Modelling of piezoelectric structures–a Hamiltonian approach

Abstract

This contribution is dedicated to the geometric description of infinite-dimensional port Hamiltonian systems with in- and output operators. Several approaches exist, which deal with the extension of the well-known lumped parameter case to the distributed one. In this article a description has been chosen, which preserves useful properties known from the class of port controlled Hamiltonian systems with dissipation in the lumped scenario. Furthermore, the introduced in- and output maps are defined by linear differential operators. The derived theory is applied to the piezoelectric field equations to obtain their port Hamiltonian representation. In this example, the electrical field strength is assumed to act as distributed input. Finally it is shown, that distributed inputs, that are in the kernel of the input map act similarly on the system as certain boundary inputs.

Keywords:

• infinite dimensional systems
• Hamiltonian formulation
• differential geometry
• differential operators

1. Introduction

Port controlled Hamiltonian systems with dissipation (PCHD-systems) are well known in the context of modelling and control, especially in the lumped parameter case, see for example 1 and references therein. The main advantage of the PCHD systems is that the mathematical description separates structural properties, storage elements, dissipative parts and ports. Furthermore, in the time invariant lumped parameter case the stability analysis can often be reduced to the investigation of the Hamiltonian. Distributed parameter systems are described by partial differential equations and this leads to many difficulties not known from the lumped parameter case. Especially the theorem concerning the existence and uniqueness of the initial value problem for explicit differential equations helps to link the properties of the differential equations with the properties of their solution. As no analogous theorem exists for partial differential equations in this contribution, only the formal properties of the equations will be discussed, which means that we will not focus on the properties of the solutions.

The extension of lumped parameter PCHD systems to the distributed parameter case is neither straight-forward nor unique. The determination of a geometrical description of infinite-dimensional port Hamiltonian systems with dissipation, also called I-pHd systems, is an actual field of research. Several publications on that topic as for example 2-6 visualize that different Hamiltonian representations are available. The description used in this contribution is based on the demand that useful properties known from the class of PCHD Systems in the lumped scenario should be preserved, see 4. Furthermore, we will analyse the case where the in- and output maps are given by linear differential operators and give an interpretation of ports on the domain and on the boundary in this case, which is an extension to the theory shown in 4. As an example, the piezoelectric field equations, a problem with two physical domains, is presented to show how the derived theory can be used for modelling.

The contribution is organized as follows. In Section 2 the subsequently applied mathematical framework is introduced. The geometrical description of infinite-dimensional port Hamiltonian systems using first order differential operators as input maps is the content of the third part of this contribution, where also the impact of differential input operators on the corresponding boundary ports of the infinite-dimensional system is investigated. Finally, the derived theory is applied to the geometric representation of the piezoelectric field equations. Here, we will consider nonlinear constitutive relations.

Some remarks on further extensions of the introduced framework and possible applications close this contribution.

2 Mathematical framework

This contribution uses the language of differential geometry. An introduction and much more detail concerning differential geometry can be found in many textbooks for example in 5,7,8. In the sequel we will summarize only some important constructions, which will be of frequent use in the following. The notation is similar to the one presented in 7.

2.1 Manifolds and bundles

A fibred manifold is a triple with the total manifold , the base manifold and the surjective submersion . For each point , the subset is called the fibre over p. If the fibres are diffeomorphic to a so-called typical fibre, then is a bundle. In the following, a triple will always denote a bundle. We can introduce the adapted coordinates (X ⁱ , x ^α) to at least locally with the independent coordinates X ⁱ , i = 1,…, r and the dependent ones x ^α, α = 1,…, s. Often, we will write instead of , whenever the projection π and the base manifold follow from the context. Bundles, whose fibres are vector spaces, are referred to as vector bundles. A section σ of is a map such that is met, where denotes the identity map on . We do not require that a section σ exists globally and write for the set of all sections Γ . From now on we use Latin indices for the independent and Greek indices for the dependent variables. Additionally a domain of integration is defined as an orientable, bounded manifold with global volume form together with a coherently oriented boundary manifold .

Let be a smooth m-dimensional manifold, then its tangent and cotangent bundles are denoted by . These vector bundles possess the coordinates , respectively. Using local coordinates, we write for sections of are met. Furthermore, we already applied the Einstein convention for sums to keep the formulas short and readable. From these vector bundles one derives further bundles, like the exterior k-form bundle or other tensor bundles. We denote the exterior algebra over ,

is the exterior derivative and

is the interior product written as v⌋ω with . The symbol ∧ denotes the exterior product of the exterior algebra . The Lie derivative of along the field is written as f (ω). Additionally, we will use Stokes's theorem 8

whereby the manifold and its boundary are related using the inclusion mapping .

A vector field is said to be π-projectable, if there exists a field such that

is met, where π_∗ denotes the push forward along the map π. We say v is π-vertical in the case of π_∗ ˆ v = 0. It is easy to show that the set of all π-vertical vector fields – the vertical tangent bundle  – is a subbundle of . The vertical bundle is equipped with the induced coordinates with respect to the holonomic fibre base {∂_α}.

2.2 Jet manifolds

Let γ be a smooth section of a bundle with adapted coordinates (X ⁱ , x ^α), i = 1,…, r, α = 1,…, s. The kth order partial derivatives of γ^α will be denoted by

with J = j ₁ ⋯ j _r , and . J is nothing else than an ordered multi-index 9. The special index J = j ₁ ⋯ j _r , j _i  = δ _il , l ∈ {1,…, r} will be denoted by 1 _l and J + 1 _l is a shorthand notation for j _i  + δ _il with the Kronecker symbol δ _il . Using adapted coordinates we can extend γ to a map

the first jet of γ. One can provide the set of all first jets of sections with the structure of a differentiable manifold, which is denoted by . An adapted coordinate system of induces an adapted system on , which is denoted by with the r · s new coordinates . The manifold has two natural projections

which correspond to the bundles . Analogously to the first jet of a section γ, we define the nth jet j ⁿ (γ) of γ by

The nth jet manifold may be considered as a container for nth jets of sections of . Furthermore, an adapted coordinate system of induces an adapted system on . These jet manifolds are connected by the following sequence

The unique operator d _i , which meets

for all functions and sections , is the vector field . It is called the total derivative with respect to the independent coordinate X ⁱ and is defined by

in adapted coordinates (X ⁱ ,x ^α). The introduction of the total derivative d _i enables us to introduce the horizontal derivative d _h through

or in local coordinates d _h = dX ⁱ ∧ d _i (see e.g. 6). Furthermore, we have

for , which is nothing else than Stokes' theorem adapted to bundles. In the sequel we will suppress the pull backs and write instead of for instance if the pull back is clear from the context.

3 Geometrical structure of I-pHd systems

The state of a distributed parameter system is given by a certain set of functions defined on the bounded base manifold . Therefore, it is obvious that we have to use a bundle to describe the state in the infinite dimensional case. We use the local coordinates (X ⁱ ), i = 1,…, r for , where these coordinates will represent the independent spatial coordinates according to the analysed plant. Let denote the state bundle with local coordinates (X ⁱ ,x ^α), α = 1,…, s, where x ^α represents the dependent coordinates. Consequently, a section defines a state of the system by x ^α = σ^α(X). From the state bundle we derive four important structures. The nth jet manifold with adapted coordinates , the vertical tangent bundle with coordinates (X ⁱ ,x ^α,[xdot] ^α), and the exterior bundles

with coordinates (X ⁱ ,x ^α,w), and the volume form

The interior product

induces the canonical product

The Hamiltonian functional ℌ is a map which is given as

where in the general case the Hamiltonian also depends on the jet coordinates with m > 0. Let us consider an evolutionary vectorfield , which corresponds to the set of partial differential equations

This field v does not generate a flow on but it may generate a semi group φ_τ that maps sections to sections of the bundle , i.e. . In general the semi flow and the evolutionary vectorfield are linked by

In the sequel, we restrict ourselves to the case of first-order Hamiltonians.

3.1 First-order Hamiltonian

We confine ourselves to the case in equation (4) such that n = 1 holds in the relation (5). The change of the functional ℌ (σ) along the semi flow φ_τ can be computed as

for first order Hamiltonians, where the first prolongation j ¹ (v)

is used. Let us inspect the expression

and integration by parts leads to

Using the variational derivative δ and the horizontal derivative d _h the equation (7) can be rewritten as

where the variational derivative δ is a map

which has the coordinate expression

It is easily seen that the total derivative d splits into the variational derivative δ and an exact form. Furthermore, the additional map δ^∂ can be introduced with

which in coordinates is given as

3.2 Evolutionary equations

We propose the following set of equations

together with . The maps ℑ, ℜ are of the form

which are differential operators (see 9) in general. As the input space we choose the vector bundle with local coordinates (X ⁱ ,u ^ς), ς = 1, … , m and basis {e _ς}. Of course, the output space is given by the dual vector bundle, where we use the coordinates (X ⁱ ,y _ς) and the basis {e ^ς ⊗ dX}. Furthermore, we conclude that there exists a bilinear map

given by the interior product

The input map reads as denotes the adjoint output map .

Here we confine ourselves to the case, where ℑ, ℜ are linear maps and thus no differential operators. The map ℑ is assumed to be skew symmetric i.e.

and ℜ to be a symmetric positive semidefinite map defined by

The in- and output maps 𝔅 (·) and 𝔅* (·) are given by linear differential operators of first order.

We make use of linear differential operators of the form

as introduced for example in 5. These operators meet

as well as

due to their linearity. Additionally, their adjoint map is defined by

with . Using the horizontal derivative d _h we obtain

Already this definition of the in- and output maps visualizes, that the use of differential in- and output operators introduces additional boundary conditions to the system. It is worth mentioning that the application of the total derivative in equation (10) is essential, as this guaranties a clear geometrical interpretation of the used differential operator. Let us consider an extended Hamiltonian density of the form

then it is obvious that for the variational derivative δh _e reads as

which shows that the input map contains a differential operator and this justifies the choice made in equation (10).

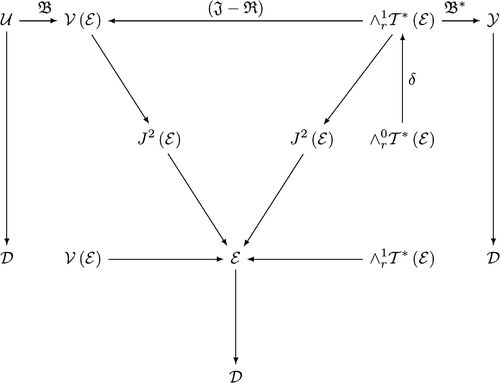
The constructions presented so far can be visualized in the following commutative diagram

where the pull backs and the projections have been omitted.

3.3 Infinite-dimensional Hamilton operator and collocation

Let the π-vertical operator (this operator is not a vector field, but a submanifold on parametrized in u) from equation (8) denote the Hamilton operator. The Lie derivative of ℌ along the Hamilton operator of the corresponding I-pHd system which is the total time derivative of the Hamiltonian functional along the solution

as in equation (6) consequently leads to

Let us apply the relations (11). Then the domain expression reads as

with

and the boundary term follows to

The equations (12) and (13) state, that the dissipative operator ℜ, the pairing u ^ς y _ς, which is a port distributed over , and the boundary term

with

determine the Lie derivative of the Hamiltonian functional ℌ. In equation (14) the boundary bundle , the boundary section and the r – 1 boundary volume form

are used as geometric objects, where the inclusion map ι is assumed to be given by

3.4 Boundary ports

The form λ_∂ stated in equation (14) is now assumed to equal the natural pairing of the boundary in- and outputs. In contrary to the determination procedure of the collocated output y on the domain, as stated in equation (9), it is no more possible to give a unique separation of the in- and output variables at the boundary visualized by the use of in the following expression

To overcome this problem we investigate two cases of boundary pairings on vector bundles.

Let us consider the boundary input vector bundle with local coordinates and the basis and its dual – the boundary output vector bundle with local coordinates and basis . We make use of the tensor and formulate a boundary input map which is defined by

The adjoint map is then clearly given by

and we obtain as desired. The second pair is given by the boundary input vector bundle with local coordinates and the basis and its dual – the boundary output vector bundle with local coordinates and basis . The tensor is used to define the boundary input map to construct

and consequently the adjoint map is given by

If one vector or form part of λ_∂ vanishes, that is for a certain α, then the corresponding pairing does not represent a port anymore.

Now we are able to conclude, that the evolution of the Hamiltonian functional along the solution (here we assume the existence and uniqueness of the solution of the I-pHd systems) of a first order I-pHd system with in- and output operators is determined by the internal damping, the collocation of the in- and output on the domain and boundary and an additional term

on the boundary due to the application of an input operator .

It is worth mentioning, that the adjoint map of the considered input map also becomes a differential operator with a non-trivial kernel. If one applies an input to the systems that leads to a collocated output lying in the kernel of the output map, then this input influences the evolution of the system through the corresponding boundary conditions, that is this input acts similarly to a boundary input.

To provide this mathematical construction with a physical example, we investigate the piezo-electric field equations in the derived framework.

4 Application – the piezoelectric field

In this contribution, we consider models of linearized elasticity, linearized quasi static electrodynamics combined with nonlinear constitutive relations. Let denote the domain of the three-dimensional mechanical structure equipped with the Euclidean coordinates (X ⁱ ), i = 1,2,3, which are used to mark the positions of the mass points. The actual position of a mass point X is given by , where u ^α, α = 1,2,3 are the displacements. The state of the elastic structure, is given by the positions, or equivalently by the displacements u ^α, and linear momenta with the mass density . The total manifold of the state bundle is equipped with the local coordinates

We assume, that there exists a stored energy density e _S dX, which meets

with the stress

the strain

the electrical field strength E = E _ψ dX ^ψ and the electric displacement D = D ^ψ∂_ψ⌋dX. This assumption guaranties due to the exactness of de _S ∧ dX that the stored energy is purely defined by the actual state of the system (see e.g. 10).

Here we introduce the nonlinear constitutive equations of the form

Remark 1: A subclass of these equations are the well-known linear constitutive equations of piezoelectric materials given by

with τ, δ, ν = 1, 2, 3, and . These relations supply

and finally

if the integrability conditions C ^αβτδ = C ^βατδ = C ^αβδτ = C ^τδαβ, G ^αβψ = G ^βαψ, F ^ψν = F ^νψ are met.

The kinetic energy density e _K dX is defined by

with .

Finally, we are able to determine the exterior derivative of the Hamiltonian h as the sum of the exterior derivative of the stored and kinetic energy i.e.

The electrical field strength is considered as input and the variational derivative of the Hamiltonian density hdX can be rewritten in the form

with x ^μ = (u ^α, p _γ), whereby it is visualized that the exterior derivative of h is sufficient in the determination of the variational derivative. Consequently, there is no need to know the stored energy function – its existence and its exterior derivative already enables the determination of the equations of motion.

Remark 2: The choice of the coordinates (X ⁱ ,u ^α,p _γ) obviously leads to a Hamiltonian, which contains first-order jet variables. This should be compared with the approach presented in 11 where the authors consider infinite dimensional systems and avoid the use of jet variables in the Hamiltonian, by considering the map ℑ as a differential operator. In the piezoelectric case, this approach leads to the choice of different state variables, namely the strain instead of the displacement. In this case additional partial differential equations appear as restrictions. Therefore, one has to deal with restricted I-pHd systems.

The equations of motion are given by

using the mechanical coordinates (u ^α,p _γ). The achieved Hamiltonian representation does not currently qualify as a port Hamiltonian representation, as the input – the electric field strength E – acts on the system in a nonlinear fashion. This problem can be solved by the introduction of new and less general constitutive relations

This restriction leads us to

Consequently, we obtained the I-pHd structure

where the free Hamiltonian h ₀ meets

and the input map of interest appears in the form of the operator

From these investigations we see that the input map meets the specifications of equation (10). It is worth mentioning that in the case where the piezoelectric material is an insulator d _ξ D ^ξ = 0 has to be met, because the volume charge density has to vanish. This relation has been omitted in the calculations above.

Finally, the Lie derivative of the Hamiltonian functional stated in equation (6) leads to

because no dissipative effects have been taken into account. The integral over the domain in equation (16) can be written as

Let us apply the the definition of the adjoint operator from equation (11), which enables us to obtain

where the adjoint map reads as

because we use the electric field strength as the distributed input. The boundary expression from the relation (16) is given as

which represents the boundary ports, where

is used and an additional boundary term arises due to the application of the adjoint operator, which reads as

If is in the kernel of the output map 𝔅* (·), then the domain port generated by the input map vanishes completely. In the case of piezoelectric systems this is for example given by

In contrary to the domain port, the boundary port generated by the input operator does not vanish and consequently a domain input could act on the system like a boundary input does. These investigations show, that the spatial shape of the distributed input and collocated output is mainly responsible for its appearance within the field equations, boundary conditions and evolution of the free Hamiltonian h ₀.

5 Conclusions

Piezoelectric materials enable fascinating new ways of interaction (actuation and sensing) between control equipment and flexible structures. To derive passivity based control strategies a geometric description of the system in a port Hamiltonian setting is of main interest.

This contribution introduces a geometrical representation of infinite-dimensional port Hamiltonian systems with in- and output maps using differential operators. It is shown, that the extension of the description shown in 4 results in the appearance of additional boundary conditions in the Lie derivative of the Hamiltonian functional. As the presented approach is a formal one, based on differential geometric considerations, several aspects from functional analysis are missing. For example, Sobolev norms on linear spaces and manifolds have not been introduced, see for example 12-13, also the existence of solutions has not been discussed.

The analysis of the piezoelectric field equations on the introduced I-pHd framework yields a very interesting explanation of the frequently used method of “electrode shaping” for piezoelectric devices. The existence of a linear differential input operator enables the use of spatial output distributions such that the output is in the kernel of the domain output operator. Consequently, the distributed domain input acts in a similar fashion on the system as a boundary input.

It is obvious that linear input operators of higher order provide more complex output kernels, and consequently, additional degrees of freedom in the application of control action are given.

Finally, it is worth mentioning, that the mappings ℑ, ℜ could also be replaced by appropriate differential operators. Such an extension will enable the treatment of coupled field problems like piezo-thermo-elasticity on the basis of port Hamiltonian systems. This represents the content of future investigations.

Acknowledgements

Partly, this work has been done in the context of the European sponsored project GeoPlex with reference code IST-2001-34166. Further information is available at http://www.geoplex.cc.