Stability-preserving parametric model reduction by matrix interpolation

Abstract

In this article, a method to preserve stability in parametric model reduction by matrix interpolation is presented. Based on the matrix measure approach, sufficient conditions on the original system matrices are derived. Once they are fulfilled, the stability of each of the reduced models is guaranteed as well as that of the parametric model resulting from interpolation. In addition, it is shown that these sufficient conditions are met by port-Hamiltonian systems and by a relevant set of second-order systems obtained by the finite element method. The new approach is illustrated by two numerical examples.

Keywords:

• parametric model order reduction
• stability preservation
• contractivity
• port-Hamiltonian systems

1. Introduction

Accurate modelling of complex processes in several fields, for instance engineering, biology and economics, leads to large-scale dynamical systems that often depend on one or several parameters. Reaching from geometric dimensions up to material properties, the parameters can even define modes of operation. To allow the reduction of such a class of dynamical systems, while preserving the parameter-dependency in the reduced-order model, there is a need to adapt and further develop the existing reduction methods or possibly create new ones. This relatively new and emerging branch of model order reduction (MOR) is known as parametric model order reduction (pMOR).

Consider a parametric multi-input multi-output generalized state-space model

(1)

where , are parameter-dependent matrices with constant coefficients, with being the vector of parameters, and where , and are, respectively, the inputs, outputs and states of the system of order n. The main goal of pMOR is to calculate a reduced model that preserves the parameter-dependency, allowing a variation of any of the parameters without the need to repeat the reduction step. Thereby, the reduction method should ideally be able to cope with any number of parameters and with systems where no analytical expression of the parameter dependency in the matrices is available. In addition, it should be numerically efficient to be suitable for the reduction of large-scale systems while preserving important system properties such as stability or passivity.

The first work dealing with pMOR for large-scale state-space systems was presented in [1], where the moment-matching approach has been generalized to a parametric system with a matrix linearly dependent on one parameter. It was shown how to calculate a projection matrix, such that the resulting reduced model matches some of the first moments of the transfer function with respect to both the Laplace variable s and the parameter p. This work has been generalized in [2] to the multiple parameter case, where the coefficients of the multivariate Taylor series having s and the parameters as variables are matched. One of the main drawbacks of the method is that it suffers from the curse of dimensionality, as the order of the reduced system grows very rapidly even for a low number of parameters.

Another widely used technique consists of calculating local projection matrices from several local models in the parameter space, merging these matrices together and then applying a common projection to the original parametric model [3,4]. The main advantage of this method is its simplicity and transparent calculation of the projection matrices. However, to result in a parametric reduced-order model, an affine parameter dependency in the original model is required.

In [5], a method based on truncated balanced realization (TBR) using interpolation and a soft switching between weighted linear transfer functions of different non-parametric reduced models has been presented. For the choice of the local reduced models, the sparse grids method was proposed. The order of the resulting model depends on the order and number of involved local models and the method faces difficulties when these systems have weakly damped modes. In [6], an alternative approach has been presented and the approach has been further developed and coupled to the interpolatory -optimal model reduction method.

A framework for the reduction of linear time-invariant (LTI) parametric systems with no analytically expressed parameter dependency was recently introduced in [7–9]. After generating and reducing several local original models in the parameter space, a parametric reduced-order model is calculated by interpolating the system matrices of the local reduced models. Within this framework, the order of the reduced model remains constant, independent of the number of local models considered. This allows increasing the number of these models to better capture the generally unknown parameter dependency, without increasing the complexity of the resulting reduced model. In addition, the reduction method to be applied can be freely chosen.

Stability preservation has been an active and important research field in MOR, as stability is an important requirement for the analysis, proper operation and control of any dynamical system. Hence, the reduced-order model is required to be stable in order to be a valid approximation of the original one.

When dealing with small to medium-sized systems, MOR techniques such as the TBR- and the Hankel-based reduction methods guarantee stable reduced systems. However, due to their comparably high numerical effort, they cannot be applied to large-scale systems without further modifications, after which stability preservation is, theoretically, no longer ensured.

For the reduction of large-scale systems, Krylov subspace methods are nowadays among the best choices. However, stability is not generally guaranteed. Towards solving this problem, several approaches have been developed in the last decade. The first family of methods is based on deleting the unstable poles of the reduced system through post-processing, by using algorithms such as the implicitly and explicitly restarted Arnoldi and Lanczos [10–12]. Another group of methods is the interpolation-based ones that preserve passivity (and thus stability) of the original system through spectral-zero interpolation [13–15]. In addition, methods that combine aspects of the TBR- and Krylov-based approximation methods have been presented in [16–18].

Preserving the stability becomes even more complex when dealing with parametric systems, as stability of the reduced system for all possible parameter values has to be guaranteed. This is one of the major difficulties behind the generalization of the existing stability-preserving methods to parametric systems. Hence, all the reduction methods based on moment matching such as, for example, [2] and those using a common projector, for example, [3] cannot ensure stability of the resulting reduced system. Moreover, the reduced parametric model obtained by interpolation of locally reduced ones (except [5]) is not necessarily stable even if each of the involved models is stable.

In this article, the pMOR framework by matrix interpolation [7,8] is further developed to ensure stability of the resulting parametric system. This is first achieved by using a new approach [19] based on the concept of matrix measure that guarantees obtaining stable local reduced models. Accordingly, the pMOR framework is adapted to also guarantee stability during matrix interpolation. Furthermore, special attention is paid to systems in port-Hamiltonian and second-order forms, where stability preservation can be achieved without additional numerical effort.

The rest of this article is organized as follows: in the next section, a short overview on projection-based MOR is presented. In Section 3, the stability-preserving framework using the matrix measure together with its link to port-Hamiltonian systems is introduced. The pMOR framework by matrix interpolation is reviewed in Section 4 followed by the stability-preserving pMOR reduction approach in Section 5. The suitability and performance of the proposed method are illustrated by numerical examples in the last section.

2. Projection-based order reduction

Consider the LTI dynamical system

(2)

of order , where , and are matrices with constant coefficients; , and are, respectively, the input, output and state vectors of the system.

Projection-based MOR aims at approximating the state vector by a lower dimensional vector , consisting of only variables

(3)

where . Inserting Equation (3)(3) in Equation (2)(2) yields an overdetermined system with q unknowns but n equations,

(4)

which can only be solved with a remainder [20]. To obtain a well-determined system of equations while fulfilling the Galerkin condition , the state equation (4)(4) is multiplied from the left by , leading to the reduced LTI system [16,20]

(5)

This procedure, known as Galerkin-type or one-sided projection, can be regarded as a projection of the large-scale state equation (4)(4) onto a rank-q subspace spanned by the columns of along its orthogonal complement using the projector

(6)

for which applies if is an orthonormal matrix.

Another option is the so-called Petrov–Galerkin or two-sided projection, where Equation (4)(4) is premultiplied by , with fulfilling . This approach is advantageous to increase the accuracy of the reduced models; however, the choice is beneficial for the purposes of this article as matrix properties such as definiteness and stability are preserved independently of the choice of the projection matrix .

Existing MOR methods such as Krylov subpace methods (also known as moment matching) [20–22] or proper orthogonal decomposition aim at computing a suitable projection matrix that guarantees a good approximation of the original system while preserving important system properties.

3. Stability preservation in MOR

In this section, the problem of stability preservation during MOR is tackled using the matrix measure approach with the port-Hamiltonian and second-order systems as special cases. Based on sufficient conditions on the system representation, the proposed approach is well suited for the pMOR framework by matrix interpolation with arbitrary projection matrices.

3.1. The matrix measure approach for stability preservation

Most of the works tackling the stability problem in model reduction are based on quadratic Lyapunov equations, , ¹ that is, where is the assumed Lyapunov function. In [19], a more general framework based on the matrix measure

(7)

and Lyapunov equations defined in any vector p-norm was introduced. The possible choice of other computationally cheaper norms and all the literature regarding the matrix measure [23–25] offer a wider range of options that could be more suitable to the considered problem. However, for the purpose of this article, it is sufficient to restrict the discussion to the 2-norm case.

The concept of matrix measure appears naturally when dealing with the Lyapunov stability theory for linear systems. Namely, if a system is asymptotically stable, there exists a Lyapunov function satisfying in the conditions:

i.	, radially unbounded.
ii.

Choosing as a vector norm , where is a full-rank matrix, and applying the state transformation to system (2)

(8)

leads to . According to this choice of , condition (i) is automatically fulfilled as the result of any vector norm is positive and unbounded. From condition (ii) and , the definition of matrix measure appears:

Consequently, if then , which implies asymptotic stability of the system. Similarly, implies stability. A system fulfilling is called contractive. The matrix measure in the 2-norm has been defined in [24] as

(9)

where is the most right eigenvalue.

For systems involving a symmetric E matrix, the following Lemma is derived.

Lemma 3.1:

A continuous-time LTI system (2) with and is stable.

Proof:

The positive-definite symmetric matrix E admits the Cholesky factorization . Applying the change of basis to Equation (2)(2) and premultiplying by leads to a contractive system representation with and , which can be shown to fulfil .

A system representation that fulfils this sufficient condition can be found in different ways, for instance, by a state transformation based on low-rank approximations of the solution of a quadratic Lyapunov equation [26–29] or by balancing the A matrix with a diagonal state transformation [30,31]. Other trivial cases are systems with balanced or normal A matrices (symmetric, skew-symmetric and so on). Additionally, in some important cases, the sufficient condition of Lemma 3.1 can be easily fulfilled without additional computational effort, for example, for systems obtained by the finite element method or by the port-Hamiltonian modelling approach (Section 3.2).

Accordingly, the sufficient condition for stability preservation in MOR can be derived.

Lemma 3.2:

Sufficient Condition (2-norm): Given a continuous-time system with and , reduced stable models are obtained when a full column-rank projection matrix is used [ 19 ].

Proof:

The positive definiteness of E is preserved in , as

In addition, the contractivity of A is retained in :

Therefore, the reduced system fulfils and and is stable according to Lemma 3.1.

3.2. Relevant system classes

In this section, it is shown that the theory of contractivity can be directly applied to second-order systems obtained by the finite element method, as well as to port-Hamiltonian models, without any additional numerical effort. Hence, these system classes are obviously best suited candidates for stability-preserving parametric model reduction by matrix interpolation as shown in Section 5.

3.2.1. Port-Hamiltonian systems

The port-Hamiltonian system representation [32] provides a generic framework for interdisciplinary modelling of complex dynamical systems. Consider a LTI port-Hamiltonian system of the form

(10)

The symmetric, positive-definite matrix , , defines the quadratic Hamiltonian , representing the total stored energy. The symmetric, positive semi-definite matrix , , describes the dissipation or damping in the system. The interconnection between the energy-storing states is represented by the skew-symmetric matrix , . Due to the so-called collocated input and output vectors, the derivative of the Hamiltonian indicates the passivity of port-Hamiltonian systems. As every passive system is stable, can be used to prove Lyapounov stability.

A main challenge in MOR of this class of systems is to preserve the port-Hamiltonian structure in the reduced system. Towards this aim, a structure-preserving Krylov-based method has been presented in [33]. Hence, the stability of the obtained reduced system is guaranteed due to the passivity property of port-Hamiltonian systems.

An alternative proof for this stability preservation property can be derived based on Lemma 3.2. Consider that the state transformation has been applied to the original port-Hamiltonian system (10):

(11)

Clearly the matrix and the matrix measure . Consequently, two observations are made:

•	Port-Hamiltonian systems can be expressed as contractive systems in the 2-norm case so that stable reduced systems are obtained when applying one-sided projection.
•	Physical interpretations can be added to the theory of contractivity, because the matrix E assigns a Lyapunov function to the system regarded as the virtual stored energy. Accordingly, the symmetric part of A describes the dissipation of this virtual energy, whereas the skew-symmetric part defines the interconnection, that is, the exchange of virtual energy inside the system.

3.2.2. Second-order systems

Consider the following second-order system

(12)

where the matrices M, D and K are called mass, damping and stiffness matrices, respectively. For a large class of finite element models, , and can be assumed. The system (13) can be written as a first-order LTI system:

(13)

with F being an arbitrary non-singular matrix of appropriate dimensions. In [34], was suggested as a beneficial choice for a stability-preserving reduction, confirmed by the following Lemma.

Lemma 3.3:

If is chosen in the LTI system (13), then reduced stable models are obtained when applying a one-sided projection by a full column-rank projection matrix .

Proof:

By defining

it is clear that and . Lemma 3.2 completes the proof.

Remark 3.1:

Note that with the choice in Equation (13)(13), the same stable system is described. This leads to the conclusion that the conditions in Lemma 3.2 are sufficient to ensure stability; however, they do not have to be necessarily fulfilled.

4. pMOR by matrix interpolation

In the following section, the pMOR framework presented in [7,8] is reviewed for the case of a one-sided projection.

Consider the parametric LTI dynamical system (1) given at the discrete parameter values for ,

(14)

Each of the k models is reduced separately using local projection matrices , leading to

(15)

This procedure allows to individually tune the approximation of each of these models, which generally have different dynamics. In fact, it is even possible to employ different order reduction methods.

Once all the local reduced models are obtained, the resulting parametric reduced model is calculated as a weighted sum of the system matrices,

(16)

where

(17)

and , for , .

According to Equation (3)(3), the prolongated reduced states represent different vectors in the original state space, as different projection matrices have been employed for the reduction of the respective models at different parameter values.

It was presented in [7] that the interpolation (17) is, in fact, not meaningful unless the states are made compatible ² by regular local state transformations beforehand. It was shown that applying a transformation to each of the systems (15) and premultiplying them by from the left before the interpolation (17),

(18)

leaves the individual transfer behaviour unchanged, but strongly affects the dynamics of the resulting parametric reduced model (16). It was proposed to choose the transformation matrices as

(19)

where the columns of should span the subspace containing the important dynamics of the original system at the parameter value of interest.

To this end, the concatenation of the local projection matrices is built and followed by a singular value decomposition,

(20)

where

The matrix R is then chosen to be the first q columns in , which offer an orthonormal basis of the dominant directions of the column span of . With this choice, the dynamics at the parameter value of interest is approximated using the available information from the reference points.

In some cases, even cheaper ways for the calculation of R may be viable. For instance, if the subspaces spanned by the different matrices are sufficiently close to one another, it is often satisfactory to choose , where is the projection matrix associated with a model in the centre of the parameter space. For further possibilities, see [9].

Once R and the transformation matrices have been determined, the transformed system matrices , , and are calculated. Their corresponding state vectors are compatible to each other with respect to the subspace spanned by R. Accordingly, these matrices are employed for the interpolation (17) instead of , , and [7].

Note that within this framework, all parameter-independent calculations involving constant matrices can be computed beforehand. On the contrary, all other parameter-dependent operations need to be computed in real time. The former are called offline computations whereas the latter are online computations.

5. Stability preservation in pMOR by matrix interpolation

The method presented in the previous section turned out to be suitable for the reduction of systems emerging from various industrial applications. Hence, it does not require an analytical expression for the parameter dependency and delivers good results with little numerical effort once the local models have been reduced.

However, a main drawback of this approach is that it cannot guarantee stability of the resulting reduced-order model. On the one hand, stability is not in general preserved during the reduction of the local models; on the other hand, even if all local reduced models are stable, the parametric reduced system resulting from the interpolation (17) may still happen to possess poles on the right-hand side of the complex plane.

Making use of the theory from Section 3, a solution to this problem is presented in the following.

Lemma 5.1:

Given that and is satisfied for each of the local reduced-order models, the parametric system resulting from the matrix interpolation (17) with non-negative weights, , is stable.

Proof:

The positive definiteness of the matrices is equivalent to for all . Therefore, the following holds true for non-negative weights ,

and hence is positive definite.

The definition of the matrix measure in the 2-norm implies that if . As the proof given above holds true also for negative semi-definiteness, we can conclude that

and it follows that .

According to Lemma 3.1, the parametric reduced system (16) is stable.

Due to the concept of compatibility presented in the previous section, no state transformations may be applied to the state vectors of the original local models. Accordingly, if the contractivity of these systems is not given a priori, it may not be achieved in the way presented in Section 3. Instead, the state equation should be premultiplied by , which keeps the state vector of the system unchanged:

The system now, however, meets the requirements of Lemma 3.2 if P is chosen such that

The results of this article are summarized by the following algorithm:

PArametric STability preserving model Order Reduction by matrix interpolation (PASTOR)

Starting point

The large-scale parametric model is given by the matrices , , and at k discrete reference points , together with non-negative weighting functions for all admissible parameter values.

Offline computations

•	For all systems that do not fulfil and , find suitable matrices such that and and use , , instead of , , for the following steps.
•	Reduce each of the models locally by a one-sided projection, for example, using a Krylov subspace method.

Online computations

•	Evaluate the weighting functions for the given parameter value .
•	Concatenate the projection matrices to build , perform an economy singular value decomposition of and define R as the first q columns of . Alternative possibilites for the choice of R can be found in [9].
•	Compute and transform the local reduced models according to Equation (18)(18).
•	Conduct the interpolation (17) to obtain the reduced model for the parameter value .

6. Numerical examples

In this section, the performance and suitability of the presented approach are illustrated using two numerical examples from two different fields of engineering.

6.1. Thermal model of an H-bridge

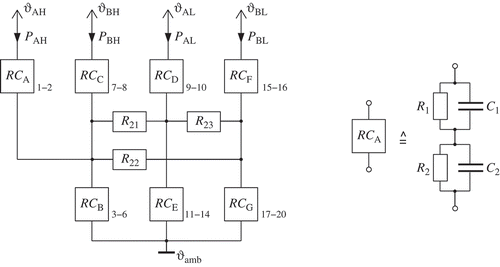
As a first example, the thermal fitting model for the STMicroelectronics H-bridge motor driver VNH2SP30-E [35] is considered. The integrated power circuit consists of four power metal oxide semi-conductor field-effect translators (MOSFETs) arranged on three separate chip areas (dice) – the high potential MOSFETs mounted on a common dice. The thermal behaviour is described by an equivalent thermal network of 20 thermal capacitances [J/°C] and 23 thermal resistances [°C/W], whose values are listed in [35]. The lumped elements of the equivalent network are arranged in 20 parallel RC-circuits and 3 singular resistors. The RC-circuits can be combined in seven series ³ to model the vertical heat exchange according to the chip geometry. The three values and describe the mutual (horizontal) thermal resistances between the three dice.

The port-Hamiltonian system describing the thermal characteristics of the circuit is

where is the state vector of heat energy stored in the lumped capacitances of the corresponding RC-series connections and is the thermal power introduced at each MOSFET junction. Due to the irreversible transformation of thermal energy, . The dissipation matrix R and input matrix are given by

where indicates an n-dimensional column vector containing only ones. The off-diagonal submatrices

and the diagonal submatrices of R

contain the values of the thermal resistances. With the Hamiltonian function

the collocated output describes the temperatures at the MOSFET junctions. In the following, only the first transistor is considered in operation. The thermal power P _AH introduced at the junction and the resulting temperature _AH (see Figure 1) are, respectively, the input and collocated output of the single-input singal-output (SISO) system with the first column of as input vector.

Figure 1. Thermal equivalent RC-circuits.

The copper area on the chip is assumed to be the free parameter that can vary from the minimum pad layout to . Four local original models at the parameter values footprint, , and are obtained by varying the resistors , and and the capacitors , and . Images of the chips with various copper areas can be found in [35].

Each of the local models is reduced to order by a one-sided Krylov subspace method, while matching one moment about and four moments about .

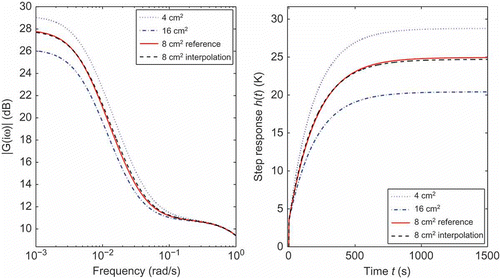
To obtain the parametric reduced system with area, we interpolate using linear weights between two reduced-order models that correspond to the copper areas and . Additionally, a reduced model with of copper area is used for comparison with the interpolated reduced system.

Figure 2 shows the frequency and step responses of both reduced local models, the reference model and the parametric model resulting from interpolation. The new method delivers a stable and accurate reduced system that almost matches the transfer behaviour of the reference model in both frequency and time domains.

Figure 2. System response for the H-bridge model. (a) Frequency response. (b) Step response.

6.2. The cantilever beam

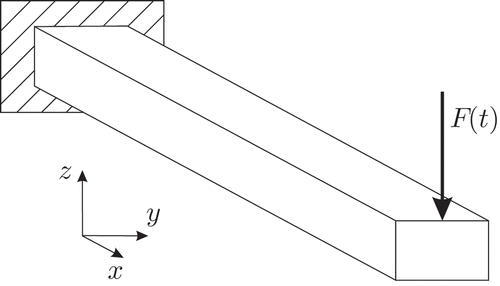
In the second example, the new framework is applied to a second-order system describing the motion of a 3D cantilever Timoshenko beam [36]. Its length L is assumed to be a free geometry parameter that varies between and . The model input is the vertical force applied at the beam's free end, whereas the output is considered to be the displacement at this point (Figure 3).

Figure 3. The cantilever beam.

As a result of the FEM modelling, the order of the LTI system for both considered lengths is . This results from taking 200 nodes along the beam, each having six degrees of freedom: three translational displacements u, v and w and three rotational degrees of freedom , and with respect to the x-, y- and z-axis, respectively. For model reduction, we apply a one-sided Krylov subspace method with and an expansion point . 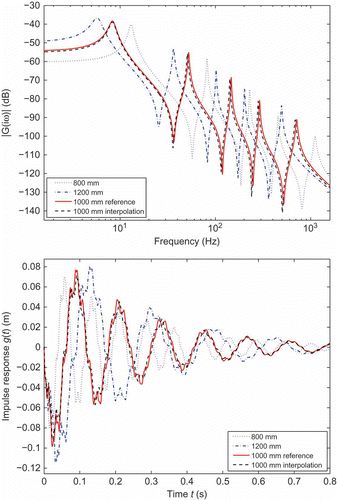To obtain the parametric reduced system, we interpolate using linear weights between two reduced-order models that correspond to the lengths and . In addition, a reduced reference model with is used to evaluate the quality of the approximation.

Figure 4 shows the frequency and impulse responses of both reduced local models, of the reference model and of the parametric model resulting from interpolation.

Figure 4. System response for the cantilever beam. (a) Frequency response. (b) Impulse response.

The new approach is suitable for the reduction of this class of models, as it can be clearly seen that the responses are accurately approximated, whereas a minor discrepancy in the time domain is observed.

7. Conclusion

The pMOR framework by matrix interpolation is improved by further exploiting the stability-preserving matrix measure approach with the aim of generating stable parametric reduced models.

Starting from a large-scale parametric system given at k discrete values in the parameter space, the representation of each of the local models is suitably transformed to possess a contractive matrix A and, if existent, a symmetric positive-definite matrix E. This guarantees obtaining stable reduced models by the matrix interpolation framework. For the case of models in second-order or port-Hamiltonian forms, it was shown that the sufficient conditions required to preserve stability for all parameter values are automatically fulfilled within the modelling step, thus, without any additional numerical effort.

A number of open problems have still to be solved to further develop the presented framework. These include the sampling method of the parameter space, the choice of the weighting functions, numerically efficient algorithms to find contractive representations for large-scale systems in the general case and error estimates to judge the quality of the obtained models.

Acknowledgements

This work has been partially supported by the Elite Network of Bavaria and the Cusanuswerk Scholarship Award Programme, which are gratefully acknowledged. The authors also thank Paul Kotyczka for providing the H-bridge thermal model.

Notes

1.For ease of presentation, it is assumed here that E = I.

2.For a definition of compatibility in this context, refer to [7].

3.The numbers beside the blocks in Figure 1 indicate the contained RC-circuits.