Two-sided projection methods for model reduction of MIMO bilinear systems

Abstract

Two-sided projection methods are presented for model reduction of large scale multi-input multi-output bilinear systems. By properly choosing projection matrices, the reduced model possesses a superior moment matching property and we prove it from a new perspective by means of linear equations. The preservation of stability for reduced models is also considered. In contrast to the most existing approaches, we construct the reduced model directly instead of using an iterative procedure, thereby saving much computational cost. As two-sided methods are more likely to produce badly ill-conditioned system matrices, a mixed algorithm having the benefits of one-sided and two-sided methods is proposed at the cost of roughly doubling the dimension of reduced models. Theoretical analysis and numerical experiments show the efficiency of our approach.

Keywords:

• bilinear system
• two-sided method
• model reduction
• moment matching
• H₂ norm

1. Introduction

Model reduction is an important robust tool allowing for fast numerical simulation of complicated models [1,2]. It aims to replace a large scale system by an approximate system of lower order, which not only preserves the basic input–output behaviour of the original system but also requires significantly less effort.

In this paper, we consider time invariant multi-input multi-output (MIMO) bilinear systems, which are described by the following differential equations:

(1)

Here, is the system state, is the output, and is the input, in which denotes the ith component. Further, , , , are constant matrices. For simplicity, we assume the initial condition . Bilinear systems arise in various engineering fields, such as nuclear fission, optical communication, modelling of chemical and thermal processes [3–5]. As a special sort of nonlinear system, such systems can be also used to approximate weakly nonlinear systems [6–8].

Model reduction for bilinear systems has been investigated by several researchers in the past decades. The basic gramian-based methods were studied initially in [9] and the latest development on this topic was stated in [10]. The optimal model reduction problem for bilinear systems has been also addressed via the analysis of the reachability and observability gramians [11,12]. Recently, the relation to the interpolation-based methods was investigated in [13]. On the other hand, moment matching methods have been exploited by virtue of the Volterra series representation of a bilinear system [14]. Similar to the case of linear systems, reduced order systems are produced to match a desired number of moments to guarantee accurate approximations. Contributions involved in [7,15–19] fall into this category and use one-sided projection. In addition, two-sided projection methods have also been applied to single-input single-output (SISO) bilinear systems [20–22]. Although there is currently no error bound for moment matching methods, it is desirable to preserve as many moments as possible for a fixed reduced order and given interpolation points, from which at least good local approximation can be hoped for.

In this paper, two-sided projection methods are studied in the MIMO case for bilinear systems. We prove the property on moment matching from a new point of view which is concise and intelligible. How to determine the interpolation points in a multi-points framework is addressed via analysis based on the norm of the error system and specifically accomplished by constructing the projection matrices directly instead of employing an iterative procedure. The issue the preservation of stability is also considered. A scheme used to avoid badly ill-conditioned reduced order system matrices in the two-sided framework is proposed. As a consequence, our algorithm takes on the advantages of the one-sided and two-sided projection methods.

The paper is organized as follows. In Section 2, the relevant concepts of bilinear systems and model reduction are formally defined. In Section 3, we present two-sided projection methods for bilinear systems and the properties of moment matching are proven from a new point of view. The practical algorithms are also presented. In Section 4, we discuss the preservation of stability together with the norm. In Section 5, two numerical examples are used to test our theoretical results. Finally, some conclusions are given in Section 6.

2. Bilinear system and model reduction

The Volterra series is a model for nonlinear behaviour and frequently used to denote a functional expansion of a time-invariant nonlinear dynamic system [14]. Specifically, the input–output behaviour of (Equation (1)) has the infinite series expression [23]

where the kth subsystem has the convolution representation

The associated degree-k regular kernel has the following expression:

where and denotes Kronecker product. By the multi-variable Laplace transformation, the kth transfer function is defined as

Let be not an eigenvalue of A for , and then is invertible. Using the properties of Kronecker product (on page 275 of [24]) and Neumann expansions, we have the expansion

where are defined as the moments at and given as

Likewise, when expanding at , we have

where are defined as Markov parameters

Model reduction for bilinear systems aims to construct a reduced model of the same form as (Equation (1)) but with fewer states. In [7,18] a reduced order system was defined as

(2)

where , and for . The orthonormal matrix V was designed to satisfy

(3)

where was defined by the following Krylov subspaces:

(4)

In this paper, for a given square matrix T and a rectangular matrix R, Krylov subspace is defined as . In particular, it should be noted that . With the above choice, the reduced model preserves the first moments of the jth subsystem of the original system [7,18], that is

Generally, the dimension of reduced model (Equation (2)) is , which may grow rapidly as m or q increases, even for relatively small k. To alleviate this disadvantage, we consider two-sided methods for model reduction of MIMO bilinear systems.

3. Two-sided projection methods

In this section, we present a projection framework of two-sided methods for MIMO bilinear systems, and a practical algorithm is proposed to avoid the potential singularity.

3.1. Framework of two-sided methods

By confining the state of system (Equation (1)) in a specified subspace , the approximation is available, where is a base matrix of , and . If the matrix is nonsingular, we get a reduced order system as follows:

(5)

where the coefficient matrices are given by

For convenience, we denote .

By properly choosing V and W, we expect reduced order system (Equation (5)) preserves as many moments as possible so as to provide a better approximation when the choice of interpolation points is not taken into account. The basic idea is first considered for . In this case, we always assume that A is invertible. We give the following lemma prepared for the main results.

Lemma 3.1:

Let V be defined by (Equation (3)) and (Equation (4)). If is invertible, the moments of systems (Equation (5)) and (Equation (1)) satisfy for and .

Proof:

For ease of presentation, we define the denotations

for , . We first prove the following equality by induction:

(6)

When , by the definition of V, can be rewritten as , where are matrices with compatible dimensions. Further, note that solves the linear equation

Multiplying each row of the above equation by from left produces

which precisely is the equation for . So we get , then .

Suppose that (Equation (6)) is valid for . When , according to the identity

we have

The definition of V yields the expression , where are matrices with compatible dimensions. Likewise, by multiplying each row of the above equation with , the following equation is obtained

Additionally, using the assumption, we have

The above equalities imply that , and then

That is, equality (Equation (6)) is valid.

In the end, the lemma is proved by multiplying equality (Equation (6)) with from the left.

□

Remark 3.1:

An alternative proof of Lemma 3.1 can be extracted from a variation on the method used to prove Theorem 1 in [22], where a similar result for SISO bilinear systems was obtained. In comparison, our proof focuses on MIMO systems and also applicable to SISO systems.

Now we define V and W for the two-sided method. Let the integers satisfy , and . Construct the following Krylov subspaces:

(7)

V is defined as a base matrix of the union of the above Krylov subspaces

(8)

On the other hand, W is defined as a base matrix of the union space

(9)

determined by the Krylov subspaces

(10)

Theorem 3.1:

Let V be defined by (Equation (7)) and (Equation (8)), W by (Equation (9)) and (Equation (10)). If is nonsingular, then for , , the moments of systems (Equation (5)) and (Equation (1)) satisfy

Proof:

First, it follows from (Equation (6)) that

(11)

Similar to the proof of Lemma 3.1, it can be verified that for ,

(12)

From the above equality, we obtain

(13)

Noting that the moments of systems (Equation (5)) and (Equation (1)) can be expressed as the products of the left and right sides of (Equation (11)), (Equation (12)) and (Equation (13)), respectively, the theorem is shown straightforwardly.

□

Remark 3.2:

From the proof of Theorem 3.1, it is clear that moments which can be expressed as the products of the right sides of (Equation (12)) and (Equation (13)), or (Equation (11)) and (Equation (12)) are all preserved in model reduction.

As a special case, Lemma 3.1 corresponds to the choice , and in Theorem 3.1. The other critical situation versus Lemma 3.1 is , and .

Corollary 3.1:

Let W be an orthonormal base matrix of the subspace , where for . If is nonsingular, the moments of systems (Equation (5)) and (Equation (1)) satisfy for and .

Given the desired number of matched-moments, Theorem 3.1 allows us to determine the parameters and l according to our requirements. If there is no deflation occurrence [25], the numbers of the columns of matrices V and W are, respectively,

(14)

Based on (Equation (14)), the following algorithms are given to determine the parameters which allow V and W to possess the same number of columns in principle and thereby produce a much lower dimensional reduced model.

Algorithm 3.1:

Choice of , and l when .

1. When k is even, set ;

2. When k is odd, and q is even, set ;

3. When both k and q are odd, set .

Algorithm 3.2:

Choice of , and l when .

1. If there exists a positive integer such that set ; otherwise, go into the step (2);

2. Find a positive integer solving the following inequalities and set ,

3. Find a positive integer solving the following inequalities and set ,

As is well known, two-sided methods are more likely to produce badly ill-conditioned coefficient matrices [21,22]. To this end, one can proceed to define a new orthonormal matrix Z using the calculated V and W such that

(15)

The following algorithm is designed to produce a reduced model which matches the moments at for .

Algorithm 3.3:

Two-sided methods for MIMO bilinear systems.

Input: Coefficient matrices of (1) and parameters:

Output: Coefficient matrices of (5):

1. If , fix and l by Algorithm 3.1; otherwise by Algorithm 3.2.

2. Construct the matrix V by (Equation (7)) and (Equation (8)).

3. Construct the matrix W by (Equation (9)) and (Equation (10)).

4. If is singular or nearly singular, construct an orthonormal matrix Z by (Equation (15)). Then set .

5. Compute , for

A few remarks are in order:

• As the definitions of V and W are grounded in a series of Krylov subspaces, one can construct them by the block Arnoldi algorithm with deflation [25,26] instead of using direct calculations.

• Due to the deflation occurrence, V and W derived from steps (2) and (3) generally have a different number of columns. If V has fewer columns, one just needs to continue computing the associated Krylov subspace until the necessary number is reached. Otherwise, perform the similar manipulation for W.

• The singularity of may be avoided through repeatedly adjusting parameters k and q, but the procedure is entirely through intuition. Therefore, in practice one can directly run the step (4) regardless of the singularity of , which roughly doubles the dimension of the reduced model. Despite an increase of the reduced order, this scheme has the accuracy benefits of two-sided methods and the numerical stability properties of one-sided methods. Note that this method is completely different from conventional one-sided methods and more efficient in terms of producing much lower order reduced models. For example, for a bilinear system with , we set and , and want moments and to be preserved for . The dimension of the reduced model produced by Algorithm 3.3 along with a direct execution of step (4) is 16, but the reduced order reaches when constructing the reduced model by the conventional one-sided methods.

• The stability of the reduced model cannot be guaranteed automatically even if the step (4) is implemented directly. Some pretreatment may be undertaken beforehand for varied bilinear systems. The issue on the system stability is discussed in detail in Section 4 and is addressed properly by the proposed approach.

3.2. Extension to the general cases

So far we have considered two-sided methods for the Maclaurin series expansion of . We extend the underlying idea to more general cases in this subsection.

The following definitions for V and W enable the reduced model to preserve some Markov parameters. Let integers be such that , and . In order to define V, construct the Krylov subspaces

(16)

Likewise, for the definition of W construct the Krylov subspaces

(17)

Theorem 3.2:

Let V be defined by (Equation (8)) and (Equation (16)), W by (Equation (9)) and (Equation (17)). If is nonsingular, then for , , the Markov parameters of systems (Equation (5)) and (Equation (1)) satisfy

Proof:

Similar to the proof of Lemma 3.1, we can verify by induction that, for and ,

Meanwhile, for and , there holds

The theorem is then obtained directly from the above equalities. □

We now consider matching the moments at . To construct V, we define the Krylov subspaces

(18)

We also construct the following Krylov subspaces for the definition of W:

(19)

Theorem 3.3:

Let V be defined by (Equation (8)) and (Equation (18)), W by (Equation (9)) and (Equation (19)). If the matrices and are nonsingular, then the moments of systems (Equation (5)) and (Equation (1)) at satisfy for and .

Proof:

Except for replacing A by , the proof is almost the same as that of Theorem 3.1.

□

Similar to the case for linear systems, the multi-points projection methods are also applicable to bilinear systems. Give a series of points , here . In order to match a desired number of moments at points , we can construct and according to Theorem 3.3 for each point , and subsequently define V and W such that

(20)

That is, V and W span subspaces which contain all associated vectors at each expansion point.

In the general cases, the denotations can be also properly defined to simplify the proof of properties on moment matching. Algorithms for preserving Markov parameters and moments at multi-points are the same as Algorithm 3.3 except the definitions of V and W in steps (2) and (3). We omit the details for brevity. Another important point is the choice of the interpolation points in the multi-points framework. We touch on this point in the next section.

4. Stability for bilinear systems

We consider the bounded-input-bounded-output (BIBO) stability definition in this paper. As it is well-known a system is stable if its outputs remain bounded on provided that all inputs are bounded [23]. Generally, a bilinear system is BIBO stable if the coefficient matrices are sufficiently bounded and meanwhile A is stable. In most cases a minimal requirement is that A is stable, that is all its eigenvalues have the strictly negative real parts.

The stability of reduced models cannot be ensured automatically by Algorithm 3.3. As the entire stability definition for bilinear systems is more complicated, in the following we just enforce the reduced models to satisfy the minimal requirement if the original system is stable.

If the matrix is negative definite, Algorithm 3.3 with a direct execution of step (4) generates a reduced model and therefore the reduced model has the stable coefficient matrix . Inspired by the case of linear systems [27], the negative definite condition can be achieved by the intermediary system

which results from the original system by a similarity transformation, where L is the Cholesky decomposition of solving the Lyapunov equation Theoretically, the minimal requirement can be always fulfilled by this method. Note that as the order of the original system might be very large, the solution P of a Lyapunov equation can be numerically expensive.

Next, based on the analysis of the norm, we present a new method which not only preserves the stability but also provides us with fresh insight concerning the assignation of the interpolation points for moment matching methods. The norm of a bilinear system is first introduced in [11] and can alternatively be expressed via transfer functions as

Let be eigenvalues of A. Similar to the analysis for discrete bilinear systems [12], with the aid of residue theorem the above equality is rewritten as

(21)

where is a generalized residue associated with the ith transfer function. Consequently, from (Equation (21)) we get the following theorem.

Theorem 4.1:

Let and be the original and reduced order systems, and be the spectrum of matrices A and , respectively. Then the norm of the error system reads

Theorem 4.1 indicates that the error, assessed by the norm, is induced by the mismatch of the transfer functions at the mirror images of eigenvalues of matrices A and . This directs us to take the interpolation points as the eigenvalues of A and in the multi-points framework. As the matrix cannot be known a priori, we directly construct projection matrices to ensure the interpolation property at the mirror images of the poles of the reduced model (namely the eigenvalues of ).

Theorem 4.2:

Let be a subset of eigenvalues of , U be a basis matrix of the corresponding invariant subspace. Define V according to (Equation (20)) with interpolation points . Then the reduced order system

interpolates the original system at the mirrors of its poles. Moreover, is stable.

Proof:

As U spans an invariable subspace of , there holds , where is a matrix having eigenvalues . Then we obtain and is stable. Since we take as interpolation points, the interpolation property follows easily from the preceding discussion in Section 3. □

Remark 4.1:

Due to the duality, the results in Theorem 4.2 are also valid if U is used to guarantee the interpolation property, while V is specified to span an invariable subspace of A.

Remark 4.2:

In order to match moments at the mirror images of the poles of the reduced model, an iterative procedure Bilinear-IRKA is introduced in [28]. Although the procedure generally converges rapidly in practice, there is no guarantee of convergence and stability in theory at this stage. The particular idea of IRKA is that the reduced poles converge to a local -optimum, which is not the case in Theorem 4.2. However, Theorem 4.2 presents a method for modal reduction, being optimal, once the reduced poles are fixed. This is a completely different approach than IRKA.

5. Simulation examples

In this section, two numerical examples are presented to illustrate the efficiency of our approach. We compare our methods with one-sided methods [7,18] and the scheme proposed to avoid the singularity is also testified. We perform all our experiments in Matlab and use ode15s to solve ordinary differential equations (ODE) under investigation.

Example 1.

In this example, the system is of order 500 and its coefficient matrices are given as

, and with all entries being 0 except . Four reduced models are constructed for this example. Reduced model-2 is produced by two-sided methods to preserve moments at 0 for and . For comparison, Reduced model-1 is produced by one-sided methods to preserve moments at 0 for and . Consequently, they are of order 20. Reduced model-4 is constructed to preserve moments at multi-points 0, 100, and for , by two-sided methods, and accordingly Reduced model-3 is constructed by one-sided methods to preserve moments at multi-points 0, 100 and for , . Reduce model-3 and model-4 are of order 18. 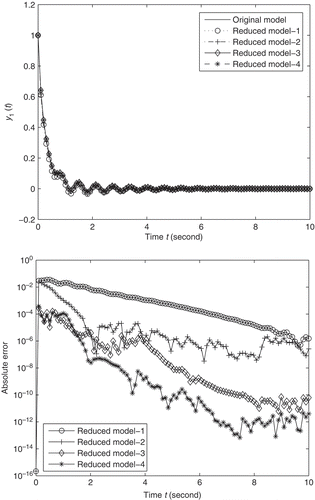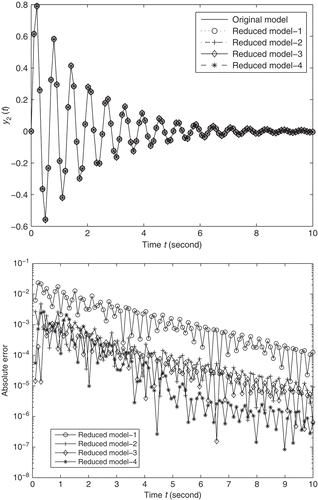Given the initial condition , Figure 1 shows the outputs and the absolute errors.

Figure 1. Left: outputs , Right: absolute errors, for .

During the simulation, there is no singularity occurrence and step (4) of Algorithm 3.3 is not executed for this example. The dynamical behaviour of the original model is excellently approximated by reduced models and we can hardly distinguish them clearly from Figure 1. It is clear that two-sided methods produce better approximations for this example, especially in the multi-points framework, due to the preservation of much more moments.

Example 2.

We consider the bilinear system resulting from the Carleman bilinearization of a semi-discretized nonlinear equation, which is obtained from the nonlinear partial differential equation

(22)

Such one-dimensional viscid Burgers equation typically is used to model gas dynamics and traffic flow [29]. In this paper, we use it to illustrate the relevance of model reduction.

For simpleness, we assume parameter is constant and . We execute spatial discretization for (Equation (22)) using an equidistant step size in interval . By the central difference approximations

and the notations , for , we get a multiple input nonlinear system

where and

Truncating the Taylor series of the nonlinear function up to second order, we obtain a bilinear system with the new state vector as follows:

(23)

where and are the first and second derivative matrices of ; are the Jacobian matrices of the first and second columns of , respectively. Further, , and are the first and second columns of . We specify the system output as , where with all entries being 0 except .

In our simulation, we set and thereby the dimension of original model (23) is 930. We construct Reduced model-2 by two-sided methods to preserve moments at 0 for and . Accordingly, Reduced model-1 is generated by one-sided methods to preserve moments at 0 for and . The order of Reduced model-1 and model-2 are 42. Using two-sided methods, Reduced model-4 is designed to preserve moments at multi-points , and for . For Reduced model-4, step (4) of Algorithm 3.3 is adopted as the matrix has the condition number , which causes the ode15s to fail to accurately solve the relevant ODEs. So the resulting Reduced model-4 is of order 36. For a fair comparison, we also plot Reduced model-3 of order 60, which is produced in a one-sided framework to preserve moments at , and for . Figure 2 displays the outputs and the absolute errors for the given inputs.

Figure 2. Left: outputs , Right: absolute errors, for .

6. Conclusions

Two-sided projection methods have been studied for MIMO bilinear systems. The issue of the stability is addressed properly by directly constructing the projection matrices instead of using an iterative procedure and thereby the computational load is light. We have also proposed a scheme to get rid of the potential singularity in the two-sided framework at the cost of roughly doubling the reduced order, which allows the approach to take on accuracy benefits of two-sided methods and stability properties of one-sided methods. The simulation results indicate that the scheme is very efficient.

Acknowledgements

The authors would like to thank the editors and the anonymous referees for their helpful comments and suggestions which greatly improved the presentation of the paper.

This work was supported by the Natural Science Foundation of China (NSFC) under grant 11071192, the International Science and Technology Cooperation Program of China under grant 2010DFA14700, and the NPU Foundation for Fundamental Research under grant JCY20130142.