A POD–EIM reduced two-scale model for precipitation in porous media

ABSTRACT

A time-dependent two-scale multiphase model for precipitation in porous media is considered, which has recently been proposed and investigated numerically. For numerical treatment, the microscale model needs to be finely resolved due to moving discontinuities modelled by several phase-field functions. This results in high computational demands due to the need of resolving many such highly resolved cell problems in course of the two-scale simulation. In this article, we present a model order reduction technique for this model, which combines different ingredients such as proper orthogonal decomposition for construction of the approximating spaces, the empirical interpolation method for parameter dependency and multiple basis sets for treating the high solution variability. The resulting reduced model experimentally demonstrates considerable acceleration and good accuracy both in reproduction as well as generalization experiments.

KEYWORDS:

• Porous media
• precipitation
• model reduction
• two-scale model
• cell problems
• proper orthogonal decomposition
• empirical interpolation

1. Introduction

The present paper develops and shows numerically the efficiency of a model reduction scheme for a time-dependent two-scale model for a precipitation process in a porous medium that was recently introduced in [29]. A porous medium is a domain that is perforated by so-called grains, cf. [4]. The domain of interest is the pore space, which is the complementary domain to the union of the grains. The considered situation in [29] and here is the following one. The pore space is occupied by a mixture of three substances: water, oil and a precipitate (e.g. salt). The water contains dissolved (salt) particles that precipitate on the grain boundary and form a crystalline solid if the concentration of the dissolved particles in the water exceeds a certain threshold. The reverse reaction is also possible, that is particles of the precipitate dissolve in the water if the concentration in the water is below this threshold. Therefore, the boundary between water and precipitate is a-priori unknown and moved besides curvature effects by precipitation and dissolution. The location of the boundaries water–oil and oil–water is also a-priori unknown but only driven by curvature effects, since it is assumed that particles of the precipitate cannot dissolve in oil and that water and oil are immiscible and incompressible. The evolution of the concentration of the particles in the water is driven by the precipitation process but also by diffusion.

Since the spatial scale of the diffusion process is much larger than the scale of the pores on which a phase transition takes place, the model of [29] consists of two spatial length scales: a macroscopic so-called Darcy scale and a microscopic so-called pore scale. It was developed by the application of a homogenization technique to a pure pore-scale model for simplifying the numerical treatment; for an introduction to homogenization in porous media, see [8]. In the two-scale model, the unknown on the macroscopic scale is the concentration of the dissolved particles in the water, and on the microscopic scale, the evolution of the phase boundaries is modelled by three phase-fields; see [8,9] for a general introduction to phase-field modelling with one phase-field,[6,7] for the handling of three phase-fields and [8] for the diffuse domain approximation method that is used in [29] in order to model the evolution of the characteristic functions of the three pore-space’s subdomains that are each occupied by one of the three constituents, water, oil and precipitate. Furthermore, an auxiliary function on the microscale is described that results from the upscaling and which acts as a microscopic correction of the diffusion tensor in the evolution equation for the macroscopic concentration. The two scales are coupled, that is the evolution of the phase-fields is influenced by the macroscopic concentration of dissolved particles in the water, and conversely, the evolution of the macroscopic concentration is influenced by the rate of microscopic precipitation and the microscopic auxiliary function.

The usual two-scale model’s (detailed/high-dimensional) discretization (as described in [29]) consists of an evolution scheme for the concentration on a macroscopic numerical grid and for every macroscopic grid point of a microscopic cell problem describing the evolution of the three phase-fields and of the auxiliary function. The number of cell problems that must be solved in course of a simulation is equal to the product of the number of macroscopic nodes times the number of time steps. This soon becomes numerically very demanding if both numbers increase, since in order to solve a cell problem accurately, a fine discretization is necessary.

The present study presents a model reduction approach for the two-scale model described above. Existing approaches dealing with model reduction for multiscale problems involve reduced basis approaches for cell problems [5, 22, 24], the localized reduced basis multiscale method [20,2] or kernel surrogate models for microscale models [14]. While the former are used in the context of linear problems, the latter allows nonlinear problems but only is applicable in the case of few number of inputs/outputs in the coupling of the scales.

Our approach is projection-based and aims at a reduction of the most expensive part of the cell problems in order to accelerate the computation of the overall two-scale model, where it is the discretization of the auxiliary function that is most expensive. The problem for the auxiliary function strongly depends on the shape of the microscale subdomain occupied by the water, that is the problem depends on the phase-field modelling this subdomain. The problem is elliptic but, since the phase-field for water evolves in course of a simulation, it is implicitly time-dependent, that is a good approximation of complete trajectories and a high solution variability must be accounted for by the reduction approach. In [28], a similar procedure was developed for a two-scale model for crystal growth.

The detailed model for the auxiliary function will be projected to a low-dimensional solution subspace generated via a proper orthogonal decomposition (POD; [19,30]) strategy based on high-dimensional snapshots. The empirical interpolation method (EIM, [3,15]) deals with the parameter dependency enabling to evaluate local parametric discretization operators efficiently. In particular, we refer to the empirical operator interpolation approach for linear and nonlinear operators [11,17], as well as the discrete empirical interpolation method (DEIM) for nonlinear parametric ordinary differential equations [10] or extensions as the matrix DEIM used in [33]. In addition to full precomputation of the offline data, recently also online adaptation procedures have been introduced that accept online complexities linear in the full dimension H and continuously update the reduced model throughout the simulation [2,26]. As last step in our reduction, the reduced models are subdivided into submodels where each of them is capable of producing accurate low-dimensional approximations to the high-dimensional solutions for certain shapes of the water domain. Local subdomain basis approaches can also be found in other articles on model order reduction [1, 12, 13, 16, 25, 31], where time, parameter or state–space distance is used as partitioning criterion. As an alternative to partitioning, also interpolation of local models is a possible approach, for example [14]. But here, we follow the partitioning idea and the utilized partitioning criterion will be the volume of the precipitate.

The paper is structured as follows. Section 2 will present the detailed two-scale model as introduced in [29] and additionally gives a matrix-based formulation of the microscale problem that will be reduced. This microscale equation then is subject to a POD/EIM-based model reduction, which is explained in Section 3. The extensive Section 4 then presents numerical results, which illustrate the efficiency of the reduced model over the full model both in reproduction, as well as generalization settings. The paper is concluded with comments in Section 5.

2. The detailed two-scale model

This section briefly discusses the detailed discrete two-scale model describing the evolution of the dissolved particles’ concentration in the water phase on a Darcy-scale (macroscopic) and the evolution of the boundaries of the three substances, water, oil and the precipitate, on a pore-scale (microscopic) of a porous medium. Note that this description will be very concise only focussing on the relevant parts for the derivation of our subsequent reduced model. A detailed development and explanation of the model is presented in [29]. The model consists of a macroscopic homogenized equation modelling the evolution of the concentration u of the dissolved particles in water, and at each point of the macroscopic domain of microscopic cell-problems with periodic boundary conditions modelling the evolution of the three substances and of two auxiliary functions w₁ and w₂. The evolution of the substances is modelled by three phase-fields which smoothly approximate the characteristic functions (in a sharp-interphase sense) of the three subdomains occupied each by one of the substances.

Consider a time-interval J(T): = [0,T] with the end time T > 0 and $\overline{J(T)}=[0,T]$, a macroscopic spatial domain $\mathrm{\Omega }\subset {\mathbb{R}}^d$ of dimension d = 2 with a boundary ${\mathrm{\Gamma }}_{\mathrm{\Omega }}=\mathrm{\partial }\mathrm{\Omega }$ and a microscopic spatial domain Y = (0,1)^d. The domain Y is subdivided into a pore-space $\mathcal{P}$, a grain $\mathcal{G}$ and the grain’s boundary ${\mathrm{\Gamma }}_{\mathcal{G}}$, that is $Y=\mathcal{P}\cup \mathcal{G}\cup {\mathrm{\Gamma }}_{\mathcal{G}}$. The boundary ${\mathrm{\Gamma }}_{\mathcal{P}}$ of the pore-space $\mathcal{P}$ equals $\mathrm{\partial }Y\cup {\mathrm{\Gamma }}_{\mathcal{G}}$. Let n_Ω be the outer-normal to ${\mathrm{\Gamma }}_{\mathrm{\Omega }}$ and $n_{\mathcal{G}}$ the inner-normal to ${\mathrm{\Gamma }}_{\mathcal{G}}$.

As mentioned above, the pore-space $\mathcal{P}$ is occupied by three substances P_i, i_μI = {1,2,3}: two immiscible, incompressible fluids P₁ (water) and P₂ (oil) and the precipitate P₃. In a sharp-interface setting, the substances would occupy three disjoint time-dependent a-priori unknown regions $P_1^s$, $P_2^s$ and $P_3^s$. In the phase-field setting considered in this article, three phase fields smoothly approximate the characteristic functions ${\chi }_1$, ${\chi }_2$ and ${\chi }_3$ of $P_1^s$, $P_2^s$ and $P_3^s$, that is for i_μI = {1,2,3}, the phase-field smoothly approximates ${\chi }_i$. The model ensures a perfect mixture of the three phase fields $\mathrm{\Phi }=({\varphi }_1,{\varphi }_2,{\varphi }_3)$ in the sense that their sum equals 1 and each of them is not less than 0, that is $\mathrm{\Phi }\in \mathcal{S}:=\left\{\mathrm{\Phi }=({\varphi }_1,{\varphi }_2,{\varphi }_3)\in {[0,1]}^3|{\sum }_{i\in I}{\varphi }_i=1\right\}$.

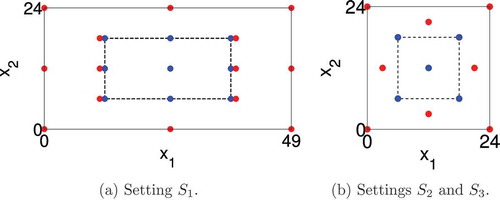
In the considered initial configuration, μ of the three phases, depicted in Figure 1, the precipitate P₃ surrounds the grain which is located in the centre of the microscopic domain Y, the fluid P₂ is located in the corners of Y and the fluid P₁ occupies the remainder of the pore-space $\mathcal{P}=Y\mathrm{\setminus }\overline{\mathcal{G}}$. Due to the considered periodic boundary conditions onμY, both P₂ and $P_3$ are spherical, where P₃ is perforated by the grain.

Figure 1. The considered initial configuration ℐ of the three substances in the microscopic pore-space μ, where $Y=\mathcal{G}\cup {\mathrm{\Gamma }}_{\mathcal{G}}\cup \mathcal{P}$. The grain μ is located in the centre of Y and the pore-space μ is occupied by the two immiscible and incompressible fluids P₁ (water) and P₂ (oil) as well as the precipitate P₂. The spherical perforated precipitate P₃ is attached to the boundary Г_μ of the grain μ, the spherical fluid P₂ domain is located in the corners of the microscopic domain Y and the fluid P₁ occupies the remainder.

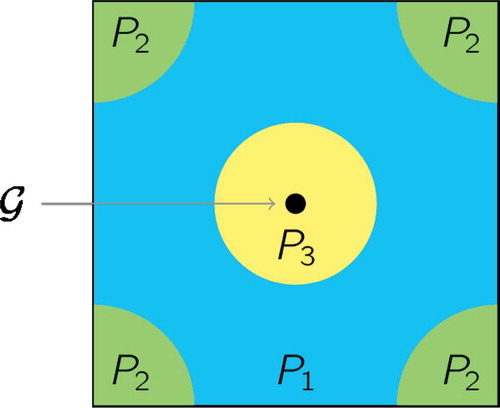
The fluid P₁ contains dissolved particles that can precipitate on the grain-boundary Г_μμ as well as on the boundary of an already existent precipitate μμP₁. By assumption, P₂ cannot contain particles, hence the concentration is 0 in P₂. Furthermore, ρ > 0 is the fixed concentration of particles in the precipitate region P₃.

The upscaled model considered here is derived in [29] by a homogenization technique from a pure microscopic model for the concentration u and the phase-fields Φ for the idealized situation of periodically distributed grains. The cell problems for the auxiliary functions w₁ and w₂ result from the homogenization process.

2.1. The homogenized macroscopic equation for the concentration

In our presentation, we will use the notational convention that variables related to the partial differential equation model are put in normal font, independent of whether they are scalar or low-dimensional vectors. We then discriminate the resulting discretized high-dimensional coefficient vectors and matrices by consistently using an underline under the corresponding variable. The macroscopic spatial variable will be denoted by x ∈ Ω, the microscopic spatial variable by y ∈ Y. These are used as subscript for denoting the corresponding spatial differential operators, in particular ${\mathrm{\nabla }}_x,{\mathrm{\nabla }}_y,{\mathrm{\Delta }}_y$. Applying these conventions, we can formulate the macroscopic equation for the concentration:

Problem 2.1: Given the diffusion coefficient $D>0$, the fixed concentration $\rho >0$ of particles in the precipitate P₃ and the regularization parameter $\delta >0$, the microscopic field variables $\mathrm{\Phi }:\overline{J(T)}\times \mathrm{\Omega }\times \mathcal{P}\to \mathcal{S}$ and $w_1,w_2:\overline{J\left(T\right)}\times \mathrm{\Omega }\times \mathcal{P}\to \mathbb{R}$ and the initial conditions $u_0:\mathrm{\Omega }\to [0,\rho )$, find the macroscopic concentration $u:\overline{J(T)}\times \mathrm{\Omega }\to \mathbb{R}$ satisfying

${\mathrm{\partial }}_t\left({\overline{{\varphi }_1+\delta }}^{\mathcal{P}}u\right)-D{\mathrm{\nabla }}_x\cdot \left({\overline{K\left({\varphi }_1+\delta ,w_1,w_2\right)}}^{\mathcal{P}}{\mathrm{\nabla }}_{x}u\right)-\rho {\overline{g_{\delta }\left(\mathrm{\Phi }\right){\mathrm{\partial }}_t{\varphi }_1}}^{\mathcal{P}}=0\mathrm{i}\mathrm{n}J\left(T\right)\times \mathrm{\Omega },$

(1) $-D{\overline{K\left({\varphi }_1+\delta ,w_1,w_2\right)}}^{\mathcal{P}}{\mathrm{\nabla }}_{x}u\cdot n_{\mathrm{\Omega }}=0\mathrm{o}\mathrm{n}J(T)\times {\mathrm{\Gamma }}_{\mathrm{\Omega }},$(1)

$u(0,\cdot )=u_0\mathrm{i}\mathrm{n}\mathrm{\Omega },$

where the input of the microscopic variables is averaged on $\mathcal{P}$ as follows:

(2) ${\overline{v\left(t,x,\cdot \right)}}^{\mathcal{P}}=\frac{1}{\left|\mathcal{P}\right|}\underset{\mathcal{P}}{\int }v\left(t,x,y\right)\mathrm{d}\mathrm{y}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}v:\overline{J\left(T\right)}\times \mathrm{\Omega }\times P\to \mathbb{R}$(2)

(3) ${\left({\overline{K\left({\varphi }_1+\delta ,w_1,w_2\right)\left(t,x,\cdot \right)}}^{\mathcal{P}}\right)}_{ij}={\overline{\left({\varphi }_1+\delta \right)\left({\delta }_{ij}+{\mathrm{\partial }}_{y_i}{w}_j\right)}}^{\mathcal{P}}\mathrm{f}\mathrm{o}\mathrm{r}1\le i,j\le d,$(3)

with Kronecker’s delta ${\delta }_{ij}$, and where

(4) $g_{\delta }\left(\mathrm{\Phi }\right)=\left\{21\mathrm{i}\mathrm{f}\delta =0\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{\Phi }{=(1,0,0)}^{\mathrm{T}},\frac{{\varphi }_3}{{\varphi }_2+{\varphi }_3+\delta }=\frac{{\varphi }_3}{1-{\varphi }_1+\delta }\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}.\right.$(4)

The function $g_{\delta }(\mathrm{\Phi })$ approximates a linear function interpolating between 1 in a water–precipitate- and 0 in a water–oil-interface. Therefore, the last term on the left-hand side of the first equation in (1) accounts for the conservation of the particles’ mass.

Remark 2.2: The symmetry of the considered initial configuration ℐ of the three phases yields

(5) ${\overline{K\left({\varphi }_1+\delta ,w_1,w_2\right)}}^{\mathcal{P}}={\overline{K\left({\varphi }_1+\delta ,w_1\right)}}^{\mathcal{P}}={\overline{\left({\varphi }_1+\delta \right)\left(1+{\mathrm{\partial }}_{y_1}{w}_1\right)}}^{\mathcal{P}}\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$(5)

in $\overline{J(T)}\times \mathrm{\Omega }$. A thorough investigation of the considered symmetry’s implications will be carried out in the Remarks 2.4 and 2.6.

2.2. The microscopic cell problems

The microscopic cell problems describe the evolution of the phase-fields Φ and the auxiliary functions w₁ and w₂.

Problem 2.3: Given the time-relaxation parameter α > 0, the parameter ξ > 0 that is proportional to the width of the phase transition regions, the parameters $c_{u,0},c_{u,1}>0$ with $c_{u,1}<\rho$ (where ρ > 0 is the fixed concentration of particles in the precipitate P₃), the macroscopic field variable $u:J(T)\times \mathrm{\Omega }\to [0,1]$, and the initial conditions ${\mathrm{\Phi }}_0=\left({\varphi }_{1,0},{\varphi }_{2,0},{\varphi }_{3,0}\right):\mathrm{\Omega }\times \mathcal{P}\to \mathcal{S}$, for every x μμ Ω find the Y-periodic microscopic phase-fields $\mathrm{\Phi }:\overline{J\left(T\right)}\times \left\{x\right\}\times \mathcal{P}\to \mathbb{R}$ satisfying for i ∈ I

(6) $\alpha {\xi }^2{\mathrm{\partial }}_t{\varphi }_i-\frac{3}{4}{\xi }^2{\mathrm{\Delta }}_y{\varphi }_i+G_i(\mathrm{\Phi },u)=0\mathrm{i}\mathrm{n}J(T)\times \{x\}\times \mathcal{P},-\frac{3}{4}{\xi }^2{\mathrm{\nabla }}_y{\varphi }_i\cdot n_{\mathcal{G}}=0\mathrm{o}\mathrm{n}J(T)\times \{x\}\times {\mathrm{\Gamma }}_{\mathcal{G}},{\varphi }_i(0,\cdot ,\cdot )={\varphi }_{i,0}\mathrm{i}\mathrm{n}\{x\}\times \mathcal{P},$(6)

with the potentials

(7) $G_i(\mathrm{\Phi },u)=\left(\sum _{j\in I\mathrm{\setminus }\{i\}}\left({\mathrm{\partial }}_{{\varphi }_i}-{\mathrm{\partial }}_{{\varphi }_j}\right)W\left(\mathrm{\Phi }\right)\right)+f_i(\mathrm{\Phi },u)\mathrm{f}\mathrm{o}\mathrm{r}i\in I,$(7)

where

(8) $\begin{array}{rl}& W\left(\mathrm{\Phi }\right)=2\sum _{i\in I}{\varphi }_i^2{\left(1-{\varphi }_i\right)}^2,f_1(\mathrm{\Phi },u)=\alpha \xi \hspace{0.17em}{\gamma }_{13}(\mathrm{\Phi })f(u),f_2(\mathrm{\Phi },u)=0,\\ & f_3(\mathrm{\Phi },u)=-f_1(\mathrm{\Phi },u),{\gamma }_{13}(\mathrm{\Phi })=4\hspace{0.17em}{\varphi }_1{\varphi }_3,f(u)=c_{u,0}\left(u-c_{u,1}\right)\end{array}$(8)

The function W(Φ) is non-convex in $S$ and minimal for the pure states $\mathrm{\Phi }\in \left\{{\left(1,0,0\right)}^{\mathrm{T}},{\left(0,1,0\right)}^{\mathrm{T}},{\left(0,0,1\right)}^{\mathrm{T}}\right\}$. Since γ₁₃ is an indicator of the diffuse interface $\left({\varphi }_1,{\varphi }_3\approx \frac{1}{2}\right)$ between water and precipitate and $f(u)$ is an affine linear rate function with a given constant rate $c_{u,0}>0$ and a constant threshold $0<c_{u,1}<\rho$ that separates precipitation and dissolution, the forces f₁ and f₃ drive the precipitation process. If u is larger than $c_{u,1}$, then dissolved particles precipitate and the precipitate phase expands, otherwise it recedes if $u<c_{u,1}$.

Remark 2.4: Since the subspace $\mathcal{S}$ of the admissible states of Φ is an invariant subspace of the solution operator ${\mathrm{\Phi }}_0\mapsto \mathrm{\Phi }$ of Problem 2.3, it is sufficient to solve the problem for i = 2,3 and subsequently to set ${\varphi }_1=1-{\varphi }_2-{\varphi }_3$, see [29]. Furthermore, the considered initial configuration μ of the three phases satisfies for $y_1{y}_2\mathrm{T}\in \mathcal{P}$ in $J(T)\times \mathrm{\Omega }$.

(9) $\mathrm{\Phi }\left(\cdot ,\cdot ,\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\right)=\mathrm{\Phi }\left(\cdot ,\cdot ,\left(\begin{array}{c}1-y_1\\ y_2\end{array}\right)\right)=\mathrm{\Phi }\left(\cdot ,\cdot ,\left(\begin{array}{c}{y}_1\\ 1-y_2\end{array}\right)\right)=\mathrm{\Phi }\left(\cdot ,\cdot ,\left(\begin{array}{c}1-y_1\\ 1-y_2\end{array}\right)\right).$(9)

To be precise, Φ is rotational symmetric of order 4: a rotation of Φ by an angle of 90 does not change it.

Problem 2.5: Given the diffusion coefficient D = 0 and the regularization parameters δ > 0, the microscopic field variable ${\varphi }_1:J(T)\times \mathrm{\Omega }\times \mathcal{P}\to [0,1]$, for j = 1,2 for every x ∈ Ω find the Y-periodic microscopic solution $w_j:J\left(T\right)\times \left\{x\right\}\times \mathcal{P}\to \mathbb{R}$ with vanishing average in μ satisfying

(10) $\begin{array}{rl}& -D{\mathrm{\nabla }}_y\cdot \left(({\varphi }_1+\delta ){\mathrm{\nabla }}_y{w}_j\right)\\ & =D{\mathrm{\nabla }}_y({\varphi }_1+\delta )\cdot e_j\mathrm{i}\mathrm{n}J(T)\times \{x\}\times \mathcal{P},\\ & -D({\varphi }_1+\delta ){\mathrm{\nabla }}_y{w}_j\cdot n_{\mathcal{G}}\\ & =D({\varphi }_1+\delta )e_j\cdot n_{\mathcal{G}}\mathrm{o}\mathrm{n}J(T)\times \{x\}\times {\mathrm{\Gamma }}_{\mathcal{G}}.\end{array}$(10)

Remark 2.6: Since Problem 2.5 is completed by periodic boundary conditions, it is only uniquely solvable owing to the constraint demanding that the solution vanishes on average. Furthermore, due to the considered rotational symmetry of the three phases, the solutions satisfy

(11) $w_1\left(\cdot ,\cdot ,\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\right)=w_2\left(\cdot ,\cdot ,\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\right)\mathrm{f}\mathrm{o}\mathrm{r}\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\in \mathcal{P}$(11)

in J(T × Ω. Furthermore, $w_1$ is symmetric to the axis $\left\{{\left(\begin{array}{cc}{y}_1& \frac{1}{2}\end{array}\right)}^{\mathrm{T}}|y_1\in [0,1]\right\}\subset Y$ and anti-symmetric to $\left\{{\left(\begin{array}{cc}\frac{1}{2}& y_2\end{array}\right)}^{\mathrm{T}}|y_2\in [0,1]\right\}\subset Y$. In combination with (9), these observations yield

(12) $1{\overline{({\varphi }_1+\delta ){\mathrm{\partial }}_{y_1}{w}_1}}^{\mathcal{P}}={\overline{({\varphi }_1+\delta ){\mathrm{\partial }}_{y_2}{w}_2}}^{\mathcal{P}}\mathrm{i}\mathrm{n}J(T)\times \mathrm{\Omega },{\overline{({\varphi }_1+\delta ){\mathrm{\partial }}_{y_2}{w}_1}}^{\mathcal{P}}={\overline{({\varphi }_1+\delta ){\mathrm{\partial }}_{y_1}{w}_2}}^{\mathcal{P}}=0\mathrm{i}\mathrm{n}J(T)\times \mathrm{\Omega }.$(12)

Therefore, it is sufficient to solve Problem 2.5 for w₁ only.

2.3. Discretization

Problems 2.1, 2.3 and 2.5 are discretized by the explicit Euler method with respect to the time, and by standard second-order finite differences on uniform rectangular grids Ω_hg and Y_hμ with respect to the spatial domain, where h_g > 0 denotes the macroscopic and h_μ > 0 the microscopic space-increment. The discrete microscopic pore-space μ_hμ is a subset of Y_hμ. The time-increment μⁿt depends on ${\overline{{\varphi }_1^{n-1}+\delta }}^{\mathcal{P}}$, due to the CFL-condition for the discretization of Problem 2.1.

Since it is demanding to solve the microscopic cell Problems 2.3 and 2.5 in all macroscopic nodes, the problem is solved adaptively in the sense of [27], that is only the microscopic problems in active macroscopic nodes $A^n\subset {\mathrm{\Omega }}_{h_g}$ are solved and the microscopic data of inactive nodes ${\mathrm{\Omega }}_{h_g}\mathrm{\setminus }{A}^n$ is approximated. Details are also given in [1]. This results in the following algorithm:

Algorithm 1:

1. Set n = 0, $u^n={\left. u_0\right|}_{{\mathrm{\Omega }}_{h_g}}$ and ${\mathrm{\Phi }}^n={\left. {\mathrm{\Phi }}_0\right|}_{{\mathrm{\Omega }}_{h_g}\times Y_{h_{\mathrm{\ell }}}}$.

2. Set n = n + 1 and $t_n=t_{n-1}+{\mathrm{\Delta }}^{n}t$.

3. Adjust the set Aⁿ of the active macroscopic nodes.

4. For every node in Aⁿ solve the discretization of the microscopic Problem 2.5 for ${\varphi }_2^n$ and ${\varphi }_3^n$ with parameter uⁿ⁻¹ and set ${\varphi }_1^n=1-{\varphi }_2^n-{\varphi }_3^n$.

5. For every node in $A^n$ solve the discretization (15) of the microscopic Problem 2.5 for $w_1^n$ with parameter ${\varphi }_1^n$.

6. Approximate the microscopic parameters ${\overline{{\varphi }_1^n+\delta }}^{\mathcal{P}}$, ${\overline{K\left({\varphi }_1^n+\delta ,w_1^n\right)}}^{\mathcal{P}}$ and ${\overline{g_{\delta }({\mathrm{\Phi }}^n){\mathrm{\partial }}_t{\varphi }_1^n}}^{\mathcal{P}}$ in Ω_hg.

7. Solve the discretization of the macroscopic Problem 2.1 for $u^n$ with the parameters of Step 6.

8. Go back to Step 1 if t_n = T.

In this algorithm, the computation of the elliptic problem for $w_1$ in Step 1 is the crucial expensive component – a detailed complexity discussion follows in Section 3. Therefore, only the microscopic Problem 2.5 for $w_1^n$ will be solved in a reduced sense in the reduced two-scale model to be developed. The detailed model’s discretization of 2.5 reads

(13) $\begin{array}{rl}& 1\frac{D}{2h_{\mathrm{\ell }}^2}{\sum }_{\bar{y}\in {\overline{Y}}_{h_{\mathrm{\ell }}}(y)}\left({\varphi }_1^n(y)+{\varphi }_1^n(\bar{y})+2\delta \right)\left(w_1^n(y)-w_1^n(\bar{y})\right)\\ & =\frac{D}{2h_{\mathrm{\ell }}^2}\left({\varphi }_1^n\left(y_1+h_{\mathrm{\ell }},y_2\right)-{\varphi }_1^n\left(y_1-h_{\mathrm{\ell }},y_2\right)\right),\end{array}$(13)

where $y={\left(y_1,y_2\right)}^{\mathrm{T}}\in {\mathcal{P}}_{h_{\mathrm{\ell }}}$ and ${\overline{Y}}_{h_{\mathrm{\ell }}}(y)$ is the set of first-order neighbours of $y$, that is

(14) ${\overline{Y}}_{h_{\mathrm{\ell }}}(y)=\left\{{\left(y_1+h_{\mathrm{\ell }},y_2\right)}^{\mathrm{T}},{\left(y_1-h_{\mathrm{\ell }},y_2\right)}^{\mathrm{T}},{\left(y_1,y_2+h_{\mathrm{\ell }}\right)}^{\mathrm{T}},{\left(y_1,y_2-h_{\mathrm{\ell }}\right)}^{\mathrm{T}}\right\}.$(14)

As this, problem will be reduced, a compactly written vector–matrix formulation is provided in the following, which is more accessible than the above detailed formulation. For this, define $H:=|{\mathcal{P}}_{h_{\mathrm{\ell }}}|$ as the (high) dimension of the field variable $w_1$ and introduce the vectors of degrees of freedom (DOF) ${\underset{\_}{w}}_{1,H}^n:=(w_1^n(y){)}_{y\in {\mathcal{P}}_{h_{\mathrm{\ell }}}}$ and ${\underset{\_}{\varphi }}_{1,H}^n:=({\varphi }_1^n(y){)}_{y\in {\mathcal{P}}_{h_{\mathrm{\ell }}}}$, assuming a suitable enumeration of μ_hμ. The auxiliary function ${\underset{\_}{w}}_1^n$ is characterized by the system of equations

(15) ${\underset{\_}{L}}_H({\underset{\_}{\varphi }}_{1,H}^n){\underset{\_}{w}}_{1,H}^n={\underset{\_}{R}}_H({\underset{\_}{\varphi }}_{1,H}^n),$(15)

where the matrix ${\underset{-}{L}}_H({\underset{-}{\varphi }}_{1,H}^n)\in {\mathbb{R}}^{H\times H}$ and the vector ${\underset{-}{R}}_H({\underset{-}{\varphi }}_{1,H}^n)\in {\mathbb{R}}^{H\times 1}$ depend linearly on the solution ${\underset{\_}{\varphi }}_{1,H}^n$ of the microscopic Problem 2.3. To be precise, let $N_i$ define the set of indices of the first-order neighbours of the node $i$ and r_i (and correspondingly μ_i) define the index of the first-order neighbour to the right (left) of the node i, then for all $i,j=1,\dots ,H$ the matrix and the right-hand side are given by

(16) $1{\left({\underset{\_}{L}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)\right)}_{i,j}=\left\{\begin{array}{c}2{\sum }_{k\in N_i}\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_i+{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_k+2\delta \right)\mathrm{i}\mathrm{f}j=i,\\ -\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_i+{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_j+2\delta \right)\mathrm{i}\mathrm{f}j\in N_i,\\ 0\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e},\end{array}\right.$(16)

${\left({\underset{\_}{R}}_H({\underset{\_}{\varphi }}_{1,H}^n)\right)}_i=h_{\mathrm{\ell }}\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{r_i}-{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{{\mathrm{\ell }}_i}\right).$

The solution of the system is approximated by a CG procedure with the following abort criterion: stop the iteration if the maximum norm of the residuum is less or equal than the product of the tolerance δ and the maximum norm of the right-hand side. A Lagrange-multiplier ensures uniqueness by enforcing the vanishing average.

3. The reduced two-scale model

The discretization of the microscopic Problem 2.3 describing the evolution of the phase-fields ${\varphi }_2$ and ${\varphi }_3$ in each step of time in each active macroscopic node is solvable in $O$ (H), and the complexity of the discrete macroscopic Problem 2.1 for u is insignificant. However, the complexity of solving the sparse linear system (15) for $w_1^n$ in each step of time in each active macroscopic node is roughly $O\left(H^2\right)$, if we assume a standard iterative solver, where the number of iterations as well as the cost for matrix–vector products grows linearly with H. Consequently, the overall complexity of the discrete two-scale model is reducible significantly by reducing the complexity of the model for w₁. In the overall reduced two-scale model, operations of complexity $O\left(H\right)$ are accepted. Therefore, only the model for w₁ is reduced, that is Step 1 of Algorithm 1 is replaced by

• For every node in Aⁿ approximate the high-dimensional solution $w_{1,H}^n$ of (15) with parameter ${\varphi }_{1,H}^n$ by the low-dimensional solution $w_{1,L}^n$ to the projection of (15) (with parameter ${\varphi }_{1,H}^n$) to a low-dimensional snapshot-based approximation space.

The reduced model must account for the dependency on a time-dependent parameter, that is it must provide a good approximation of complete trajectories and a high solution variability, and the coupling of the microscopic equations. To consider this, a POD for the trajectory treatment, EIM for the parametrization and a partitioning approach to account for different solution regimes will be applied. As we refer to [28] at various places, we want to comment on the relation to that previous study in order to clarify the contribution of the current paper. The commonality to [28] is that we also consider an instationary macroscopic two-scale problem that is coupled to multi-field microscopic models, where the microscopic models are reduced by POD/EIM and a partitioning approach resulting in multiple bases. But the fundamental difference of the current study to [28] is that we have a completely different application setting (here precipitation in contrast to crystal growth), with different field variables, different equations and nonlinear coupling of the microscopic fields into the macroscopic model. This requires various changes in the methodology. In particular, we merely reduce the most costly component of the model, which is only one microscopic field variable, we leave other microscopic field variables unreduced.

As typical in parametrized model reduction procedures, the overall reduction process consists of an offline and an online phase. In the offline phase, the reduced basis and further quantities are pre-computed, this phase is accepted to be costly, but only performed once. The online phase of the reduced model then will be of low complexity and allows the reduced scheme to be used rapidly and multiply. We summarize these stages for our current problem in order to clarify the overall workflow from parameter inputs to solutions from the reduced two-scale model:

In the offline phase for a given parameter setting of the two-scale model (e.g. choice of initial values, boundary conditions, macro grid resolutions), we solve the full two-scale model for this training setting by Algorithm 1. During this computation, we collect snapshots for ${\underset{\_}{w}}_{1,H}^n$ and the right hand side $\underset{\_}{R}({\varphi }_{1,H}^n)$ for the construction of the reduced model for ${\underset{\_}{w}}_{1,H}^n$. The construction of the corresponding basis and further offline quantities will be explained in Section 3.1.

In the online phase, for various parameter settings of the two-scale model, the two-scale model is solved by Algorithm 1 but using step (5ʹ) instead of step (5). This means, for all active macroscopic nodes, the macroscopic value u^n − 1 is used as input parameter into the microscopic model. More precisely, the pointwise value of $u^{n-1}(x)$ enters the microscopic fields ${\varphi }_2^n$ and ${\varphi }_3^n$, these determine ${\varphi }_1^n$, which is the final field that enters the reduced model for the microscopic variable $w_1^n$. The detailed explanation of the computations for this reduced microscopic problem for the auxiliary variable w₁ is given in Section 3.2. Then the suitably averaged microscopic fields enter the macroscopic evolution problem enabling the macroscopic timestep to obtain uⁿ. So, clearly, the reduced model for $w_1^n$ is used multiply for all timesteps and all active macroscopic nodes and different macroscopic simulation runs by varying macroscopic parameter settings.

3.1. The offline phase

The following steps are processed in the offline phase.

1. Solve the detailed two-scale model and collect snapshots

   1. of the microscopic solution ${\underset{\_}{w}}_{1,H}^n$ of (15) in the set П_w

   2. and of the right hand side ${\underset{\_}{R}}_H({\underset{\_}{\varphi }}_{1,H}^n)$ of (15) in the set П_r.

2. Construct a reduced basis Φ_w by POD: ${\mathrm{\Phi }}_w=\{{\phi }_{w,1},\dots ,{\phi }_{w,N_w}\}\subset \mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\left({\mathrm{\Pi }}_w\right)$ with size $N_w=|{\mathrm{\Phi }}_w|$. For $i=1,\dots ,N_w$, the $N_w$ vectors ${\phi }_{w,i}$ are exactly the eigenvectors of the correlation operator of П_w corresponding to the $N_w$ largest eigenvalues. If the eigenvalues λ_i are sorted decreasingly, then N_w is the smallest number fulfilling the condition ${\sum }_{i=1,\dots ,N_w}{\lambda }_i\ge \left(1-{\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}\right){\sum }_{i=1,\dots ,|{\mathrm{\Pi }}_w|}{\lambda }_i$ with a tolerance $0<{\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}<1$.

3. Perform the offline phase of the Empirical Interpolation Method EIM [3] to generate an approximation of the high-dimensional microscopic model (15). Use as training data the snapshot set ${\mathrm{\Pi }}_r$, define the tolerance $0<{\epsilon }_{EI}<1$, determine the indices $Y_M\subset {\mathcal{P}}_H$ of the magic points and generate the collateral basis ${\mathrm{\Phi }}_w^{EI}$. Note, that training snapshots ${\underset{\_}{L}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right){\underset{\_}{w}}_{1,H}^n-{\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ as required for the considered model are always zero, therefore, snapshots of only ${\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ are used.¹

   Furthermore, with respect to the five-point-stencil which discretizes the spatial derivatives, determine the indices $Y_{N_M}\subset {\mathcal{P}}_H$ of the magic points’ neighbours, but only of those neighbours which are not magic points themselves, that is $Y_M\cap Y_{N_M}=\mathrm{\varnothing }$. Define $Y_M^{\star }=Y_M\cup Y_{N_M}$ and introduce an enumeration by $Y_M^{\star }(i)=Y_M(i)$ for all $i=1,\dots ,|Y_M|$ and $Y_M^{\star }(i)=Y_{N_M}\left(i-|Y_M|\right)$ for all $i=|Y_M|+1,\dots ,|Y_M|+|Y_{N_M}|$.

4. Determine the reduced operators which are required for solving the reduced model; details on the operators are given in the following.

Although these offline quantities comprise a reduced basis and the interpolation points, this set of quantities is denoted a reduced basis set

(17) $\mathcal{B}=[4]\left\{{\mathrm{\Phi }}_w,Y_M,Y_M^{\star }\right\}.$(17)

Similar as for a crystal growth model [28], not only one but also many basis sets are used for different solution regimes. Aim of the reduction is to obtain an accurate solution in much less online time than needed for the detailed model. Accuracy increases with increasing numbers N_w, μY_Mμμ andμμY_NMμμ. Contrary to this relation, speed of computation increases with decreasing numbers N_w, μY_Mμμ andμμY_NMμμ. In order to keep those numbers low but still to gain accurate results, multiple basis sets are used. A problem-specific feature extraction is used to partitioning the solution space. The utilized criterion is the volume of the precipitate P₃. Since the fluid domain for P₂ is almost unchanged, microscopic configurations of the three phases with similar precipitates’ volumes are similar themselves. Similar configurations result in similar solutions w₁,_H.

The construction of the $N_{\mathcal{B}}\in \mathbb{N}\mathrm{\setminus }\{0\}$ basis sets ${\mathcal{B}}_1,\dots ,{\mathcal{B}}_{N_{\mathcal{B}}}$ in the offline and their usage in the online phase is now straightforward. The collected snapshots are partitioned into subsets for different subintervals of the precipitates volume. This is done such that the number of snapshots is (roughly) equal for each subset, and results in volume subintervals of different size, as will be demonstrated in the experiments. For each of these snapshot subsets, the steps (2), (3), (4) mentioned at the beginning of this subsection are performed in order to generate the basis set for each subinterval.

As known in local basis construction, it can be beneficial to guarantee a certain overlap of snapshot sets for local bases [28]. Identical to [28], we introduce an overlapping parameter ${\epsilon }_{\mathcal{B}}\in [0,1]$, which extends the snapshot sets for an interval to cover some snapshots from both neighbouring intervals. In particular, ${ϵ}_{\mathcal{B}}=0$ corresponds to the non-overlapping situation as just explained, while ${ϵ}_{\mathcal{B}}=1$ implies a full inclusion of the snapshot sets for the previous and next interval. In practice, a value of the overlapping parameter will be chosen close to 0.

In the online phase, the volume of the local precipitate is computed, the corresponding subinterval is determined and the corresponding basis-set is then used for computing the reduced approximation of the microscopic field w₁.

3.2. The reduced model for w₁

The standard empirical interpolation system approximating the detailed system (15) for the auxiliary function $w_{1,H}^n$ reads

(18) ${\underset{\_}{\mathrm{\Phi }}}_w^{EI}{\underset{\_}{L}}_H{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{Y_M}{\underset{\_}{\mathrm{\Phi }}}_w{\underset{\_}{w}}_{1,N_w}^n={\underset{\_}{\mathrm{\Phi }}}_w^{EI}{\underset{\_}{R}}_H{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{Y_M},$(18)

with ${\underset{}{\underset{\_}{L}}}_H{\left({\underset{}{\underset{\_}{\varphi }}}_{1,H}^n\right)}_{Y_M}\in {\mathbb{R}}^{\left|Y_M\right|,H}$ and ${\underset{}{\underset{\_}{R}}}_H{\left({\underset{}{\underset{\_}{\varphi }}}_{1,H}^n\right)}_{Y_M}\in {\mathbb{R}}^{\left|Y_M\right|,1}$, where the index Y_M denotes that only the rows of the matrices belonging to the magic points’ indices are considered, where ${\underset{\_}{\Phi }}_w\in {ℝ}^{H,N_w}$ is the matrix with columns equal to the DOF-vectors of the current appropriate POD-basis Φ_w, and where ${\underset{}{\underset{\_}{\mathrm{\Phi }}}}_w^{\mathrm{E}\mathrm{I}}\in {\mathbb{R}}^{H,\left|Y_M\right|}$ is the matrix with columns equal to the DOF-vectors of the current appropriate collateral basis ${\mathrm{\Phi }}_w^{\mathrm{E}\mathrm{I}}$. This system is not suitable because a high-dimensional system must be solved in the online phase and, furthermore, it is unknown whether the system is of full rank and it is over-determined. Therefore, ${\underset{\_}{\mathrm{\Phi }}}_w^{\mathrm{E}\mathrm{I}}$ is eliminated from the equation by a suitable biorthogonal matrix multiplication, resulting in

(19) ${\underset{\_}{L}}_{Y_M}\left({\underset{\_}{\varphi }}_{1,H}^n\right){\underset{\_}{w}}_{1,N_w}^n={\underset{\_}{R}}_{Y_M}\left({\underset{\_}{\varphi }}_{1,H}^n\right),$(19)

with a matrix ${\underset{-}{L}}_{Y_M}\left({\underset{-}{\varphi }}_{1,H}^n\right)\in {\mathbb{R}}^{\left|Y_M\right|,N_w}$ and a vector ${\underset{-}{R}}_{Y_M}\left({\underset{-}{\varphi }}_{1,H}^n\right)\in {\mathbb{R}}^{\left|Y_M\right|,1}$. This system is suitable for an online phase because it is low-dimensional. It is solved for ${\underset{\_}{w}}_{1,N_w}^n$ by a Least-Squares procedure via the pseudoinverse, as it still will be over-determined in general when $|Y_M|>N_w$.

In correspondence to (15), the low-dimensional matrix and vector are defined as follows:

(20) $\begin{array}{rl}& {\underset{\_}{L}}_{Y_M}\left({\underset{\_}{\varphi }}_{1,H}^n\right)=\underset{\_}{L}\left({\underset{\_}{\varphi }}_{1,H}^n\right){\underset{\_}{\tau }}_{Y_M^{\star }}{\underset{\_}{\mathrm{\Phi }}}_w,\\ & {\left({\underset{\_}{R}}_{Y_M}\left({\underset{\_}{\varphi }}_{1,H}^n\right)\right)}_i=h_{\mathrm{\ell }}\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{r_{Y_M(i)}}-{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{{\mathrm{\ell }}_{Y_M(i)}}\right),\end{array}$(20)

with $\underset{}{\underset{\_}{L}}\left({\underset{}{\underset{\_}{\varphi }}}_{1,H}^n\right)\in {\mathbb{R}}^{\left|Y_M|,|Y_M^{\star }\right|}$ defined as

(21) ${\left(\underset{\_}{L}\left({\underset{\_}{\varphi }}_{1,H}^n\right)\right)}_{i,j}=\left\{\begin{array}{c}1\sum _{k\in N_{Y_M(i)}}\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{Y_M(i)}+{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_k+2\delta \right)\mathrm{f}\mathrm{o}\mathrm{r}j=i,\\ -\left({\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{Y_M(i)}+{\left({\underset{\_}{\varphi }}_{1,H}^n\right)}_{Y_M(j)}+2\delta \right)\mathrm{i}\mathrm{f}{Y}_M^{\star }(j)\in N_{Y_M(i)},\\ 0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$(21)

and with the restriction-matrix ${\underset{}{\underset{\_}{\tau }}}_{Y_M^{\star }}\in {\mathbb{R}}^{\left|Y_M^{\star }\right|,H}$ defined as

(22) ${\left({\underset{\_}{\tau }}_{Y_M^{\star }}\right)}_{i,j}=\left\{\begin{array}{c}11\mathrm{f}\mathrm{o}\mathrm{r}j=Y_M^{\star }(i),\\ 0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$(22)

The matrix ${\underset{}{\underset{\_}{\tau }}}_{Y_M^{\star }}{\underset{}{\underset{\_}{\mathrm{\Phi }}}}_w\in {\mathbb{R}}^{\left|Y_M^{\star }\right|,N_w}$ is pre-computed in the offline phase. What remains to be computed in the online phase’s time-step $n$ is

1. the sparse matrix $\underset{-}{L}\left({\underset{-}{\varphi }}_{1,H}^n\right)\in {\mathbb{R}}^{\left|Y_M\right|,\left|Y_M^{\star }\right|}$ and the product of the two matrices $\underset{-}{L}\left({\underset{-}{\varphi }}_{1,H}^n\right)\in {\mathbb{R}}^{\left|Y_M\right|,\left|Y_M^{\star }\right|}$ and ${\underset{-}{\tau }}_{Y_M^{\star }}{\underset{-}{\mathrm{\Phi }}}_w\in {\mathbb{R}}^{\left|Y_M^{\star }\right|,N_w}$ – in order to assemble the matrix ${\underset{\_}{L}}_{Y_M}\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ on the left-hand side of (19),

2. the vector ${\underset{-}{R}}_{Y_M}({\underset{-}{\varphi }}_{1,H}^n)\in {\mathbb{R}}^{\left|Y_M\right|,1}$ on the right-hand side of (19) and

3. finally, the least-squares solution ${\underset{-}{w}}_{1,N_w}^n\in {\mathbb{R}}^{N_w,1}$ of (19).

All of these computations for the online phase of the reduced model are completely independent of the high dimension H. The computational complexity only scales with $N_w,|Y_M|$ and $|Y_M^{\star }|$. Consequently, the reduced model for w₁ provides an ideal offline/online decomposition.

However, in order to approximate the microscopic parameter ${\overline{K\left({\varphi }_1^n+\delta ,w_1^n\right)}}^{\mathcal{P}}$ in ${\mathrm{\Omega }}_{h_g}$ in Step 6 of Algorithm 1 the high-dimensional solution $w_{1,H}^n$ must necessarily be approximated, which is done by the reconstruction operation $w_{1,H}^n:={\mathrm{\Phi }}_w{\underset{\_}{w}}_{1,N_w}^n$ of complexity linear in $H$. This complexity could also be reduced by involving an additional empirical interpolation step for this averaging equation. However, for our purposes, it is acceptable to have this moderate linear dependency on H in this coupling step.

4. Numerical results

This section presents numerical solutions of the two-scale problem for precipitation in porous media computed by the Algorithm 1 – with high-dimensional and reduced (i.e. low-dimensional) solutions of the auxiliary function w₁. Three test settings S₁, S₂ and S₃ in two spatial dimensions are considered, where S₂ and S₃ are variations of S₁. Initially, reduced models are developed from high-dimensional snapshots of the setting S₁ which therefore is the training setting. After demonstrating the significant efficiency gain of the reduced models in comparison to a high-dimensional discretization of S₁, it is shown that the reduced models’ solutions of the settings S₂ and S₃ also approximate the corresponding high-dimensional solutions.

4.1. The three settings S₁, S₂ and S₃

The varying parameters of the settings S₁, S₂ and S₃ are specified in Table 1: the final time T of the time-interval, the number of the macroscopic nodes H_g in x₁ and x₂ direction, the initial macroscopic concentration u₀, a function u_(t) that is relevant for the macroscopic boundary condition of u, and the precipitates’ initial radii r₀. The following paragraph presents further explanations for the varying parameters and specifies the remaining common parameters of the three settings.

Table 1. The varying parameters of the three settings S₁, S₂ and S₃, which are explained in Section 4.1 and Figure 2. The function u_(t) = a:b increases linearly from a to b with the time-steps in the course of a simulation. For i = 1,2 an initial precipitate’s radius $r_0(i)$ results in a precipitate’s initial portion of ${\overline{{\varphi }_3}}^{\mathcal{P}}(i)$ on the overall pore-space’s volume, analogously the water’s initial portion is ${\overline{{\varphi }_1}}^{\mathcal{P}}(i)$, and the oil’s initial portion is ${\overline{{\varphi }_2}}^{\mathcal{P}}(i)=0.07$ due to a radius ${\tilde{r}}_0(i)=30h_{\mathrm{\ell }}$.

Setting	T	H	$u_0$	$u_{\mathrm{\perp }}(t)$	$r_0$	${\overline{{\varphi }_1}}^{\mathcal{P}}$	${\overline{{\varphi }_3}}^{\mathcal{P}}$
S1	5	{50,25}	0.4	0.6:0.9	$\{30h_{\mathrm{\ell }},70h_{\mathrm{\ell }}\}$	$\{0.86,0.54\}$	$\{0.07,0.39\}$
S2	2.5	{25,25}	0.5	0.5:0.8	$\{70h_{\mathrm{\ell }},30h_{\mathrm{\ell }}\}$	$\{0.54,0.86\}$	$\{0.39,0.07\}$
S3	2.5	{25,25}	0.5	0.5:0.75	$\{68h_{\mathrm{\ell }},35h_{\mathrm{\ell }}\}$	$\{0.56,0.83\}$	$\{0.37,0.10\}$

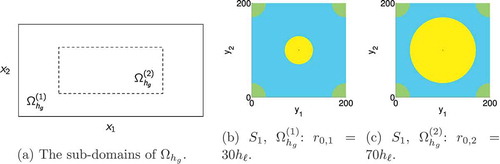
Figure 2. The initial phase configurations in the microscopic pore-space ${\mathcal{P}}_{h_{\mathrm{\ell }}}$ in the two subdomains ${\mathrm{\Omega }}_{h_g}^{(1)}$ and ${\mathrm{\Omega }}_{h_g}^{(2)}$ of the macroscopic domain ${\mathrm{\Omega }}_{h_g}$. The black points in the very centre of ${\mathcal{P}}_{h_{\mathrm{\ell }}}$ in (b) and (c) represent the small spherical grains ${\mathcal{G}}_{h_{\mathrm{\ell }}}$. Each grain is surrounded by a precipitate $P_3$ (yellow). For $i=1,2$, $r_{0,i}$ defines the initial radius of the precipitates in the subdomain ${\mathrm{\Omega }}_{h_g}^{(i)}$. Each precipitate is surrounded by water (blue) and a spherical oil phase $P_2$ (green) is located in the corners of ${\mathcal{P}}_{h_{\mathrm{\ell }}}$. The coloured subdomains P_i are characterized by ${\varphi }_i\ge \frac{1}{2}$ for $i\in I$. Full colour available online.

The time interval $\overline{J(T)}=[0,T]$ is discretized by $J_{{\mathrm{\Delta }}^{n}t}(T)$ using the time-dependent increments ${\mathrm{\Delta }}^{n}t=0.001\left(\delta +{min}_{x\in {\mathrm{\Omega }}_{h_g}}{\overline{{\varphi }_1\left(t_{n-1},x\right)}}^{{\mathcal{P}}_{h_{\mathrm{\ell }}}}\right)$, where $\delta =1e-6$, which results from stability considerations. This δ is also used as error tolerance of the CG-method solving the high-dimensional elliptic system (15) for the auxiliary function $w_1$. The microscopic pore-space ${\mathcal{P}}_{h_{\mathrm{\ell }}}$ is perforated by a small spherical grain ${\mathcal{G}}_{h_{\mathrm{\ell }}}$ located in the centre of $Y_{h_{\mathrm{\ell }}}$ and consisting of one node. Let H_ = 200 denote the number of the microscopic nodes in each space dimension. Then, the microscopic domain $Y_{h_{\mathrm{\ell }}}$ and the pore-space ${\mathcal{P}}_{h_{\mathrm{\ell }}}$ are given by

(23) $Y_{h_{\mathrm{\ell }}}=\left\{y_{h_{\mathrm{\ell }}}=(k_1{h}_{\mathrm{\ell }},k_2{h}_{\mathrm{\ell }})|k_1,k_2\in \{0,1,\dots ,H_{\mathrm{\ell }}\}\right\}\mathrm{a}\mathrm{n}\mathrm{d}{\mathcal{P}}_{h_{\mathrm{\ell }}}=Y_{h_{\mathrm{\ell }}}\mathrm{\setminus }{\mathcal{G}}_{h_{\mathrm{\ell }}}.$(23)

The edge-length $h_g=H_{\mathrm{\ell }}{h}_{\mathrm{\ell }}$ of $Y_{h_{\mathrm{\ell }}}$ defines the macroscopic space-increment $h_g$. The macroscopic domain ${\mathrm{\Omega }}_{h_g}$ is defined as

(24) ${\mathrm{\Omega }}_{h_g}=\left\{x_{h_g}=(k_1{h}_g,k_2{h}_g)|k_1\in \{0,1,\dots ,H_{g,1}-1\},k_2\in \{0,1,\dots ,H_{g,2}-1\}\right\}.$(24)

The initial concentration $u_0$ and the diffusion coefficient $D=2e+4$ are fixed. For simplifying the numerical boundary treatment, it is assumed that Ω is surrounded by a virtual domain ${\mathrm{\Omega }}_V$ of one cell row such that the mixture in Ω is surrounded by a virtual mixture in ${\mathrm{\Omega }}_V$. The diffusion tensor in a node $x_V\in {\mathrm{\Omega }}_V$ shall be the same as in the node $x_{\mathrm{\perp }}(x_V)\in \overline{\mathrm{\Omega }}$, which is the orthogonal projection of $x_V$ on $\overline{\mathrm{\Omega }}$ that is the point with shortest distance to x_y, ergo $x_{\mathrm{\perp }}(x_V)={\left(\begin{array}{cc}{x}_{\mathrm{\perp },1}(x_V)& x_{\mathrm{\perp },2}(x_V)\end{array}\right)}^{\mathrm{T}}:=arg{min}_{x\in \overline{\mathrm{\Omega }}}|x-x_V|$. Hence, for $(t,x_V)\in \overline{J(T)}\times {\mathrm{\Omega }}_V$,

(25) ${\overline{K({\varphi }_1+\delta ,w_1)(x_V)}}^{\mathcal{P}}:={\overline{K({\varphi }_1+\delta ,w_1)(x_{\mathrm{\perp }}(x_V))}}^{\mathcal{P}}.$(25)

By definition, the concentration in the surrounding virtual domain Ω_v yields on the one hand that dissolved particles flow into Ω across its upper and its right boundary and on the other hand that the remaining part of the boundary is not permeable. Precisely, for all $(t,x_V)\in \overline{J(T)}\times {\mathrm{\Omega }}_V$, the concentration is defined as

(26) $u(x_V,t)=\left\{\begin{array}{c}2u_{\mathrm{\perp }}(t)\mathrm{i}\mathrm{f}{x}_{\mathrm{\perp },1}(x_V)=H_{g_1}{h}_g\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{f}{x}_{\mathrm{\perp },2}(x_V)=H_{g_2}{h}_g,\\ u(x_{\mathrm{\perp }}(x_V))\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}.\end{array}\right.$(26)

The remaining microscopic physical parameters are prescribed as $\alpha =100$, $\xi =0.25$, and the concentration of particles in the precipitate P₃ satisfies $\rho =1$. The parameters of the rate-function f from (8) are fixed as $c_{u,0}=100$ and $c_{u,1}=0.5$, that is dissolved particles precipitate if their concentration exceeds the threshold of $0.5$ and contrarily, the precipitate dissolves if the concentration falls below 0.5. Due to the initial concentration $u_0=0.4$ in setting S₁, the precipitates dissolve in the beginning of the time-interval and grow again as soon as, due to the boundary condition, the concentration exceeds 0.5. On the contrary, the precipitates never dissolve in settings S₂ and S₃.

What remains to be specified is the initial configuration of the phase-fields and the parameters of the adaptive solution strategy. The grain is surrounded by a spherical precipitate P₃ as displayed in Figure 2. The fluid P₂ is located in the corners of the microscopic domain Y. Due to the periodic boundary conditions, P₂ is spherical with prescribed radius ${\tilde{r}}_0=30h_{\mathrm{\ell }}$. The macroscopic domain ${\mathrm{\Omega }}_{h_g}$ is subdivided into the two subdomains ${\mathrm{\Omega }}_{h_g}^{(1)}={\mathrm{\Omega }}_{h_g}\mathrm{\setminus }{\mathrm{\Omega }}_{h_g}^{(2)}$ and ${\mathrm{\Omega }}_{h_g}^{(2)}$, where

(27) ${\Omega }_{h_g}^{(2)}=\left\{x_{h_g}\in {\Omega }_{h_g}|x_{h_g}\in \left[\lfloor \frac{H_{g,1}}{4}\rfloor h_g,3\lfloor \frac{H_{g,1}}{4}\rfloor h_g\right]\times \left[\lfloor \frac{H_{g,2}}{4}\rfloor h_g,3\lfloor \frac{H_{g,2}}{4}\rfloor h_g\right]\right\},$(27)

with the floor-function $x\left|\to \right. \left[x\right]=max\left\{k\in \mathbb{Z}\left|k\le x\right. \right\}$. By definition, the initial perforated spherical precipitates in ${\mathrm{\Omega }}_{h_g}^{(1)}$ are of radius r_0,1 and in ${\mathrm{\Omega }}_{h_g}^{(2)}$ of r_0,2. Finally, for completeness, the parameters of the adaptive solution strategy are specified as follows, see [33]: $\lambda =0.1$, $c_{\mathrm{t}\mathrm{o}{\mathrm{l}}_c}=0.2$, $c_{\mathrm{t}\mathrm{o}{\mathrm{l}}_e}=0.01$, $\mathrm{R}\mathrm{U}=0$, $eC=1$, $M_A=2$, IT-CA, the copy method; the initial set of active nodes contains, respectively, one node from both subdomains ${\mathrm{\Omega }}_{h_g}^{(1)}$ and ${\mathrm{\Omega }}_{h_g}^{(2)}$, and the refining tolerance is defined as

(28) $to{l}_r(t):={10}^{-3/2}\underset{i=1,2}{max}\underset{x,\tilde{x}\in {\mathrm{\Omega }}_{h_g}^{(i)}}{max}\left\{d_E\left(u(\cdot ,x),u(\cdot ,\tilde{x});t,\lambda \right)\right\},$(28)

where $d_E\left(u(\cdot ,x),u(\cdot ,\tilde{x});t,\lambda \right)$ is a metric with a fading memory measuring the distance of the concentration evolution in two macroscopic grid points.

In each setting, the macroscopic concentration u does never and nowhere fall below u₀ (initial condition) or exceed $max(u_{\mathrm{\perp }})$ (boundary condition), that is $u_0\le u\le max(u_{\mathrm{\perp }})$ in the macroscopic time-space cylinder $Q=J_{{\mathrm{\Delta }}^{n}t}(T)\times {\mathrm{\Omega }}_{h_g}$. Therefore, due to similar initial microscopic conditions of the three settings, and since similar evolutions of the macroscopic concentration result in similar microscopic evolutions of the three phases Φ and hence of the auxiliary function w₁, it is expectable that the reduced models developed from high-dimensional snapshots of setting $S_1$ are capable of approximating the high-dimensional solutions of $S_2$ and $S_3$, despite the fact that the macroscopic domains and the time-interval of the three settings vary significantly.

The quality of an approximation $\{u_{\mathrm{a}\mathrm{p}\mathrm{p}},{\mathrm{\Phi }}_{\mathrm{a}\mathrm{p}\mathrm{p}},w_{1,\mathrm{a}\mathrm{p}\mathrm{p}}\}$ to a high-dimensional solution $\{u_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}},{\mathrm{\Phi }}_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}},w_{1,\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}\}$ is estimated by

(1) the $L_{\mathrm{\infty }}(Q)$-norm of $\mathrm{\Delta }u:=u_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-u_{\mathrm{a}\mathrm{p}\mathrm{p}}$,

(2) the $L_{\mathrm{\infty }}(Q)$-norm of $\mathrm{\Delta }{K}_{\mathrm{c}\mathrm{o}\mathrm{r}}:=K_{\mathrm{c}\mathrm{o}\mathrm{r},\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-K_{\mathrm{c}\mathrm{o}\mathrm{r},\mathrm{a}\mathrm{p}\mathrm{p}}$,

(3) the $L_{\mathrm{\infty }}(Q^{\star })$-norm of $\mathrm{\Delta }\mathrm{\Phi }:={\mathrm{\Phi }}_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-{\mathrm{\Phi }}_{\mathrm{a}\mathrm{p}\mathrm{p}}$,

(4) and the $L_{\mathrm{\infty }}(Q^{\star })$-norm of $\mathrm{\Delta }({\varphi }_1^{\delta }{w}_1):=({\varphi }_{1,\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}+\delta )w_{1,\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-({\varphi }_{1,\mathrm{a}\mathrm{p}\mathrm{p}}+\delta )w_{1,\mathrm{a}\mathrm{p}\mathrm{p}},$

where the following abbreviations are used $\parallel \cdot {\parallel }_Q=\parallel \cdot {\parallel }_{L_{\mathrm{\infty }}(Q)}$, $\parallel \cdot {\parallel }_{Q^{\star }}=\parallel \cdot {\parallel }_{L_{\mathrm{\infty }}(Q^{\star })}$. The term $K_{\mathrm{c}\mathrm{o}\mathrm{r}}:={\overline{({\varphi }_1+\delta ){\mathrm{\partial }}_{y_1}{w}_1}}^{\mathcal{P}}$ defines the microscopic correction of the macroscopic diffusion tensor $K$ of (5), $Q=J_{{\mathrm{\Delta }}^{n}t}(T)\times {\mathrm{\Omega }}_{h_g}$ represents the macroscopic time-space cylinder and $Q^{\star }=J_{{\mathrm{\Delta }}^{n}t}^{\star }(T)\times {\mathrm{\Omega }}_{h_g}^{\star }\times {\mathcal{P}}_{h_{\mathrm{\ell }}}$ represents a subset of the microscopic time-space cylinder. $J_{{\mathrm{\Delta }}^{n}t}^{\star }(T)$ contains every 100th step of time and ${\mathrm{\Omega }}_{h_g}^{\star }$ contains the macroscopic nodes highlighted in Figure 3. The subset $Q^{\star }$ instead of $Q$ is used to measure the microscopic quality because of the large number of the microscopic DOF and due to limitations of memory resources. However, since the microscopic solutions do not change significantly from one step of time to another one, and since the nodes of ${\mathrm{\Omega }}_{h_g}^{\star }$ are well distributed in the macroscopic grid ${\mathrm{\Omega }}_{h_g}$, an accurate approximation of the overall error can be expected.

Figure 3. The nodes in the subset ${\mathrm{\Omega }}_{h_g}^{\star }$ of the macroscopic grid ${\mathrm{\Omega }}_{h_g}$: nodes of ${\mathrm{\Omega }}_{h_g}^{\star }\cap {\mathrm{\Omega }}_{h_g}^{(1)}$ are indicated in red, and in blue those of ${\mathrm{\Omega }}_{h_g}^{\star }\cap {\mathrm{\Omega }}_{h_g}^{(2)}$. Full colour available online.

4.2. Setting $S_1$: the reproduction ability of the reduced models

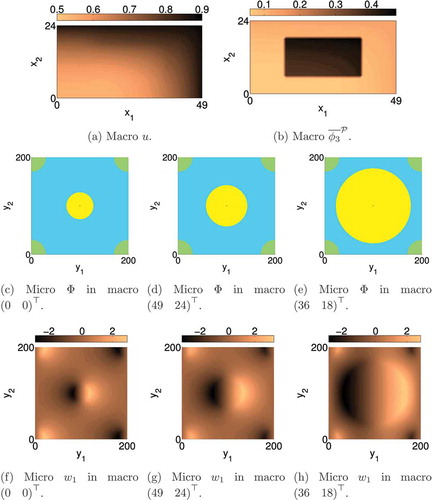
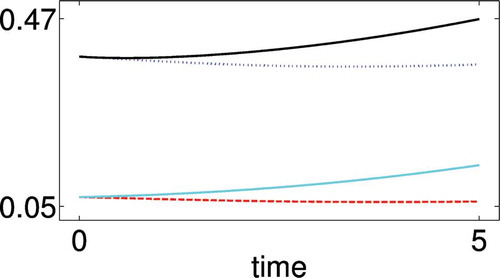
Setting $S_1$’s high-dimensional solution at the final time $T=5$ is depicted in Figure 4 and the evolution of the precipitates’ volume fractions in Figure 5. The setting’s initial concentration $u_0=0.4$ is below the threshold $c_{u,1}$ separating precipitation and dissolution. Therefore, in the beginning of the time-interval the precipitates dissolve and their portion on the pore-space’s volume decreases, and in contrast, the concentration of dissolved particles in the water increases inversely proportional. A further burst of growth of the concentration results from the boundary condition on the upper and the right boundary of $\mathrm{\Omega }$, that is from the prescribed increase of the concentration in the virtual mixture surrounding the mixture in $\mathrm{\Omega }$ on top and on the right. As soon as the concentration exceeds the threshold $c_{u,1}$, dissolved particles precipitate and the precipitates’ volume portions increase. The edges in the macroscopic field $u$ result from the strong diffusion in ${\mathrm{\Omega }}_{h_g}^{(1)}$ and the weak diffusion in ${\mathrm{\Omega }}_{h_g}^{(2)}$. The larger the volume fraction of the water the stronger the diffusion of the dissolved particles on the macroscopic length scale. The shape of a microscopic field $w_1$ is strongly influenced by the shape of the water-indicator ${\varphi }_1$. In areas characterized by small absolute first derivatives of ${\varphi }_1$, the auxiliary function $w_1$ is almost constant. On the contrary, areas characterized by large absolute first derivatives of ${\varphi }_1$ are also characterized by large absolute values of $w_1$, where the sign of $w_1$ and ${\mathrm{\partial }}_{y_1}{\varphi }_1$ is the same.

Figure 4. High-dimensional solution of setting $S_1$ at the end of the time-interval for $T=5$.

Figure 5. High-dimensional solution of the setting $S_1$: the evolution of the precipitates’ volume portion on the pore-space in the macroscopic nodes $(00{)}^{\mathrm{T}}$ (red dashed), $(126{)}^{\mathrm{T}}$ (blue dotted), $(3618{)}^{\mathrm{T}}$ (black) and $(4924{)}^{\mathrm{T}}$ (cyan). In ${\mathrm{\Omega }}_{h_g}^{(1)}$ the node $(00{)}^{\mathrm{T}}$ (and respectively, $(4924{)}^{\mathrm{T}}$) is host of the precipitate with the minimum (maximum) volume portion throughout the time-interval. The same relation holds in ${\mathrm{\Omega }}_{h_g}^{(2)}$ for $(126{)}^{\mathrm{T}}$ (minimum) and $(3618{)}^{\mathrm{T}}$ (maximum). Full colour available online.

Applying Algorithm 1 (high-dimensional), the solution has been computed by $27$ processors of type Intel(R) Xeon(R) CPU [email protected] GHz in roughly 57 h. On average, roughly $65$ and in maximum $81$ macroscopic nodes have been active that is the microscopic problems in these nodes have been solved. Consequently, in maximum every processor had to solve three high-dimensional microscopic problems per step in time and the number of steps in time was roughly $10,000$.

The reduced models are constructed from snapshots of the setting $S_1$’s high-dimensional solution. Every 16th step of time the solution ${\underset{\_}{w}}_{1,H}^n$ and the right-hand side ${\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ in every active macroscopic node are memorized. As explained earlier, the developed reduced models do not consist of only one but $100$ reduced basis sets (with the overlapping parameter ${\epsilon }_{\mathcal{B}}=0.1$), by the ultra-small tolerance ${\epsilon }_{\mathrm{E}\mathrm{I}}=1e-12$ it is guaranteed that the number $|Y_M|$ of the magic points $Y_M$ is not smaller than the size $N_w$ of the POD-basis ${\mathrm{\Phi }}_w$ in each reduced basis set, such that the systems are not under-determined, and finally, the second stopping condition $|Y_M|\le N_w+50$ assures that the number of the magic points is not much larger than the size of the corresponding POD basis.

Table 2 tabulates results of six reduced models ($R_2$, $R_4$, $R_6$, $R_8$, $R_{10}$ and $R_{12}$) with varying tolerance ${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}$, where ${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}=1e-k$ in $R_k$ ($k\in \{2,4,6,8,10,12\})$, and of a high-dimensional approximation ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$ with prescribed vanishing auxiliary function $w_1=0$. Since the high-dimensional solution’s macroscopic concentration $u$ varies in the course of the simulation between $0.4$ and $0.9$, the high-dimensional approximation ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$’s error of $u$ is (at least) roughly $4\mathrm{\%}$, which is not insignificant. It is roughly $50\mathrm{\%}$(!) for the phase fields $\mathrm{\Phi }$. And the total error of $w_1$ in the water region is $2.52$ which at the same time is the maximum of $\parallel {\varphi }_1^{\delta }{w}_1{\parallel }_{Q^{\star }}$ of the solution of the high-dimensional model that does not neglect the auxiliary function $w_1$. Therefore, approximating the high-dimensional solution by ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$ results on the one hand indeed in a vast speed-up of the computation time, but on the other hand, its accuracy is unacceptable. This result indicates the need and is a justification for using the two-scale model including $w_1$ instead of neglecting the quantity.

Table 2. Results for setting $S_1$: the column entitled by ‘speed-up’ presents the rough speed-up of the approximations’ computation time in comparison to the high-dimensional solution of $S_1$ in 57 h (as for the high-dimensional solution $27$ processors of type Intel(R) Xeon(R) CPU [email protected] GHz were used), and the columns entitled by $\parallel \mathrm{\Delta }u{\parallel }_Q$, $\parallel \mathrm{\Delta }{K}_{\mathrm{c}\mathrm{o}\mathrm{r}}{\parallel }_Q$, $\parallel \mathrm{\Delta }\mathrm{\Phi }{\parallel }_{Q^{\star }}$ and $\parallel \mathrm{\Delta }({\varphi }_1^{\delta }{w}_1){\parallel }_{Q^{\star }}$ present the approximations’ accuracy. The line entitled by ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$ presents the results of a high-dimensional approximation with prescribed $w_1=0$ resulting in $K_{\mathrm{c}\mathrm{o}\mathrm{r}}=0$ and ${\varphi }_1^{\delta }{w}_1=0$.

Model	${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}$	Speed-up	$\parallel \mathrm{\Delta }u{\parallel }_Q$	$\parallel \mathrm{\Delta }{K}_{\mathrm{c}\mathrm{o}\mathrm{r}}{\parallel }_Q$	$\parallel \mathrm{\Delta }\mathrm{\Phi }{\parallel }_{Q^{\star }}$	$\parallel \mathrm{\Delta }({\varphi }_1^{\delta }{w}_1){\parallel }_{Q^{\star }}$
${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$	–	$211$	$3.84e-02$	$1.71e-01$	$5.06e-01$	$2.52e+00$
$R_2$	$1e-02$	$201$	$3.52e-05$	$2.58e-03$	$3.17e-04$	$1.06e-01$
$R_4$	$1e-04$	$200$	$1.57e-05$	$2.58e-03$	$1.95e-04$	$1.06e-01$
$R_6$	$1e-06$	$194$	$5.83e-06$	$7.62e-04$	$1.83e-05$	$1.89e-02$
$R_8$	$1e-08$	$190$	$2.29e-06$	$4.37e-04$	$5.22e-06$	$6.52e-03$
$R_{10}$	$1e-10$	$174$	$4.43e-08$	$1.16e-05$	$3.47e-08$	$5.00e-04$
$R_{12}$	$1e-12$	$149$	$6.49e-09$	$1.45e-06$	$6.63e-09$	$7.39e-05$

Almost the same speed-up as the model ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$ is gained by the reduced model $R_2$ with ${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}=1e-02$. Every error indicator shows that $R_2$ is much more accurate than ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$. The weakest accuracy with a relative error of around $4\mathrm{\%}$ is observed by the indicator $\parallel \mathrm{\Delta }({\varphi }_1^{\delta }{w}_1){\parallel }_{Q^{\star }}$ measuring the error of the auxiliary function $w_1$ in the water region. However, the results presented in Table 3 show that for $R_2$ each basis set consists of solely one POD mode ($N_w=1.01$) for $w_1$. Considering this, the accuracy is surprisingly high.

Table 3. Results for setting $S_1$: the columns entitled by $N_w$, $|Y_M|$ and $|Y_M^{\ast }|$ present the average sizes of the $100$ basis sets of a reduced model, and the column entitled by ‘reduction time’ presents the time that one processor of type Intel(R) Xeon(R) CPU [email protected] GHz needs to construct the reduced models from the pre-computed snapshots of the high-dimensional solution of $S_1$. In particular, this time is not the full offline time, as it does not include the 57-h for the snapshots computation.

Model	${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}$	$N_w$	$|Y_M|$	$|Y_M^{\ast }|$	$\sim$Reduction time (h)
$R_2$	$1e-02$	$1.01$	$50.91$	$197.36$	$1.5$hours
$R_4$	$1e-04$	$1.46$	$51.36$	$198.52$	$1.5$hours
$R_6$	$1e-06$	$3.61$	$53.47$	$204.95$	$1.5$hours
$R_8$	$1e-08$	$8.38$	$58.17$	$219.31$	$1.7$hours
$R_{10}$	$1e-10$	$21.75$	$71.11$	$256.47$	$2.1$hours
$R_{12}$	$1e-12$	$51.04$	$95.81$	$318.64$	$3.5$hours

The reduction of the POD-tolerance ${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}$ yields an increase of the mean number of POD modes, magic points and their neighbours. The increase of the mean number of POD modes and the mean number of magic points is roughly the same, due to the second stop condition for the procedure determining the magic points: it stops once the EI-error falls below ${\epsilon }_{\mathrm{E}\mathrm{I}}$ or $|Y_M|=N_w+50$. The increase of the mean number of the magic points’ neighbours is a little weaker since some of them are magic points themselves. Summarizing, a decrease of the tolerance yields an increase of the basis sets’ sizes. The larger their sizes the more must be computed and the longer it takes. This is observed in both phases of the reduction procedure, that is in the part of the offline time for the reduced model construction from precomputed snapshots (Table 3, column ‘reduction time’) and the online phase (Table 2). A speed-up of $201$ corresponds to an online computation time of roughly 0.3 h, and for $149$, it is 0.4 h. In comparison to the high-dimensional solution, this is a significant speed up.

What is even more important to observe than the modest deceleration of the computation time, is the fact that for the POD-tolerance ${ϵ}_{POD}$ tending to $0$ the reduced converges to the high-dimensional solution. In fact, for the reduced model $R_{12}$ with ${ϵ}_{POD}=1e-12$, the errors of the macroscopic concentration $u$ and of the phase-fields $\mathrm{\Phi }$ vanish numerically. The error of the microscopic correction $K_{\mathrm{c}\mathrm{o}\mathrm{r}}$ of the macroscopic diffusion tensor $K$ and of the auxiliary function $w_1$ in the water region $\left({\varphi }_1^{\delta }{w}_1\right)$ are five orders of magnitude smaller than the error for ${\hspace{0.17em}}^{\star }{w}_1=0^{\star }$, which actually indicates a relative error of the same order.

As mentioned above, each two-scale model, that is both the high-dimensional and the reduced ones, are solved adaptively by Algorithm 1, where Step (5) is replaced by a reduced approximation (5ʹ) for the reduced two-scale model. As described in [29], the selection of the active macroscopic nodes is only determined with respect to the evolution of the concentration $u$ in the macroscopic nodes of ${\mathrm{\Omega }}_{h_g}$. Since, as tabulated in Table 2, the differences of the high-dimensional and the reduced models in the macroscopic concentration field are very small, the same nodes are active and consequently the same microscopic cell problems are solved in the high-dimensional and in the reduced simulations. Therefore, the adaptive strategy does not falsify the error estimates.

Note that indeed the problem of the moving phase boundary is a hard problem to reduce as it is “almost” a discontinuity. This is reflected in the requirement of many local bases for adequate approximation. Certainly, the overall sum of local basis sizes may be very well in the range or beyond the original full dimension. But still the model represents a valid reduced model, as each single microscopic model is approximated by a low-dimensional problem.

The presented results are a justification of the employed strategy constructing the reduced models, since they show the desired online speed-up and the reproduction ability: the reduced models can be solved much quicker than the high-dimensional model and their results are a good approximation to the high-dimensional ones.

Figure 6 shows for the macroscopic points $(00{)}^{\mathrm{T}}$, $(126{)}^{\mathrm{T}}$, $(3618{)}^{\mathrm{T}}$ and $(4924{)}^{\mathrm{T}}$ the evolution of the microscopic precipitate’s volume (a) and the corresponding evolution of the utilized basis set (b) in the reduced model $R_{10}$ with ${\epsilon }_{POD}=1e-10$. The larger a precipitate’s volume the higher the index of the basis set used to approximate $w_1$. Important to note is that, despite the fact that the volumes in $(4924{)}^{\mathrm{T}}$ and $(126{)}^{\mathrm{T}}$ are far from similar, the same basis set with index $73$ is used in the end of the time-interval. This is due to the fact that $(4924{)}^{\mathrm{T}}$ is host of the cell problem with the largest precipitate’s volume in the subdomain ${\mathrm{\Omega }}_{h_g}^{(1)}$ and $(126{)}^{\mathrm{T}}$ hosts the smallest in ${\mathrm{\Omega }}_{h_g}^{(2)}$. The smallest in ${\mathrm{\Omega }}_{h_g}^{(2)}$ is way larger than the largest in ${\mathrm{\Omega }}_{h_g}^{(1)}$, but the volume interval of basis set $73$ contains both of them, which can also be seen in Figure 7(a).

Figure 6. Results for the setting $S_1$ and the low-dimensional solution $R_{10}$ with ${ϵ}_{POD}=1e-10$: (a) presents the evolution of the precipitates’ volumes ${\overline{{\varphi }_3}}^{\mathcal{P}}$ and (b) the utilized basis sets in the course of the simulation in the macroscopic nodes $(00{)}^{\mathrm{T}}$ (red dashed), $(126{)}^{\mathrm{T}}$ (blue dotted), $(3618{)}^{\mathrm{T}}$ (black) and $(4924{)}^{\mathrm{T}}$ (cyan). Full colour available online.

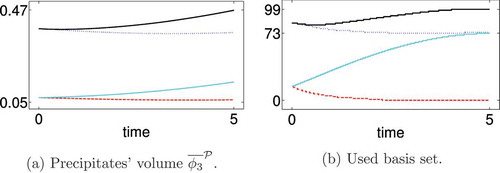
Figure 7. Results for the setting $S_1$ and the low-dimensional solution $R_{10}$: (a) depicts the minimum (black) and maximum (cyan) of the volume interval for the precipitates for the $100$ basis sets that are used in the online phase to determine the proper basis set in order to approximate the reduced solution of $w_1$, where the minimum is $-\mathrm{\infty }$ for basis set $0$ and the maximum is $\mathrm{\infty }$ for basis set $99$; (b) shows the number of POD modes (cyan) and the number of magic points (black) of the basis sets and (c) depicts exemplary for the basis set $73$ for the increasing number of modes the decay of ${log}_{10}$ of the eigenvalues of the correlation operator in the construction of the POD basis (cyan) and for the increasing number of magic points the error decay of the EI (black). Full colour available online.

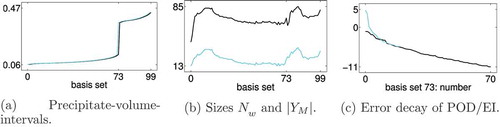
Figure 7(b) shows furthermore that the number of the magic nodes is roughly $50$ higher than the number of POD modes as expected due to the choice of the two stop conditions for the EIM. Also depicted in Figure 7(c) is the error decay of the POD and EIM. Both errors decay rapidly indicating a strong compressing ability of the high-dimensional model for $w_1$. 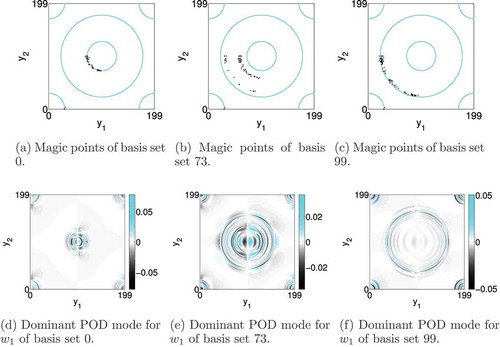For the basis sets $0$, $73$ and $99$, the distribution of the magic points and the dominant POD mode are illustrated in Figure 8. For each basis set, the magic points are located in the water domains’ diffuse boundaries of the used snapshots. Therefore, for an increasing index of the basis sets the magic points move from inner regions of the pore-space to outer ones, due to the increasing volume of the precipitates. There are two locations in basis set $73$, since it handles a large interval of precipitate volumes, and there is a gap between the smaller and the larger ones. The characteristic shapes of the dominant POD modes also travel from inner to outer regions of the pore-space.

Figure 8. Results for setting $S_1$ and the low-dimensional solution $R_{10}$, which consists of $100$ basis sets: (a), (b) and (c) illustrates the distribution of the magic points in the basis sets $0$, $73$ and $99$, where the inner circle marks the smallest and the outer one the largest subdomain supporting the precipitate in the snapshots, and the four quarters of a circle indicate the almost unchanged oil phase; (d), (e) and (f) depict the dominant POD mode for $w_1$ for the corresponding basis sets.

In summary, this subsection showed that the reduced models are capable of reproducing the training data and demonstrated their desired efficiency in comparison to the high-dimensional discretization.

4.3. The settings S₂ and S₃: the generalization ability of the reduced models

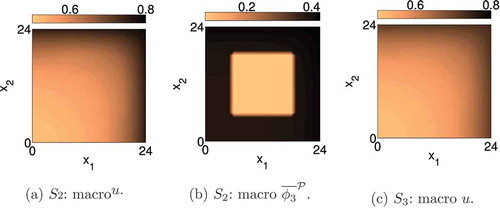
The reduced models of the previous subsection were constructed from snapshots of the setting $S_1$. In this subsection, the generalization ability of these models is tested for. Figure 9 illustrates high-dimensional results for the settings $S_2$ and $S_3$ that differ from $S_1$ in the parameters tabulated in Table 1. The time-interval of $S_2$ and $S_3$ is $(0,2.5]$ instead of $(0,5]$, the macroscopic domains are quadratic and also only half the size of $\mathrm{\Omega }$ in $S_1$ and the precipitates with larger volumes are located in the outer subdomain ${\mathrm{\Omega }}_{h_g}^{(1)}$ of $\mathrm{\Omega }$. The initial macroscopic concentration $u_0=0.5$ instead of $0.4$ in $S_1$, the macroscopic function $u_{\mathrm{\perp }}$ increases monotonically from $0.5$ to $0.8$ in $S_2$ and to $0.75$ in $S_3$ instead of from $0.6$ to $0.9$ in $S_1$, and the initial radii of the microscopic precipitates are $30h_{\mathrm{\ell }}$ for $S_1$, $70h_{\mathrm{\ell }}$ for $S_2$ and $68h_{\mathrm{\ell }}$ for $S_3$ in ${\mathrm{\Omega }}_{h_g}^{(1)}$ as well as $70h_{\mathrm{\ell }}$ for $S_1$, $30h_{\mathrm{\ell }}$ for $S_2$ and $35h_{\mathrm{\ell }}$ for $S_3$ in ${\mathrm{\Omega }}_{h_g}^{(1)}$. The shape of the time-interval and the macroscopic domain do not influence the microscopic evolution of $\mathrm{\Phi }$ and $w_1$, but on the other hand the evolution of the macroscopic concentration $u$ certainly does, as well as obviously do the initial radii $r_0$ of the precipitates.

Figure 9. High-dimensional solutions of the settings $S_2$ and $S_3$ in the end of the time-interval at $T=2.5$.

For $S_2$, Table 4 shows that the reduced solution converges to the high-dimensional solution for the POD tolerance ${\epsilon }_{\mathrm{P}\mathrm{O}\mathrm{D}}$ tending to zero. In contrast, in case of $S_3$ the reduced results do not converge to the high-dimensional solution (Table 5) but instead remain on an acceptable level of accuracy. Since the reduced models were developed from snapshots of $S_1$, these observations yield that the high-dimensional solution space for $w_1$ of $S_2$ must to be closer to $S_1$’s solution space than the one of $S_3$, where the initial radius $r_0$ of the precipitates seems to make the significant difference.

Table 4. Setting S₂: the approximations’ accuracy.

Model	${ϵ}_{POD}$	$\parallel \mathrm{\Delta }u{\parallel }_Q$	$\parallel \mathrm{\Delta }{K}_{11}{\parallel }_Q$	$\parallel \mathrm{\Delta }\mathrm{\Phi }{\parallel }_{Q^{\star }}$	$\parallel \mathrm{\Delta }({\varphi }_1^{\delta }{w}_1){\parallel }_{Q^{\star }}$
*w1 = 0*	–	3.12e − 02	1.71e − 01	1.61e − 01	2.34e + 00
R6	1e − 06	2.23e − 05	3.26e − 04	1.31e − 04	1.93e − 02
R8	1e − 08	7.22e − 06	1.00e − 04	3.40e − 05	1.15e − 02
R10	1e − 10	2.04e − 06	1.32e − 05	1.36e − 06	1.21e − 03
R12	1e − 12	2.21e − 06	1.24e − 05	3.06e − 06	4.13e − 04

Table 5. Setting S₃: the approximations’ accuracy.

Model	${ϵ}_{POD}$	$\parallel \mathrm{\Delta }u{\parallel }_Q$	$\parallel \mathrm{\Delta }{K}_{11}{\parallel }_Q$	$\parallel \mathrm{\Delta }\mathrm{\Phi }{\parallel }_{Q^{\star }}$	$\parallel \mathrm{\Delta }({\varphi }_1^{\delta }{w}_1){\parallel }_{Q^{\star }}$
*w1 = 0*	–	2.46e − 02	1.71e − 01	1.68e − 01	2.42e − 00
R6	1e − 06	2.89e − 05	9.65e − 04	1.23e − 04	2.10e − 02
R8	1e − 08	1.04e − 05	4.29e – 04	9.69e − 05	1.80e − 02
R10	1e − 10	2.36e − 05	1.16e − 03	1.45e − 04	2.63e − 02
R12	1e − 12	2.70e − 05	1.22e − 03	1.44e − 04	2.25e − 02

To sum up, the constructed efficient reduced two-scale models produce accurate results for a wide range of settings as long as the settings’ solution spaces for $w_1$ are close enough to the training setting’s one.

5. Conclusion and outlook

This article presented a model reduction procedure for a complex time-dependent two-scale model for precipitation in porous media. The model used advanced model reduction tools, in particular POD for state compression, EIM for the parameter dependency and multiple basis sets for treating the difficult problem of evolving phase boundaries. Numerical results comparing the overall high- and low-dimensional solutions of the two-scale model demonstrate that the reduced model is on the one hand capable of reproducing the high-dimensional training data and on the other hand can approximate solutions of generalized parameter settings – both extremely efficiently.

This study clearly put a methodological and numerical focus. Future work may address rigorous error analysis for the presented model reduction. The resulting reduced model avoids any operations of complexity $\mathcal{O}(H^p),p\ge 2$ (or even any operations of superlinear complexity) during its online phase. But still it requires operations linear in H, which may be prohibitive in more refined space discretizations or in three-space dimensions. Therefore, a further step could consist in providing a reduced scheme that approximates all fields on the microscale (i.e. spaces for all unknowns) and avoids any operation of complexity H. However, the acquired efficiency already fulfils our current requirements.

Acknowledgements

The authors would like to thank the Baden-Württemberg Stiftung gGmbH for funding this project. Also, we thank the German Research Foundation (DFG) for financial support within the Cluster of Excellence in Simulation Technology: [Grant Number EXC 310/1] and within the International Research Training Group ‘Nonlinearities and upscaling in porous media’ [NUPUS, IRTG 1398] at the University of Stuttgart.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Deutsche Forschungsgemeinschaft [EXC 310/1, NUPUS IRTG 1398].

Notes

1. We give a short motivation for this choice of snapshots for EI: Equation (15) is equivalent to the root finding problem $0=\underset{\_}{F}\left({\underset{\_}{w}}_{H,1}^n\right):={\underset{\_}{L}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right){\underset{\_}{w}}_{1,H}^n-{\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$. Standard training snapshots $\underset{\_}{F}\left({\underset{\_}{w}}_{1,H}^n\right)$ are always zero, hence carry no suitable information. Motivated by the Newton fixpoint iteration $D\underset{\_}{F}\left({\underset{\_}{w}}^{(k+1)}\right)=D\underset{\_}{F}\left({\underset{\_}{w}}^{(k)}\right)-\underset{\_}{F}\left({\underset{\_}{w}}^{(k)}\right)={\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ we realize that for good approximation of this system (and thus good approximation of the fixpoint, i.e. the root) it seems reasonable to collect snapshots ${\underset{\_}{R}}_H\left({\underset{\_}{\varphi }}_{1,H}^n\right)$ for constructing an EI space. In this sense, we are realizing an EI for the linearized root finding problem, which in our case is the original linear problem (15).