Port-Hamiltonian modelling of nonlocal longitudinal vibrations in a viscoelastic nanorod

ABSTRACT

Analysis of nonlocal axial vibration in a nanorod is a crucial subject in science and engineering because of its wide applications in nanoelectromechanical systems. The aim of this paper is to show how these vibrations can be modelled within the framework of port-Hamiltonian systems. It turns out that two port-Hamiltonian descriptions in physical variables are possible. The first one is in descriptor form, whereas the second one has a non-local Hamiltonian density. In addition, it is shown that under appropriate boundary conditions these models possess a unique solution which is non-increasing in the corresponding ‘energy’, i.e., the associated infinitesimal generator generates a contraction semigroup on a Hilbert space, whose norm is directly linked to the Hamiltonian.

KEYWORDS:

• Descriptor port-Hamiltonian
• viscoelastic
• nonlocal vibration

1. Introduction

The micro and nanoscale physical phenomena have different properties from macro-scale [1–3]. Carbon nanotubes (CNTs) are allotropes of carbon. They have diameters as small as 1 nm and lengths up to several centimetres. CNTs have amazing mechanical and electrical properties such as high electrical conductivity, chemical stability, high stiffness and axial strength [4]. These excellent properties have led to wide practical application of CNTs in NanoElectroMechanical Systems (NEMS). Due to novel properties and vast applications of CNTs in industry, there is a lot of research on static, buckling and vibration analysis of CNTs using the local and the nonlocal models [5]. For example, Li et al. investigate dynamics and stability of transverse vibrations of nonlocal nanorods [6]. Nonlocal longitudinal vibration of viscoelastic-coupled double-nanorod systems is studied by Karlicic et al. [7]. Heidari investigates controllability and stability analysis of a nanorod [2].

Many electrical, mechanical and electromechanical systems can be suitably modelled in port-Hamiltonian (pH) framework. This modelling exposes fruitful information on physical characteristics of the system such as the relation between the energy storage, dissipation, and interconnection structure [8,9].

This information is of great interest in analysing and simulating complex network system. Over the last years, many researchers worked on port-Hamiltonian systems, extending the theory and/or solving applied control problems, see, e.g., Jeltsema and Doria-Cerezo [10], Macchelli and Melchiorri [11], and Ramirez et al. [12]. For an overview and more details we refer the reader to [9].

To the best of our knowledge, in spite of a large amount of research on vibration of nanorod and pH systems, there is only little research on pH modelling of vibration of nanorods. In [13] we studied the problem, but there a pH formulation was found using non-physical variables. Therefore, pH modelling of vibration of an elastic nanorod using physical variables is considered in this paper. The rest of paper is organized as follows. In Section 2, a short review on nonlocal theory and governing equations are given. Section 3 presents the first port-Hamiltonian formulation. This is in descriptor form, the existence of its solutions is done in Section 4. In Section 5, a second pH formulation is given. The relation between the two formulations is discussed in Section 6. We end the paper with the conclusions and discussion on future works.

2. Model formulation

In this section, we recall from [7] the mathematical modelling of vibration in nanorods.

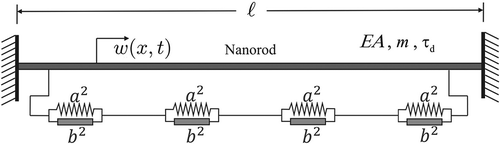
We consider a nanorod with length $\ell$ and cross-sectional area $A$ which is depicted in Figure 1.

Figure 1. Schematic of the present study.

In our case, the cross-sectional area is constant along the $x$-coordinate, but in general it could have arbitrary shapes along this $x$-coordinate. We assume that the material of a nanorod is elastic and homogeneous. Also, we consider the free longitudinal vibration of the nanorod in the $x$-direction. An infinitesimal element of length $dx$ is taken at a typical coordinate location $x$. Further, we take that the force $N$ is the resultant of an axial stress ${\sigma }_{xx}$ acting internally on $A$, where ${\sigma }_{xx}$ is assumed to be uniform over the cross-section. The stress resultant $N$ may vary along the length, and is also a function of time, i.e., $N=N(x,t)$. Using our assumptions, we find that

(1) $N(x,t)={\int }_A{\sigma }_{xx}(x,t)dA={\sigma }_{xx}(x,t)A.$(1)

In addition, an axially distributed force $\tilde{F}$ is assumed, having dimensions of force per unit length, which results from external sources, either internally or externally applied. The equilibrium of forces in the $x$-direction is

(2) $-N+\left(N+\frac{\mathrm{\partial }N}{\mathrm{\partial }x}dx\right)-\tilde{F}dx=\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}dm,$(2)

where $dm=\rho Adx$ is the mass of an infinitesimal element and $w$ is the displacement in the $x$-direction. Substituting $dm=\rho Adx$ and simplifying (2) gives

(3) $\frac{\mathrm{\partial }N}{\mathrm{\partial }x}=\tilde{F}+\rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}.$(3)

Next, we model the stress–strain relation. Based on nonlocal Eringen’s theory, it is assumed that the stress at a point is related to the strain (${ϵ}_{xx}$) at all other points in the domain. The nonlocal constitutive equation for an elastic medium is as follows

(4) ${\sigma }_{xx}-\mu \frac{{\mathrm{\partial }}^2{\sigma }_{xx}}{\mathrm{\partial }{x}^2}=E\left({ϵ}_{xx}+{\tau }_d\frac{\mathrm{\partial }}{\mathrm{\partial }t}{ϵ}_{xx}\right),$(4)

where $E$ is the elastic modulus, $\mu$ is the nonlocal parameter (length scales) [7] and ${\tau }_d$ is the viscous damping coefficient of the nanorod. We remark that we assume all parameters to be constant. We consider the following standard relation between the strain and $w$, see [14],

(5) ${ϵ}_{xx}=\frac{\mathrm{\partial }w}{\mathrm{\partial }x}.$(5)

By substituting Equations (1) and (5) into (4), the stress resultant for the nonlocal theory is obtained as

(6) $N-\mu \frac{{\mathrm{\partial }}^{2}N}{\mathrm{\partial }{x}^2}=EA\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }x}+{\tau }_d\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }x\mathrm{\partial }t}\right),$(6)

where the last term, $\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }x\mathrm{\partial }t}$, is the strain rate in the nanorod. Finally, we consider an external force

(7) $\tilde{F}=a^{2}w+b^2\frac{\mathrm{\partial }w}{\mathrm{\partial }t}$(7)

in which the parameter $a$ is the stiffness coefficient of the viscoelastic layer and the last term represents uniform damping, see [7]. In the following sections, we show that the Equations (3), (6), and (7) can be written in a port-Hamiltonian form. In some papers, one can find one (scalar) equation describing the motion. To write the Equations (3), (6) into one equation, we have first differentiate Equation (6) with respect to $x$ and next use (3), to get the following equation of motion

(8) $\tilde{F}+\rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}-\mu \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\left(\tilde{F}+\rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}\right)=EA\left(\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{x}^2}+{\tau }_d\frac{{\mathrm{\partial }}^{3}w}{\mathrm{\partial }{x}^2\mathrm{\partial }t}\right),$(8)

which is mentioned in [7].

3. Descriptor port-hamiltonian formulation

As many physical models, our model can also be written in a port-Hamiltonian form. However, it is not the standard formal as for instance studied in [8], but there will appear a non-invertible operator in front of the derivative of the state, i.e., it is of descriptor form. Hence, we show that for a suitable state $z$ our model can be written as

(9) $\mathbb{E}\frac{dz}{dt}=P_1\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left({\mathcal{H}}_{e}z\right)+P_0\left({\mathcal{H}}_{e}z\right)-R_0\left({\mathcal{H}}_{e}z\right)$(9)

with $\mathbb{E}$, ${\mathcal{H}}_e$, and $R_0$ bounded operators on the Hilbert space $L^2((0,\mathrm{\ell });{\mathbb{R}}^n)$, $P_1$ a symmetric $n\times n$ matrix and $P_0$ an anti-symmetric $n\times n$ matrix both consisting only of $-1$, $0$, and $1$‘s, and ${\mathbb{E}}^{\ast }{\mathcal{H}}_e$ and $R_0+R_0^{\ast }$ self-adjoint and non-negative.

The state $z$ that we choose is given by

(10) $z=\left(\begin{array}{c}w\\ \rho A\frac{\mathrm{\partial }w}{\mathrm{\partial }t}\\ \mu \rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}\\ \frac{\mathrm{\partial }w}{\mathrm{\partial }x}\\ N\end{array}\right).$(10)

Equation (3) implies

(11) ${\dot{z}}_2=\rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}=\frac{\mathrm{\partial }N}{\mathrm{\partial }x}-\tilde{F}=\frac{\mathrm{\partial }N}{\mathrm{\partial }x}-a^{2}w-b^2\frac{\mathrm{\partial }w}{\mathrm{\partial }t}$(11)

(12) $=\frac{\mathrm{\partial }}{\mathrm{\partial }x}{z}_5-a^2{z}_1-\frac{b^2}{\rho A}{z}_2,$(12)

where we used (10) and (7).

Using Equations (10) and (11), the time derivative of $z_3$ is written as

(13) ${\dot{z}}_3=\mu \rho A\frac{{\mathrm{\partial }}^{3}w}{\mathrm{\partial }{t}^2\mathrm{\partial }x}=\mu \frac{\mathrm{\partial }}{\mathrm{\partial }x}({\dot{z}}_2)=\mu \frac{{\mathrm{\partial }}^{2}N}{\mathrm{\partial }{x}^2}-a^2\mu \frac{\mathrm{\partial }w}{\mathrm{\partial }x}-b^2\mu \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x},$(13)

where we used the assumption that the parameters are constants. Using Equation (6), this becomes

${\dot{z}}_3=N-(EA+a^2\mu )\frac{\mathrm{\partial }w}{\mathrm{\partial }x}-(EA{\tau }_d+b^2\mu )\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}$

(14) $=z_5-(EA+a^2\mu )z_4-\frac{EA{\tau }_d+b^2\mu }{\mu \rho A}{z}_3.$(14)

Using (12) and the above equality, we find that

(15) $\mathbb{E}\dot{z}=\left(\begin{array}{ccccc}0& \frac{1}{\rho A}& 0& 0& 0\\ -a^2& -\frac{b^2}{\rho A}& 0& 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}\\ 0& 0& \frac{-EA{\tau }_d-\mu b^2}{\mu \rho A}& -EA-\mu a^2& 1\\ 0& 0& \frac{1}{\rho A\mu }& 0& 0\\ 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}\frac{1}{\rho A}& -\frac{1}{\rho A\mu }& 0& 0\end{array}\right)z,$(15)

where $\mathbb{E}=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$. We write the matrix of the right-hand side as a product,

$\left(\begin{array}{ccccc}0& 1& 0& 0& 0\\ -1& -b^2& 0& 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}\\ 0& 0& -EA{\tau }_d-\mu b^2& -1& 1\\ 0& 0& 1& 0& 0\\ 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}& -1& 0& 0\end{array}\right)\left(\begin{array}{ccccc}{a}^2& 0& 0& 0& 0\\ 0& \frac{1}{\rho A}& 0& 0& 0\\ 0& 0& \frac{1}{\mu \rho A}& 0& 0\\ 0& 0& 0& EA+\mu a^2& 0\\ 0& 0& 0& 0& 1\end{array}\right).$

From this we see that our model (15) can be written in the form (9) with

(16) $P_1=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\end{array}\right),{\mathcal{H}}_e=\left(\begin{array}{ccccc}{a}^2& 0& 0& 0& 0\\ 0& \frac{1}{\rho A}& 0& 0& 0\\ 0& 0& \frac{1}{\mu \rho A}& 0& 0\\ 0& 0& 0& EA+\mu a^2& 0\\ 0& 0& 0& 0& 1\end{array}\right),$(16)

(17) $P_0=\left(\begin{array}{ccccc}0& 1& 0& 0& 0\\ -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 1\\ 0& 0& 1& 0& 0\\ 0& 0& -1& 0& 0\end{array}\right),\mathrm{a}\mathrm{n}\mathrm{d}{R}_0=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& b^2& 0& 0& 0\\ 0& 0& EA{\tau }_d+\mu b^2& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right).$(17)

It is easy to see that these expressions satisfy the conditions stated below (9). If we assume that $z$ is a classical solution of (9), then $H_e(t):=\frac{1}{2}{\int }_0^{\mathrm{\ell }}z(t{)}^T{\mathbb{E}}^{\ast }{\mathcal{H}}_{e}z(t)dx$ satisfies the following equality

(18) ${\dot{H}}_e(t)=\frac{1}{2}{\left[{({\mathcal{H}}_{e}z)}^T{P}_1{\mathcal{H}}_{e}z\right]}_0^{\mathrm{\ell }}-\frac{1}{2}{\int }_0^{\mathrm{\ell }}({\mathcal{H}}_{e}z{)}^T(R_0+R_0^{\ast }){\mathcal{H}}_{e}zdx.$(18)

For our model this becomes

(19) $H_e(t)=\frac{1}{2}{\int }_0^{\mathrm{\ell }}{a}^{2}w(x,t{)}^2+\rho A\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(x,t{)}^2+\mu \rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}(x,t{)}^2+(EA+\mu a^2)\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(x,t{)}^{2}dx,$(19)

(20) ${\dot{H}}_e(t)=\frac{1}{2}{\left[\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(x,t)N(x,t)\right]}_0^{\mathrm{\ell }}-{\int }_0^{\mathrm{\ell }}{b}^2\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(x,t{)}^2+\left({\tau }_{d}EA+\mu b^2\right)\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}(x,t{)}^{2}dx.$(20)

We see that the first term represents the change of Hamiltonian ($H_e(t)$) through the boundary, whereas the integral term represents internal damping.

The above power balance is very standard for port-Hamiltonian systems, see [8,9,15]. However, there are a few differences between the form (9) with $\mathbb{E}$, $P_1$, $P_0$ and $R_0$ given in (16)–(17) and the form studied by Jacob and Zwart [8]. The most obvious one is that $\mathbb{E}$ is non-invertible. Moreover, our $P_1$ is not invertible. First results for port-Hamiltonian systems with a non-invertible term in front of the time derivative can be found in [16], but only for ordinary differential equations. In Villegas [17, Chapter 6] port-Hamiltonian systems with $P_1$ non-invertible is treated. We will not follows this, but take a more direct approach. So, in the next section, we show that the model (15) possesses a unique solution which is non-increasing in the Hamiltonian $H_e(t).$

4. Existence of solutions

We study the existence of solutions under the assumption that the rod is fixed, i.e.,

(21) $\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(0,t)=\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(\mathrm{\ell },t)=0.$(21)

As state space, we take all states with finite energy but satisfying the constraints

(22) $Z_t:=\left\{z_t=\left(\begin{array}{c}{z}_1\\ z_2\\ z_3\\ z_4\end{array}\right)\right.\in L^2((0,\mathrm{\ell });{\mathbb{R}}^4)|z_2\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{b}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{l}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{u}\mathrm{o}\mathrm{u}\mathrm{s}$(22)

$\left.\frac{d{z}_2}{dx}\in L_2(0,\mathrm{\ell }),z_2(0)=z_2(\mathrm{\ell })=0,\mathrm{a}\mathrm{n}\mathrm{d}\mu \frac{d{z}_2}{dx}=z_3\right\}.$

As inner product on $Z_t$, we take the inner product associated to the Hamiltonian (19), i.e.,

(23) $⟨z_t,{\tilde{z}}_t{⟩}_1:=⟨z_t,{\mathcal{H}}_{e,1}{\tilde{z}}_t⟩,$(23)

where the latter inner product is the standard inner product on $L^2((0,\mathrm{\ell });{\mathbb{R}}^4)$ and ${\mathcal{H}}_{e,1}$ is the upper four by four block of ${\mathcal{H}}_e$, i.e., ${\mathbb{E}}^{\ast }{\mathcal{H}}_e$

(24) ${\mathcal{H}}_{e,1}=\left(\begin{array}{cccc}{a}^2& 0& 0& 0\\ 0& \frac{1}{\rho A}& 0& 0\\ 0& 0& \frac{1}{\mu \rho A}& 0\\ 0& 0& 0& EA+\mu a^2\end{array}\right).$(24)

Lemma 4.1 $Z_t$ is a closed subspace of $L^2((0,\mathrm{\ell });{\mathbb{R}}^4)$.

(25)

Proof. Since all physical parameters in (24) are positive, the norm associated to the inner product (23) is equivalent to the standard norm on $L^2((0,\mathrm{\ell });{\mathbb{R}}^4)$. This directly implies that if the sequence $\{z_{t,n},n\in \mathbb{N}\}$ converges in $Z_t$, then the first, third, and fourth component converge in $L^2((0,\mathrm{\ell });\mathbb{R})$. Hence it remains to show that the second component converges as well. By (22) and the convergence of $z_{3,n}$, the third component of $z_{t,n}$, we have that

$z_{2,n}(x)={\int }_0^x\frac{1}{\mu }{z}_{3,n}(\tau )d\tau \to {\int }_0^x\frac{1}{\mu }{z}_3(\tau )d\tau ,x\in [0,\mathrm{\ell }].$

On the other hand, by assumption $z_{2,n}\to z_2$, and combining this with (25) gives that $z_2$ is absolutely continuous with $z_2(0)=0$ and $\mu \frac{d{z}_2}{dx}=z_3$. Using this equation once more together with the fact that $z_{2,n}(\mathrm{\ell })=0$ gives that $z_2$ satisfies the condition of $Z_t$, and thus $Z_t$ is closed subspace of $L^2((0,\mathrm{\ell });{\mathbb{R}}^4)$.               ⁏

From this lemma, we find that $Z_t$ with the inner product (23) is a Hilbert space. Next, we define the (candidate) infinitesimal generator associated with our p.d.e. We refer to Chapter 5 and 6 of [8] for more detail on semigroup theory.

For $z_t\in D(\mathbb{A})$ we define

(26) $\begin{array}{rl}& \mathbb{A}{z}_t=\left(\begin{array}{ccccc}0& \frac{1}{\rho A}& 0& 0& 0\\ -a^2& -\frac{b^2}{\rho A}& 0& 0& \frac{d}{dx}\\ 0& 0& \frac{-EA{\tau }_d-\mu b^2}{\mu \rho A}& -EA-\mu a^2& 1\\ 0& 0& \frac{1}{\rho A\mu }& 0& 0\end{array}\right)\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\\ & =:A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),\end{array}$(26)

where

(27) $D(\mathbb{A})=\{z_t\in Z_t|\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{s}{z}_5\in H^1(0,\mathrm{\ell })\mathrm{s}.\mathrm{t}.A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\in Z_t\}.$(27)

Since $\mathbb{A}$ is defined implicitly, it is important to know that it is well defined, i.e., the outcome $\mathbb{A}{z}_t$ is uniquely defined. This is shown next.

Lemma 4.2 The operator $\mathbb{A}$ with domain $D(\mathbb{A})$ is well-defined.

Proof. So what we have to show is that the $z_5$ needed to define $\mathbb{A}$ is unique. Let us assume that there are two, i.e., $z_5,{\tilde{z}}_5\in H^1(0,\mathrm{\ell })$ are such that $A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)$ and $A_1\left(\begin{array}{c}{z}_t\\ {\tilde{z}}_5\end{array}\right)\in Z_t.$ Since $A_1$ is linear, we see that this implies that $A_1\left(\begin{array}{c}0\\ z_5-{\tilde{z}}_5\end{array}\right)\in Z_t$. So if we can show that for an arbitrary $z_5\in H^1(0,\mathrm{\ell })$ the condition $A_1\left(\begin{array}{c}0\\ z_5\end{array}\right)\in Z_t$ implies that $z_5=0$, then we have shown that $\mathbb{A}$ is well-defined.

Assume that there exists $z_5\in H^1(0,\mathrm{\ell })$ is such that $A_1\left(\begin{array}{c}0\\ z_5\end{array}\right)\in Z_t$. Using (26) and (22) this implies that $\frac{d{z}_5}{dx}\in H^1(0,\mathrm{\ell })$, $\frac{d{z}_5}{dx}(0)=\frac{d{z}_5}{dx}(\mathrm{\ell })=0$ and $\mu \frac{d^2{z}_5}{d{x}^2}=z_5$. Since $\mu >0$ this implies that $z_5=0$.                          ⁏

Theorem 4.3. The operator $\mathbb{A}$ defined in (26) and (27) generates a contraction semigroup on $Z_t$.

(28)

Proof. Using Lumer-Phillips Theorem, see e.g. [18, Theorem II.3.15] or [8, Theorem 6.1.7], we have to show two properties of $\mathbb{A}$, namely for all $z_t\in D(\mathbb{A})$

$⟨\mathbb{A}{z}_t,z_t{⟩}_1+⟨z_t,\mathbb{A}{z}_t{⟩}_1\le 0,$

and for all $g\in Z_t$ there exists an $f\in D(\mathbb{A})$ such that

$(I-\mathbb{A})f=g.$

We begin by showing (28).

Using the definition of $\mathbb{A}$ and the inner product on $Z_t$

$⟨\mathbb{A}{z}_t,z_t{⟩}_1+⟨z_t,\mathbb{A}{z}_t{⟩}_1=⟨\mathbb{A}{z}_t,{\mathcal{H}}_{e,1}{z}_t⟩+⟨{\mathcal{H}}_{e,1}{z}_t,\mathbb{A}{z}_t⟩$

$=⟨A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),{\mathcal{H}}_{e,1}{z}_t⟩+⟨{\mathcal{H}}_{e,1}{z}_t,A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)⟩$

$=⟨\left(\begin{array}{c}{A}_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\\ 0\end{array}\right),{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)⟩+⟨{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),\left(\begin{array}{c}{A}_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\\ 0\end{array}\right)⟩,$

where the last equality is in $L^2(0,\mathrm{\ell });{\mathbb{R}}^5)$. Since $A_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\in Z^t$, we have that

$\left(\begin{array}{c}{A}_1\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)\\ 0\end{array}\right)=\left(\begin{array}{ccccc}0& \frac{1}{\rho A}& 0& 0& 0\\ -a^2& -\frac{b^2}{\rho A}& 0& 0& \frac{d}{dx}\\ 0& 0& \frac{-EA{\tau }_d-\mu b^2}{\mu \rho A}& -EA-\mu a^2& 1\\ 0& 0& \frac{1}{\rho A\mu }& 0& 0\\ 0& \frac{d}{dx}\frac{1}{\rho A}& -\frac{1}{\rho A\mu }& 0& 0\end{array}\right)\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)$

$=\left(\begin{array}{ccccc}0& 1& 0& 0& 0\\ -1& -b^2& 0& 0& \frac{d}{dx}\\ 0& 0& -EA{\tau }_d-\mu b^2& -1& 1\\ 0& 0& 1& 0& 0\\ 0& \frac{d}{dx}& -1& 0& 0\end{array}\right){\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)$

$=\left[P_1\frac{d}{dx}+P_0-R_0\right]{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),$

see (16) and (17). Since $P_0+P_0^T=0$ and $R_0+R_0^{\ast }\ge 0$, we find that

$⟨\mathbb{A}{z}_t,z_t{⟩}_1+⟨z_t,\mathbb{A}{z}_t{⟩}_1$

$\le ⟨P_1\frac{d}{dx}{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)⟩+⟨{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right),P_1\frac{d}{dx}{\mathcal{H}}_e\left(\begin{array}{c}{z}_t\\ z_5\end{array}\right)⟩$

$={\left[\frac{1}{\rho A}{z}_2{z}_5\right]}_0^{\mathrm{\ell }}=0,$

where we have used the boundary conditions of $z_2$. So we see that (28) holds. Next, we show (29).

Let $g=\left(\begin{array}{c}{g}_1\\ g_2\\ g_3\\ g_4\end{array}\right)\in Z_t$ be given. Then, we have to find $f^t=\left(\begin{array}{c}{f}_1\\ f_2\\ f_3\\ f_4\end{array}\right)\in D(\mathbb{A})$ and $f_5\in H^1(0,\mathrm{\ell })$ such that

(30) $f_1-\frac{1}{\rho A}{f}_2=g_1,$(30)

(31) $a^2{f}_1+s_2{f}_2-\frac{d{f}_5}{dx}=g_2,$(31)

(32) $s_3{f}_3+(EA+\mu a^2)f_4-f_5=g_3,$(32)

(33) $-\frac{1}{\mu \rho A}{f}_3+f_4=g_4,,$(33)

where $s_2=1+b^2$ and $s_3=1+\frac{EA{\tau }_d+\mu b^2}{\mu \rho A}$. Furthermore, we have the conditions, see (22)

(34) $\mu \frac{d{f}_2}{dx}=f_3,f_2(0)=0=f_2(\mathrm{\ell }).$(34)

By considering Equation (32) and Equation (33), we have

(35) $\left(\begin{array}{cc}{s}_3& EA+\mu a^2\\ -\frac{1}{\mu \rho A}& 1\end{array}\right)\left(\begin{array}{c}{f}_3\\ f_4\end{array}\right)=\left(\begin{array}{c}{f}_5+g_3\\ g_4\end{array}\right).$(35)

Since $s_3+\frac{EA+\mu a^2}{\mu \rho A}\ne 0$, we find

(36) $f_3=\frac{\mu \rho A}{\mu \rho A{s}_3+EA+\mu a^2}\left[f_5+g_3-(EA+\mu a^2)g_4\right]$(36)

(37) $f_4=\frac{1}{\mu \rho A{s}_3+EA+\mu a^2}\left[f_5+g_3+\mu \rho A{s}_3{g}_4\right].$(37)

From (30) and (31) it follows that

$(\frac{a^2}{\rho A}+s_2)f_2-\frac{d{f}_5}{dx}=-a^2{g}_1+g_2.$

Combining this with (34) and using (36) we find the following differential equation in $f_2$ and $f_5$

(38) $\frac{d}{dx}\left(\begin{array}{c}{f}_2\\ f_5\end{array}\right)=\left(\begin{array}{cc}0& a_{12}\\ a_{21}& 0\end{array}\right)\left(\begin{array}{c}{f}_2\\ f_5\end{array}\right)+\left(\begin{array}{c}{\tilde{g}}_1\\ {\tilde{g}}_2\end{array}\right),$(38)

where $a_{12},a_{21}$ are positive constants, and ${\tilde{g}}_1,{\tilde{g}}_2$ are a linear combination of $g_1,\cdots ,g_5$. The solution of (38) is given by

(39) $\left(\begin{array}{c}{f}_2(x)\\ f_5(x)\end{array}\right)=\left(\begin{array}{cc}cosh(\lambda x)& \sqrt{\frac{a_{12}}{a_{21}}}sinh(\lambda x)\\ \sqrt{\frac{a_{21}}{a_{12}}}sinh(\lambda x)& cosh(\lambda x)\end{array}\right)\left(\begin{array}{c}0\\ f_5(0)\end{array}\right)+{\int }_0^x\left(\begin{array}{cc}cosh(\lambda (x-\tau ))& \sqrt{\frac{a_{12}}{a_{21}}}sinh(\lambda (x-\tau ))\\ \sqrt{\frac{a_{21}}{a_{12}}}sinh(\lambda (x-\tau ))& cosh(\lambda (x-\tau ))\end{array}\right)\left(\begin{array}{c}{\tilde{g}}_1(\tau )\\ {\tilde{g}}_2(\tau )\end{array}\right)d\tau ,$(39)

where $\lambda =\sqrt{a_{12}{a}_{21}}$ and we used the first boundary condition of (34). To satisfy the second boundary condition, we have to solve

$0=f_2(\mathrm{\ell })=\sqrt{\frac{a_{12}}{a_{21}}}sinh(\lambda \mathrm{\ell })f_5(0)+$

${\int }_0^{\mathrm{\ell }}\left[cosh(\lambda (\mathrm{\ell }-\tau )){\tilde{g}}_1(\tau )+\sqrt{\frac{a_{12}}{a_{21}}}sinh(\lambda (\mathrm{\ell }-\tau )){\tilde{g}}_2(\tau )\right]d\tau .$

Since $\lambda$ and $\mathrm{\ell }$ are positive constants, this is solvable and so the $f_2$ and $f_5$ are given by (39) with

$f_5(0)=\frac{-1}{sinh(\lambda \mathrm{\ell })}{\int }_0^{\mathrm{\ell }}\left[\sqrt{\frac{a_{21}}{a_{12}}}cosh(\lambda (\mathrm{\ell }-\tau )){\tilde{g}}_1(\tau )+sinh(\lambda (\mathrm{\ell }-\tau )){\tilde{g}}_2(\tau )\right]d\tau .$

Note that these functions lie in $H^1(0,\mathrm{\ell })$ and $f_2$ satisfies the boundary conditions of (34). Given these solutions, the functions $f_3$ and $f_4$ follows from (36) and (37), respectively. Equation (30) gives $f_1$. Summarizing we see that $I-\mathbb{A}$ is surjective, and so $\mathbb{A}$ generates a contraction semigroup on $Z_t$.                      ⁏

5. Second hamiltonian formulation

In this section we show that there is a second port-Hamiltonian formulation for the nanorod. Therefore, we use the boundary conditions already in the formulation. So we assume that $w$ is zero at $x=0$ and $x=\mathrm{\ell }$ for all time, see also (21). Using Equation (3) and (7) this implies that

(40) $\frac{\mathrm{\partial }N}{\mathrm{\partial }x}(0,t)=0,\frac{\mathrm{\partial }N}{\mathrm{\partial }x}(\mathrm{\ell },t)=0,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}t\ge 0.$(40)

We use these boundary conditions to solve (see (6))

$N-\mu \frac{{\mathrm{\partial }}^{2}N}{\mathrm{\partial }{x}^2}=f,$

for $f\in L^2(0,\mathrm{\ell })$. We find, see e.g. [19, Section 7.5]

(41) $N(x)={\int }_0^{\mathrm{\ell }}g(x,\zeta )f(\zeta )d\zeta$(41)

with (Green’s function)

(42) $g(x,\zeta )=\frac{\gamma }{sinh(\gamma \mathrm{\ell })}\left(\begin{array}{cc}cosh(\gamma x)cosh(\gamma (\zeta -\mathrm{\ell }))& x<\zeta \\ cosh(\gamma (x-\mathrm{\ell }))cosh(\gamma \zeta )& x>\zeta \end{array}\right.,$(42)

where ${\gamma }^2={\mu }^{-1}$.

Choose now the state

(43) $z=\left(\begin{array}{c}w\\ \rho A\frac{\mathrm{\partial }w}{\mathrm{\partial }t}\\ \frac{\mathrm{\partial }w}{\mathrm{\partial }x}\end{array}\right).$(43)

Using (3), (6) and (7) we find (for ${\tau }_d=0$)

$\dot{z}=\left(\begin{array}{c}\frac{1}{\rho A}{z}_2\\ a^2{z}_1-\frac{b^2}{\rho A}{z}_2+\frac{\mathrm{\partial }N}{\mathrm{\partial }x}\\ \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }x\mathrm{\partial }t}\end{array}\right)=\left(\begin{array}{c}\frac{1}{\rho A}{z}_2\\ a^2{z}_1-\frac{b^2}{\rho A}{z}_2+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[G(EA\frac{\mathrm{\partial }w}{\mathrm{\partial }x})\right]\\ \frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\frac{1}{\rho A}{z}_2\right]\end{array}\right),$

where $G$ is the mapping defined by (41) and (42), i.e.

(44) $\left(G(f)\right)(x)={\int }_0^{\mathrm{\ell }}g(x,\zeta )f(\zeta )d\zeta .$(44)

Hence our model can be written as

(45) $\dot{z}(t)=\left(\begin{array}{ccc}0& 1& 0\\ -1& -b^2& \frac{\mathrm{\partial }}{\mathrm{\partial }x}\\ 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}& 0\end{array}\right)\left[\left(\begin{array}{ccc}{a}^2& 0& 0\\ 0& \frac{1}{\rho A}& 0\\ 0& 0& EA\cdot G\end{array}\right)z(t)\right].$(45)

This we can write in the port-Hamiltonian format (9) with $\mathbb{E}$ the identity,

(46) $P_1=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),P_0=\left(\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 0\end{array}\right),R_0=\left(\begin{array}{ccc}0& 0& 0\\ 0& b^2& 0\\ 0& 0& 0\end{array}\right),$(46)

and

(47) $\mathcal{H}z=\left(\begin{array}{ccc}{a}^2& 0& 0\\ 0& \frac{1}{\rho A}& 0\\ 0& 0& EA\cdot G\end{array}\right)z.$(47)

Note that since $g(x,\zeta )=g(\zeta ,x)>0$ for all $x,\zeta \in [0,\mathrm{\ell }]$, $G$ is a self-adjoint bounded, strictly positive operator. Using this and the fact that the physical parameters are positive, we find that $\mathcal{H}$ is a coercive operator on $L^2((0,\mathrm{\ell });{\mathbb{R}}^3)$. As in [8, Chapter 7] we choose as our state space $Z=L^2((0,\mathrm{\ell });{\mathbb{R}}^3)$ with inner product

(48) $⟨f,g{⟩}_Z=\frac{1}{2}⟨f,\mathcal{H}(g)⟩,$(48)

where the latter is the standard inner product on $L^2((0,\mathrm{\ell });{\mathbb{R}}^3)$.

For $z\in D(\bar{A})$ we define

(49) $\bar{A}z=\left(\begin{array}{ccc}0& 1& 0\\ -1& -b^2& \frac{\mathrm{\partial }}{\mathrm{\partial }x}\\ 0& \frac{\mathrm{\partial }}{\mathrm{\partial }x}& 0\end{array}\right)\left[\left(\begin{array}{ccc}{a}^2& 0& 0\\ 0& \frac{1}{\rho A}& 0\\ 0& 0& EA\cdot G\end{array}\right)z\right]$(49)

with domain

(50) $D(\bar{A})=\{z\in Z|z_2\in H^1(0,\mathrm{\ell }),z_2(0)=z_2(\mathrm{\ell })=0,G(z_3)\in H^1(0,\mathrm{\ell })\}.$(50)

From Lemma 7.2.3 and Theorem 7.2.4 of [8] the following theorem follows.

Theorem 5.1. For $b\in \mathbb{R}$, the operator $\bar{A}$ with domain $D(\bar{A})$ as defined in (49) and (50) generates a contraction semigroup on the state space $Z$. If $b=0$, then $\bar{A}$ generates a unitary group on $Z$.

Note that we have written the domain of $\bar{A}$ in the standard form, verify e.g. [8, Equation (7.22)] or [15]. However, since $G$ maps $L^2$-functions onto $H^2$-functions, the last condition in (50) is always satisfied, and thus could be removed.

In the formulation (45), and thus Theorem 5.1, we have assumed that ${\tau }_d=0$. Using (6) we see that for ${\tau }_d\ne 0$ our model can be written as

(51) $\begin{array}{rl}& \dot{z}(t)=[P_1\frac{\mathrm{\partial }}{\mathrm{\partial }x}+P_0-R_0]\left(\mathcal{H}z(t)\right)-\left(\begin{array}{c}0\\ \frac{\mathrm{\partial }}{\mathrm{\partial }x}\\ 0\end{array}\right)G\left(\frac{{\tau }_d}{\rho A}\left(\begin{array}{ccc}0& -\frac{\mathrm{\partial }}{\mathrm{\partial }x}& 0\end{array}\right)\left(\mathcal{H}z(t)\right)\right)\\ & =:[P_1\frac{\mathrm{\partial }}{\mathrm{\partial }x}+P_0-R_0]\left(\mathcal{H}z(t)\right)-{\mathcal{G}}_{R}S{\mathcal{G}}_R^{\ast }\left(\mathcal{H}z(t)\right).\end{array}$(51)

Since ${\tau }_d,\rho ,A$ are positive constants, and $G$ is a positive operator, the operator $S$ is positive. Using Theorem 5.1 and Theorem 2.2 of [20], we see that under the same boundary conditions as formulated in (50) this model generates a contraction semigroup on the state space $Z$.

6. Relation between the two formulations

In Sections 3 and 5 we have shown that the model of the nanorod as presented in Section 2 allows for two port-Hamiltonian formulations. These formulations are both leading to a well-posed differential equation, and so it is only natural to ask for the relation between these two. Let us begin by stating that it is not exceptional to have more than one Hamiltonian, see, e.g. [21]. In the study of partial differential equations, the knowledge of conserved quantities, e.g. Hamiltonian is very useful for gaining insight in the system. Thus, knowing more than one Hamiltonian is seen as a positive fact.

For the formulation found in Section 3 the Hamiltonian is given by

$H_e(z_t)=\frac{1}{2}{\int }_0^{\mathrm{\ell }}{a}^{2}w(x{)}^2+\rho A\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(x{)}^2+\mu \rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}(x{)}^2+(EA+\mu a^2)\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(x{)}^{2}dx,$

whereas the Hamiltonian associated to the formulation in Section 5 equals

$H_2(z)=\frac{1}{2}{\int }_0^{\mathrm{\ell }}{a}^{2}w(x{)}^2+\rho A\frac{\mathrm{\partial }w}{\mathrm{\partial }t}(x{)}^{2}dx+\frac{1}{2}EA{\int }_0^{\mathrm{\ell }}{\int }_0^{\mathrm{\ell }}\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(x)g(x,\zeta )\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(\zeta )d\zeta dx.$

Although they have the same unit [J] and are equal in the first two terms, for $\mu \ne 0$ they differ in the last term(s). Best to see this is by noticing that there is an $a^2$ in last term of $H_e$, whereas this missing in $H_2$. Since the last term in $H_2$ comes from (6), in which the $a^2$ is absent, we conclude that $H_e$ and $H_2$ measure different quantities for $\mu \ne 0$.

When there is no damping, then both Hamiltonians are constant. Thus, along solutions, we will have that

${\int }_0^{\mathrm{\ell }}\mu \rho A\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }t\mathrm{\partial }x}(x,t{)}^2+(EA+\mu a^2)\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(x,t{)}^{2}dx-EA{\int }_0^{\mathrm{\ell }}{\int }_0^{\mathrm{\ell }}\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(x,t)g(x,\zeta )\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(\zeta ,t)d\zeta dx=c,$

where $c$ is a constant, only depending on the initial condition. As said above this relation does not follow from an equality like (6), but is a property of the complete model.

In [8] there is no example with two Hamiltonians, and so it surprising that the model of the nanorod has two. Looking at the derivation of the model once more, we notice that the first model cannot be derived when the parameters are spatially depending, see the third equality in (13). The second model has a natural extension to spatially depending coefficients by replacing the left-hand side of (6) by

$N-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\mu \frac{\mathrm{\partial }N}{\mathrm{\partial }x}\right),$

where $\mu =\mu (x)>0$. Since this is a Sturm-Liouville operator, existence, uniqueness, and other properties of the differential equation

$N(x)-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\mu (x)\frac{\mathrm{\partial }N}{\mathrm{\partial }x}\right)(x)=f(x)$

are well known, see, e.g. [19, Section 7.5]. For instance, the solution map will again be a strictly positive operator, and so Equation (45) still hold (with another $G$). So we feel that the bi-Hamiltonian property only holds in the constant parameter case.

7. Conclusions and further work

Concluding we see that we have derived two different port-Hamiltonian formulations corresponding to the same differential equation. Since the original model was build under the assumption of constant parameters, we have kept this assumption throughout this paper. For many port-Hamiltonian systems the step from constant to spatial varying (physical) parameters is easy, see the examples in, e.g. [8]. However, for the model of the nanorod this is less obvious. For the model derived in Section 5 this is possible if one replaces the left-hand side of (6) by, see also the discussion in the previous section,

$N-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\mu \frac{\mathrm{\partial }N}{\mathrm{\partial }x}\right).$

For the model derived Section 3 this is much less clear. However, this should only be done, when the correct nanorod model for spatial dependent coefficients has been derived.

If damping is present, i.e., $b>0$, then the time-derivative of both Hamiltonians is non-positive. We believe that in this case both semigroups are strongly stable, i.e., the solutions converge to zero as time goes to infinity. A possible proof could be to apply [18, Corollary V.2.22]. To check if the system is exponentially stable, the eigenvalues need to be calculated/estimated.

We have only studied the nanorod under one set of boundary conditions. For standard port-Hamiltonian systems, all boundary conditions could somehow be treated in the same theorem. Here the situation is different. For instance, when the boundary conditions $w(0,t)=w(\mathrm{\ell },t)=0$ are replaced by no force at the boundary, i.e., $N(0,t)=N(\mathrm{\ell },t)=0$, then for the formulation in Section 4 the boundary conditions must be removed from the state space, see (22), and enter the domain (27) as boundary conditions on $z_5$. In the formulation of Section 5, the expression of $g$ changes, since the differential equation for $N$ has to be solved under the condition $N(0)=N(\mathrm{\ell })=0$.

Another topic which we like to study in the future is the port-Hamiltonian formulation when one of the boundary conditions is non-zero, i.e., for instance when there is a control at the boundary. Since we had to put the boundary conditions into the state space (Section 3) or use it to reformulate our problem (Section 5), this problem is non-trivial. It is by no means clear that it will lead to a boundary control system, like standard port-Hamiltonian p.d.e.’s do.

Nomenclature

Table

Symbol	Meaning	Unit
$A$	cross sectional area	$m^2$
$a^2$	stiffness coefficient of the light viscoelastic layer	$gm{s}^{-2}$
$b^2$	damping coefficient of the light viscoelastic layer	$g{s}^{-1}$
$E$	elastic modulus	$g{m}^{-1}{s}^{-2}$
${ϵ}_{xx}$	strain	-
$\tilde{F}$	axially distributed force	$g{s}^{-2}$
$\mu$	nonlocal parameter	$m^2$
$N$	resultant force of axial stress	$gm{s}^{-2}$
$\rho$	mass density	$g{m}^{-3}$
${\sigma }_{xx}$	axial stress	$g{m}^{-1}{s}^{-2}$
${\tau }_d$	viscous damping	$s$
$w$	displacement of nanorod in $x$ direction	$m$

Acknowledgments

We want to express our thanks to Serge Nicaise and Marius Tucsnak for their useful comments which really helped our research on this problem further.

Disclosure statement

No potential conflict of interest was reported by the authors.