Two strains model of infectious diseases for mathematical analysis and simulations

ABSTRACT

In this study, we study a two-strain nonlinear model for the transmission of COVID-19 with a vaccinated class. Here, it is remarkable that the model we consider contains two kinds of viruses known as Omicron and Delta variants denoted by $\mathit{A}$ and $\mathit{B}$, respectively. Also, the uninfected population is denoted by $\mathit{S}$, the vaccinated class by $\mathit{V}$ and the recovered individuals by $\mathit{R}$. In the presented study, we consider the proposed model under conformable fractional order derivatives. The fundamental reproductive number and equilibrium points are computed. Moreover, we determine the existence and uniqueness of the solution to the suggested model using fixed-point theory. Furthermore, we provide a suitable methodology by applying the Euler numerical method to calculate the approximate solution of each compartment of the proposed model. Additionally, using MATLAB-16, we simulate the given results graphically for a variety of fractional orders using some real values of the parameters and initial conditions.

KEYWORDS:

• Nonlinear model
• conformable differential derivative
• Euler method

1. Introduction

Recently, the infectious disease due to coronavirus has greatly attracted the attention from researchers. This is because the said disease has greatly affected human life on this globe during the past four years. According to WHO report, millions of people have lost their lives in this outbreak (World Health Organization [WHO] 2020). Both health and economic conditions of all most all countries of the world have badly been affected during the outbreak caused by COVID-19 (Zhao et al. 2020; Nesteruk 2020). Since the said disease is still a great threat to human life on this globe (Hui et al. 2020), researchers, bioengineers and others are working day and night to prepare proper vaccine for its cure. They have now succeeded in preparing proper vaccines. The required vaccines are now available in the market of different organizations. Most of the countries have bought vaccines for their public from various organization according to the availability (Le et al. 2020). As we know that epidemiology has been a highly popular field among researchers, the study of how infectious diseases propagate across a community and the causes of their emergence falls under the heading of the aforementioned field. Since epidemiology is a crucial area of medical science, numerous infectious diseases are being researched for possible treatments, controls, cures and so on. In this perspective, mathematical biology is one of the primary subfields. Researchers are now more interested in biomathematics and bio-maths engineering than they were in the past. We refer to some important contributions by Molyneux (1997), Lotka (2002) and Gumel et al. (2004) in the said area. Keeping this importance, researchers have also investigated vaccination strategies against COVID-19 and the diffusion of anti-vaccination with the help of bioengineering (Prieto Curiel and González Ramrez 2021).

Mathematical modelling is regarded as a potent technique for describing a wide range of real-world issues. The aforementioned location has been thoroughly evaluated for a variety of physical and biological issues. The SIR model is one of the well-known versions that Kermack and McKendrick debuted in 1927. The concerned model, which defines the interaction between susceptible, infected and recovered persons in a society, is seen as being relatively simplistic. In other words, the model may also be used to explain the connection between groups that are healthy, infected and recovered to represent the transmission of illness in a community. Therefore, to comprehend the principles of transmission, make predictions and select the most effective control measures, numerous researchers have employed many forms of mathematical models of infectious illnesses. Here, for various works on biological models, mathematical biology and patterns of change in vector-borne diseases, we refer to Leah (2005) and Britton (2003). Mathematical models have been applied to provide framework for understanding the dynamics of various infectious diseases. For the effective study of various diseases, mathematical modelling is using the most powerful tools (Goel et al. 1971). By means of mathematical models, we make various predictions and develop control procedures for diseases in a community. Keeping these points in view, researchers have been greatly attracted to the aforementioned area. Here, we remark that there has been significant attention dedicated to the use of applications of taxis-driven partial differential equations to investigate the mathematical models of infection spread. Columbu et al. (2024) studied the zero-flux attraction-repulsion chemotaxis models and deduced interesting and useful results. In addition, Li et al. (2023) investigated by combining the effects ensuring boundedness in an attraction-repulsion chemotaxis model with production and consumption and created valuable results. In addition, the mentioned area has also been significantly used in mathematical models of atmospheric diffusion problems in science and regulation. The mentioned tools are applied when there are no monitoring data to approximate the atmospheric concentration field. Recently, researchers have published numerous good results in this regard (see, Viglialoro and Woolley 2018; Li and Viglialoro 2021).

Following the significant use of mathematical models, researchers have also formulated large numbers of mathematical models for COVID-19. For instance, Zhang et al. (2020) studied the dynamics of COVID-19 using stochastic perturbation. In the same way, Atangana and Araz (2020) investigated the propagation of the mentioned disease in Turkey and South Africa via mathematical models. Subsequently, researchers investigated the origin, aetiology and transmission, with more details provided in the study by Zhou et al. (2020), Li et al. (2020) and Bogoch et al. (2020), respectively. Researchers have predicted the transmission dynamics, control procedures of the disease in community, person-to-person propagation of infection, and so on, through mathematical models. In additions, they have also investigated the effect of vaccine by developing mathematical models. Here, we refer to some useful contributions by Wu et al. (2020) and Zeb et al. (2020) in this regard and the analysis of sensitivity discussed in Zhang et al. (2021). In the same way, Diagne et al. (2021) have also investigated vaccination and treatment via mathematical models.

Here, it is interesting to mention that all the mentioned studies have considered classical derivative in their models. Currently, it has been proved that derivative of arbitrary orders in comparison with the classical one has greater advantages because fractional calculus generalizes the operators of differentiations and integrations to any real or complex numbers. Fractional derivatives also incorporate the memory and genetic effects that are vital in the development of infectious diseases and increase the plausibility of the scenario. Therefore, utilizing fractional order derivatives, multiple researchers have lately investigated various models of epidemic diseases. For instance, researchers have considered, in this regards, many important applications of fractional differential operators have been investigated in the past three decades. For some significant uses in rheology, bioengineering, photoelasticity, signal and image processing phenomenon, diseases dynamics and so on, we refer to some reputed work such as those by Rossikhin and Shitikova (1997), Richard (2004), Liu and Burrage (2011), Mainardi (2012) and Wagner et al. (2017). Also, for COVID-19 models, the said concepts have been used very well, and we refer to Zhang et al. (2020), Shah et al. (2021), Atangana and Araz (2021) and Boccaletti et al. (2020). Researchers have constructed different numerical and analytical tools to simulate the results of various fractional orders systems. Here, we refer to some work such as Wang et al. (2020) and Arenas et al. (2016).

As traditional product, quotient and chain rules are not satisfied by the usual fractional order derivatives given by Riemann-Liouville, Caputo, and so on, mathematicians extended the concepts of fractional calculus to conformable derivative of fractional order. The concerned operator obeys the product, quotient and chain rules. Further, we state that the said operator is free of memory terms and therefore also called the local differential operator with arbitrary order. Numerous researchers have done important work in this area. For instance, some new definitions of the said operators were introduced, and we refer to Abdeljawad (2015). Further results on the mentioned area have been published; see Mostafa and Rezazadeh (2015). An integral method for the Wu-Zhang dynamical system under the said concept was given by Ünal et al. (2015). Solutions to some problems under the aforementioned operator have been deduced in Chung (2015). Moreover, the mentioned concept has been applied in Newtonian mechanics (Zhong and Wang 2018). Basic theory for some initial value problems of conformable operators has been established in Al-Rifae and Abdeljawad (2017). Asawasamrit et al. (2016) investigated Sturm-Liouville problems under the said operator. Utilizing conformable derivative, a periodic boundary value problem has been investigated in Silva et al. (2018).

Here, it is noteworthy that in very few cases, biological models have been investigated via the tools of the conformable fractional calculus. Hence, motivated from the aforementioned significance of the conformable derivative of non-integer order, we consider the following two strains model of COVID-19 containing Omicron and Delta virus with vaccinated class. It should be noted that the two strains models have been considered for the said infected disease very well. For instance, Tchoumi et al. (2022) have studied classical order two strains models for the mentioned disease. Therefore, we extend the model studied (Tchoumi et al. 2022) under the conformable differential operators as

(1) $\left\{\begin{array}{cc}{\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{S}(\mathit{t})& =(1-\mathit{\beta })\mathit{\alpha }-\left(\frac{k({\mu }_1\mathcal{A}+{\mu }_2\mathcal{A})}{\mathcal{N}}+\mathit{\eta }+d_0\right)\mathcal{S}+\mathit{\gamma }\mathcal{R}\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{V}(\mathit{t})& =\mathit{\beta \alpha }+\mathit{\eta }\mathcal{S}-\left(\frac{k{\mu }_2\mathcal{B}}{\mathcal{N}}+\frac{k{\mu }_1\mathcal{A}(1-\mathit{\delta })}{\mathcal{N}}+d_0\right)\mathcal{V}\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{A}(\mathit{t})& =\frac{k{\mu }_1\mathcal{A}\mathcal{S}}{\mathcal{N}}+\frac{k{\mu }_1\mathcal{A}(1-\mathit{\delta })\mathcal{V}}{\mathcal{N}}-(r_1+d_0+d_{\mathcal{A}})\mathcal{A}\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{B}(\mathit{t})& =\frac{k{\mu }_2\mathcal{B}(\mathcal{S}+\mathcal{V})}{\mathcal{N}}-(r_2+d_0+d_{\mathcal{B}})\mathcal{B}\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{R}(\mathit{t})& =r_1\mathcal{A}+r_2\mathcal{B}-(\mathit{\gamma }+d_0)\mathcal{R}\\ \mathcal{S}\ge 0,& \mathcal{V}\ge 0,\mathcal{A}\ge 0,\mathcal{B}\ge 0,\mathcal{R}\ge 0.\end{array}\right.$(1)

Further, $\mathcal{N}$ represents the total population, and the parameters involved in the model we proposed are described in Table 1.

Table 1. The parameters and description in model (1).

Parameters	Description	Parameters	Description
$\mathcal{S}$	Susceptible compartment	$\mathit{\eta }$	Vaccination rate of susceptible class
$\mathcal{V}$	Vaccinated compartment	$\mathit{k}$	Contact rate
$\mathcal{A}$	Delta virus infected compartment	${\mu }_1$	Transmission of delta virus
$\mathcal{B}$	Omicron virus infected compartment	${\mu }_2$	Transmission of omicron virus
$\mathcal{R}$	Recovered compartment	$\mathit{\delta }$	Delta virus vaccine efficacy
$\mathit{\alpha }$	Birth rate	$\mathit{\gamma }$	Loss of immunity
$d_{\mathcal{A}}$	Disease death rate of delta virus	$\mathit{\beta }$	Vaccination rate
$d_0$	Natural death rate	$r_1$	Recovery from delta virus
$d_{\mathcal{B}}$	Disease death rate of omicron virus	$r_2$	Recovery of omicron virus

Here, we mentioned that Tchoumi et al. (2022) have studied the above model under ordinary differential equations. They investigated the global and local stability, backward bifurcation analysis and including some control strategies. Our analysis is quiet different from the mentioned one. We investigate the model under some new scenarios by using conformable fractional derivative. We establish the existence theory by using fixed point approach, positivity and boundedness of solution. Also, we extend the traditional numerical Euler technique to conformable fractional order model (1) and simulate the results for various fractional order values. In addition, we derive the basic results of the model, also the reproductive number is provided using the procedure mentioned by Zhao et al. (2020). Moreover, the qualitative theory of solution has also been established via fixed point theory. A suitable numerical scheme based on Taylor series is also developed by following Toprakseven (2019). Also, we graphically interpret our results using some real values for the initial data and parameters. For the initial values of compartments, we take information from https://data.covid19taskforce.com/data/countries/Philippines.

2. Preliminaries

Some important findings are remembered here.

Definition 2.1.

[44] The conformable derivative of a function $\mathrm{f}:[t_0,\mathrm{\infty })\to \mathrm{IR}$ of order $\mathrm{p}\in (0,1]$ is given by

${\mathbf{D}}_{t_0}^{\mathrm{p}}\mathrm{f}(\mathit{t})=\underset{\kappa \to t_0}{lim}\frac{\mathrm{f}(t+\kappa {\mathit{t}}^{1-\mathrm{p}})-\mathrm{f}(\mathit{t})}{\mathit{\kappa }},\mathit{for}\mathit{every}\mathit{t}>t_0,$

provided that if ${\mathbf{D}}_{t_0}^{\mathrm{p}}\mathit{\xi }(\mathit{t})={lim}_{t\to t_0}{D}_{\mathrm{p}}^{t_0}\mathrm{f}(\mathit{t}).$

Definition 2.2.

[44] For function $\mathrm{f}:[t_0,\mathrm{\infty })\to \mathrm{IR}$ with order $\mathrm{p}\in (0,1]$, integral is given by

${\mathbf{I}}_{t_0}^{\mathrm{p}}\mathrm{f})(\mathit{t})={\int }_{t_0}^{\mathit{t}}(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{f}(\mathit{\tau })\mathit{d\tau },\mathit{for}\mathit{every}\mathit{t}>t_0,$

such that the right hand side exists.

Lemma 2.3.

Let $\mathrm{f}:[t_0,\mathrm{\infty })\to \mathrm{IR}$ is continuous, one has

${\mathbf{D}}_{t_0}^{\mathrm{p}}[{\mathbf{I}}_{t_0}^{\mathrm{p}}\mathrm{f})(\mathit{t})]=\mathrm{f}(\mathit{t}),\mathrm{p}\in (0,1],\mathit{for}\mathit{every}\mathit{t}>t_0.$

Lemma 2.4.

[45] Also the result for

${\mathbf{D}}_{t_0}^{\mathrm{p}}\mathrm{f}(\mathit{t}))=\mathrm{h}(\mathit{t})$

holds as

$\mathrm{f}(\mathit{t})=\mathrm{f}(t_0)+{\int }_{t_0}^{\mathit{t}}(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{h}(\mathit{\tau })\mathit{d\tau },\mathrm{p}\in (0,1].$

To show boundedness of solution, we give the result as follows:

Theorem 2.5.

All solutions $(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})$ of model (1) are bounded and lie in the positively invariant feasible region given by

$\mathrm{\Omega }=\{(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})\in \mathcal{R}{+}^5):\mathcal{N}\le \frac{\alpha }{d_0}\}.$

Proof.

We know that $\mathcal{N}=\mathcal{S}+\mathcal{V}+\mathcal{A}+\mathcal{B}+\mathcal{R}$, one has

${\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{N}=\mathit{\alpha }-d_A\mathcal{A}-d_B\mathcal{B}-d_0\mathcal{N}$

(2) $\le \mathit{\alpha }-d_0\mathcal{N}.$(2)

Applying the conformable Laplace transform as used in Silva et al. (2018), and then use $\mathit{t}\to \mathrm{\infty }$, we have

$\mathcal{N}\le \frac{\alpha }{d_0}.$

Thus,

$\mathcal{S}+\mathcal{V}+\mathcal{A}+\mathcal{B}+\mathcal{R}\le \frac{\alpha }{d_0}$

which implies that all solutions

$\mathcal{S}\le \frac{\alpha }{d_0},\mathcal{V}\le \frac{\alpha }{d_0},\mathcal{A}\le \frac{\alpha }{d_0},\mathcal{B}\le \frac{\alpha }{d_0},\mathcal{R}\le \frac{\alpha }{d_0}$

are bounded. In addition, the feasible region where all solutions are attracted is given by

$\mathrm{\Omega }=\{(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})\in \mathcal{R}{+}^5):\mathcal{N}\le \frac{\alpha }{d_0}\}$

is required region.

Theorem 2.6. Given that

$\mathcal{S}(0)\ge 0,\mathcal{V}(0)\ge 0,\mathcal{A}(0)\ge 0,\mathcal{B}(0)\ge 0,\mathcal{R}(0)\ge 0,$

the solutions $(\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t}))$ of the proposed model are positive for all $\mathit{t}>0.$

Proof.

From first equation of model (1), we have

${\left.{\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{S}(\mathit{t})\right|}_{\mathcal{S}=0}=(1-\mathit{\beta })\mathit{\alpha }+\mathit{\gamma }\mathcal{R},$

applying Lemma 2.4, we have

$\mathcal{S}(\mathit{t})=\mathcal{S}(t_0)+{\int }_{t_0}^{\mathit{t}}(\mathit{\tau }-\mathit{t}{)}^{\mathrm{p}-1}[(1-\mathit{\beta })\mathit{\alpha }+\mathit{\gamma }\mathcal{R}]\mathit{d\tau }>0,\mathrm{for}\mathrm{all}\mathit{t}>0,$

which yields that $\mathcal{S}(\mathit{t})>0,\mathrm{forall}\mathit{t}>0.$ In the same way, for other compartments we can deduce that

$\mathcal{V}(\mathit{t})>0,\mathcal{A}(\mathit{t})>0,\mathcal{B}(\mathit{t})>0,\mathcal{R}(\mathit{t})>0,\mathrm{for}\mathrm{all}\mathit{t}>0.$

In addition, the trivial equilibrium point is given by ${\mathcal{E}}^0=({\mathcal{S}}^0,{\mathcal{V}}^0,0,0,0),$ where

${\mathcal{S}}^0=\frac{(1-\mathit{\beta })\mathit{\alpha }}{\eta +d_0},{\mathcal{V}}^0=\frac{(d_0\mathit{\beta }+\mathit{\eta })\mathit{\alpha }}{d_0(\mathit{\eta }+d_0)}.$

Let the population $\mathcal{N}(\mathit{t})=\mathbb{N}$ be constant at the point where the endemic equilibrium is occurred given by ${\mathcal{E}}^{\ast }=({\mathcal{S}}^{\ast },{\mathcal{V}}^{\ast },{\mathcal{A}}^{\ast },{\mathcal{B}}^{\ast },{\mathcal{R}}^{\ast },$ where

$\begin{array}{rl}& {\mathcal{S}}^{\ast }=\frac{(1-\mathit{\beta })\mathit{\alpha }-\mathit{\gamma }{\mathcal{R}}^{\ast }}{\frac{k{\mu }_1{\mathcal{A}}^{\ast }+\mathit{k}{\mu }_2{\mathcal{B}}^{\ast }}{\mathbb{N}}+\mathit{\eta }+d_0},{\mathcal{V}}^{\ast }=\frac{\mathit{\beta \alpha }+\mathit{\eta }{\mathcal{S}}^{\ast }}{\frac{k{\mu }_2{\mathcal{B}}^{\ast }+(1-\mathit{\delta })\mathit{k}{\mu }_1{\mathcal{A}}^{\ast }}{\mathbb{N}}+d_0}\\ & {\mathcal{A}}^{\ast }=\frac{\frac{k{\mu }_1{\mathcal{A}}^{\ast }{\mathcal{S}}^{\ast }}{\mathbb{N}}+(1-\mathit{\delta })\frac{k{\mu }_1{\mathcal{A}}^{\ast }}{\mathbb{N}}{\mathcal{V}}^{\ast }}{r_1+d_{\mathcal{A}}+d_0},{\mathcal{B}}^{\ast }=\frac{k{\mu }_2{\mathcal{B}}^{\ast }({\mathcal{S}}^{\ast }+{\mathcal{V}}^{\ast })}{(r_2+d_{\mathcal{B}}+d_0)\mathbb{N}},{\mathcal{R}}^{\ast }=\frac{r_1{\mathcal{A}}^{\ast }+r_2{\mathcal{B}}^{\ast }}{\mathit{\gamma }+d_0}.\end{array}$

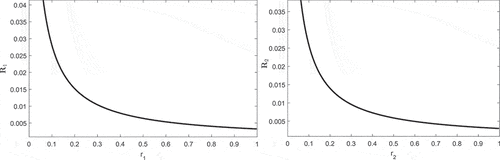
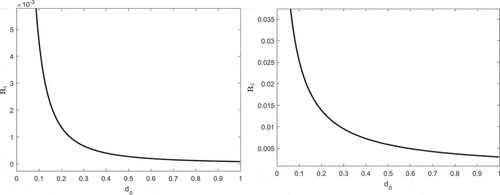
Addition, following the methodology given in Zhao et al. (2020), we compute the basic reproduction number ${\mathbf{R}}_0$ as

${\mathbf{R}}_0=max\{{\mathbf{R}}_1,{\mathbf{R}}_2\},$

where

${\mathbf{R}}_1=\frac{{\mu }_1\mathit{k}[d_0(1-\mathit{\beta })+(1-\mathit{\delta })(d_0\mathit{\beta }+\mathit{\eta })]}{(d_0+\mathit{\eta })(r_1+d_0+d_{\mathcal{A}})}$

also known as infection rate of delta virus, and

${\mathbf{R}}_2=\frac{k{\mu }_2}{r_2+d_{\mathcal{B}}+d_0},$

${\mathbf{R}}_2$ represents infection rate of omicron infection. For effective reproductive number, we consider the maximum of the two ${\mathbf{R}}_1,{\mathbf{R}}_2$, respectively. Here, in Figures 1 and 2, we present the behaviours of ${\mathbf{R}}_1$ and ${\mathbf{R}}_2$, respectively, using numerical values of Table 2.

Figure 1. 2D profile of ${\mathbf{R}}_1$ and ${\mathbf{R}}_2$ against $r_1,r_2$.

Figure 2. 2D profile of ${\mathbf{R}}_1$ and ${\mathbf{R}}_2$ using different vales of $d_0$.

Table 2. Values of nomenclatures of model (1).

Parameters	Value	Parameters	Value
$\mathcal{S}$	22.12 (https://data.covid19taskforce.com/data/countries/Philippines, August, 2023a)	$\mathit{\eta }$	0.009 estimated
$\mathcal{V}$	79.9 (https://www.statista.com/statistics/1236727/philippines-coronavirus-covid19-vaccine-rollout/, August, 2023b)	$\mathit{k}$	0.24 estimated
$\mathcal{A}$	4.174106 (https://data.covid19taskforce.com/data/countries/Philippines, August, 2023a)	${\mu }_1$	0.0127 estimated
$\mathcal{B}$	0.007037 (https://data.covid19taskforce.com/data/countries/Philippines, August, 2023a)	${\mu }_2$	0.0127 estimated
$\mathcal{R}$	4.103828 (https://www.statista.com/statistics/1236727/philippines-coronavirus-covid19-vaccine-rollout/, August, 2023b)	$\mathit{\delta }$	0.016 estimated
$\mathit{\alpha }$	0.99 assumed	$\mathit{\gamma }$	0.0012 estimated
$d_{\mathcal{A}}$	0.0099 (https://data.covid19taskforce.com/data/countries/Philippines, August, 2023a)	$\mathit{\beta }$	0.99 estimated
$d_0$	0.0082 (https://data.covid19taskforce.com/data/countries/Philippines, August, 2023a)	$r_1$	0.011 estimated
$d_{\mathcal{B}}$	0.0099 estimated	$r_2$	0.011 estimated

3. Qualitative theory (1)

In this section, we deduce the necessary criteria for at least one solution to the put forward problem to exist and be unique. Applying some fixed point tools, we create the necessary conditions for the existence of at least one solution in order to accomplish this goal. We express the considered system (1) with $\mathrm{p}\in (0,1]$ as

(3) $\left\{\begin{array}{cc}{\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{S}(\mathit{t})& =\mathrm{I}{\mathrm{F}}_1(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t})),\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{V}(\mathit{t})& =\mathrm{I}{\mathrm{F}}_2(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t})),\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{A}(\mathit{t})& =\mathrm{I}{\mathrm{F}}_3(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t})),\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{B}(\mathit{t})& =\mathrm{I}{\mathrm{F}}_4(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t})),\\ {\mathbf{D}}_{t_0}^{\mathrm{p}}\mathcal{R}(\mathit{t})& =\mathrm{I}{\mathrm{F}}_5(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t})),\end{array}\right.$(3)

where $\mathrm{Y}=(\mathcal{S},\mathcal{E},\mathcal{I},\mathcal{R}),{\mathrm{Y}}_0=({\mathcal{S}}_0,{\mathcal{E}}_0,{\mathcal{I}}_0,{\mathcal{R}}_0)$ and $\mathrm{I}{\mathrm{F}}_i:[t_0,\mathit{T}]\times {\mathbb{R}}^r{ }_{+}\to \mathbb{R}$ is continuous for $\mathit{i}=1,2,..,5$. On applying ${\mathbf{I}}_0^{\mathrm{p}}$ to (16) yields

(4) $\left\{\begin{array}{c}\mathcal{S}(\mathit{t})={\mathcal{S}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ \mathcal{V}(\mathit{t})={\mathcal{V}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_2(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ \mathcal{A}(\mathit{t})={\mathcal{A}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_3(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ \mathcal{B}(\mathit{t})={\mathcal{B}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_4(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ \mathcal{R}(\mathit{t})={\mathcal{R}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_5(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }.\end{array}\right.$(4)

If $\mathrm{IH}=\mathit{C}[t_0,\mathit{T}]$ be the Banach space, then the product space $\mathrm{IB}=\mathrm{IH}\times \mathrm{IH}\times \mathrm{IH}\times \mathrm{IH}\times \mathrm{IH}$ is also the Banach space under the norm

$\parallel (\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}=\underset{t\in [t_0,\mathit{T}]}{sup}[|\mathcal{S}(\mathit{t})|+|\mathcal{V}(\mathit{t})|+|\mathcal{A}(\mathit{t})|+|\mathcal{B}(\mathit{t})|+|\mathcal{R}(\mathit{t})|].$

Additionally, $\mathrm{Q}=({\mathrm{Q}}_1,{\mathrm{Q}}_2,{\mathrm{Q}}_3,{\mathrm{Q}}_4,{\mathrm{Q}}_5):\mathrm{IB}\to \mathrm{IB}$ be the operator defined by

(5) $\left\{\begin{array}{c}{\mathrm{Q}}_1[\mathcal{S}(\mathit{t})]={\mathcal{S}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ {\mathrm{Q}}_2[\mathcal{V}(\mathit{t})]={\mathcal{V}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_2(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ {\mathrm{Q}}_3[\mathcal{A}(\mathit{t})]={\mathcal{A}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_3(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ {\mathrm{Q}}_4[\mathcal{B}(\mathit{t})]={\mathcal{B}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_4(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\\ {\mathrm{Q}}_5[\mathcal{R}(\mathit{t})]={\mathcal{R}}_0+{\int }_0^t(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_5(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }.\end{array}\right.$(5)

Let the given hypothesis hold.

(A₁) If there exist constants $C_{\mathrm{I}{\mathrm{F}}_i},M_{\mathrm{I}{\mathrm{F}}_i},>0$, for $\mathit{i}=1,2,..,5,$ such that

$|\mathrm{IF}(\mathit{t},\mathcal{S}(\mathit{t}),\mathcal{V}(\mathit{t}),\mathcal{A}(\mathit{t}),\mathcal{B}(\mathit{t}),\mathcal{R}(\mathit{t}))|\le C_{\mathrm{I}{\mathrm{F}}_i}[|\mathcal{S}(\mathit{t})|+|\mathcal{V}(\mathit{t})|+|\mathcal{A}(\mathit{t})|+|\mathcal{B}(\mathit{t})|+|\mathcal{R}(\mathit{t})|]+M_{\mathrm{I}{\mathrm{F}}_i}.$

(A₂) There exist constants $\mathrm{I}{\mathrm{L}}_{\mathrm{I}{\mathrm{F}}_i},$ such that for $(\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ}),(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ})\in \text{IB}$ with

$|{\text{IF}}_i(\mathit{t},\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ})-{\text{IF}}_i(\mathit{t},\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ})|\le {\text{IL}}_{{\text{IF}}_i}[|\mathit{S}-\overline{S}|+|\mathit{V}-\overline{V}|+|\mathit{A}-\overline{A}|+|\mathit{ℬ}-\overline{ℬ}|+|\mathit{ℛ}-\overline{ℛ}|].$

Theorem 3.1.

Inview of hypothesis $(A_1)$, the system (16) has at least one fixed point. Consequently, the system (1) has at least one solution.

Proof.

Let $\mathbf{D}=\left\{(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})\in \mathrm{IB}:\parallel (\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r}\right\}\subseteq \mathrm{IB}$ with

$\mathit{r}\ge \frac{{\mathit{T}}^{\mathrm{p}}{M}_{\mathrm{I}{\mathrm{F}}_i}}{5\mathrm{p}-T^{\mathrm{p}}{\sum }_{i=1}^5{C}_{\mathrm{I}{\mathrm{F}}_i}}.$

Now, for every $(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})\in \mathbf{D}$, one has

(6) $\begin{array}{rl}& \parallel {\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}=\underset{t\in [t_0,\mathit{T}]}{sup}\left|{\mathcal{S}}_0+{\int }_{t_0}^{\mathit{t}}{(\tau -t_0)}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\right|\\ & \le |{\mathcal{S}}_0|+{\int }_{t_0}^{\mathit{t}}(\mathit{\tau }-t_0{)}^{\mathrm{p}-1}|\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))|\mathit{d\tau }\\ & \le \frac{{\mathit{T}}^{\mathrm{p}}[C_{\mathrm{I}{\mathrm{F}}_1}\mathit{r}+M_{\mathrm{I}{\mathrm{F}}_1}]}{\mathrm{p}}\\ & \le \mathit{r}.\end{array}$(6)

Repeating the same arguments for other operators ${\mathrm{Q}}_2,{\mathrm{Q}}_3,{\mathrm{Q}}_4,{\mathrm{Q}}_5$, one has

(7) $\parallel {\mathrm{Q}}_2(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r},$(7)

(8) $\parallel {\mathrm{Q}}_3(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r},$(8)

(9) $\parallel {\mathrm{Q}}_4(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r},$(9)

and

(10) $\parallel {\mathrm{Q}}_5(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r}.$(10)

Then, adding (6)–(10) gives

(11) $\parallel \mathrm{Q}(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \frac{{\mathit{T}}^{\mathrm{p}}}{\mathrm{p}}\left[\sum _{\mathit{i}=1}^k(C_{\mathrm{I}{\mathrm{F}}_i}\mathit{r}+M_{\mathrm{I}{\mathrm{F}}_i})\right]\le \mathit{r}.$(11)

Hence, (11) implies that $\parallel \mathrm{Q}(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}){\parallel }_{\mathrm{IB}}\le \mathit{r}$ which implies that $\mathrm{Q}(\mathbf{D})\subset \mathbf{D}.$ $\mathrm{IF}$ is continuous means that $\mathrm{Q}$ is also. Additionally, let $t_1<t_2\in [t_0,\mathit{T}],$ such that

$|{\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_2)-{\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_1)|=\left|{\int }_{t_0}^{t_2}{(t_2-\mathit{\tau })}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\right.$

(12) $\begin{array}{rl}& \left.-{\int }_{t_0}^{t_1}{(t_1-\mathit{\tau })}^{\mathrm{p}-1}\mathrm{I}{\mathrm{F}}_1(\mathit{\tau },\mathcal{S}(\mathit{\tau }),\mathcal{V}(\mathit{\tau }),\mathcal{A}(\mathit{\tau }),\mathcal{B}(\mathit{\tau }),\mathcal{R}(\mathit{\tau }))\mathit{d\tau }\right|\\ & \le \frac{{\mathit{C}}_{\mathrm{I}{\mathrm{F}}_1}\mathit{r}+M_{\mathrm{I}{\mathrm{F}}_1})}{\mathrm{p}}[(t_2-t_0{)}^{\mathrm{p}}-(t_1-t_0{)}^{\mathrm{p}}].\end{array}$(12)

As the right hand side of (12) goes to zero with $t_2\to t_1$, so

$|{\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_2)-{\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_1)|\to 0\mathrm{as}{t}_2\to t_1.$

The same arguments can be repeated for other operators ${\mathrm{Q}}_2,{\mathrm{Q}}_3,{\mathrm{Q}}_3,{\mathrm{Q}}_4,{\mathrm{Q}}_5$. Thus, $\mathrm{Q}$ is equi-continuous and also ${\mathrm{Q}}_1$ bounded.

$\parallel {\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_2)-{\mathrm{Q}}_1(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})(t_1){\parallel }_{\mathrm{IB}}\to 0\mathrm{as}{t}_2\to t_1$

implies the uniform continuity. Hence, the proposed system (1) has at least one solution.

Theorem 3.2.

Let hypothesis $(A_2)$ holds along with the condition $\mathrm{W}=\frac{\mathrm{I}{\mathrm{L}}_{\mathrm{IF}}{T}^{\mathrm{p}}}{\mathrm{p}}<\frac{1}{5}$, then system (1) has a unique solution.

Proof.

Consider $(\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ}),(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ})\in \text{IB}$, then we have

(13) $\parallel {\text{Q}}_1(\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ})-{\text{Q}}_1(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ}){\parallel }_{\text{IB}}\le \frac{{\text{IL}}_{{\text{IF}}_1}{T}^{\text{p}}}{\text{p}}\parallel (\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ})-(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ}){\parallel }_{\text{IB}}.$(13)

Upon repeating the same process, we and adding all relations, we have From (13), one has

$\parallel \text{Q}(\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ})-\text{Q}(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ}){\parallel }_{\text{IB}}\le \text{W}\parallel (\mathit{S},\mathit{V},\mathit{A},\mathit{ℬ},\mathit{ℛ})-(\overline{S},\overline{V},\overline{A},\overline{ℬ},\overline{ℛ}){\parallel }_{\text{IB}}.$

Hence, the operator $\mathrm{Q}$ is a contraction. In view of Banach Fixed point theorem, model (1) has a unique solution.

4. Numerical analysis and explanation

Here, in this part, we establish a numerical scheme for the proposed model (1). Here, we recall some basic results (Toprakseven 2019) as:

Definition 4.1.

If $\mathrm{Y}\in ([t_0,\mathrm{\infty }),\mathbb{R})$ be $\mathrm{p}-$ differentiable mapping with $\mathrm{p}\in (0,1],$ at a neighborhood of a point $t_0$, then we can describe the fractional order power series for $\mathrm{Y}$ as

(14) $\mathrm{Y}(\mathit{t})=\sum _{\mathit{k}=0}^{\mathrm{\infty }}\frac{{\left({\mathbf{D}}_{t_0}^{\mathrm{p}}\mathrm{Y}\right)}^{\mathit{k}}(t_0)(\mathit{t}-t_0{)}^{\mathit{k}\mathrm{p}}}{{\mathrm{p}}^k\mathrm{\Gamma }(\mathit{k}+1)},t_0<\mathit{t}<{\rho }^{\frac{1}{\mathrm{p}}},\mathit{\rho }>0.$(14)

Definition 4.2.

Following Definition 4.1, we can express the fractional order Taylor series of $\mathrm{Y}(t_{\mathit{n}+1})$ at $\mathit{t}=t_n$ as

(15) $\mathrm{Y}(t_{\mathit{n}+1})=\mathrm{Y}(t_n)+{\mathbf{D}}_{t_0}^{\mathrm{p}}\mathit{Y}(t_n)\frac{{\mathrm{\Delta }}_1}{\mathrm{p}}+{\rho }_1(t_{\mathit{n}+1},t_n,t_0),$(15)

where ${\mathrm{\Delta }}_1=h^{\mathrm{p}}\left[{(\mathit{n}+1)}^{\mathrm{p}}-n^{\mathrm{p}}\right]$, and ${\rho }_1(t_{\mathit{n}+1},t_n,t_0)$ represents the remainder term.

Consider the

(16) $\left\{\begin{array}{c}{\mathbf{D}}_{t_0}^{\mathrm{p}}\mathrm{Y}(\mathit{t})=\mathrm{IF}(\mathit{t},\mathrm{Y}(\mathit{t})),\mathit{t}\in [t_0,\mathit{T}],\\ \mathrm{Y}(0)={\mathrm{Y}}_0,\end{array}\right.$(16)

then using (15), we can write the solution of (16) as

(17) $\mathrm{Y}(t_{\mathit{n}+1})=\mathrm{Y}(t_n)+\mathrm{IF}(t_n,\mathrm{Y}(t_n))\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}+{\rho }_1(t_{\mathit{n}+1},t_n,t_0),$(17)

where

(18) $a_n=(\mathit{n}+1{)}^{\mathrm{p}}-n^{\mathrm{p}}.$(18)

If we ignore the remainder term, then from (19) using $\mathit{n}=0,1,2,\dots ,\mathit{N}$ at $t_n$, the fractional conformable Euler method is deduced for $\mathrm{Y}(t_n)={\mathrm{Y}}_n$ as

(19) $\begin{array}{rl}& {\mathrm{Y}}_{\mathit{n}+1}={\mathrm{Y}}_n+\mathrm{IF}\left(t_n,\mathrm{Y}(t_n)\right)\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}},\\ & \mathrm{Y}(\mathit{t}){|}_{t=t_0}={\mathrm{Y}}_0.\end{array}$(19)

In addition, the remainder term ${\rho }_1(t_{\mathit{n}+1},t_n,t_0)$ can be explained using Definition 4.1, step size $\mathit{h}$ and fractional order $\mathrm{p}$ as (see Toprakseven 2019)

(20) ${\rho }_1(t_{\mathit{n}+1},t_n,t_0)=h^{2\mathrm{p}}\left[\left(\frac{C_1{n}^{\mathrm{p}}}{{\mathrm{p}}^2}-\frac{C_2{(\mathit{hn})}^{\mathrm{p}}}{2{\mathrm{p}}^2}\right)a_n+\frac{C_3{n}^{3\mathrm{p}}}{2{\mathrm{p}}^2}\right],$(20)

where $\mathit{a}$ is given in (18), and $C_i,(\mathit{i}=1,2,3)$ are bounded constants. The error bound can be computed as

$|\mathrm{Y}(t_{\mathit{n}+1})-{\mathrm{Y}}_{\mathit{n}+1}|\le \mathit{C}{h}^{\mathrm{p}}.$

Following the above method, the proposed system (1) can be described as

(21) $\left\{\begin{array}{cc}{\mathcal{S}}_{\mathit{n}+1}& ={\mathcal{S}}_n+\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}\mathrm{I}{\mathrm{F}}_1(t_n,{\mathcal{S}}_n,{\mathcal{V}}_n,{\mathcal{A}}_n,{\mathcal{B}}_n,{\mathcal{R}}_n),\\ {\mathcal{V}}_{\mathit{n}+1}& ={\mathcal{V}}_n+\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}\mathrm{I}{\mathrm{F}}_2(t_n,{\mathcal{S}}_n,{\mathcal{V}}_n,{\mathcal{A}}_n,{\mathcal{B}}_n,{\mathcal{R}}_n),\\ {\mathcal{A}}_{\mathit{n}+1}& ={\mathcal{A}}_n+\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}\mathrm{I}{\mathrm{F}}_3(t_n,{\mathcal{S}}_n,{\mathcal{V}}_n,{\mathcal{A}}_n,{\mathcal{B}}_n,{\mathcal{R}}_n),\\ {\mathcal{B}}_{\mathit{n}+1}& ={\mathcal{B}}_n+\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}\mathrm{I}{\mathrm{F}}_4(t_n,{\mathcal{S}}_n,{\mathcal{V}}_n,{\mathcal{A}}_n,{\mathcal{B}}_n,{\mathcal{R}}_n),\\ {\mathcal{R}}_{\mathit{n}+1}& ={\mathcal{R}}_n+\frac{{\mathit{h}}^{\mathrm{p}}{a}_n}{\mathrm{p}}\mathrm{I}{\mathrm{F}}_5(t_n,{\mathcal{S}}_n,{\mathcal{V}}_n,{\mathcal{A}}_n,{\mathcal{B}}_n,{\mathcal{R}}_n).\end{array}\right.$(21)

5. Numerical simulations and discussion

Here, we simulate our proposed model by using the aforesaid numerical scheme using the values given in Table 2. Here, we consider the real initial data of Philippines from ht tps://da ta.covid19taskforce.com/data/countries/Philippines (2023a, August) and htt ps://ww w.statista.com/statistics/1236727/philippines-coronavirus-covid19-vaccine-rollout/ (2023b, August).

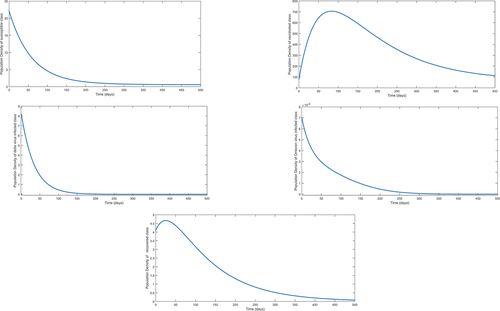
Here, we have considered the population of Philippines for initial data. During the past three years, $79.9$ million people have been given full vaccine in the country. Moreover, the other values of parameters have been estimated. We present the concerned population dynamics in Figures 3, 4, 5, 6 and 7, respectively, of different compartment by considering fractional order in $[0.90,1.0]$ for 1200 days.

Figure 3. Numerical interpretation for susceptible compartment’s of the model (1) for given fractional orders.

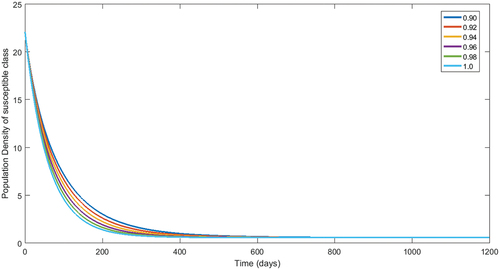
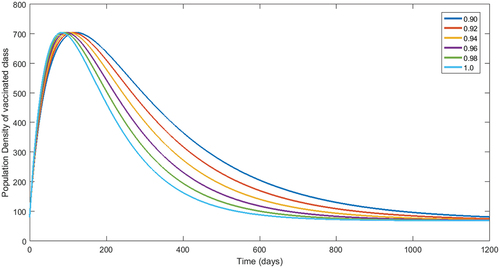
Figure 4. Numerical interpretation for vaccinated compartment’s of model (1) for given fractional orders.

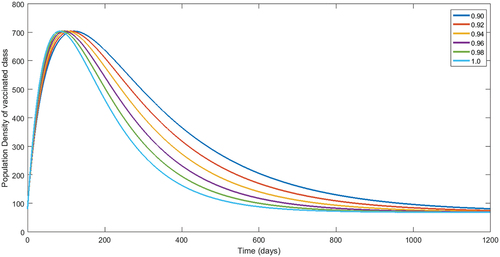
Figure 5. Numerical interpretation for class having delta virus of model (1) for given fractional orders.

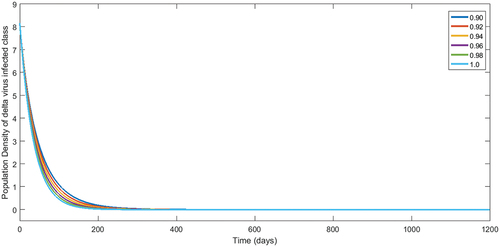
Figure 6. Numerical interpretation for compartment’s having omicron type virus of model (1) for given fractional orders.

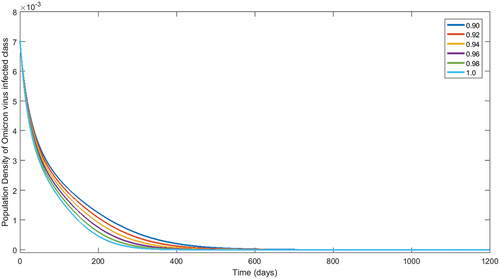
Figure 7. Numerical interpretation for recovered compartment’s of the model (1) for given fractional orders.

Another set of fractional orders have been considered to simulate numerically our results for the numerical data given in Table 2. Therefore, we present population dynamics in Figures 8, 9, 10, 11 and 12, respectively, of different compartment by considering fractional order in $[0.90,1.0]$ for 1200 days.

Figure 8. Numerical interpretation for susceptible compartment’s of the model (1) for given fractional orders.

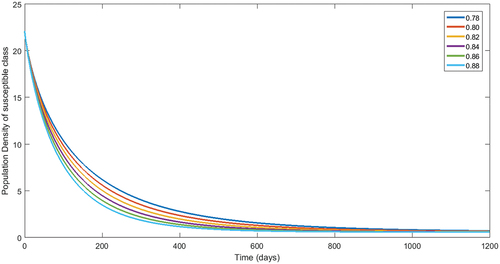
Figure 9. Numerical interpretation for vaccinated compartment’s of model (1) for given fractional orders.

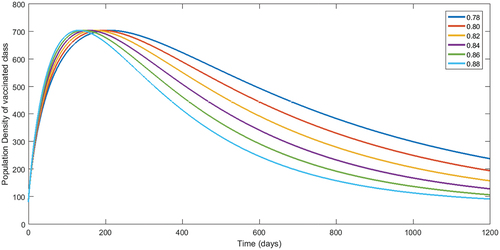
Figure 10. Numerical interpretation for class having delta virus of model (1) for given fractional orders.

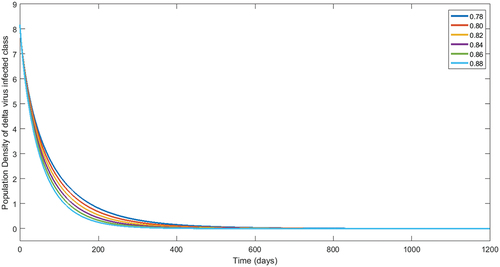
Figure 11. Numerical interpretation for compartment having omicron type virus of model (1) for given fractional orders.

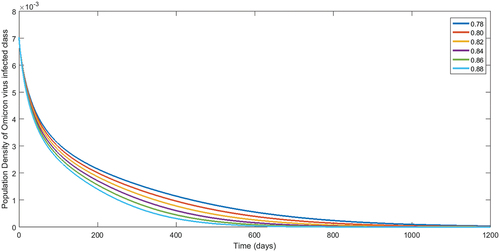
Figure 12. Numerical interpretation for recovered compartment of model (1) for given fractional orders.

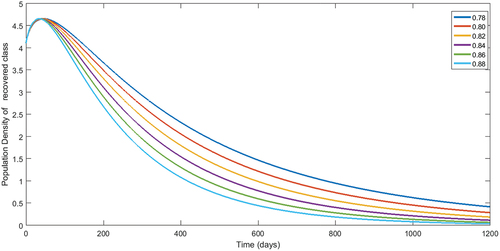
From Figures 3 and 8, we see decay in population of susceptible class. The concerned decay is different due to to different fractional orders. On the other hand, the population dynamics during first 200 days is increasing of vaccinated class as shown in Figures 4 and 9, respectively, corresponding to different fractional order. In the same way, after 200 days, the concerned population is going to decrease. Following the procedure, we see that the classes related to infection of different virus are decaying during vaccination time for various fractional orders. The reader should see Figures 5 and 10 for delta virus class, and Figures 6 and 11 for class having omicron virus. Also, the recovered population during first 200 days is increasing corresponding to different fractional orders. Readers should see the Figures 7 and 12, respectively. From the numerical interpretation, we see that the suggested fractional differential operator is an alternative way for the investigation of different epidemiological problems as well as real-world process. Additionally, we present the simulation for $\mathrm{p}=1$ in Figure 13. The concerned dynamics coincide with the results of the classical model studied in Tchoumi et al. (2022).

Figure 13. Numerical interpretation of model (1) for $\mathrm{p}=1$.

6. Conclusion

In this study, a nonlinear two-strain COVID-19 model with a vaccinated class has been taken into account. The suggested model has been investigated using conformable fractional derivatives. The fixed-point approach has been used to study the existence and uniqueness criteria. We have also created a general technique to compute numerical solutions of various compartments using the Euler method. Additionally, we computed fundamental results of the model including equilibrium points and ${\mathbf{R}}_0$. The approximations for the various fractional orders have been graphically shown using MATLAB-16. For illustrative purpose, some actual values have been used. All the results conclude the significance of the conformable fractional calculus as an alternative tool to be used in epidemiology for modelling.

Acknowledgements

The authors Kamal Shah and Thabet Abdeljawad would like to express their gratitude to Prince Sultan University for supporting them through the TAS research lab.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The author(s) reported there is no funding associated with the work featured in this article.