Experimental and numerical analysis of asphalt flow in a slump test

Abstract

The mechanical behaviour of uncompacted asphalt mixtures is still not well understood, threatening directly to the pavement practices such as control of mixture's workability and segregation. This situation may become even worse due to the gradually increasing complexity and advances in paving materials and technologies. This study adopts a slump flow test based on concrete technology and a Discrete Element (DE)-based numerical tool to investigate the mechanical behaviour of uncompacted asphalt mixture from a microstructural point of view, particularly focusing on the bituminous binder effects. The combined experimental and numerical analysis indicates that bitumen distinctly influences the contact interactions within the mixture and thus its macroscopic flow, which can be physically interpreted as a combined effect of lubricated friction and bonding force. Additional case studies demonstrate that the DE model is capable of simulating the flow response of asphalt mixtures under changed particle contact conditions and driven force.

Keywords:

• Asphalt mixture
• slump test
• discrete element method
• large displacement

1. Introduction

1.1. Background

Good functionality and performance of asphalt pavements depend not only on the optimal structural and material design principles, but also the right practices of field construction. Due to the complex mechanical behaviour of asphalt before and during compaction, some challenging field issues may popup, such as workability and size segregation-related problems, eventually creating uneven rough surfaces and reduced durability of the pavements after construction (Gudimettla, Cooley, & Brown, 2004; Stroup-Gardiner & Brown, 2000). Moreover, in order to meet the sustainability goals for roads, development and application of new materials have gained momentum, including such as polymer modified bitumen as well as additives for warm or cold mixing technologies with foamed/emulsified bitumen, often in combination with reclaimed asphalt or industrial waste. Such innovations, however, make the mechanical behaviour of asphalt mixtures even more complex and variable. This is not only true for the mixtures after placing but also during construction, since workability and compactability of asphalt mixtures are closely influenced by type and gradation of aggregates, viscosity of binder, and temperature (Bayer, 1994; Leiva & West, 2008). In the meanwhile, some studies claimed that the correlation between compactability and bitumen viscosity is not as evident for warm mix asphalt as the reduction in friction between particles (Canestrari, Ingrassia, Ferrotti, & Lu, 2017; Hanz, Faheem, Mahmoud, & Bahia, 2010). Thus, it appears that the mechanical behaviour of asphalt mixtures at these large displacement situations is very sensitive and variable, and difficult to be adequately assessed or predicted through existing modelling or experimental techniques.

Generally speaking, improved understanding of the material's macroscopic responses can be achieved by a close link to the properties of its individual constituents and their interactions at microstructural level. In order to fill this gap, different numerical simulation explorations have been found while among which, the Finite Element (FE) and Discrete Element (DE) methods are frequently used. In comparison to the FE method, The DE method is more flexible in quantitatively defining particles' shape and size distribution while, more importantly, it allows for simulating discrete flow of the elements with large translational and rotational movements, which suits with the situation of this study. The DE method was firstly introduced for studying granular assemblies by Cundall and Strack (1979). Asphalt mixture, nearly 90% of which is crushed stones, can also be taken as a granular system under certain assumptions. The method has thus been applied to predict the mechanical behaviour of both compacted and uncompacted asphalt mixtures. For compacted asphalt mixture, studies are found on using the method for predicting and analysing bulk modulus, dilation, fracture or permanent deformation of the mixture (Collop, McDowell, & Lee, 2006; Kim & Buttlar, 2009; Ma, Zhang, Zhang, Wang, & Huang, 2018; You, Adhikari, & Dai, 2008). For uncompacted asphalt mixture, the method has been employed to investigate the mixture's compactability by simulating its densification process under different compaction modes and with different aggregate characteristics (Chen, Huang, Chen, & Shu, 2012; Chen, Huang, Shu, & Hu, 2014; Gong, Liu, Zhou, & You, 2018; Roozbahany & Partl, 2016). These studies indiate that DE method is able to simulate asphalt flow under certain conditions whereas, the mechanisms of the involved microstructural activities and how they affect the macroscopic responses of the mixture are still poorly understood.

1.2. Goal and objectives of this research

Since the mechanical behaviour of asphalt mixtures under large displacement situations is complex, effective investigation tools, either experimentally or numerically, are still missing. This study aims at developing such an analysis approach for studying the flow response of uncompacted asphalt mixture and, in which, the microstructual properties are considered in a rational way. To proceed, the following specific objectives are included: (i) feasibility analysis of using a slump test for evaluating the flow of uncompacted asphalt mixture; (ii) development of a DE-based numerical tool suitable for quantitatively studying the mechanical behaviour of uncompacted asphalt material and, capable of explicitly capturing the influence of binder on material flow characteristics; (iii) demonstration of the approach's capability by investigating the flow of the mixtures under different contact conditions and changed driven force, e.g. vibration.

2. Methodology

The first important task is to identify a simple, quick and reliable test method in order to capture the flow response of an uncompacted asphalt mixture in a quantifiable way, keeping in mind that the test should be numerically modelled with finite computation effort. Hence, the slump test, a typical flow test widely used in checking workability of fresh cement mortar or concrete, is selected. Meanwhile, in order to develop a numerical model which can reasonably simulate the flow response of asphalt mixture, the numerical model should be developed by a proper application of microstructural mechanics and, importantly as well, with an acceptable calibration. To proceed, this section presents the detailed descriptions of the experimental test as well as the development of the numerical model.

2.1. Experimental study

2.1.1. Test setup

The setup used for performing the slump flow test is known as Abraham's cone, sizing of 200 mm (bottom diameter)×100 mm (top diameter)×300 mm (height). The experimental procedure consists of several steps in succession: (i) a certain mass of hot mixing asphalt mixture is prepared and maintained at a fixed temperature. (ii) The uncompacted asphalt mixture is gradually filled into the cone by a hand shovel until reaching the cone's height of 300 mm, without any pressing. This important step should be carried out cautiously for minimising inhomogeneity of the microstructure, but, at the same time as fast as possible in order to minimise non-uniformity of temperature distribution. (iii) The cone, supported by a metal cavity with smooth surface, is subsequently lifted up in an instant manner, pushing the particles to fall and roll apart under their own weights. The final slump height, being inversely proportional to the flowability of a material, can be selected as an index for quantitatively assessing the degree of a mixture's flow. From an experimental point of view, the suitability of slump test for studying the flow of asphalt mixture can be evaluated according to the following criteria: (i) the capability of the test, i.e. whether the test can reasonably capture the flow responses of different mixture types at varying environmental and loading conditions; (ii) the repeatability of the test, i.e. whether the quantitative index is measured in a repeatable way.

2.1.2. Materials and test plan

Asphalt mixtures of SMA16 type (i.e. stone mastic asphalt with a nominal maximum size of 16 mm) were prepared in the laboratory. The aggregates are natural crushed granite stones, with filler sieved from the granite fines (0 ∼ 2 mm). As binder, 70/100 pen grade neat bitumen was selected and its effect to the flow of the mixture was investigated by preparing mixture specimens with varying bitumen content 0.0%, 3.1%, 3.75% and 6.1% by weight. In order to check the effect of temperature, tests were carried out at two different temperatures (155${}^{\circ }$C and 135${}^{\circ }$C), approaching the boundary limits of the typical temperature range for compaction. The test results and theoretical discussions are given in Section 3.

2.2. Numerical simulation study

DE method is a numerical method to study the interactions among discrete elements, using Newton's second law and force-displacement law. Newton's second law describes the motion of a particle resulting from the forces acting on it and the force-displacement law is used to find contact forces from displacements. The calculations cycled in the computation alternate between invoking Newton's second law to the particles and force-displacement law at the contacts through a time-stepping finite difference scheme. For the interest of this contribution, during the model development the main concerns are the identification of the relevant physics and their incorporation into the model, followed by parameter identification and capability demonstration of the model.

2.2.1. Contact model for uncompacted asphalt mixture

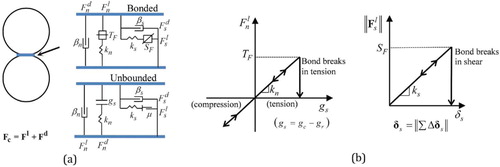
In a discrete element study, all the particles are assumed to be rigid bodies while the interactions at contacts between the bodies are closely tacked, and these interactions are primarily determined by the selected contact model. In this study, asphalt mixture is simulated to consist of graded granular particles that are coated with a thin film of bituminous matrix (mineral fillers and bitumen binder). Therefore, the differences in responses between the unbound and bound granular material (i.e. asphalt mixture) can be ascribed to the bituminous coating. The most important impacts on contact behaviours of the particles from bituminous coating are lubricated friction in shear, as well as a certain adhesion force in both shear and normal directions of contact. If the lubrication effect of bituminous film is active, a reduction in friction between the asperities can occur; if the adhesion effect of bituminous film is active, adhesive force can be induced at the contacting plane, preventing the particles from sliding or separating.

In the actual model, the bituminous coating is assumed to have a negligible thickness while its effects on particle interaction are governed by the selected contact models presented in Figure 1. In the contact model, for both normal and shear directions, the contact force ${\mathbf{F}}_{\mathbf{c}}$ is resolved into linear ${\mathbf{F}}^{\mathbf{l}}$ and dashpot components ${\mathbf{F}}^{\mathbf{d}}$. The linear component provides elastic, frictional and bonding behaviour, while the dashpot component is a force imposed to account for viscous damping. When bonded, the contact behaviour is linear elastic until the linear force exceeds the tensile or shear strength limit. After breakage of the bond, the behaviour is linear elastic and the friction is accommodated by imposing a Coulomb-slip condition on the shear direction. For this specific study, the sliding friction can be utilised to inspect the lubrication effect of bitumen, while contact bonds can be utilised to capture the adhesion effect. In the following, all lateral simulations and analyses will be essentially based on this assumption. Several remarks for the model should be noted: (a) the model is activated if the contact is bonded or if the surface gap between contact points is less than or equal to zero; (b) if a new contact is detected, a new bond is assigned; (c) slip cannot occur if a contact bond is present; (d) the dashpot force can become tensile if a contact bond is present; (e) the dashpot force does not depend on the slip state if a contact bond is present; (f) if the tensile-strength limit is exceeded, breaking of the bond in tension occurs. If the bond has not broken in tension, then the shear strength limit must be enforced. If the shear-strength limit is exceeded, then shear break of the bond occurs; and (g) the strength limits are enforced prior to the enforcement of the sliding condition and update of the force in the dashpot. Table 1 lists the associated contact model parameters used in the simulations. Some of them might have an important effect on flow and are further discussed as follows:

Figure 1. (a) Contact models and (b) force–displacement relations for normal and shear directions.

Table 1. List of the important contact model parameters.

Parameter	Value	Unit
Effective modulus	1×10${}^8$	Pa
Normal to shear stiffness ratio	1.0	–${}^{\mathrm{a}}$
Bulk density	2.7×10${}^3$	kg/m${}^3$
Sliding friction coefficient, $\mu$	To be determined	−
Normal and shear bond strength, $St{}_{n,t}$	To be determined	Pa
Critical viscous damping ratios, normal and shear	0.3	−
Local damping ratio	0.1	−

${}^{\mathrm{a}}$ Not available.

• Coefficient of sliding friction. The bituminous film affects the sliding friction condition between the coated aggregates. The situation can be taken as a general lubrication problem, where the coefficient of sliding friction between two lubricated asperities can be affected by thickness and viscosity of the coating film (Maru & Tanaka, 2007). Depending on the binder type and content, the coefficient of friction between coated aggregates can vary as well, e.g. ranging from around 0.5 for unbound granular material to 0.1 for pure bitumen (Ingrassia, Lu, Canestrari, & Ferrotti, 2018).

• Contact bond strengths. A bond with certain strength limit is installed at contacts between aggregates to introduce the adhesive/cohesive force from bituminous coating which, in general, would impose some extra resistance to the flow of mixture in bulk. This bonding force is difficult to be experimentally determined and will be calibrated via slump test.

• Damping parameters. In adopted PFC software, three types of mechanical damping are available for dissipating extra kinetic energy in the particle system: (1) viscous damping: a damping approach to reproduce realistic response of free vibration; it is appropriate for dynamic problems such as the slump flow test of this study; (2) local damping: a damping acts on each particle, by applying a damping force with a magnitude proportional to the summated unbalanced force. It is normally used in static or quasi-static problems; (3) hysteretic damping: similar to local damping; it is considered for problems dominated by rapid impacts. In the circumstance of large flow, sliding friction and the viscous damping are major energy dissipation means, while a very low local damping coefficient is used to further stabilise the system.

2.2.2. Particle shape effect

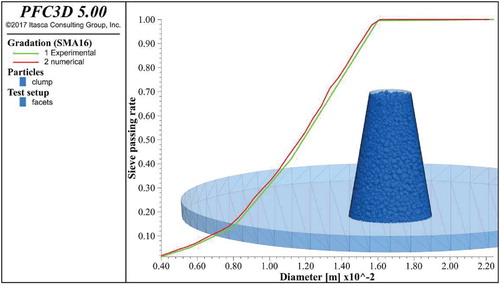
Particle interlocking that reduces the rotations of particles is introduced into the model by using non-spherical shape particles. As shown in Figure 2, a clump template consisting of five spherical pebbles of the same radius is created via the clumping technique in PFC. The gravitational centres of the pebbles have equal distance between each other, while their connections form a standard triangular bipyramid. The length of each connection line is 0.6 times the pebble diameter. Meanwhile, the diameter of a clumped particle is defined as diameter of a spherical particle with equivalent volume. In the simulation, all particles are produced using the same clump template, while the size distribution of particles is determined by fitting to the gradation curve of the SMA16 mixture that has been used in experimental tests. One should also note that the effects to mixture's flow behaviour by aggregates will not be systematically examined in this paper, since only one type of granular material is selected without any change in shape or size distribution. Instead, a sole inspection is recommended to be conducted in future inquires, as in principle the flow behaviour of asphalt mixtures may considerably depend on the type, size distribution, and shape (e.g. form, angularity and surface smoothness) of the complex granular particles.

Figure 2. Clump template used to introduce the particle shape effect.

2.2.3. Simulation of slump flow test

The numerical setup for the DE model was established following the described slump test. Initially, particles, possessing the defined clump template shape and the size distribution of the SMA16 mixture used in experiments, were randomly generated and distributed in the Abraham's cone. Very fine particles ($<$4 mm in dimeter) saturate into the bituminous matrix and are not counted in the particle system. Figure 3 illustrates the initial particle system generated for simulation of the slump test, which consists of 41,845 clumps in total. The contact model presented in Section 2.1 is assigned to the particle–particle and particle–wall contacts within the system. The cone is then vertically lifted up, spontaneously propelling the particles to fall and roll under their own weights. The flow simulation stops until the particles are mostly settled down in the cavity.

Figure 3. Generation of the initial particle system for slump test simulation.

3. Experimental results and discussion

3.1. Laboratory measurements

The final slump heights of different mixtures, each of which was averaged by two repetition tests, are presented in Table 2. Since the standard deviations are small in comparison to the mean values of the measured slump heights, a satisfactory repeatability of the test can be concluded.

Table 2. Slump height measurements of asphalt mixture with varying binder content.

SMA mixture	0.0$\mathrm{\%}$ bitumen	3.1$\mathrm{\%}$ bitumen		3.75$\mathrm{\%}$ bitumen		6.1$\mathrm{\%}$ bitumen
		155${}^{\circ }$C	135${}^{\circ }$C	155${}^{\circ }$C	135${}^{\circ }$C	155${}^{\circ }$C	135${}^{\circ }$C
Slump height (cm)	9.3	9.75	9.85	10.7	10.8	8.25	8.8
	(0.14)^a	(0.21)	(0.07)	(0.28)	(0.28)	(0.07)	(0.14)

${}^{\mathrm{a}}$Standard devitaion.

Apart from the macroscopic measurements, a few pertinent findings on the microstructural activities during flow are worth mentioning: (i) the unbound granular mixture slumps promptly, completing in less than one second. With increasing bitumen content, the slump process takes more time to complete, which can be due to the viscous nature of bituminous matrix. For the same reason, the movements of particles are becoming less vigorous with increasing binder content, ending with different accumulation shapes as shown in Figure 4. (ii) In the second graph of Figure 4, some fines are found piled up on the top, which can be taken as indication of a certain degree of segregation of the mixture's gradation. The potential reason is that at very low binder content there is a lack of adhesion within the system. Hence, the bituminous fines, instead of rolling away with particles, just drop through the free paths and accumulate over the particles that do not move. More delicate experimental design is needed to quantitatively investigate these microstructural activities which, however, is not the main focus of this contribution and left as future work.

Figure 4. Views of the final slump state of uncompacted asphalt mixtures with varying binder content.

3.2. Flow mechanisms of asphalt mixture

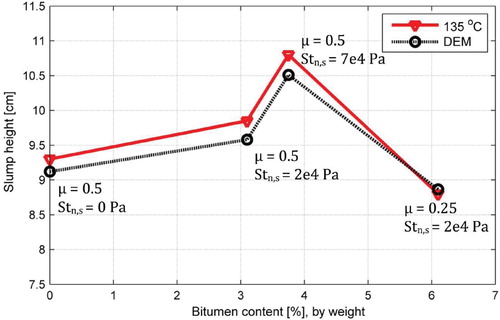
The above slump flow test demonstrates that bitumen distinctly affects the free flow response of asphalt mixture. Thus, the possible causes and mechanisms are investigated and, accordingly, the slump height of asphalt versus bitumen content is plotted in Figure 5. The plot shows the slump height increases progressively with increasing binder content from 0% up to 3.75%; however, when bitumen content reaches a level above 6.1%, the slump height conversely drops to a level lower than for the unbound mixture. These test results confirm that the bitumen content plays an important role in the flow behaviour of uncompacted asphalt mixtures. On the other hand, little difference is noted between tests at 135${}^{\circ }$C and 155${}^{\circ }$C, indicating that within the typical compaction temperature range the slump height measurement of asphalt mixture is not very sensitive to the temperature variations, i.e. viscosity change of bitumen. From the microstructural perspective, the bituminous matrix would primarily affect the contact interactions among the coated aggregate particles, mainly referring to the sliding friction condition and adhesive/cohesive bonding.

Figure 5. Measurement results of final slump height versus binder content.

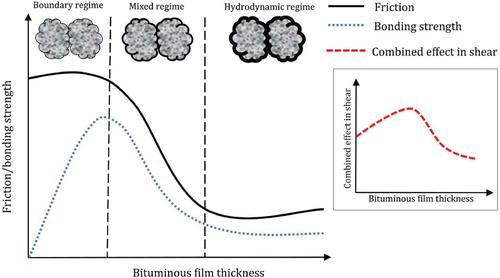
• Sliding friction. In tribology science (Bayer, 1994; Maru & Tanaka, 2007), the sliding friction between asperities of two rough surfaces can described by the lubricant's film thickness that is affected by a factor of $\eta V/W$, where $\eta$ is the lubricant's viscosity, V is the average sliding velocity and W is the normal load. The relationship, as qualitatively shown in the dark full curve in Figure 6, consists of several regimes: (i) the boundary regime, where the friction is controlled by the direct contacts between asperities and keeps almost constant with increasing film's thickness as long as this film thickness is significantly lower than the size of the asperities; (ii) the mixed regime, in which the direct contact between two solids is reduced, causing to a continuous reduction in friction; and (iii) the hydrodynamic regime, where the two asperities do not longer have physical contact and the lubricant controls the friction which is at a very low level. For the interest of this study, by gradually increasing the bitumen content a similar trend of friction between bituminous coated aggregates can be assumed.

• Bonding force. At high temperature, the adhesion/cohesion force between asphalt particles is an integrated action of such as viscous, capillary, adhesion, and gravitational forces induced by the bituminous matrix. The force, which is complex and difficult to be accurately measured, depends on the rheological and chemical properties of the bituminous matrix as well as the composition and characteristics of aggregate particles (Huang, Robertson, Branthaver, & McKay, 1999; Poulikakos, Tiwari, & Partl, 2013). In order to capture the effects in a rough way, a brittle bond with certain strength limit, which involves with film's thickness, can be assumed. According to some macroscopic tests (Frolov, Vasil'eva, Frolova, & Ovchinnikova, 1983), the relation of bonding strength versus bituminous film thickness is qualitatively shown as dotted blue curve in Figure 6. Its shape can be explained as follow: (i) At the beginning, with gradually increasing film thickness, the aggregate particles of the two substances experience progressively complete coating and the mainly adhesive bonding strength between them grows accordingly; (ii) with continuously increasing film thickness, cohesion failure within the bituminous film develops and since cohesion strength is normally lower than adhesion, the overall bonding strength curve gradually changes from increase to decline; (iii) by the end, the cohesive failure becomes dominant and the bonding strength infinitely approaches to a minimum level. In reality, both friction and bonding effects are at presence in asphalt mixture in shear direction of a contact and, therefore, a combined effect of the both is further qualitatively explained as the dashed red curve in Figure 6.

Based on the mechanisms illustrated in Figure 6, the experimental results in Figure 5 can be further interpreted from a microstructural point of view. Firstly, by increasing bitumen content from 0% to 3.1% the system is still in boundary friction regime where the particles have direct collisions and the lubrication effect of the bituminous coating is negligible. Further to 3.75%, at the same time, the observed progressive increase in slump height can be attributed to the gradual increase of adhesion bonding strength. With increasing bitumen content up to 6.1%, the friction within mixture changes to the mixed or hydrodynamic regime, the adhesive bond loses its influence and the cohesion within bituminous matrix dominates bonding effect; both friction and bonding force are thus low at high bitumen content, leading to the increase in the mixture's flow ability and correspondingly a decrease in slump height. Hence, bitumen profoundly affects the mechanical flow of asphalt mixture which, theoretically, can be interpreted as combined action of friction and adhesive/cohesive bonding force at microstructural scale.

Figure 6. Qualitative illustrations of friction and bonding strength versus bituminous film thickness.

4. DE analysis of asphalt mixture flow

In order to properly simulate the flow response of asphalt mixtures, it is very important to choose suitable values for the contact bond model parameters. Among them, the bitumen-related model parameters, mainly the coefficient of sliding friction and bond strength, are the important ones and therefore identified using previous slump tests. Apart from that, the capability of the simulation tool in predicting the macroscopic flow of the mixtures is further demonstrated via additional case studies at different contact and force conditions.

4.1. Model parameter identification

The parameter identification process consists of two successive steps: (i) identification of the effects from granular particles such as size distribution and irregular particle shape, using slump test results of the unbound mixture; and (ii) calibration of bitumen-related contact model parameters using slump test results of asphalt mixtures and associated theoretical interpretations. Figure 7 shows a general example of the final state of slump flow test from simulation (asphalt mixture, 3.75% binder). The slump height in each simulation is collected by averaging the position height of the top 10 particles.

Figure 7. Illustration of the DE simulation result of a complete slump test.

Firstly, at binder content of 0.0%, the particle system is taken as an unbound mixture consisting of irregularly shaped particles. By choosing 0.5 for the coefficient of friction (typical level for unbound materials) and bond strength of 0 Pa, trial simulations were performed to identify a suitable aggregate shape. Accordingly, the clump template explained in Section 2.2.2 was identified and fixed, since a good fit between the model simulation and experimentally determined slump height of the unbound mixture was found. Thereafter, the effects of bitumen on slump flow were further calibrated based on the experiments and associated to the interpretations in Figure 6. At binder content of 3.1% and 3.75%, the thickness of coating is too low to change the sliding condition between two asperities and still falls into the boundary friction regime. Meanwhile, the formation of adhesion between aggregates increases with continuously adding bitumen and, accordingly, the bonding strength grows. Hence, at binder content of 3.1% and 3.75%, asphalt particles are assumed to experience the same sliding friction as in the unbound mixture with a friction coefficient of 0.5. The bond strengths are numerically evaluated, finding St${}_{n,t}$= 2×10${}^4$ Pa for the mixture with 3.1% of binder and St${}_{n,t}$ = 7×10${}^4$ Pa for the mixture with 3.75% of binder. By increasing the binder content to 6.1%, a significant rise in coating film thickness occurs causing huge reduction in both sliding friction and bonding force. By assuming a friction coefficient of 0.25, a friction level between unbound granular material and pure bitumen material, the bond strengths are numerically identified to be 2×10${}^4$ Pa. As seen in Figure 8, the model simulations closely agree with the experimentally measured slump heights. To conclude, the developed simulation tool could well reproduce the experimentally determined flow response of asphalt mixtures and, importantly, the effect from bituminous matrix is well captured in a reasonable way.

Figure 8. Comparison of final slump height between measurements and DE model prediction.

4.2. Model evaluation

In this subsection, the capability of the simulation tool in predicting the macroscopic flow of an asphalt mixture is further investigated. Hence, several case studies based on slump tests are performed, where wide range selection of the contact conditions as well as another driven force, i.e. vibration, are made.

4.2.1. Model parametric study

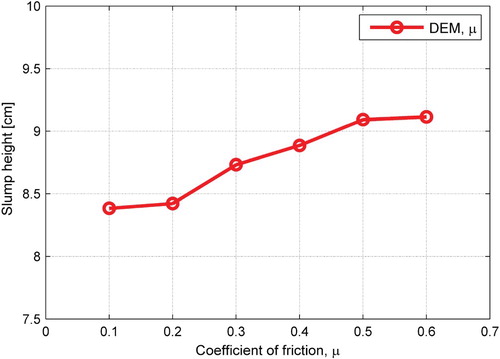
The influences of physical contact conditions on macroscopic flow response of the mixture as a whole are examined. To proceed, a parametric sweep study is firstly conducted to examine the effect of friction to the macroscopic flow, while the bonding force is excluded by assigning bond strengths of 0 Pa in the contact model. A number of simulations are launched at varying coefficients of sliding friction $\mu$. The final slump height results are plotted in Figure 9. With increasing coefficient of friction, a gradual increase in slump height is observed, which proves that friction prevents particles from shear sliding and thus restrains the macroscopic flow of a mixture. However, from a quantitative perspective, less than 10% increase in slump height is observed for a wide selection range of $\mu$ (varying from 0.1 to 0.6), suggesting the effect from friction alone is, in general, is not very strong.

Figure 9. Slump height versus coefficient of sliding friction at zero bonding strength.

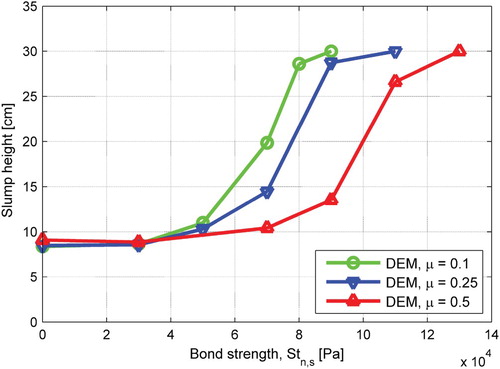
Apart from friction, the bonding force due to the rheological nature of the bituminous matrix can also play an indispensable role in the microstructural interactions within a mixture. A number of simulations are launched for a wide range of bond strength and friction coefficients, aiming at quantifying the possible effects from bonding strength and its coupling with sliding friction. Information on slump heights from the simulations is plotted in Figure 10. It shows that the adhesive/cohesive bonding force between particles resists the macroscopic flow of mixtures while the resistance greatly depends on the amplitude of bonding force as well as the coefficient of friction.

Figure 10. Slump height versus bonding strength at varying sliding friction.

At a constant friction condition, the slump height starts with little change when the bond strength is low and easily exceeded by the particle's contact forces; as the bond is difficult to break with increasing bond strength, an exponential increase in resistance to flow is observed. Hence, the resistance to the flow of asphalt mixtures due to the bonding effect is nonlinearly proportional to the adhesion/cohesion strength of the bituminous film, indicating a parabolic trend. Moreover, the bonding force has a coupling effect with sliding friction, which notably affects the mixture's flow. The general trend shows that for lower friction coefficients the resistance to flow versus bond strength increases at a faster pace, and thus the entire system reaches the cut-off of 'zero' flow (i.e. slump height of 30 cm) at a lower strength limit.

It is known that a Coulomb friction criterion is imposed in shear direction after breakage of the bond. This influences directly the update of the shear force at the contact point and thus the state of contact (e.g. sliding or not). For explaining the higher flow at a larger coefficient of friction (fixed bond strength), the summated shear forces (absolute values) within the system at different friction levels are extracted and compared in Figure 11(a), at the same bonding strength of 7×10${}^4$ Pa (corresponding to 3.16 N of the maximum bonding force at contact plane). Figure 11(a) shows that for all friction levels, a high total shear contact force within the system is noted at the start of slumping (at mechanical age of 1×10${}^{-3}$ s), which can be taken as the trigger of bond breakages and massive flow of the particles. High peak values of the total shear contact force are observed for high coefficients of friction. The corresponding cumulative distribution of all shear contact forces at the peak values of the total is further shown in Figure 11(b). Combing Figure 11(a, b), one can confirm that the number of shear contact forces exceeding the bonding force limit (3.16 N) is higher at high friction level, which induces more bond breakages and thus more flow of the particles.

Figure 11. (a) Total shear force as function of mechanical age; (b) cumulative distribution of individual shear forces at mechanical age of 1×10${}^{-3}$ s.

4.2.2. Mixture's flow under vibrational force

Another demonstration study is carried out to investigate the flow under vibrational loading, aiming to shed some light on mixture's segregation issue, e.g. during its transporting process. The initial particle system was regenerated using the same gradation (SMA16), whereas the total number of particles is reduced by half in order to save computational effort. As shown in Figure 12(a) left, these particles are randomly distributed in a cylindrical container ($\mathrm{\Phi }=200$ mm) and classified into two groups based on their diametrical sizes: ‘Small size’ group with diameters of 0 ∼ 8 mm, and ‘Big size’ group with dimeters of 8 ∼ 16 mm. A displacement-controlled vibration load, i.e. ${\delta }_d\sin \left(2\pi ft\right)$ is applied to the container alone the vertical direction, in which a displacement amplitude ${\delta }_d$ of 8 mm and frequency f of 10 Hz are used. Two cases are studied: (i) unbound mixture with friction coefficient of 0.5 and bonding strength of 0 Pa; (ii) asphalt mixture with friction coefficient of 0.5 and bonding strength of 7×10${}^4$ Pa. The vibration is applied for 0.5 s, i.e. 5 cycles of vibrating, and then a 0.5 s of pause is given for the particles to settle down.

Figure 12. Before and after vibration: (a) particles' distribution within asphalt mixture; and (b) comparison of mean heights of small and big particles.

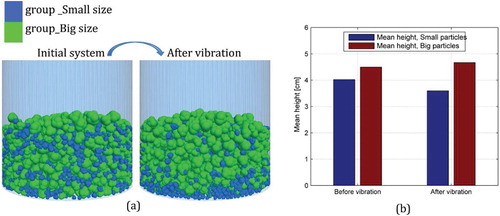
Figure 12(a) presents also the particles' spatial distribution within asphalt mixture (case ii) after vibration. One can notice that due to the vibration loading small particles tend to non-uniformly distribute along vertical direction and with a tendency to accumulate at the bottom of container, whereas for big particles an opposite trend of flow is indicated. A further quantitative analysis is conducted by comparing the mean vertical height of small particles and big particles before and after vibration, as shown in Figure 12(b). The mean height of small particles increases after vibration whereas a decrease trend is observed for big particles, displaying again that particle segregations are induced within asphalt mixture. An index named $H_{\mathrm{small}/\mathrm{big}}$ is proposed to characterise the level of segregation, which is defined as the ratio of averaged position height of small particles with that of the big particles. The calculated $H{}_{\mathrm{small}/\mathrm{big}}$ in the initial particle system is 0.894 while, after vibration, $H{}_{\mathrm{small}/\mathrm{big}}$ decreases to be 0.771 for asphalt mixture and 0.772 for unbound mixture. Hence, vibration-induced segregation is confirmed in both asphalt and unbound mixtures; meanwhile, the weak bonding force from bituminous matrix does not notably influence mixture's segregation under the selected vibration condition. In future analysis, it's worth noting that the segregation difference between the unbound and asphalt mixtures at high frequency vibration might be better captured by taking the viscoelastic effect of binder into account.

5. Concluding remarks

The mechanical behaviour of uncompacted asphalt mixture is complex while the bottleneck mainly lies in a lack of theoretical understanding of the microstructural mechanisms and how they affect the macroscopic responses of the mixture. In this paper, a combined experimental and DE-based numerical approach suitable for examining flow of asphalt mixtures has been developed. Based on this novel approach, an in-depth analysis of the flow responses from uncompacted asphalt mixtures was conducted resulting in the following conclusions:

• The slump test, which explicitly demonstrates the free flow behaviour of a material, is found to be a promising experimental tool for studying the flow of uncompacted asphalt mixture. Major findings from the actual measurements include: (i) an acceptable repeatability of the slump height measurement is found, indicating the reliability of the test method. (ii) The effects to the mixture's macroscopic flow are captured from the bituminous matrix through a comparison of measured slump heights while the underlying mechanisms are qualitatively described by a combined effect of lubricated friction and adhesion/cohesion bonding between the aggregate contacts. (iii) The slump flow is not sensitive to temperature in the tested range (i.e. 135${}^{\circ }$C ∼ 155${}^{\circ }$C) which, however, does not imply that the test is insensitive at another temperature range (e.g. lower than 135${}^{\circ }$C).

• A DE model suitable for investigating the mechanical behaviour of uncompacted asphalt mixtures has been developed and, particularly, the important physical mechanisms determining the microstructural interactions were properly modelled. These physics mechanisms rely on parameters such as size distribution and irregular shape of graded aggregates, as well as the lubricated friction and adhesive/cohesive bonding induced by the bituminous matrix. By choosing model parameter values in a rational way, a satisfactory agreement between model simulation and experimental measurement of the slump height is found. This suggests that the numerical approach can model the microstructural interactions within a mixture and thus capture its macroscopic flow response in a reasonable way. Additional case studies demonstrate that the DE model is capable of simulating the flow response of asphalt mixtures under changed contact condition and driven force.

In next research stage, the computational tool has to be applied for investigating mixture-related field issues, such as aggregate segregations. In addition, the contact model can also be further advanced. For instances, (i) the identified contact model parameters must be expressed as function of bitumen-related factors, such as viscosity, volume content, and temperature. (ii) Since the viscous features of the bituminous matrix might not be sufficiently captured in the current contact bond model, e.g. the bonding effect is more likely to vanish in a ductile way, a viscoelastic contact model should be considered in future for improving the prediction of the flow versus time.

Nomenclature

$\mathrm{Notation}$	=	$\mathrm{Commentary}$
${\mathbf{F}}_{\mathbf{c}}$	=	Contact force
${\mathbf{F}}^{\mathbf{l}}$	=	Linear force component
${\mathbf{F}}^{\mathbf{d}}$	=	Dashpot force component
$S{t}_{n,s}$	=	Tensile and shear strengths
η	=	Viscosity
λ	=	Film's thickness
$T_F\mathrm{\&}{S}_F$	=	Tensile force and shear force
${\beta }_s\mathrm{\&}{\beta }_n$	=	Normal and shear critical damping ratios
$g_s$	=	Surface gap
$g_c$	=	Contact gap
$g_r$	=	Reference gap
${\delta }_s$	=	Relative shear displacement
$k_n\mathrm{\&}{k}_s$	=	Contact normal and shear stiffness [force/length]
$F_n^l\mathrm{\&}{F}_s^l$	=	Normal and shear components of the linear force
μ	=	Coefficient of sliding friction
V	=	Sliding velocity
W	=	Normal load
f	=	Frequency, Hz
${\delta }_d$	=	Displacement amplitude

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The authors would like to acknowledge the financial support from Swedish Research Council Formas under FORMAS with project grant nr. 2012-1349.