On an efficient multiple time step Monte Carlo simulation of the SABR model

Abstract

In this paper, we will present a multiple time step Monte Carlo simulation technique for pricing options under the Stochastic Alpha Beta Rho model. The proposed method is an extension of the one time step Monte Carlo method that we proposed in an accompanying paper Leitao et al. [Appl. Math. Comput. 2017, 293, 461–479], for pricing European options in the context of the model calibration. A highly efficient method results, with many very interesting and nontrivial components, like Fourier inversion for the sum of log-normals, stochastic collocation, Gumbel copula, correlation approximation, that are not yet seen in combination within a Monte Carlo simulation. The present multiple time step Monte Carlo method is especially useful for long-term options and for exotic options.

Keywords:

• SABR model
• Exact simulation
• Monte Carlo methods
• Copulas
• Stochastic collocation
• Fourier techniques
• Exotic options

AMS Subject Classifications:

• C15
• C63

1. Introduction

The Stochastic Alpha Beta Rho (SABR) model (Hagan et al. 2002) is an established stochastic differential equation (SDE) model which, in practice, is often used for interest rates and foreign-exchange (FX) modelling. It is based on a parametric local volatility component in terms of a model parameter, , and reads(1)

Here, denotes the forward price of the underlying asset , with r an interest rate, the spot price and T the maturity. Further, represents a stochastic volatility process, with , and are correlated Brownian motions with constant correlation coefficient (i.e. ). The parameters of the SABR model are (the volatility of volatility, vol-vol), (the variance elasticity) and (the correlation coefficient). Because of a practically very useful closed-form expression for the implied volatility, Hagan et al. (2002) and Obloj (2008), the model has gained its popularity. However, since this expression is derived by perturbation theory, the formula is not always accurate for small strike values or for long time to maturity. By the one time step SABR method in Leitao et al. (2017), we can efficiently calculate accurate implied volatilities for any strike, however, only for short times to maturity (less than two years). This fits well to the context of FX markets.

Here, we extend the one time step Monte Carlo method from Leitao et al. (2017), and propose a multiple time step Monte Carlo simulation technique for pricing options under the SABR dynamics. We call it the mSABR method. With this new simulation approach, we can price options with longer maturities, payoffs relying on the transitional distributions and exotic options (like path-dependent options) under the SABR dynamics, overcoming the limitations of Hagan’s formula in the mentioned situations.

Because a robust and efficient SABR simulation scheme may be involved and quite expensive, we aim for using as few time steps as possible. This fact, together with the long-time horizon assumption, implies that we focus on larger time steps. In this context, the important research line is called exact simulation, where, rather than Taylor-based simulation techniques, the probability density of the SDE under consideration is highly accurately approximated. Point-of-departure is Broadie and Kaya’s exact simulation for the Heston stochastic volatility model (Broadie and Kaya, 2006). That method is, however, time-consuming because of multiple evaluations of Bessel functions and the use of Fourier inversion techniques on each Monte Carlo path. Inspired by this approach, in Smith (2007) and van Hasstrecht and Pelsser (2010), computational improvements were proposed. Furthermore, Andersen (2008) presented two efficient alternatives to the Broadie and Kaya scheme, the so-called Truncated Gaussian and the Quadratic Exponential (QE) schemes.

For the SABR model, exact Monte Carlo simulation is nontrivial because the forward process in (1(1) ) is governed by constant elasticity of variance (CEV) dynamics (Cox 1996, Schroder 1989). In Islah (2009), the connection between the CEV and a squared Bessel processes was explained, and an analytic approximation for the SABR conditional distribution based on the non-central distribution was presented. The expression relies on the stochastic volatility dynamics, but also on the integrated variance process (which itself also depends on the volatility).

An (approximately) exact SABR simulation can then be subdivided in to the simulation of the volatility process, the simulation of the integrated variance (conditional on the volatility process) and the simulation of the underlying CEV process (conditional on the volatility and the integrated variance processes). Based on this, Chen et al. (2012) proposed a low-biased Monte Carlo scheme with moment-matching (following the techniques of the QE scheme by Andersen (2008)) and a direct inversion approach. For the simulation of the integrated variance, they also employed moment-matching based on conditional moments that were approximated by a small disturbance expansion. In Cai et al. (forthcoming), the authors employed direct inversion for the forward distribution and used a Laplace transform inversion technique to simulate the integrated variance. Kennedy and Pham (2014) provided the moments of the integrated variance for specific SABR models (like the normal, log-normal and displaced diffusion SABR models) and derived an approximation of the SABR distribution. In Lord and Farebrother (2014), a summary of different approaches was presented.

In this work, we approximate the distribution of the integrated variance conditional on the volatility dynamics by joining the two involved marginal distributions, i.e. the stochastic volatility and integrated variance distributions, by means of copula techniques. With both marginal distributions available, we use the Archimedean Gumbel copula to define a multivariate distribution which approximates the conditional distribution of the integrated variance given the stochastic volatility.

An approximation of the cumulative distribution function (CDF) of the integrated variance can be obtained by a recursive procedure, as described in Zhang and Oosterlee (2013), originally employed to price arithmetic Asian options. This iterative technique is based on the derivation of the characteristic function of the integrated variance process and Fourier inversion to recover the probability density function (PDF).

The fact that we need to apply recursion and compute the corresponding characteristic function, PDF and CDF of the integrated variance for each Monte Carlo sample at each time step, makes this approach however computationally very expensive (even with the improvements already made in Leitao et al. (2017)), like the Heston exact simulation. In order to reduce the use of this procedure as much as possible, highly efficient sampling from the CDF of the integrated variance is proposed, which is based on the so-called Stochastic Collocation Monte Carlo sampler (SCMC), see Grzelak et al. (2015). The technique employs a sophisticated interpolation (based on Lagrange polynomials and collocation points) of the CDF under consideration.

As will be seen, the resulting ‘almost exact’ Monte Carlo SABR simulation method that we present here (the mSABR method), contains several interesting (and not commonly used) components, like the Gumbel copula, a recursion plus Fourier inversion to approximate the CDF of the integrated variance and efficient interpolation by means of the SCMC sampler. The proposed mSABR scheme allows for fast and accurate option pricing under SABR dynamics, providing a better ratio of accuracy and computational cost than Taylor-based simulation schemes. Compared to the other approaches mentioned in this introduction, we provide a highly accurate SABR simulation scheme, based on only a few time steps.

The paper is organized as follows. In section 2, SABR model simulation is introduced. In section 3, the different parts of the multiple time step copula-based technique are described, including the derivation of the marginal distributions and the application of the copula. Some numerical experiments are presented in section 4. We conclude in section 5. In the derivation of the CDF of the integrated variance, we need to perform several approximations, which comes with approximation errors. In appendix 1, we list and discuss these errors.

2. ‘Almost exact’ SABR simulation

The SABR model with dependent Brownian motions was already given in (1(1) ). The multiple time step Monte Carlo SABR simulation is based on the corresponding SDE system with independent Brownian motions and , i.e.(2)

The forward dynamics are governed by a CEV process. Based on this fact and the work by Schroder (1989) and Islah (2009), an analytic approximation for the CDF of the SABR conditional process has been obtained. For some generic time interval [s, t], , assuming , the conditional cumulative distribution for forward S(t) with an absorbing boundary at , given , and , is given by(3)

where

and is the non-central chi-square CDF.

This formula is exact in the case of and constitutes an approximation otherwise (because the CEV process is approximated by a shifted process with an approximated initial condition for in the derivation). Based on equation (3(3) ), an approximately exact simulation of SABR model is feasible by inverting the conditional SABR cumulative distribution when the conditional integrated variance is known, see section 2.1.

2.1. SABR Monte Carlo simulation

In order to apply an ‘almost exact’ multiple time step Monte Carlo method for the SABR model, several steps need to be performed, that are described in the following:

• Simulation of the SABR volatility process, given . By equation (2(2) ), the stochastic volatility process of the SABR model exhibits a log-normal distribution. The solution is a geometric Brownian motion, i.e. the exact simulation of reads(4)

• Simulation of the SABR integrated variance process, . This conditional distribution is not available in closed form. We will therefore derive an approximation of the conditional distribution of the SABR integrated variance given and . The integrated variance sampling can be done by simply inverting it.

• Simulation of the SABR forward price process. The forward price S(t) can be simulated by inverting the CDF in equation (3(3) ). By this, we avoid negative forward prices in the simulation, as an absorbing boundary at zero is considered. There is no analytic expression for the inverse distribution and therefore this inversion has to be computed by means of some numerical approximation.

The multiple time step Monte Carlo simulation for the SABR model is thus summarized in algorithm 1. Input parameters are the initial conditions ( and ), the maturity time, T, the SABR parameters , and , the number of Monte Carlo samples (n) and the number of time steps (m).

In section 3.3, we propose a procedure to sample based on the Gumbel copula. For this, the CDF of the integrated variance given the initial volatility, , (as a marginal distribution) must be derived. In section 3.1, a recursive technique to obtain an approximation of this CDF is presented. Because we need to apply this recursion to approximate the characteristic function, the PDF and the CDF of for each sample of at each time step, this approach is expensive in terms of computational cost. To overcome this drawback, an efficient alternative will be employed here, based on Lagrange interpolation, as in the SCMC (Grzelak et al., 2015). In section 2.2, this methodology is briefly described.

2.2. Stochastic collocation Monte Carlo sampler

In a multiple time step exact simulation Monte Carlo method we need to perform a significant number of computations each time step on each Monte Carlo path. This often hampers the applicability of the exact simulation for systems of SDEs. One of the important components of the multiple time step Monte Carlo SABR simulation is therefore an accurate and highly efficient interpolation, as proposed in the SCMC sampler in Grzelak et al. (2015).

In this section, we will introduce the SCMC technique. The details in the SABR conditional integrated variance context will be presented in section 3.2.

The SCMC technique relies on the property that a CDF of a distribution (if it exists) is uniformly distributed. A well-known standard approach to sample from a given distribution, Y, with CDF reads

where means equality in distributional sense, and are samples from . The computational cost of this approach highly depends on the cost of the inversion , which is assumed to be expensive.

We therefore consider another, ‘cheap’, random variable X, whose inversion, , is computationally much less expensive. In this framework, the following relation holds

The samples of Y, and of X, are thus related via the following inversion,

However, this does not yet imply any improvement since the number of expensive inversions remains the same. The goal is to compute using a function , such that

where evaluations of function do not require many inversions .

In Grzelak et al. (2015), function is approximated by means of Lagrange interpolation, which is a well-known interpolation also used in the Uncertainty Quantification (UQ) context. The result is a polynomial, , which approximates function , and the samples can be obtained by employing as

where is a vector of samples from X and and are so-called collocation points. represents the number of collocation points and the exact inversion value of at the collocation point , i.e. . By applying this interpolation, the number of inversions is reduced and, with only expensive inversions , we can generate any number of samples by evaluating the polynomial . This constitutes the 1D version of SCMC sampler in Grzelak et al. (2015).

According to the definition of the SCMC technique, a crucial aspect for the computational cost is parameter : the fewer collocation points are required, the more efficient will be the sampling procedure. The collocation points must be optimally chosen in a way to minimize their number. For any random variable X, the optimal collocation points will be based on the moments of X. The optimal collocation points are here chosen to be Gauss quadrature points that are defined as the zeros of the related orthogonal polynomial. This approach leads to a stable interpolation under the probability distribution of X. The complete procedure to compute the collocation points is described in Grzelak et al. (2015).

In section 3.2, the application of SCMC technique to generate samples from the CDF of is presented. Since we deal with a conditional distribution, the 2D version of SCMC needs to be used.

3. Components of the mSABR method

In this section, we will discuss the different components of the mSABR method. For simplicity, hereafter, we denote the SABR’s integrated variance process by . We will explain how to efficiently sample the integrated variance given the initial and the final volatility, i.e. , as well as its use in a complete SABR simulation. Since the distribution is not available in closed form, some approximations need to be made. In section 3.3, we propose an accurate sampling method based on copula theory (Sklar, 1959), which is employed to approximate the required conditional distributions. The copula relies on the availability of the marginal distributions to simulate the joint distribution. As the marginal distributions, and appear as the natural choices. In section 3.1, a procedure to recover the CDF of the integrated variance process given the initial volatility is presented.

3.1. CDF of using the COS method

We present a technique to approximate the CDF of , i.e. . We will work in the log-space, so an approximated CDF of , , will be derived. We have employed this technique in the one time step SABR method (Leitao et al. 2017), but the multiple time step version is more involved. We approximate Y(s, t) by its discrete equivalent, i.e.(5)

where M is the number of intermediate or discrete time points,¹ and , . is subsequently transformed to the logarithmic domain, with(6)

and the PDF of .

Density is, in turn, found by approximating the associated characteristic function, , and applying a Fourier inversion procedure. The characteristic function and the desired PDF of form a Fourier pair. Based on the work in Benhamou (2002) and Zhang and Oosterlee (2013), we can define a recursive procedure to recover the characteristic function of .

3.1.1. Recursive procedure to recover

We start by defining the sequence,(7)

where is the logarithmic increment of between and , . As the volatility process follows log-normal dynamics, and increments of Brownian motion are independent and identically distributed, the are also independent and identically distributed, i.e. . In addition, the characteristic function of is well known and reads, ,(8)

with as in (1(1) ) and the imaginary unit. By the definition of in equation (7(7) ), we write as(9)

At this point, a backward recursion procedure in terms of will be defined by which we can recover . We define(10)

with .

By equations (9(9) ) and (10(10) ), the discrete integrated variance can be expressed as follows:(11)

From equation (11(11) ) and by applying the definition of characteristic function, we determine , as follows:(12)

We have reduced the computation of to the computation of . As is defined recursively, its characteristic function can be obtained by a recursion as well. According to the definition of the (backward) sequence in equation (10(10) ), the initial and recursive characteristic functions are given by the following expressions,(13)

where equation (8(8) ) is used in both expressions and the independence of and is also employed. By definition, the characteristic function of reads

PDF is not known. To approximate it, the Fourier cosine series expansion on is applied. We first truncate the integration range to [a, b]. The calculation of integration boundaries a and b follows the cumulant-based approach as described in Zhang and Oosterlee (2013) and Fang and Oosterlee (2008). After truncation of the integral and by applying a cosine series expansion to , we have(14)

with N the number of cosine expansion elements, and where

We wish to compute , for . Considering equation (14(14) ), we rewrite in matrix–vector form, as follows:(15)

where(16)

with(17)

By the recursion procedure in equation (15(15) ), we obtain the approximation of the characteristic function of .

3.1.2. Numerical approximation of integral

For the approximation in equation (15(15) ), we must compute matrix in equation (16(16) ) highly efficiently. The fast computation of the integral occurring for each element of is a key aspect for the performance of the mSABR method. The number of elements in matrix can be large, as it corresponds to the number of elements in the cosine series expansion, i.e. . The efficiency also depends on the required accuracy. In this work, we take advantage of the performed analysis in Leitao et al. (2017). Among several options, the authors have shown that a numerical approximation based on a piecewise linear approximation provides a good balance between performance and accuracy. Following this approximation, we rewrite the considered integral as follows:(18)

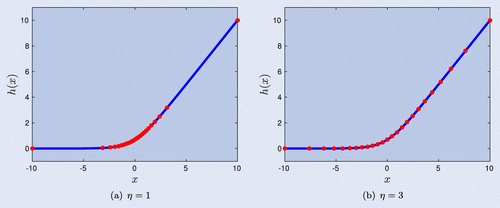
with and as in (17(17) ). Although function h(x) is not linear, it is smooth and monotonic (see figure 1). Hence, the proposed numerical technique is to define sub-intervals of the integration range [a, b] in which h(x) is almost constant or linear, i.e.

so that we can perform a first-order expansion in each sub-interval , . In order to guarantee continuity of the approximation, h(x) is approximated by a linear function in each interval as follows:

This gives us an approximation , as follows(19)

In each sub-interval , we need to determine a simple integral, , which can be computed analytically.

The optimal integration points and in equation (19(19) ) are found by differentiation of h(x) w.r.t. x, i.e.

giving a relation between the derivative of h(x) and the logistic distribution. This representation indicates that H(x) is the CDF of the logistic distribution, with a so-called location parameter and a scale parameter . In order to determine the optimal integration points so that their positions correspond to the logistic distribution, we need to compute the quantiles. The quantiles of the logistic distribution are analytically available and given by

The algorithm for the optimal integration points, given integration interval [a, b] and the number of intervals L, is then as follows:

• Determine an interval in the probability space: .

• Divide the interval equally into L parts: , .

• Determine and by calculating the quantiles, and , .

The algorithm above ensures that integration points are optimally distributed (see figure 1(a)). However, for the particular problem, the integration interval can be rather large. As the integration points are typically concentrated near the function’s curved part, the errors in the outer sub-intervals dominate the overall error and more points at the beginning and at the end of the interval are required to reduce this error. A more evenly distribution of the integration points can be achieved by introducing a scale parameter, , which implies that the integration points correspond to a CDF with increased variance. In figure 1(b), the case of is presented. When , the expression for the quantiles reads,

Through the experiments in Leitao et al. (2017), we concluded that the choice provided accurate results in this context.

Figure 1. Optimal integration points. .

3.1.3. Recovering by COS method

Once the approximation of , , has been efficiently derived, we can recover from by employing the COS method (Fang and Oosterlee 2008), as follows:(20)

with

and

where N is the number of COS terms, is the support² of and the prime and symbols in equation (20(20) ) mean division of the first term in the summation by two and taking the real part of the complex-valued expressions in the brackets, respectively. CDF can be obtained by integration, plugging the approximated from equation (20(20) ) into equation (6(6) ).

The characteristic function and PDF need to be derived for each sample of and this makes the computation of (and also its subsequent inversion) very expensive. In order to overcome this issue, the SCMC technique (see section 2.2) will be employed approximating these rather expensive computations by means of an accurate interpolation.

3.2. Efficient sampling of

By employing the SCMC technique, instead of directly computing for each sample of , we only have to compute at the collocation points. In general, only a few collocation points are sufficient to obtain accurate approximations, which is a well-known fact from the UQ research field. This fact allows us to drastically reduce the computational cost of sampling the required distribution.

For the problem at hand, we require samples from the integrated variance conditional on the initial volatility, . Therefore, we need to make use of the 2D version of the SCMC technique. Two levels of collocation points need to be chosen, one for each dimension. If we denote them by and , respectively, the resulting number of inversions equals . The formal definition of the 2D SCMC technique applied to our context reads(21)

where are the samples from , which is used as the cheap variable, and the samples of ; and are the collocation points for approximating variables and , respectively. The Lagrange polynomials and are defined by

The collocation points and are calculated based on the moments of the random variables. The two involved variables in the application of the 2D SCMC technique are the collocation variables, , and . The moments of a normal variable, are analytically available, and are given by

where p is the moment order and the expression !! represents the double factorial. In order to compute the optimal collocation points, , the precalculated collocation points by means of the moments need to be shifted according to the mean, i.e. .

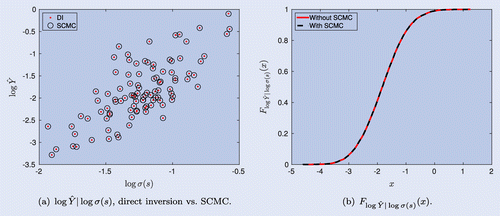
We first test numerically the accuracy of the SCMC technique for our problem. In figure 2, two experiments are presented. In figure 2(a), we compare the samples obtained by direct inversion and by the SCMC technique. The fit is highly accurate, already with only seven collocation points. In figure 2(b), the empirical CDFs are depicted, where the excellent match is confirmed.

Figure 2. (a) Points cloud by direct inversion (DI) sampling (red dots) and SCMC sampling (black circles). (b) Empirical CDFs of with and without using SCMC.

In order to show the performance of SCMC technique for the simulation of , the execution times of generating different numbers of samples are presented in table 1.

In appendix 1, the different sources of error due to the approximations made in the sections 3.1 and 3.2 are analysed.

3.3. Copula-based simulation of

In this section, we present an algorithm for the simulation of the integrated variance given and by means of a copula. In order to obtain the joint distribution, we require the marginal distributions. In our case, the required CDFs are and . In section 3.1, an approximated CDF of , , has been derived. Since follows a log-normal distribution, by definition, is normally distributed, and the conditional process given , follows a normal distribution,(22)

Table 1. SCMC time in seconds.

		With SCMC
Samples	Without SCMC
100	1.0695	0.0449	0.0466	0.0660
10000	16.3483	0.0518	0.0588	0.0798
1000000	1624.3019	0.2648	0.5882	1.0940

3.3.1. Pearson’s correlation coefficient

For any copula some measure of the correlation between the marginal distributions is needed. We will employ the Pearson correlation coefficient for and . For this quantity, an approximated analytic formula can be derived. By definition, we have

We employ the following approximation

where the logarithm and the integral are interchanged. Since the function is concave, this approximation forms a lower bound for the true value. This can be seen by applying Jensen’s inequality, i.e.

It has been numerically shown that, under the model settings with an interval size less than two years, the results based on this approximation are highly satisfactory (further details in Leitao et al. (2017)). The correlation coefficient can then be approximated by

To compute the covariance, we need , and . From equation (4(4) ), the last expectation as well as are known. We find that

and

Based on these equations, using

we obtain the following expressions for the remaining expectation,

For the variance of , we first compute

where

and the variance reads

An approximation of the Pearson correlation coefficient is then obtained as follows:(23)

Some copulas do not employ, in their definition, Pearson’s coefficient as the correlation measure. For example, Archimedean copulas employ the Kendall’s rank correlation coefficient. However, a relation between both Pearson’s and Kendall’s coefficients is available,

3.3.2. Gumbel copula

In this work, we will use Archimedean Gumbel copula. The Gaussian copula may seem a natural choice, as follows a log-normal distribution and can be seen as summation of squared log-normal processes. However, in Leitao et al. (2017), we have empirically shown that the Gumbel copula performs most accurately in this context for a variety of SABR parameter values. The formal definition of the Archimedean Gumbel copula, considering as the marginal distributions, reads(24)

where , is the so-called generator function of the Gumbel copula. In order to calibrate parameter , a relation between and the rank correlation coefficient Kendall’s can be employed, i.e. .

So, we have derived approximations for all the components required to apply the copula-based technique for the integrated variance simulation. The algorithm to sample given and then consists of the following steps:

(1)	Determine by equation (22(22) ).
(2)	Determine by equation (6(6) ).
(3)	Determine the correlation between and by equation (23(23) ).
(4)	Generate correlated uniform samples, and from the Gumbel copula by equation (24(24) ).
(5)	From , invert the CDF to get the samples of . This procedure is straightforward since the normal distribution inversion is analytically available.
(6)	From , invert the CDF to get the samples of . We propose an inversion procedure based on linear interpolation. First, we evaluate the CDF function at some discrete points. Then, the insight is that, by rotating the CDF under consideration, we can interpolate over probabilities. This is possible when the CDF function is a smoothly increasing function. The interpolation polynomial provides the quantiles of the original distribution from some given probabilities. Since is indeed a smooth and increasing function, the interpolation-based inversion is definitely applicable. This procedure together with the use of 2D SCMC sampler (see section 3.2) results in a fast and accurate inversion.
(7)	The samples of and of are obtained by simply taking exponentials as follows:

3.4. Simulation of S(t) given S(s), , and

We complete the mSABR method by the conditional sampling of S(t). The most commonly used techniques can be classified in two categories: direct inversion of the SABR distribution function given in equation (3(3) ) and moment-matching approaches. The direct inversion procedure has a higher computational cost because of the evaluation of the non-central distribution. However, some recent developments make this computation affordable. Chen et al. (2012) proposed a forward asset simulation based on a combination of moment-matching (Quadratic Gaussian) and enhanced direct inversion procedures. We employ this technique also here. Note however that, for some specific values of , the simulation of the conditional S(t) given S(s), , and enables analytic expressions.

3.4.1. Case

For , it is easily seen from equation (2(2) ) that the asset process (in integral form) becomes

where(25)

and(26)

Since this allows negative asset prices, the simulation of S(t) with must be corrected. If the price at the initial time is less or equal to zero, i.e. , the price S(t) must remain zero for all time. Otherwise,

This correction is performed to be consistent within the whole simulation procedure, since the distribution of the ‘exact’ SABR simulation in equation (3(3) ) relies on the condition . If negative values are permitted, this must be handled in a different way (see Hagan et al. (2014) or Antonov et al. (2015), for example).

3.4.2. Case

In the case of , the asset dynamics in equation (1(1) ) become log-normal and the solution is given by

If we take the log-transform,

and by considering again equations (25(25) ) and (26(26) ), we obtain the distribution of , which reads(27)

By employing equation (27(27) ), the asset dynamics S(t) can be sampled from(28)

where X is the standard normal.

3.4.3. Case ,

As mentioned before, for the generic case of , we employ the enhanced inversion of the SABR asset price distribution in equation (3(3) ) as introduced in Chen et al. (2012). We briefly summarize this approach. The asset simulation is performed either by a moment-matched quadratic Gaussian approximation or by an enhanced direct inversion. The authors in Chen et al. (2012) proposed a threshold value to choose the suitable technique among these two. The moment-matching approach relies on the fact that, for , the distribution function in equation (3(3) ) can be approximated by

By definition, the mean, and the variance, , of a generic non-central chi-square distribution are and , respectively. A variable is accurately approximated by a quadratic Gaussian distribution, as follows

with

Applying this to the case in equation (3(3) ), we can sample the conditional asset dynamics, , by

The moment-matching approximation is safely and accurately applicable when and (Chen et al. 2012). Otherwise, a direct inversion procedure must be employed. A root-finding Newton method is then used. In order to reduce the number of Newton iterations (and the expensive evaluation of the non-central chi-square CDF), the first iterations are based on an approximated formula for the non-central chi-square distribution, which is based on the normal CDF and derived by Sankaran (1963). Then, the obtained value is employed as the initial guess for the Newton algorithm. The result is a significant reduction in the number of iterations and, hence, in the computational cost. Furthermore, this root-finding procedure consists of only basic operations, so that the whole procedure can be easily vectorized, leading to a further efficiency improvement.

As in the case of , the absorbing boundary at zero needs to be prescribed to avoid negative prices.

The resulting sampling procedure is robust and efficient.

3.4.4. Martingale correction

As already pointed by Andersen (2008) and Chen et al. (2012), the almost exact simulation of the asset price in some stochastic volatility models can produce a loss of the martingale property, due to the approximation of a continuous process by its discrete equivalent. This is especially seen, when the size of time step is large and for certain configurations of the SABR parameters, like small values, close-to-zero initial asset values , high vol-vol parameter or large initial volatility . In order to overcome this issue, we incorporate to the mSABR method the use of a simple but effective numerical martingale correction, as follows:

where represents the th Monte Carlo sample. Note, however, that, for practical SABR parameters, the martingale error is very small and can be easily controlled by increasing the number of overall time steps m.

4. Numerical experiments

In this section, we benchmark the mSABR method by pricing options under the SABR dynamics. We will consider several parameter configurations, extracted from the literature (see table 2), a zero-correlation set as in Grzelak et al. (2015) (set I), a set under log-normal dynamics as in Chen et al. (2012) (set II), a medium long time to maturity set as in Antonov et al. (2013) (set III) and a more extreme set as in Antonov et al. (2015) (set IV). The strikes, , are chosen following the expression

introduced by Piterbarg (2005).

Table 2. Data sets.

						T
Set I (Grzelak et al. 2015)	0.5	0.5	0.4	0.5	0.0	4
Set II (Chen et al. 2012)	0.04	0.2	0.3	1.0		5
Set III (Antonov et al. 2013)	1.0	0.25	0.3	0.6		20
Set IV (Antonov et al. 2015)	0.0056	0.011	1.080	0.167	0.999	1

Other parameters include:

• Step size in equation (5(5) ): .

• Number of terms in equations (14(14) ) and (20(20) ): .

• Number of intervals for piecewise linear approximation in equation (19(19) ): .

• Number of collocation points in equation (21(21) ): .

• Number of samples: .

The experiments were performed on a computer with CPU Intel Core i7-4720HQ 2.6 GHz and RAM memory of 16 Gigabytes. The employed software package was Matlab r2015b.

As usual, the European option prices are obtained by averaging the maximum of the forward asset values at maturity minus the strike and zero, i.e. (call option). Subsequently, the Black–Scholes formula is inverted to determine the implied volatilities. Note that, once the forward asset is simulated by the mSABR method, we can price options at multiple strikes simultaneously.

4.1. Convergence test

We perform a convergence study in terms of the number of time steps, m and, subsequently, in terms of the number of samples, n. Set I is considered suitable for this experiment, since an analytic solution is available by Antonov et al. (2013) when , and it can be used as a reference. Also, as equation (3(3) ) is employed to sample the forward asset dynamics, the case results in an exact simulation.

In table 3, the implied volatilities obtained by the mSABR method for several choices of the number of time steps m are presented. We observe by the errors in basis points (bp) that, by increasing the number of time steps, the technique converges very rapidly. Furthermore, only a few time steps are required to obtain accurate results: with only time steps (one per year) the error is already less than ten basis points and with (the time step size is a quarter of year), the error remains below one basis points. Compared to the low-bias SABR simulation scheme proposed in Chen et al. (2012), the mSABR method is more accurate, since it relies on the exact simulation of the integrated variance, whereas the low-bias scheme approximates the integrated variance by a small disturbance expansion and moment-matching techniques. That scheme performs worse when bigger time steps are considered.

Table 3. Implied volatility, increasing m: Antonov vs. mSABR. Set I.

Strikes
Antonov				N/A
Error(bp)		2.54	24.38	N/A	61.71	76.66	89.26
Error(bp)		4.94	12.71	N/A	25.48	30.40	34.73
Error(bp)				N/A	0.92	2.21	3.17
Error(bp)				N/A
Error(bp)	0.15	0.58	0.78	N/A	0.43	0.04

Table 4. Implied volatility, increasing n: Antonov vs. mSABR. Set I.

Strikes
Antonov				N/A
RE				N/A
RE				N/A
RE				N/A

Figure 3. Convergence of the mSABR method.

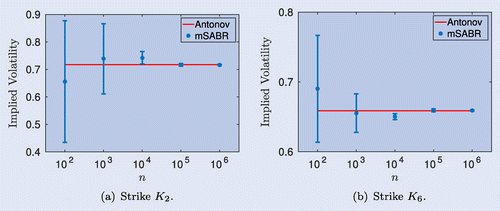
We also perform a convergence test in the number of samples, n. According to the previous experiment and in order to guarantee that the errors do not increase by the time discretization, we set . In table 4, the implied volatilities for increasing n are presented. By the relative error (RE), we can see that, as expected, the error is approximately reduced by a factor of . Furthermore, we wish to show how the number of samples affects the variance of the mSABR method. In figure 3, the standard deviations³ for several choices of n are presented. Two strikes are evaluated, one in-the-money strike, , and one out-of-the-money strike,⁴. An identical behaviour can be observed for all other strikes as well. Again, we see a fast convergence and variance reduction in terms of n.

4.2. Performance test

Next to the convergence of the mSABR method in terms of m and n, another important aspect is the computational cost. Specifically, we will measure the execution times of an option pricing experiment using different alternative Monte Carlo-based methods and compare them with the mSABR method. Again, parameter Set I is employed since a reference value is available for this case. We consider a plain Monte Carlo Euler (MC Euler) discretization scheme for the forward asset, S(t). Note that the absorbing boundary at zero must be handled with care. Since our main contribution here is the exact simulation of the integrated variance, it is natural to also compare the performance with other, less involved, techniques. We therefore also present a comparison between the mSABR method and two techniques where the integrated variance is either approximated by (left rectangular rule) or (trapezoidal rule). We denote these alternatives as the Y -Euler and Y -trpz schemes, respectively. The simulation of S(t) is, in both cases, carried out as explained in section 3.4. In table 5, we present execution times (in seconds) of the MC Euler, Y -Euler, Y -trpz and mSABR schemes, to achieve a certain level of accuracy (measured as the error of the implied volatilities in basis points). In addition, the required number of time steps is presented in parentheses to provide an insight in the efficiency. Furthermore, the speedup obtained by our method is included in table 6. We observe that the mSABR method is superior in terms of the ratio between computational cost and accuracy. The accuracy of Y-Euler or Y-trpz can be improved by adding intermediate time steps, but then also the computational cost increases.

Table 5. Execution times and time steps, m (parentheses).

Error	100 bp	50 bp	25 bp	10 bp
MC Euler	6.85 (200)	10.71 (300)	27.42 (800)	42.90 (1200)
Y-Euler	2.18 (4)	6.55 (16)	11.85 (32)	45.12 (128)
Y-trpz	2.17 (3)	4.24 (8)	7.25 (16)	14.47 (32)
mSABR	3.46 (1)	2.98 (2)	3.72 (3)	4.89 (4)

Table 6. Speedups provided by the mSABR method.

Error	100 bp	50 bp	25 bp	10 bp
MC Euler	1.98	3.59	7.37	8.77
Y-Euler	0.63	2.19	3.18	9.22
Y-trpz	0.62	1.42	1.94	2.95

4.3. ‘Almost exact’ SABR simulation by varying

As a next experiment we test the stability of the mSABR method when correlation parameter varies from negative to positive values. As stated before, equation (3(3) ) is only exact for . For that, we use Set II since the conditional forward asset simulation enables a closed-form solution (given by equation (28(28) )) for . The considered values are . Following the outcome of the previous experiment, we set . As a reference, a Monte Carlo (MC) simulation with a very fine Euler time discretization (1000T time steps) in the forward asset process is employed. In table 7, the resulting implied volatilities are provided. The differences between the Monte Carlo volatilities and the ones given by the mSABR method are within 10 basis points for all choices of .

Table 7. Implied volatility, varying : Euler Monte Carlo vs. mSABR. Set II.

Strikes
MC
mSABR
Error(bp)	3.59	2.86	1.78	0.95
MC
mSABR
Error(bp)	0.04
MC
mSABR
Error(bp)

4.4. Pricing barrier options

We will price barrier options with the mSABR method. The up-and-out call option is considered here, with the barrier level, B, . The price of this type of barrier option reads

where represents the indicator function and are the predefined times where the barrier condition (whether or not it is hit) is checked.

As a reference, a Monte Carlo method with very fine Euler time discretization is employed, as in the previous experiment. The number of time steps for the mSABR scheme is again set to . In tables 8, 9 and 10, the obtained prices are presented for the parameter sets I, II and III, respectively. The prices are multiplied by a factor of 100. Also, the mean squared error (MSE) is shown. We define the MSE as

where and are the barrier option prices provided by Monte Carlo method and by the mSABR method, respectively.

Table 8. Pricing barrier options with mSABR: . Set I.

Strikes
MC	6.2868	5.4577	4.6330	3.8263	3.0551	2.3358	1.6869
mSABR	6.3264	5.4890	4.6566	3.8436	3.0677	2.3452	1.6953
MSE
MC	10.2271	9.1568	8.0718	6.9856	5.9142	4.8753	3.8899
mSABR	10.2249	9.1507	8.0609	6.9702	5.8960	4.8572	3.8737
MSE
MC	13.5740	12.3571	11.1118	9.8513	8.5910	7.3477	6.1403
mSABR	13.5915	12.3686	11.1174	9.8507	8.5851	7.3380	6.1276
MSE

Table 9. Pricing barrier options with mSABR: . Set II.

Strikes
MC	1.1702	0.9465	0.7268	0.5215	0.3423	0.1996	0.0987
mSABR	1.1724	0.9486	0.7285	0.5226	0.3428	0.1997	0.0986
MSE
MC	1.3099	1.0766	0.8462	0.6290	0.4367	0.2794	0.1626
mSABR	1.3092	1.0761	0.8456	0.6282	0.4355	0.2782	0.1618
MSE
MC	1.3521	1.1168	0.8841	0.6644	0.4695	0.3093	0.1891
mSABR	1.3518	1.1166	0.8838	0.6639	0.4686	0.3080	0.1880
MSE

Table 10. Pricing barrier options with mSABR: . Set III.

Strikes
MC	29.1174	23.4804	17.2273	10.7825	5.0203	1.1750	0.0036
mSABR	29.2346	23.5828	17.3086	10.8327	5.0385	1.1805	0.0036
MSE
MC	41.3833	34.5497	26.8311	18.6089	10.7281	4.4893	0.9434
mSABR	41.3394	34.5097	26.7948	18.5747	10.6943	4.4546	0.9320
MSE
MC	48.5254	41.1652	32.7980	23.7807	14.9344	7.5364	2.6692
mSABR	48.5008	41.1515	32.7888	23.7655	14.9097	7.5117	2.6549
MSE

Figure 4. The mSABR method in the context of negative interest rates.

The resulting accuracy is very satisfactory. As expected, higher option prices are obtained for bigger barrier levels, B, and/or lower strikes, .

4.5. Negative interest rates

The SABR model is very popular in the interest rate context. One of the most important current features in this market is the occurrence of negative interest rate values and strikes. Approaches dealing with this issue have appeared in the literature, like Antonov et al. (2015) or Hagan et al. (2014). To apply the mSABR scheme in the case of negative interest rates, we will use the shifted SABR model by Schlenkrich et al. (2014). The shifted SABR model is defined as follows:

where is a displacement, or shift, in the underlying. The volatility process, , remains invariant (see equation (1(1) )). Parameter can be seen as the maximum level of negativity that is expected in the rates. This generalization of the SABR model is widely used by market practitioners due to its simplicity, and, precisely, the advantage of keeping the existing simulation schemes. In mSABR, the assumption is required to employ the method.

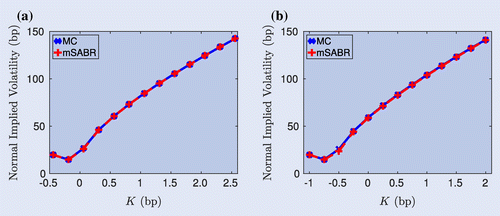
In order to test the mSABR scheme in the context of negative interest rates, we employ the set IV. The SABR model parameters were obtained by Antonov et al. (2015) after a calibration process to real data⁵ under the shifted SABR model. Note that this configuration corresponds to an extreme situation with high values of the correlation, , and vol-vol, . As a shift parameter, is chosen. We compare the normal implied volatilities⁶ obtained by employing Monte Carlo with very fine (1000T) time discretization (as a reference) and the mSABR method with . In figure 4(a), these curves are depicted and a perfect fit is observed. The strikes, K are chosen to permit negative values. We perform an even more extreme experiment, by setting . The resulting normal implied volatilities are presented in figure 4(b), again with a excellent fit.

Table 11. Execution times and time steps, m (parentheses).

Error	bp	bp	bp	bp
Y-Euler	2.47 (4)	9.64 (16)	14.32 (24)	19.25 (32)
Y-trpz	1.32 (2)	4.99 (8)	9.75 (16)	14.52 (24)
mSABR	1.61 (1)	2.57 (2)	3.52 (3)	4.57 (4)

Table 12. Speedups provided by the mSABR method.

Error	bp	bp	bp	bp
Y-Euler	1.57	3.75	4.07	4.21
Y-trpz	0.82	1.94	2.77	3.17

Due to the complexity of the negative interest rates experiment and this particular set of parameters (), we wish to test the performance of our method under these conditions. In tables 11 and 12 the execution times obtained are presented. Again, the small number of time steps due to the ‘almost’ exact simulation of the mSABR method provides an important gain in terms of performance.

5. Conclusions

In this work, we have proposed an accurate and robust multiple time step Monte Carlo method to simulate the SABR model with only a few time steps. The mSABR method employs many nontrivial components that have not been seen before in combination within a Monte Carlo simulation. A copula methodology to generate samples from the conditional SABR’s integrated variance process has been introduced. The marginal distribution of the integrated variance has been derived by employing Fourier techniques. We have dealt with an increasing computational complexity, due to the multiple time steps and the almost exact simulation, by applying an interpolation based on stochastic collocation. This has resulted in an efficient SABR simulation scheme. We have numerically shown the convergence and the stability of the method. In terms of convergence, the mSABR method requires only very few time steps to achieve high accuracy, due to the focus on almost exact simulation (in contrast to the low-bias SABR scheme Chen et al. 2012). This fact impacts the performance, obtaining an excellent ratio between accuracy and computational cost. As a multiple time step method, it can be employed to price path-dependent options. As an example, a pricing experiment for barrier options has been carried out. Furthermore, we have shown that the mSABR scheme is also suitable in the context of negative interest rates, in combination with a shifted model.

Additional information

Funding

The first author is supported by the EU in the FP7-PEOPLE-2012-ITN Program [Agreement number 304617] (FP7 Marie Curie Action, Project Multi-ITN STRIKE—Novel Methods in Computational Finance).

Notes

No potential conflict of interest was reported by the authors.

1 So, we have the m large time steps, for the multiple time step Monte Carlo simulation, and we have M intermediate dates for the integrated variance, . We suggest to prescribe , and use , in order to avoid over-discretization issues. This makes the value of M dependent on the interval size, .

2 It can be calculated given the support of , [a, b].

3 Computed by performing 100 realizations.

4 We consider European call options.

5 1Y15Y Swiss franc swaption from 10 February 2015.

6 Determined using the normal Bachelier model instead of the log-normal Black–Scholes model.

Appendix

Error analysis of simulation

Errors in the CDF of

In section 3.1, we have proposed a method to compute the approximated CDF for the conditional integrated variance, i.e. . Here, we perform an error analysis, indicating how to reduce or bound the errors. The sources of error in the approximation include , the discretization of Y(s, t) in equation (5(5) ), , the truncation in equations (14(14) ) and (20(20) ), , due to the cosine expansion in equations (14(14) ) and (20(20) ) and , the numerical computation of in equation (19(19) ).

Error

This error occurs because SABR’s time-integrated variance is approximated by its discrete equivalent, i.e. . Note that the process is the solution of the SDE

which, by employing the same time discretization as for in Equation (5(5) ), can be written as follows:

This is essentially the Euler–Maruyama discretization scheme. Indeed, it is easy to see that, if we sum the right-hand side of the equality over the M discrete time points, we recover the discrete approximation , as follows:

The error (or convergence) of the Euler–Maruyama discretization scheme has been intensively studied in the literature (see, e.g. Kloeden and Platen 1992). Two errors can be defined when a stochastic process is discretized: strong and weak. It was proved by Kloeden and Platen (1992) that, under some conditions of regularity, the Euler–Maruyama scheme has strong convergence of order and weak convergence of order . We focus on the strong error between Y(s, t) and . Then, error can be computed and bounded by employing the usual strong convergence expression as

for some constant .

In the actual experiments, we consider and . This will reduce the error further. In Leitao et al. (2017), we have presented numerical results that confirm the expected behaviour of this error.

Error

The use of cosine expansions and the COS method implies a truncation of the integration range to interval [a, b]. This gives rise to a truncation error, which is defined by

where H corresponds to and , according to equations (14(14) ) and (20(20) ), respectively. By a sufficiently large integration range [a, b], this error can be reduced and does not dominate the overall error.

Error

The convergence due to the number of terms N in the cosine series expansion was derived in Fang and Oosterlee (2008). For any , can be bounded by

being a constant and a term which varies less than exponentially with respect to N. As the integrated variance is a very smooth function, will decay exponentially with respect to N.

Error

When the piecewise approximation in equation (19(19) ) is employed, the convergence in terms of the number of sub-intervals, L, is numerically tested. In table A1, we observe a reduction of the error by a factor four, when going from to integration points. However, with the error reduces more drastically due to the choice of optimal integration points.

Table A1. MSE vs. L for in equation (19(19) ).

Equidistant
Optimal ()
Optimal ()

Error in the application of SCMC to

In Grzelak et al. (2015), where SCMC sampler was proposed, an error analysis of the technique was carried out. Here we summarize the most important results related to our context and refer the reader to the original paper for further details.

To measure the error which results from the collocation method in a more general case (see section 2.2), we can consider either the difference between functions g(X) and (X the cheap variable) or the error associated with the approximated CDF. The first type of error is due to Lagrange interpolation, so the corresponding error estimate is well known. The error with collocation points is given by the standard Lagrange interpolation reads(A1)

where are the collocation points, and , . The error can be bounded by defining as the point where has its maximum. A small probability of large errors in the tails can be observed by deriving the error , by substituting the uniformly distributed random variable in the previous equation, using ,

A ‘close-to-linear’ relation between the involved stochastic variables, meaning being small, gives a small approximation error. On the other hand, when approximating the CDF of the expensive variable Y, we have , which is exact at the collocation points ,

A deeper analysis can be found in the original paper of SCMC (Grzelak et al., 2015), including a theoretical convergence in and the convergence within the distribution tails.

We have chosen X to be standard normal, and can be seen as the logarithm of a sum of log-normal variables. Therefore, it is a ‘close-to-normal’ distribution which can be efficiently approximated by a linear combination of standard normal distributions. In order to measure the error when SCMC is applied to the sampling of (see section 3.2), we can consider the difference between the functions and in equation (21(21) ). By following the same derivation as in equation (A1(A1) ), we have

where and are the number of collocation points in each dimension and are the collocation points corresponding to the conditional random variable .