From optimal martingales to randomized dual optimal stopping

Abstract

In this article we study and classify optimal martingales in the dual formulation of optimal stopping problems. In this respect we distinguish between weakly optimal and surely optimal martingales. It is shown that the family of weakly optimal and surely optimal martingales may be quite large. On the other hand it is shown that the surely optimal Doob-martingale, that is, the martingale part of the Snell envelope, is in a certain sense robust under a particular random perturbation. This new insight leads to a novel randomized dual martingale minimization algorithm that doesn't require nested simulation. As a main feature, in a possibly large family of optimal martingales the algorithm may efficiently select a martingale that is as close as possible to the Doob martingale. As a result, one obtains the dual upper bound for the optimal stopping problem with low variance.

Keywords:

• Optimal stopping problem
• Doob-martingale
• Randomization

2000 Mathematics Subject Classification:

• 91G60
• 65C05
• 60G40

JEL classifications:

• G10
• G12
• G13

1. Introduction

The last decades have seen a huge development of numerical methods for solving optimal stopping problems. Such problems became very prominent in the financial industry in the form of American derivatives. For such derivatives one needs to evaluate the right of exercising (stopping) a certain cash-flow (reward) process Z at some (stopping) time τ, up to some time horizon T. From a mathematical point of view this evaluation comes down to solving an optimal stopping problem $Y^{\star }=\underset{\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}\tau \le T}{sup}\mathsf{E}\mathsf{[}\underset{\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}{Z_{\tau }}].$ Typically the cash-flow Z depends on various underlying assets and/or interest rates and as such is part of a high dimensional Markovian framework. Particularly for high dimensional stopping problems, virtually all generic numerical solutions are Monte Carlo based. Most of the first numerical solution approaches were of primal nature in the sense that the goal was to construct a ‘good’ exercise policy and to simulate a lower biased estimate of $Y^{\star }.$ In this respect we mention, for example, the well-known regression methods by Longstaff and Schwartz (2001), Tsitsiklis and Van Roy (2001), and the stochastic mesh approach by Broadie and Glasserman (2004), and the stochastic policy improvement method by Kolodko and Schoenmakers (2006). For further references we refer to the literature, for example Glasserman (2003) and the references therein.

In this paper we focus on the dual approach developed by Rogers (2002), and Haugh and Kogan (2004), initiated earlier by Davis and Karatzas (1994). In the dual method the stopping problem is solved by minimizing over a set of martingales, rather than a set of stopping times, (1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) A canonical minimizer of this dual problem is the martingale part, $M^{\star }$ of the Doob(-Meyer) decomposition of the Snell envelope $Y_t^{\star }=\underset{t\le \mathrm{s}\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}\tau \le T}{sup}{\mathsf{E}}_{{\mathcal{F}}_t}\left[Z_{\tau }\right],$ which moreover has the nice property that (2) $Y_0^{\star }=\underset{0\le s\le T}{max}(Z_s-M_s^{\star })\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{y}.$(2)

That is, if one would succeed in finding $M^{\star }$, the value of $Y^{\star }$ can be obtained from one trajectory of $Z-M^{\star }$ only.

Shortly after the development of the duality method in Rogers (2002) and Haugh and Kogan (2004), various numerical approaches for computing dual upper bounds for American options based on it appeared. May be one of the most popular methods is the nested simulation approach by Andersen and Broadie (2004), who essentially construct an approximation to the Doob martingale of the Snell envelope via stopping times obtained by the Longstaff & Schwartz method (Longstaff and Schwartz 2001). A few years later, a linear Monte Carlo method for dual upper bounds was proposed in Belomestny et al. (2009). In fact, as a common feature, both Andersen and Broadie (2004) and Belomestny et al. (2009) aimed at constructing (an approximation of) the Doob martingale of the Snell envelope via some approximative knowledge of continuation functions obtained by the method of Longstaff & Schwartz or in another way. Instead of relying on such information, the common goal in later studies (Desai et al. 2012, Belomestny 2013, Schoenmakers et al. 2013, Belomestny et al. 2014), was to minimize the expectation functional in the dual representation (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) over a linear space of generic ‘elementary’ martingales. Indeed, by parameterizing the martingale family in a linear way and replacing the expectation in (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) by the sample mean over a large set of trajectories, the resulting minimization comes down to solving a linear program. However, it was pointed out in Schoenmakers et al. (2013) that in general there may exist martingales that are ‘weakly’ optimal in the sense that they minimize (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ), but fail to have the ‘almost sure property’ (2(2) $Y_0^{\star }=\underset{0\le s\le T}{max}(Z_s-M_s^{\star })\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{y}.$(2) ). As a consequence, the estimator for the dual upper bound due to such martingales may have high variance. Moreover, an example in Schoenmakers et al. (2013) illustrates that a straightforward minimization of the sample mean corresponding to (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) may end up with a martingale that is asymptotically optimal in the sense of (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) but not surely optimal in the sense of (2(2) $Y_0^{\star }=\underset{0\le s\le T}{max}(Z_s-M_s^{\star })\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{y}.$(2) ), when the sample size tends to infinity. As a remedy to this problem, in Belomestny (2013) variance penalization is proposed, whereas in Belomestny et al. (2014) the sample mean is replaced by the maximum over all trajectories.

In this paper we first extend the study of surely optimal martingales in Schoenmakers et al. (2013) to the larger class of weakly optimal martingales. As a principal contribution, we give a complete characterization of weakly and surely optimal martingales and moreover consider the notion of randomized dual martingales. In particular, it is shown that in general there may be infinitely martingales that are optimal but not surely optimal. In fact, straightforward minimization procedures based on the sample mean in (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) may typically return martingales of this kind, even if the Doob martingale of the Snell envelope is contained in the martingale family (as illustrated already in Schoenmakers et al. (2013), though at a somewhat pathological example with partially deterministic cash-flows). As another main contribution we will show that surely optimal martingales play a distinguished role within the family of all optimal martingales. Namely, it will be proved that by perturbing a surely optimal martingale by particular randomization it will remain surely optimal, while any other martingale under this particular randomization turns to a suboptimal one. In the context of the surely optimal Doob martingale, this turns out to be a very useful feature, since the corresponding ‘ideal’ randomization involves information of the Doob martingale itself that can be estimated from an estimate of the Snell envelope. More specifically, under this ‘ideal’ randomization the Doob martingale, perturbed with it, remains guaranteed (surely) optimal, while any other surely or weakly optimal martingale turns to a suboptimal one. Of course, as a rule, this ‘ideal’ randomization is not known or available in practical applications. But, fortunately, it turns out that by just incorporating some simple (‘naive’) randomization using uniform random variables, the sample-mean minimization may return a martingale that is closer to the Doob-martingale than the one obtained without randomization. We thus end up with a martingale having a lower variance, which in turn guarantees that the corresponding upper bound based on (1(1) $Y^{\star }=\underset{M:\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{l}\mathrm{e},M_0=0}{inf}\mathsf{E}\left[\underset{0\le s\le T}{max}(Z_s-M_s)\right].$(1) ) is tight (see Belomestny 2013, Schoenmakers et al. 2013). Compared to Belomestny et al. (2014) and Belomestny (2013), the benefit of this new randomized dual approach is its computational efficiency related to the fact that the resulting optimization problem can be solved via linear programing (in the case of linear classes of martingales). We have carried out numerical experiments for a couple of stylized examples that are simple enough to be treated analytically but yet rich enough to exhibit most features in the context of our study.

Finally, we underline that in this paper our emphasis is on the theoretical aspects and classification of the optimal martingales with potential applications to randomization procedures for selecting martingales with low variance. An extensive numerical analysis of a randomized dual martingale approach (albeit with slightly different randomization) as well as a comprehensive convergence analysis based on the theory of empirical processes is available in the follow-up work (Belomestny et al. 2022).¹

The structure of the paper is as follows. Section 2 carries out a systematic theoretical analysis of optimal martingales. In Section 3 we deal with randomized optimal martingales and the effect of randomizing the Doob-martingale. More technical proofs are given in Section 4 and some first numerical examples are presented in Section 5.

2. Characterization of optimal martingales

Since practically any numerical approach to optimal stopping is based on a discrete exercise grid, we will work within in a discrete time setup. That is, it is assumed that exercise (or stopping) is restricted to a discrete set of exercise times $t_0=0,\dots ,t_J=T,$ for some time horizon T and some $J\in {\mathbb{N}}_{+}.$ For notational convenience we will further identify the exercise times $t_j$ with their index j, and thus monitor the reward process $Z_j,$ at the ‘times’ $j=0,\dots ,$ J.

Let $(\mathrm{\Omega },\mathcal{F},\mathrm{P})$ be a filtered probability space with discrete filtration $\mathcal{F}=({\mathcal{F}}_j{)}_{j\ge 0}.$ An optimal stopping problem is a problem of stopping the reward process $(Z_j{)}_{j\ge 0}$ in such a way that the expected reward is maximized. The value of the optimal stopping problem with horizon J at time $j\in \{0,\dots ,J\}$ is given by (3) $Y_j^{\star }=\underset{\tau \in \mathcal{T}[j,\dots ,J]}{\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{p}}{\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{\tau }\right],$(3) provided that Z was not stopped before j. In (3(3) $Y_j^{\star }=\underset{\tau \in \mathcal{T}[j,\dots ,J]}{\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{p}}{\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{\tau }\right],$(3) ), $\mathcal{T}[j,\dots ,J]$ is the set of $\mathcal{F}$-stopping times taking values in $\{j,\dots ,J\}$ and the process $(Y_j^{\star }{)}_{j\ge 0}$ is called the Snell envelope. It is well known that $Y^{\star }$ is a supermartingale satisfying the backward dynamic programing equation (Bellman principle): $Y_j^{\star }=max(Z_j,{\mathsf{E}}_{{\mathcal{F}}_j}[Y_{j+1}^{\star }\left]\right),0\le j<J,Y_J^{\star }=Z_J.$ Along with a primal approach based on the representation (3(3) $Y_j^{\star }=\underset{\tau \in \mathcal{T}[j,\dots ,J]}{\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{p}}{\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{\tau }\right],$(3) ), a dual method was proposed in Rogers (2002) and Haugh and Kogan (2004). Below we give a short self-contained recap while including the notions of weak and sure optimality.

Let $\mathcal{M}$ be the set of martingales M adapted to $\mathcal{F}$ with $M_0=0.$ By using the Doob's optimal sampling theorem one observes that (4) $Y_j^{\star }\le {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right],j=0,\dots ,J,$(4) for any $M\in \mathcal{M},$ see Rogers (2002) and Haugh and Kogan (2004). We will say that a martingale M is weakly optimal, or just optimal, at j, for some $j=0,\dots ,J,$ if (5) $Y_j^{\star }={\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right].$(5) The set of all martingales (weakly) optimal at j will be denoted by ${\mathcal{M}}^{\circ ,j}.$ The set of martingales optimal at j for all $j=0,\dots ,J,$ is denoted by ${\mathcal{M}}^{\circ }.$ We say that a martingale M is surely optimal at j, for some $j=0,\dots ,J,$ if (6) $Y_j^{\star }=\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\text{almost surely.}$(6) The set of all surely optimal martingales at j will be denoted by ${\mathcal{M}}^{\circ \circ ,j}.$ The set of surely optimal martingales at j for all $j=0,\dots ,J,$ is denoted by ${\mathcal{M}}^{\circ \circ }.$ Note that, obviously, ${\mathcal{M}}^{\circ \circ }$ ⊂${\mathcal{M}}^{\circ }$⊂ $\mathcal{M}.$

Now there always exists at least one surely optimal martingale, the so-called Doob-martingale coming from the Doob decomposition of the Snell envelope $(Y_j^{\star }{)}_{j\ge 0}.$ Indeed, consider the Doob decomposition of $Y^{\star },$ that is, (7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) where $M^{\star }$ is a martingale with $M_0^{\star }=0,$ and $A^{\star }$ is predictable with $A_0^{\star }=0.$ It follows immediately that (8) $\begin{array}{r}{M}_j^{\star }=\sum _{l=1}^j(Y_l^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{l-1}}[Y_l^{\star }\left]\right),A_j^{\star }=\sum _{l=1}^j(Y_{l-1}^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{l-1}}[Y_l^{\star }\left]\right),\end{array}$(8) and so $A^{\star }$ is non-decreasing due to the fact that $Y^{\star }$ is a supermartingale. One thus has by (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ) on the one hand $\begin{array}{rl}& \underset{j\le r\le J}{max}(Z_r-M_r^{\star }+M_j^{\star })\\ & =Y_j^{\star }+\underset{j\le r\le J}{max}(Z_r-Y_r^{\star }+A_j^{\star }-A_r^{\star })\le Y_j^{\star }\end{array}$ and due to (4(4) $Y_j^{\star }\le {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right],j=0,\dots ,J,$(4) ) on the other hand ${\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}\right(Z_r-M_r^{\star }+M_j^{\star }\left)\right]\ge Y_j^{\star }.$ Thus, it follows that (6(6) $Y_j^{\star }=\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\text{almost surely.}$(6) ) holds for arbitrary j, hence $M^{\star }\in {\mathcal{M}}^{\circ \circ }.$ Furthermore we have the following properties of the sets $\left({\mathcal{M}}^{\circ ,j}\right)$ and $\left({\mathcal{M}}^{\circ \circ ,j}\right).$

Proposition 1

The sets ${\mathcal{M}}^{\circ ,j}$ and ${\mathcal{M}}^{\circ \circ ,j}$ for $j=0,\dots ,J,$ ${\mathcal{M}}^{\circ },$ and ${\mathcal{M}}^{\circ \circ }$ are convex.

As an immediate consequence of Proposition 1; if there exist more than one weakly (respectively surely) optimal martingale, then there exist infinitely many weakly (respectively surely) optimal martingales.

Proposition 2

It holds that M $\in {\mathcal{M}}^{\circ ,j}$ for some $0\le j\le J,$ if and only if for any optimal stopping time ${\tau }_j^{\star }\ge j$ satisfying $Y_j^{\star }=\underset{\tau \ge j}{sup}{\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{\tau }\right]={\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{{\tau }_j^{\star }}\right],$ one has that $\underset{j\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }}.$

Proof.

Let ${\tau }_j^{\star }\ge j$ be an optimal stopping time. Suppose that M $\in {\mathcal{M}}^{\circ ,j}.$ On the one hand, one trivially has $\underset{j\le r\le J}{max}(Z_r-M_r)-(Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }})\ge 0$ and on the other, since M $\in {\mathcal{M}}^{\circ ,j}$ (see (5(5) $Y_j^{\star }={\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right].$(5) )), (9) $\begin{array}{rl}& {\mathsf{E}}_{{\mathcal{F}}_j}[\underset{j\le r\le J}{max}(Z_r-M_r)-(Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }})]\\ & =Y_j^{\star }-M_j-(Y_j^{\star }-M_j)=0,\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{j\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }}\text{almost surely.}\end{array}$(9) The converse follows from (9(9) $\begin{array}{rl}& {\mathsf{E}}_{{\mathcal{F}}_j}[\underset{j\le r\le J}{max}(Z_r-M_r)-(Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }})]\\ & =Y_j^{\star }-M_j-(Y_j^{\star }-M_j)=0,\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{j\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_j^{\star }}-M_{{\tau }_j^{\star }}\text{almost surely.}\end{array}$(9) ) by taking conditional ${\mathcal{F}}_j$-expectations.

It will be shown below that the class of the optimal martingales ${\mathcal{M}}^{\circ }$ may be considerably large. In fact, any such martingale can be seen as a perturbation of the Doob martingale $\left(M_j^{\star }\right).$ For this, let us introduce some further notation and define ${\tau }^0:=0^{-}$ with $0^{-}<0$ by convention and let, for $l\ge 1,$ ${\tau }^l$ be the first optimal stopping time strictly after ${\tau }^{l-1}.$ That is, if ${\tau }^{l-1}<J,$ we define recursively ${\tau }^l=inf\{{\tau }^{l-1}<i\le J:Z_i\ge {\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right]\},$ where $Y_{J+1}^{\star }:=0.$ There so will be a last number, $l_J$ say, with ${\tau }^{l_J}=J.$ Further, the family $({\tau }_i^{\star }{)}_{i\ge 0}$ defined by (10) ${\tau }_i^{\star }={\tau }^l\mathrm{f}\mathrm{o}\mathrm{r}{\tau }^{l-1}<i\le {\tau }^l,l\ge 1,$(10) is a consistent optimal stopping family in the sense that $Y_j^{\star }={\mathsf{E}}_{{\mathcal{F}}_j}\left[Z_{{\tau }_j^{\star }}\right]$ and that ${\tau }_i^{\star }>i$ implies ${\tau }_i^{\star }={\tau }_{i+1}^{\star }.$

The next lemma provides a corner stone for an explicit structural characterization of (weakly) optimal martingales.

Lemma 3

$M\in {\mathcal{M}}^{\circ }$ if and only if M is a martingale with $M_0=0$ such that the identities $\begin{array}{rl}\left(\mathrm{i}\right)& \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-M_r)=Z_{{\tau }^l}-M_{{\tau }^l}\text{if}l\ge 1,\\ \left(\mathrm{i}\mathrm{i}\right)& \underset{{\tau }^{l-1}\le r\le {\tau }^l}{max}(Z_r-M_r)=Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}}\text{if}l>1\end{array}$ hold.

The following lemma anticipates sufficient conditions for a martingale M to be optimal, that is, to be a member of ${\mathcal{M}}^{\circ }.$

Lemma 4

Let $({\mathcal{S}}_i{)}_{0\le i\le J}$ be an adapted sequence with ${\mathcal{S}}_0=0$ and consider the ‘shifted’ Doob martingale $M_i=M_i^{\star }-{\mathcal{S}}_i,0\le i\le J.$ Let $l_i\ge 1$ be the unique number such that ${\tau }^{l_i-1}<i\le {\tau }^{l_i}$ for any $0\le i\le J.$ If $\mathcal{S}$ satisfies for all $0\le i\le J,$ (11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) (12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) for ${\tau }^{l_i-1}<i\le {\tau }^{l_i}$ and $l_i>1$, then M satisfies the identities (i)–(ii) in Lemma 3.

The next lemma is merely a reformulation of the previous one in terms of the increments of $\mathcal{S}$.

Lemma 5

Let us represent an (arbitrary) adapted $\mathcal{S}$ with ${\mathcal{S}}_0=0$ by (13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) where each ${\zeta }_{i+1}$ is a ${\mathcal{F}}_{i+1}$-measurable random variable. Then the conditions (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) are equivalent to the following ones.

(i)

On the ${\mathcal{F}}_i$-measurable event $\{{\tau }^{l_i-1}<i<{\tau }^{l_i}\}$ it holds that (14) $\begin{array}{rl}{\zeta }_{i+1}& \ge \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\text{and}\end{array}$(14) (15) $\begin{array}{rl}{\zeta }_{i+1}& \le Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\text{for}{l}_i>1;\end{array}$(15)

(ii)

On $\{{\tau }^{l_i}=i\}$ one has that (16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16)

Proof.

Indeed, take j such that $\{{\tau }^{l_j-1}<j\le {\tau }^{l_j}\},$ $l_j\ge 1.$ If $j-1>{\tau }^{l_j-1}$ then $l_{j-1}=l_j$ and (14(14) $\begin{array}{rl}{\zeta }_{i+1}& \ge \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\text{and}\end{array}$(14) ) and (15(15) $\begin{array}{rl}{\zeta }_{i+1}& \le Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\text{for}{l}_i>1;\end{array}$(15) ) imply with i = j−1 via (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ), $\begin{array}{rl}0& \ge \underset{{\tau }^{l_j-1}<r\le j-1}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_j)\mathrm{a}\mathrm{n}\mathrm{d}\\ 0& \le Z_{{\tau }^{l_j-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_j-1}}}\left[Y_{{\tau }^{l_j-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_j-1}}-{\mathcal{S}}_j\mathrm{f}\mathrm{o}\mathrm{r}{l}_j>1,\end{array}$ respectively, which in turn imply (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) (note that $Z_j-Y_j^{\star }\le 0$) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ), respectively. Further if $j-1={\tau }^{l_j-1}$ we have to distinguish between $(j=0)\wedge (l_0=1)$ and $(j={\tau }^{l_j-1}+1)\wedge (l_j>1).$ In both cases (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) is trivially fulfilled, while (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) is void in the first case, and in the second case it reads, $0\le Z_{{\tau }^{l_j-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_j-1}}}\left[Y_{{\tau }^{l_j-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_j-1}}-{\mathcal{S}}_{{\tau }^{l_j-1}+1},l_j>1,$ which is implied by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ) and (16(16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16) ) for $i=j-1={\tau }^{l_i}={\tau }^{l_{j-1}}={\tau }^{l_j-1}.$ The converse direction, that is from (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) to (14(14) $\begin{array}{rl}{\zeta }_{i+1}& \ge \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\text{and}\end{array}$(14) ), (15(15) $\begin{array}{rl}{\zeta }_{i+1}& \le Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\text{for}{l}_i>1;\end{array}$(15) ), (16(16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16) ), goes similarly and is left to the reader.

Corollary 6

Any martingale $\mathcal{S}$ with ${\mathcal{S}}_0=0$ that satisfies (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ), or (i) and (ii) via (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ), is an optimal martingale. (Note that $\mathcal{S}=0$ trivially satisfies these conditions.)

Interestingly, the converse to Corollary 6 is also true and we so have the following characterization theorem.

Theorem 7

It holds that $M\in {\mathcal{M}}^{\circ }$ if and only if $M=M^{\star }-\mathcal{S},$ where $\mathcal{S}$ is a martingale with ${\mathcal{S}}_0=0$ that satisfies (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) in Lemma 4.

The proofs of Lemmas 3–4 and Theorem 7 are given in Section 4. In fact, Theorem 7 reveals that in general, besides the Doob martingale, there may exist a large set of optimal martingales $M\in {\mathcal{M}}^{\circ }.$ From Theorem 7 we also obtain a characterization of the surely optimal martingales which is essentially the older result in Schoenmakers et al. (2013), Thm. 6 (see Section 4 for the proof).

Corollary 8

It holds that $M\in {\mathcal{M}}^{\circ \circ }$ if and only if $M=M^{\star }-\mathcal{S}$ with $\mathcal{S}$ represented by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ) with all ${\mathsf{E}}_{{\mathcal{F}}_i}\left[{\zeta }_{i+1}\right]=0,$ ${\zeta }_{i+1}$ satisfying (16(16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16) ) for $i={\tau }^{l_i}$, and ${\zeta }_{i+1}=0$ for ${\tau }^{l_i-1}<i<{\tau }^{l_i},$ $l_i\ge 1.$

In applications of dual optimal stopping, hence dual martingale minimization, it is usually enough to find martingales M that are ‘close to’ surely optimal ones, merely at some specific point in time i, that is, M ∈${\mathcal{M}}^{\circ \circ ,i}$. Naturally, since ${\mathcal{M}}^{\circ ,i}$ $\supset$ ${\mathcal{M}}^{\circ },$ we may expect that in general the family of undesirable (not surely) optimal martingales at a specific time may be even much larger than the family ${\mathcal{M}}^{\circ }$ characterized by Theorem 7. A characterization of ${\mathcal{M}}^{\circ ,i}$ and ${\mathcal{M}}^{\circ \circ ,i}$ is given by the next theorem, where we take i = 0 without loss of generality. The proof is given in Section 4.

Theorem 9

The following statements hold.

(i)

$M=M^{\star }-\mathcal{S}\in {\mathcal{M}}^{\circ ,0}$ for some martingale $\mathcal{S}$ represented by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ), if and only if (17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) (18) $\begin{array}{rl}& {\mathcal{S}}_j-{\mathcal{S}}_{{\tau }^{\star }}\le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J\end{array}$(18) with ${\tau }^{\star }:={\tau }_0^{\star },$ where $A_j^{\ast }=0$ (see (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) )) for all $0\le j\le {\tau }^{\star }.$

(ii)

$M=M^{\star }-\mathcal{S}\in {\mathcal{M}}^{\circ \circ ,0},$ if and only if (19) $\begin{array}{rl}{\mathcal{S}}_j& =0\text{for}0\le j\le {\tau }^{\star },\end{array}$(19) (20) $\begin{array}{rl}{\mathcal{S}}_j& \le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J.\end{array}$(20)

After dropping the nonnegative term $Y_j^{\star }-Z_j$ in the right-hand-sides of (18(18) $\begin{array}{rl}& {\mathcal{S}}_j-{\mathcal{S}}_{{\tau }^{\star }}\le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J\end{array}$(18) ) and (20(20) $\begin{array}{rl}{\mathcal{S}}_j& \le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J.\end{array}$(20) ) we may obtain tractable sufficient conditions for a martingale to be optimal or surely optimal at a single date, respectively. In the spirit of Lemma 5 they may be formulated in the following way.

Corollary 10

Let $M=M^{\star }-\mathcal{S}$ for some martingale $\mathcal{S}$ represented by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ), then

(i)

$M\in {\mathcal{M}}^{\circ ,0}$ if (21) $\begin{array}{rl}{\zeta }_j& \ge \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{j-1}+{\mathcal{S}}_r)\text{for}1\le j\le {\tau }^{\star }\text{and}\\ {\zeta }_j& \le A_j^{\ast }+{\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_{j-1}\text{for}{\tau }^{\star }<j\le J,\end{array}$(21)

(ii)

$M\in {\mathcal{M}}^{\circ \circ ,0}$ if ${\zeta }_j=0$ for $0\le j\le {\tau }^{\star },$ and (22) ${\zeta }_j\le A_j^{\ast }-{\mathcal{S}}_{j-1}\text{for}{\tau }^{\star }<j\le J.$(22) In particular, the right-hand-sides in (21(21) $\begin{array}{rl}{\zeta }_j& \ge \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{j-1}+{\mathcal{S}}_r)\text{for}1\le j\le {\tau }^{\star }\text{and}\\ {\zeta }_j& \le A_j^{\ast }+{\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_{j-1}\text{for}{\tau }^{\star }<j\le J,\end{array}$(21) ) and (22(22) ${\zeta }_j\le A_j^{\ast }-{\mathcal{S}}_{j-1}\text{for}{\tau }^{\star }<j\le J.$(22) ) are ${\mathcal{F}}_{j-1}$-measurable.

Remark 11

While the class of optimal martingales ${\mathcal{M}}^{\circ ,0}$ may be quite large in general, it is still possible that it is just a singleton (containing the Doob martingale only). For example, let the cash-flow $Z\ge 0$ be a martingale itself, then it is easy to see that the only optimal martingale (at 0) is $M=M^{\star }=Z-Z_0$ (the proof is left as an easy exercise).

3. Randomized dual martingale representations

Let $({\mathrm{\Omega }}_0,\mathcal{B})$ be some auxiliary measurable space that is ‘rich enough’. Let us consider random variables on $\tilde{\mathrm{\Omega }}:=\mathrm{\Omega }\times {\mathrm{\Omega }}_0$ that are measurable with respect to the σ-field $\tilde{\mathcal{F}}:=\sigma \{F\times B:F\in \mathcal{F},B\in \mathcal{B}\}.$ While abusing notation a bit, $\mathcal{F}$ and ${\mathcal{F}}_j$ are identified with $\sigma \{F\times {\mathrm{\Omega }}_0:F\in \mathcal{F}\}\subset \tilde{\mathcal{F}}$ and $\sigma \{F\times {\mathrm{\Omega }}_0:F\in {\mathcal{F}}_j\}\subset \tilde{\mathcal{F}},$ respectively. Let further $\mathsf{P}$ be the given ‘primary’ measure on $(\mathrm{\Omega },\mathcal{F}),$ and $\tilde{\mathsf{P}}$ be an extension of $\mathsf{P}$ to $(\tilde{\mathrm{\Omega }},\tilde{\mathcal{F}})$ in the sense that $\tilde{\mathsf{P}}({\mathrm{\Omega }}_0\times F)=\mathsf{P}\left(F\right)\text{for all}F\in \mathcal{F}.$ In particular, if $X:\tilde{\mathrm{\Omega }}\to \mathbb{R}$ is $\mathcal{F}$-measurable, then $\left\{\right(\omega ,{\omega }_0):X(\omega ,{\omega }_0)\le x\}=$  $\left\{\right(\omega ,{\omega }_0):\omega \in F_x\}$ for some $F_x\in \mathcal{F}$, that is, X does not depend on ${\omega }_0.$ We now introduce randomized or ‘pseudo’ martingales as random perturbations of $\mathcal{F}$-adapted martingales $M\in \mathcal{M}$. Let $({\eta }_j{)}_{j\ge 0}$ be random variables on $(\tilde{\mathrm{\Omega }},\tilde{\mathcal{F}},\tilde{\mathsf{P}})$ such that ${\tilde{\mathsf{E}}}_{\mathcal{F}}\left[{\eta }_j\right]=0$ for $j=0,\dots ,J.$ Then (23) ${\tilde{M}}_j:=M_j-{\eta }_j$(23) is said to be a pseudo martingale. As such, $\tilde{M}$ is not an $\mathcal{F}$-martingale but ${\tilde{\mathsf{E}}}_{\mathcal{F}}\left[\tilde{M}\right]$ is. The results below on pseudo-martingales provide the key motivation for randomized dual optimal stopping. All proofs in this section are deferred to Section 4.

Proposition 12

(i)	For any $\tilde{M}$ of the form (23(23) ${\tilde{M}}_j:=M_j-{\eta }_j$(23) ) one has the upper estimate (24) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]\ge Y_0^{\star }.$(24)
(ii)	Suppose $M^{\circ \circ ,0}=M_j^{\star }-{\mathcal{S}}_j^{\circ \circ ,0}\in {\mathcal{M}}^{\circ \circ ,0},$ i.e. ${\mathcal{S}}^{\circ \circ ,0}$ satisfies Theorem 9-(ii). Then (25) $M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\ge 0,\text{for}0\le j\le J.$(25)
(iii)	If the mean zero random perturbations $\left({\eta }_j\right)$ satisfy in addition (26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) then for the pseudo martingale (27) ${\tilde{M}}_j=M^{\circ \circ ,0}-{\eta }_j=M_j^{\star }-{\mathcal{S}}_j^{\circ \circ ,0}-{\eta }_j,$(27) one has the almost sure identity (28) $Y_0^{\star }=\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)\tilde{\mathsf{P}}-a.s.$(28) Moreover, for the first optimal stopping time ${\tau }^{\star }$ : = ${\tau }_0^{\star }$ (see (10(10) ${\tau }_i^{\star }={\tau }^l\mathrm{f}\mathrm{o}\mathrm{r}{\tau }^{l-1}<i\le {\tau }^l,l\ge 1,$(10) )) one has that ${\eta }_{{\tau }^{\star }}=0$ a.s.

The next theorem states that, loosely speaking, there exists a particular randomization of the form (26(26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) ) connected with $M^{\circ \circ ,0}$ with the following property: Any martingale different from $M^{\circ \circ ,0}$ fails to be optimal under this particular randomization.

Theorem 13

Now suppose that $M=M^{\circ \circ ,0}-\mathcal{S}\in \mathcal{M}$ with $M^{\circ \circ ,0}\in {\mathcal{M}}^{\circ \circ ,0}$ and $\mathcal{S}$ being some martingale of the form (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ). Let $\left({\eta }_j\right)$ be a sequence of random variables given by (29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) where the $\left({\xi }_j\right)$ are assumed to be i.i.d. distributed on $(-\mathrm{\infty },1],$ independent of $\mathcal{F}$ with $\tilde{\mathsf{E}}\left[{\xi }_j\right]=0.$ It is further assumed that the r.v. $\left({\xi }_j\right)$ have a density p that is continuous in the interval $(-\mathrm{\infty },1]$, vanishes on $(1,\mathrm{\infty })$, and is such that $p\left(1\right)>0$. As such the randomizers (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ) satisfy (26(26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) ). Proposition 12 provides an upper bound (24(24) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]\ge Y_0^{\star }.$(24) ) due to the pseudo martingale $\tilde{M}=M-\eta .$ Now, for the randomized martingale $\tilde{M}$ one has (30) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]>Y_0^{\star }$(30) if $\mathcal{S}\ne 0,$ that is, if $M\ne M^{\circ \circ ,0}$.

The following corollary states that any martingale $M\in$ $\mathcal{M}$ randomized with (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ), which is suboptimal in the sense of (30(30) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]>Y_0^{\star }$(30) ), cannot have zero variance. The proof relies on Theorem 13.

Corollary 14

Let M and $\left({\eta }_j\right)$ as in Theorem 13, and $\tilde{M}=M-\eta$. Then $\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)=0$ if and only if $M=M_j^{\circ \circ ,0}.$

Randomizing the Doob the martingale

Proposition 12 shows that, in principle, there is a remarkable freedom of perturbing any surely optimal martingale $M^{\circ \circ ,0}$ randomly while (28(28) $Y_0^{\star }=\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)\tilde{\mathsf{P}}-a.s.$(28) ) remains true. The message of Theorem 13 is, on the one hand, that a particular randomization, namely (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ), of any martingale different from $M^{\circ \circ ,0}$ results in a non optimal (pseudo) martingale in the sense of (30(30) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]>Y_0^{\star }$(30) ). On the other hand, any randomization of $M^{\circ \circ ,0}$ under (26(26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) ) remains surely optimal in the sense (28(28) $Y_0^{\star }=\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)\tilde{\mathsf{P}}-a.s.$(28) ). However, when one thinks of implementing this idea in practice the question arises: which target martingale $M^{\circ \circ ,0}$ (there may be infinitely many) do we have in mind? Of course, the canonical candidate is the Doob martingale. An approximation may be directly inferred, for instance from any accompanying standard primal algorithm such as the Longstaff-Schwartz method. With $M^{\circ \circ ,0}=M^{\star }$ the randomization (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ) takes by (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ) the form (31) ${\eta }_j={\xi }_j(M_j^{\star }-Z_j+Y_0^{\star })={\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }).$(31) Thus, if ${\overline{c}}_j\left(x\right)\approx {\mathsf{E}}_{{\mathcal{F}}_j}[Y_{j+1}^{\star }|X_j=x]$ are approximate continuation functions due to some underlying Markovian process X obtained by the method of Longstaff-Schwartz for example, one may consider the randomizations (32) $\begin{array}{rl}{\overline{\eta }}_j& ={\xi }_j(\phantom{\sum _{r=1}^j}max(Z_0,{\overline{c}}_j\left(X_0\right))-Z_j(X_j)\\ & +\sum _{r=1}^{j}max\left(Z_r\right(X_r),{\overline{c}}_j(X_r\left)\right)-{\overline{c}}_{r-1}\left(X_{r-1}\right)).\end{array}$(32) As a bottomline, if the (surely optimal) Doob martingale is a member of some larger martingale family that includes many weakly optimal martingales, by randomizing with (31(31) ${\eta }_j={\xi }_j(M_j^{\star }-Z_j+Y_0^{\star })={\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }).$(31) ) (or (32(32) $\begin{array}{rl}{\overline{\eta }}_j& ={\xi }_j(\phantom{\sum _{r=1}^j}max(Z_0,{\overline{c}}_j\left(X_0\right))-Z_j(X_j)\\ & +\sum _{r=1}^{j}max\left(Z_r\right(X_r),{\overline{c}}_j(X_r\left)\right)-{\overline{c}}_{r-1}\left(X_{r-1}\right)).\end{array}$(32) )) all (or approximately all) weakly optimal members of this family can be sorted out in a suitable dual expectation minimization procedure. For first numerical examples we refer to Section 5.

4. Proofs

4.1. Proof of Lemma 1

It is enough to show the convexity of ${\mathcal{M}}^{\circ ,j}$ and ${\mathcal{M}}^{\circ \circ ,j}$ for any j. For any $M,M^{\mathrm{\prime }}\in {\mathcal{M}}^{\circ ,j}$ and $\theta \in (0,1)$ one has $\begin{array}{rl}& {\mathsf{E}}_{{\mathcal{F}}_j}[\underset{j\le r\le J}{max}(Z_r-(\theta M_r+(1-\theta \left)M_r^{\mathrm{\prime }}\right))+\theta M_j+(1-\theta \left)M_j^{\mathrm{\prime }}\right]\\ & =\mathsf{E}[\underset{j\le r\le J}{max}(\theta (Z_r-M_r+M_j)\\ & +(1-\theta )(Z_r-M_r^{\mathrm{\prime }}+M_j^{\mathrm{\prime }}))]\\ & \le \theta \mathsf{E}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right]\\ & +(1-\theta )\mathsf{E}\left[\underset{j\le r\le J}{max}(Z_r-M_r^{\mathrm{\prime }}+M_j^{\mathrm{\prime }})\right]=Y_j^{\star }\end{array}$ while by (4(4) $Y_j^{\star }\le {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right],j=0,\dots ,J,$(4) ), $\begin{array}{rl}& {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-(\theta M_r+(1-\theta \left)M_r^{\mathrm{\prime }}\right)+\theta M_j+(1-\theta \left)M_j^{\mathrm{\prime }}\right)\right]\\ & \ge Y_j^{\star }.\end{array}$ Similarly, for any $M,M^{\mathrm{\prime }}\in {\mathcal{M}}^{\circ \circ ,j}$ and $\theta \in (0,1)$ we have $\begin{array}{rl}& \underset{j\le r\le J}{max}(Z_r-(\theta M_r+(1-\theta )M_r^{\mathrm{\prime }}+\theta M_j+(1-\theta \left)M_j^{\mathrm{\prime }}\right))\\ & =\underset{j\le r\le J}{max}(\theta (Z_r-M_r+M_j)+(1-\theta \left)(Z_r-M_r^{\mathrm{\prime }}+M_j^{\mathrm{\prime }})\right)\\ & \le \theta \underset{j\le r\le J}{max}(Z_r-M_r+M_j)+(1-\theta )\\ & \times \underset{0\le r\le J}{max}(Z_r-M_r^{\mathrm{\prime }}+M_j^{\mathrm{\prime }})=Y_j^{\star }\end{array}$ while by (4(4) $Y_j^{\star }\le {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-M_r+M_j)\right],j=0,\dots ,J,$(4) ), $\begin{array}{rl}& {\mathsf{E}}_{{\mathcal{F}}_j}\left[\underset{j\le r\le J}{max}(Z_r-(\theta M_r+(1-\theta \left)M_r^{\mathrm{\prime }}\right)+\theta M_j+(1-\theta \left)M_j^{\mathrm{\prime }}\right)\right]\\ & \ge Y_j^{\star }.\end{array}$ In both cases the sandwich property completes.

4.2. Proof of Lemma 3

Suppose that M is a martingale with $M_0=0$ such that Lemma 3-(i) and (ii) hold. Then (ii) implies for $q\ge 1$ that (33) $Z_{{\tau }^1}-M_{{\tau }^1}\ge Z_{{\tau }^2}-M_{{\tau }^2}\ge \cdots \ge Z_{{\tau }^q}-M_{{\tau }^q}$(33) Now take $0\le i\le J$ arbitrarily, and let $q_i\ge 1$ be such that ${\tau }^{q_i-1}<i\le {\tau }^{q_i}$ (Note that $q_i$ is unique and ${\mathcal{F}}_i$ measurable). Then due to Lemma 3-(i) and (33(33) $Z_{{\tau }^1}-M_{{\tau }^1}\ge Z_{{\tau }^2}-M_{{\tau }^2}\ge \cdots \ge Z_{{\tau }^q}-M_{{\tau }^q}$(33) ), $\begin{array}{rl}& \underset{i\le r\le J}{max}(Z_r-M_r)\\ & =max\left(\underset{i\le r\le {\tau }^{q_i}}{max}\right(Z_r-M_r),\underset{q>q_i}{max}\underset{{\tau }^{q-1}<r\le {\tau }^q}{max}(Z_r-M_r\left)\right)\\ & =max(Z_{{\tau }^{q_i}}-M_{{\tau }^{q_i}},\underset{q>q_i}{max}(Z_{{\tau }^q}-M_{{\tau }^q}))\\ & =max(Z_{{\tau }^{q_i}}-M_{{\tau }^{q_i}},Z_{{\tau }^{q_i+1}}-M_{{\tau }^{q_i+1}})=Z_{{\tau }^{q_i}}-M_{{\tau }^{q_i}}.\end{array}$ On the other hand, one has ${\tau }_i^{\star }={\tau }^{q_i}$ (see (10(10) ${\tau }_i^{\star }={\tau }^l\mathrm{f}\mathrm{o}\mathrm{r}{\tau }^{l-1}<i\le {\tau }^l,l\ge 1,$(10) )). Thus, by Proposition 2, $M\in {\mathcal{M}}^{\circ ,i}$ and hence $M\in {\mathcal{M}}^{\circ }$ since i was taken arbitrarily.

Conversely, suppose that $M\in {\mathcal{M}}^{\circ }.$ So for any $0\le i\le J,$ $\underset{i\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_i^{\star }}-M_{{\tau }_i^{\star }}$ by Proposition 2. For l = 1 one thus has $\begin{array}{rl}\underset{{\tau }^0<r\le J}{max}(Z_r-M_r)& =\underset{0\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_0^{\star }}-M_{{\tau }_0^{\star }}\\ & =Z_{{\tau }^1}-M_{{\tau }^1}\end{array}$ and for l>1 it holds that $\begin{array}{rl}\underset{{\tau }^{l-1}<r\le J}{max}(Z_r-M_r)& =\sum _{k=0}^{J-1}{1}_{\{{\tau }^{l-1}=k\}}\underset{k+1\le r\le J}{max}(Z_r-M_r)\\ & =\sum _{k=0}^{J-1}{1}_{\{{\tau }^{l-1}=k\}}(Z_{{\tau }_{k+1}^{\star }}-M_{{\tau }_{k+1}^{\star }})\\ & =\sum _{k=0}^{J-1}{1}_{\{{\tau }^{l-1}=k\}}(Z_{{\tau }^l}-M_{{\tau }^l})=Z_{{\tau }^l}-M_{{\tau }^l}.\end{array}$ That is, (i) is shown. Next, for any l>1 it holds $\begin{array}{rl}\underset{{\tau }^{l-1}\le r\le J}{max}(Z_r-M_r)& =\sum _{k=0}^L{1}_{\{{\tau }^{l-1}=k\}}\underset{k\le r\le J}{max}(Z_r-M_r)\\ & =\sum _{k=0}^L{1}_{\{{\tau }^{l-1}=k\}}(Z_{{\tau }_k^{\star }}-M_{{\tau }_k^{\star }})\\ & =Z_{{\tau }_{{\tau }^{l-1}}^{\star }}-M_{{\tau }_{{\tau }^{l-1}}^{\star }}=Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}}\end{array}$ which implies (ii).

4.3. Proof of Lemma 4

Assume that $\mathcal{S}$ is adapted with ${\mathcal{S}}_0=0$ and that $\mathcal{S}$ satisfies (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ). For l>1 and ${\tau }^{l-1}<r\le {\tau }^l$ we may write, (34) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+M_{{\tau }^{l-1}}^{\star }-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r-\sum _{k={\tau }^{l-1}+1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r\\ & -\sum _{k={\tau }^{l-1}+1}^r{Y}_k^{\star }+\sum _{k={\tau }^{l-1}+1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }-M_{{\tau }^{l-1}}^{\star }+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]+{\mathcal{S}}_r.\end{array}$(34) By taking $r={\tau }^l$ in (34(34) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+M_{{\tau }^{l-1}}^{\star }-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r-\sum _{k={\tau }^{l-1}+1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r\\ & -\sum _{k={\tau }^{l-1}+1}^r{Y}_k^{\star }+\sum _{k={\tau }^{l-1}+1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }-M_{{\tau }^{l-1}}^{\star }+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]+{\mathcal{S}}_r.\end{array}$(34) ) and using $Z_{{\tau }^l}=Y_{{\tau }^l}^{\star }$ we then get $Z_{{\tau }^l}-M_{{\tau }^l}=-M_{{\tau }^{l-1}}^{\star }+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^l}$ and thus $\begin{array}{rl}{Z}_r-M_r& =Z_{{\tau }^l}-M_{{\tau }^l}+Z_r-Y_r^{\star }+{\mathcal{S}}_r\\ & -{\mathcal{S}}_{{\tau }^l},{\tau }^{l-1}<r\le {\tau }^l.\end{array}$ So from (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) we obtain with $i={\tau }^l,$ $l_i-1=l-1,$ $Z_r-M_r\le Z_{{\tau }^l}-M_{{\tau }^l}\mathrm{f}\mathrm{o}\mathrm{r}{\tau }^{l-1}<r\le {\tau }^l,$ i.e. Lemma 3-(i) for $l>1.$ If l = 1 and ${\tau }^1=0,$ Lemma 3-(i) is trivially fulfilled. So let us consider l = 1 and ${\tau }^1>0.$ Analogously, we then may write for ${\tau }^0=0^{-}<0<r\le {\tau }^1,$ (35) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r=Z_r+{\mathcal{S}}_r\\ & -\sum _{k=1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r+{\mathcal{S}}_r-\sum _{k=1}^r{Y}_k^{\star }+\sum _{k=1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }+{\mathsf{E}}_{{\mathcal{F}}_0}\left[Y_1^{\star }\right]+{\mathcal{S}}_r.\end{array}$(35) It is easy to see that (35(35) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r=Z_r+{\mathcal{S}}_r\\ & -\sum _{k=1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r+{\mathcal{S}}_r-\sum _{k=1}^r{Y}_k^{\star }+\sum _{k=1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }+{\mathsf{E}}_{{\mathcal{F}}_0}\left[Y_1^{\star }\right]+{\mathcal{S}}_r.\end{array}$(35) ) is also valid for $r=0,$ due to our assumption ${\tau }^1>0.$ Thus, for l = 1 and taking $r={\tau }^1>0,$ we get from (35(35) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r=Z_r+{\mathcal{S}}_r\\ & -\sum _{k=1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r+{\mathcal{S}}_r-\sum _{k=1}^r{Y}_k^{\star }+\sum _{k=1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }+{\mathsf{E}}_{{\mathcal{F}}_0}\left[Y_1^{\star }\right]+{\mathcal{S}}_r.\end{array}$(35) ), $Z_{{\tau }^1}-M_{{\tau }^1}={\mathsf{E}}_{{\mathcal{F}}_0}\left[Y_1^{\star }\right]+{\mathcal{S}}_{{\tau }^1},$ whence (35(35) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r=Z_r+{\mathcal{S}}_r\\ & -\sum _{k=1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r+{\mathcal{S}}_r-\sum _{k=1}^r{Y}_k^{\star }+\sum _{k=1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }+{\mathsf{E}}_{{\mathcal{F}}_0}\left[Y_1^{\star }\right]+{\mathcal{S}}_r.\end{array}$(35) ) implies for ${\tau }^0=0^{-}<r\le {\tau }^1$ $Z_r-M_r=Z_r-Y_r^{\star }+Z_{{\tau }^1}-M_{{\tau }^1}\le Z_{{\tau }^1}-M_{{\tau }^1},$ that is Lemma 3-(i) holds also for $l=1.$

Let us now consider (ii) and take $l>1.$ Now for ${\tau }^{l-1}<r\le {\tau }^l$ (34(34) $\begin{array}{rl}{Z}_r-M_r& =Z_r-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+M_{{\tau }^{l-1}}^{\star }-M_r^{\star }+{\mathcal{S}}_r\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r-\sum _{k={\tau }^{l-1}+1}^r(Y_k^{\star }-{\mathsf{E}}_{{\mathcal{F}}_{k-1}}\left[Y_k^{\star }\right])\\ & =Z_r-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_r\\ & -\sum _{k={\tau }^{l-1}+1}^r{Y}_k^{\star }+\sum _{k={\tau }^{l-1}+1}^{r-1}{\mathsf{E}}_{{\mathcal{F}}_k}\left[Y_{k+1}^{\star }\right]\\ & +{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & =Z_r-Y_r^{\star }-M_{{\tau }^{l-1}}^{\star }+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]+{\mathcal{S}}_r.\end{array}$(34) ) implies with $M_{{\tau }^{l-1}}^{\star }=$ ${\mathcal{S}}_{{\tau }^{l-1}}+M_{{\tau }^{l-1}},$ (36) $\begin{array}{rl}{Z}_r-M_r& =Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}}+Z_r-Y_r^{\star }+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l-1}}}\left[Y_{{\tau }^{l-1}+1}^{\star }\right]\\ & -Z_{{\tau }^{l-1}}+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^{l-1}}.\end{array}$(36) Hence, since always $Z_r\le Y_r^{\star },$ (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) implies for ${\tau }^{l-1}<r\le {\tau }^l,$ (37) $Z_r-M_r\le Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}},{\tau }^{l-1}<r\le {\tau }^l,$(37) i.e. Lemma 3-(ii) is proved.

4.4. Proof of Theorem 7

If $M=M^{\star }-\mathcal{S}$, where $\mathcal{S}$ is a martingale with ${\mathcal{S}}_0=0$ that satisfies (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) in Lemma 4 then $M\in {\mathcal{M}}^{\circ }$ due to Corollary 6.

Let us now consider the converse and assume that $M=M^{\star }-\mathcal{S}\in {\mathcal{M}}^{\circ }$ with $M_0={\mathcal{S}}_0=0.$ Then $\mathcal{S}$ is adapted and may be written in the form (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ) where the ${\zeta }_{i+1}$ are ${\mathcal{F}}_{i+1}$-measurable and ${\mathsf{E}}_{{\mathcal{F}}_i}\left[{\zeta }_{i+1}\right]=0$ for $0\le$ $i<J.$ Since $M\in {\mathcal{M}}^{\circ }$ Lemma 3-(i) implies that for $l\ge 1,$ (38) $\begin{array}{rl}& \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Z_{{\tau }^l}+M_{{\tau }^l}^{\star }-M_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0,\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0\end{array}$(38) since for each r with ${\tau }^{l-1}<r\le {\tau }^l$ one has $Z_{{\tau }^l}-M_{{\tau }^l}^{\star }+M_r^{\star }=Z_{{\tau }_r^{\star }}-M_{{\tau }_r^{\star }}^{\star }+M_r^{\star }=Y_r^{\ast }$ because $M^{\star }\in {\mathcal{M}}^{\circ \circ }.$ We now show for any i with ${\tau }^{l-1}<i\le {\tau }^l$ that (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) holds with $l_i=l$ by backward induction. For $i={\tau }^{l_i}$ it follows from (38(38) $\begin{array}{rl}& \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Z_{{\tau }^l}+M_{{\tau }^l}^{\star }-M_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0,\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0\end{array}$(38) ). Now suppose that for some i with ${\tau }^{l_i-1}<i<i+1\le {\tau }^{l_i}$ it holds that (39) $\begin{array}{r}{1}_{\{{\tau }^{l_{i+1}-1}<i+1\le {\tau }^{l_{i+1}}\}}\underset{{\tau }^{l_{i+1}-1}<r\le i+1}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{i+1})\le 0.\end{array}$(39) One has by construction $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_i)\\ & ={\zeta }_{i+1}+\underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{i+1}).\end{array}$ Hence, since $\{{\tau }^{l_i-1}<i<{\tau }^{l_i}\}=\{{\tau }^{l_i-1}<i\}\cap \{{\tau }^{l_i-1}<i+1\le {\tau }^{l_i}\}$ with $\{{\tau }^{l_i-1}<i\}\in {\mathcal{F}}_i$ and $\{{\tau }^{l_i-1}<i+1\le {\tau }^l\}\in {\mathcal{F}}_i$ (!), ${\mathsf{E}}_{{\mathcal{F}}_i}\left[{\zeta }_{i+1}\right]=0,$ $l_i=l_{i+1},$ and taking ${\mathcal{F}}_i$-conditional expectations, $\begin{array}{rl}& 1_{\{{\tau }^{l_i-1}<i<{\tau }^{l_i}\}}\underset{{\tau }^{l-1}<r\le i}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_i)\\ & =1_{\{{\tau }^{l_i-1}<i\}}{\mathsf{E}}_{{\mathcal{F}}_i}\\ & \times \left[\underset{{\tau }^{l_i-1}<r\le i}{max}\right(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{i+1}\left)1_{\{{\tau }^{l_i-1}<i+1\le {\tau }^{l_i}\}}\right]\\ & \le 1_{\{{\tau }^{l_i-1}<i\}}{\mathsf{E}}_{{\mathcal{F}}_i}\\ & \times \left[\underset{{\tau }^{l_{i+1}-1}<r\le i+1}{max}\right(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{i+1}\left)1_{\{{\tau }^{l_{i+1}-1}<i+1\le {\tau }^{l_{i+1}}\}}\right]\\ & \le 0,\end{array}$ using the induction hypothesis (39(39) $\begin{array}{r}{1}_{\{{\tau }^{l_{i+1}-1}<i+1\le {\tau }^{l_{i+1}}\}}\underset{{\tau }^{l_{i+1}-1}<r\le i+1}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{i+1})\le 0.\end{array}$(39) ). In view of (38(38) $\begin{array}{rl}& \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Z_{{\tau }^l}+M_{{\tau }^l}^{\star }-M_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0,\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Y_r^{\ast }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^l})=0\end{array}$(38) ) it follows that (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) holds for ${\tau }^{l_i-1}<i\le {\tau }^{l_i}.$

Next, on the other hand, $M\in {\mathcal{M}}^{\circ }$ implies by Lemma 3-(ii) that for any fixed l>1, (40) $\begin{array}{rl}& \underset{{\tau }^{l-1}\le r\le {\tau }^l}{max}(Z_r-M_r^{\star }+{\mathcal{S}}_r)=Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_{{\tau }^{l-1}},\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Z_{{\tau }^{l-1}}+M_{{\tau }^{l-1}}^{\star }-M_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^{l-1}})=0.\end{array}$(40) Suppose that ${\tau }^{l-1}<i\le {\tau }^l$ and hence $l_i=l.$ Then (40(40) $\begin{array}{rl}& \underset{{\tau }^{l-1}\le r\le {\tau }^l}{max}(Z_r-M_r^{\star }+{\mathcal{S}}_r)=Z_{{\tau }^{l-1}}-M_{{\tau }^{l-1}}^{\star }+{\mathcal{S}}_{{\tau }^{l-1}},\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \underset{{\tau }^{l-1}<r\le {\tau }^l}{max}(Z_r-Z_{{\tau }^{l-1}}+M_{{\tau }^{l-1}}^{\star }-M_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_{{\tau }^{l-1}})=0.\end{array}$(40) ) implies by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ) after a few manipulations, $\begin{array}{rl}& Z_i-Z_{{\tau }^{l_i-1}}+M_{{\tau }^{l_i-1}}^{\star }-M_i^{\star }+{\mathcal{S}}_i-{\mathcal{S}}_{{\tau }^{l_i-1}}\\ & ={\zeta }_{{\tau }^{l_i-1}+1}+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]-Z_{{\tau }^{l_i-1}}+Z_i-Y_i^{\star }\\ & +\sum _{r={\tau }^{l_i-1}+1}^{i-1}{\zeta }_{r+1}+\sum _{r={\tau }^{l_i-1}+1}^{i-1}{\mathsf{E}}_{{\mathcal{F}}_r}\left[Y_{r+1}^{\star }\right]-\sum _{r={\tau }^{l_i-1}+1}^{i-1}{Y}_r^{\star }\le 0\end{array}$ with the usual convention $\sum _{r=p}^{p-1}:=0.$ Thus, either the last three sums are zero due to $i={\tau }^{l_i-1}+1,$ or we may use that $Y_r^{\star }={\mathsf{E}}_{{\mathcal{F}}_r}\left[Y_{r+1}^{\star }\right]$ for ${\tau }^{l_i-1}<r<i.$ We thus get for ${\tau }^{l-1}<i\le {\tau }^l,$ (41) $\begin{array}{rl}& {\zeta }_{{\tau }^{l_i-1}+1}+{\mathsf{E}}_{{\tau }^{l_i-1}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]-Z_{{\tau }^{l_i-1}}+Z_i-Y_i^{\star }+{\mathcal{S}}_i-{\mathcal{S}}_{{\tau }^{l_i-1}+1}\\ & \le 0.\end{array}$(41) In particular, due to $Z_{{\tau }^l}=Y_{{\tau }^l}^{\star },$ for $i={\tau }^l$ this gives (42) $\begin{array}{r}{\zeta }_{{\tau }^{l_i-1}+1}+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]-Z_{{\tau }^{l_i-1}}+{\mathcal{S}}_{{\tau }^{l_i}}-{\mathcal{S}}_{{\tau }^{l_i-1}+1}\le 0.\end{array}$(42) Let us now show that (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) holds for ${\tau }^{l_i-1}<i\le {\tau }^{l_i}$ and $l_i>1$ by backward induction. For $i={\tau }^{l_i}$ it follows from (42(42) $\begin{array}{r}{\zeta }_{{\tau }^{l_i-1}+1}+{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]-Z_{{\tau }^{l_i-1}}+{\mathcal{S}}_{{\tau }^{l_i}}-{\mathcal{S}}_{{\tau }^{l_i-1}+1}\le 0.\end{array}$(42) ) by ${\zeta }_{{\tau }^{l_i-1}+1}-{\mathcal{S}}_{{\tau }^{l_i-1}+1}=-{\mathcal{S}}_{{\tau }^{l_i-1}}$ that $Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_{{\tau }^{l_i}}\ge 0$ that is (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) for $i={\tau }^{l_i}.$ Now suppose that for some i with ${\tau }^{l_i-1}<i<i+1\le {\tau }^{l_i}$ it holds that $\begin{array}{rl}& 1_{\{{\tau }^{l_{i+1}-1}<i+1\le {\tau }^{l_{i+1}}\}}(Z_{{\tau }^{l_{i+1}-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_{i+1}-1}}}\left[Y_{{\tau }^{l_{i+1}-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_{i+1}-1}}\\ & -{\mathcal{S}}_{i+1}\phantom{\left[Y_{{\tau }^{l_{i+1}-1}+1}^{\star }\right]})\ge 0.\end{array}$ One thus has by construction $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\\ & =Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_{i+1}+{\zeta }_{i+1}^{-}.\end{array}$ It then follows similarly by taking ${\mathcal{F}}_i$-conditional expectations that $\begin{array}{rl}& 1_{\{{\tau }^{l_i-1}<i<{\tau }^{l_i}\}}(Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i)\\ & =1_{\{{\tau }^{l_i-1}<i<{\tau }^{l_i}\}}\\ & \times {\mathsf{E}}_{{\mathcal{F}}_i}[(Z_{{\tau }^{l_{i+1}-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_{i+1}-1}}}\left[Y_{{\tau }^{l_{i+1}-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_{i+1}-1}}-{\mathcal{S}}_{i+1})\\ & \times 1_{\{{\tau }^{l_{i+1}-1}<i+1\le {\tau }^{l_{i+1}}\}}]\ge 0\end{array}$by the induction hypothesis (note again that $l_{i+1}=l_i$). Thus, (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) holds for ${\tau }^{l_i-1}<i\le {\tau }^{l_i}$ and so (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ) is proved. We thus conclude that $\mathcal{S}$ is a martingale that satisfies (11(11) $\begin{array}{rl}& \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\le 0\end{array}$(11) ) and (12(12) $\begin{array}{rl}& Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\ge 0,\end{array}$(12) ). The theorem is proved.

4.5. Proof of Corollary 8

Suppose that $M=M^{\star }-\mathcal{S}\in {\mathcal{M}}^{\circ \circ }$ for some martingale $\mathcal{S}$ represented by (13(13) ${\mathcal{S}}_{i+1}={\mathcal{S}}_i+{\zeta }_{i+1},0\le i<J,$(13) ). Since $M\in {\mathcal{M}}^{\circ \circ }\subset$ ${\mathcal{M}}^{\circ },$ Theorem 7 implies (via Corollary 5) that the ${\zeta }_{i+1}$ satisfy (16(16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16) ) for $i={\tau }^{l_i}$. Further, for any $0\le i\le J$ one has $\begin{array}{rl}{Y}_i^{\star }& =\underset{i\le r\le J}{max}(Z_r-M_r+M_i)\\ & =\underset{i\le r\le J}{max}(Z_r-M_r^{\star }+M_i^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\\ & \le Z_{{\tau }_i^{\star }}-M_{{\tau }_i^{\star }}^{\star }+M_i^{\star }+{\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i=Y_i^{\star }+{\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i\end{array}$ since $M^{\star }\in {\mathcal{M}}^{\circ \circ }.$ So ${\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i\ge 0\mathrm{w}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{e}{\mathsf{E}}_{{\mathcal{F}}_i}[{\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i]=0,$ by Doob's sampling theorem. Hence, by the sandwich property, ${\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i=0$ for all $0\le i\le J.$ This implies for any i with ${\tau }^{l-1}<i<{\tau }^l$ that ${\zeta }_{i+1}={\mathcal{S}}_{i+1}-{\mathcal{S}}_i={\mathcal{S}}_{{\tau }_{i+1}^{\star }}-{\mathcal{S}}_{{\tau }_i^{\star }}=0$ due to ${\tau }_i^{\star }={\tau }_{i+1}^{\star }={\tau }^l.$

Conversely, if the ${\zeta }_{i+1}$ satisfy (16(16) ${\zeta }_{i+1}\le Z_i-{\mathsf{E}}_{{\mathcal{F}}_i}\left[Y_{i+1}^{\star }\right].$(16) ) for $i={\tau }^{l_i}$ and further ${\zeta }_{i+1}=0$ for any i with ${\tau }^{l_{i-1}}<i<{\tau }^{l_i}={\tau }_i^{\star },$ they also trivially satisfy (15(15) $\begin{array}{rl}{\zeta }_{i+1}& \le Z_{{\tau }^{l_i-1}}-{\mathsf{E}}_{{\mathcal{F}}_{{\tau }^{l_i-1}}}\left[Y_{{\tau }^{l_i-1}+1}^{\star }\right]+{\mathcal{S}}_{{\tau }^{l_i-1}}-{\mathcal{S}}_i\text{for}{l}_i>1;\end{array}$(15) ) and (14(14) $\begin{array}{rl}{\zeta }_{i+1}& \ge \underset{{\tau }^{l_i-1}<r\le i}{max}(Z_r-Y_r^{\star }+{\mathcal{S}}_r-{\mathcal{S}}_i)\text{and}\end{array}$(14) ), and so one has $M\in {\mathcal{M}}^{\circ }$ by Theorem 7 (via Corollary 5). Furthermore it follows that ${\mathcal{S}}_{{\tau }_i^{\star }}={\mathcal{S}}_i$ for any i with ${\tau }^{l_{i-1}}<i<{\tau }^{l_i}={\tau }_i^{\star },$ so by Proposition 2 $\begin{array}{rl}& \underset{i\le r\le J}{max}(Z_r-M_r)=Z_{{\tau }_i^{\star }}-M_{{\tau }_i^{\star }}=Z_{{\tau }_i^{\star }}-M_{{\tau }_i^{\star }}^{\star }+{\mathcal{S}}_{{\tau }_i^{\star }}\\ & =Y_i^{\star }-M_i^{\star }+{\mathcal{S}}_{{\tau }_i^{\star }}=Y_i^{\star }-M_i+{\mathcal{S}}_{{\tau }_i^{\star }}-{\mathcal{S}}_i\\ & =Y_i^{\star }-M_i.\end{array}$ Hence, $M\in {\mathcal{M}}^{\circ \circ ,i}$ and so $M\in {\mathcal{M}}^{\circ \circ }$ since i was arbitrary.

4.6. Proof of Theorem 9

• Due to Proposition 2, $M\in {\mathcal{M}}^{\circ ,0}$ if and only if $0=\underset{0\le r\le J}{max}(Z_r-M_r-Z_{{\tau }^{\star }}+M_{{\tau }^{\star }})$ with ${\tau }^{\star }:={\tau }_0^{\star },$ which is equivalent with (43) $\begin{array}{rl}\underset{0\le r<{\tau }^{\star }}{max}(Z_r-M_r-Z_{{\tau }^{\star }}+M_{{\tau }^{\star }})& \le 0\mathrm{a}\mathrm{n}\mathrm{d}\end{array}$(43) (44) $\begin{array}{rl}\underset{{\tau }^{\star }<r\le J}{max}(Z_r-M_r-Z_{{\tau }^{\star }}+M_{{\tau }^{\star }})& \le 0.\end{array}$(44) Since ${\tau }^{\star }={\tau }_r^{\star }$ for $0\le r<{\tau }^{\star },$ (43(43) $\begin{array}{rl}\underset{0\le r<{\tau }^{\star }}{max}(Z_r-M_r-Z_{{\tau }^{\star }}+M_{{\tau }^{\star }})& \le 0\mathrm{a}\mathrm{n}\mathrm{d}\end{array}$(43) ) reads (45) $\begin{array}{rl}& \underset{0\le r<{\tau }^{\star }}{max}(Z_r-M_r^{\star }-Z_{{\tau }_r^{\star }}+M_{{\tau }_r^{\star }}^{\ast }-{\mathcal{S}}_{{\tau }_r^{\star }}+{\mathcal{S}}_r)\\ & =\underset{0\le r<{\tau }^{\star }}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{{\tau }_r^{\star }}+{\mathcal{S}}_r)\\ & =\underset{0\le r<{\tau }^{\star }}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{{\tau }^{\star }}+{\mathcal{S}}_r)\le 0\end{array}$(45) which in turn is equivalent with (17(17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) ). Indeed, suppose that (45(45) $\begin{array}{rl}& \underset{0\le r<{\tau }^{\star }}{max}(Z_r-M_r^{\star }-Z_{{\tau }_r^{\star }}+M_{{\tau }_r^{\star }}^{\ast }-{\mathcal{S}}_{{\tau }_r^{\star }}+{\mathcal{S}}_r)\\ & =\underset{0\le r<{\tau }^{\star }}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{{\tau }_r^{\star }}+{\mathcal{S}}_r)\\ & =\underset{0\le r<{\tau }^{\star }}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{{\tau }^{\star }}+{\mathcal{S}}_r)\le 0\end{array}$(45) ) holds. Then (17(17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) ) clearly holds for $j=$ ${\tau }^{\star }.$ Now assume that (17(17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) ) holds for $0<j\le {\tau }^{\star }.$ Then, by backward induction, $\begin{array}{rl}& \underset{0\le r<j-1}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_{j-1}+{\mathcal{S}}_r)\\ & =\underset{0\le r<j-1}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)+{\zeta }_j\le {\zeta }_j\end{array}$ By next taking ${\mathcal{F}}_{j-1}$-conditional expectations we get (17(17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) ) for $j-1.$ For the converse, just take $j=$ ${\tau }^{\star }$ in (17(17) $\begin{array}{rl}& \underset{0\le r<j}{max}(Z_r-Y_r^{\ast }-{\mathcal{S}}_j+{\mathcal{S}}_r)\le 0\text{for}0\le j\le {\tau }^{\star }\text{and}\end{array}$(17) ). We next consider (44(44) $\begin{array}{rl}\underset{{\tau }^{\star }<r\le J}{max}(Z_r-M_r-Z_{{\tau }^{\star }}+M_{{\tau }^{\star }})& \le 0.\end{array}$(44) ), which may be written as $\underset{{\tau }^{\star }<r\le J}{max}(Z_r-M_r^{\ast }+M_{{\tau }^{\star }}^{\ast }-Z_{{\tau }^{\star }}-{\mathcal{S}}_{{\tau }^{\star }}+{\mathcal{S}}_r)\le 0$ Using the Doob decomposition of the Snell envelope (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ), $A_{{\tau }^{\star }}^{\ast }=0,$ and that $Y_{{\tau }^{\star }}^{\star }=Z_{{\tau }^{\star }},$ this is equivalent with (18(18) $\begin{array}{rl}& {\mathcal{S}}_j-{\mathcal{S}}_{{\tau }^{\star }}\le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J\end{array}$(18) ).

• Suppose that $M\in {\mathcal{M}}^{\circ \circ ,0}.$ One has that $M=M^{\star }-\mathcal{S}\in {\mathcal{M}}^{\circ \circ ,0},$ if and only if $\begin{array}{rl}0& =\underset{0\le r\le J}{max}(Z_r-M_r-Y_0^{\ast })\\ & =\underset{0\le r\le J}{max}(Z_r-M_r^{\ast }+{\mathcal{S}}_r-Y_0^{\ast }).\end{array}$ Since $Z_{{\tau }^{\star }}-M_{{\tau }^{\star }}^{\ast }=Y_0^{\ast }$ a.s., this implies ${\mathcal{S}}_{{\tau }^{\star }}\le 0$ a.s., and so by ${\mathsf{E}}_{{\mathcal{F}}_0}\left[{\mathcal{S}}_{{\tau }^{\star }}\right]=0,$ that ${\mathcal{S}}_{{\tau }^{\star }}=0$ by the sandwich property. Now note that ${\tilde{\mathcal{S}}}_j={\mathcal{S}}_{j\wedge {\tau }^{\star }},$ $j=0,\dots ,J,$ is also a martingale with ${\tilde{\mathcal{S}}}_J=0$ a.s. Let us write (assuming that $J\ge 1$) $0={\tilde{\mathcal{S}}}_J=\sum _{j=1}^J{\tilde{\mathcal{S}}}_j-{\tilde{\mathcal{S}}}_{j-1}={\tilde{\mathcal{S}}}_J-{\tilde{\mathcal{S}}}_{J-1}+\sum _{j=1}^{J-1}{\tilde{\mathcal{S}}}_j-{\tilde{\mathcal{S}}}_{j-1}.$ That is, ${\tilde{\mathcal{S}}}_J-{\tilde{\mathcal{S}}}_{J-1}$ is ${\mathcal{F}}_{J-1}$-measurable with ${\mathsf{E}}_{{\mathcal{F}}_{J-1}}[{\tilde{\mathcal{S}}}_J-{\tilde{\mathcal{S}}}_{J-1}]=0,$ so ${\tilde{\mathcal{S}}}_J-{\tilde{\mathcal{S}}}_{J-1}=0$ and thus ${\tilde{\mathcal{S}}}_{J-1}=0$ a.s. By proceeding backwards in the same way we see that ${\tilde{\mathcal{S}}}_j-{\tilde{\mathcal{S}}}_{j-1}=0$ for all $1\le j\le J,$ which implies ${\tilde{\mathcal{S}}}_j-{\tilde{\mathcal{S}}}_{j-1}=\sum _{r=1}^{j\wedge {\tau }^{\star }}{\zeta }_r-\sum _{r=1}^{(j-1)\wedge {\tau }^{\star }}{\zeta }_r=1_{\{{\tau }^{\star }\ge j\}}{\zeta }_j=0,$ whence ${\mathcal{S}}_j=0$ for $0\le j\le {\tau }^{\star },$ i.e. (19(19) $\begin{array}{rl}{\mathcal{S}}_j& =0\text{for}0\le j\le {\tau }^{\star },\end{array}$(19) ). Since ${\mathcal{M}}^{\circ \circ ,0}\subset {\mathcal{M}}^{\circ ,0}$ (20(20) $\begin{array}{rl}{\mathcal{S}}_j& \le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J.\end{array}$(20) ) follows from (18(18) $\begin{array}{rl}& {\mathcal{S}}_j-{\mathcal{S}}_{{\tau }^{\star }}\le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J\end{array}$(18) ) with ${\mathcal{S}}_{{\tau }^{\star }}=0.$ Conversely, if (19(19) $\begin{array}{rl}{\mathcal{S}}_j& =0\text{for}0\le j\le {\tau }^{\star },\end{array}$(19) ) and (20(20) $\begin{array}{rl}{\mathcal{S}}_j& \le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J.\end{array}$(20) ) hold, then $\begin{array}{rl}& \underset{0\le r\le J}{max}(Z_r-M_r^{\ast }+{\mathcal{S}}_r-Y_0^{\ast })\\ & =\underset{0\le r\le {\tau }^{\star }}{max}(Z_r-M_r^{\ast }-Y_0^{\ast })\\ & \vee \underset{{\tau }^{\star }<r\le J}{max}(Z_r-M_r^{\ast }+{\mathcal{S}}_r-Y_0^{\ast })\\ & =0\vee \underset{{\tau }^{\star }<r\le J}{max}(Z_r-M_r^{\ast }+{\mathcal{S}}_r-Y_0^{\ast })\end{array}$ and due to (20(20) $\begin{array}{rl}{\mathcal{S}}_j& \le Y_j^{\star }-Z_j+A_j^{\ast }\text{for}{\tau }^{\star }<j\le J.\end{array}$(20) ), for each ${\tau }^{\star }<r\le J$ $Z_r-M_r^{\ast }+{\mathcal{S}}_r-Y_0^{\ast }\le Y_r^{\star }-M_r^{\ast }+A_r^{\ast }-Y_0^{\ast }=0$ by (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ). That is $\underset{0\le r\le J}{max}(Z_r-M_r)=Y_0^{\ast }$ and so $M\in {\mathcal{M}}^{\circ \circ ,0}.$

4.7. Proof of Proposition 12

It holds that $\begin{array}{rl}\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)\right]& =\tilde{\mathsf{E}}{\tilde{\mathsf{E}}}_{\mathcal{F}}\left[\underset{0\le j\le J}{max}(Z_j-M_j+{\eta }_j)\right]\\ & \ge \tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}(Z_j-M_j+{\tilde{\mathsf{E}}}_{\mathcal{F}}\left[{\eta }_j\right])\right]\\ & =\mathsf{E}\left[\underset{0\le j\le J}{max}(Z_j-M_j)\right]\ge Y_0^{\star },\end{array}$ by duality, hence (24(24) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]\ge Y_0^{\star }.$(24) ). Further, if $M=M_j^{\circ \circ ,0}=M_j^{\star }-{\mathcal{S}}^{\circ \circ ,0}$ one has with (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ), for $j=0,\dots ,J,$ $\begin{array}{rl}{M}_j^{\circ \circ ,0}+Y_0^{\star }-Z_j& =M_j^{\star }-{\mathcal{S}}_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\\ & =Y_j^{\star }-Z_j+A_j^{\star }-{\mathcal{S}}_j^{\circ \circ ,0}\ge 0,\end{array}$ due to Theorem 9-(ii), hence (25(25) $M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\ge 0,\text{for}0\le j\le J.$(25) ). For $\tilde{M}$ given by (27(27) ${\tilde{M}}_j=M^{\circ \circ ,0}-{\eta }_j=M_j^{\star }-{\mathcal{S}}_j^{\circ \circ ,0}-{\eta }_j,$(27) ) with $\left({\eta }_j\right)$ satisfying (26(26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) ), we thus have (46) $Z_j-{\tilde{M}}_j=Z_j-M_j^{\circ \circ ,0}+{\eta }_j\le Y_0^{\star },j=0,\dots ,J.$(46) Then (28(28) $Y_0^{\star }=\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)\tilde{\mathsf{P}}-a.s.$(28) ) follows by (24(24) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]\ge Y_0^{\star }.$(24) ) and the sandwich property.

As for the last statement: By (26(26) ${\eta }_j\le M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.j=0,\dots ,J,$(26) ) one has ${\eta }_{{\tau }^{\star }}\le M_{{\tau }^{\star }}^{\circ \circ ,0}+Y_0^{\star }-Z_{{\tau }^{\star }},$ and by Theorem 9-(ii) and Doobs decomposition (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ), $M_{{\tau }^{\star }}^{\circ \circ ,0}=M_{{\tau }^{\star }}^{\star }=Y_{{\tau }^{\star }}^{\star }-Y_0^{\star }+A_{{\tau }^{\star }}^{\star }.$ That is, ${\eta }_{{\tau }^{\star }}\le Y_{{\tau }^{\star }}^{\star }-Z_{{\tau }^{\star }}+A_{{\tau }^{\star }}^{\star }=A_{{\tau }^{\star }}^{\star }=0,$ since $A_j^{\star }=0$ for $j=0,\dots ,{\tau }^{\star }.$ Then, since $\mathsf{E}\left[{\eta }_{{\tau }^{\star }}\right]=0,$ it follows that ${\eta }_{{\tau }^{\star }}=0$ a.s.

4.8. Proof of Theorem 13

Let $M=M^{\circ \circ ,0}-\mathcal{S},$ and $\left({\eta }_j\right)$ be as stated, and let us assume that for $\tilde{M}=M-\eta$ one has (47) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]=Y_0^{\star }.$(47) We then have to show that $\mathcal{S}=0,$ i.e. $M=M^{\circ \circ ,0}.$ We may write $\begin{array}{rl}\underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)& =\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}+{\mathcal{S}}_j+{\eta }_j)\\ & =Y_0^{\star }+\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j).\end{array}$ By (47(47) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]=Y_0^{\star }.$(47) ) we must have (48) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\right]=0.$(48) Let us observe that (49) $\begin{array}{rl}& \underset{0\le j\le J}{max}(Z_j-M^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\\ & \ge Z_{{\tau }^{\star }}-M_{{\tau }^{\star }}^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_{{\tau }^{\star }}+{\eta }_{{\tau }^{\star }}={\mathcal{S}}_{{\tau }^{\star }},\end{array}$(49) using $M_{{\tau }^{\star }}^{\circ \circ ,0}=M_{{\tau }^{\star }}^{\star }=Y_{{\tau }^{\star }}^{\star }-Y_0^{\star }+A_{{\tau }^{\star }}^{\star }=Z_{{\tau }^{\star }}-Y_0^{\star }$ due Theorem 9-(ii) and (7(7) $Y_j^{\star }=Y_0^{\star }+M_j^{\star }-A_j^{\star },$(7) ) and $A_{{\tau }^{\star }}^{\star }=0,$ and ${\eta }_{{\tau }^{\star }}=0$ due to Proposition 12. Since, by assumption, $\mathcal{S}$ is some martingale with ${\mathcal{S}}_0=0$, we have $\tilde{\mathsf{E}}\left[{\mathcal{S}}_{{\tau }^{\star }}\right]=\mathsf{E}\left[{\mathcal{S}}_{{\tau }^{\star }}\right]=0$ by Doob's sampling theorem, and so (48(48) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\right]=0.$(48) ) and (49(49) $\begin{array}{rl}& \underset{0\le j\le J}{max}(Z_j-M^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\\ & \ge Z_{{\tau }^{\star }}-M_{{\tau }^{\star }}^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_{{\tau }^{\star }}+{\eta }_{{\tau }^{\star }}={\mathcal{S}}_{{\tau }^{\star }},\end{array}$(49) ) imply by the sandwich property, (50) $\begin{array}{r}\begin{array}{rl}& \underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j-{\mathcal{S}}_{{\tau }^{\star }}+{\eta }_j)\\ & =0,\text{a.s., whence}\\ & {\eta }_j\le {\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j+M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,\text{a.s. for all}0\le j\le J.\end{array}\end{array}$(50) Now inserting (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ) yields, (51) $({\xi }_j-1)(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j)\le {\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j\tilde{\mathsf{P}}-\mathrm{a}.\mathrm{s}.$(51) By applying Lemma 15 below to $U\equiv {\xi }_j-1,$ $V\equiv M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j,$ and $W\equiv {\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j$ it follows that ${\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j\ge 0,\mathsf{P}-\mathrm{a}.\mathrm{s}.$ However, $\mathcal{S}$ is a martingale with ${\mathcal{S}}_0=0,$ so by Doob's sampling theorem $\mathsf{E}\left[{\mathcal{S}}_{{\tau }^{\star }}\right]=0,$ i.e. $\mathsf{E}[{\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j]=0,$ and we thus must have ${\mathcal{S}}_{{\tau }^{\star }}-{\mathcal{S}}_j=0.$ Since j, $0\le j\le J,$ was arbitrary it now follows that ${\mathcal{S}}_{{\tau }^{\star }}={\mathcal{S}}_j={\mathcal{S}}_0=0$ for all j, hence $M=M^{\circ \circ ,0}.$

Lemma 15

Let U, V, W be real valued random variables with $U\le 0$, $V\ge 0,$ and $UV\le W$ almost surely, and, U being independent of the pair $(V,W)$ with $\mathsf{P}(-\delta <U<0)>0$ for any $\delta >0$. One then must have $W\ge 0$ a.s.

Proof.

For arbitrary $ϵ>0$ and K>0 we have, since $UV\le W$ a.s., $\begin{array}{rl}0& =\mathsf{P}((-\frac{ϵ}{2K}\le U<0)\wedge (V\le K)\wedge (W\le -ϵ))\\ & =\mathsf{P}(-\frac{ϵ}{2K}\le U<0)\mathsf{P}((V\le K)\wedge (W\le -ϵ)),\end{array}$ using that U is independent of the pair $(V,W).$ Hence $\mathsf{P}\left(\right(V\le K)\wedge (W\le -ϵ\left)\right)=0$ and it thus follows that the set $\begin{array}{rl}\{W<0\}& =\bigcup _{n=1}^{\mathrm{\infty }}\{W\le -\frac{1}{n}\}=\bigcup _{n=1}^{\mathrm{\infty }}\bigcup _{m=1}^{\mathrm{\infty }}\{W\le -\frac{1}{n}\}\\ & \cap \{V\le m\}\end{array}$ has probability zero.

4.9. Proof of Corollary 14

If $M=M^{\circ \circ ,0}$ one has $\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)=0$ due to Proposition 12. Let us take some $M\ne M^{\circ \circ ,0}$ and assume that $\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)=0.$ From here we will derive a contradiction. As in the proof of Theorem 13 we write (52) $\begin{array}{r}\begin{array}{rl}& \underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)=Y_0^{\star }+\underset{0\le j\le J}{max}\\ & (Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)\\ & =\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\right)=0.\end{array}\end{array}$(52) Now, $M\ne M^{\circ \circ ,0}$ implies by Theorem 13 that (53) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j\left)\right]>0.$(53) That is, due to (52(52) $\begin{array}{r}\begin{array}{rl}& \underset{0\le j\le J}{max}(Z_j-{\tilde{M}}_j)=Y_0^{\star }+\underset{0\le j\le J}{max}\\ & (Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\\ & \mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)\\ & =\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)\right)=0.\end{array}\end{array}$(52) ) and (53(53) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j\left)\right]>0.$(53) ), there exists a constant c>0 such that $\underset{0\le j\le J}{max}(Z_j-M_j^{\circ \circ ,0}-Y_0^{\star }+{\mathcal{S}}_j+{\eta }_j)=c>0.$ Using (29(29) ${\eta }_j={\xi }_j(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j),0\le j\le J,$(29) ) and the fact that for any j, $M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\ge 0$ (see Proposition 12), and ${\xi }_j\le 1,$ this implies (54) $\begin{array}{r}0<c=\underset{0\le j\le J}{max}({\mathcal{S}}_j+({\xi }_j-1)(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\left)\right)\le \underset{0\le j\le J}{max}\left({\mathcal{S}}_j\right).\end{array}$(54) Consider the stopping time $\sigma :=inf\{j\ge 0:{\mathcal{S}}_j\ge c\}.$ Then, using ${\mathcal{S}}_0=0$ and (54(54) $\begin{array}{r}0<c=\underset{0\le j\le J}{max}({\mathcal{S}}_j+({\xi }_j-1)(M_j^{\circ \circ ,0}+Y_0^{\star }-Z_j\left)\right)\le \underset{0\le j\le J}{max}\left({\mathcal{S}}_j\right).\end{array}$(54) ), we must have that $0<\sigma \le J$ almost surely. Since $\mathcal{S}$ is a martingale, Doob's sampling theorem then implies $0={\mathcal{S}}_0=\mathsf{E}\left[{\mathcal{S}}_{\sigma }\right]\ge c,$ hence a contradiction. That is, the assumption $\mathrm{V}\mathrm{a}\mathrm{r}\left(\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right)=0$ was false.

5. Stylized numerical examples

5.1. Simple stylized numerical example

We first reconsider the stylized test example due to Schoenmakers et al. (2013, Section 8), also considered in Belomestny et al. (2014), where J = 2, $Z_0=0$, $Z_2=1$, and $Z_1=\mathcal{U}$ is a random variable which uniformly distributed on the interval $[0,2]$. The optimal stopping time ${\tau }^{\ast }$ is thus given by ${\tau }^{\ast }=\{\begin{array}{ll}1,& \mathcal{U}\ge 1,\\ 2,& \mathcal{U}<1.\end{array}$ and the optimal value is $Y_0^{\star }=\mathsf{E}max(\mathcal{U},1)=5/4$. Furthermore, it is easy to see that the Doob martingale is given by $M_0^{\star }=0,M_1^{\star }=M_2^{\star }=max\{\mathcal{U},1\}-\frac{5}{4}.$ As an illustration of the theory developed in Sections 2–3, let us consider the linear span $M\left(\alpha \right)=\alpha M^{\star }$ as a pool of candidate martingales and randomize it according to (31(31) ${\eta }_j={\xi }_j(M_j^{\star }-Z_j+Y_0^{\star })={\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }).$(31) ). We thus consider the objective function (55) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\alpha \right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right],\end{array}$(55) for some fixed $\theta \ge 0,$ where $\left({\xi }_j\right)$ are i.i.d. random variables with uniform distribution on $[-1,1].$ Note that for this example $Y_1^{\star }=max(\mathcal{U},1),$ $Y_2^{\star }=1,$ and $A_0^{\star }=A_1^{\star }=0,$ $A_2^{\star }=max\{\mathcal{U},1\}-1,$ is the non-decreasing predictable process from the Doob decomposition. Moreover, it is possible to compute (55(55) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\alpha \right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right],\end{array}$(55) ) in closed form (though we omit detailed expressions which can be conveniently obtained by Mathematica for instance). In figure 1 (left panel) we have plotted (55(55) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\alpha \right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right],\end{array}$(55) ) for $\theta =0$ and $\theta =1,$ together with the objective function ${\overline{\mathcal{O}}}_1\left(\alpha \right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+{\xi }_j)\right],$ due to a ‘naive’ randomization, not based on knowledge of the factor $Y_j^{\star }-Z_j+A_j^{\star }.$ Also, in figure 1 (right panel), the relative standard deviations $\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}(\cdot )}/Y_0^{\star }$ of the corresponding random variables $\begin{array}{rl}{\mathcal{Z}}_{\theta }\left(\alpha \right)& :=\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star })),\\ & \theta =0,1,\mathrm{a}\mathrm{n}\mathrm{d}\\ {\overline{\mathcal{Z}}}_1\left(\alpha \right)& :=\underset{0\le j\le 2}{max}(Z_j-\alpha M_j^{\star }+{\xi }_j)\end{array}$ are depicted as a function of α.

Figure 1. Left panel: objective functions ${\mathcal{O}}_0\left(\alpha \right)$ (no randomization), ${\mathcal{O}}_1\left(\alpha \right)$ (optimal randomization), and ${\overline{\mathcal{O}}}_1$ (‘naive’ randomization); right panel: relative deviations of ${\mathcal{Z}}_0\left(\alpha \right)$ (without randomization), ${\mathcal{Z}}_1\left(\alpha \right)$ (optimal randomization), ${\overline{\mathcal{Z}}}_1\left(\alpha \right)$ (‘naive’ randomization)

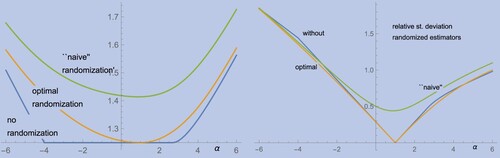
From Schoenmakers et al. (2013, Section 8) we know that, and from the plot of ${\mathcal{O}}_0\left(\alpha \right)$ in figure 1 (left panel) we see that, $M\left(\alpha \right)\in {\mathcal{M}}_0^{\circ }$ for $\alpha \in [-4,8/3]$. On the other hand, the right panel plot shows that $\mathrm{V}\mathrm{a}\mathrm{r}\left({\mathcal{Z}}_0\right(\alpha \left)\right)$ may be relatively large for $\alpha \ne 1,$ and that the Doob martingale (i.e. $\alpha =1$) is the only surely optimal one in our parametric family. Moreover, the objective function due to the optimal randomization attains its unique minimum at the Doob martingale, i.e. for $\alpha =1.$ Further, the variance of the corresponding optimally randomized estimator attains its unique minimum zero also at $\alpha =1.$ Let us note that these observations are anticipated by Theorem 13 and Corollary 14. The catch is that for each $\alpha \ne 1$ the randomized $M\left(\alpha \right)$ fails to be optimal in the sense of (30(30) $\tilde{\mathsf{E}}\left[\underset{0\le j\le J}{max}\right(Z_j-{\tilde{M}}_j\left)\right]>Y_0^{\star }$(30) ). We also see that both the optimal and the ‘naive’ randomization render the minimization problem to be strictly convex. Moreover, while the minimum due to the ‘naive’ randomization lies significantly above the true solution, the argument where the minimum is attained, $\overline{\alpha }$ say, identifies nonetheless a martingale that virtually coincides with the Doob optimal one. That is, $\overline{\alpha }\approx 1$ and $M\left(\overline{\alpha }\right)$ is optimal corresponding to variance $\mathrm{V}\mathrm{a}\mathrm{r}\left({\mathcal{Z}}_0\right(\overline{\alpha }\left)\right)\approx 0$, which can be seen in the right panel.

5.2. Stylized Bermudan call option

In order to exhibit the merits of randomization based on the theoretical results in this paper in a more realistic case, we have constructed an example that contains all typical features of a real life Bermudan option, but, is simple enough to be treated numerically in all respects on the other hand.

As in the previous example we take J = 2, and specify the (discounted) cash-flows $Z_j$ as functions of the (discounted) stock prices $S_j$ by (56) $Z_0=0,Z_1=(S_1-{\kappa }_1{)}^{+},Z_2=(S_2-{\kappa }_2{)}^{+}$(56) For S we take the log-normal dynamics (57) $S_j=S_0\exp (-\frac{1}{2}{\sigma }^{2}j+\sigma W_j),j=0,1,2,$(57) where $W_1\sim \mathcal{N}(0,1)$ and $W_{1,2}:=W_2-W_1\sim \mathcal{N}(0,1),$ independent of $W_1.$

For the continuation function at j = 1 we thus have (58) $\begin{array}{rl}{C}_1\left(W_1\right)& ={\mathsf{E}}_{W_1}\left[{(S_0\exp (-{\sigma }^2+\sigma W_2)-{\kappa }_2)}^{+}\right]\\ & =\int {(S_0\exp (-{\sigma }^2+\sigma W_1+\sigma z)-{\kappa }_2)}^{+}\varphi \left(z\right)\mathrm{d}z,\end{array}$(58) where $\varphi \left(z\right)=(2\pi {)}^{-1/2}\exp (-z^2/2)$ is the standard normal density. While abusing notation a bit we will denote the cash-flows by $Z_1\left(W_1\right)$ and $Z_2\left(W_2\right)=Z_2\left(W_{1,}{W}_{1,2}\right),$ respectively. For the (discounted) option value at j = 0 one thus has $\begin{array}{rl}{Y}_0^{\star }& =\mathsf{E}[max\left(Z_1\right(W_1),C_1(W_1\left)\right)]\\ & =\int max({(S_0\exp (-\frac{1}{2}{\sigma }^2+\sigma z)-{\kappa }_1)}^{+},C_1(z\left)\right)\\ & \times \varphi \left(z\right)\mathrm{d}z\end{array}$ Further we obviously have $\begin{array}{rl}& Y_1^{\star }\left(W_1\right)=max\left(Z_1\right(W_1),C_1(W_1\left)\right)\mathrm{a}\mathrm{n}\mathrm{d}\\ & Y_2^{\star }\left(W_2\right)=Z_2\left(W_2\right)=Z_2\left(W_{1,}{W}_{1,2}\right).\end{array}$ The Doob martingale for this example is thus given by $\begin{array}{rl}& M_0^{\star }=0,M_1^{\star }=Y_1^{\star }\left(W_1\right)-Y_0^{\star },\\ & M_2^{\star }-M_1^{\star }=Z_2\left(W_{1,}{W}_{1,2}\right)-C_1\left(W_1\right)\end{array}$ and the non-decreasing predictable component $A^{\star }$ is given by $A_0^{\star }=A_1^{\star }=0,A_2^{\star }=Y_1^{\star }\left(W_1\right)-C_1\left(W_1\right).$ For demonstration purposes we will quasi analytically compute the optimal randomization coefficient in (31(31) ${\eta }_j={\xi }_j(M_j^{\star }-Z_j+Y_0^{\star })={\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }).$(31) ), $Y^{\star }-Z+A^{\star }=\{\begin{array}{ll}{Y}_0^{\star }& j=0,\\ \left(C_1\right(W_1)-Z_1(W_1){)}^{+},& j=1,\\ \left(Z_1\right(W_1)-C_1(W_1){)}^{+},& j=2.\end{array}$ by using a Black(-Scholes) type formula $\begin{array}{rl}{C}_1\left(W_1\right)& =S_0\exp (-\frac{1}{2}{\sigma }^2+\sigma W_1)\mathcal{N}(W_1+\frac{1}{\sigma }\ln (S_0/{\kappa }_2\left)\right)\\ & -{\kappa }_2\mathcal{N}(W_1+\frac{1}{\sigma }\ln (S_0/{\kappa }_2)-\sigma ),\end{array}$ and a numerical integration for obtaining the target value $Y_0^{\star }$. We now consider two martingale families.

(M-Sty)

For any $\mathit{\alpha }=({\alpha }_{11},{\alpha }_{12},{\alpha }_{21},{\alpha }_{22})$ we set (59) $\begin{array}{rl}{M}_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :={\alpha }_{11}\left(Y_1^{\star }\right(W_1)-Y_0^{\star }-W_1)\\ & +{\alpha }_{12}{W}_1\\ M_2^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :=M_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)\\ & +{\alpha }_{21}\left(Z_2\right(W_{1,}{W}_{1,2})\\ & -C_1\left(W_1\right)-W_{1,2})\\ & +{\alpha }_{22}{W}_{1,2}.\end{array}$(59) Note that $M^{\mathrm{s}\mathrm{t}\mathrm{y}}\left(\right(1,1,1,1),W)=M^{\star }\left(W\right).$

(M-Hermite)

Using that the (probabilistic) Hermite polynomials given by $\begin{array}{rl}H{e}_k\left(x\right)& =(-1{)}^k{\mathrm{e}}^{\frac{x^2}{2}}\\ & \times {\left(\frac{\mathrm{d}}{\mathrm{d}x}\right)}^k{\mathrm{e}}^{-\frac{x^2}{2}},k=0,1,2,\dots ,\end{array}$ are orthogonal with respect to the standard Gaussian density we consider a martingale family (60) $\begin{array}{rl}{M}_1^{\mathrm{H}}(\mathit{\alpha },W)& =\sum _{k=1}^K{\alpha }_{1,k}H{e}_k\left(W_1\right)\\ M_2^{\mathrm{H}}(\mathit{\alpha },W)& =M_1^H(\mathit{\alpha },W)\\ & +\sum _{k=0}^K\sum _{l=1}^L{\alpha }_{2,k,l}H{e}_k\left(W_1\right)\\ & \times H{e}_l\left(W_{1,2}\right),\end{array}$(60) with obvious definition of $\mathit{\alpha }\in {\mathbb{R}}^K\oplus {\mathbb{R}}^{(K+1)}\times {\mathbb{R}}^L$ (note that $H{e}_0\equiv 1$). Since our mere goal is to exhibit the effect of randomization, for the examples below we restrict ourselves to the choice $K=L=3.$

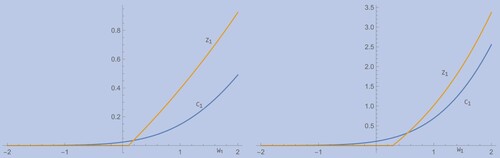
The parameters in (56(56) $Z_0=0,Z_1=(S_1-{\kappa }_1{)}^{+},Z_2=(S_2-{\kappa }_2{)}^{+}$(56) ) and (57(57) $S_j=S_0\exp (-\frac{1}{2}{\sigma }^{2}j+\sigma W_j),j=0,1,2,$(57) ) are taken to be such that with a medial probability optimal exercise takes place at $j=1.$ In particular, we consider two cases specified with parameter sets $\begin{array}{rl}\left(\mathrm{P}\mathrm{a}1\right)& :S_0=2,{\sigma }^2=\frac{1}{3},{\kappa }_1=2,{\kappa }_2=3,\\ & \text{target value }{Y}_0^{\star }=0.164402,\\ \left(\mathrm{P}\mathrm{a}2\right)& :S_0=2,{\sigma }^2=\frac{1}{25},{\kappa }_1=2,{\kappa }_2=\frac{5}{2},\\ & \text{target value }{Y}_0^{\star }=0.496182,\end{array}$ respectively. From figure 2 we see that the probability of optimal exercise at j = 1 is almost 50% for (Pa1) and almost 30% for (Pa2). Let us visualize on the basis of martingale family (M-Sty) and parameters (Pa1) the effects of randomization. Consider the objective function (61) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\mathit{\alpha }\right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha })+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right].\end{array}$(61) where θ scales the randomization due to i.i.d. random variables $\left({\xi }_j\right),$ uniformly distributed on $[-1,1]$. I.e.for $\theta =0$ there is no randomization and $\theta =1$ gives the optimal randomization. Now restrict (61(61) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\mathit{\alpha }\right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha })+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right].\end{array}$(61) ) to the sub domain $\mathit{\alpha }=({\alpha }_1,{\alpha }_1,{\alpha }_2,{\alpha }_2)=:({\alpha }_1,{\alpha }_2)$ (while slightly abusing notation), i.e. ${\alpha }_{11}={\alpha }_{12}={\alpha }_1$ and ${\alpha }_{21}={\alpha }_{22}={\alpha }_2.$ The function ${\mathcal{O}}_0({\alpha }_1,{\alpha }_2),$ i.e. 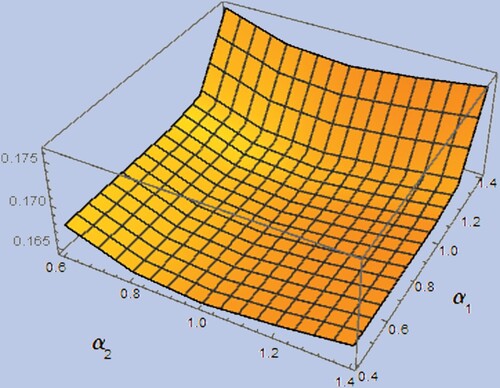(61(61) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\mathit{\alpha }\right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha })+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right].\end{array}$(61) ) without randomization is visualized in figure 3, where expectations are computed quasi-analytically with Mathematica. From this plot we see that the true value $Y_0^{\star }=0.164402$ is attained on the line $({\alpha }_1,1)$ for various ${\alpha }_1$ (i.e. not only in $(1,1)$). 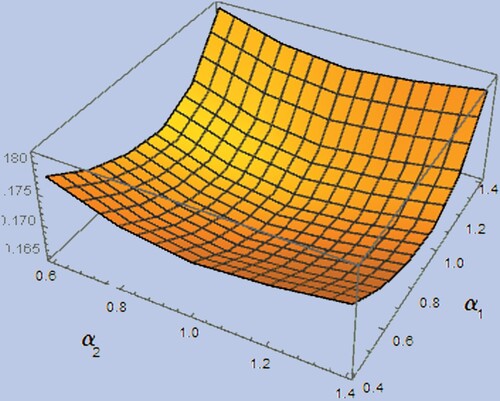On the other hand, ${\mathcal{O}}_1({\alpha }_1,{\alpha }_2)$ i.e. (61(61) $\begin{array}{r}{\mathcal{O}}_{\theta }\left(\mathit{\alpha }\right):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha })+\theta {\xi }_j(Y_j^{\star }-Z_j+A_j^{\star }))\right].\end{array}$(61) ) with optimal randomization, has a clear strict global minimum in $(1,1)$, see figure 4. Let us have a closer look at the map ${\alpha }_1\to {\mathcal{O}}_{\theta }({\alpha }_1,{\alpha }_1,1,1)$ for $\theta =0$ and $\theta =1,$ respectively, and also at ${\alpha }_1\to {\overline{\mathcal{O}}}_{0.16}({\alpha }_1,{\alpha }_1,1,1)$ due to the ‘naive’ randomization

Figure 2. Cash-flow Z₁ versus continuation value C₁ as a function of W₁ for (Pa1) (left) and (Pa2) (right).

Figure 3. Objective function for BS-Call (Pa1) without randomization as function of $({\alpha }_1,{\alpha }_2)$.

Figure 4. Objective function for BS-Call (Pa1) with optimal randomization as function of $({\alpha }_1,{\alpha }_2)$.

${\overline{\mathcal{O}}}_{0.16}({\alpha }_1,1):=\tilde{\mathsf{E}}\left[\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}({\alpha }_1,1)+0.16{\xi }_j)\right],$ where the scale parameter $\theta =0.16$ is taken to be roughly the option value. (It turns out that the choice of this scale factor is not critical for the location of the minimum.) In fact, the results, plotted in figure 5, tell there own tale. The second panel depicts the relative deviation of

Figure 5. Left panel: objective functions of ${\alpha }_1$ with ${\alpha }_2=1$ fixed, for BS-Call (Pa1) without, optimal, and ‘naive’ randomization; right panel: relative deviation of ${\mathcal{Z}}_0({\alpha }_1,1)$ (i.e. without randomization).

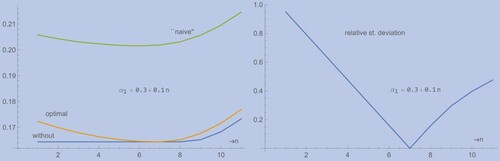
${\mathcal{Z}}_0({\alpha }_1,1):=\underset{0\le j\le 2}{max}(Z_j-M_j^{\mathrm{s}\mathrm{t}\mathrm{y}}({\alpha }_1,1\left)\right).$ In fact, similar comments as for the example in Section 5.1 apply. The ‘naive’ randomization attains its minimum at ${\overline{\alpha }}_1=0.9,$ which we read off from the tables that generated this figure. We thus have found the martingale $M^{\mathrm{s}\mathrm{t}\mathrm{y}}(0.9,1),$ which may be virtually considered surely optimal, as can be seen from the variance plot (second panel). Analog visualizations for the parameter set (Pa2) with analog conclusions may be given, though are omitted due to space restrictions.

Let us now pass on to a Monte Carlo setting, where we mimic the approach in real practice more closely. Based on N simulated samples of the underlying asset model, i.e. $S^{\left(n\right)},$ $n=1,\dots ,N,$ we consider the minimization (62) $\begin{array}{rl}{\hat{\mathit{\alpha }}}_{\theta }& :=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })\\ & +\theta {\xi }_j(Y_j^{\star \left(n\right)}-Z_j^{\left(n\right)}+A_j^{\star \left(n\right)}))]\end{array}$(62) for $\theta =0$ (no randomization) and $\theta =1$ (optimal randomization), along with the minimization (63) $\begin{array}{r}{\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}:=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N\left[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })+{\theta }_j^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}{\xi }_j)\right]\end{array}$(63) based on a ‘naive’ randomization where the coefficients ${\theta }_j^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}},$ j = 0, 1, 2 are pragmatically chosen. In (62(62) $\begin{array}{rl}{\hat{\mathit{\alpha }}}_{\theta }& :=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })\\ & +\theta {\xi }_j(Y_j^{\star \left(n\right)}-Z_j^{\left(n\right)}+A_j^{\star \left(n\right)}))]\end{array}$(62) ) and (63(63) $\begin{array}{r}{\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}:=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N\left[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })+{\theta }_j^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}{\xi }_j)\right]\end{array}$(63) ) M stands for a generic linearly structured martingale family, such as (59(59) $\begin{array}{rl}{M}_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :={\alpha }_{11}\left(Y_1^{\star }\right(W_1)-Y_0^{\star }-W_1)\\ & +{\alpha }_{12}{W}_1\\ M_2^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :=M_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)\\ & +{\alpha }_{21}\left(Z_2\right(W_{1,}{W}_{1,2})\\ & -C_1\left(W_1\right)-W_{1,2})\\ & +{\alpha }_{22}{W}_{1,2}.\end{array}$(59) ) and (60(60) $\begin{array}{rl}{M}_1^{\mathrm{H}}(\mathit{\alpha },W)& =\sum _{k=1}^K{\alpha }_{1,k}H{e}_k\left(W_1\right)\\ M_2^{\mathrm{H}}(\mathit{\alpha },W)& =M_1^H(\mathit{\alpha },W)\\ & +\sum _{k=0}^K\sum _{l=1}^L{\alpha }_{2,k,l}H{e}_k\left(W_1\right)\\ & \times H{e}_l\left(W_{1,2}\right),\end{array}$(60) ) for example. The minimization problems (62(62) $\begin{array}{rl}{\hat{\mathit{\alpha }}}_{\theta }& :=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })\\ & +\theta {\xi }_j(Y_j^{\star \left(n\right)}-Z_j^{\left(n\right)}+A_j^{\star \left(n\right)}))]\end{array}$(62) ) and (63(63) $\begin{array}{r}{\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}:=\underset{\mathit{\alpha }}{\arg min}\frac{1}{N}\sum _{n=1}^N\left[\underset{0\le j\le 2}{max}(Z_j^{\left(n\right)}-M_j^{\left(n\right)}(\mathit{\alpha })+{\theta }_j^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}{\xi }_j)\right]\end{array}$(63) ) may be solved by linear programing (LP). They may be transformed into a suitable form such that the (free) LP package in R can be applied. This transformation procedure is straightforward and spelled out in Desai et al. (2012) for example. In the latter paper it is argued that the required computation time scales with N due to the sparse structure of the coefficient matrix involved in the LP setup. However, taking advantage of this sparsity requires a special treatment of the implementation of the linear program in connection with more advanced LP solvers (as done in Desai et al. 2012). Since this paper is essentially on the theoretical justification of the randomized duality problem (along with the classification of optimal martingales), we consider an in-depth numerical analysis beyond scope of this paper.

For both parameter sets (Pa1) and (Pa2), and both martingale families (59(59) $\begin{array}{rl}{M}_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :={\alpha }_{11}\left(Y_1^{\star }\right(W_1)-Y_0^{\star }-W_1)\\ & +{\alpha }_{12}{W}_1\\ M_2^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)& :=M_1^{\mathrm{s}\mathrm{t}\mathrm{y}}(\mathit{\alpha },W)\\ & +{\alpha }_{21}\left(Z_2\right(W_{1,}{W}_{1,2})\\ & -C_1\left(W_1\right)-W_{1,2})\\ & +{\alpha }_{22}{W}_{1,2}.\end{array}$(59) ) and (60(60) $\begin{array}{rl}{M}_1^{\mathrm{H}}(\mathit{\alpha },W)& =\sum _{k=1}^K{\alpha }_{1,k}H{e}_k\left(W_1\right)\\ M_2^{\mathrm{H}}(\mathit{\alpha },W)& =M_1^H(\mathit{\alpha },W)\\ & +\sum _{k=0}^K\sum _{l=1}^L{\alpha }_{2,k,l}H{e}_k\left(W_1\right)\\ & \times H{e}_l\left(W_{1,2}\right),\end{array}$(60) ) with $K=L=3,$ we have carried out the LP optimization algorithm sketched above. We have taken N = 2000 and for the ‘naive’ randomization $\begin{array}{rl}& {\theta }_0^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}=1.6\mathrm{f}\mathrm{o}\mathrm{r}\left(\mathrm{P}\mathrm{a}1\right),\\ & {\theta }_0^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}=4.8\mathrm{f}\mathrm{o}\mathrm{r}\left(\mathrm{P}\mathrm{a}2\right),\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{y}{\theta }_1^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}={\theta }_2^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}=0.\end{array}$ In the table 1, for (Pa1), and table 2, for (Pa2), we present for the minimizers ${\hat{\mathit{\alpha }}}_0,{\hat{\mathit{\alpha }}}_1,{\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$ the in-sample expectation $\hat{m}$, the in-sample standard deviation $\hat{\sigma }/\sqrt{N},$ and the path-wise maximum due to a single trajectory $\hat{\sigma },$ followed by the corresponding ‘true’ values $m^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}},$ ${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}/\sqrt{N^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}},$ ${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}},$ based on a large ‘test’ simulation of $N^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}={10}^6$ samples.

Table 1. LP minimization results due to $M^{\mathrm{s}\mathrm{t}\mathrm{y}}$ and $M^{\mathrm{H}}$ for (Pa1).

	$M^{\mathrm{s}\mathrm{t}\mathrm{y}}$			$M^{\mathrm{H}}$
(Pa1)	${\hat{\mathit{\alpha }}}_0$	${\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$	${\hat{\mathit{\alpha }}}_1$	${\hat{\mathit{\alpha }}}_0$	${\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$	${\hat{\mathit{\alpha }}}_1$
$\hat{m}$	0.16243	0.16399	0.16403	0.16268	0.16560	0.16696
$\hat{\sigma }/\sqrt{N}$	0.00573	0.00036	0.00029	0.00574	0.00113	0.00118
$\hat{\sigma }$	0.25639	0.01608	0.01278	0.25676	0.05063	0.05293
$m^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$	0.16490	0.16445	0.16442	0.16709	0.16664	0.16685
${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}/\sqrt{N^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}}$	0.00026	0.00001	0.00001	0.00026	0.00005	0.00005
${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$	0.26096	0.01460	0.01064	0.26439	0.05083	0.05153

Table 2. LP minimization results due to $M^{\mathrm{s}\mathrm{t}\mathrm{y}}$ and $M^{\mathrm{H}}$ for (Pa2).

	$M^{\mathrm{s}\mathrm{t}\mathrm{y}}$			$M^{\mathrm{H}}$
(Pa2)	${\hat{\mathit{\alpha }}}_0$	${\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$	${\hat{\mathit{\alpha }}}_1$	${\hat{\mathit{\alpha }}}_0$	${\hat{\mathit{\alpha }}}_{{\theta }^{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$	${\hat{\mathit{\alpha }}}_1$
$\hat{m}$	0.48748	0.49471	0.49490	0.49329	0.50082	0.50546
$\hat{\sigma }/\sqrt{N}$	0.02064	0.00201	0.00152	0.02076	0.00318	0.00308
$\hat{\sigma }$	0.92301	0.08981	0.06801	0.92852	0.14222	0.13762
$m^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$	0.49820	0.49639	0.49633	0.51079	0.50870	0.50912
${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}/\sqrt{N^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}}$	0.00095	0.00009	0.00007	0.00097	0.00016	0.00015
${\sigma }^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$	0.95415	0.09038	0.06674	0.97272	0.16047	0.15103

The results in tables tables 1–2 show that even a simple (naive) randomization at j = 0 leads to a substantial variance reduction (up to 10 times) not only on training samples but also on the test ones. We think that for more structured examples and more complex families of martingales even more pronounced variance reduction effect may be expected. For example, in general it might be better to take Wiener integrals, i.e. objects of the form $\int \alpha (t,X_t)dW,$ where α runs through some linear space of basis functions, as building blocks for the martingale family. Also other types of randomization can be used, for example one may take different distributions for the r.v. ξ. However all these issues will be analyzed in a subsequent study.

Acknowledgments

J.S. gratefully acknowledges financial support from the German science foundation (DFG) via the cluster of excellence MATH+, project AA4-2.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 This work started after the first version of the present paper was available on arXiv:2102.01533, Febr. 2, 2021.