A mathematical model of continuous flotation deinking

Abstract

A mathematical model is formulated to study the evolution of a continuous flotation process; the model yields a lower bound for the long-time deinking efficiency. Some of the theoretical predictions of the model are analysed using data obtained at a recycle mill.

Keywords:

• Continuous flotation
• Deinking
• Kinetic model
• Rate constant
• Microprocess probabilities

Nomenclature

1.	Bo′modified Bond number
2.	C
3.	C Bparameter characterizing the bubble surface mobility
4.	C 1 gas constant
5.	d p particle diameter
6.	Eff(t) global process efficiency at time t, equal to 1 −
7.	erf(x) error function
8.	f fluid flow friction factor
9.	g acceleration due to gravity
10.	g(r)
11.	G dimensionless particle settling velocity
12.	h 0 initial thickness of the film separating a bubble and a particle
13.	h crit film thickness at which the film ruptures spontaneously
14.	k(r)
15.	k 1 forward (attachment) rate parameter
16.	k 2 reverse (detachment) rate parameter
17.
18.	K maximum number of particles that can attach to a bubble along an arc, on one hemisphere, of a great circle on the bubble
19.	n B constant (total) bubble concentration
20.	concentration of bubbles with attached particles
21.	concentration of bubbles available to capture particles
22.	concentration of bubbles with j particles attached, 0 ⩽ j ⩽ K
23.	free bubble concentration
24.	n p constant particle concentration
25.	concentration of free particles
26.	n p0 initial concentration of particles ( )
27.	initial concentration of free particles
28.	P the overall probability of the formation of a stable bubble – particle aggregate, ( =P c P asl P tpc P stab),
29.	P asl probability of adhesion by sliding
30.	P c probability of collision between a particle and a bubble
31.	P destab probability of destabilization of a bubble – particle aggregate
32.	P stab probability of stability of a bubble – particle aggregate
33.	P tpc probability of the formation of a three-phase contact
34.	r radial distance from the centre of a bubble
35.	R B bubble radius
36.	R p particle radius
37.	Re B bubble Reynolds number
38.
39.	Re p particle Reynolds number
40.	relative velocity between a bubble and the fluid
41.	relative velocity between a particle and the fluid
42.	υB bubble rise velocity
43.	υp particle velocity
44.	υps particle settling velocity
45.	Z collision frequency divided by the number of bubbles available to capture particles at time t > 0
46.	Z′ detachment frequency of particles from bubbles
47.	α system parameter mediating the stability of bubble/particle aggregates
48.	γ
49.	ϵ (Kolmogorov) turbulent energy density
50.	θ contact angle
51.	dimensionless friction factor
52.	(t) average number of particles, at time t, which are attached to a bubble in the exit stream
53.	time-averaged
54.	μl fluid viscosity
55.	υl kinematic viscosity
56.	ρ B bubble (gas) density
57.	ρ l fluid density
58.	ρ p particle density
59.	σ surface tension
60.	standard deviation of a normally distributed random variable

1 The continuous flotation model

We present, in this paper, a mathematical model, of chemical kinetics type, to describe the overall flotation deinking process. We begin, in section 1, by making explicit those expressions for the microprocess probabilities which are used in the formulation of the relevant kinetic constants; this, in turns, leads to the basic nonlinear ordinary differential equation governing the evolution of free (ink) particles. The relevant model system is solved in section 2 and is followed in section 3 by a theoretical discussion of model predictions, including an explicit lower bound for the asymptotic (i.e., long-time) efficiency of the process. Section 4 is concerned with a description of the experimental methodology that has been employed in the process of conducting flotation deinking trials in a recycle mill in Texas. Finally, in section 5, we compare some of the ‘experimental’ results obtained in the aforementioned trials with the corresponding model predictions, including long-time deinking efficiency.

In modelling continuous flotation processes associated with deinking the balance equation for the concentration of free ink particles can be shown to have the form given by Bloom and Heindel [1]

In (1), k ₁ and k ₂ are the rate parameters for the forward and reverse reactions respectively; these two parameters depend upon the various microprocess probabilities that constiture the mechanism of bubble – particle aggregate formation and destruction and are functions of the bubble, particle, fluid and system properties. In (1), the rate parameters, both of which have the dimensions of frequency (i.e. s^− 1), are given by

and

for the case in which it was assumed that only free bubbles may attract a particle; in (2a),

plays the role of a collision frequency for the interaction of particles and free bubbles, P _c is the probability of collision between a particle and bubble, P _asl is the probability of adhesion by sliding, P _tpc is the probability of three-phase contact, P _stab is the probability of stability of a bubble – particle aggregate, P _destab is the probability of destabilization of a bubble – particle aggregate and Z′ is the detachment frequency (of particles from bubbles). The probability of the formation of a three-phase contact between liquid, bubble and particle has been shown to be nearly one over a wide range of parameters and has been specified to be exactly one in this paper. In the appendix we provide a brief (but broad) overview of the flotation deinking process and those basic elements underlying the development of comprehensive mathematical models to describe this process.

By combining (1) with (2a) we observe that

may be interpreted as the ‘collision’ rate (per unit volume, per unit time) of free bubbles with free particles, while P = P _c P _asl P _tpc P _stab is the overall probability that a collision will lead to the formation of a stable bubble – particle aggregate. In an analogous manner,

may be interpreted as the rate at which bubbles with an attached particle interact (per unit volume, per unit time) with the turbulent vortices in the cell which are responsible for particle detachment, while P _destab = 1−P _stab is the probability that such an interaction will actually result in particle detachment. We note that

is time dependent because of the time dependence of the quantity

. In this paper we shall replace

in (2a) by

(the number of bubbles, per unit volume, at time t, which are ‘available’ to capture particles,

); the subsequent replacement of

in (2a) by

will still render k ₁ time dependent and for this reason we have denoted k ₁ and k ₂ as ‘rate’ parameters rather than true ‘rate’ constants. Only in the most naive model, where all bubbles are available to capture particles, resulting in the replacement, in (2a), of

by Zn _B, may k ₁ be termed a ‘rate’ constant.

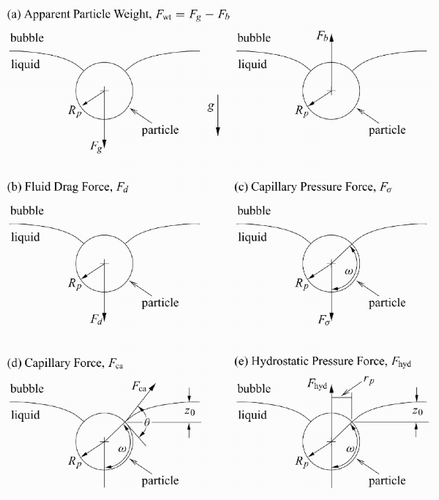
The probability P _stab of stability, addresses the stabilization and destabilization of a bubble – particle aggregate. Modifying the work of Schulze [2], we take as the form for P _stab

where the modified Bond number Bo′ is defined as the ratio of detachment to attachment forces, that is

and α (0 < α < 1), is a stability parameter which depends on the relative particle and bubble radii.

The various other parameters introduced in (4) are defined as follows:

In our computations we employ the following relationship between the surface tension, maximum bubble radius and turbulent energy density [3]:

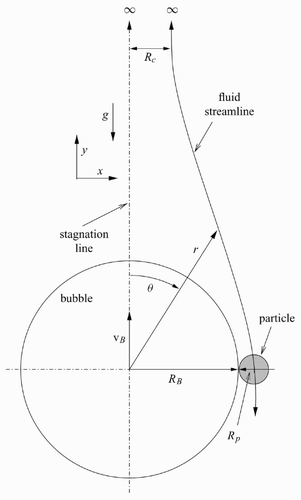
For the probability (P _c) of collision and probability (P _asl) of adhesion by sliding we use, in this paper, new results which were developed in [4] and [5] respectively for flotation deinking conditions. Beginning with P _c, if υ_p represents the particle velocity, and Re _p is the particle Reynolds number given by

where ν_l = μ _l /ρ _l is the kinematic viscosity (μ _l being the usual fluid viscosity), then for an intermediate flow about the bubble surface, in which 2  < Re _p  < 500, it follows from the work by Bloom and Heindel that [4]

In (8), G is the dimensionless particle settling velocity, that is

where υ_ps is the particle settling velocity and υ_B is the bubble (terminal) rise velocity. Also,

where Re _B given by,

is the bubble Reynolds number. For the same kind of intermediate flow over the bubble surface (see for example [6]) it follows from the work of Bloom and Heindel [5] that

where

and

while

is the dimensionless friction factor (f is the usual fluid flow friction factor). Also, C _B is a measure of the bubble surface mobility and is a parameter that varies between one (for a completely immobilized or rigid bubble surface) and four (for an unrestrained bubble surface), h ₀ is the (initial) thickness of the liquid film about the bubble at the instant at which the particle makes contact with the film and begins the sliding process, and h _crit  < h ₀ is the film thickness at which the film spontaneously ruptures.

In (12) it is still necessary to insert the value of h ₀ /h _crit ≡ γ; in fact, because of the manner in which equation (12) is derived, γ = γ* (h ₀ /h _crit) in (12) where the asterisk indicates that we are using that specific value of h ₀ /h _crit that corresponds to φ₀ = φ* ≡ φ*_crit. However, in recent work [7], it has been shown that, for the intermediate flow given by Yoon and Luttrell [6], γ*∼1.5 and, furthermore, that (12) may be replaced by

where

In order to use (15), we consider (16) as a system for (φ*,α*). We may proceed in any of the following ways: solve (16) for φ*; compute α* using (16a) and (16b) and then P _asl by employing (15); by using the computed value of φ*, calculate P _asl as sin² φ*. This new algorithm for computing P _asl has been used in the work reported here.

Finally it has been shown by Bloom and Heindel [8] that Z, which mediates the collision frequency, and Z′, the bubble – particle detachment frequency, may be written in the following forms:

with erf(x) the standard error function and

and

the effective values of relative velocity between (respectively) particles (bubbles) and the fluid, while

with C ₁ a constant whose value in this report has been taken to be C ₁ = 2.

As

with

denoting the number of particles per unit volume attached to bubbles at time t, and it is assumed that

, we may rewrite (1) in the form

where

, i.e.

Equation (21) must be solved subject to the initial condition that

, where

is the number density of free ink particles at time t = 0.

The work that we present here is in the realm of population balance-type models for flotation which date back to the work of Schuhmann [9]; it is closest in spirit to the work of Schulze [2, 3] in that it allows, as we believe no other work in this area does, for the destabilization of bubble – particle aggregates. Almost without exception, other theoretical work on flotation deinking efficiency has involved the study of a particular microprocess probability, for example collision or adhesion as a result of the sliding process, or has looked at one or more of the phenomena underlying such microprocess probabilities, for example thin-film rupture; the work of Bloom and Heindel [1,4,5,8] contains a fairly complete survey of such papers as does the Encyclopedia article [10] by the same authors. A recent exception to the rule noted above occurs in the recent paper by Bloom and Heindel [11] where a comprehensive model of the overall deinking process has been synthesized and experimentally validated in the laboratory, albeit for a semibatch flotation process instead of the continuous flotation deinking process which is employed in an industrial setting and studied here. In the semibatch process described in [11] a WEMCO laboratory flotation cell was employed in which a fixed volume of the liquid – particle mixture is maintained while air is continuously bubbled through the mixture; unlike the situation addressed in the present paper, this is a steady-state process in which the total number of bubbles entering the vessel is identical to the total number of bubbles leaving the flotation cell (per unit time).

In the balance equation (1) for the concentration of free ink particles it was explicitly assumed that only bubbles which do not already have an ink particle attached to them are capable of picking up a particle and removing it from the flotation cell; we now relax this assumption by replacing

in (2a) by

where

represents the concentration of bubbles that are available to pick up ink particles. Assuming no bubble – particle aggregate rotation as it rises in the flotation cell,

represents all bubbles up to (and including) those with one particle less than the maximum number of particles that may be packed, geometrically, on the upper hemisphere of a given bubble. We also assume that the expressions for P _c, P _asl, P _stab , Z and Z′ have the explicit forms and values delineated in this section irrespective of the number of particles actually attached to individual bubbles.

Finally, because we no longer assume that the concentration of bubbles with particles attached to them is identical with the concentration of particles attached to bubbles, in the detachment term on the right-hand side of (1) we must replace

by

. Therefore, in lieu of the balance equation (1) we consider the model whose first equation has the form

where k ₂ is still given by (2b) but, now,

We also let Λ(t) represent the average number of particles, at time t, which are attached to a bubble in the exit stream. If each bubble with attached particles is carrying only one ink particle, then Λ(t)≡1.

The following relations are a direct consequence of the definitions of n _B,

,

,

,

and n _p, namely

and

By virtue of (25),

Using this result in (23) we have, in view of (24),

The differential inequality (28) is coupled to the initial condition

We shall study solutions of the system (28) and (29) with the goal of producing an upper bound for

; an upper bound for

will, of course, yield a lower bound for the efficiency

By virtue of (28) we have

However, in view of the definition of Λ, that is

therefore, (31) may be rewritten in the form

A particularly conservative approach, at this junction, consists, for example, of taking the maximum carrying capacity of a bubble to be the maximum number (K) of particles that can attach to a typical bubble in the flotation cell along an arc (on one hemisphere) of a great circle on the bubble. We note that K is a function only of the radii R _p and R _B of the particle and bubble respectively; in fact it is easily shown that (2α) K < π so that, in fact, we may take

if

is odd and

if

is even, where [z] denotes the greater integer less than or equal to z. For Rp ≪ R _B we have

so that

Thus, for the concentration of bubbles available to capture particles at any time t we have

while, for the concentrations of bubbles with particles attached to them and of particles attached to bubbles respectively, we have

and

Therefore,

and

We note that Λ ⩾ 1 and Λ = 1 if and only if

for j ⩾ 2.

In order to specify the quantity Λ more precisely we may assume the existence of an experimentally determined distribution function

to represent the concentration of bubbles that have exactly x particles attached to them. In actuality, of course, the concentration of bubbles that have a fixed number x of particles attached to them will fluctuate with time; in a first model, however, we may assume that, for fixed x, f (x) represents an average over a time interval [0, T] of interest in the problem, that is

In implementing the model, this assumption is used only to deal with the coefficient involving Λ in (32).

In (43), x is a non-negative integer which varies from zero up to the maximum carrying capacity of one hemisphere of a typically sized bubble. In order to illustrate the type of results that are possible with an experimentally determined distribution function f (x), we may assume, for example, that f (x) is proportional to a normally distributed random variable with mean

, variance

, and standard deviation

, that is with the constant of proportionality denoted by k:

for 0 ⩽ x < ∞, with f (x) ≡ 0 for x < 0. We may think of f (x), as given by (44), as interpolating the values of f at non-negative integer values x because

is meaning-ful, physically, only at such values. The constant of proportionality k in (44) can be determined as follows: for x = K/2

Thus,

so that

From (47) it follows that

If we note that

then

where

Using (49) and (50), we may rewrite (47) in the form

In (32),

as given by (41) will, in general, fluctuate with time; so as not to have to deal, in this paper, with a system with time-dependent coefficients we replace

in (41) by

so that

in which case (32) holds with

replaced by

. From (52), (43) and (44) it now follows that

The model under consideration is based on the differential inequality (32); this inequality is subject to the constraint that n _B and n _p are constant as well as to the initial condition (29).

In (32),

and

is the (time-averaged) average number of particles attached to those bubbles with attached particles; for the Gaussian distribution considered above for example,

would be given by G(K; σ), as defined in (54). An upper bound for the set of solutions of (32) and (29) is obtained by considering (32) with the inequality replaced by equality, that is

which we may rewrite in the form

If we set

then (57) assumes the form

Finally, we assume that

and set

where

Employing the definitions (60) and (61) and replacing γ(t) by Γ(t) = −γ(t) in (59), we obtain

with the associated initial condition

2 Model solutions

To integrate the model system (62a) and (62b) we write (62a) in the form

Because

there exists a μ > 0 such that

Thus, if we set

then (63) becomes, for t > 0,

and associated with (66) is the initial condition

if x ²(t)  > μ ², for all t > 0, then as A > 0 it follows that

(t) > 0 for all t > 0 and this, in turn, is equivalent to

(t) < 0 for all t > 0.

Remark: In view of the definitions of A and B we have the explicit expressions

or

and

while

By virtue of (61), x(0) < 0.□

Returning to the model system written in terms of x(t), we note that (66) is a separable first-order equation which may be integrated explicitly so as to yield

for t > 0. Now (71) has been obtained under the hypothesis that x ²(t) > μ ², for all t >  0; this hypothesis will be substantiated below. If we set

then it follows from (71) that

As x(0)  < 0, x(0) − μ < 0, where μ is given explicitly by (69). In order, therefore, to conclude that β ₀ as defined by (72) satisfies β ₀  > 0, we need a condition which implies that x(0) + μ < 0. However,

while

Thus

as B< 0. On the other hand

so that

Combining (76) and (78) we obtain

Therefore, x(0) + μ < 0 provided that C< A, that is provided that

As x(0) < 0, x(0) = −|x(0)|, and (72) may be written in the form

but we have shown that (80) implies that β ₀  > 0 and, as μ > 0, it then follows from (81) that |x(0)| > μ in which case β ₀  > 1. From (73) we obtain

However β ₀  > 1, and so 1 − β ₀ exp (2μAt) ≠ 0, ∀ t ⩾ 0, and it then follows from (82) that

(t) > 0, for all t > 0. A direct computation shows that x(t), as defined by (73), satisfies both (66) and (67) and, therefore, by local uniqueness of the solution of the initial-value problem we conclude that (73) is the unique solution of (66) and (67). Thus, x(t),as given by (73) satisfies

However

(t) > 0, t > 0 and A > 0 and so x(t), as given by (73), also satisfies x ²(t) > μ ², for all t > 0.

3 Theoretical model predictions

We write the solution (73) to the initial-value problem (66) and (67) in the form

or, as B < 0,

It follows at once from (83) that

or, in view of (60), (61) and (69), and the definition of γ,

Furthermore, for

small (the expected situation) the mean-value theorem may be used to approximate the right-hand side of (84) as follows:

in which case (84) yields

Alternatively, we may write for the long-time asymptotic limit of the number of free particles

From (85) and the fact that Γ(t) = −γ(t) we obtain

in which case (82) produces

for all t > 0. From (88) we infer that the graph of

is (strictly) monotonically decreasing for all t > 0. Furthermore,

for all t > 0, so that the graph of γ(t) is convex for all t > 0. The initial slope

of the graph of γ(t) is given by

and, thus, the equation of the tangent line to the graph of γ(t) at time t = 0 is

From (91) we easily obtain the value of that time t̄ at which the tangent line

to γ(t), at t = 0, intersects the asymptotic level γ = γ_∞ (as given by (86)):

The larger the initial rate of decline of free particles, the smaller is the value of t̄.

Now let t* represent the time required for γ(t), the ratio of free ink particles to the (constant) total number of ink particles, to fall to a specified level γ*, γ _∞  < γ* < 1.

Then from (83) we easily compute that

In particular, if γ* = 

then t* = t _1/2, the time required for the ratio of free ink particles to the (constant) total number of ink particles to fall to

; by virtue of (93) this ratio is given by

A useful approximation to t _1/2 may be obtained by working with the tangent line to the graph of γ(t) at t = 0, i.e., with

as given by (9); we let t̄_1/2 represent the time at which this tangent line intersects the level γ = 

, that is,

Now,

so that

and, thus, (95) may be reduced to

Using (89) and (90) we easily obtain

Thus, from (60), (96) and (97),

Also, the magnitude of the initial rate of decrease of free particles is, by virtue of (90),

Because both (98) and (99) are based on the tangent line approximation to the graph of γ(t) at t = 0, neither result involves the kinetic constant k ₂ which mediates detachment of particles from bubbles. A measure of the efficiency of the deinking process which involves both

and k ₂ is, of course, t _1/2 which may be written in the form

A second measure of the efficiency of the deinking process which we have is represented by the long-time limit of the ratio

as given either by (85) or by the approximate expression (86); this measure also exhibits the competition between attachment and detachment of particles to and from bubbles and may be written as

if we work with the approximation in (86). Clearly, for fixed n _p , n _B, and

, as

↑, γ _∞↓ and as k ₂ ↓, γ _∞↓. A lower bound for the actual efficiency of the deinking process, as gauged by the model, is given by (30) and (83), that is

while a lower bound for the asymptotic (long-time) efficiency is determined, by virtue of (101), as

Remark: By using the definitions of

and k ₂ it is an easy algebraic exercise to rewrite the lower bound (103) for the asymptotic efficiency Eff(∞) in the form

where

Insertion of (3) for P _stab, into (104) then yields as a lower bound

where

Bo′ is the modified bond number, as given by (4), and α, 0 < α ⩽ 1, is the stability parameter associated with particle – bubble aggregate stability. Thus (106) displays the functional dependence of the asymptotic efficiency Eff (∞) on the parameter α.□

4 Experimental methodology

Flotation deinking trials were performed on the B-line at Abitibi's recycle mill in Sheldon, Texas. The B-line consists of a mixing cell, seven primary Ecocells and two secondary cells manufactured by Voith Sulzer. Only two variables, namely the feed flow rate and feed consistency, were varied for the initial experiments. Table 1 shows the experimental conditions that were varied for the five experiments that were conducted. A total of 17 samples were collected from experiment 1; 12 samples were collected from each of the remaining four experiments. The samples were shipped immediately and stored in a cold room upon arrival. The samples were then tested for consistency, made into handsheets, and used for analysis and dirt count measurements. The analysis and dirt count measurements were performed at the laboratories of Eka Chemicals in Marietta, Georgia, USA.

Table 1. Factors varied during the mill trial.

Experiment	Feed flow rate (g/min)	Feed consistency (%)
1	4040	1.24
2	3640	1.24
3	3640	1.11
4	4030	1.37
5	4440	1.24

4.1 Surface tension measurement

Aliquots of the 64 mill samples were filtered through a Whatman No. 4 filter paper and the filtrates were used to determine the surface tension. Approximately 100 ml of the filtrates was collected from each sample. Surface tension was measured using a Cahn DCA 312 apparatus (Wilhelmy plate method). Tables 2  – 6 list the data for the surface tension measurements. It is observed that the surface tension of the overflows is lower than that of the other samples for all the experiments. In general, the range of surface tension values lies between 41 and 44 dyn/cm for all overflows and primary rejects, and between 45 and 50 dyn/cm for all other samples.

Table 2. Surface tension measurements on filtrates from pulp samples: experiment 1.

	Cycle 1 (dynes/cm)	Cycle 2 (dynes/cm)	Average surface tension (dynes/cm)
Discharge cell 1	49.32	49.11	49.22
Discharge cell 2	49.43	49.30	49.37
Discharge cell 3	46.35	46.87	46.61
Discharge cell 4	50.60	50.57	50.59
Discharge cell 5	49.21	49.11	49.16
Discharge cell 6	46.74	47.04	46.89
Overflow cells 1	42.02	42.31	42.17
Overflow cells 2	41.36	41.71	41.54
Overflow cells 3	44.21	43.58	43.90
Overflow cells 4	43.98	43.48	43.73
Overflow cells 5	43.12	43.00	43.06
Overflow cells 6	44.50	44.04	44.27
Mix-cell discharge	49.73	50.28	50.01
Feed flow	50.77	50.51	50.64
Accepts from second secondary cell	44.93	45.15	45.04
Rejects 1 – 6 from primary cell	45.93	45.58	45.76
Flotation accepts	48.57	48.63	48.60

Table 3. Surface tension measurements on filtrates from pulp samples: experiment 2.

	Cycle 1 (dyn/cm)	Cycle 2 (dyn/cm)	Average surface tension (dyn/cm)
Discharge cell 1	49.26	49.20	49.23
Discharge cell 2	47.97	47.68	47.83
Discharge cell 3	47.09	46.80	46.95
Discharge cell 5	48.72	48.66	48.69
Discharge cell 6	50.71	50.50	50.61
Overflow cell 1	41.25	40.85	41.05
Overflow cell 3	44.08	44.08	44.08
Overflow cell 6	44.27	43.85	44.06
Feed pump	46.39	46.15	46.27
Primary accepts from cell 7	46.41	47.71	47.06
Primary rejects	45.00	44.44	44.72
Discharge cell 2	48.66	48.13	48.40

Table 4. Surface tension measurements on filtrates from pulp samples: experiment 3.

	Cycle 1 (dyn/cm)	Cycle 2 (dyn/cm)	Average surface tension (dyn/cm)
Discharge cell 1	49.60	49.14	49.37
Discharge cell 2	46.22	46.39	46.31
Discharge cell 3	48.66	48.53	48.60
Discharge cell 5	48.90	48.10	48.50
Discharge cell 6	49.83	49.40	49.62
Overflow cell 1	43.66	43.22	43.44
Overflow cell 3	44.81	44.31	44.56
Overflow cell 6	42.55	42.00	42.28
Mix-cell discharge	46.89	46.75	46.82
Feed flow	51.02	50.51	50.77
Primary accepts from cell 7	49.66	49.94	49.80
Primary rejects	45.53	45.02	45.28

Table 5. Surface tension measurements on filtrates from pulp samples: experiment 4.

	Cycle 1 (dyn/cm)	Cycle 2 (dyn/cm)	Average surface tension (dyn/cm)
Discharge cell 1	49.17	48.83	49.00
Discharge cell 2	50.43	50.14	50.29
Discharge cell 3	48.87	48.49	48.68
Discharge cell 5	45.46	45.90	45.68
Discharge cell 6	46.90	47.14	47.02
Overflow cell 1	44.20	44.45	44.33
Overflow cell 3	45.67	45.67	45.67
Overflow cell 6	43.72	43.34	43.53
Mix-cell discharge	50.80	50.08	50.44
Feed flow	46.41	46.84	46.63
Primary accepts from cell 7	49.00	49.12	49.06
Primary rejects	40.42	41.27	40.85

Table 6. Surface tension measurements on filtrates from pulp samples: experiment 5.

	Cycle 1 (dyn/cm)	Cycle 2 (dyn/cm)	Average surface tension (dyn/cm)
Discharge cell 1	46.46	46.47	46.47
Discharge cell 2	47.85	47.66	47.76
Discharge cell 3	48.72	48.70	48.71
Discharge cell 5	49.36	49.55	49.46
Discharge cell 6	46.64	46.64	46.64
Overflow cell 1	43.63	43.18	43.41
Overflow cell 3	42.14	41.98	42.06
Overflow cell 6	41.16	41.03	41.10
Mix-cell discharge	49.62	49.21	49.42
Feed flow	47.43	47.35	47.39
Primary accepts from cell 7	49.91	49.67	49.79
Primary rejects	485.79	45.25	45.52
Primary rejects	42.86	43.17	43.02

4.2 Handsheet-making procedure

First, the consistency of the pulp samples was determined. The amount of pulp necessary for making a 3 g handsheet was calculated. The desired amount of pulp was transferred to a graduated cylinder and diluted to 1000 ml using deionized water. A 150 mm filter paper was placed in a levelled fritted-glass Buchner funnel and wetted with deionized water from a wash bottle. Suction was applied to seat the filter paper. With no suction applied to the funnel the 1000 ml stock was rapidly poured. Subsequently, suction was applied until all the excess water was removed. The Buchner funnel was inverted over a standard blotter paper, and the test sheet and filter paper were dislodged from the funnel by blowing into the funnel stem. The blotter paper, test sheet and filter paper were placed on a flat surface, covered with an additional blotter paper and couch plate. A couch roll was rolled five times with no pressure being applied except for the weight of the roll, then the couch plate and top blotter were removed, and an indelible pencil was used to identify the test sheet. Next, a sheet of blotter paper was placed on the press. On this blotter was placed a clean drying plate with its polished surface facing upwards. The test sheet with the filter paper was placed face down on the drying plate. Two more blotter papers were then placed on top. The stack (from the bottom) then consisted of one blotter, a drying plate, the test sheet, filter paper and the two blotters. On this stack a clean drying plate for the next test sheet was added. This sequence was continued until eight test sheets were accumulated. Care was taken to centre the drying sheets. The cover was placed over the final stack and tightened. The pressure was raised to 50 1bf/in²g in 30 s and then maintained for an additional 90 s. After removing the press cover, the filter paper was removed from the test sheets. The handsheets were dried using a commercial drum dryer and were then left in a TAPPI humidity- and temperature-controlled environment until analysis.

4.3 Measurement of handsheet properties

An ERIC value is a measure of the ink attachment to the fibres. ERIC values represent an estimate of the amount of ink below 10 μm that is in the fibre. Two handsheets were made for each pulp sample that was obtained from the mill. To obtain an ERIC value, three measurements were made on the top side of each handsheet and three measurements were made on the bottom side of each handsheet. The results were tabulated as the average of the six readings for each side. The ERIC measurements in table 7 were performed on a Technidyne Color Touch ISO instrument. The ink scan evaluates the ink particle distribution from 10 to 200 μm. Five measurements were made from the top side of each handsheet and five measurements from the bottom side of each sheet, for a total of 20 measurements per pulp sample. The average of the 20 measurements is reported in table 8. The particles were divided into three size ranges and the overall efficiency for the flotation line was calculated for the three individual size ranges.

Table 7. ERIC measurements on handsheets.

	ERIC Value
Experiment	Feed	Accepts
1	924.3	221.8
2	971.6	238.1
3	929.6	199.4
4	956.7	248.3
5	839.8	233.8

Table 8. Dirt count measurement on handsheets.

Experiment	Particle size (μm)	Number of particles in feed	Number of particles in accepts	Experimental efficiency (%)
1	8 – 20	11 897	1316	88.93
1	24 – 52	19 32	184	90.47
1	56 – 224	94	30	68.10
2	8 – 20	10 942	1567	85.60
2	24 – 52	1 524	220	85.60
2	56 – 224	69	34	50.72
3	8 – 20	11 543	1164	89.91
3	24 – 52	1 643	235	85.60
3	56 – 224	89	30	66.29
4	8 – 20	13 323	1283	90.37
4	24 – 52	1 771	252	85.77
4	56 – 224	105	32	69.52
5	8 – 20	11 348	1429	87.40
5	24 – 52	1440	263	81.70
5	56 – 224	119	42	64.70

4.4 Determination of model parameter values

The data obtained from the five experiments conducted at the recycle mill were compared with the modified model for continuous flotation; as a first step the parameters used in the model had to be identified. The modified model requires 13 parameters to evaluate the long-time deinking efficiency Eff (∞). Many of these parameters were measured and some that could not be measured were input as ‘educated guesses’.

The Density of fluid and the viscosity of the pulp in the model were specified to correspond to those of water. The viscosity of fibre suspensions is known to be highly non-Newtonian and will deviate significantly from that of water. Also, the consistency of the fibre suspension will affect the apparent viscosity of the suspension. The effect of viscosity will be further discussed in the section on model parametric variations.

The particle diameter was fixed at the upper value in the data range. Since a significant portion of the ink particles were determined to be in the 8 – 20 μm size range, the radius of the particles was fixed at 10 μm. The particle density was specified to be 1.2 g/cm³.

The particle concentration was calculated from the dirt count measurements and the consistency of the feed suspension. Because a narrow range of 45 – 50 dyn/cm was measured for most of the samples in all five experiments, the surface tension parameter was assumed to be a constant with a value of 50 dyn/cm. The contact angle, a tough parameter to measure, was set at 60°. The bubble surface mobility C_B , was set to a constant value of 1, signifying that the bubbles behaved as rigid spheres.

The power input was computed to be approximately 7.18 W/kg cell for a recycle line processing 300 ton/day at 1.3% consistency (M. Kemper, Voith Sulzer, personal communications 2003); this calculation is presented below. It was assumed that the entire power consumed by the line was converted into turbulent mixing energy. The calculation proceeds as follows. The inlet pressure of an Ecocell is 0.9 bar. The specific power consumption of a standard Ecocell line is about 27 kW h/ton. A standard Ecocell line consists of five primary cells and one secondary cell. About 12.5 ton/h are processed. Thus

is the power consumption for a line producing 300 ton/day, which is the production rate on line B at Houston. For five primary cells and one secondary cell we have a total volume of 46 917 l (again, the Houston Mill data). As we assume a density for the slurry of ρ_slurry = 1 g/cm³ , 46 917 l = 46917 kg slurry. Thus

The gas hold-up was not measured and was estimated to be 10%.

The bubble diameter is a parameter that is currently guessed and needs to be measured in a mill setting; this parameter appears in each of the equations that determine the probability of the individual microprocesses. Flash X-ray radiography is not suitable for measuring bubble diameter in a mill environment and an alternate technique has to be utilized. An optical method described by O'Connor et al. [12] and Hunold et al. [13] is a good candidate for initial investigation. Using (6) an R _B,max of 1.1194 mm may be computed as follows. As 1 W/kg = 10⁴ cm²/s³, ϵ = 7.18 W/kg = 7.18 × 10⁴ cm²/s³. For ρ _l we take a value of 1 g/cm³ while σ is estimated at 50 dyn/cm. Since 1 dy = 1 g cm/s² we have σ = 50 g/s². Solving (6) for R _B,max we find that

As R _B,max = 1.1194 mm, a value for R _B of 0.75 mm was selected for use in the model. With R _B and ϵ known, the constant bubble concentration can be calculated.

The two remaining parameters are

and α.

represents the average number of ink particles attached to a bubble. There is no known method of determining this parameter in a mill. For model validation purposes, the value of

was set equal to its minimum value of 1; a parametric variation in

was conducted while maintaining all other parameters constant. The stability parameter α was treated as a fitting parameter. It may be shown that the model is very sensitive to the value of α. In future work, the parameter α either will be modelled directly or will be backed out (curve fitted) from a set of experimental data.

5 Some model predictions

In this section we present some model predictions based on the data reported in section 4. It is important to note that we do not view the results presented below as being indicative of the kind of more complete study that would be needed for ‘industrial’ validation of the model. Experimental flotation efficiencies (of ink particles in the 8 – 20 μm range) for the five experiments at the mill varied between 85 and 90%; the upper limit of the size range was used as the particle diameter in the model. Data from experiment 1, wherein standard operating conditions were maintained, was used to determine the value of the fitting parameter α. Maintaining α fixed, the predicted efficiencies of the other experiments were computed. Similar comparisons were made for the deinking efficiency of particles in the 24 – 52 μm range. The bubble radius was set at 0.75 mm for all the comparisons. Table 9 lists the values of the parameters that were used in the parametric study. In the figures and discussion that follow it is assumed that all parameters, except the parameter being varied, are fixed at the values given in table 9. Table 10 lists the comparison of the experimental data with the long time deinking efficiency predicted by the mathematical model.

Table 9. Parameter values used in calculating the predicted long-time efficiency.

Parameter	Initial value
Bubble radius	750 μm
Number of bubbles	3.96 × 10^8
Particle radius	10 μm
Number of particles	3.00 × 10^7
Turbulent energy density	50.26
Gas hold-up	0.10
Surface tension	50 dyn/cm
Contact angle	60°
Viscosity	1 mm^2/s
Bubble density	0.001 kg/m^3
Fluid density	1000 kg/m^3
Particle density	1200 kg/m^3

Table 10. Comparison of experimental and predicted efficiencies.

Particle size (μm)	Experiment	Model efficiency (%)	Experimental efficiency (%)
10	1	89.36	88.94
10	3	89.54	89.92
10	4	89.03	90.37
50	1	85.98	90.48
50	3	86.04	85.70
50	4	85.98	85.77

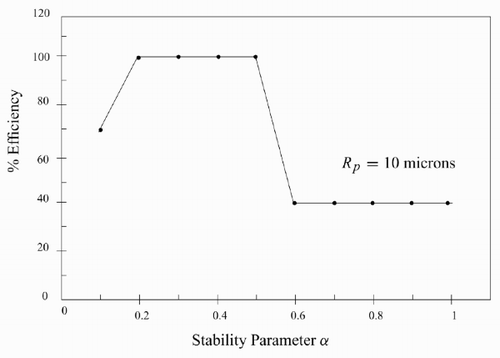
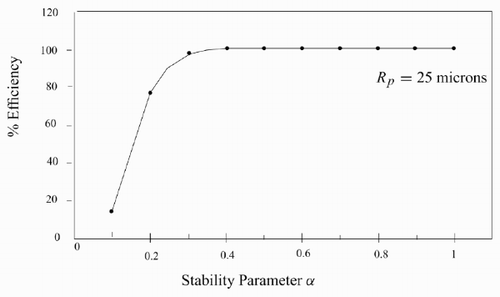
Figure 1 shows the effect of parameter α on the long-time deinking efficiency. It is interesting to note that there are two ranges within which the efficiency is independent of α. The lower range 0.2 < α < 0.5 predicts 100% efficiency for the removal of particles with a radius of 10 μm. The 0.6 < α < 1 range predicts an efficiency of 34% for the same particles. In figure 2 we see the effect of the parameter α on the flotation of ink particles with a radius of 25 μm by bubbles with a radius of 0.75 mm. Here the efficiency increases with increasing α values and attains 99% at an α value of 0.3.

Figure 1. Effect of the parameter α on the predicted long-time efficiency (R _p = 10 μm).

Figure 2. Effect of the parameter α on the predicted long-time efficiency (R _p = 25 μm).

As the modified Bond number Bo ^′ is a monotonically increasing function of Rp (see (4)) the behaviour displayed here indicates (in view of the expression adopted for P _stab in (3)) that the stability parameter α is also a function of R _p, and probably of R _B as well, as has already been noted in section 1. The precise nature of the dependence of α on the particle and bubble radii has yet to be addressed. It is entirely possible that α exhibits a dependence on other factors as well, for example the turbulent energy density ϵ.

Variations in the turbulent energy density ϵ influence the predicted removal efficiency through the collision rates and the probability of stability. Figure 3 shows the dependence of the efficiency on ϵ for α values of both 0.2 and 0.7.

Figure 3. Turbulent energy density versus percentage efficiency for α equal to 0.2 and 0.7 respectively.

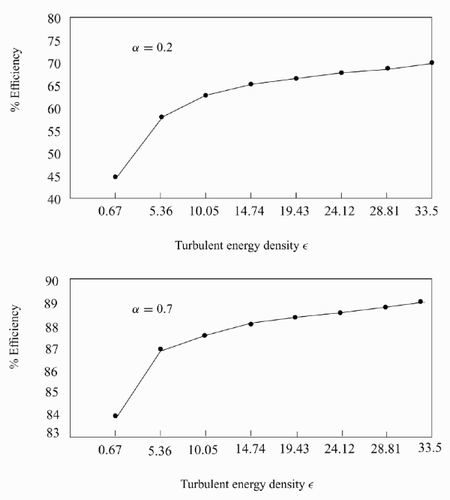
It is clear that, in both cases in figure 3, the efficiency is a monotonically increasing function of turbulent energy density which is not an unexpected result in view of the role that increasing ϵ has in facilitating particle – bubble collisions. As ϵ also plays a role in destabilizing particle – bubble aggregates, the implication is that the favourable impact of an increasing ϵ on particle – bubble collision supersedes its negative impact on the stability of particle – bubble aggregates.

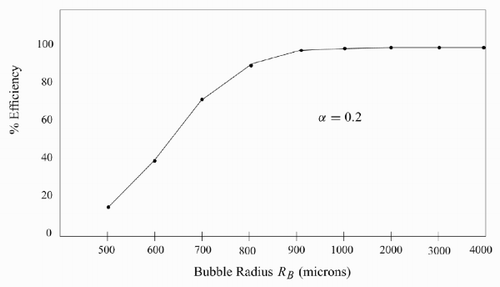
The bubble radius has a variable influence on the long-time efficiency. For the value of α = 0.2 in figure 4 a bubble larger than 0.90 mm in radius has a negligible effect on the removal efficiency for particles with an R _p of 10 μm.

Figure 4. Dependence of the predicted long-time efficiency on the bubble radius R _B.

As an increasing bubble radius R _B, with fixed particle radius R _p, tends to facilitate particle – bubble collisions, adhesion by sliding, and the stability of particle – bubble aggregates, the monotonic increase in efficiency with increasing bubble radius displayed in figure 4 is to be expected. For very large R _B the detrimental effect of increasing R _B on, for example, υ_B could possibly explain the levelling off of the graph in figure 4.

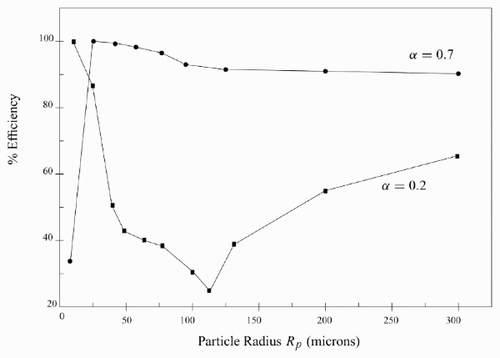
Figure 5 shows the effect of the particle radius R _p on the long-time efficiency. A high efficiency is predicted by an α of 0.2 at R _p 10 μm, but the efficiency drops significantly for higher values of R _p. For an α value of 0.7 the efficiency rises sharply for particles larger than 10 μm and decreases slightly for particles larger than 75 μm.

Figure 5. Dependence of the predicted long-time efficiency on the particle radius R _p.

As was the case for the results displayed in figures 1 and 2, the unusual behaviour displayed in figure 5 may not be explainable on physical grounds until a better understanding of the dependences inherent in α are understood.

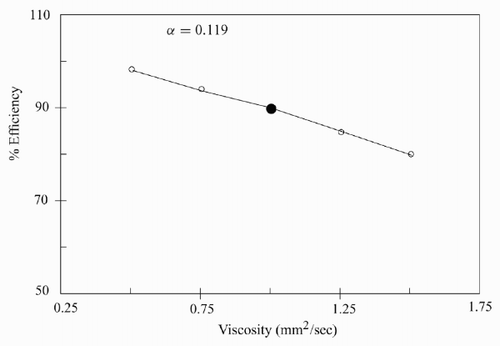
Experimentally, the feed consistency and feed flow rate were the two factors that were varied during the mill trials. Both of these parameters are not directly required for testing the model. Consistency will be related to the viscosity parameter in the model and a search of the literature should provide a mathematical relationship relating viscosity to consistency, but this has not yet been carried out. A parametric study of viscosity, holding all the other parameters at the values given in table 10, is shown in figure 6. The experimental efficiency is shown as the full circle. The predicted long-time efficiency decreases almost linearly with increasing viscosity.

Figure 6. Effect of the viscosity on the predicted long-time efficiency.

An increase in viscosity υ_l results in a decrease in the bubble Reynolds number Re _B and, almost certainly, a decrease in the particle settling velocity, both of which, by virtue of (8), impact the probability P _c of collision in a negative way; the effect of a decrease in υ_l on P _asl and P _stab are not as clear and represent an issue that requires further study.

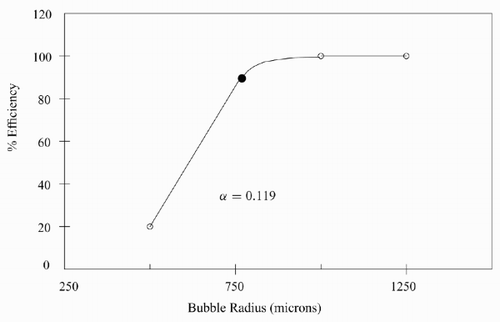
It is widely accepted that there is bubble coalescence at higher consistencies. The effect of bubble coalescence might dominate over the increase in viscosity. Figure 7 shows the change in efficiency due to the increase in bubble radius. The experimental efficiency is denoted by the full circle. For a fixed particle radius, an increase in bubble radius leads to an asymptotic increase in efficiency, which is consistent with the similar result shown in figure 4.

Figure 7. Effect of the bubble radius on the predicted long-time efficiency for α = 0.119.

The two main conclusions which follow from the work presented here are the following.

	The continuous flotation model shows great promise for being able to predict industrial recycle mill efficiencies if the remaining ‘gaps’ in the model can be closed, specifically the measurement of bubble size, the functional form of the stability parameter α and the relationship between consistency and viscosity.
	Once these ‘gaps’ in the model are closed the model can also be used to optimize mill performance; that is, it can be used to predict, for example, the optimal bubble size to use for particles sizes (in a specific range) so as to maximize long-time efficiency. The model may also be used to determine efficiency at conditions beyond the regime of current equipment.

Acknowledgments

The author wishes to acknowledge the support of the Institute of Paper Science and Technology of the Georgia Institute of Technology, Atlanta, Georgia, during the period when the research leading to this paper was conducted; the author is especially grateful for the help provided by Dr Suresh Shrauti, who conducted the experimental trials, and to the staff of the Abitibi recycle mill in Sheldon, Texas, for their cooperation during the period when those trials were performed.

Appendix

Some basic concepts of flotation separation

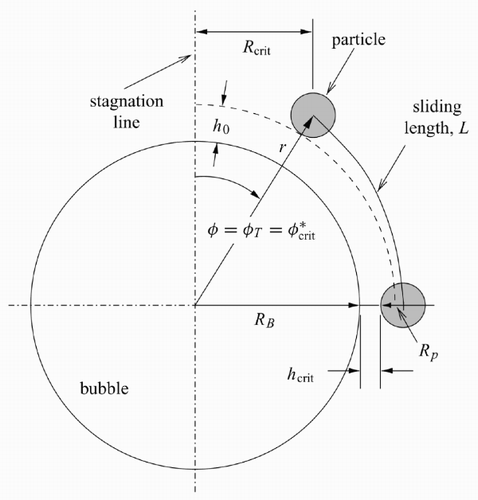
Flotation separation is a process used in many industries to separate one constituent from another. Dispersed air flotation is commonly found in mineral processing (mineral flotation) and paper recycling (flotation deinking). In these processes, relatively large bubbles are formed by mechanical agitation or sparger air injection. Bubble – particle aggregates then form between bubbles and naturally or chemically induced hydrophobic particles. Bubbles with sufficient buoyant force carry the particles to the surface for removal. Dispersed air flotation is a selective process in that it separates, for example, hydrophobic mineral or contaminant particles from gangue or desired fibre in mineral flotation and flotation deinking respectively. In particular, flotation deinking is a separation process used to remove ink and other contaminant particles from reclaimed cellulose fibre. Despite the many differences between mineral flotation and flotation deinking, all flotation cells operate on similar principles. In modern flotation cells, three separate processes take place in tandem:

	aeration, where air bubbles are introduced into the system;
	mixing, where bubbles and particles are intimately mixed to maximize bubble – particle interaction;
	separation, where bubbles and bubble – particle aggregates are allowed to separate from the bulk mixture and are skimmed away.

The modelling of this complex process must be based on the fundamentals of bubble – particle interaction, aggregate formation and aggregate stability. Based on experimental observations, the flotation separation process is thought to be analogous to a chemical reactor which can be described by an ordinary differential equation. In what has become a common assumption in the attempt to develop a model of the flotation process that is independent of the flotation equipment, the overall macroprocess of flotation separation is thought to be composed of a series of microprocesses. These microprocesses include the following:

	the approach of a particle to an air bubble and the subsequent interception of that particle by the bubble;
	the sliding of the particle along the surface of the thin liquid film that separates the particle from the bubble, which leads to film rupture;
	upon film rupture, the formation of a three-phase contact between the bubble, particle and fluid;
	the stabilization of the bubble – particle aggregate and its transport to the froth layer for removal from the flotation cell.

Each of these microprocesses has probabilities associated with it that will successfully occur. The overall probability that a stable bubble particle aggregate will form and be lifted to the froth layer is a product of the various microprocess probabilities; this leads to a kinetic- or population balance-type model where the population of free particles is modelled. Bloom and Heindel [1] extended the idea of a population-balance model to include a forward and reverse reaction (i.e. the birth and death of free particles); this model has the form (1) in this paper where

represents the concentration of bubbles with attached particles. The first term on the right-hand side of (1) represents the successful formation of a bubble – particle aggregate and its subsequent rise to the froth layer. The second term is a measure of the probability that a bubble – particle aggregate will become unstable before it reaches the froth layer and split to yield a ‘new’ free particle. The kinetic rate constants k ₁ and k ₂, are positive numbers described by k ₁ = ZP _overall

and k ₂ = Z′P _destab = Z′(1 − P _stab), where P _destab is the probability that a bubble – particle aggregate will become unstable, P _stab is the probability that the bubble – particle aggregate will remain stable and Z′ is the detachment frequency of particles from bubbles. As we have already noted, in modelling the flotation process, the overall probability P _overall that a bubble – particle aggregate will form and be carried to the froth layer must be determined. Following Schuhmann [9], and assuming that the individual microprocess probabilities are independent, it is common to describe P _overall by P _overall = P _c P _asl P _tpc P _stab, where P _c is the probability of bubble – particle collision or capture, P _asl is the probability of bubble – particle attachment by sliding, P _tpc is the probability of forming a three-phase contact and, as already indicated, P _stab is the probability that a bubble – particle aggregate will remain stable on its journey to the froth layer. Some investigators imply that P _tpc ≈ 1 and omit this term from P _overall. The expression for P _overall assumes that, once a bubble – particle aggregate reaches the froth layer, it is removed from the system. A probability may also be associated with the particle removal from the froth layer. In flotation deinking, mixing is used to maximize bubble – particle interaction, and flotation cells can be assumed to have regions of complex, highly turbulent flows. However, as the distance separating the particle from the bubble decreases, the flow conditions relative to the bubble – particle pair are typically idealized and simplified to be that of unperturbed flow; this allows for considerable simplifications that are universally applied in modelling the flotation microprocesses and, indeed, such assumptions have been used in developing the expression for P _c in (8) and that for P _asl in (12). Most models developed to describe microprocess probabilities assume that the bubble and particle are spherical. In addition, most of the microprocess analyses consider the interaction of one particle with one bubble. Efforts to include non-spherical particles, multiple particles interacting with a single bubble, or bubble swarms add additional mathematical complications to the modelling process. The various forces acting on a particle in the vicinity of a bubble in a flotation tank are depicted in figure 8. In figure 9 we depict the ‘collision’ of a particle with a bubble while, in figure 10, we show that diagram of the sliding process which is relevant for the development of P _asl in (12).

Figure 8. Forces acting on a particle in the neighbourhood of a bubble.

Figure 9. Particle – bubble collision.

Figure 10. Sliding of a particle along the ‘surface’ of a bubble.