Self-referential order

Abstract

We introduce the concept of self-referential order which provides a way to quantify structural organization in non-crystalline materials. The key idea consists in the observation that, in a disordered system, where there is no ideal, reference, template structure, each sub-portion of the whole structure can be taken as reference for the rest and the system can be described in terms of its parts in a self-referential way. Some parts carry larger information about the rest of the structure and they are identified as motifs. We discuss how this method can efficiently reduce the amount of information required to describe a complex disordered structure by encoding it in a set of motifs and matching rules. We propose an information-theoretic approach to define a self-referential-order-parameter and we show that, by means of entropic measures, such a parameter can be quantified explicitly. A proof of concept application to equal disk packing is presented and discussed.

Keywords:

• self-referential order
• disordered structure
• information theory
• order
• structural encoding

Introduction

Complex, non-crystalline materials are everywhere and the capability of understanding and mastering disordered atomic packings is crucial to enhance properties of materials. The quest for understanding the internal structure of matter has been central to human curiosity since the beginning of science and, despite the remarkable achievements obtained since the Platonic theory of matter (Timaeus BC), still we are only able to describe the structure of a very special class of materials where regular periodic (or quasi-periodic) arrangements of atoms are present. However, disorder is not randomness and nor it is a defective, degenerate form of order, real disordered structures show high degrees of organization that can propagate hierarchically through the material. Nonetheless, these structures do not present any periodic, predictable pattern and the absence of such regularity is precisely what makes disorder difficult to describe and encode in a way that is both accurate and compact. Science is measurement, but disorder is difficult to quantify. For instance, in an ordered, crystalline, system one can introduce a quantity called ‘order parameter’ that measures how close the system is to the perfect crystalline reference structure. This parameter is extremely useful to predict the properties of the material. But in a disordered system, there is not a unique, ideal, reference structure and a simple parameter that quantifies the kind and amount of disorder cannot be used. Even common language lacks of terms to define non-ordered structures. Indeed, we are limited to the use of negative identifications: disorder (i.e. disturbance of order) or amorphous (i.e. absence of shape). Such a lack of vocabulary is probably consequence of the fact that the classification of crystalline structures has been one of the great success stories of modern science which has induced us to overlook the evidence that “disordered” and “amorphous” materials are everywhere and the mastering of good techniques to describe atomic disorder is crucial to enhance material performances. It has been recently shown that ‘order’ in amorphous structures can be identified by looking at ‘patches’ that repeat more often than typical [1]. This approach reveals diverging correlation lengths at glass transition [2] shading light on the relations between thermal glass transition and athermal jamming of discrete matter [3]. In this paper, we follow a similar approach to [1] using information-theoretic methods to quantify, in a self-referential way, an ordered parameter and identifying the locally most referential structures.

There are two main technical challenges that have so far slowed down the progress in this field. The first has been the lack of experimental data. Indeed, until recently, diffraction techniques have been the main experimental tools to study atomic structures inside the bulk of materials. However, diffraction gives insights only on the average relative positions of the constituents and the reconstruction of the structure from diffraction data becomes very hard in absence of regularly repeated local units. Now, for the first time, atomic-scale tomography techniques are providing us a way to directly “see” the complex atomic architectures inside materials. Indeed, in the last few years, techniques such as Atom Probe Tomography and Electron Tomography have started to provide direct information about the position of millions of atoms in the bulk of materials [4–9]. In the next few years, we will witness a large production of experimental data concerning large-scale complex atomic aggregates. However, this brings up the second technical challenge concerning the huge size of data to process demanding the development of specific tools and a novel theoretical framework for their interpretation and use. Indeed, in absence of a compact way to encode structural complexity, the processing of this amount of information is still beyond the capability of the world’s largest supercomputers. The total world information storage capacity, currently estimated bits, would not be enough to encode the structure of a gram of disordered matter. There is therefore a demand to develop a general approach to encode complex structures and reduce the amount of information to the relevant part related to the material’s functional properties. In principle, in a disordered material positions, properties and the interactions of every atom must be recorded independently. In some special cases, when the structure is a regular periodic repetition of identical parts (i.e. crystals), the problem can be reduced to the study of the unit cell: a local sub-structure that repeats periodically in space, however this cannot be directly extended to non-crystalline materials. Nonetheless, even in these ‘disordered’ materials, geometrical, physical and chemical laws impose local regularities that spontaneously develop into a structural organization spanning the whole system. In this paper, we show that these regularities can be identified as a set of local motifs that combine together into a hierarchically organized space-filling complex network in a analogous way as an alphabet combines into words which assemble into phrases forming the whole text. Retrieving the ‘alphabet’, identifying the ‘words’, uncovering the ‘grammatical’ rules and ultimately, decoding the ‘syntax’ is the key to describe the structure of non-crystalline matter.

Describing the structure in terms of itself: self-referential order

The key-idea at the basis of the present work is very simple: in the absence of a pre-definite template reference structure, we can use a part of the material as a reference structure for another part. The structure is consequently encoded with a self-referential description. For instance, from a general information-theoretic perspective, we can re-interpret the identification of the unit cell of a crystalline structure has a very efficient way to encode a structure with the amount of data required to encode the structure passing from order to order . Even in the absence of any previous knowledge of crystallography it is still rather straightforward to identify the unit cell from the information about the positions of all atoms. Indeed, it is sufficient to take a portion of the structure, translate it in space and see when and where it perfectly overlaps with another part of the structure. The smallest portion of the structure that periodically overlaps with all other parts of the structure is the unit cell. In the context of this paper, this is the simplest case of self-referential description where only one local motif -the unit cell- is sufficient to entirely describe the whole crystal.

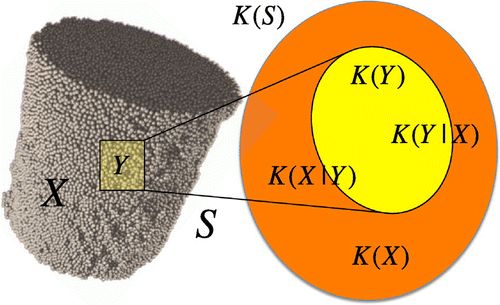
Fig. 1 (colour online) In the absence of a pre-defined template reference structure, one can use a portion () of the structure to describe the whole structure . The knowledge about the portion can reduce the uncertainty about the rest of the structure . Kolmogorov complexity, here denoted with and , measure the information contained in and , respectivelly. For instance, in the case in which the rest of the structure is completely determined by the knowledge of the portion , we have . In this case, the conditional information about given , , is equal to zero.

An ideal approach

Let us consider a structure and let us consider it as composed of a large portion and a smaller portion , so that . To measure the amount of self-referential order, we need to be able to quantify how the knowledge about the portion reduces the amount of information needed to encode . Formally, we need a measure of information content such as the Kolmogorov complexity [10–13]. In simple terms, the quantity is the amount of information necessary to describe . Its conditional counterpart, , is the amount of information necessary to describe , given the full knowledge of . When the knowledge about a portion of the structure is sufficient to describe the rest of the structure, we must have and . Conversely, when the knowledge about a portion does not add any knowledge about the rest of the structure we must have .

We could therefore introduce the self-referential order parameter(1) which is equal to one if the system is fully self-referentially ordered and it is equal to zero if completely random. This approach formally defines self-referential order and it would solve the problem. However, –unfortunately– Kolmogorov complexity is not a computable quantity.

The entropic way

A computable quantity that measures information content is the entropy that, in the Shannon formulation [14], can be written as:(2) where is the probability of occurrence, in , of a configuration with a given set of structural properties, denoted with . Entropy is everywhere in physics; it is a thermodynamic state variable and the Shannon formula coincides with the Gibbs derivation (with base- log and multiplied by [15]) of the entropy for the canonical ensemble. Here, we shall use entropy for its information significance: is the amount of information encoded into a structure when its properties are considered. We shall therefore use entropic measure of information instead of the Kolmogorov complexity. Let us note that Kolmogorov complexity of is the size of the smallest programme that generates , instead Shannon entropy measures smallest number of bits required, on average, to describe [13]. The two measures can coincide in some special cases (signals computable by a Turing machine) but not in general, though they are related [16].

In analogy with the previous section, we can therefore look for the information about provided by the knowledge of . The remaining entropy of variable when variable is known is quantified by the conditional entropy . Therefore, an entropic measure of self-referential order is:(3) We have , therefore this quantity is defined in the interval where 0 is associated to a random state and 1 is instead observed for perfect self-referential order. We can use the identity obtaining the equivalent expression(4) which also reads(5) One may notice that the quantity on the numerator is the mutual information: , therefore this measure quantifies the relative mutual dependence between structures and .

Motifs

There must be parts of the structure that carry larger amount of information about the whole structure with respect to others. These high information-content portions are repeated similarly in the structure more often that others and therefore they are of particular relevance. We look for local sub-structures containing maximal relative information. We shall call them ‘motifs’ these are equivalent to the ‘patches’ used in [1]. In general, more than one motif is necessary to encode a disordered structure. Furthermore, these motifs do not repeat perfectly across the structure and therefore they must be described in statistical terms. Motifs are the set of local structures from which the whole structure can be most efficiently encoded. Frequency of occurrence, fluctuations and relations between motifs characterize and quantify the kind and amount of disorder in the structure. We then use these motifs as an encoding alphabet and we search for an efficient description of the entire structure with the shortest code-length. By identifying the recurrent structural motifs and by uncovering the rules governing their combination into a space-filling network, we can encode the structure of complex materials into a compressed format.

Motifs can be identified from Equations 1(1) or 3(3) by looking at the local parts that maximally contribute to the information about the whole structure, i.e. the portions associated with the largest . Once the motifs are identified, one must quantify their recurrence in the structure. This can be done in three steps: (i) count the relative frequency of occurrence of each local motif; (ii) compute the probability distribution of its fluctuations; and (iii) estimate the entropy. A computationally fast identification of the motifs in presence of structural fluctuations is a very challenging task. Another challenge is associated with possible overlaps between motifs that makes their unique identification ambiguous and requires the introduction of “exclusion rules” (i.e. when two motifs overlap, only one must be counted at the time) and statistical ensamble analysis (i.e. all encodings resulting from the different exclusions) must be considered.

Motifs are building blocks that connect to each-other forming a space-filling three-dimensional structure. When described in terms of motifs, the structure is characterized by two aspects: (1) topology – a network of interconnected motifs; and (2) geometry, where position and orientation of each motif is specified. Due to the possible overlaps between motifs, there can be more than one network for a given structure, the ensamble all these networks must be considered. For a given network, the matching rules can be identified from a statistical study of local co-occurrences. Matching rules are both topological and geometrical. Indeed, motifs can join together only in specific relative positions and orientations.

The description of a structure in terms of the network of motifs and their matching rules provides a compact encoding of the structure. For example, a crystal is reduced to only one motif (a parallelepipedal unit cell), one topological matching rule (6 neighbors) and one geometrical matching rule (unit cells join by opposite faces). In general, for a complex structure we have a large – but finite and non-scaling – number of motifs and a order of matching rules. Therefore, the amount of information required to encode the structure is of the order . A-priori it is quite hard guesswork to estimate the size of , which -of course- varies from system to system. The experience acquired with disordered sphere packings [17–19] suggests us that in these systems is of the order of , and the matching rules are of the order of (note that resolving all the reciprocal orientations can be demanding). This may seem a large number but it must be pointed out that in terms of information compression, we are passing from an information size of the order of (hundreds of billions of gigabytes), which is certainly beyond computable sizes, to a size of bytes (tens of kilobytes), which is computationally insignificant. Furthermore, for many practical purposes, a precise definition of the local geometrical configuration and its orientation is often irrelevant and the information can therefore be further reduced. Let us here explain this point with an example from the results on sphere packings in [20] where it was shown that local tetrahedral motifs are related to the description of a structural transition at the Random Close Packing limit. In that paper, it was shown that the controlling parameter were the length of the tetrahedral edges with an effective differentiation between “short” or “long” edges. In terms of motifs, given that each tetrahedron has six edges and each edge has two states, in this special case we can count relevant motifs. To compute the matching rules, we must then consider that tetrahedra match face by face and they have 4 faces giving matching rules. However, these numbers can be greatly reduced, for instance, in [20], it was shown that the most relevant motifs were only 2: all-short-edges or not. And the relevant matching statistics was given by the chains of all-short-edges tetrahedra.

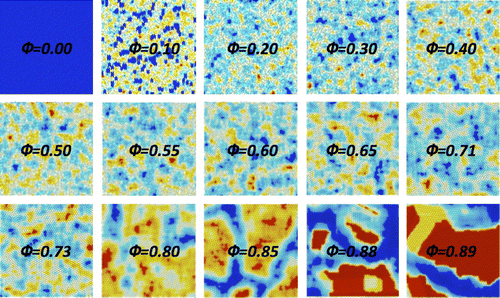
Fig. 2 (colour online) Snapshots of the local self-referential order parameter . The local portion is a square of edge 5 disc diameters. The pictures are a heat map (blue low red high, color online) representing the relative values of for a portion centred in each given part of the packing. indicates the packing fraction of each sample. Colourmap is rescaled for each image.

Fig. 3 Global values of the self referential order parameter vs. packing fraction displayed in both linear and semi-logarithmic scale. Different curves ( symbols) correspond to different sizes of the local portion , which are squares, respectively, with edges equal to 3, 5 or 10 disk-diameters.

Fig. 4 Average maximum local values of the self referential order parameter for each sample. The average is over the 10% largest . Different curves ( symbols) correspond to different sizes of the local portion , which are squares, respectively, with edges equal to 3, 5 or 10 disk-diameters.

Results

In this paper, we report a preliminary investigation about the quantification of self-referential order in two-dimensional disks packings generated via molecular dynamic simulations. The results presented here are a ‘proof of concept’ demonstrating that this method can be used quantitatively. Extended applications to three-dimensional structures from simulations and experiments are under investigation.

We generate several packings of disks at various packing fractions by using the algorithm proposed by [21], which is a molecular dynamic simulation with constant compression rate. We terminate the simulation when a desired packing fraction is reached, before the reach of (local) jamming. We report results for 15 samples comprising 5,000 disks representing a range of packing fractions between 0 to .

We compute the self referential order parameter by looking at the Voronoï volumes around each disk and identifying a set of kinds of motifs classified in terms of their different volumes. We verify that the method is robust against this choice with analogous results obtained for or . We then take a local square portion of the sample and compute by applying Equation 5(5) . We repeat the process in 10,000 different portions regularly displaced across each sample.

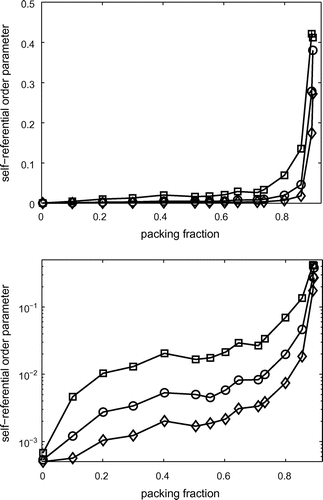
In Figure 2, distributions of the local self-referential order parameter inside each sample and across the samples are shown. One can note that the values are low at low packing fractions where the system is essentially in a random state. Conversely, they are large at high packing factions where the system starts nucleating crystalline regions. This is quantified and shown in Figure 3 where we report a global measure of self referential order parameter () computed by estimating the joint probability to have given fractions of Voronoï volumes simultaneously present in any of the portions and in the rest of the sample . One can see that the self referential order parameter increases with packing fraction to reach a maximum at the largest packing of . From the semi-log plot in Figure 3, we can note that this parameter ranges over 4 order of magnitude, with an interesting plateau appearing between packing fractions and . Let us note that the largest packing fraction attainable for equal disks is [22], which corresponds to a perfectly ordered, crystalline, triangular packing. Our densest packing has still some defects that lower slightly its packing fraction. These defects are clearly visible in Figure 2 where one can appreciate that in correspondence with miss-alignment of the crystalline order we observe lower values of . 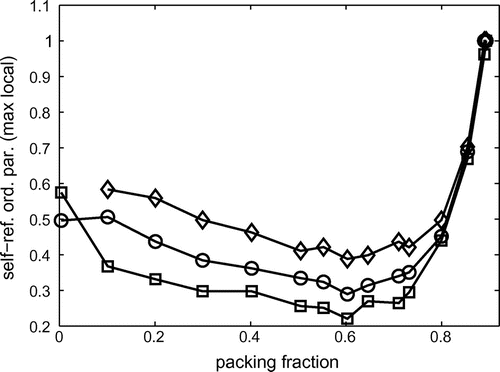Indeed, these defective regions are less representative of the sample. We can also note that, conversely, at lower packing fractions the most representative local portions are not compact configurations with crystalline symmetry but rather more complex and less compact configurations. In general, at different packing fractions different local configurations carry more or less information about the rest of the sample structure. We investigated the presence of highly referential motifs by looking at the maximum values of in each sample. Specifically, we quantified the portions of sub structures carrying the largest information by identifying the 10% largest per each sample. In Figure 4, we show the values of the average self referential order parameter in this top 10% subset of most representative configurations. One can note that at large packing fractions, where the structure is essentially crystalline, only few configurations carry all structural information. Interestingly, also at very low packing fractions, where the structure is essentially random, again a small part of the most informative configurations characterize well the whole structure. On the other hand, at intermediate packing fractions -around – the structure is more complex and even the most informative local configurations carry, in average, a smaller amount of information about the rest of the system.

Conclusion

We addressed the intriguing question concerning how atoms organize themselves inside non-crystalline, complex materials and how to extract, filter and encode this information in an efficient and meaningful way. To this purpose we introduced the concept of self-referential-order and we proposed a method to quantify it from entropic measures. There are over one billion trillion atoms in a gram of matter, and in the absence of a regular, ordered arrangement, the characterization of an amorphous structure would require accounting for the position of every atom. This is an impossible task that would require over a billion terabytes. However, the material functional properties are associated with a much smaller amount of information. In this paper, we have illustrated a general approach to encode complex structures and to reduce this overwhelming amount of information to the relevant part related to the material’s functional properties. Our method can be used to select the most informative portions of the material, the ‘motifs’, and encode the complex structure in a set of motifs and matching rules reducing dramatically the amount of information required. In this paper, we present a ‘proof of concept’ with application to equal disk packing at different packing fractions. We found that the self-referential-order parameter well characterizes globally the transition towards crystallization, but also it identifies locally the emergence of an increasing complexity at intermediate packing fractions. Future studies will be dedicated to the analysis of three-dimensional structures from experiments and large scale simulations. Our information filtering and encoding techniques can be directly applied to very different kinds of complex structures which are defined in high-dimensional phase-spaces: the study of the structure of dependency in financial systems [23, 24] or the structure of gene co-expressions in biological systems [25].