On low temperature glide of dissociated 〈1 1 0〉 dislocations in strontium titanate

Abstract

An elastic interaction model is presented to quantify low temperature plasticity of SrTiO₃ via glide of dissociated 〈1 1 0〉{1 1 0} screw dislocations. Because 〈1 1 0〉 dislocations are dissociated, their glide, controlled by the kink-pair mechanism at T < 1050 K, involves the formation of kink-pairs on partial dislocations, either simultaneously or sequentially. Our model yields results in good quantitative agreement with the observed non-monotonic mechanical behaviour of SrTiO₃. This agreement allows to explain the experimental results in terms of a (progressive) change in 〈1 1 0〉{1 1 0} glide mechanism, from simultaneous nucleation of two kink-pairs along both partials at low stress, towards nucleation of single kink-pairs on individual partials if resolved shear stress exceeds a critical value of 95 MPa. High resolved shear stress allows thus for the activation of extra nucleation mechanisms on dissociated dislocations impossible to occur under the sole action of thermal activation. We suggest that stress condition in conjunction with core dissociation is key to the origin of non-monotonic plastic behaviour of SrTiO₃ at low temperatures.

Keywords:

• Strontium titanate
• plastic deformation
• non-monotonic plastic behaviour
• dissociated dislocations
• dislocation glide

1. Introduction

SrTiO₃ strontium titanate has gained wide interest because of its technological applications. It is widely used as a substrate, especially to grow other perovskite thin films [1,2]. Although bulk SrTiO₃ itself is paraelectric, it can exhibit ferroelectricity when strained as a thin film, which makes it a potential candidate for thin-film memory applications [3,4]. As such, a deep knowledge of its response to stress and of the properties of extended defects (e.g. stacking faults, dislocations) is of paramount importance. The mechanical behaviour of strontium titanate has turned out to be complex over a wide temperature range [5–14]. Despite its brittleness at high temperatures between 1050 and 1270 K [5,8], this oxide ceramic with a perovskite structure deforms in a ductile regime at temperatures below 1050 K, now commonly referred to as regime A [5–8,12]. In this low-temperature regime, plastic flow is driven by 〈1 1 0〉{1 1 0} slip systems. In addition, it has been shown by Brunner [7] that single crystal plasticity in regime A is characterised by a non-monotonic increase of the critical resolved shear stress (CRSS) with decreasing temperature. Brunner [7] subdivided regime A further into three regimes: A₁ (from 1050 K down to 225 K), A₂ (between 225 and 205 K) and A₃ (below 205 K). Transmission electron microscopy (TEM) observations of deformed SrTiO₃ single crystals have demonstrated that its microstructure was predominantly governed by 〈1 1 0〉{1 1 0} screw dislocations aligned with their Peierls potential minima along close packed directions in the perovskite structure [8,12] over the whole temperature range of regime A [7], thus discarding the hypothesis of a change of slip system to explain the non-monotonous mechanical behaviour. Both TEM at room temperature [9] and high-resolution transmission electron microscopy (HRTEM) below room temperature [11,12] of strained SrTiO₃ single crystals revealed that 〈1 1 0〉 screw dislocations are systematically dissociated by glide in {1 1 0} planes in the whole temperature range of regime A, impeding the hypothesis of a change in core structure of these dislocations. The 〈1 1 0〉 dislocations dissociate into (collinear) partials following the Burgers vector reaction: 〈1 10 〉 → ½〈1 1 0〉 + ½〈1 1 0〉, partial dislocations being separated by an antiphase boundary (APB). The latter has been confirmed by theoretical calculations of the core structure of 〈1 1 0〉 dislocations in SrTiO₃ [13–15]. Deformed single crystal microstructure being predominantly composed of straight 〈1 1 0〉 screw dislocations, together with the general (albeit non-monotonic) increase in CRSS with decreasing temperature, are typical signs of lattice friction controlled plasticity in the low temperature regime A, characterised by stress-assisted thermally activated dislocation glide.

Thermally activated and stress-assisted glide of dislocations is usually controlled by kink-pair formation [16,17]. In this context, Castillo-Rodríguez and Sigle [12] proposed that the discontinuous evolution of the CRSS with decreasing temperature below 1050 K in SrTiO₃ may be associated with a change in kink-pair mechanism. They interpret this change in terms of kink-pair formation that is controlled either by nucleation (short-segment limit) or by propagation (long-segment limit) of kinks. However, so far, no consensus has been reached about the origin of this particular behaviour. In this work, we propose a kink-pair nucleation-based model that is able to explain the non-monotonic behaviour of the temperature dependence of the CRSS in regime A. We show that this particular mechanical behaviour can be reproduced in terms of a change in kink-pair mechanism of dissociated 〈1 1 0〉 screw dislocations, which above a critical stress condition at high CRSS, is essentially governed by individual motion of ½〈1 1 0〉 partials and towards low CRSS by coherent motion of both ½〈1 1 0〉 partial dislocation lines. In this work, we describe the motion of dissociated dislocations (such as those governing SrTiO₃ plasticity in regime A) using an elastic interaction model [18]. Our model depends explicitly on the core properties of dissociated 〈1 1 0〉{1 1 0} screw dislocations that is characterised by its core geometry, stacking fault energy, Peierls potential and associated Peierls stress. Plastic behaviour in low temperature regime A by glide of 〈1 1 0〉 dislocations is finally determined via the stress dependent nucleation rate of kink-pairs. The rate of kink-pair nucleation is controlled by the critical energy variation of kink-pair formation which is determined with the elastic interaction model. A comparison between our results and the available experimental data will be finally presented.

2. Modelling the kink-pair mechanism

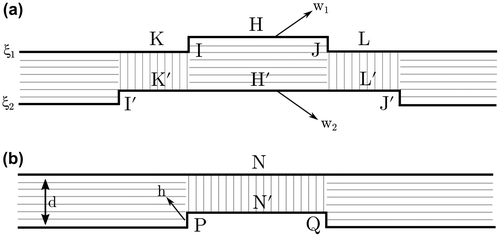
When lattice friction controls plastic deformation, stress-assisted thermally activated dislocation glide essentially occurs by nucleation and migration of kinks along dislocation lines [17]. Based on the experimental occurrence of long straight screw dislocations in SrTiO₃ deformed at low temperature, we assume that kink migration is not the limiting mechanism. Our approach therefore is purely nucleation-based, i.e. the rate of kink-pair formation is controlled by the total energy variation H associated with the local bow-out of the dislocation over its Peierls potential. In SrTiO₃, one complexity arises from the fact that 〈1 1 0〉 dislocations are dissociated, hence the model must consider nucleation mechanisms on both partials (Figure 1), as previously discussed by Möller [19] and Mitchell et al. [20]. Depending on the applied shear stress τ, kink-pair nucleation may occur on the partial dislocations either simultaneously or sequentially. In the latter scenario, a first kink-pair is nucleated on one of the partials, followed by a second kink-pair nucleating on the second partial. This process (hereafter called ‘uncorrelated nucleation’) involves a change in stacking fault width d and energy, and a variation in elastic interaction between the partials (Figure 1(b)). In the former scenario, two pairs of kinks nucleate on both partials simultaneously (hereafter called ‘correlated nucleation’) (Figure 1(a)). Considering that kink-pairs are rectangular with a height h and a width w, the energy variation ΔH of kink-pair formation on dissociated dislocations depends on the activated scenario and consists of four terms:(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1)

Figure 1. Nucleation of rectangular kink-pairs of width w and height h on (collinear) dissociated dislocations with equilibrium stacking fault width d. (a) Correlated kink-pair nucleation with their centres coinciding along both partial dislocation lines ξ₁ and ξ₂ and widths corresponding to w₁ = H and w₂ = K′ + H’ + L′, respectively. (b) Uncorrrelated kink-pair nucleation that starts from the trailing partial. This process can occur only above a critical applied shear stress τ_c. In both nucleation processes, vertically shaded areas correspond to a change in equilibrium stacking fault width d, whereas horizontally shaded areas remain equal to d. The length of the line segments H, H′, N, N′, K = K′ = L = L′ are associated with their corresponding shaded areas. Length of the segments I, I′, J, J′, P and Q correspond to the height h of individual kinks.

In Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) ), the first term ΔE_el is the variation in elastic energy resulting from the increase of dislocation length, and the change of the separation distance between the partials. This term is computed in Section 3 according to the elastic interaction model [18]. ΔW_sf corresponds to the change in stacking fault energy. ΔP is the variation in Peierls energy related to one partial line segment w leaving its Peierls valley. Finally, W_τ = τb_phw is the plastic work of the resolved shear stress on one of the partials, of Burgers vector b_p. The constant c is equal to 1 or 2 for uncorrelated or correlated kink-pair nucleation, respectively.

Let us define V_p as the Peierls potential of the full straight dislocation. Since the dislocation is dissociated into two identical partials, one can assume that each partial overcomes half of the maximum of the potential [21], i.e. V_p/2. The variation of the Peierls energy ΔP associated with a single partial dislocation line can be thus written as(2) $$\mathrm{\Delta }P={\int }_{x_0}^{x_0+h}{V}_p\text{d}x+\frac{w}{2}\left[V_p\left(x_0+h\right)-V_p(x_0)\right]$$(2)

where x₀ is the new equilibrium position of a given partial under the resolved shear stress τ. Since both partials experience the same stress condition, x₀ can be solved for by $\tau b={\left|\text{d}{V}_p(x)/\text{d}x\right|}_{x=x_0}$ with full Burgers vector b. In the framework of the Peierls–Nabarro model [22,23], the Peierls potential V_p is the sum of two contributions, the non-elastic misfit energy V_m between m pairs of crystal planes [24,25] and the elastic strain strain V_e [26]:(3) $$V_m=\sum _{m=-\infty }^{m=+\infty }\gamma \left(u_m\right)a^{\prime }$$(3) (4) $$V_e=\frac{1}{2}{a}^{\mathrm{\prime }}\{\frac{u_m}{2}[\sum _{m=-\mathrm{\infty }}^{m=+\mathrm{\infty }}\frac{\mathrm{\partial }\gamma }{\mathrm{\partial }{u}_m}(u_m)]+\frac{-u_m}{2}[\sum _{m=-\mathrm{\infty }}^{m=+\mathrm{\infty }}\frac{\mathrm{\partial }\gamma }{\mathrm{\partial }{u}_m}(-u_m)]\}$$(4)

where a′ is the distance between two Peierls valleys, u_m is the relative displacement between two consecutive crystal planes across the glide plane, and γ is the generalised stacking fault energy of {1 1 0} plane along the 〈1 1 0〉 Burgers vector direction. To compute V_p as shown in Figure 2, we use the γ-surface calculations of Hirel et al. [13], and u_m is derived from the dislocation core structure provided by Hirel et al. [14]. It yields a Peierls stress τ_p = 500 GPa. One can then rewrite the maximum of this potential as $$V_p^{max}=\frac{1}{\pi }{a}^{\mathrm{\prime }}b{\tau }_p=0.02$$ eV/Å. As pointed out earlier, each partial dislocation overcomes half of this potential, i.e. $$V_{p_p}^{max}=\frac{1}{\pi }{a}^{\mathrm{\prime }}{b}_p{\tau }_p$$.

3. Elastic interaction model

The elastic interaction model, as proposed by Koizumi et al. [18], is used throughout this study to calculate the variation in elastic energy ΔE_el between a straight and a kinked dislocation appearing in Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) ). Considering straight line segments as illustrated in Figure 1 and the coplanar elastic interaction formalism [27], the variation in elastic energy of one (partial) screw dislocation is given by:(5) $$\mathrm{\Delta }{E}_{{\xi }_n}=\frac{\mu b_p^2}{2\pi }\left[\sqrt{w^2+h^2}-w-h+w\log \left(\frac{2w}{w+\sqrt{w^2+h^2}}\right)-\frac{1}{1-\nu }\left[w-\sqrt{w^2+h^2}+h\log \left(\frac{h+\sqrt{w^2+h^2}}{w}\right)-h\left[\log \left(\frac{h}{r_c}\right)-1\right]\right]\right]$$(5)

where μ is the shear modulus of the material, and ν its Poisson ratio (Table 1). Equation (5(5) $$\mathrm{\Delta }{E}_{{\xi }_n}=\frac{\mu b_p^2}{2\pi }\left[\sqrt{w^2+h^2}-w-h+w\log \left(\frac{2w}{w+\sqrt{w^2+h^2}}\right)-\frac{1}{1-\nu }\left[w-\sqrt{w^2+h^2}+h\log \left(\frac{h+\sqrt{w^2+h^2}}{w}\right)-h\left[\log \left(\frac{h}{r_c}\right)-1\right]\right]\right]$$(5) ) depends on the kink-kink interaction (segments P and Q of edge character in Figure 1(b)) and includes a change in self-energy of the line. The latter is due to creation of new edge segments which depends on the inelastic distortion field of the dislocation core (i.e. core extension) and is here parameterized through a cut-off radius r_c.

Table 1. Elastic properties (shear modulus μ and Poisson ratio ν) of SrTiO₃ and dislocation core structure parameters of the 〈1 1 0〉{1 1 0} screw dislocation (as inferred from atomistic modelling [14]). b_p is the modulus of the partial Burgers vector. a′ is the Peierls periodicity (equivalent to the lattice constant). According to Hirel et al. [14], we use in the model an equilibrium stacking fault width d between collinear partial dislocations (of half-width ξ_h) in association with an APB energy γ.

〈1 1 0〉{1 1 0} screw dislocation	bp (Å)	a′ (Å)	ξh (Å)	d (Å)	γ (J/m^2)	μ (GPa)	ν
	2.78	3.94	4.0	30	0.45	112	0.25

Nucleation of individual kink-pairs on either the leading or the trailing partial (Figure 1(b)) induces a local change h in the stacking fault width, thus a variation in stacking fault energy ΔW_sf = ± γhw. Due to the spreading of the partial dislocation cores, and to maintain consistency with the elastic interaction model, we use an effective stacking fault energy of γ = 0.45 J/m² (Table 1) to describe the APB [11]. As a result, the interaction energy $$\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}$$ between the partials ξ₁ and ξ₂ (involving the interaction between segments N and N’ in Figure 1(b)) becomes:(6) $$\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}=\frac{\mu b_p^2}{4\pi }\left[\pm 2h-2\sqrt{w^2+d_f^2}-wlog\left(\frac{\sqrt{w^2+d_f^2}-w}{\sqrt{w^2+d_f^2}+w}\right)+2\sqrt{w^2+d_i^2}+wlog\left(\frac{\sqrt{w^2+d_i^2}-w}{\sqrt{w^2+d_i^2}+w}\right)\right]$$(6)

Equation (6(6) $$\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}=\frac{\mu b_p^2}{4\pi }\left[\pm 2h-2\sqrt{w^2+d_f^2}-wlog\left(\frac{\sqrt{w^2+d_f^2}-w}{\sqrt{w^2+d_f^2}+w}\right)+2\sqrt{w^2+d_i^2}+wlog\left(\frac{\sqrt{w^2+d_i^2}-w}{\sqrt{w^2+d_i^2}+w}\right)\right]$$(6) ) depends on the kink-pair nucleation process (i.e. nucleation on leading or trailing partial) with d_i and d_f corresponding to the initial and final stacking fault width, respectively. The total variation in elastic energy related to uncorrelated kink-pair nucleation can now be written as ΔE_el = $$\mathrm{\Delta }{E}_{{\xi }_n}+\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}$$. Such an event in this uncorrelated kink-pair nucleation scenario is, therefore, characterised by a competition between $$\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}$$ and ΔW_sf (Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) )). As previously suggested by Möller [19] and Mitchell et al. [20], uncorrelated kink-pair nucleation requires the applied stress to be greater than a critical value τ_c obtained by minimisation of the resolved shear stress τ with respect to kink-pair geometry h and w formulated as(7) $$\tau \left(h,w\right)=\frac{1}{b_{p}hw}\left[\mathrm{\Delta }{E}_{{\xi }_1,{\xi }_2}\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}(h,w)\right]$$(7)

On the contrary, the scenario of correlated nucleation can occur even at resolved shear stress lower than the previous critical stress τ_c [19]. Therefore, in the low stress regime (τ < τ_c) only correlated kink-pair nucleation determines the dislocation mobility. Correlated nucleation of kink-pairs (Figure 1(a)) is based on the following geometry: a constant kink height h = a′ (a classical assumption valid under low stress conditions [18]) and two variable widths w₁ and w₂ on each partial (it can be useful to further define w_k = ½(w₂ − w₁) > 0). Compared to previous work [19,20], the use of variable widths w₁ and w₂ implies potential changes in the total stacking fault area. The simultaneous nucleation of two kink-pairs is then associated with a variation of the elastic interaction energy composed of three terms, ΔE_el = $$2\mathrm{\Delta }{E}_{{\xi }_n}+\mathrm{\Delta }{E}_{{\xi }_{1,2}}+\mathrm{\Delta }{W}_I$$. For each partial, $\mathrm{\Delta }{E}_{{\xi }_n}$ is taken from Equation (5(5) $$\mathrm{\Delta }{E}_{{\xi }_n}=\frac{\mu b_p^2}{2\pi }\left[\sqrt{w^2+h^2}-w-h+w\log \left(\frac{2w}{w+\sqrt{w^2+h^2}}\right)-\frac{1}{1-\nu }\left[w-\sqrt{w^2+h^2}+h\log \left(\frac{h+\sqrt{w^2+h^2}}{w}\right)-h\left[\log \left(\frac{h}{r_c}\right)-1\right]\right]\right]$$(5) ). $$\mathrm{\Delta }{E}_{{\xi }_{1,2}}$$ describes the variation in elastic energy between the partial lines (involving the interaction between segments K and K′, L and L′ in Figure 1(a)) and is given by Equation (8(8) $$\mathrm{\Delta }{E}_{{\xi }_{1,2}}=\frac{\mu b_p^2}{2\pi }\left[-2a^{\prime }-2\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-w_{k}log\left(\frac{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-w_k}{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+w_k}\right)+2\sqrt{w_k^2+d^2}+w_{k}log\left(\frac{\sqrt{w_k^2+d^2}-w_k}{\sqrt{w_k^2+d^2}+w_k}\right)\right]$$(8) ).(8) $$\mathrm{\Delta }{E}_{{\xi }_{1,2}}=\frac{\mu b_p^2}{2\pi }\left[-2a^{\prime }-2\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-w_{k}log\left(\frac{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-w_k}{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+w_k}\right)+2\sqrt{w_k^2+d^2}+w_{k}log\left(\frac{\sqrt{w_k^2+d^2}-w_k}{\sqrt{w_k^2+d^2}+w_k}\right)\right]$$(8)

ΔW_I, as given below by Equation (9(9) $$\mathrm{\Delta }{W}_I=\frac{\mu b_p^2}{2\pi \left(1-\nu \right)}\left[2\sqrt{w_k^2+d^2}-dlog\left(\frac{\sqrt{w_k^2+d^2}+d}{\sqrt{w_k^2+d^2}-d}\right)-\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}+\frac{1}{2}\left(d+a^{\prime }\right)log\left(\frac{\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}+\left(d+a^{\prime }\right)}{\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}-\left(d+a^{\prime }\right)}\right)-\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+\frac{1}{2}\left(d-a^{\prime }\right)log\left(\frac{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+\left(d-a^{\prime }\right)}{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-\left(d-a^{\prime }\right)}\right)\right]$$(9) ), corresponds to the contribution of elastic interactions between the kinks of both lines: ΔW_I = W_I(II′) + W_I(IJ′) + W_I(JJ′) + W_I(JI′), which reduces to ΔW_I = W_I(II′) + W_I(JJ′) under low stress conditions (where one can assume w_k = K ≪ H). Without any further assumptions on w₁ and w₂ or w_k, this scenario may include a variation in the stacking fault energy ΔW_sf = −2γa′w_k.(9) $$\mathrm{\Delta }{W}_I=\frac{\mu b_p^2}{2\pi \left(1-\nu \right)}\left[2\sqrt{w_k^2+d^2}-dlog\left(\frac{\sqrt{w_k^2+d^2}+d}{\sqrt{w_k^2+d^2}-d}\right)-\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}+\frac{1}{2}\left(d+a^{\prime }\right)log\left(\frac{\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}+\left(d+a^{\prime }\right)}{\sqrt{w_k^2+{\left(d+a^{\prime }\right)}^2}-\left(d+a^{\prime }\right)}\right)-\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+\frac{1}{2}\left(d-a^{\prime }\right)log\left(\frac{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}+\left(d-a^{\prime }\right)}{\sqrt{w_k^2+{\left(d-a^{\prime }\right)}^2}-\left(d-a^{\prime }\right)}\right)\right]$$(9)

4. Results

As mentioned in Sections 1 and 2, our model is applied to dissociated 〈1 1 0〉 screw dislocations in SrTiO₃ using the parameters given in Table 1 and the Peierls potential as given in Figure 2. The cut-off radius r_c (Equation (5(5) $$\mathrm{\Delta }{E}_{{\xi }_n}=\frac{\mu b_p^2}{2\pi }\left[\sqrt{w^2+h^2}-w-h+w\log \left(\frac{2w}{w+\sqrt{w^2+h^2}}\right)-\frac{1}{1-\nu }\left[w-\sqrt{w^2+h^2}+h\log \left(\frac{h+\sqrt{w^2+h^2}}{w}\right)-h\left[\log \left(\frac{h}{r_c}\right)-1\right]\right]\right]$$(5) )), used to quantify the intrinsic energy of dislocation line, is set to 0.56 Å, corresponding to ~10% of the complete Burgers vector b [18]. For a given applied stress, the metastable kink-pair configuration corresponds to a saddle point of the total energy variation ΔH given by Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) ). For uncorrelated nucleation, the variables h and w (characterising one kink pair) are considered and the critical configuration corresponds to the condition ∂ΔH/∂h = ∂ΔH/∂w = 0. For correlated nucleation, the metastable configuration is obtained by solving ∂ΔH/∂w₁ = ∂ΔH/∂w₂ = 0.

For uncorrelated nucleation, two different mechanisms can be distinguished: (1) forward motion of the leading partial, described by H_u,l1, followed by the forward migration of the trailing partial, corresponding to H_u,t2. Independently of the applied stress, we always find H_u,t2 ≪ H_u,l1, meaning that this sequence of events is governed by the nucleation on the leading partial. (2) Alternatively, the trailing partial may move first, associated with a critical energy H_u,t1, followed by the motion of the leading partial, characterised by H_u,l2. Independently of the applied stress, we always find H_u,t1 ≪ H_u,l2, i.e. this sequence is also limited by nucleation on the leading partial. In other words, uncorrelated kink-pair nucleation by which the leading partial starts to move is characterised by H_u,l1, whereas nucleation starting from the trailing partial is determined by H_u,l2. Furthermore, we always find that H_u,l1 ≫ H_u,l2 (as an example, with an applied stress of 0.2τ_p, H_u,l1 = 1.1 eV and H_u,l2 = 0.56 eV), i.e. the sequence (1) can be neglected and the uncorrelated process is always expected to start at the trailing partial (Figure 1(b)). Therefore, uncorrelated kink-pair nucleation will be essentially determined by H_u,l2, hereafter called H_u (Figure 3(a)). This is in agreement with what has been previously suggested by Möller [19] based on earlier theories of Celli et al. [28], Rybin and Orlov [29], and Hirth and Lothe [27]. For this uncorrelated scenario, saddle points are numerically found only at resolved shear stresses above a critical stress τ_c = 0.19τ_p = 95 MPa. On the contrary, we find that correlated nucleation of kink-pairs occurs for any resolved shear stress 0 < τ ≤ τ_p and involves a single critical energy H_c.

Figure 2. Peierls potential V_p and Peierls force Σ of 〈1 1 0〉{1 1 0} screw dislocations based on previous atomistic simulations [13,14] and calculated in the framework of the Peierls–Nabarro model. The Peierls stress τ_p = 500 GPa is equal to the maximum of Σ.

The evolution of the critical nucleation energies as a function of the resolved shear stress τ is presented in Figure 3(a) for correlated H_c (blue symbols) and uncorrelated kink-pair nucleation H_u (red symbols). Since the elastic interaction model is most accurate at low stress conditions [30], H_c and H_u are extrapolated in the whole stress range 0 < τ ≤ τ_p using a classical power-law relationship [31]. It can be seen in Figure 3(a) that the nucleation energy for uncorrelated kink-pair nucleation (H_u) becomes significantly smaller with increasing resolved shear stress above τ_c, which implies that 〈1 1 0〉 glide in the {1 1 0} plane is mainly controlled by uncorrelated kink-pair nucleation on the ½〈1 1 0〉 partials above τ_c, whereas glide below τ_c can only be the result of correlated kink-pair nucleation. Both Möller [19] and Takeuchi [32] already demonstrated that uncorrelated nucleation of kink-pairs is energetically favourable at τ ≥ τ_c, since only one pair of kinks needs to be formed at a time.

Regarding the critical kink-pair geometry, the critical height h associated with uncorrelated nucleation is found to be ~0.5a′ at τ_c and decreases monotonically with increasing stress following the same trend as in Koizumi et al. [18], Ritterbex et al. [33], and Ritterbex et al. [34]. The variation in critical kink-pair width w₁ and w₂ (Figure 1(a)) as a function of resolved shear stress is presented in Figure 3(b). The critical widths w₁ and w₂ are equivalent and large at lowest stress conditions and decrease rapidly to almost constant values near the critical stress τ_c, with a difference of about one order of magnitude in between. Large critical widths under low stress conditions are due to the interaction between kinks of opposite sign, which attract each other and tend to annihilate. Consequently, increasing the stress leads to a decrease in the critical kink-pair width [35]. On the other hand, the critical width w corresponding to uncorrelated kink-pair formation is found to be more or less constant at resolved shear stresses τ ≥ τ_c with a value close to 80 b_p. This shows that at lowest stress conditions, equivalent and very wide kink-pairs (K = K′ = L = L′ → 0 in Figure 1(a)) are nucleated on both individual partials with no stacking fault change due to the absence of sufficient work performed by the stress. With increasing stress, the kink-pair widths on both partials become progressively smaller with a difference in between converging to one order of magnitude. Above τ_c, the width of one of the kink-pairs tends to become as small as 5b_p whereas the other one is found to be in the same order of magnitude as the width associated with uncorrelated kink-pair nucleation (Figure 3(b)). The above suggests a continuous and progressive evolution from purely correlated to uncorrelated kink-pair nucleation with increasing resolved shear stress, due to a collapse of the kink-pair on the leading partial and because the nucleation of a single kink-pair is energetically more favourable above τ_c (Figure 3(a)).

5. Temperature dependence of the CRSS

Our model can be extended to describe the plasticity of SrTiO₃ that is controlled by glide of dissociated 〈1 1 0〉{1 1 0} screw dislocations. The CRSS is usually considered as the typical stress required for plastic flow. At low temperature, like the temperature regime A in SrTiO₃, the onset of plasticity is expected to be controlled by the mobility of individual dislocations. On the contrary, above a so-called athermal temperature T_a, plastic flow is limited by other mechanisms, e.g. dislocation–dislocation interaction. At low temperature, the constitutive equation describing the plastic flow is Orowan’s equation $\dot{\epsilon }=\rho bv$, relating the strain rate $\dot{\epsilon }$ to the dislocation density ρ and the dislocation mobility v.

In SrTiO₃, the mobility of 〈1 1 0〉 dissociated dislocations depends on both the rate of correlated kink-pair nucleation J_c and the rate of uncorrelated nucleation J_u. The average glide velocity v can be formulated as v = a′J_c for τ < τ_c and v = ½a′(J_c + J_u) for τ ≥ τ_c [19]. In the framework of the transition state theory (TST), the rate of kink-pair nucleation is expressed as J = J₀(τ) exp(−H(τ)/k_bT) with k_b the Boltzmann constant. The terms J and H stand for either J_c and H_c for correlated nucleation or J_u and H_u in case of uncorrelated nucleation (Figure 3(a)). The pre-exponential factor J₀ is taken from Guyot and Dorn [36] and consists of the following two contributions: (1) the vibrational frequency ν₀b_p/w of the partials with averaged critical kink-pair width w and (2) the number of potential nucleation sites L/cb_p with constant c as given in Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) ). Inserting the average velocity into Orowan’s equation, one finds $\dot{\epsilon }={\dot{\epsilon }}_{0}exp\left(-H(\tau )/k_{b}T\right)$. For a given strain rate (chosen here as $\dot{\epsilon }={10}^{-4}$ s⁻¹), the activation energy as a function of stress (Figure 3(a)) satisfies:(10) $$H\left(\tau \right)=C{k}_{b}T$$(10)

with $$C=\log \left({\dot{\epsilon }}_0/\dot{\epsilon }\right)$$ a constant under experimental conditions [37]. It is worth noticing that since Equation (10(10) $$H\left(\tau \right)=C{k}_{b}T$$(10) ) is verified, the stress τ corresponds by definition to the CRSS. To compute the evolution of CRSS as a function of temperature, according to Equation (10(10) $$H\left(\tau \right)=C{k}_{b}T$$(10) ), we use an average length of the partial lines $L=1/\sqrt{\rho }$. To fit with experimental results and microstructures, the effect of the dislocation forest on the plasticity has to be taken into account. This is done by introducing the experimental back stress τ_f = 50 MPa [7,12], and by adding to the results of our model the amount (T/T_a) × τ_f. This ensures that above the athermal temperature T_a = 600 K the CRSS does not vanish and remains constant with the value τ_f [7]. Consequently, the dislocation density is expressed as ρ = (τ_f /αμb_p)² with α = 0.1 [12,38].

Figure 4 presents the prediction of the CRSS as a function of T from our model. Our results for 〈1 1 0〉{1 1 0} slip describe a non-monotonic behaviour of the CRSS with decreasing T, split into three different regimes. Above 200 K, the correlated kink-pair mechanism alone allows SrTiO₃ to flow at low stress (regime labelled A₁ in Figure 4). As temperature decreases, this mechanism requires higher stresses (as depicted by the increase of CRSS in regime labelled A₂). Above a threshold stress of 95 MPa, the uncorrelated mechanism activates, and flow involves both correlated and uncorrelated mechanisms (regime A₃ in Figure 4). Overall, our model reproduces with good accuracy the behaviour experimentally observed by Brunner [7] (Figure 4).

Figure 3. (colour online) (a) Critical energy H plotted against resolved shear stress τ for correlated kink-pair nucleation (solid blue circles) H_c and uncorrelated kink-pair nucleation (open red circles) H_u under low(est) stress conditions. Solid blue and red curve correspond to the extrapolated fit [31] for correlated and uncorrelated kink-pair nucleation, respectively. (b) Critical kink-pair width w₁ (open circles) and w₂ (solid circles) in conjunction with correlated kink-pair nucleation as a function of resolved shear stress τ (see Figure 1(a)). Results at high stress are given by the extrapolated dotted line.

Figure 4. (colour online) Critical resolved shear stress (CRSS) plotted versus temperature at constant strain rate $\dot{\epsilon }$ of 10⁻⁴ s⁻¹ for thermally activated glide of (collinear) dissociated 〈110〉{1 1 0} dislocations. Experimental values from Castillo-Rodríguez and Sigle [12] are presented by black circles.

6. Discussion

The good agreement of our model with the experimental data suggests that the particular non-monotonic plastic behaviour of SrTiO₃ can be explained by a (progressive) change in 〈1 1 0〉{1 1 0} glide mechanism. Glide in regime A₁ is uniquely determined by nucleation of kink-pairs on both partials (correlated nucleation), which progressively evolves towards glide governed by nucleation of kink-pairs on one of the partials at a time in regime A₃ (uncorrelated nucleation). The abrupt increase in CRSS with decreasing T near 210 K in regime A₂ as inferred from experiments is assumed to be characterised by the transition from correlated to uncorrelated kink-pair nucleation (Figure 4). This change of mechanism is a direct consequence of the dissociation into ½ 〈1 1 0〉 partials. Alternatively, Castillo-Rodríguez and Sigle [12] explain this non-monotonic mechanical behaviour in terms of a transition from kink migration (long-segment limit) to kink-pair nucleation (short-segment limit) with decreasing T. However, their model does not explicitly take the dissociation of dislocations into account, implying that such a non-monotonic mechanical behaviour may occur even in materials where dislocations are non-dissociated. On the contrary, we explain the non-monotonic behaviour explicitly in terms of core dissociation. From our model it follows that this non-monotonic plastic behaviour results from the activation of different kink-pair nucleation mechanisms related to the dissociated state of dislocations under different stress conditions. This non-monotonic CRSS(T) evolution may be more or less pronounced depending on the properties of the extended cores, especially on the stacking fault energy (i.e. dissociation width between partials) which determines whether partials are strongly or weakly coupled and behave more like compact cores (monotonic plastic behaviour) or rather like two distinct but interacting partials (non-monotonic plastic behaviour). Our model predicts that extended cores with substantial dissociation width and low stacking fault energy favours the appearance of non-monotonic plastic behaviour. If cores become more compact by a decrease in dissociation width between the partials, the critical stress τ_c is found to increase leading to a smoother CRSS transition from correlated to uncorrelated kink-pair nucleation. The fact that SrTiO₃ exhibits a pronounced non-monotonic plastic behaviour in contrast to other types of perovskite is likely due to the dissociated state of the core of the active dislocations (large dissociation width and low APB energy). Comparable pronounced non-monotonic evolution of CRSS(T) may be found in other perovskites if their plasticity is governed by glide of dissociated dislocations with low stacking fault energies. Potential candidates may be potassium niobate (KNbO₃) [39] or barium titanate (BaTiO₃).

According to our model, regime A₂ should be marked by a transition from the correlated mechanism alone towards the contributions of both correlated and uncorrelated kink-pair nucleation, with the CRSS increasing as temperature decrease. This transition remains poorly described in our approach because the elastic interaction model relies on independent formulations of the total energy variation ΔH for correlated and uncorrelated kink-pair nucleation (Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) )). Our results of the critical kink-pair width (Figure 3(b)) clearly suggest the evolution from purely correlated nucleation to evolve progressively towards uncorrelated kink-pair nucleation starting from the trailing partial (with the collapse of one of the kink-pairs at resolved shear stress close to τ_c). However, our discontinuous model set-up does not allow for this collapse to occur. Moreover, for correlated nucleation of two kink-pairs, we chose to parameterize Equation (1(1) $$\mathrm{\Delta }H\left(h,w\right)={\mathrm{\Delta }E}_{\mathit{el}}\left(h,w\right)+c\mathrm{\Delta }P\left(h,w\right)+\mathrm{\Delta }{W}_{\mathit{sf}}\left(h,w\right)-c{W}_{\tau }(h,w)$$(1) ) with variable widths w₁ and w₂ on each partial, considering a constant kink-pair height of h = a′ in regime A₁ and A₂ (blue curve in Figure 4). This assumption is valid under the low stress conditions of regime A₁, but the kink-pair height generally decreases monotonically with increasing stress [18]. Indeed, the model solution of the critical kink-pair height for uncorrelated nucleation at τ_c is found to be equal to ~0.5a′. This suggests inaccurate model solutions for the evolution of CRSS(T) in regime A₂ (near τ_c) in relation to correlated kink-pair nucleation. The above may explain the discrepancy between our model and experimental results in regime A₂. Nevertheless, our model allows to interpret the strong CRSS(T) gradient observed experimentally in regime A₂ as the transition from correlated to uncorrelated kink-pair nucleation with decreasing T. In addition, purely uncorrelated kink-pair nucleation cannot occur just below the critical stress τ_c. To maintain the opening of the critical kink-pairs, at a stress close to τ_c, a small decrease in thermal activation (i.e. decrease in T) may require a strong increase in CRSS. Overall, the evolution of CRSS(T) obtained from our model is able to reproduce satisfyingly the experimental data both qualitatively and quantitatively.

7. Conclusion

We derived an analytical model describing the motion of 〈1 1 0〉 screw dislocations in SrTiO₃, based on kink-pair nucleation. Because these dislocations are dissociated, their motion may occur either by simultaneous (correlated) nucleation of kink-pairs on both partial dislocations, or by consecutive (uncorrelated) nucleation of a kink-pair on one partial, followed by nucleation of another kink-pair on the other partial. The estimation of activation energies for these mechanisms show that at low stress, the correlated mechanism is the only one to be thermally activated, while at high stress both correlated and uncorrelated mechanisms occur. Nucleation rates, estimated from TST, allow to derive the evolution of the CRSS as a function of temperature. Low temperature plasticity of SrTiO₃ is then characterised by a non-monotonic evolution of the CRSS, in agreement with experimental results. This suggests that the non-monotonic plastic behaviour of SrTiO₃ in the low temperature regime A arises from the occurrence of dissociated dislocation cores. Our model can be extended to other materials for which plastic flow is dominated by glide of dissociated dislocations. For such materials, a non-monotonic behaviour of the CRSS can be thus anticipated. It can be remarkably pronounced depending on the material properties such as elastic properties or stacking fault energies.

Acknowledgements

We would like to kindly thank M. Castillo-Rodríguez for making the experimental data set of Brunner [7] available to us.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the European Research Council under the Seventh Framework Programme (FP 7), ERC [grant number 290424 RheoMan].