3D DDD modelling of dislocation–precipitate interaction in a nickel-based single crystal superalloy under cyclic deformation

Abstract

Strain-controlled cyclic deformation of a nickel-based single crystal superalloy has been modelled using three-dimensional (3D) discrete dislocation dynamics (DDD) for both [0 0 1] and [1 1 1] orientations. The work focused on the interaction between dislocations and precipitates during cyclic plastic deformation at elevated temperature, which has not been well studied yet. A representative volume element with cubic γ′-precipitates was chosen to represent the material, with enforced periodical boundary conditions. In particular, cutting of superdislocations into precipitates was simulated by a back-force method. The global cyclic stress–strain responses were captured well by the DDD model when compared to experimental data, particularly the effects of crystallographic orientation. Dislocation evolution showed that considerably high density of dislocations was produced for [1 1 1] orientation when compared to [0 0 1] orientation. Cutting of dislocations into the precipitates had a significant effect on the plastic deformation, leading to material softening. Contour plots of in-plane shear strain proved the development of heterogeneous strain field, resulting in the formation of shear-band embryos.

Keywords:

• Dislocation–precipitate interaction
• representative volume element
• crystallographic orientation
• dislocation structures
• precipitation
• slip bands

1. Introduction

Nickel-based superalloys are widely applied as rotating turbine blades and discs in the hottest sections of gas turbine engines. Their exceptional mechanical properties at high temperature are due to the coherent double-phase microstructure, i.e., a L1₂-ordered -precipitate phase and a ductile -matrix phase. The precipitates, dispersed in the -matrix, play a significant role in increasing the strength and enhancing the fatigue and creep behaviour of the alloys at elevated temperature [1–3]. In order to achieve further improved mechanical properties, new development of nickel-based superalloys is normally pursued by increasing the volume fraction. For instance, the volume fraction may reach above 70% for the latest single crystal nickel alloys. Nickel-based superalloys are often subjected to severe cyclic or sustained loads in harsh environments, thus a reliable characterisation and prediction of their mechanical behaviour at high temperature, such as plastic deformation under low cycle fatigue, is critical in order to accurately assess damage tolerance of their components.

Discrete dislocation dynamics (DDD) has been developed during recent years to study plastic deformation in metals and alloys by directly modelling the evolution of collective dislocation segments. The DDD model can simulate dislocation motion, multiplication and interaction under applied loading conditions. For instance, Déprés et al. [4] modelled local plastic deformation of AISI 316L steel by 3D DDD simulations during low cycle fatigue. They confirmed that dislocation cross-slip played the crucial role for the initial strain spreading within the grain and also the subsequent strain localisation for forming slip bands. Huang et al. [5] studied crack-tip deformation of a polycrystalline nickel-base superalloy under model I cyclic loading condition using 2D DDD simulations. Results showed that the ratchetting strain ahead of the crack tip is associated with dislocation accumulation, climb and penetration across grain boundaries, amongst which dislocation climb seems to be the dominant mechanism for the cases studied at elevated temperature. 3D DDD simulations were also carried out to study strain hardening in Al-TiN nanolayered composites [6]. When the layer thickness ratio kept constant, the rate of strain hardening was caused by plastic incompatibility solely and independent of dislocation density and layer thickness. On the other hand, the yield stress of the composites showed a strong size effect, i.e., the dependence of yield stress on the thickness of Al layer (significant increase of yield stress was observed with the decreasing thickness of Al layer when the layer thickness ratio kept unchanged).

The DDD approach is able to model the interaction between dislocations and material microstructures explicitly, including the formation of heterogeneous dislocation networks such as slip bands. Huang et al. [7] and Hafez Haghighat et al. [8] simulated dislocation network formation in nickel-base single crystal superalloys during monotonic loading, showing that the movement of dislocations was in the γ channels and close to the γ′ cubes, and most dislocation segments were deposited on the γ/γ′ interfaces to form the dislocation network. Shin et al. [9] modelled fatigue deformation in precipitation hardened metals, with a fixed precipitate volume fraction (14%). They showed that large monomodal precipitates (radius ) caused only a small effect on the material’s cyclic response. For small monomodal precipitates (radius ), strain localised into persistent slip bands (PSBs) with features similar to single phased materials and a large effect on the cyclic mechanical response (evolution of the stress amplitude) was found in the initial loading cycles. In grains with a bimodal precipitate, the simulated mechanical behaviour (such as stress–strain behaviour, PSBs, dislocation densities and cyclic response) fell between the above two cases. Yashiro et al. [10] studied dislocation shearing into γ′ precipitates by applying a back-force model, and the model was used to explore the dependence of precipitate-shearing resistance on the dislocation spacing in the interfacial dislocation network for nickel-base superalloys.

In nickel alloys, precipitates play a very important role in obstructing dislocation motion and high volume fraction of γ′ precipitates tend to confine dislocations in the narrow channels of the γ phase, resulting in increased material strength. In fact, Rao et al. [11] conducted discrete dislocation simulations to study the influences of volume fraction on critical resolved shear stress (CRSS) needed to overcome the precipitate barrier. Their simulation results showed that the CRSS varied with the square root of the precipitate volume fraction. Vattré et al. [12] also demonstrated that the CRSS increased strongly with the increase in precipitate volume fraction when the average spacing of precipitates was kept constant. However, the existing 3D DDD simulations are largely limited to monotonic loading condition, without considering the effect of loading reversal. In this paper, 3D DDD was performed to gain a better understanding of dislocation–microstructure interaction under cyclic deformation of a nickel-based single crystal superalloy at high temperature (850 °C). A representative volume element (RVE), with γ′ cubic precipitates of 70% volume fraction, was chosen to represent a Ni-based single crystal superalloy, on which a periodic boundary condition was enforced. A back-force model was applied to simulate the cutting of superdislocations into precipitates. Detailed studies on dislocation evolution during cyclic loading were conducted for both [1 1 1] and [0 0 1] orientations. The dislocation-dynamics induced plastic deformation and the corresponding dislocation networks were then discussed, including the cutting of superdislocations into precipitates and the formation of shear-band embryos.

2. 3D DDD simulation methodology

2.1. Peach–Kohler force calculation

In 3D DDD model, a dislocation network of arbitrary topology is represented by sets of nodes which are connected to form straight segments with non-zero Burgers vectors. The evolution of dislocation segments was dependent on the motion of dislocation nodes. The Peach–Koehler (PK) force controls the motion of dislocation nodes and can be calculated by [13]:(1)

where F_i is the Peach–Koehler (PK) force acting on dislocation segment i, N is the total number of dislocation segments, ξ_i is the line sense vector, and F_i,i+1 and F_i,i-1 are the interaction forces between dislocation segments i and i + 1 and i and i − 1, respectively, which are computed by following the method presented in Zbib et al. [13] and Hirth and Lothe [14], is long range stress from a remote segment j and σ^app is externally applied stress on segment i.

During a simulated time increment, the glide velocity for each dislocation segment, , was governed by:

(2)

where is the glide component of the PK force F_i, τ_int is an internal stress caused by the anti-phase boundary in γ′ precipitate, τ_F is the friction stress in the γ phase, B is the drag coefficient and is the absolute value of x.

For efficient computation of the PK force F_i in Equation (1(1) ), the RVE was further partitioned into a series of equal-sized subcells. For dislocations within a subcel and its neighbouring subcells, their contributions to PK force on dislocation i were calculated at the centre of the dislocation segment i directly, and for dislocations in remote subcells, their contributions to PK force were calculated at the centre of the subcell which contains the dislocation segment i. The dislocation stress field in Equation (1(1) ) was calculated by applying the analytical Hirth and Lothe formulation [14]. In addition, the interaction stresses between dislocations in remote subcells were calculated from a multipole expansion method, which reduces the computational cost. Also in order to further improve the efficiency of computing, a parallel OpenMP interface was utilised to calculate the long-range stresses.

In the precipitates, when the screw superdislocations on the octahedral slip planes cross slip to {1 0 0} planes, a Kear–Wilsdorf (KW) lock was introduced to hinder the dislocation motion. In this paper, a KW unlocking stress τ_KW, acting as a friction stress in the precipitates and corresponds to the term τ_F in Equation (2(2) ), was used to consider the KW locks and can be expressed as [12]:

(3)

where f_D is a Debye frequency factor, l_s is the length of the screw dislocation segment, ΔH₀ is the activation enthalpy for KW locks, T is the absolute temperature and k is the Boltzmann constant. The KW lock inside the precipitates was not simulated directly but considered by a KW unlocking stress τ_KW, which has a constant value of 425 MPa as calculated from Equation (3(3) ).

In nickel-based single crystal superalloys with high precipitate volume fraction, TEM imaging revealed that dislocation–precipitate interactions may result in shearing of precipitate by dislocation pairs separated by anti-phase boundary (APB), i.e., superdislocation [15,16]. Based on these experimental observations, a back-force model suggested by Yashiro et al. [10] was applied to simulate precipitate shearing by series of superdislocations explicitly. When a leading dislocation cuts into a precipitate, it leaves an antiphase boundary (APB) on the slip plane with a back force F_b (equals to antiphase boundary energy χ_APB) acting on it. Meanwhile, a follow-on trailing dislocation on the same slip plane is attracted by F_b and enters the precipitate subsequently. The leading and the trailing dislocations form a superdislocation which glides in the precipitate. The following criterion was applied in the 3D DDD code to decide whether the dislocation entering the γ′ phase is a trailing or a leading dislocation [7]:

•	If Fapp∙Fint ≥ 0 and abs(Fint) > 0.25χAPB, the dislocation is a leading dislocation;
•	If Fapp∙Fint < 0 and abs(Fint) > 0.25χAPB, the dislocation is a trailing dislocation.

Here, represents the inherent APB energy density, is the glide force caused by the externally applied load and is the dislocation–interaction stress computed at the centre of the dislocation segment i. They are defined by the following two equations:

(4) (5)

where n is the normal vector of the slip plane of dislocation segment i, σ_app is the externally applied stress and σ_int is the centre stress of dislocation segment i induced by an interacting dislocation. Also, the back force (F_b, per unit length), acting on the pair of superdislocations (i.e. leading and trailing dislocations) cutting into the precipitate, literally corresponds to τ_intb_i in Equation (2(2) ), i.e., .

2.2. DDD short/long range interactions

The interactions of dislocations are very important because of their influence on the mobility of dislocations and hence on the plastic deformation of crystals. Broadly, the interaction can be classified as either short range or long range. The local interactions between dislocations with a small distance (core level) are described by short-range interactions. Basically, when the distance between two dislocations is close to the size of the core where the elasticity field is not valid anymore and short-range interaction occurs [17]. In the present DDD model, short-range interactions included the formation of jogs and junctions as well as the annihilation of dislocations. Long range interactions are defined here as non-contact elastic interactions between dislocation segments in a three-dimensional microstructure. Modelling of the interacting dislocation segments in a large model is far too computationally expensive, since the computation every step would be proportional to the square of dislocation segment numbers. The multipolar expansion method is a numerical technique [13] developed to reduce the order of computation to N_s log without losing the required accuracy. In this method, the dislocations far away from the point of interest are grouped into a set of equivalent monopoles and dipoles. For numerical implementation, one would divide the 3D cell into a number of subcells, and the dislocations in each subcell are grouped into monopoles and dipoles whose far stress field can then be computed more efficiently using the multipolar expansion method.

In particular, the mechanisms of cross-slip and collinear annihilations have been implemented in the 3D DDD code. The cross slip of screw dislocation was determined numerically using a Monte-Carlo type simulation [18], and the collinear annihilations of dislocations AB and CD are possible if short-range interaction is possible and and b_AB + b_CD = 0 (or and b_AB − b_CD = 0). Here, b is the Burgers vector and ξ is the dislocation line sense vector [17]. Our simulations showed that cross slip (threshold stress for cross slip was chosen to be 122 MPa) leads to softer stress–strain response and higher dislocation densities, which is consistent with the DDD simulation results for single-crystal nickel by Zhou et al. [19].

2.3. Evaluation of plastic strains and computation of external stress

Glide of many dislocations results in plastic deformation in crystalline materials. The motion of each dislocation segment produces plastic deformation, which is associated with the macroscopic plastic strain . In the 3D DDD model, a homogeneous macroscopic stress state is assumed in the RVE, and thus a macroscopic plastic strain is computed by [20](6)

where dA represents the area incrementally swept over by the segment of dislocation, n_i is the vector normal to the glide plane, V is the volume of the RVE and A_slip is the collection of deforming surfaces. Equation (6(6) ) describes the rigorous relationship between the macroscopic plastic strain and the dislocation motion.

If the external load is applied along the z axis of the RVE with a strain rate of , the total strain along the loading axis should be:(7)

By referring to Equations (6(6) ) and (7(7) ), the elastic strain is written as:(8)

Then, the time-dependent external stress is:(9)

where E is the Young’s modulus.

2.4. RVE model

Representative volume elements (RVE) containing 1, 8 and 27 cubic precipitates, as sketched in Figure 1, were built, representing a new-generation nickel-based single-crystal superalloy MD2. The RVE has a precipitate volume fraction of 70% and a channel width of 0.0475 μm. The γ′ volume fraction in MD2 was estimated based on the assumption that the γ′ precipitate is perfectly cubic. Periodical boundary conditions (PBCs) were imposed on dislocation movement which is critical in 3D DDD simulations and should always be considered. Basically, when a dislocation leaves the RVE from one side, it enters the RVE from the opposite side to maintain the continuity of dislocation lines [21]. The corresponding elastic stress fields were calculated directly from the updated dislocation networks. In addition, the elastic stress field induced by imaging dislocations in the rest of periodical RVEs were considered by the multipolar expansion method [13]. Transmission electron microscopy (TEM) observations have revealed that dislocations are initially contained in the γ matrix, whereas no dislocations were found in the γ′ precipitates [22]. Also, the TEM observations [23,24] demonstrated that dislocation motion was not found on cubic slip planes. Consequently, in this work random initial dislocations were distributed on 12 octahedral slip systems in γ phase as Frank-Read sources. These initial dislocations are also randomly oriented on the slip plane. The dependency of initial dislocations on loading axis was not considered in this work. When an initial length of dislocation sources is less than γ channel width, unreal macroscopic mechanical behaviour is produced [25]. To prevent such issues, the initial lengths of all dislocation sources were set to be 0.0875 μm (>channel width of 0.0475 μm). The initial dislocation density of nickel-based superalloy adopted in previous 3D DDD simulations [7,8,25,26] ranged from 1.4 × 10¹² to 6.7 × 10¹³ m⁻². In this study, the initial dislocation density was chosen to be 2.5 × 10¹³ m⁻², which fell within the range reported in literature.

Figure 1. (colour online) RVEs with (a) 1, (b) 8 and (c) 27 precipitates, where initial Frank-Read dislocation sources are randomly distributed in the -phase matrix.

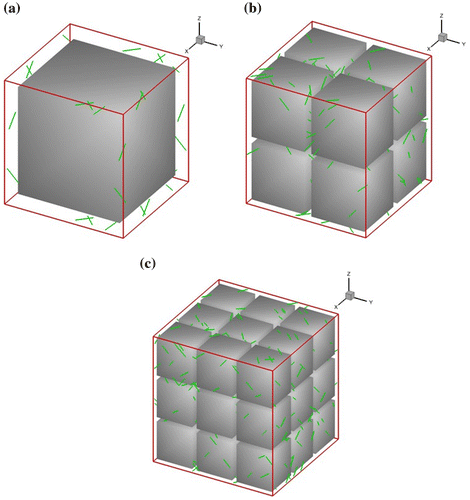
Both the and phases were treated as isotropic and have the same elastic constants (modulus and Poisson’s ratio). Due to the PBCs imposed to the RVE, portions of dislocation loops may self-annihilate to reduce the mean free-path of dislocations [27], which may affect the microstructure arrangement as well as the strain hardening behaviour. To avoid these, a non-perfect cubic shape is applied to the RVE. The dimensions of the RVE with 1, 8 and 27 precipitates are 1420b × 1500b × 1580b, 3220b × 3380b × 3540b and 4830b × 5070b × 5310b, respectively (see Figure 1), corresponding to 70% precipitate volume fraction and a channel width of 190b (0.0475 μm), where b is the Burgers vector magnitude.

2.5. Contour plot of maximum plastic shear strain

The RVE is divided into equal-sized sub-cells in 3D DDD model, and the plastic strain produced by the dislocation segments in sub-cells is computed at the centre of each sub-cell in the 3D DDD simulations. The plastic strain at nodes of sub-cells was calculated by a written post-processing program in the present study. The plastic strain at a node k is computed by averaging the plastic strains at the centre of all sub-cells sharing the node k:

(10)

where n is the number of neighbouring sub-cells sharing the node k, is the plastic shear strain at the centre of the mth sub-cell.

Then the maximum plastic shear strain is computed by:

(11)

where i and j refer to coordinate axes. In the present simulation, we used Equation (11(11) ) to calculate the in-plane maximum plastic shear strain on the surface of the 3D RVE model. The contour plot of maximum plastic shear strain can be created easily with the assistance of commercial software Tecplot once the nodal values are determined by Equations (10(10) ) and (11(11) ).

3. Results

3.1. RVE size and model parameter identification

Using the 3D DDD framework given in the above section, numerical analyses were conducted for three RVEs, consisting of 1, 8 and 27 precipitates with randomly distributed Frank–Read dislocation sources in the γ-phase matrix as shown in Figure 1. The stress–strain response and the dislocation density evolution for the RVEs with different number of precipitates were compared in Figures 2 and 3 for both [0 0 1] and [1 1 1] orientations. It was seen that a good convergence was achieved for an 8-precipitate RVE, especially for the evolution of dislocation density. Consequently, a RVE with 8-precipitates was adopted in our simulations.

Figure 2. (colour online) Stress–strain response for RVEs with different number of precipitates for (a) [0 0 1] orientation; (b) [1 1 1] orientation.

Figure 3. (colour online) Dislocation density against time for RVEs with different number of precipitates for (a) [0 0 1] orientation; (b) [1 1 1] orientation.

To determine the DDD model parameters for the actual material (MD2), we adopted a fitting procedure based on iterative simulations of monotonic and cyclic stress–strain responses for both [0 0 1] and [1 1 1] orientations. Prior to the fitting process, some fundamental material parameters such as Poisson’s ratio and modulus were directly obtained from experimental measurements. Initial values of other dislocation-dynamics related parameters were estimated based on the literature [7,26]. Following each simulation, the stress–strain responses were obtained and compared with those measured experimentally to assess the difference. This essentially is an inverse parameter-fitting process. Basically, we manually change the values of the parameters until the simulated stress–strain responses matched the low-cycle-fatigue test data for both [0 0 1] and [1 1 1] orientations. Here, we focused on monotonic and the first cycle of fatigue loading. The procedure consisted of a series of iterations until an acceptable agreement was achieved between model simulations and experimental data. The material parameters obtained for 3D DDD simulations are given in Table 1, where the elastic moduli for [0 0 1] and [1 1 1] orientation were taken from the linear part of the stress–strain responses. Shear modulus for [1 1 1] orientation was also calculated using the following equation [28]:(12)

Table 1. The parameters used in 3D DDD simulations.

Orientation	[0 0 1]	[1 1 1]
Young’s modulus (GPa)	99.3	247.3
Poisson ratio	0.402	0.24
APB energy (mJ/m^2)	150
Drag coefficient (Pa s)	1.0e–4
KW unlocking stress (MPa)	425
Friction stress in γ phase (MPa)	180

where

Here, E_{[0 0 1]} and v_{[0 0 1]}are the elastic modulus and Poisson’s ratio in [0 0 1] orientation, respectively. For single crystals, the elastic modulus in [1 1 1] orientation is higher while the corresponding shear modulus is lower when compared to those in [0 0 1] orientation [29]. In the code, the shear modulus G_{[1 1 1]}, calculated as 43.7 GPa, was used for calculations of Orowan stress and critical resolved shear stress, which control the dislocation glide on {1 1 1} slip planes.

Experimental stress–strain responses were obtained from our own low-cycle-fatigue tests. The tests were carried out using standard cylindrical specimens (a diameter of 6.4 mm and a gauge length of 36.5 mm) at a temperature of 850 °C which reflects the typical working environment of nickel superalloys. The specimens were subjected to strain-controlled cyclic loading, with 2 s–2 s–2 s–2 s (2 s dwell at both maximum and minimum load levels) and 200 s–200 s–200 s–200 s (200 s dwell at both maximum and minimum load levels) loading waveforms, for both 〈0 0 1〉 and 〈1 1 1〉 directions. The maximum level of strain applied to the specimen was 1%, with a strain ratio of -1.

3.2. stress–strain response

The simulated macroscopic stress–strain responses by the DDD model under monotonic and cyclic loading (1st cycle) are presented in Figure 4(a) and (b) for [0 0 1] and [1 1 1] orientations, respectively, in a direct comparison with the experimental results. It is noted that the model simulations have a good agreement with the experimental data for the two cases. Both the stress–strain responses and the shape of cyclic loops were captured by 3D DDD model. Results exhibited the narrow hysteresis loop for the [0 0 1] orientation, which demonstrated the very limited amount of plastic deformation for this orientation. While for the [1 1 1] orientation, the stress–strain loop is much fatter (see Figure 4(b)), indicating considerably more plastic deformation in the alloy for this orientation. It is noted from Figure 4(b) that the present 3D DDD model could not capture the strain hardening behaviour very well followed by load reversal in the [1 1 1] loading direction, which may be attributed to a lack of additional hardening mechanisms for the material. In nickel-based single crystal superalloys, majority of dislocations are deposited at the γ/γ′ phase interfaces rather than in the γ channels, which is also the dominant hardening mechanism. There is an absence of additional hardening mechanisms such as Taylor hardening. Specifically, a generalised form for Taylor hardening can be written as [30], for which the coefficients are the components of a matrix that describe the average interaction strength between slip system m and slip system n, and they are related with the formation of dislocation junctions and jogs. This implies that the formation of junctions and jogs will lead to high hardening rate, as also reported in Rhee et al. [17]. However, as reported in our previous work [7], the density of dislocations with jogs and junctions (5.2 × 10¹¹ and 6 × 10¹³ m⁻² at 0.4% plastic strain) are two to four orders less than the total dislocation density 1.25 × 10¹⁵ m⁻² for nickel-based superalloys. Basically, junction and jog dislocations make negligible contributions to the total dislocation density in nickel-based superalloys, indicating an absence of Taylor hardening. This is also the case for our current simulations.

Figure 4. (colour online) Cyclic stress–strain response simulated with 3D DDD model at for (a) [0 0 1] and (b) [1 1 1] orientations.

3.3. Evolution of dislocation networks

Dislocation networks developed at different loading stages are shown in Figures 5 and 6 for [0 0 1] and [1 1 1] orientations, respectively. During the loading stage, the initial dislocation segments of Frank-Read sources are activated and tend to bow out (i.e. multiplication process) when an applied resolved shear stress exceeds a critical value [31]. The activated dislocations in the slip plane can climb over, shear or loop around precipitates, which results in the deposition of most dislocation segments on the γ/γ′ interfaces. These deposited dislocations constituted a type of dislocation network, in which dislocation lines are normal to each other, as shown in Figures 5 and 6, consistent with the TEM observation by Tian et al. [32]. These dislocations on the γ/γ′ interfaces can cause high internal back stresses that lower the PK force and subsequently the dislocation mobility in the channels, leading to strain hardening. When the applied stress is reduced (the unloading stage), the dislocation loop tends to shrink due to the reduction of dislocation line tension and some of the deposited segments would disappear if not hindered [33]. Moreover, the mutual dislocation annihilation can happen during the reversed loading stage [34]. Therefore, a reduction of dislocation density, as shown in Figures 5 and 6, is a direct outcome of the annihilation and shrinkage of dislocations.

Figure 5. (colour online) Dislocation networks for [0 0 1] orientation at (a) time = 1 s, (b) time = 4 s, (c) time = 5 s, (d) time = 8 s and (e) time = 9 s.

Figure 6. (colour online) Dislocation networks for [1 1 1] orientation at (a) time = 1 s, (b) time = 4 s, (c) time = 5 s, (d) time = 8 s and (e) time = 9 s.

It is noted that simulated dislocation density was much higher for the [1 1 1] orientation (compared with the density for [0 0 1] orientation), which is because cross slip and junction formation take place more easily for [1 1 1] orientation [35]. The evolution of dislocation density has a direct influence on plastic strain or plastic deformation, and a lower yield stress is shown for [1 1 1] orientation which is associated with the higher density of dislocations for this orientation (compared to [0 0 1] orientation). This also reflects different Schmid factors for these two orientations. From the Orowan formula (), which relates the plastic strain rate to the mobile dislocation density ρ, Burgers vector magnitude b, and average dislocation velocity v, the higher density of mobile dislocations would result in a softer response due to the increasing plastic strain rate, and, consequentially, reduce the flow stress. Our work showed that dislocation networks for both [0 0 1] and [1 1 1] orientations are similar to those reported in Vattré’s work [25]. For the [0 0 1] orientation, dislocations deposited on the surface of precipitates form a network and are normal to each other; for the [1 1 1] orientation, due to the multiplication of dislocations in one single crystallographic direction, the dislocations on the surface of precipitates are restricted to one direction. On the other hand, this work showed that [1 1 1] orientation had a significantly higher dislocation density than [0 0 1] orientation (as opposed to the results in Vattré et al. [25]), which is consistent with the more severe plastic deformation observed experimentally for the [1 1 1] orientation (Figure 4). It should be noted that Vattré et al. [25] used the same modulus for [0 0 1] and [1 1 1] orientation in their simulations. In fact, [1 1 1] orientation has much higher modulus than [0 0 1] orientation (i.e. 247.3 GPa for [1 1 1] and 99.3 GPa for [0 0 1]) and also experiences more plastic deformation. This is measured by our experiments, but not reflected in Vattré et al. work [25]. In our work, we used the correct modulus which was able to capture the behaviour.

3.4. Contour plot of maximum shear strain

To examine shear-related material deformation behaviour, contour plots of the maximum shear plastic strain were also produced for both [0 0 1] and [1 1 1] orientations at a total strain of 1% and shown in Figure 7(a) and (b), respectively. Again, the simulations showed heterogeneous shear deformation at precipitate level. It was particularly noted that shear-band embryos were formed in the RVE, with an inclination of 45° with respect to the loading direction (z-axis). Here, we used shear-band ‘embryos’ to reflect the modest RVE size (0.355 × 0.375 × 0.395 μm) used in our simulations (due to the high computing cost for 3D DDD simulations). The shear-band embryos developed with a characteristic orientation and a regular spacing, similar to those observed in f.c.c. polycrystalline metals using digital image correlation method [36]. Due to more plastic deformation developed for the [1 1 1] orientation the intensity of shear deformation in the shear-band embryos is much stronger for [1 1 1] orientation than that for [0 0 1] orientation. These shear-band ‘embryos’ will eventually develop into shear bands at large scale. This has been confirmed by our 2D DDD simulations using a larger RVE (3 × 3 μm²), showing a direct correlation between dislocation networks and shear bands. Basically, ‘bands’ of localised high-density dislocations tend to develop along certain slip planes, which are discrete and accommodate a significant amount of shear strain. They also appear as shear bands in the contour plots of maximum in plane shear strain.

Figure 7. (colour online) Maximum-shear plastic strain contour at strain = 1% for (a) [0 0 1] and (b) [1 1 1] orientations.

4. Discussions

4.1. Dislocation-precipitate interaction

Discrete dislocation dynamics and its computer simulation have advanced significantly over the past two decades, where such important features as dislocation intersection, slip geometry, multiplication, line tension effects and cross-slip have been successfully modelled to simulate dislocation patterning observed in experiments. However, almost all studies are limited to isotropic and homogeneous media, and the interactions between dislocations and material microstructure, which is the major source for heterogeneous dislocation arrangements and the generation of internal stress concentration and initiation of cracks, is generally excluded for simplicity. One of our aims is to understand how the dislocation–microstructure interaction affects the global stress–strain behaviour during plastic deformation, which cannot be captured by the classical continuum model (e.g. crystal plasticity).

To illustrate this, DDD simulaitons were carried out for RVE without precipitates for both [0 0 1] and [1 1 1] orientations. For like-to-like comparison, the DDD parameters and the initial dislocation distributions were kept exactly the same as the RVEs with precipitates. The stress–plastic strain curves obtained are shown in Figure 8, in direct comparison with those for RVEs with precipitates. It was noted that stress–plastic strain response for RVE without precipitates has a sharp drop after the initial elastic stage and is well below those for RVE with precipiates. Following a sharp drop, the stress tends to reach a steady level for both [0 0 1] and [1 1 1] orientations and no further strain hardening occurs. This confirms that the strength of nickel alloys is mainly controlled by the dislocation–precipitates interaction, especially the accumulation of dislocation loops at the matrix–precipitate interfaces. These accumulated dislocation loops form a strong network and make the mobile dislocations more difficult to bow-out between the precipitates, leading to significant strain-hardening effect [37,38]. As also demonstrated in Huang et al. [7], the morphology of precipitates also affects the evolution of dislocation networks in the matrix channel, leading to alteration of mechanical behaviour of the material. The effect of varied internal microstructure features (e.g. volume fraction, shape and morphologies of precipitates) on material behaviour will be further studied in future research.

Figure 8. (colour online) Stress–strain response with and without precipitate for (a) [0 0 1] and (b) [1 1 1] orientations.

4.2. Shearing of precipitates by superdislocations

The simulated stress–plastic strain responses for single-precipitate RVE along [0 0 1] and [1 1 1] orientations are presented in Figure 9 for the cases with and without introducing precipitate shearing in the 3D DDD model. It can be seen that shearing of precipitates had a great effect on the stress–strain response for both [0 0 1] and [1 1 1] orientations, and three-stage deformation (elastic, hardening and softening stages) was observed (Figure 9). During the elastic stage, since the initial sources of dislocations in the γ channels are not activated or just move slightly to the γ/γ′ interfaces, both the γ and γ′ phases remain elastic and no plastic deformation or increase of dislocation density is expected. When the resolved shear stress on the slip systems exceeds the critical shear stress, dislocations bow out and the initial yielding occurs. With the increase of load level, more Orowan dislocation loops are produced and most of them are deposited at the γ/γ′ surface, which results in strain hardening, i.e. the second stage deformation. With further increase of strain level (beyond ~1%), shearing of precipitates by superdislocations occurred, which reduced the resistance of the material to further slip and produced a softer mechanical response of the material [39,40]. Based on our simulations, it is concluded that the shearing of precipitates by dislocations is a major cause of the softening behaviour of nickel superalloys, especially at high strain levels. These findings have also been observed in experimental studies [22,41–43].

Figure 9. (colour online) Stress–strain response with and without shearing of precipitate by dislocations for (a) [0 0 1] and (b) [1 1 1] orientations.

As mentioned in Section 2.1, precipitates are generally sheared by a series of superdislocations formed by leading and trailing dislocations. When a leading dislocation enters into the precipitate, it destroys the L1₂ order in the slip plane, thus creating an antiphase boundary (APB) [44]. The following trailing dislocation moving on the same slip plane intends to restore the initial L1₂ structure. We checked the dislocation networks of single-precipitate RVE under monotonic loading conditions (strain rate = 1%/s and strain level = 2%), and superdislocations clearly sheared into the precipitate for both [0 0 1] and [1 1 1] orientations at strain levels of 1 and 2%, as shown in Figures 10 and 11. It is noted that, when loading level reached to a higher value, more superdislocations sheared into the precipitate, which further demonstrated that precipitate shearing resulted in the softening of material’s stress–strain response.

Figure 10. (colour online) Shearing of dislocations into precipitate for [0 0 1] orientation at: (a) strain = 1% and (b) strain = 2%.

Figure 11. (colour online) Shearing of dislocations into precipitate for [1 1 1] orientation at: (a) strain = 1% and (b) strain = 2%.

In fact, TEM images have confirmed that the precipitates were cut by superdislocations for nickel-based superalloys, especially at elevated temperature and increased loading level [15,16]. For example, TEM study in Grant et al. [16] revealed that the precipitates were cut by series of superdislocations for a nickel-based superalloy tested under tensile loading at 500 °C (with a strain rate of 10⁻⁴/s). Cui et al. [45] studied the creep deformation mechanisms of a nickel-base superalloy, and pointed out that, at low temperature region, the favourable deformation mechanism for shearing of γ′ precipitates was dominated by stacking faults. However, it changed to antiphase boundaries (APBs) shearing (e.g. superdislocations) at high temperatures. Their TEM observations confirmed the shearing of γ′ precipitates by superdislocations under creep (760 MPa) and at high temperature (800~1000 °C). In our simulations, the stress levels for both [0 0 1] and [1 1 1] orientations are up to 1000 MPa and the temperature is 850 °C, so the cutting of γ′ precipitates by superdislocations should be considered in our 3D DDD model. To study such phenomenon in simulations, we artificially put some dislocation sources on the same slip planes, which allowed an increased chance (probability) of formation of superdislocations. For comparison purposes, we are currently carrying out systematic TEM studies of the tested samples to investigate the cutting of precipitates by superdislocations, which will be reported in our future work.

4.3. Evolution of dislocation densities during cyclic loading

The evolution of the dislocation density for [0 0 1] and [1 1 1] orientations is shown in Figure 12(a) for the 1st loading cycles. Density reached the peak at the end of monotonic loading (time = 1 s), then kept increasing during the dwell period (despite the stress relaxation behaviour). Decrease in dislocation density was observed during the unloading and reached a minimum value at the end of load reversal. Following subsequent re-loading, density was increasing again with the time and reached another peak value, larger than the 1st peak, at the maximum load level (time = 9 s). These are consistent with the in situ measurements by Huang et al. [34], who obtained dislocation densities at seven points within the 1st fatigue cycle using Neutron diffraction method (see Figure 12(b)). The measurement at point 7 (end of the 1st loading cycle) has a higher dislocation density than that at point 1 (beginning of the 1st loading cycle), which shows the strain hardening even within the 1st cycle. The measured dislocation densities for the 1st and 100th cycles were also compared in the work, as shown in Figure 12(b). Although the same load level was maintained during the fatigue test, the observed dislocation density for 100th cycle is several times higher than that for the 1st cycle, indicating the significant accumulation of dislocations during the cyclic plastic deformation. Due to the excessive amount of computing time required for simulating a large number of cycles under dwell-fatigue, only one cycle was modelled in this paper. However, additional simulations were carried out by removing the dwell period in the fatigue cycles. The dislocation density against time for the 1st and the 5th cycles are shown in Figures 13(a) and 14(a) for [0 0 1] and [1 1 1] orientations, respectively. The increase in dislocation density with cyclic loading number is clearly shown, indicating the accumulation of dislocations during fatigue. The dislocation networks at the end of the 1st and the 5th cycles are shown in Figure 13(b) and (c) for [0 0 1] orientation and Figure 14(b) and (c) for [1 1 1] orientation, respectively, which further confirmed the accumulation of dislocations with the number of fatigue cycles. This is consistent with the in situ neutron measurements by Huang et al. [34] and the 3D DDD simulation results by Shin et al. [9].

Figure 12. (colour online) Evolution of the dislocation density: (a) simulations in this work for both [0 0 1] and [1 1 1] orientations and (b) the in situ measurements by Huang et al. [34].

Figure 13. (colour online) (a) Evolution of dislocation density; dislocation networks at the end of the first (b) and the fifth (c) cycles for [0 0 1] orientation.

Figure 14. (colour online) (a) Evolution of dislocation density; dislocation networks at the end of the first (b) and the fifth (c) cycles for [1 1 1] orientation.

4.4. Limitations of current work

The misfit strains and the associated coherency stress, produced by the lattice mismatch between the γ/γ′ phases in nickel-base single crystal superalloys, are not considered in this work. However, the work of Huang et al. [7] demonstrated that the influence of coherency stress on stress–strain behaviour can be negligible, which is also confirmed by the work of Vattré et al. [12]. The simulations in this study focused on the macroscopic stress–strain responses and dislocation networks for [0 0 1] and [1 1 1] loading directions, which should not be much affected by the misfit strain. But further work is needed to fully understand the effects of lattice mismatch.

The dislocation climb was not considered in our 3D DDD code, so its effect on relaxation of hardening was not simulated in our work. The recent 3D DDD simulation results on nickel-based superalloys by Gao et al. [46] demonstrated that dislocation climb was capable to promote dislocation glide and multiplication, and rearrange the dislocation configuration to relax the hardening due to dislocations filling in the γ channel. 2D DDD simulations by Huang et al. [47] also showed that dislocation climb decreased significantly the flow stress and hardening rate while increased the dislocation density by relieving the dislocation pile-ups against the grain boundaries (GBs). We are in the process of incorporating climb into our 3D DDD code, but it requires a significant amount of efforts and additional work. Also in this paper, we are more focused on the interaction between dislocations and precipitate, especially looping and cutting of precipitates by dislocations, under cyclic loading. The effect of climb on dislocation-precipitate interaction will be reported in our future work.

The DDD method seems to be phenomenological to a certain extent, as it still relies on some governing laws to describe generation, evolution and interaction of dislocations. But it makes sense to say that DDD is a more physically based approach compared to crystal plasticity model. For instance, the dislocation networks can naturally introduce strain hardening without the need of phenomenological hardening variables. Specifically, the long-range dislocation interaction may contribute to the isotropic hardening, while the short-range interaction to the kinematic hardening. Finally, it needs to be noted that the DDD simulations are based on isotropic response and further work is required to incorporate anisotropic elastic constants into the 3D DDD code.

5. Conclusions

Cyclic deformation of a nickel-based single crystal superalloy has been modelled by 3D DDD at high temperature (850 °C). RVE-size study confirmed the convergence of stress–strain behaviour and dislocation density for 8-precipitate RVE, which was used in simulations of stress–strain response and dislocation evolution. The DDD model parameters were calibrated from strain-controlled cyclic experimental data at 850 °C. Simulation results are in good agreement with experimental data for both [0 0 1] and [1 1 1] loading orientations, in terms of stress/strain responses (monotonic and cyclic loading). The simulation results also confirmed the orientation-dependence of the global stress–strain response ([0 0 1] vs. [1 1 1]). The dislocation networks deposited on the γ/γ′ interface made major contributions to strain hardening while the precipitate shearing by superdislocations played a significant role in the material softening. The dislocation densities also evolved accordingly with the cyclic loading, and increased with the number of loading cycles. Maximum shear plastic strain contour plots of the deformed RVE at total strain of 1% showed heterogeneous shear deformation, which led to the development of shear bands.

Funding

The work was funded by the EPSRC [grant number EP/M000966/1], [grant number EP/K026844/1] of the UK and in collaboration with GE Power, Dstl (Matthew Lunt) and Rolls-Royce (Mark Hardy).

Disclosure statement

No potential conflict of interest was reported by the authors.

Acknowledgments

The authors also would like to thank Prof. Philippa Reed at the University of Southampton and Prof. Michael Preuss and Dr. João Quinta da Fonseca at the University of Manchester for several useful discussions of the results. Research data for this paper is available on request from the project principal investigator Prof Liguo Zhao at Loughborough University.