A new theory of the solid-state growth of embryos during nucleation: the fundamental role of interfacial mobility

Abstract

One of the major challenges in nucleation theory is to explain the kinetic pathway allowing multicomponent precipitates to grow until they reach stability. This problem is particularly challenging when the supersaturation is low, so that the critical size of nucleation is large and requires the condensation of thousands of atoms. A new theory is proposed to explain the growth of embryos before they reach the critical size of nucleation. This theory is not a substitute of the classical nucleation theory, but a complement aiming to understand the kinetic pathway allowing unstable embryos to grow at the expense of their neighbours. The theory stands on the strong interactions between embryos. The latter may exchange atoms via impingement and coarsening, which are possible when there are no concentration gradients between the embryos. This condition is supposed to be met during the unstable growth regime of nucleation considering that the growth is limited by the interface during that period. Assuming that the embryos behave in a collective manner when they are grouped in a cloud, we show that the growth velocity of the most active embryos will be limited only by their interfacial mobility and the available driving force.

Keywords:

• Nucleation
• interfacial mobility
• multi-component, coarsening

Introduction

The occurrence of a phase transformation is governed by nucleation kinetics, which dictates the number of nuclei that are produced per unit volume and time and where they should appear. The basic problem of nucleation theories is the kinetic pathways followed by the system to assist the formation and growth of subcritical embryos [1]. According to the classical nucleation theory, thermal fluctuations are responsible of the formation of embryos, as if the latter should appear almost spontaneously after a certain incubation time. A portion of them should cross the energy barrier at a pace ruled by the atomic condensation rate. This scenario was experimentally demonstrated with microgel colloidal spheres by Peng et al. [2]. In movies 2, 3 and 4 available in their supplementary materials [2], one can see that embryos form and disappear rapidly when their size is below the critical size (40–60 spheres), while the sudden apparition of an embryo having the critical size trigger the start of the phase transition. If this scenario can explain the nucleation of a new phase in a one component system, it is more difficult to imagine how thermal fluctuations can help the stabilisation of a multicomponent embryo during a first-order phase transition, knowing that the solute atoms have to migrate over a relatively long distance in this case. In fact, this depends on the critical size itself because if the latter is small then a lot of scenarios are possible but if it is large and the embryo contains thousands of atoms, then one has to find out how it is possible that such a large amount of atoms can migrate and combine to form a stable nucleus. As an example, the critical size of a penny shaped Al₂Cu – θ′ phase growing in the Al rich corner of the Al-Cu system should be around 1.2 nm thick and 2.4 nm wide at 0 K according to the atomistic calculations made by Hu et al. [3]. Such a nucleus contains approximately 400 atoms. Since the chemical driving force decreases at higher temperature, it is expected that the critical size will be much higher at temperatures in the 400–500 K range, which are typical of those used for artificial ageing. Assuming that these precipitates have an aspect ratio of around 20 at these temperatures, one can estimate that the oblate spheroid nucleus will contain thousands of atoms at the critical size. The pathway explaining how a subcritical embryo containing around 50 atoms can grow up to a stable nucleus containing thousands of atoms has not been determined experimentally neither theoretically. Some new ideas have been put forward by Fallah et al. [4,5] regarding the clustering phenomenon in the Al-Cu system. Their model predicts the formation of Al-Cu clusters for which the Cu concentration varies gradually while the surface is fully coherent with the matrix. The nucleation of clusters was helped by the dislocations present in the matrix. According to their model, the energy barrier was sufficiently reduced to initiate the post critical growth thanks to sufficiently large local solutal fluctuations or to the movement of random dislocations. The critical size of the clusters had only 10 atoms however and the morphology of the clusters was roughly spherical. Such clusters were not found in their samples when examined with a high-resolution transmission electronic microscope (HRTEM) but they detected some small fluctuations of low Cu content with a high-resolution scanning transmission electronic microscope (HRSTEM). They proposed that these early clusters/GP zones of low Cu-content and spherical morphology could be the potential precursors of the well-developed plate-shaped clusters of higher Cu content. No experimental evidence was given however to support the idea that the precursor participates in a chemical reaction producing the new phase. This standpoint about the role of precursors in phase transition is largely accepted by researchers as one of the possible kinetic pathways. The exact evolution of precursors is however difficult to schematize since the vast majority of them will dissolve while simultaneously a minority may react to become a more stable phase. The contribution of Fallah and co-workers indicates however that the clustering phenomenon can give birth to clusters having different compositions. Soon after, one may expect that the different types of clusters will transform into different phases, called embryos, each one having a definite structure and composition.

Keeping the Al-Cu system as an example, one can find in textbooks that the sequence of precipitation is:(1)

This sequence suggests that each phase is the direct product of the transformation of its precursor. Another possibility is that all these phases are in competition and the reason explaining why some phases grow extensively before the others is their favourable kinetics. After the generation of clusters and their subsequent transformation into sub-critical embryos of metastable and stable phases, it is likely that the latter grow at different paces according to their growth kinetics. Once a more stable phase reaches a certain volume fraction, the less stable phase starts to dissolve and eventually disappear to the profit of the more stable phase. Such a process means that all phases grow essentially at the expense of the matrix and not at the expense of its precursor. This is very likely considering that the direct transformation from one intermetallic particle to another type of intermetallic is a very slow process at standard ageing temperatures. Indeed, such a transformation involves diffusion inside the intermetallics, where the atomic mobility of elements is presumed to be very low in comparison to the atomic mobility in the supersaturated solid solutions. This assumption, which is largely accepted by researchers developing precipitation models, comes from the limited solubility of most intermetallics and the partially covalent nature of the atomic bounds. The combination of these two factors slow down significantly the migration of atoms inside these phases and prevents the reaction to occur swiftly, especially when the less stable phase has grown extensively. In fact, the best opportunity for a reorganisation of a phase into another one is expected to happen during the clustering phenomenon, where the number of atoms involved is very small. According to the scenario suggested by Fallah and co-workers, it seems realistic that the transformation of clusters into embryos occurs when the latter are very small. But, once embryos of the new phases have formed, their growth is not guaranteed because the surface energy is then sufficiently large to exert a negative driving force. Indeed, the capillarity forces are such that they impaired the growth of embryos until the latter reach their theoretical critical size of nucleation r ^* . This variable (r ^* ) stands for an isolated particle trying to grow at the expense of a matrix free of defect and its value differs from the initial size of the embryo (r ₀) since the former refers to the evolution in a matrix free of defects while the latter refers to the formation of an embryo on a lattice defect. The subcritical growth regime is defined in this scenario as the period spent during the time the embryo grows from r ₀ to r ^* .

In this paper, we will propose a mechanism explaining how subcritical embryos can grow up to their critical size in spite of the global negative driving force. The theory will be based on the coarsening of subcritical embryos, which is activated and governed by the nucleation of ledges on the crystallographic facets of the embryos.

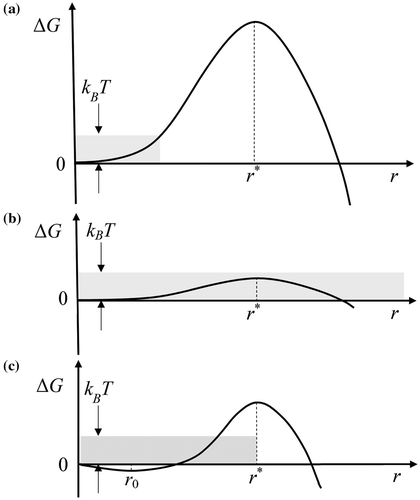
The role of thermal fluctuations

According to the classical nucleation theory [6–8], thermal fluctuations generate a steady state population of clusters after a lag time. A certain number (N ^* ) of these clusters have the critical size and a portion of them given by Z·N ^*, where Z is the Zeldovich factor, will grow with a velocity determined by the condensation rate. The variation of free energy with the size of a precipitate during homogeneous nucleation is schematised in Figure 1(a). Thermal fluctuations can generate embryos having a size belonging to the shaded area but the probability of creating an embryo having the critical size r ^* in a matrix free of defect, is so small, that one cannot expect this scenario to be plausible. A large defect like a grain boundary can reduce the height of the energy barrier to such a point (see Figure 1(b)), that clusters having the critical size have a much higher probability to nucleate in a one step process and grow steadily afterwards. But when a precipitate nucleates on a dislocation, the cluster is limited to the distorted zone. Its size is not expected to extend far from the dislocation line (1–2 nm typically), especially when the cluster has to grow in more than one direction. Such a cluster has a certain stability depending on the depth of the valley of the curve free energy ΔG vs. size, as this is schematised in Figure 1(c). The cluster can be stable for a while but its growth is not guaranteed. As mentioned earlier, if the matrix is free of defect around the cluster of size r ₀, further growth will produce an increase in surface free energy, which will encompass the decrease in bulk free energy.

Figure 1. Variation of free energy with the size of a precipitate when nucleating (a) homogeneously, (b) on a grain boundary and (c) on a dislocation.

Thermal activation can hardly be visualised experimentally, but it is possible to illustrate its effects with Monte-Carlo simulation models. Soisson and Martin [9] investigated the decomposition of a metastable binary solid solution using the so-called residence time algorithm [10] and reported interesting results showing the gradual increase in size of subcritical embryos and the reduction of their number density during the incubation regime. Figure 2 presents the evolution of the number of atoms condensing onto an embryo during the early stages of the simulation. With the set of parameters given in the paper, one can calculate that the critical number of atoms in the embryo was 12 in this particular simulation. This plot reveals that the growth of an embryo reaching the critical size was gradual during the incubation regime.

Figure 2. Time evolution of the number (i) of atoms in one cluster. “Reprinted (Fig. 7b) with permission from [9] Copyright (2000) by the American Physical Society”.

More recently, an experimental investigation conducted by Liu et al. [11] on an Al-Cu alloy showed that the growth rate of the plate-like θ′ particles was rather constant during ageing at 140 °C, as this can be seen on their Figure S5-a. At this low temperature, it is likely that the precipitation process was still in its incubation regime during the first hours of ageing. The authors concluded that the process was diffusion-controlled on the basis that a good correlation was found between the precipitate diameter and the square root of time for 20 precipitates growing at 140, 160 and 180 °C. Considering that many precipitates were experiencing dissolution and impingement, it is also possible that the limited growth rate experienced by many precipitates resulted from a less favourable location for growth. At 160 °C, some particles had their diameter growing linearly with time from 10 to 155 nm but others had their diameter growing linearly with the square root of time, though in the last case, their diameter reached a plateau at around 30–40 nm. These particles were likely candidates for an eventual dissolution.

From the above numerical and experimental observations, one can highlight the following points:

(1)	During the incubation regime, some clusters grow until they reach the critical size (the winners) while many others are dissolving (the losers).
(2)	The growth rate of the winners can be considered as being constant during the incubation regime.

The gradual increase in size of some particles occurring concomitantly with the dissolution of others is a phenomenon called coarsening. Usually, this phenomenon is invoked when the volume fraction of precipitates reaches a plateau, but the conditions allowing coarsening seems to be there during the incubation regime.

Most of the time, coarsening is described as the biggest particles growing at the expense of the smallest. This stands from the classical coarsening theory developed by Lifshitz and Slyozov [12] and Wagner [13], referred as the LSW theory, where the kinetic equation was developed using a mean field approach. The limit of such an approach is that the coarsening rate of a precipitate is assumed to be independent of its immediate surroundings. One consequence of this assumption is that coarsening is not active if all precipitates have exactly the same size. But the precipitates are dispersed in space and do not have the same surroundings. Because of the thermal fluctuations, some will experience high pressure (causing dissolution) while others will experience negative pressures (causing growth). This fact has already been taking into account in modern coarsening theories (see [14]). So, in all cases, a system will find its way to reduce its total energy via coarsening even though the particles have the same size. This illustrates that thermal fluctuations are the root cause of coarsening and the reduction of total energy is its driving force. Consequently, it is obvious that coarsening is acting in all stages of precipitation. If nucleation is activated by thermal fluctuations, one can say that thermal fluctuations activate the coarsening mechanism during the incubation regime and that the incubation time depends essentially on the coarsening rate of unstable embryos.

Coarsening rates are very slow when the volume fraction of precipitates reaches a plateau, and one can imagine that the atoms are transferred from the dissolving precipitates to the growing precipitate, driven by the concentration gradient existing between the two precipitates. But this picture does not reflect the reality. In fact, to record a coarsening event, an atom emitted from a precipitate does not have to travel the distance separating that precipitate to another one. The sequence presented in Figure 3 shows that after few jumps, the precipitate on the left is gaining one solute atom while the precipitate on the right is losing one solute atom. The matrix keeps the same amount of solute atoms. The two processes can be completely independent one of each other. The precipitates do not have to be close one to each other. The two events do not have to be simultaneous. The exchange is done via the matrix. If the sequence (R→L) is repeated, the precipitate on the left will grow while the precipitate on the right will dissolve. This sequence will dominate the reverse sequence (L→R) since the free energy of the system will decrease by the repetition of the same sequence. This mechanism is certainly realistic and can be used to explain the results of the Monte-Carlo simulations showing that coarsening occurs until a given proportion of the precipitates reach the critical size.

Figure 3. Illustration of the exchange mechanism for interface controlled kinetics. Repetition of the same sequence will produce coarsening and reduction of the free energy.

The role of the interfacial mobility

If the growth of subcritical embryos during the incubation regime is made possible via the exchange mechanism depicted in Figure 3, it follows that the atomic attachment rates must be regulated by the interfacial mobility. Sietsma and van der Zwaag [15] stated that precipitation starts as an interface-controlled transformation because of the large ratio between the surface area and the volume. This statement was reaffirmed by the author with the analytical solution of the quasi-stationary growth in the mixed-mode regime of an ellipsoidal precipitate [16]. During the incubation regime, the growth of embryos is not limited by the migration of atoms in the matrix, which accommodates the growth in a very efficient way, but by the formation of ledges on the surface of the precipitates which governs the interfacial mobility. When the precipitates are very small, the number of ledges is likely not sufficient to attach the atoms migrating nearby, which allows time for the flattening of concentration gradients in the matrix.

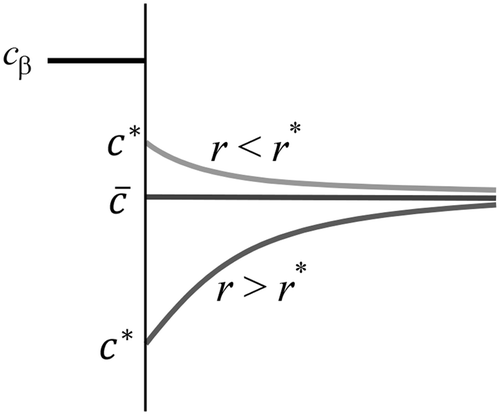
The exchange mechanism explained above is possible if there is no diffusional driving force between the embryos and the matrix. Figure 4 schematises the three possible situations that could prevail in a binary system near the interface of a precipitate. The two first situations occur if local equilibrium is assumed at the interface while the system is not at equilibrium. In these cases, the concentration of solute at the interface is c ^*. If r < r ^*, r ^* being the critical radius of nucleation, the matrix solute concentration at the interface should be higher than the nominal composition of the matrix because of the Gibbs-Thomson effect. Under such a condition, each embryo loses more solute atoms than it will gain because of the up-hill diffusion required to get atoms from the matrix. The dissolution is then the only option since the embryos are isolated by their diffusion field. The inverse situation occurs when r > r ^*. All embryos grow and compete for the solute atoms in the matrix. Here also, the embryos are isolated by their diffusion field and will interact only via the decrease in . The third situation occurs when one assumes that the growth is 100% controlled by the interface. The only resistance for growth under such a condition is the mobility of the interface. The mixing of atoms in the matrix is fast so that concentration gradients are flattened rapidly. The exchange mechanism between the embryos is then fully operative and coarsening becomes possible even if r < r ^*. The interface control mode of growth requires that the interface is not at equilibrium and that the boundary migration velocity depends on the interfacial mobility. The velocity of a spherical interface is proportional to its mobility according to the following equation [17]:(2)

Figure 4. Solute concentration profile near the interface under different regimes.

where M is the mobility of the interface, V _m is the molar volume of the precipitate and is the driving force. The driving force acting on the boundary of a precipitate β growing in a matrix α is given by [18]:(3)

where is the molar fraction of element i in the precipitate, is the chemical potential of element i in phase φ at the interface and I is the number of species in the precipitate. The surface free energy variation is given by [19,20]:(4)

where is the chemical potential of element i in phase α when the particle of a given size and shape is in equilibrium with the matrix and is the chemical potential of element i in phase α when the interface is planar and the system at equilibrium. We will assume that the composition of the precipitate is invariant and equal to the equilibrium composition. Hence, one can set in Equation (3(3) ) to obtain:(5)

Combining Equations (4(4) ) and (5(5) ) and assuming that the thermodynamic factors are constant for concentrations below the nominal composition of the matrix, one can show that:(6)

where is the matrix molar fraction of solute i at the interface, is the equilibrium matrix molar fraction as given by the phase diagram (planar interface), R is the gas constant and T is the absolute temperature. The first term on the right-hand side of Equation (6(6) ) accounts for the increase of surface free energy when the precipitate is growing. Notice that a strain energy term can be added on the right hand side of Equation (6(6) ) to take into account the increase of lattice and volume misfits caused by the growth of a precipitate. If ΔG _s is the molar strain energy produced by the growth of the precipitate, then one can modify Equation (6(6) ) as:(7)

This term has for immediate effect to reduce the driving force by rising the solubility limit of the matrix at a given temperature. Let the composition being defined as:(8)

The exponential term now gives the increase of solubility related to the strain energy. Combining the 2 last equations one obtains:(9)

An accurate estimation of the strain energy term is very difficult. When the phase diagram is based on experimental data, one can expect that the solubility of the matrix extracted from this phase diagram includes up to a certain point the impact of the strain energy because of the unavoidable stress field surrounding precipitates in almost all experimental conditions. In this case, it is advisable to use the solubility data from the phase diagram and neglect the extra strain energy term. But if the phase diagram is entirely plotted based on ab initio calculations of the thermodynamic variables of fully relaxed phases, then one should add the elastic strain energy contribution. Therefore, some attention must be paid to the value of used when modelling growth kinetics.

The frequency factor

In the classical nucleation theory, the time-dependent nucleation rate is given by [21]:(10)

where N ₀ is the potential nucleation sites density, β ^* is the frequency factor, Z is the Zeldovich factor, ΔG ^* is the nucleation energy barrier, τ is the incubation time and t is the isothermal reaction time. The simplest expression used to evaluate the frequency factor is [22]:(11)

where S ^* is the “effective” area of the nucleus- matrix interface, Γ is the jump frequency, a is the lattice parameter of the matrix and c is the molar fraction of solute in the matrix. The frequency factor β* represents the condensation rate of the embryo and not the net condensation rate , the latter being equal to the condensation rate less the evaporation rate. The evaporation rate is taken into account by the Zeldovich factor Z in the classical nucleation theory [23]. Figure 5 illustrates the time evolution of a hypothetical cluster size distribution. In this figure, the dotted curve represents the cluster size distribution at time t ₀ and the solid curve represents the modified size distribution after a certain time t ₁ > t ₀. In this scenario, there are winners and losers. The winners grow at a pace given by the condensation rate, Equation (11(11) ), while the losers are dissolving. There is no capillarity term in the expression for β* in the classical nucleation theory, which suggests that the growth rate of the winners is not affected by this term. If this is true when the winners have the critical size, it is likely that this could also be true before that time.

Figure 5. Evolution of a cluster size distribution from time t ₀ to t ₁. Adapted from [23].

To evaluate the condensation rate, it is usual to estimate Γ from the jump frequency of atoms in the matrix according to this relationship [24]:(12)

where D is the coefficient of diffusion and α is the jump distance. The problem with this relationship is that it does not reflect the jump frequency at the interface, which can be very different from the jump frequency in the matrix, particularly if two species have similar volume diffusivities but different stoichiometry in the precipitate. The parameter characterising at best the jump frequency of atoms across the interface is the interfacial mobility. For an isolated particle, the velocity of the interface is obtained by combining Equations (2(2) ) and (6(6) ):(13)

where has been replaced by the nominal composition of the matrix on the basis that the phase transformation is interface controlled during the subcritical growth regime. When the term into brackets, which represents the driving force per mole of atoms, is equal to zero, one obtains the standard critical size of nucleation:(14)

If the velocity of the interface is zero at the critical size for an isolated embryo, it follows from the mean field approach that the average velocity of the interfaces is zero for a population of embryos. But if the population is divided between winners and losers, the former will have a positive velocity while the latter will have a negative velocity. The condensation rate of the winners can then be expressed without the capillarity term, similarly to the classical nucleation theory. For a spherical embryo, the condensation rate can be expressed as:(15)

where V _at is the atomic volume. Ignoring the capillarity term in Equation (13(13) ) to determine the interfacial velocity of the winners, one obtains:(16)

Notice that this expression stands for a multicomponent embryo and that the term being thermally activated is M and not D.

The dissolution rate of unstable embryos

Considering that the winners can grow with an interfacial velocity υ given by:(17)

a certain amount of losers must dissolve at a pace allowing such a growth rate for the winners. The mass conservation equation in the embryos size space can be written as [25]:(18)

where C _n is the number density of embryos in a given size class and S is the source term taking into account the loss of embryos. The source term is by definition the total differential , which can be estimated by imposing a constraint. In standard coarsening theories, developed for situations where the volume fraction of precipitates is near the equilibrium value (late coarsening), it is advisable to use a constraint imposing that the volume fraction is conserved. During late coarsening, the dissolution of a precipitate has for effect to increase the total energy of the system, which is eventually decreased by the growth of another precipitate. So, the return of atoms into the matrix increases the total energy. But when the coarsening occurs during the incubation regime (sub-critical coarsening), the dissolution of precipitates decreases the total energy. The return of atoms into the matrix is therefore an event which has favourable probabilities to occur. It means that the probability that one atom remains in the matrix is not zero. For that reason, the volume conservation constraint is unlikely during the incubation regime.

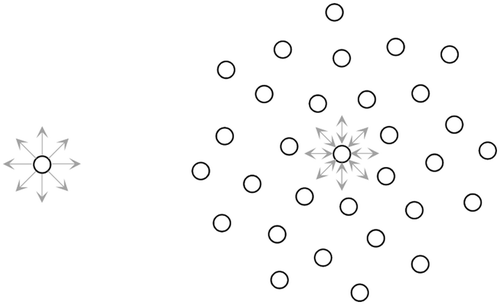
The probability that an isolated sub-critical precipitate dissolves is equal to 1, because the matrix is large enough to capture the atoms with an infinitesimal increase in the average molar fraction. If the dissolution is the only option for an isolated subcritical embryo, the situation is different for a group of interacting embryos. Figure 6 depicts the two situations. On the left, the isolated embryo experiences a net loss of atoms if its size is below the critical size. On the right, many subcritical embryos will receive more atoms than they will lose because they are surrounded by a high number of neighbours. This is happening because the liberation of solutes inside the cloud generates a positive solutal fluctuation having for effect to slow down the evaporation rate inside the cloud. But some embryos will dissolve because they are more isolated. Among them, the subcritical embryos located at the periphery will dissolve at a higher rate because of their limited number of neighbours.

Figure 6. On the left: An isolated subcritical embryo experiencing a net loss of atoms. On the right: A cloud of subcritical embryos.

It is likely that a cloud, containing a population of embryos of size r ₀ at the start of the coarsening process, will successfully transform to a cloud of precipitates having the critical size if the initial number density C ₀ is large enough, otherwise the positive solutal fluctuation will not be large enough. This supposes that nucleation is possible only if the number density of defects is above a certain critical value called C _c . When C ₀ < C _c , the embryos behave like isolated particles and their growth is impaired by the energy required to increase the combined interface area. But if C ₀ = C _c, the minimal condition for successful nucleation is reached, which corresponds to a combined interface area that remains constant during the coarsening process. For spherical embryos, the constraint would therefore be written as:(19)

Because the main barrier to nucleation is the growth of interfaces, Equation (19(19) ) tells that the energy barrier can be bypassed if, at least, the combined interface area does not increase during the coarsening of embryos. This is a minimal requirement. When C ₀ > C _c , one should expect that the combined interface area decreases during the coarsening process. However, because a portion of the atoms liberated by the dissolving embryos remain in the matrix during the incubation regime, a net reduction of the interface area is not granted. The time evolution of the volume fraction of embryos during the coarsening process is given by:(20)

where V _β is the volume of one embryo and y represents the proportion of atoms liberated by the dissolving embryos that remains in the matrix. If y = 0, the volume fraction of embryos remains constant and this corresponds to the volume conservation constraint. But if y = 1/2, Equation (20(20) ) can be transformed to obtain:(21)

which is strictly equivalent to Equation (19(19) ) for shape conservative growing particles (invariant aspect ratios). The combined interface area of the embryos is reduced or constant only if 0 < y < 1/2. Above 1/2, the combined interface area increases preventing nucleation to occur. The critical number density of embryos corresponds to the situation where y = 1/2. It is difficult to evaluate the value of y when C ₀ > C _c except for the extreme case where the embryos are very close one to each other. If a cloud contains a high number density of embryos, like the one depicted in Figure 7, it is expected that the cloud will dissolve layer by layer, like a snowball above 0 °C. Therefore, it is reasonable to think that around 50% of the atoms liberated on the periphery of the cloud will escape out of the cloud while the other 50% of atoms are going to condensate on the internal embryos. If the cloud fills the volume of a grain, the escaping atoms will condensate on the grain boundaries. This scenario results also on a surface conservative constraint since, as we have shown above, when 50% of the atoms liberated by the dissolving embryos do not condensate on the remaining embryos, this results in a surface conservative constraint. Since the two extreme cases resulting in a successful nucleation are surface conservative, we will postulate that the coarsening process always occurs under the constraint expressed by Equation (21(21) ) for spherical embryos. For a monosize distribution of spherical embryos, the dissolution rate will therefore be deduced from Equation (19(19) ) so that:(22)

Figure 7. Left: A cloud containing a high number density of embryos. Right: One of the dissolving embryos located at periphery.

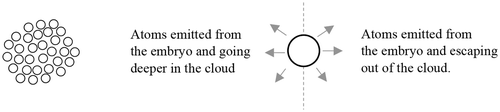
For embryos growing with variable aspect ratios, it can be postulated that coarsening occurs under the constraint that the combined surface energy remains constant.

The incubation time

Accepting that the combined surface energy remains constant during the coarsening of embryos, one may expect that the growth rate of the winners will be given by Equation (17(17) ), not only at the critical size, but also during the entire sub-critical growth regime. Since the average molar fractions in the matrix do not change a lot during the incubation regime, a nearly constant growth rate should be observed, unless the interfacial mobility changes for some reason. This is supported by the observations of Liu et al. [11], as mentioned before.

Defining the incubation time θ as the time needed for the embryos to increase in size up to their critical size, one obtains:(23)

Assuming that r ₀ << r ^*, one obtains after insertion of Equations (14(14) ) and (17(17) ) into Equation (23(23) ):(24)

The incubation time will be long when the interfacial mobility or the driving force will be low. The expression proposed by Aaronson et al. [26], which is based on the treatment of Feder et al. [27], can be written as:(25)

where is the driving force. It is worthwhile to notice that Equation (25(25) ) is identical to Equation (24(24) ) if one makes the following substitution:(26)

If the coefficient of diffusion has an Arrhenius-type temperature dependency, it is expected that the term M ⋅ k _B T also have such a temperature dependency. According to Christian [17], the interfacial mobility is indeed related to the absolute temperature by an equation like:(27)

where E is the activation energy and Ω is a pre-exponential factor. The same temperature dependency is therefore obtained for the incubation time. It is important to mention that the activation energy related to the interfacial mobility can differ significantly from the activation energy related to the migration of atoms in the matrix as the former is largely determined by the energy required to form a new ledge at the interface.

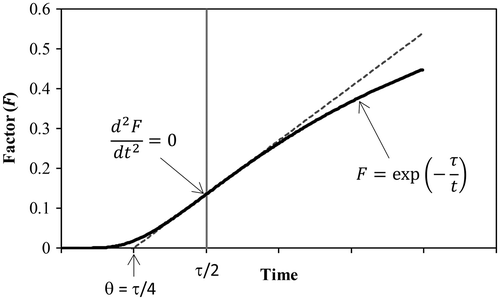
The expression frequently used for the incubation time in the classical nucleation theory is included in the factor F = exp(–τ/t) appearing in Equation (10(10) ). Figure 8 presents a plot of this factor vs. time. It is easy to show that F has a zero curvature at t = τ/2. The straight line tangent to F at this point crosses the horizontal axis at t = τ/4. This time can be used to represent the incubation time, since F starts to rise significantly afterwards. The incubation time θ, which is given by Equation (24(24) ), should therefore be multiplied by 4 to compare with incubation times calculated with expressions used for τ in the literature.

Figure 8. Plot of the factor F vs. time.

Evolution of the number density of embryos

The nucleation of precipitates will be considered as a two-steps process. In the first step, embryos are generated on lattice defects following a clustering process and a rapid transition toward a phase having a definite structure and composition. At the end of this step, a population of embryos of radius r ₀ is present and ready to coarsen. The second step of nucleation is the sub-critical growth regime for which the model will apply. This step begins by considering an initial concentration of spherical embryos (C ₀) of radius r ₀ already formed at time t = 0. Two phenomena will affect the evolution of the number density of embryos, the first one being coarsening and the second one being autocatalytic nucleation. The calculation will be made by adopting a very simplified formulation, which is to assume that the population of embryos can be represented by a population having a monosize distribution. This supposes that the dissolution of losers is very fast and that the natural dispersion of growth rates produced by the thermal fluctuations is not considered. In fact, the formulation will not be useful to calculate the evolution of the size distribution, but will give a correct prediction of the evolution of the number density of precipitates in a one-size-class approach. In a spatial distribution of embryos of equal size, the activation of coarsening by thermal fluctuations will generate the highest pressure on the losers, causing their rapid dissolution, as if their apparent size (corresponding to the pressure calculated on a mean field approach) was much smaller than the rest of the population. Once they disappear, they no longer emit atoms, and this has for effect to increase the pressure on another subset of precipitates. So the dissolution of precipitates in a population is sequential and fast in comparison to the growth of the rest of the population. In terms of size space, the instantaneous disappearing of the shrinking embryos is justified since the complete dissolution of one embryo corresponds to a small increment in the size of the winners.

For a monosize distribution of particles, the evolution of the number density C _n will be calculated by solving Equation (18(18) ) with the appropriate source term. The surface conservative source term defined from Equation (19(19) ) is very restrictive and obliterates the fact that the growth of an embryo can stimulate the nucleation of new embryos close to it. This phenomena is called autocatalytic nucleation and has been clearly demonstrated by Perovic et al. [28] on the precipitation of θ′ platelets in an Al-3 wt.%Cu alloy. Taking this phenomenon into consideration, we assume that the following constraint can be used instead:(28)

where I _A is the autocatalytic nucleation rate and r ₀ is the radius of the new embryos, which is assumed to be the same as the initial radius of the embryos of the first generation. The new embryos generated by thermal fluctuations create a “free” supplement of surfaces, which is slowing down the dissolution rate of the first generation of embryos. It is understood that the new small embryos dissolve or combined very rapidly after their apparition because of the intense pressure applied on them. Notice that this phenomenon has been observed experimentally by Liu et al. [11] and will be discussed in the next section. The monosize distribution is recovered rapidly after the dissolution or combination of the smallest embryos. This is a major simplification, but it does not alter the main principles of the problem. From the last equation, the source term becomes:(29)

Inserting Equation (29(29) ) in Equation (18(18) ), one obtains:(30)

An analytical solution of this equation is possible by assuming that I _A and υ are constant. As mentioned above, the interfacial velocity should not change according to Equation (14(14) ), unless the composition of the precipitate changes significantly during the growth. In such a case, the variables appearing in Equation (14(14) ) could be updated and Equation (27(27) ) solved numerically with a time integration procedure. Such a procedure should be adopted for instance if the formation of a precipitate occurs via the evolution of precursors. To develop the analytical solution, the interfacial velocity υ will be assumed constant for the rest of the demonstration. With these assumptions, one can show that the solution of Equation (30(30) ). can be written as [29]:(31)

where Φ(u) is an arbitrary function of u = r – r ₀ – υt. The initial condition is that C _n  = C ₀ at t = 0. The particular solution can then be written as:(32)

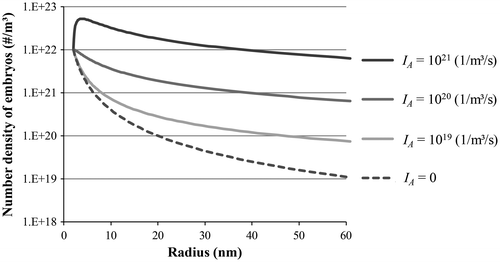
where δ(u) = 0 when u ≠ 0 and δ(u) = 1 when u = 0. Equation (32(32) ) represents a plane wave travelling in the direction of increasing r at a constant speed υ, with an amplitude varying with r as shown in Figure 9. One can see that with a sufficiently large autocatalytic nucleation rate, one may obtain a multiplication of the embryos by the combination of newly formed small embryos.

Figure 9. Evolution of the number density of embryos with respect of the radius of the embryos. Calculations were made with C ₀ = 1 × 10²² m⁻³, r ₀ = 2 nm and υ = 0.01 nm/s.

Discussion

The classical nucleation theory is a probabilistic way of predicting the nucleation rate. It does not tell how thermal fluctuations activate the process. The new theory is based on the concept that coarsening is the mechanism by which thermal fluctuations activate the process. Table 1 presents the main difference existing between the two approaches.

Table 1. Comparison between the classical nucleation theory and the subcritical growth theory (this contribution).

	Classical nucleation theory	Subcritical growth theory
Frequency Factor: β ^*
Incubation time: τ
Dissolution of embryos	Zeldovitch factor: Z	Negative source term in the equation:

The role played by the interfacial mobility is the main principle upon which is based the new theory. The expressions found for the frequency factor and the incubation time are truly multicomponent and put the focus on the growth kinetics right at the interface of the embryos.

According to the present model, the growth rate of the surviving embryos is constant under isothermal conditions and depends on the driving force and the mobility of the interface. Liu and co-workers wrote that the linear growth may have been assisted by the free surface of the specimen [11]. This is certainly a possibility but it is not clear that the diffusion of atoms along the surface of the specimen and along the interface can be the root cause explaining this phenomenon since the concentration gradients along these surfaces are likely insufficient. Another possibility is that the generation of new ledges at the junction of the free surface and the matrix-precipitate interface has been promoted, increasing the interfacial mobility for these precipitates. It is worthwhile to mention that the best way to evaluate whether the growth is interface or diffusion control is to measure the concentration gradients around the precipitate and not the time dependency of the growth rate. The absence of long range concentration gradients would indicate that the mode of growth is interface controlled, which does not mean that the migration of species is not significant. On the contrary, the species migration is sufficiently fast around the small embryos to flatten the concentration profiles and get conditions assimilated to interface control. Another important observation reported by Liu and co-workers [11] is about the role played by a dislocation to boost the growth rate of a precipitate. This can be seen in their movie S2 supplied in the supplementary information section of their report [11]. At the ageing time approaching 7h00, a dislocation reacts with the rim of a precipitate, which has for effect to boost its growth velocity by an important factor. The dislocation stayed connected to the rim of the precipitate for the rest of the experiment. Our interpretation of this phenomenon is that the dislocation has promoted the nucleation of new ledges on the rim of the precipitate, which has accidentally increased the mobility of the semi-coherent interface. It is worth to recall that the ledge formation mechanism is central in the interface migration kinetics when the growth is controlled by the interface. Finally, Liu and co-workers showed a direct interaction between precipitates in their movie S5, where one can see two precipitates nucleating and dissolving rapidly. This sequence is schematised in Figure 10.

Figure 10. Schematized events captured by Liu et al. [11] during the precipitation of θ′ in an Al-5.7 wt.%Cu specimen. Precipitates 1 and 3 are created and are then dissolved under the influence of precipitates 2 and 4. The boxes indicate the time in hours and minutes.

According to Perovic et al. [28] the autocatalytic nucleation of precipitates is energetically favoured when they are aligned with a pre-existing precipitate. This suggests that precipitates 2 and 3 may have nucleated under the influence of precipitates 1 and 4 (the latter growing from the left). The growth of precipitate 4 was slowing down a little bit when it met precipitate 1. The latter was absorbed rapidly as well as precipitate 3, which was aligned with precipitate 4. This illustrates very well how autocatalytic nucleation can help the growth of pre-existing embryos in their path to reach stability. The high supersaturation of Cu in their alloy (5.7 wt.%) and the plate-like shape of the θ′ particles promoted direct interactions between the precipitates instead of an indirect exchange mechanism via the matrix. But the result was the same: a collective increase of the size of the winners at a very low cost of surface energy creation allowed by the dissolution of many precipitates. It is not excluded that this mechanism operates beyond the critical point when the interaction between the particles is strong via impingement (short-range interaction) or via coarsening (long-range interaction).

Existing nucleation theories focused mainly their attention on the surface energy of the precipitates to explain the kinetic pathways and precipitation sequences. But the fact that the interfacial mobility was ignored surely did not help to get an accurate description of the mechanisms involved. For instance, existing theories do not explain the precipitation sequence in Al-Cu system as given by Equation (1(1) ). Let us first consider the interfacial energies of θ and θ′. The values reported in the literature are scarce but it seems that they are comparable for θ and θ′. The theoretical values reported for θ′ are 0.156–0.190 J·m⁻² for the coherent face and 0.520–0.694 J·m⁻² for the semi-coherent rim [30,31]. For the θ phase, an average value of 0.456 J·m⁻² with a minimum value of 0.24 J·m⁻² occurring at specific orientations was estimated by Kokotin et al. [32]. The only experimental value reported for θ was 0.23 J·m⁻², which was determined from the migration rate of Al–Al–Al₂Cu tri-junctions [33]. Using the Generalised Broken-Bond (GBB) model developed in [34], Kozeschnik calculated interfacial energies of 0.091 J·m⁻² and 0.088 J·m⁻² for respectively the θ′ and θ phases in an Al-3at% Cu alloy [19]. We conclude from these values that the interfacial energies of θ′ and θ are close enough to not be the decisive factor explaining why the fraction transformed of θ′ increases at a much higher speed than θ during an ageing treatment. The elastic strain energy cannot also explain the precipitation sequence since the lattice misfit energy created by the formation of a θ′ particle exceeds the volume misfit energy created by the formation of a θ particle having the same size and shape. This can be demonstrated by calculating the strain energy associated to the lattice misfit of coherent precipitates (ΔG _sc ) and the strain energy associated to the volume misfit of incoherent precipitates (ΔG _si ). Assuming that the matrix is elastically isotropic, has a Poisson ratio of 1/3 and has the same elastic moduli than the precipitate, one can approximate the value of ΔG _sc with the following equation [24]:(33)

where μ is the shear modulus, V is the volume of the precipitate and δ is the lattice misfit. For the zone surrounding a semi-coherent precipitate like θ′, the lattice misfit is estimated to be around −10.5% [24]. The expression calculating the elastic strain energy created by a homogeneous incompressible incoherent precipitate in an isotropic matrix was given by Nabarro [35]:(34)

where Δ is the volume misfit and is a shape factor <1. The volume misfit between the θ phase and the Al matrix is −9.3% based on the molar volume calculated from the unit cell of each phase. It is clear from this analysis that ΔG _si of θ < ΔG _sc of θ′, which should help the θ phase to nucleate before the θ′ phase. Finally, considering that the same species diffuse in the matrix and that the incoherent stable θ phase has the same composition, similar interfacial energies, a lower strain energy, a larger driving force than the θ′ phase, it seems likely that the θ phase nucleates before the θ′ phase. Based on these facts, it is not surprising that existing models fail to predict the precipitation sequence in Al-Cu alloys. By considering that the growth of precipitates is interface controlled during the incubation regime as suggested by the new theory, then one can advocate that the controlling variable is the interfacial mobility. If the creation of a new ledge on the surface of a θ precipitate is more difficult than it is for a θ′ precipitate, then one may conclude that the interfacial mobility of θ is lower than the interfacial mobility of θ′. It seems reasonable to think that the creation of a new ledge having no continuity with the lattice structure of the matrix requires a higher activation energy than a new ledge created in continuity with the matrix. The activation energies (E _a ) reported for θ′ and θ phases and deduced from differential scanning calorimetric analyses gives a strong indication about the validity of this idea. The values of E _a are in the range of 66–101 kJ·mol⁻¹ for θ′ and in the range of 200–360 kJ·mol⁻¹ for θ [36,37]. While many authors explain that the activation energies are essentially linked to the diffusion of species, which is consistent with their idea that the reactions would be diffusion controlled, it is difficult to understand why Cu atoms would migrate more easily toward a θ′ precipitate rather than toward a θ precipitate. In fact, what is clearly distinctive is the jump frequency of atoms across the interface and this is exclusively related to the mobility of the interface. So, if the reaction is interface controlled during the incubation regime and that the interfacial mobility of the θ phase is reduced by a large factor in comparison of the θ′, then one can explain that the growth rate of θ is very small at temperatures below 200 °C in comparison to the growth rate of θ′. This is possible in spite of the fact that the other factors are in favour of the stable phase θ.

In light of the theory proposed in this paper, it is legitimate to question the relevance of the critical size of nucleation in a practical perspective. As mentioned before, the concept of a critical size of nucleation stands for an isolated precipitate. But in a real system, precipitation occurs as a collective phenomenon where strong interactions occur between the embryos. The winners of the competition will grow at the speed allowed by the driving force while the losers will dissolve. The modelling of this competition requires advanced numerical techniques like Monte Carlo simulations. However, if one is more interested to mimic the macroscopic evolution of the microstructure, our model could be useful by providing a simple way of calculating the growth rate during the incubation regime for those precipitates surviving up to the point where the number density is stabilised for a while. This point likely coincides with the time where interface controlled mode is replaced by a mixed-mode control, the latter evolving continuously toward a diffusion control mode as demonstrated by the author [16]. This point is likely more relevant for macroscopic simulation purposes than the critical size of nucleation of an isolated particle since one can hardly determine the actual critical size of nucleation of an embryo when the latter is located in a large ensemble of similar particles. Indeed, an embryo can grow above the classical value of r ^* and being dissolved soon afterwards because of the interactions with others. The notion of stability is therefore somewhat complicated in a group of embryos. We think that it is preferable to define the end of instability as the point where the number density of precipitates becomes stable, which likely occurs at the beginning of the mixed-mode regime where concentration profiles start to appear around the precipitates.

Conclusion

A kinetic pathway was proposed to explain how it is possible for embryos to reach large critical sizes of nucleation during solid-state precipitation. The mechanism has been described using the concept of coarsening (simultaneous growth and dissolution of particles) when strong interactions are possible during the time the concentration gradients in the matrix are negligible. The growth regime during this incubation period was assumed to be interface controlled, which means that the interfacial mobility is of prime importance to predict the growth velocity of embryos. Making the necessary simplifications to avoid the complex mathematical description of a large group of embryos, we showed that the interactions between embryos promote a collective transformation where capillarity forces can be ignored to predict the evolution of those embryos growing with the available driving force. The model explains notably the in situ observations made by other researchers on the early stage of growth of metastable precipitates in an Al-Cu alloy. The fundamental role of the interfacial mobility was established on the ground that no other factors can explain why the stable θ phase in the Al rich corner does not grow substantially before the θ′ phase during an ageing treatment. The explanation can likely be applied to all stable phases that precipitate only at high temperatures. By considering the interfacial mobility as a fundamental parameter, actual precipitation models will certainly gain some predictive capability.

Disclosure statement

No potential conflict of interest was reported by the author.