Effects of number of slip systems on slip transmission between neighbouring grains

ABSTRACT

Slip transmission between neighbouring grains is needed for the occurrence of plastic deformation in polycrystals. A geometric factor defined for a pair of grains with a certain orientation relationship is used to determine the slip transmission. Two slip transmission factors are calculated for randomly oriented grains. One is the slip transmission factor averaged for randomly oriented grains and the other is the minimum of the transmission factors among all possible orientation relationships. The possible number of slip systems in a grain varies for different metals and alloys. The effects of the number of slip systems on the transmission factors are discussed.

KEYWORDS:

• Deformation
• plastic deformation
• crystal symmetry
• polycrystalline
• slip transmission

1. Introduction

Plastic deformation of metals and alloys is usually caused by slip deformation which depends on their crystal structures. Because metal and alloy polycrystals are aggregates of crystal grains with different orientations, slip transmission between slip systems of neighbouring grains is necessary for plastic deformation [1–5]. In a metal with a hexagonal close-packed (hcp) crystal structure, the total number of possible slip systems in a grain is generally lower than in a metal with a face-centred cubic (fcc) crystal structure. Although slip transmission between neighbouring grains is considered to be more difficult in the former crystal structure, the degree of difficulty of slip transmission has not yet been evaluated quantitatively as a function of the number of slip systems.

With regard to the plastic deformation of polycrystals from an atomistic perspective, the microscopic structures of grain boundaries or dislocations should be included when discussing the slip transmission between neighbouring grains [4,5]. However, in such cases, it is difficult to determine the overall effects of the total number of possible slip systems on the degree of slip transmission, because atomistic analysis involves many factors. Therefore, in this study, we will discuss the slip transmission between neighbouring grains from a macroscopic perspective using a geometric slip transmission factor. We will evaluate the degree of slip transmission for randomly oriented crystal grains, and demonstrate the effects of the number of slip systems on slip transmission in a polycrystal.

2. Geometric slip transmission factor

In the present study, we adopt the geometric slip transmission factor f_LM described by Luster and Morris [3]. Figure 1 shows a schematic illustration of slip planes in neighbouring grains. The right plane is one of the slip planes of Grain A, and p_A and d_A represent the slip plane normal and the slip direction, respectively. The left plane is one of the slip planes of Grain B, and p_B and d_B represent the slip plane normal and the slip direction, respectively, of that slip system. The geometric factor f_LM is given by (1) $f_{\mathrm{L}\mathrm{M}}=\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{p}}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{d}}$(1) where ${\theta }_{\mathrm{p}}$ and ${\theta }_{\mathrm{d}}$ are the acute angles between p_A and p_B and d_A and d_B, respectively. The range of f_LM is $0\le f_{\mathrm{L}\mathrm{M}}\le 1$ and the slip transmission between the slip systems is easier for larger f_LM values.

Figure 1. Schematic illustration showing the slip systems in Grains A and B. Arrows p and d with subscripts A and B indicate the slip plane normal and slip direction in Grains A and B, respectively.

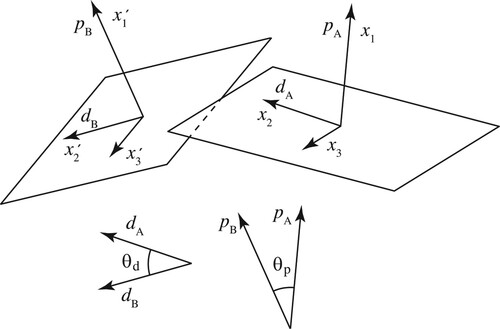
The deformation of a material is a change in the displacement $u_i$ as a function of the position $x_i$. The distortion $\mathrm{\partial }{u}_i/\mathrm{\partial }{x}_j$ is the quantity that describes the deformation. If a shear deformation as large as α occurs as a result of the activation of the slip system of p_A and d_A, using the coordinate system $x_1-x_2-x_3$ fixed to the slip system in Grain A, the following component of distortion is related to α: (2) $\mathrm{\partial }{u}_2/\mathrm{\partial }{x}_1=\alpha$(2)

We can describe the shear deformation α using the coordinate system $x_1^{\mathrm{\prime }}-x_2^{\mathrm{\prime }}-x_3^{\mathrm{\prime }}$ fixed to the slip system in Grain B. The transformation of the coordinate systems from the unprimed to the primed systems gives the magnitude of shear of the slip system of p_B and d_B written as (3) $\mathrm{\partial }{u}_2^{\mathrm{\prime }}/\mathrm{\partial }{x}_1^{\mathrm{\prime }}=\left(\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{p}}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{d}}\right)\alpha =f_{\mathrm{L}\mathrm{M}}\alpha$(3)

Therefore, the factor f_LM is a coefficient of the component of distortion given by the transformation of the coordinate systems. When f_LM is 1, all the shear deformation on the slip system of Grain A is transmitted to that of Grain B. In contrast, when f_LM is zero, the shear deformation on the slip system of Grain A is not transmitted to that of Grain B.

Other slip transmission factors have been proposed. The stress transmission factor f_LC proposed by Livingston and Chalmers is one of them [1]. The two factors f_LM and f_LC give different values for the same orientation relationship between neighbouring grains. For example, when the slip planes and directions of Grains A and B are perpendicular to each other, we have ${\theta }_{\mathrm{p}}={\theta }_{\mathrm{d}}=\pi /2$ and this causes f_LM= 0 but f_LC= 1 [1]. The factor f_LC is considered to be a coefficient of stress or strain components after the transformation of the coordinate systems. Although strain components ${ϵ}_{ij}$ for f_LM are symmetrical and always satisfy ${ϵ}_{ij}={ϵ}_{ji}$, distortion components $\mathrm{\partial }{u}_i/\mathrm{\partial }{x}_j$ for f_LC are unsymmetrical. This causes the difference in the transmission factors. As far as we consider the transmission of plastic shear deformation, slip transmission may be impossible when ${\theta }_{\mathrm{p}}={\theta }_{\mathrm{d}}=\pi /2$. The factor f_LM for unsymmetrical distortion components is appropriate as the slip transmission factor for plastic shear deformation.

In addition to the orientation relationship of slip planes and directions, there are other factors that affect slip transmission in a polycrystal [4,5]. Structure of grain boundary including its orientation is one of the factors [5]. The boundary structure affects motion and arrangement of dislocations and changes stress states near grain boundary regions in polycrystals. Such factors are not included and we cannot discuss, for example, strength of polycrystals or bicrystals with the present analysis. However, simplified geometric analysis made in the present study is useful to extract the effects of number of slip systems on slip transmission as will be shown later.

3. Polycrystals composed of randomly oriented grains

When there are two or more slip systems in a crystal grain, f_LM values for a pair of crystal grains exist for various combinations of the slip systems. Among the various values of f_LM, f_Max which is the maximum of f_LM is treated as a characteristic transmission factor for the pair of crystal grains. When the orientation relationship between the pair of crystal grains changes, f_Max also changes.

Polycrystals without texture are considered to be composed of randomly oriented grains. Such polycrystals were generated computationally. Using sets of three random numbers, three dimensionally random orientations of grains can be generated computationally [6]. In the present study, ${10}^6$ pairs of grains with random orientations were generated using the random numbers. Orientations of grains can be described by rotation axes and angles with respect to a certain reference coordinate system. Depending on the symmetry of the crystal structure of a grain, many equivalent expressions of rotation axes and angles exist for the same crystallographic orientation relationship. Among the various rotation angles, the minimum angle is called the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$. In the present study, the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ is adopted as a parameter in discussions about the dependence of f_Max on the orientation relationship. For example, the range of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for a cubic structure is $0\le {\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}\le {\cos }^{-1}\left[\left(2\sqrt{2}-1\right)/4\right]\approx {62.80}^{\circ }$ and the average value of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for random orientation has been analytically determined to be ${40.74}^{\circ }$ [7,8]. The present numerical calculations for ${10}^6$ random pairs of grains reproduce this analytical result of the average of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ well and deviations from the analytical result were smaller than 0.05% in five times trials. This demonstrates that the computationally generated number of pairs of grains, i.e. ${10}^6$, is sufficient for accurate discussion on the characteristics of a random distribution. Analytical considerations were also taken into account when interpreting the results obtained from the numerical calculations.

4. Slip transmission factor f_Max for the $\left\{111\right\}/〈01\overline{1}〉$ slip system of fcc metals

Here we first consider the slip transmission factor f_Max for the $\left\{111\right\}/〈01\overline{1}〉$ slip system of fcc metals. Because there are four $\left\{111\right\}$ and three $〈01\overline{1}〉$ on each $\left\{111\right\}$, the number N of slip systems in a grain is $12$ in this case. Figure 2 shows the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max when two neighbouring grains have all possible orientation relationships. When ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ is zero (Point O in Figure 2), the orientations of two grains are identical and f_Max is unity. For the lower-angle side of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$, f_Max generally decreases with increasing ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$, but the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max does not show one-to-one correspondence. This is because different orientation relationships with different values of f_Max exist for a certain value of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$.

Figure 2. Relationship between the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and the transmission factor f_Max for fcc metals with $\left\{111\right\}/〈01\overline{1}〉$ slip systems of $N=12$.

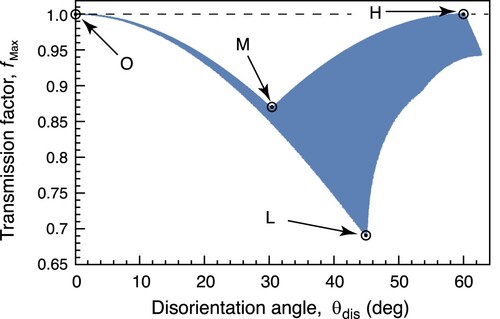
When ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ is larger than ${30}^{\circ }$, the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max is different from the lower-angle side. From Points M to H, f_Max increases with increasing ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ owing to the multiple slip systems in the grain. Analytical considerations revealed that Point H with ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}={60}^{\circ }$ and f_Max= 1 corresponds to the orientation relationship of coherent twins, where one of the slip planes and three slip directions on the slip plane are the same between two grains. The worst orientation relationship for the slip transmission is represented by Point L with ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}={45}^{\circ }$ and f_Max= 0.687. The curve in Figure 2 from Points O to L is given by the rotation around $〈100〉$, and the rotation around $〈100〉$ gives smaller values of f_Max. In contrast, the curve in Figure 2 from Points M to H is given by the rotation around $〈111〉$ from approximately ${30}^{\circ }$ to ${60}^{\circ }$, and the rotation around $〈111〉$ generally gives larger values of f_Max. Other characteristics of Figure 2 obtained by analytical considerations are explained in Appendix 1.

As shown in Figure 1, two angles, ${\theta }_{\mathrm{p}}$ and ${\theta }_{\mathrm{d}}$, between the slip plane normal and the slip directions are used to derive the slip transmission factor f_LM [3]. Hence even if the slip plane normal and the slip direction are changed and the $\left\{01\overline{1}\right\}/〈111〉$ slip system is considered for body-centred cubic (bcc) metals instead of the $\left\{111\right\}/$$〈01\overline{1}〉$ for fcc metals, the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max is not affected. Therefore Figure 2 is also considered to be the result for the $\left\{01\overline{1}\right\}/〈111〉$ slip system for bcc metals.

5. Slip transmission factor f_Max for other slip systems of cubic and hexagonal metals

Figure 3(a,b) show the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max for other slip systems of cubic metals. In Figure 3(a), the results for the $\left\{001\right\}/〈110〉$ slip system reported for high-temperature deformation of an Al-1%Mn alloy [9] are shown. The number N of the slip systems for $\left\{001\right\}/〈110〉$ is 6. In contrast to Figure 2 for $N=12$, the overall tendency of the change of f_Max is a monotonical decrease with increasing ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$. The minimum value of f_Max is 0.5 at ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}={60}^{\circ }$. This minimum value f_Max = 0.5 is smaller than the minimum value f_Max = 0.687 for $N=12$. In contrast, Figure 3(b) shows the results for $\left\{123\right\}/〈11\overline{1}〉$ which is known as one of the slip systems of bcc metals. The number N of the slip systems for $\left\{123\right\}/〈11\overline{1}〉$ is 24. In this case, as shown in Figure 3(b), there are three orientation relationships giving f_Max= 1. They are $〈111〉/{21.79}^{\circ }$, $〈111〉/{38.21}^{\circ }$ and $〈111〉/{60}^{\circ }$. The minimum value of f_Max for $N=24$ is 0.802 at ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}={45}^{\circ }$. This value is larger than the minimum value f_Max = 0.687 for $N=12$. Figure 3(c) shows the result for $\left(0001\right)/〈11\overline{2}0〉$ of the slip system of hcp metals for $N=3$. Although the overall tendency of the change of f_Max is similar to that shown in (a) of $N=6$, there is only one slip plane in a grain for this case and f_Max is zero when slip planes in neighbouring grains are perpendicular to each other. The maximum of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for a hcp structure is ${93.84}^{\circ }$[10] and the condition ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}\ge {90}^{\circ }$ is a necessary condition of f_Max$=0$.

Figure 3. Relationships between the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and the transmission factor f_Max for (a) the Al-1%Mn alloy with $\left\{001\right\}/〈110〉$ slip systems [9] of $N=6$, (b) bcc metals with $\left\{123\right\}/〈11\overline{1}〉$ slip systems of $N=24$ and (d) hcp metals with $\left(0001\right)/〈11\overline{2}0〉$ slip systems of $N=3$.

Figure 4 show the frequency of f_Max for randomly oriented grains when the grains are those of (a) fcc alloys with $\left\{001\right\}/〈110〉$ slip systems[9] of $N=6$, (b) fcc metals with $\left\{111\right\}/〈01\overline{1}〉$ slip systems of $N=12$, (c) bcc metals with $\left\{123\right\}/〈11\overline{1}〉$ slip systems of $N=24$ and (d) hcp metals with $\left(0001\right)/〈11\overline{2}0〉$ slip system of $N=3$. In Figure 4(a–c), the peaks of frequency are shown and the peaks become sharper and shift to higher values with increasing N from 6 to 24. In contrast to this tendency, the variation for $N=3$ shown in Figure 4(d) is fairly flat. The frequency of f_Max is the highest at f_Max$=0$ and decreases monotonically with increasing f_Max.

Figure 4. Frequency of the transmission factor f_Max for randomly oriented grains when the grains are (a) fcc alloys with $\left\{001\right\}/〈110〉$ slip systems [9] of $N=6$, (b) fcc metals with $\left\{111\right\}/〈01\overline{1}〉$ slip systems of $N=12$, (c) bcc metals with $\left\{123\right\}/〈11\overline{1}〉$ slip systems of $N=24$ and (d) hcp metals with $\left(0001\right)/〈11\overline{2}0〉$ slip systems of $N=3$.

6. Average and minimum slip transmission factors: F_Ave and F_Min

We will derive two slip transmission factors for the polycrystal. One is F_Ave which is the average of f_Max for randomly oriented grains. The other is F_Min which is the minimum of f_Max among all possible orientation relationships of neighbouring grains. For the initial stage of plastic deformation, occurrence of plastic deformation is resticted to regions where it occurs easily and elastic accommodation compensates the difference in the amount of plastic deformation. The average slip transmission factor F_Ave may be appropriate as a measure of the slip transmission of such initial stage of plastic deformation. On the other hand, for the occurrence of overall plastic deformation in a polycrystal, slip transmission between all neighbouring grains are needed. The minimum slip transmission factor F_Min may be appropriate as a measure of the occurrence of such deformation stage.

The values of F_Ave can be obtained from Figure 4, which are 0.752 for (a) $\left\{001\right\}/〈110〉$ of $N=6$, $0.899$ for (b) $\left\{111\right\}/〈01\overline{1}〉$ of $N=12$, $0.948$ for (c) $\left\{123\right\}/〈11\overline{1}〉$ of $N=24$ and 0.468 for (d) $\left(0001\right)/〈11\overline{2}0〉$ of $N=3$. The values of F_Min obtained from Figures 2–4 are 0.5 for $\left\{001\right\}/〈110〉$ of $N=6$, $0.687$ for $\left\{111\right\}/〈01\overline{1}〉$ of $N=12$, $0.802$ for $\left\{123\right\}/〈11\overline{1}〉$ of $N=24$ and 0 for $\left(0001\right)/〈11\overline{2}0〉$ of $N=3$.

Considering that materials have various crystal structures and slip systems, we calculated values of F_Ave and F_Min for a wide range of N values. Table 1 summarises the results, including those obtained from Figures 2–4. Although two different slip systems are considered for $N=6$ and $N=12$ as shown in Table 1, the values of F_Ave and F_Min for the slip systems with the same N values are almost the same. The slip systems for tetragonal and orthorhombic structures shown in Table 1 are those assumed from the crystal structures. The other slip systems are well known ones and have been reported previously [9,11,12]. In the numerical calculations to obtain the values of F_Ave, appropriate symmetrical operations should be made depending on the crystal structure[10]. The soundness of the symmetrical operations made in the present numerical calculations is explained in Appendix 2.

Table 1. The number N of slip systems, the average slip transmission factor F_Ave and the minimum slip transmission factor F_Min for various crystal structures and slip systems.

Crystal structure	Slip systems	No. of slip systems, N	FAve	FMin
Cubic	$\left\{123\right\}/〈11\overline{1}〉$^a	24	0.948	0.802
	$\left\{011\right\}/〈11\overline{1}〉$^a $\left\{111\right\}/〈01\overline{1}〉$^b	12	0.899	0.687
	$\left\{112\right\}/〈11\overline{1}〉$^a $\left\{111\right\}/〈11\overline{2}〉$^b	12	0.897	0.722
	$\left\{001\right\}/〈110〉$^c	6	0.752	0.5
	$\left\{011\right\}/〈01\overline{1}〉$^d	6	0.732	0.417
Hexagonal	$\left(0001\right)/〈11\overline{2}0〉$^e	3	0.468	0
Tetragonal	$\left(001\right)/\left[100\right],\left[010\right]$^f	2	0.430	0
Orthorhombic	$\left(001\right)/\left[100\right]$^f	1	0.270	0

^a Many bcc metals and alloys.

^b Many fcc metals and alloys.

^c Al-1%Mn alloy at high temperatures [9].

^d Some fcc metals and alloys at high temperatures [9,11,12].

^e Many hcp metals and alloys.

^f Assumed from the crystal structure.

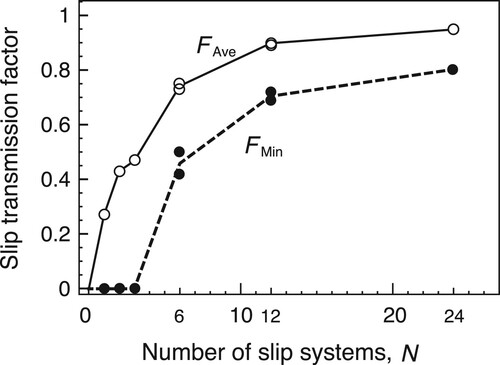
Using the values shown in Table 1, the relationship between N and F_Ave or F_Min is graphically indicated in Figure 5. F_Ave increases monotonically with increasing N for $N=1\mathrm{t}\mathrm{o}24$. On the other hand, the variation of F_Min shows no slip transmission occurs for $N=1\mathrm{t}\mathrm{o}3$. However, the increasing behaviour of F_Ave and F_Min are similar for $N\ge 6$ and shows that the slip transmission becomes easier with increasing N. Although this is the result obtained only by using the geometric factor f_LM described by Luster and Morris [3], we succeeded to extract the effect of the number N of slip systems that the slip transmission in polycrystals becomes easier with increasing N.

Figure 5. Relationships between the number N of slip systems and the average F_Ave and the minimum F_Min transmission factors for polycrystals composed of randomly oriented grains.

In the present study, we have obtained the average slip transmission factor F_Ave and the minimum slip transmission factor F_Min for polycrystals composed of randomly oriented grains. When textures with a certain tendency of grain orientations are included, the effects of texture on the average slip transmission between neighbouring grains can be discussed using the present method of analysis. This will be the subject of our future work.

7. Conclusions

In the present paper, the necessity of slip transmission between neighbouring grains for plastic deformation in polycrystals was discussed from a macroscopic perspective. The average transmission factor F_Ave and the minimum transmission factor F_Min for randomly oriented grains were used to evaluate the slip transmission in polycrystals. The number N of possible slip systems in a grain differs according to the metal or alloys. The effects of N on F_Ave and F_Min were discussed. We succeeded to extract the effect of the number N of slip systems that the slip transmission in polycrystals becomes easier with increasing N.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by JSPS KAKENHI Grant Number 19K04985.

Appendix

Appendix 1. Details of Figure 2

The curve from Points O to M illustrates the upper bound of f_Max for the range of the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$. Analysis reveals that the change along this curve is the rotation as much as ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ around the axis $v_{\mathrm{O}\mathrm{M}}$ written as $v_{\mathrm{O}\mathrm{M}}=\left(\begin{array}{c}\sqrt{6}/6\\ \left(3+\sqrt{6}\right)/6\\ -\left(3-\sqrt{6}\right)/6\end{array}\right)$

This axis $v_{\mathrm{O}\mathrm{M}}$ has the angle of ${45}^{\circ }$ with respect to both of $\left[111\right]$ and $\left[01\overline{1}\right]$. Because the change in orientation from Points M to H results from rotation around $\left[111\right]$, the coordinates of Point M are ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}={30.27}^{\circ }$ and f_Max = 0.868.

We have the following analytical expressions for the boundaries of the region shown in Figure 2:

Curve from Points from O to L: $f_{\mathrm{M}\mathrm{a}\mathrm{x}}=\left(1+\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}\right)\left(1+2\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}\right)/6.$

Curve from Points from O to M: $f_{\mathrm{M}\mathrm{a}\mathrm{x}}=\mathrm{c}\mathrm{o}{\mathrm{s}}^4\left({\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}/4\right).$

Curve from Points from M to H: $f_{\mathrm{M}\mathrm{a}\mathrm{x}}=\mathrm{c}\mathrm{o}\mathrm{s}\left(\pi /3-{\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}\right).$

Because the symmetry of the cubic crystal affects the relationship between ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ and f_Max for larger values of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$, the curve from Points L to H at the right-hand-side of Figure 2 cannot be expressed by a simple function of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$.

Appendix 2. Characteristic values of the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for various crystal structures

Characteristic values of the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for various crystal structures are shown in Table A1. The numerical results shown in this table were obtained by computationally generating ${10}^6$ pairs of randomly oriented grains. The present numerical results of average values of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for randomly oriented grains are very close to the previous analytical results of average of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ [10]. This demonstrates the soundness of the symmetrical operations used in the present numerical calculations.

Table A1. Maximum values of the disorientation angle ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for various crystal structures [10]. Analytical [10] and numerical results of average of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ for random orientations.

Crystal structure	Maximum value of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ (deg)	Average value of ${\theta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ (deg)
		Analytical	Numerical
Cubic	62.80	40.74	40.74
Hexagonal	93.84	60.07	60.07
Tetragonal	98.42	63.01	63.05
Orthorhombic	120	75.16	75.15