Corrigendum

This article refers to:

Subexponential Asymptotics of the Stationary Distributions of GI/G/1-Type Markov Chains

Article title: “Subexponential Asymptotics of the Stationary Distributions of GI/G/1-Type Markov Chains”

Authors: Tatsuaki Kimura, Hiroyuki Masuyama, and Yutaka Takahashi

Journal: Stochastic Models

Bibliometrics: Volume 29, Issue 2, pages 190–239

DOI: 10.1080/15326349.2013.783286

 The aim of this paper is to correct the minor errors of Propositions 2.4.1 and 2.4.2 of Kimura et al.^[4]

As in subsection 2.4 of Kimura et al.^[4], we consider a (possibly defective) MAdP with state space and kernel . For simplicity, we write (k₁, j₁) → (k₂, j₂) (respectively ) when there exists a path (respectively exist no paths) from state (k₁, j₁) to state (k₂, j₂) with some positive probability.

To define the period τ of the MAdP , we need the following conditions (see Assumption B.1 of Kimura et al.^[3]):

1. is irreducible (Assumption 1 (b) of Kimura et al.^[4]); and

2. for each there exists some such that (0, i) → (k_i, i), or equivalently, ∑^∞_{n = 1}A_{i, i}*ⁿ(k_i) > 0, where denotes the n-fold convolution of , i.e., and for n ⩾ 2.

The conditions (A) and (B) are necessary for the propositions, lemmas, and theorems associated with the period τ, such as Propositions 2.4.1 and 2.4.2.

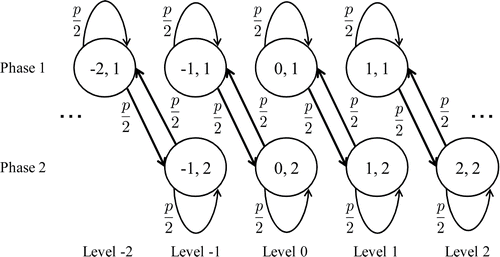
We now give an example in which the condition (B) does not hold whereas the conditions of Propositions 2.4.1 and 2.4.2 (i.e., Assumption 1 of Kimura et al.^[4]) are satisfied.

Example.

Let and Clearly, is irreducible and strictly substochastic. It also follows from for all that is irreducible and thus is positive recurrent (see Proposition 2.2.2 of Kimura et al.^[4]), which shows that this example satisfies Assumption 1 of Kimura et al.^[4]. On the other hand, if n₁ ⩾ 2; or n₃ ⩾ 2; or n₁ + n₃ ⩾ 2 and k = l. This fact implies that for all and . In addition, we can readily prove (see Figure 1) that

Therefore,∑^∞_{n = 1}A_{i, i}*ⁿ(k) = 0 for all and . As a result, the condition (B) is not satisfied and the period τ cannot be defined.

Figure 1 Transition diagram.

Probably, artificial settings such as the above example would not arise from typical queueing models (e.g. continuous-time BMAP/G/1, BMAP/PH/c queues and their variants). In other words, as far as we consider natural queueing models, the condition (B) would hold for resulting GI/G/1-type Markov chains. In addition, we can expect that the period τ (if it exists) is equal to one in many cases. From these reasons, it is assumed in the literature that τ exists and equals to one (see e.g. Bini et al.^[1] or Gail et al.^[2]).

Finally, we present a lemma, which provides a sufficient condition under which the condition (B) holds.

Lemma.

Suppose that and are irreducible. If is stochastic, then the condition (B) holds.

Proof.

We prove this lemma by contradiction. To this end, we assume that the negation of the condition (B), i.e., there exists some such that Since is an irreducible stochastic matrix, which diverges to infinity. Therefore, for each pair of phases , there exists some such that (0, i) → (k_{i, j}, j). Using this fact, we have the following path. Combining equations (1) and (2) leads to Furthermore, it follows from equations (1) and (3) that, for each , and thus must be uniquely determined. Indeed, suppose that there exist some and integer such that . We then have Note here that equation (3) yields , which is the contradiction to equation (1).

The above argument shows that, for each , which implies there exists some such that where [ · ]_i denotes the ith element of the vector in square brackets.

We now note that for all k ⩽ −1. Thus, since is stochastic, From equations (4) and (5), we have Equations (4) and (6) imply that level zero is not reachable from states {(k, i₀); k ⩾ K}. Note here that the Markov chain with transition probability matrix follows the same law as the MAdP while the former Markov chain is away from level zero. Thus, equations (4) and (6) are inconsistent with the irreducibility of . Consequently, there exists no integer such that equation (1) holds, i.e., the condition (B) is true.

The above lemma implies that the period τ is well-defined under Assumption 2 (I) of Kimura et al.^[4]. Thus, although the period τ is needed by the proofs of the lemmas and theorems in subsections 3.1 and 4.1, these results are true because they are proved under Assumption 2 (I). Similarly, Propositions 2.5.2 and 2.5.3 are true because the two propositions are proved under the conditions of the lemma presented above. On the other hand, the lemmas and theorems in subsections 3.2 and 4.2 are proved under Assumption 2 (II) of Kimura et al.^[4], independently of the period τ. As a result, for correctness, all we have to do is add the condition (B) to the conditions of Propositions 2.4.1 and 2.4.2.