Geometrically nonlinear vibration analysis of eccentrically stiffened porous functionally graded annular spherical shell segments

Abstract

This article investigates nonlinear free vibrations of porous functionally graded (FG) annular spherical shell segments surrounded by elastic medium and reinforced by circumferential stiffeners. Porous FG material contains distributed even and un-even porosities and is modeled based on refined power–law function. The governing equations of stiffened porous annular spherical shell segments have been derived according to thin shell theory with the geometrical nonlinear in von Karman–Donnell sense and the smeared stiffeners method. An analytical trend has been provided for solving the nonlinear governing equations. Obtained results demonstrate the significance of porosity distribution, geometric nonlinearity, foundation factors, stiffeners and curvature radius on vibration characteristics of porous FG annular spherical shell segments.

Keywords:

• Nonlinear vibration
• spherical shell
• annular shell segment
• porous material
• shell theory

1. Introduction

Functionally graded materials appropriately incorporate the microstructure and functions and possess preferable mechanical properties compared to usual multi-layered composites leading to their usage in promising fields of materials science (Azimi et al. 2017; Mirjavadi et al. 2017; Azimi et al. 2018; Mirjavadi, Afshari, Barati, et al. 2018; Al-Maliki, Faleh, and Alasadi 2019; Ebrahimi, Dabbagh, and Rastgoo 2019; Mirjavadi, Forsat, Hamouda, et al. 2019; Mirzaei 2019). Commonly, a functional gradient (FG) material is constructed from metallic and ceramic constituents (Abdelaziz et al. 2017; Mahmoudi et al. 2019; Wang et al. 2019; Wu et al. 2019; Trinh and Kim 2019a, 2019b). Material imperfections in a FG material are obvious during the production period, leading to dispersion of pores within the material texture (Wattanasakulpong et al. 2012; Li, Wu, Chen, Cheng, et al. 2018; Ahmed, Fenjan, and Faleh 2019; Hamad, Khalaf, and Faleh 2019; Ahmed et al. 2020). Furthermore, the shapes and distributions of porosities are controllable via the production methods. For simulating the influences of the porosities on the mechanical characteristics of an FG material, two kinds of dispersion for porosities may be introduced, namely, even (uniform) dispersion and un-even dispersion, and a refined power–law function can be used for describing the material variation. According to the refined power–law function, many researchers systematically examined the stability and vibrations of porous FG structural components at different scales (Wu et al. 2018; Addou et al. 2019; Liu et al. 2019; Trinh, Nguyen, and Kim 2019). These investigations have reported that porosities play a remarkable role in analyzing the mechanical behaviors of beam and plate structures. Although there were many articles on the mechanical behaviors of porous FG structures, no one study the nonlinear vibration behavior of porous FG annular spherical shell segments.

The annular spherical shell is broadly applied in several engineering fields including civil, mechanical, aerospace engineering. The annular spherical shell and annular spherical segment are two particular shapes of the spherical shell. Due to significant practical application of such structures, some researchers studied their mechanical behaviors via different approaches. For example, Duc, Quang, and Anh (2017) studied vibrational behavior of FG spherical shells rested on elastic substrate. Effects of elastic boundary conditions on free vibration behavior of thin spherical shells have been examined by Xie, Chen, and Li (2017). Based on an analytical solution, Duc et al. (2019) examined nonlinear dynamic behaviors of annular spherical shells made of nano-composite materials. Also, Li, Wu, et al. (2019) provided a semi-analytical approach for examining linear vibration behavior of annular spherical shells under different edge conditions. Recently, Gao et al. (2020) examined free vibrations of functionally graded spherical shell based on Ritz solution.

Recently, several researchers have focused on the static and dynamical characteristics of eccentrically stiffened plates and shells since such structural components are usually fortified with employment of stiffening elements to introduce the benefits of improved load-carrying capabilities with relatively low extra weight penalties. Furthermore, eccentrically stiffened plates and shells are main structures in engineering scheme of missile, aircraft and aerospace industries (Ninh and Bich 2016; Su et al. 2019). Despite the evident significance in practical applications, it is realized from the literature that studies on vibrations of annular spherical segment made porous FG material and reinforced by arrays of stiffeners are comparatively scarce.

Within this article, an investigation of nonlinear vibration behaviors of stiffened annular spherical shell segments constructed from porous FG materials has been presented. Porous FG material contains distributed even and un-even porosities and is modeled based on refined power–law function. The governing equations of stiffened porous annular spherical shell segments have been derived according to thin shell theory with the geometrical nonlinear in von Karman–Donnell sense and the smeared stiffeners method. Based on smeared stiffeners method, the force and moment resultants can be established as functions of stiffeners geometries and spacing (Hao et al. 2014). An analytical trend has been provided for solving the nonlinear governing equations. Obtained results demonstrate the significance of porosity distribution, geometric nonlinearity, foundation factors, stiffeners and curvature radius on vibration characteristics of porous FG annular spherical shell segments.

2. Material properties for porous FG annular spherical shell

Pores within the material texture may affect both elastic modulus and mass density of FGMs. Based upon refined power–law function, one can introduce the elastic modulus (E) and mass density ($\rho$) of FG materials as functions of porosity volume fraction (ξ) and gradient exponent (p) as (Ahmed, Fenjan, and Faleh 2019):

Even porosity distribution: (1) $$E(z)=\left(E_c-E_m\right){\left(\frac{z}{h}+\frac{1}{2}\right)}^p+E_m-\frac{\xi }{2}\left(E_c+E_m\right)$$(1) (2) $$\rho (z)=\left({\rho }_c-{\rho }_m\right){\left(\frac{z}{h}+\frac{1}{2}\right)}^p+{\rho }_m-\frac{\xi }{2}\left({\rho }_c+{\rho }_m\right)$$(2) Un-even porosity distribution: (3) $$E(z)=\left(E_c-E_m\right){\left(\frac{z}{h}+\frac{1}{2}\right)}^p+E_m-\frac{\xi }{2}\left(E_c+E_m\right)\mathrm{(}1\mathrm{}-\mathrm{}\frac{2\left|z\right|}{h}\mathrm{)}$$(3) (4) $$\rho (z)=\left({\rho }_c-{\rho }_m\right){\left(\frac{z}{h}+\frac{1}{2}\right)}^p+{\rho }_m-\frac{\xi }{2}\left({\rho }_c+{\rho }_m\right)\mathrm{(}1\mathrm{}-\mathrm{}\frac{2\left|z\right|}{h}\mathrm{)}$$(4)

In above relations, subscripts c and m respectively denote the material properties of ceramic and metallic ingredients.

3. Formulation for annular spherical shell segment

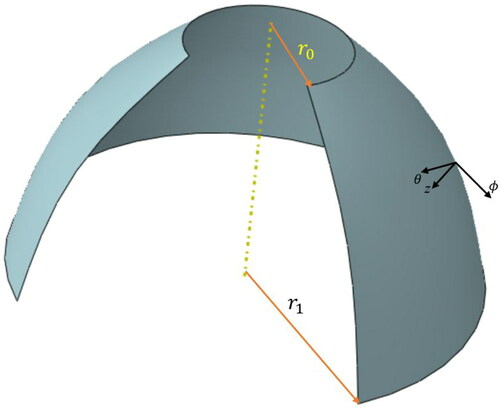
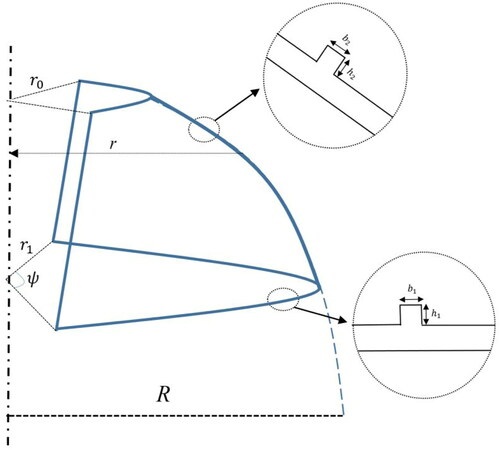
A porous FG annular spherical shell segment of thickness h has been depicted in Fig. 1 which contains radial and circumferential stiffeners as shown in Fig. 2. Here, r is radius of the spherical shell defined as a function of base radius (R) as: (5) $$r=R\hspace{0.17em}\text{sin}\hspace{0.17em}\varphi$$(5) where $\varphi$ is the meridional angle of the spherical shell. Also, considering the shallowness of the spherical shell it must be stated that $dr=Rd\varphi .$ Based on this shell assumption, the strain field may be defined in below form (Barati and Zenkour 2019): (6) $$\left\{\begin{array}{c}{\epsilon }_r\\ {\epsilon }_{\theta }\\ {\gamma }_{r\theta }\end{array}\right\}=\left\{\begin{array}{c}{\epsilon }_r^0\\ {\epsilon }_{\theta }^0\\ {\gamma }_{r\theta }^0\end{array}\right\}-z\left\{\begin{array}{c}{\chi }_r\\ {\chi }_{\theta }\\ 2{\chi }_{r\theta }\end{array}\right\}$$(6) in which (7) $$\begin{array}{c}{\epsilon }_r^0=\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R},\mathrm{}\\ {\epsilon }_{\theta }^0=\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R},\mathrm{}\\ {\gamma }_{r\theta }^0=\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta },\\ {\chi }_r=\frac{{\partial }^{2}w}{\partial r^2},\mathrm{}{\chi }_{\theta }=\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2},\mathrm{}{\chi }_{r\theta }=\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }\end{array}$$(7)

Figure 1. Configuration of annular spherical shells.

Figure 2. Geometry of the shell with stiffeners.

Above field contains (u, v, w) displacements in ($\varphi ,$θ, z) directions. By using the classic shell assumption and FG material, stress–strain relations can be summarized as (Ahmed, Fenjan, and Faleh 2019): (8) $$\{\begin{array}{c}{\sigma }_r\\ {\sigma }_{\theta }\\ {\sigma }_{r\theta }\end{array}\}=\frac{E(z)}{1-v^2}\left(\begin{array}{ccc}1& v& 0\\ v& 1& 0\\ 0& 0& (1-v)/2\end{array}\right)\{\begin{array}{c}{\epsilon }_r\\ {\epsilon }_{\theta }\\ {\gamma }_{r\theta }\end{array}\}$$(8) where σ_i (i = r, θ, r θ) are stress field components. The stresses leads to below resultants via integrating Eq. (8)(8) $$\{\begin{array}{c}{\sigma }_r\\ {\sigma }_{\theta }\\ {\sigma }_{r\theta }\end{array}\}=\frac{E(z)}{1-v^2}\left(\begin{array}{ccc}1& v& 0\\ v& 1& 0\\ 0& 0& (1-v)/2\end{array}\right)\{\begin{array}{c}{\epsilon }_r\\ {\epsilon }_{\theta }\\ {\gamma }_{r\theta }\end{array}\}$$(8) over shell thickness as: (9) $$\begin{array}{c}{N}_r=(A_{11}+\frac{E_s{A}_{s_1}}{s_1})[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+A_{12}\left[\frac{1}{r}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -(B_{11}+C_1)\frac{{\partial }^{2}w}{\partial r^2}-B_{21}[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\end{array}$$(9) (10) $$\begin{array}{c}{N}_{\theta }=A_{12}[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+(A_{22}+\frac{E_s{A}_{s_2}}{s_2})\left[\frac{1}{r}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -B_{12}\frac{{\partial }^{2}w}{\partial r^2}-(B_{22}+C_2)[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\end{array}$$(10) (11) $$N_{r\theta }=A_{66}[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2B_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }]$$(11) (12) $$\begin{array}{c}{M}_r=(B_{11}+C_1)[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+B_{12}\left[\frac{1}{r}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -(D_{11}+\frac{E_s{I}_{s_1}}{s_1})\frac{{\partial }^{2}w}{\partial r^2}-D_{12}[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\end{array}$$(12) (13) $$\begin{array}{c}{M}_{\theta }=B_{12}[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+(B_{22}+C_2)\left[\frac{1}{r}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -D_{12}\frac{{\partial }^{2}w}{\partial r^2}-(D_{22}+\frac{E_s{I}_{s_2}}{s_2})[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\end{array}$$(13) (14) $$M_{r\theta }=B_{66}[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2D_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }]$$(14) in which E_s is Young’s modulus of stiffeners; s₁ nd s₂ are spacing of stiffeners; A_s1 and A_s2 are cross sections of stiffeners and (15) $$\begin{array}{c}{A}_{11}={\int }_{-h/2}^{h/2}\frac{E(z)}{1-v^2}dz,A_{12}={\int }_{-h/2}^{h/2}\frac{E(z)v}{1-v^2}dz,\\ A_{66}={\int }_{-h/2}^{h/2}\frac{E(z)}{2(1+v)}dz,B_{11}={\int }_{-h/2}^{h/2}\frac{E(z)}{1-v^2}zdz,\\ B_{12}={\int }_{-h/2}^{h/2}\frac{E(z)v}{1-v^2}zdz,B_{66}={\int }_{-h/2}^{h/2}\frac{E(z)}{2(1+v)}zdz,\\ D_{11}={\int }_{-h/2}^{h/2}\frac{E(z)}{1-v^2}{z}^{2}dz,D_{12}={\int }_{-h/2}^{h/2}\frac{E(z)v}{1-v^2}{z}^{2}dz,\\ D_{66}={\int }_{-h/2}^{h/2}\frac{E(z)}{2(1+v)}{z}^{2}dz.\end{array}$$(15)

Detailed expressions of (A_ij, B_ij, D_ij) based on even porosity distribution have been presented in Appendix and (16) $$\begin{array}{c}{s}_1=\frac{2\pi r}{n_r},s_2=\frac{R}{n_{\theta }}(\arcsin (\frac{r_1}{R})-\arcsin (\frac{r_0}{R}))\\ I_{s_1}^{}=\frac{b_1{\left(h_1\right)}^3}{12}+A_{s_1}{\left(z_1\right)}^2,I_{s_2}^{}=\frac{b_2{\left(h_2\right)}^3}{12}+A_{s_2}{\left(z_2\right)}^2\\ C_1=\frac{E_s{A}_{s_1}{z}_1}{s_1},C_2=\frac{E_s{A}_{s_2}{z}_2}{s_2}\\ z_1=0.5(h+h_1),z_2=0.5(h+h_2)\end{array}$$(16)

Note that h₁ and h₂ are height of stiffeners; b₁ and b₂ are width of stiffeners. Also, n_r and n_θ are the number of stiffeners. Now, one can express the governing equations for an annular spherical shell surrounded by elastic medium (Li, Wu, et al. 2019) with parameters k_w, k_p as (Duc et al. 2017): (17) $$\begin{array}{c}\frac{\partial N_r}{\partial r}+\frac{1}{r}\frac{\partial N_{r\theta }}{\partial \theta }+\frac{1}{r}(N_r-N_{\theta })=I_0\frac{{\partial }^{2}u}{\partial t^2}\\ \end{array}$$(17) (18) $$\begin{array}{c}\frac{\partial N_{r\theta }}{\partial r}+\frac{1}{r}\frac{\partial N_{\theta }}{\partial \theta }+\frac{2}{r}{N}_{r\theta }=I_0\frac{{\partial }^{2}v}{\partial t^2}\\ \end{array}$$(18) (19) $$\begin{array}{c}\frac{{\partial }^2{M}_r^{}}{\partial r^2}+\frac{2}{r}\frac{\partial M_r^{}}{\partial r}+\frac{2}{r}\frac{{\partial }^2{M}_{r\theta }^{}}{\partial r\partial \theta }+\frac{2}{r^2}\frac{\partial M_{r\theta }^{}}{\partial \theta }+\frac{1}{r^2}\frac{{\partial }^2{M}_{\theta }^{}}{\partial {\theta }^2}-\frac{1}{r}\frac{\partial M_{\theta }^{}}{\partial r}+\frac{(N_r+N_{\theta })}{R}\\ +N_r\frac{{\partial }^{2}w}{\partial r^2}-2N_{r\theta }(\frac{1}{r^2}\frac{\partial w}{\partial \theta }-\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta })+N_{\theta }(\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})\\ -k_{w}w+k_P(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})=I_0\frac{{\partial }^{2}w}{\partial t^2}\\ \end{array}$$(19) where $I_0={\int }_{-h/2}^{h/2}\rho dz.$ By substituting Eqs. (9)–(14) into Eqs. (17)(17) $$\begin{array}{c}\frac{\partial N_r}{\partial r}+\frac{1}{r}\frac{\partial N_{r\theta }}{\partial \theta }+\frac{1}{r}(N_r-N_{\theta })=I_0\frac{{\partial }^{2}u}{\partial t^2}\\ \end{array}$$(17) and (19)(19) $$\begin{array}{c}\frac{{\partial }^2{M}_r^{}}{\partial r^2}+\frac{2}{r}\frac{\partial M_r^{}}{\partial r}+\frac{2}{r}\frac{{\partial }^2{M}_{r\theta }^{}}{\partial r\partial \theta }+\frac{2}{r^2}\frac{\partial M_{r\theta }^{}}{\partial \theta }+\frac{1}{r^2}\frac{{\partial }^2{M}_{\theta }^{}}{\partial {\theta }^2}-\frac{1}{r}\frac{\partial M_{\theta }^{}}{\partial r}+\frac{(N_r+N_{\theta })}{R}\\ +N_r\frac{{\partial }^{2}w}{\partial r^2}-2N_{r\theta }(\frac{1}{r^2}\frac{\partial w}{\partial \theta }-\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta })+N_{\theta }(\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})\\ -k_{w}w+k_P(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})=I_0\frac{{\partial }^{2}w}{\partial t^2}\\ \end{array}$$(19) , nonlinear governing equations in terms of displacement components are expressed as follows: (20) $$\begin{array}{c}\frac{\partial }{\partial r}\left\{\right(A_{11}+\frac{E_s{A}_{s_1}}{s_1}\left)\right[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+A_{12}[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -(B_{11}+C_1)\frac{{\partial }^{2}w}{\partial r^2}-B_{21}[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\}+\frac{1}{r}\frac{\partial }{\partial \theta }\{A_{66}[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]\\ -2B_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }]\}+(A_{11}+\frac{E_s{A}_{s_1}}{s_1}\left)\right[\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{2r}{(\frac{\partial w}{\partial r})}^2-\frac{1}{r}\frac{w}{R}]\\ +A_{12}\left[\frac{1}{r^2}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^3}{(\frac{\partial w}{\partial \theta })}^2-\frac{1}{r}\frac{w}{R}]-\frac{1}{r}(B_{11}+C_1)\frac{{\partial }^{2}w}{\partial r^2}-B_{21}[\frac{1}{r^2}\frac{\partial w}{\partial r}+\frac{1}{r^3}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\\ -A_{12}[\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{2r}{(\frac{\partial w}{\partial r})}^2-\frac{1}{r}\frac{w}{R}]-(A_{22}+\frac{E_s{A}_{s_2}}{s_2})\left[\frac{1}{r^2}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^3}{(\frac{\partial w}{\partial \theta })}^2-\frac{1}{r}\frac{w}{R}]\\ +\frac{1}{r}{B}_{12}\frac{{\partial }^{2}w}{\partial r^2}+(B_{22}+C_2)[\frac{1}{r^2}\frac{\partial w}{\partial r}+\frac{1}{r^3}\frac{{\partial }^{2}w}{\partial {\theta }^2}]=I_0\frac{{\partial }^{2}u}{\partial t^2}\end{array}$$(20) (21) $$\begin{array}{c}\frac{\partial }{\partial r}\left\{A_{66}\right[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2B_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }\left]\right\}\\ +\frac{1}{r}\frac{\partial }{\partial \theta }\left\{A_{12}\right[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+(A_{22}+\frac{E_s{A}_{s_2}}{s_2}\left)\right[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -B_{12}\frac{{\partial }^{2}w}{\partial r^2}-(B_{22}+C_2)[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\}\\ +\frac{2}{r}\left\{A_{66}\right[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2B_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }\left]\right\}=I_0\frac{{\partial }^{2}v}{\partial t^2}\end{array}$$(21) (22) $$\begin{array}{c}(\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r})\{(B_{11}+C_1)[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+B_{12}[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -(D_{11}+\frac{E_s{I}_{s_1}}{s_1})\frac{{\partial }^{2}w}{\partial r^2}-D_{12}[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\}\\ +(\frac{2}{r}\frac{{\partial }^2}{\partial r\partial \theta }+\frac{2}{r^2}\frac{\partial }{\partial \theta })\left\{B_{66}\right[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2D_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }\left]\right\}\\ +(\frac{1}{r^2}\frac{{\partial }^2}{\partial {\theta }^2}-\frac{1}{r}\frac{\partial }{\partial r})\left\{B_{12}\right[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+(B_{22}+C_2)[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -D_{12}\frac{{\partial }^{2}w}{\partial r^2}-(D_{22}+\frac{E_s{I}_{s_2}}{s_2})[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\}\\ +\frac{1}{R}(A_{11}+A_{12}+\frac{E_s{A}_{s_1}}{s_1})[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+\frac{1}{R}(A_{22}+A_{12}+\frac{E_s{A}_{s_2}}{s_2})\left[\frac{1}{r}\right(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -\frac{1}{R}(B_{11}+B_{12}+C_1)\frac{{\partial }^{2}w}{\partial r^2}-\frac{1}{R}(B_{22}+C_2+B_{21})[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\\ +\left\{\right(A_{11}+\frac{E_s{A}_{s_1}}{s_1}\left)\right[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+A_{12}[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -(B_{11}+C_1)\frac{{\partial }^{2}w}{\partial r^2}-B_{21}[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\}\frac{{\partial }^{2}w}{\partial r^2}\\ -2\left\{A_{66}\right[\frac{1}{r}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial \theta }]-2B_{66}[\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta }-\frac{1}{r^2}\frac{\partial w}{\partial \theta }\left]\right\}(\frac{1}{r^2}\frac{\partial w}{\partial \theta }-\frac{1}{r}\frac{{\partial }^{2}w}{\partial r\partial \theta })\\ +\left\{A_{12}\right[\frac{\partial u}{\partial r}+\frac{1}{2}{(\frac{\partial w}{\partial r})}^2-\frac{w}{R}]+(A_{22}+\frac{E_s{A}_{s_2}}{s_2}\left)\right[\frac{1}{r}(\frac{\partial v}{\partial \theta }+u)+\frac{1}{2r^2}{(\frac{\partial w}{\partial \theta })}^2-\frac{w}{R}]\\ -B_{12}\frac{{\partial }^{2}w}{\partial r^2}-(B_{22}+C_2)[\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}]\left\}\right(\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})\\ -k_{w}w+k_p(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2})=I_0\frac{{\partial }^{2}w}{\partial t^2}\end{array}$$(22)

4. Solution procedure

Here, the solution of nonlinear vibration problem of porous FG annular spherical shell has been provided. First, it must be stated that the edges of annular spherical shell are simply-supported based on below conditions: (23) $$\begin{array}{c}w=M_r=N_{r\theta }=0{\mathrm{}\mathrm{}\text{at}\mathrm{}\mathrm{r}=\mathrm{r}}_0\\ w=M_{\theta }=N_{r\theta }=0\mathrm{}\mathrm{}\text{at}\mathrm{}\theta =0,\psi \end{array}$$(23) where r₀ is the inner radius and $\psi$ is the open angle of annular spherical shell. In general form, the displacements of annular spherical shell may be assumed as: (24) $$u=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{U}_{mn}(t)\frac{\partial H_m(r)}{\partial r}{R}_n(\theta )$$(24) (25) $$v=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{V}_{mn}(t)H_m(r)\frac{\partial R_n(\theta )}{\partial \theta }$$(25) (26) $$w_{}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{W}_{mn}(t)H_m(r)R_n(\theta )$$(26) where ($U_{mn},$$V_{mn},$$W_{mn}$) are the displacements amplitudes and the functions $H_m$ and $R_n$ are the test functions which are selected as (Duc, Quang, and Anh 2017): (27) $$H_m(r)=\hspace{0.17em}\text{sin}\hspace{0.17em}\frac{m\pi (r-r_0)}{r_1-r_0},\mathrm{}\mathrm{}{R}_n(\theta )=\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{n\pi \theta }{\psi }\right)$$(27)

Introducing each governing equation as P_i (u, v, w)=0 with (i = 1,2,3) and placing displacement assumptions presented as Eqs. (24)–(26) into P_i results in below equations based on Galerkin’s method (Fenjan et al. 2019; Khalaf, Fenjan, and Faleh 2019; Kunbar et al. 2019; Al-Maliki et al. 2020; Abdulrazzaq et al. 2020a; 2020b; Fenjan, Hamad, and Faleh 2020): (28) $${\int }_{r_0}^{r_1}{\int }_0^{\psi }{P}_1\frac{\partial H_m(r)}{\partial r}{R}_n(\theta )\mathit{rdrd}\theta =0$$(28) (29) $${\int }_{r_0}^{r_1}{\int }_0^{\psi }{P}_2{H}_m(r)\frac{\partial R_n(\theta )}{\partial \theta }r\mathit{drd}\theta =0$$(29) (30) $${\int }_{r_0}^{r_1}{\int }_0^{\psi }{P}_3{H}_m(r)R_n(\theta )\mathit{rdrd}\theta =0$$(30)

Solving above integrals results in below equations in a simplified form neglecting in-plane inertias: (31) $$K_{11}U+K_{21}V+K_{31}W+G_1^{}{W}_{}^2=0$$(31) (32) $$K_{12}U+K_{22}V+K_{32}W+G_2^{}{W}_{}^2=0$$(32) (33) $$K_{13}U+K_{23}V+K_{33}W+G_3^{}{W}_{}^2+G_4^{}{W}_{}^3+n_{1}UW+n_{2}VW+M\ddot{W}=0$$(33) in which K_ij are stiffness matrix components; M is mass matrix and G_i are nonlinear stiffness matrices. Based on Eqs. (31)–(32) one can obtain U and V as functions of W and W² (Muhammad et al. 2019): (34) $$\begin{array}{c}U=U(W,W^2)\\ V=V(W,W^2)\\ \end{array}$$(34) Therefore, Eq. (33)(33) $$K_{13}U+K_{23}V+K_{33}W+G_3^{}{W}_{}^2+G_4^{}{W}_{}^3+n_{1}UW+n_{2}VW+M\ddot{W}=0$$(33) , with the aid of Eq. (34)(34) $$\begin{array}{c}U=U(W,W^2)\\ V=V(W,W^2)\\ \end{array}$$(34) can be reduced to below equation: (35) $$\begin{array}{c}\ddot{W}+\frac{T_1}{M}W+\frac{T_2}{M}W\left|W\right|+\frac{T_3}{M}{W}^3=0\\ \end{array}$$(35) for which (36) $$\begin{array}{c}{T}_1=K_{13}\frac{K_{21}{K}_{32}-K_{22}{K}_{31}}{K_{11}{K}_{22}-K_{12}{K}_{21}}+K_{33}+K_{23}\frac{K_{12}{K}_{31}-K_{11}{K}_{32}}{K_{11}{K}_{22}-K_{12}{K}_{21}}\\ T_2=+G_3^{}+K_{13}\frac{G_2{K}_{21}-G_1{K}_{22}}{K_{11}{K}_{22}-K_{12}{K}_{21}}+K_{23}\frac{G_1{K}_{12}-G_2{K}_{11}}{K_{11}{K}_{22}-K_{12}{K}_{21}}+n_1\frac{K_{21}{K}_{32}-K_{22}{K}_{31}}{K_{11}{K}_{22}-K_{12}{K}_{21}}+n_2\frac{K_{12}{K}_{31}-K_{11}{K}_{32}}{K_{11}{K}_{22}-K_{12}{K}_{21}}\\ T_3=+G_4^{}+n_1\frac{G_2{K}_{21}-G_1{K}_{22}}{K_{11}{K}_{22}-K_{12}{K}_{21}}+n_2\frac{G_1{K}_{12}-G_2{K}_{11}}{K_{11}{K}_{22}-K_{12}{K}_{21}}\end{array}$$(36)

The solving of Eq.(35)(35) $$\begin{array}{c}\ddot{W}+\frac{T_1}{M}W+\frac{T_2}{M}W\left|W\right|+\frac{T_3}{M}{W}^3=0\\ \end{array}$$(35) can be done based on below approximation (Mirjavadi, Forsat, Hamouda, et al. 2019): (37) $$\begin{array}{c}W(t)={\tilde{W}}_{}\hspace{0.17em}\text{cos}\hspace{0.17em}({\omega }_{NL}t)\\ \end{array}$$(37)

So that ${\omega }_{NL}$ is vibration frequency and $\tilde{W}$ is vibration amplitude. The frequency has been calculated based on the procedure provided by Mirjavadi, Forsat, Hamouda, et al. (2019). Also, some normalized parameters can be introduced in this article such as: (38) $$\Omega ={\omega }_{NL}{10}^3{h}^2\sqrt{\frac{{\rho }_c}{E_c^{}{h}^2}}\mathrm{},K_w=\frac{k_w{r}_0{}^4}{D_{11}},K_p=\frac{k_p{r}_0{}^2}{D_{11}}$$(38)

5. Results and discussions

In this study, the thickness of annular spherical shell has be assumed as h = 0.03 m. Porous FG material has two constituents which their properties are provided in Table 1. However, for simplicity the Poisson ratio is considered as constant v = 0.3. Based on above information, this section presents obtained results for nonlinear vibration frequencies of porous FG annular spherical shell surrounded by elastic medium. Porosity volume, open angle and stiffeners have great influence on nonlinear vibration behavior of annular spherical shells. In the following paragraphs, the frequency of spherical shell is validated first and then new findings from the present study have been provided and discussed. For all figures, the geometrical parameters of stiffeners are considered to be h₁ = 0.5 h, b₁ = 0.5 h.

Table 1. Material properties of FGM constituents.

Properties	Steel	Alumina ($A{l}_2{O}_3$)
E	210 (GPa)	390 (GPa)
Ρ	7800 ($kg/m^3$)	3960 ($kg/m^3$)
Ν	0.3	0.24

Table 2 presents frequency validation of spherical shells made of FG material with those of Duc, Quang, and Anh (2017). For the validation, various values of material gradient exponent (p = 0, 1, 5) have been considered. Also, it is considered that R/h = 100. Obtained frequencies are the same as Duc, Quang, and Anh (2017) which highlights the correctness of presented methodology. Also, Table 3 presents frequency validation of FG spherical shells with the article of Fadaee, Atashipour, and Hosseini-Hashemi (2013) based on different values of curvature radius (R/a) at a fixed material exponent p = 1.

Table 2. Validation of vibration frequency of spherical shell for various material gradient exponent (R/r₀=3).

	Duc et al. (2017)	Present
p = 0	0.9118	0.9118
p = 1	1.7794	1.7794
p = 5	2.2130	2.2130

Table 3. Validation of vibration frequency (Hz) of FG spherical shells at curvature radius (p = 1).

	Fadaee et al. (2013)	Present
R/a = 2.5	1578.1	1578.3
R/a = 5	2221.1	2221.2
R/a = 10	3826.7	3826.8
R/a = 20	7313.6	7313.6

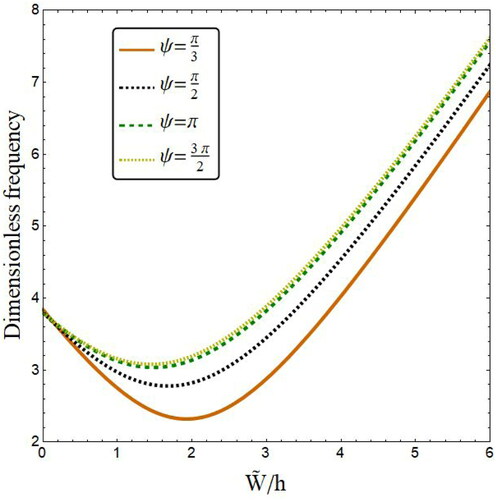
Effect of open angle ($\psi$) on the variation of nonlinear vibration frequency of FG annular spherical shell segment with respect to normalized amplitude ($\tilde{W}/h$) has been plotted in Fig. 3. The material gradient index is selected as p = 1 and shell radii are assumed to be r₁=100 h and r₀=0.5r₁. Note that the vibration frequency ignoring geometric nonlinearity can be obtained based on $\tilde{W}/h=0.$ This figure shows that nonlinear vibration behaviors of annular spherical shell segment rely on the value of open angle. Actually, as the value of open angle increases the nonlinear vibration frequency becomes larger.

Figure 3. Variation of vibration frequency versus normalized deflection of annular spherical shells for various open angles (R = 200 h, r₁=100 h, r₀=0.5r₁, p = 1, ξ = 0.2, K_w=0, K_p=0).

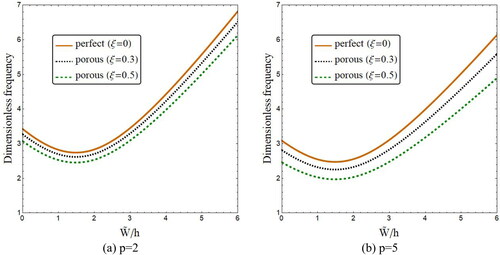
Influences of porosity volume fraction (ξ) on the variation of nonlinear vibration frequency of FG annular spherical shell segment with respect to normalized amplitude have been plotted in Fig. 4 when the material gradient exponent is set to p = 2, 5. The distribution type of porosities is considered as even. Also, the shell segment has an open angle of $\psi =\pi .$ This figure indicates the reduction of vibration frequency with the increase of porosity volume at a, prescribed value of normalized amplitude. Such finding is related to decrease of shell structural stiffness according to the growth of porosities amount. Another important finding is that an increase of FG material exponent results in lower vibration frequencies for annular spherical shell segment.

Figure 4. Variation of vibration frequency versus normalized deflection of annular spherical shells for various porosity volume fractions (R = 200 h, r₁=100 h, r₀=0.5r₁, K_w=0, K_p=0). (a) p = 2; (b) p = 5.

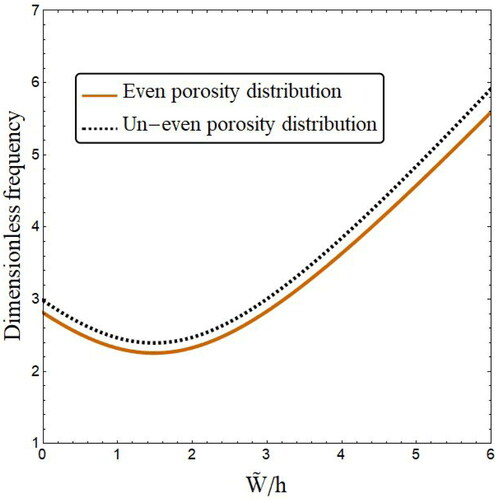
Figure 5 explores the influences of porosities distribution types on nonlinear vibration behavior of FG annular spherical shell at fixed values for material exponent p = 5 and porosities volume ξ = 0.3. One can observe that vibration frequencies based on even type of distribution are smaller than frequencies based on un-even type of distribution. This finding is owning to the fact that porosity based on even type of distribution have been dispersed all over the thickness of annular spherical shell leading to smaller shell stiffness.

Figure 5. Variation of vibration frequency versus normalized deflection of annular spherical shells for various porosity distribution types (R = 200 h, r₁=100 h, r₀=0.5r₁, p = 5, ξ = 0.3, ψ = π).

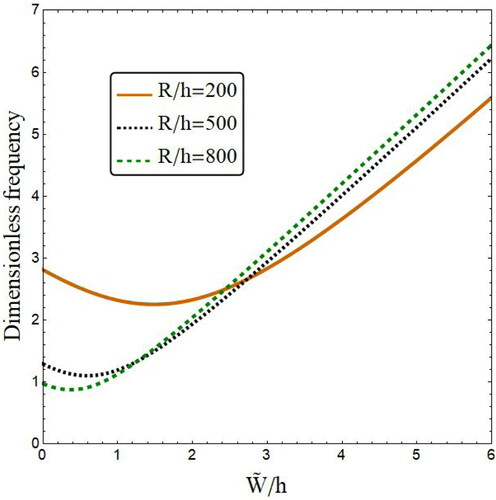
Figure 6 indicates the effect of normalized base radius (R/h) of annular spherical shell on the variation of vibration frequencies with respect to normalized amplitude. Results are presented at fixed values for material exponent p = 5 and porosities volume ξ = 0.3. Also, radii of lower and upper bases are selected as r₁=100 h, r₀=0.5 r₁ and the shell segment has an open angle of $\psi =\pi .$ As can be seen, the variation of vibration frequency with respect to vibration amplitude has higher rates as the values of R/h is greater. So, effect of R/h on vibration behavior of annular spherical shell segment depends on the value of normalized vibration amplitude.

Figure 6. Variation of vibration frequency versus normalized deflection of annular spherical shells for various porosity distribution types (r₁=100 h, r₀=0.5r₁, p = 5, ξ = 0.3, ψ = π).

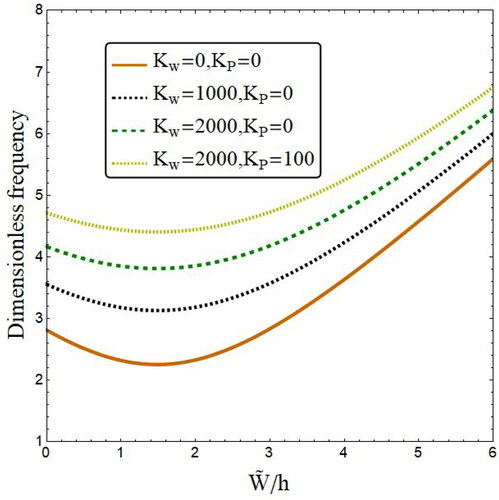
In Fig. 7, influences of foundation parameters (K_w, K_P) on the variation of nonlinear vibration frequency of FG annular spherical shell segment with respect to normalized amplitude have been plotted. This figure has been provided based on the assumption of even porosity distribution and ξ = 0.3. As can be seen, an increase of the two foundation parameters results in higher frequency–amplitude curves. However, higher values for Winkler parameter (K_w) than Pasternak parameter (K_p) are needed to affect the vibration frequency of annular spherical shells. This is due to the reason that K_w is corresponding to infinite number of springs leading to discontinuous interaction with spherical shell.

Figure 7. Variation of vibration frequency versus normalized deflection of annular spherical shells for various foundation factors (r₁=100 h, r₀=0.5r₁, p = 5, ξ = 0.3, ψ = π).

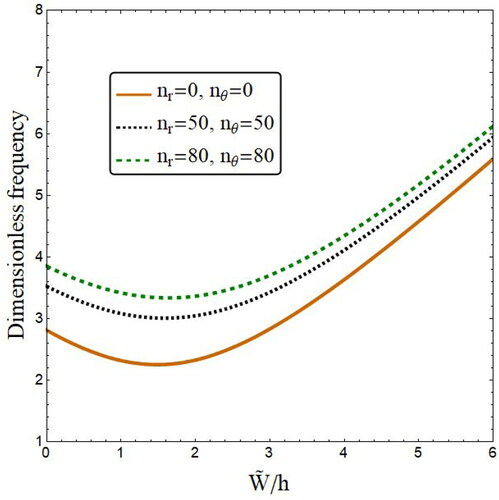
Figure 8 illustrates the effect of stiffener numbers (n_r, n_θ) of annular spherical shell on the variation of vibration frequencies with respect to normalized amplitude. Results are presented at fixed values for material exponent p = 5 and porosities volume ξ = 0.3. Also, radii of lower and upper bases are selected as r₁=100 h, r₀=0.5 r₁ and the shell segment has an open angle of $\psi =\pi .$ The geometric parameters of stiffeners are h₁=0.5 h and b₁=0.5 h. The present figure indicates that stiffened annular spherical shell has enhanced dynamic character since it is reinforced by a system of stiffeners. Therefore, vibration frequencies of stiffened annular spherical shells are higher than those without stiffeners. This issue is much important due to the fact that porous shells have lower vibration frequencies than perfect one. Hence, their vibration properties should be enhanced by adding some stiffeners.

Figure 8. Variation of vibration frequency versus normalized deflection of annular spherical shells for various number of stiffeners (r₁=100 h, r₀=0.5r₁, p = 5, ξ = 0.3, h₁=0.5 h, b₁=0.5 h, ψ = π).

6. Conclusions

In this research, nonlinear vibration frequencies of annular spherical shell segments made of porous FG materials were examined. Effects of two types of porosity distributions were considered. Also, influences of stiffeners and surrounding medium were included. An analytical trend was proposed to solve the nonlinear governing equations of annular spherical shell. Obtained findings are summarized as follows:

• As the value of open angle increases the nonlinear vibration frequency becomes larger.

• Another finding is the reduction of vibration frequency with the increase of porosity volume at a prescribed value of normalized amplitude.

• Vibration frequencies based on even type of distribution are smaller than frequencies based on un-even type of distribution.

• An increase of the two foundation parameters results in higher frequency–amplitude curves.

• Vibration frequencies of stiffened annular spherical shells are higher than those without stiffeners.

Acknowledgments

The first and second authors would like to thank FPQ (Fidar project Qaem) for providing the fruitful and useful help.

Appendix 1

(A1) $$\begin{array}{l}{A}_{11}=\frac{h\left(E_m\left(p\left(1-0.5\xi \right)-0.5\xi \right)+E_c\left(1+\left(-0.5-0.5p\right)\xi \right)\right)}{\left(1+p\right)\left(1-v^2\right)}\mathrm{}\\ A_{12}=\frac{vh\left(E_m\left(p\left(1-0.5\xi \right)-0.5\xi \right)+E_c\left(1+\left(-0.5-0.5p\right)\xi \right)\right)}{\left(1+p\right)\left(1-v^2\right)}\\ A_{66}=\frac{0.3846h\left(E_m\left(p\left(1-0.5\xi \right)-0.5\xi \right)+E_c\left(1+\left(-0.5-0.5p\right)\xi \right)\right)}{1+p}\\ B_{11}=\frac{\left(E_c-E_m\right)h^{2}p}{2\left(1+p\right)\left(2+p\right)\left(1-v^2\right)}\\ B_{12}=\frac{\left(E_c-E_m\right)v{h}^{2}p}{2\left(1+p\right)\left(2+p\right)\left(1-v^2\right)}\\ B_{66}=\frac{0.1923\left(E_c-E_m\right)h^{2}p}{\left(1+p\right)\left(2+p\right)}\\ D_{11}=\frac{h^3\left(E_m+\frac{{32}^{-p}\left(E_c-E_m\right)\left(-1+2^p\left(2+p+p^2\right)\right)}{\left(1+p\right)\left(2+p\right)\left(3+p\right)}-0.5E_c\xi -0.5E_m\xi +\frac{{32}^{-p}\left(E_c-E_m\right)\Gamma (1+p)}{\Gamma (4+p)}\right)}{12\left(1-v^2\right)}\\ D_{12}=\frac{h^{3}v\left(E_m+\frac{{32}^{-p}\left(E_c-E_m\right)\left(-1+2^p\left(2+p+p^2\right)\right)}{\left(1+p\right)\left(2+p\right)\left(3+p\right)}-0.5E_c\xi -0.5E_m\xi +\frac{{32}^{-p}\left(E_c-E_m\right)\Gamma (1+p)}{\Gamma (4+p)}\right)}{12\left(1-v^2\right)}\\ D_{66}=0.032h^3\left(E_m+\frac{{32}^{-p}\left(E_c-E_m\right)\left(-1+2^p\left(2+p+p^2\right)\right)}{\left(1+p\right)\left(2+p\right)\left(3+p\right)}-0.5E_c\xi -0.5E_m\xi +\frac{{32}^{-p}\left(E_c-E_m\right)\Gamma (1+p)}{\Gamma (4+p)}\right)\end{array}$$(A1)

where is $\Gamma$ Gamma function.