Prediction of Thermal Conductivity of Elastic Single Jersey Knitted Fabric

ABSTRACT

This work aims to derive a mathematical model that describes the thermal conductivity of the elastic single jersey knitted fabric (SJKF) based on the loop geometry and the yarn and fibers inclination on the direction of heat flow, and to assist the manufactures of elastic SJKF to predict the thermal conductivity from the fabric construction parameters. The main fabric construction parameters in this model are yarn count, loop length, and spandex weight percent. To validate the proposed model, elastic SJKF samples were produced at two different counts and five levels of loop length and spandex weight percent. The thermal conductivity of these samples was measured and compared to the predicted values from the new model rather than the previous three models (Maxwell – Eucken 2, Schuhmeister, Militky models). From the results, it could be concluded that the values of thermal conductivity from the model are very closed to the experimental values; therefore, the new model could be used to predict the thermal conductivity of elastic SJKF.

摘要

本工作旨在基于线圈几何形状以及纱线和纤维在热流方向上的倾斜，推导出描述弹性单面针织物（SJKF）导热系数的数学模型，并帮助弹性SJKF的制造商从织物结构参数中预测导热系数. 该模型中的主要织物结构参数是纱线支数、毛圈长度和氨纶重量百分比. 为了验证所提出的模型，在不同的计数和五个水平的环长和氨纶重量百分比下生产了弹性SJKF样品.测量这些样品的热导率，并将其与新模型而非前三个模型（Maxwell– Eucken 2、Schuhmeister和Militky模型）的预测值进行比较. 从结果可以得出结论，模型的热导率值与实验值非常接近; 因此，新模型可用于预测弹性SJKF的导热系数.

KEYWORDS:

• Elastic single jersey knitted fabrics
• thermal conductivity model
• fabric construction parameters
• spandex weight percent
• loop geometry
• fiber volume fraction
• air volume fraction

关键词:

• 弹性单面针织面料
• 导热系数模型
• 织物结构参数
• 氨纶重量百分比
• 回路几何
• 纤维体积分数
• air volume fraction空气体积分数

Introduction

Adding spandex to the knitted fabric enhances its dimensional stability; therefore, elastic SJKF is used for sportswear, under and outer wear for adult and kids due to its comfort feeling and free of movement with high elastic recovery compared to the fabric without spandex (Khalil and Těšinová 2022). Spandex increases the thickness of elastic SJKF by up to three times of yarn diameter and leads to stitch overlapping (Khalil et al. 2021, 2023; Khalil, Těšinová, and Aboalasaad 2021), as shown in Figure 1.

Figure 1. Stitch overlapping (Khalil et al. 2023).

Thermal comfort properties are very important issue in human comfort, and a lot of researchers are interested to evaluate the relationship between fabric construction parameters and the thermal comfort properties. This relation can be found by experimental way or by using mathematical models.

Generally, the mathematical models are needed to interpret experimental relations, estimate the expected properties, and to assist in designing and developing of a new fabric to achieve a certain property. As there are several theoretical models to predict the thermal conductivity and resistance of textile fabrics by mathematical equations, empirical equations, neural network, finite element method, and multiple regression models.

The thermal resistance and conductivity of the fabrics can be predicted by means of experimental (empirical), analytical and numerical methods (Mansoor et al. 2021). The preference of selection depends on the requisite precision and nature of the solution. Thermal conductivity and resistance were also predicted by using an Artificial Neural Network (ANN) (Alibi et al. 2012; Fayala et al. 2008; Majumdar 2011; A. E.; A. E. Mangat et al. 2015). The thermal conductivity of knitted fabrics made from cotton, viscose and spandex fibers was investigated by using an Artificial Neural Network (Alibi et al. 2012), where the fabric structure and weight, yarn count and composition, gauge, spandex percent and count, fabric thickness, and loop length were used as input parameters. There are research that predicted thermal resistance by regression model (Afzal et al. 2014; Qian and Fan 2006; Shaker et al. 2018). The thermal resistance of fabrics and socks was predicted by modeling in the wet state (Hollies and Bogaty 1964; M. M.; M. M. Mangat and Hes 2014; Mansoor et al. 2021; Zhu 2020).

Some researchers have predicted the thermal resistance and conductivity of fabrics with mathematical approaches. Several research presented a mathematical model of thermal conductivity and resistance of woven fabric based on actual construction parameters of repeat by using finite element method (Wu, Tang, and Xuan Wu 2017) and theoretical unit cell geometry (Ismail, Ammar, and El-Okeily 1988Bhattacharjee and Kothari 2009).

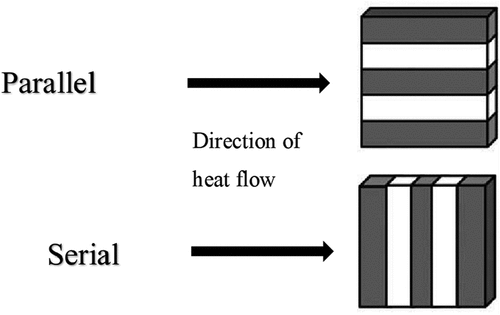
Schuhmeister summarized the relationship between the thermal conductivity and fabric structural parameters; and assumed that one-third of fibers are parallel and two-third are in series with a homogeneous distribution in all directions, as shown in Figure 2 by the empirical equation as following (Schuhmeister 1877):

(1) ${\mathit{\lambda }}_{\mathrm{fab}}\mathit{\hspace{0.17em}}=0.33\mathit{\hspace{0.17em}}({\mathrm{F}}_{\mathrm{f}}{\mathit{\lambda }}_{\mathrm{f}}+{\mathrm{F}}_{\mathrm{a}}{\mathit{\lambda }}_{\mathrm{a}})\mathit{\hspace{0.17em}}+0.67\mathit{\hspace{0.17em}}\frac{{\mathit{\lambda }}_{\mathrm{f}}\times {{\mathit{\lambda }}_{\mathrm{a}}}_{\mathit{\hspace{0.17em}}}}{{\mathit{\lambda }}_{\mathrm{f}}\mathit{\hspace{0.17em}}{\mathrm{F}}_{\mathrm{a}}+{\mathit{\lambda }}_{\mathrm{a}}\mathit{\hspace{0.17em}}{\mathrm{F}}_{\mathrm{f}}}$(1)

Figure 2. The direction of fibers compared to heat flow direction.

Where ${\mathit{\lambda }}_{\mathrm{fab}}$, ${\mathit{\lambda }}_{\mathrm{f}}$, ${\mathit{\lambda }}_{\mathrm{a}}$ are thermal conductivity coefficients of fabric, fibers, and air respectively, and F_f, F_a are the volume fractions of fibers and air respectively.

Other researchers (Mao and Russell 2007Baxter 1946) have confirmed the equation and interpreted the first term as an ideal model for a fabric construction that fibers are parallel to the heat flow. The second term has been treated as an ideal model for a fabric construction where fibers lie in series to the heat flow. Bogaty (Bogaty, Hollies, and Harris 1957) found that the percent of fibers in series and parallel is 21% and 79%, respectively, for wool fabric. Militky (Militký and Křemenáková 2011) considered that 50% fibers in series and 50% in parallel to the heat flow, as shown in the following equation:

(2) ${\mathit{\lambda }}_{\mathrm{fab}}\mathit{\hspace{0.17em}}=0.5\ast \left[\left(({\mathrm{F}}_{\mathrm{f}}{\mathit{\lambda }}_{\mathrm{f}}+{\mathrm{F}}_{\mathrm{a}}{\mathit{\lambda }}_{\mathrm{a}}\right)+\mathit{\hspace{0.17em}}\frac{{\mathit{\lambda }}_{\mathrm{f}}\times {{\mathit{\lambda }}_{\mathrm{a}}}_{\mathit{\hspace{0.17em}}}}{{\mathit{\lambda }}_{\mathrm{f}}\mathit{\hspace{0.17em}}{\mathrm{F}}_{\mathrm{a}}+{\mathit{\lambda }}_{\mathrm{a}}\mathit{\hspace{0.17em}}{\mathrm{F}}_{\mathrm{f}}}\right]$(2)

Maxwell introduced the two-phase concept (continuous and dispersed phase) for the determination of electrical conductivity. Later on, Eucken used the same concept for thermal conductivity evaluation (Eucken 1940). Maxwell – Eucken (ME) model can be used to describe the thermal conductivity of a two-component material with simple physical structures. The phase that presented in form of droplets was the dispersed phase, and the phase in which droplets were suspended was called the continuous phase. Thermal conductivity models require the naming of a continuous and dispersed phase. The materials with exterior porosity, individual solid particles are surrounded by a gaseous matrix, and hence the gaseous component (air) forms the continuous phase, and the solid component (fibers) forms the dispersed phase by Maxwell – Eucken 2 (ME2) (Kumar and Topin 2014Carson 2017). The ME2 model equation is as follows:

(3) ${\mathit{\lambda }}_{\mathit{fab}}=\frac{{\lambda }_a{F}_a+{\lambda }_{\mathit{f}}{F}_f\frac{3{\lambda }_a}{2{\lambda }_a+{\lambda }_f}}{F_a+F_f\frac{3{\lambda }_a}{2{\lambda }_a+{\lambda }_f}}$(3)

From the previous researches, there is no model that describes the thermal conductivity of elastic SJKF. Therefore, the aims of this work are

1. Investigating if some of these previous models can be valid to elastic SJKF.

2. Deriving a new model that can predict the thermal conductivity of elastic SJKF based on the construction parameters (namely, yarn count, loop length, and spandex weight percent) of fabric and the yarn and fibers inclination on the direction of heat flow.

3. Assisting the manufacturers and designers to predict the thermo-physiological properties of elastic SJKF produced from cotton yarns.

Studied material and used method

Studied materials

To achieve these aims, the full plaited SJKF were produced at two yarn counts (25 and 35 Ne), five levels of spandex weight percent, SWP, and loop length as shown in Table 1. All samples were produced on VIGNONI SJ-B (number of feeders: 57, diameter: 19-inch, machine gauge: 24 needles/inch), and were treated according to the elastic knitted fabric finishing recipe. First, heat setting at 185°C was applied, followed by dyeing at 95°C and finally compacting at 90°C.

Table 1. Elastic SJKF specifications.

Yarn count	SWP (%)		4	5	6	7	8
25 Ne	Loop length (mm)	2.7	√	√	√	√	√
		2.9	√	√	√	√	√
		3.1	√	√	√	√	√
		3.3	√	√	√	√	√
		3.4	√	√	√	√	√
35 Ne	Loop length (mm)	2.7	√	√	√	√	√
		2.9	√	√	√	√	√
		3.1	√	√	√	√	√
		3.3	√	√	√	√	√
		3.4	√	√	√	√	√

Used methods

Yarn diameter was measured by taking images of the yarns by the camera (ProgRes-CT3) attached to a microscope under transmitted light. The captured images were analyzed by using NIS-elements software. The threshold of binary images was adjusted then binary image processing was applied, such as erosion and dilation for 70 images for each count, and the yarn diameter was calculated by inserting 70 images.

Thermal conductivity and fabric thickness were measured by using Alambeta tester (nondestructive instrument) (Hes and Dolezal 1989) according to the standard ISO 8301 (1991).

Schuhmeister, Militky, and ME2 models were applied on elastic SJKF to calculate predicted values of the thermal conductivity and then compared to experimental values and see if one of them is valid to the elastic SJKF

Results and discussion

Applying three simple mathematical models (Maxwell–eucken 2, schuhmeister, Militky)

Figure 3 shows that the predicted values of thermal conductivity from ME2 model were very low compared to the experimental values. The predicted values from Schuhmeister model (one-third of fibers is parallel and two-thirds are in series) were lower than experimental values. When the percent of fibers in parallel increased to fifty percent, the predicted values from Militky model were higher than experimental values. Therefore, the predicted thermal conductivity increased when the parallel component increased. So, a new model is needed to be valid for the elastic SJKF and this is the main aim is of this work.

Figure 3. Experimental and predicted values from Schuhmeister, Militky, and ME 2 of thermal conductivity of elastic knitted fabric produced from yarn count 35 Ne.

Assumptions and equations of a new model

Assumptions

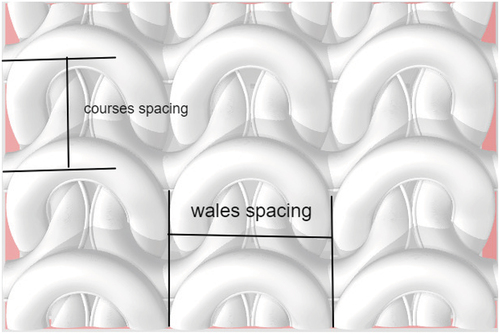
A new model was derived based on the loop geometry and fabric construction parameters, namely wales and courses spacing, yarn diameter, fibers density, fabric thickness. It was assumed that:

• Yarn in one repeat was a cylinder with diameter $\mathit{d}$ and its length equal to loop length ($\mathit{l}$).

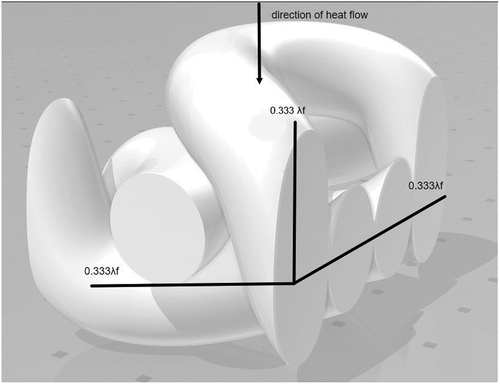
• Fibres were divided to equal three components.

• One third of fibers was in the same direction of heat flow (parallel to heat flow).

• Two thirds of fibers were in series with heat flow direction.

• Heat transfer by convection and radiation was neglected.

Equations

Thermal conductivity of fibres in one repeat

$\mathit{Total}\mathit{volume}\mathit{of}\mathit{one}\mathit{repeat},\mathit{m}{m}^3=\mathit{w}\ast \mathit{c}\ast \mathit{h}$

Where w is wales spacing (mm) = (1/wales density), c is courses spacing (mm) = (1/courses density), h is fabric thickness (mm) as shown in Figure 4.

$\mathit{Cotton}\mathit{yarn}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}(\mathit{m}{m}^3)=\frac{\pi }{4}\ast d^2\ast \mathit{l}$

$\mathit{Cotton}\mathit{fibres}\mathit{weight}\mathit{in}\mathit{one}\mathit{repeat}\left(\mathit{gm}\right)=\frac{l}{1000\ast \mathit{Nm}}$

Figure 4. Theoretical image of elastic knitted fabric with the overlapping.

Where $\mathit{Nm}$ is yarn metric count, $\mathit{l}$ is the loop length (mm), and $\mathit{d}$ is yarn diameter (mm).

$\mathit{Cotton}\mathit{fibres}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}(\mathit{m}{m}^3)=\frac{1000\ast \mathit{l}}{\mathrm{Nm}\ast {\mathit{\rho }}_{\mathrm{c}}}$

$\mathit{Cotton}\mathit{fibres}\mathit{volume}\mathit{fraction},F_c=\frac{1000\ast \mathit{l}}{\mathrm{Nm}\ast \mathrm{w}\ast \mathrm{c}\ast \mathrm{h}\ast {\rho }_c}$

$\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{cotton}\mathit{fibres}\mathit{in}\mathit{one}\mathit{repeat},{\mathit{\lambda }}_{\mathit{cotton}}=F_c\ast {\mathit{\lambda }}_c$

Where ${\rho }_c$ is the cotton fibre density (1520 kg.m⁻³), ${\mathit{\lambda }}_c$ is the thermal conductivity coefficient of cotton fibres (0.5 W.m⁻¹.K⁻¹) (Herlinger 2008).

(4) ${\mathit{\lambda }}_{\mathit{cotton}}=\frac{1000\ast \mathit{l}}{Nm\ast w\ast c\ast h\ast {\rho }_c}\ast {\mathit{\lambda }}_c$(4)

$\mathit{Spandex}\mathit{weight}\mathit{in}\mathit{one}\mathit{repeat},\mathit{gm}=\mathit{Cotton}\mathit{fibre}\mathit{weight}\mathit{in}\mathit{one}\mathit{repeat}\ast \frac{\mathit{SWP}}{100}$

$\mathit{Spandex}\mathit{weight}\mathit{in}\mathit{one}\mathit{repeat},\mathit{gm}=\frac{\mathit{l}\ast \mathit{SWP}}{{10}^5\ast \mathit{Nm}}$

$\mathit{Spandex}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat},\mathit{m}{m}^3=\frac{10\ast \mathit{l}\ast \mathit{SWP}}{\mathit{Nm}\ast {\mathit{\rho }}_{\mathrm{s}}}$

$\mathit{Spandex}\mathit{volume}\mathit{fraction},F_s=\frac{10\ast \mathit{l}\ast \mathit{SWP}}{\mathit{w}\ast \mathit{c}\ast \mathit{h}\ast \mathit{Nm}\ast {\mathit{\rho }}_{\mathrm{s}}}$

$\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{spandex}\mathit{in}\mathit{one}\mathit{repeat},{\lambda }_{\mathit{spandex}}=F_s\ast {\lambda }_s$

Where ${\mathit{\rho }}_{\mathrm{s}}$ spandex fibre density (1225 kg.m⁻³), ${\lambda }_s$ is the thermal conductivity coefficient of spandex fibres (0.15 W.m⁻¹.K⁻¹) (Herlinger 2008).

(5) ${\lambda }_{\mathit{spandex}}=\frac{10\ast \mathit{l}\ast \mathit{SWP}}{w\ast c\ast h\ast Nm\ast {\rho }_s}\ast {\lambda }_s$(5)

(6) $\mathit{Total}\mathit{thermal}\mathit{conductivity}\mathit{of}\mathit{fibres},{\lambda }_f={\mathit{\lambda }}_{\mathit{cotton}}+{\lambda }_{\mathit{spandex}}$(6)

By substituting with the Equations 4(4) ${\mathit{\lambda }}_{\mathit{cotton}}=\frac{1000\ast \mathit{l}}{Nm\ast w\ast c\ast h\ast {\rho }_c}\ast {\mathit{\lambda }}_c$(4) and 5(5) ${\lambda }_{\mathit{spandex}}=\frac{10\ast \mathit{l}\ast \mathit{SWP}}{w\ast c\ast h\ast Nm\ast {\rho }_s}\ast {\lambda }_s$(5) on Equation 6(6) $\mathit{Total}\mathit{thermal}\mathit{conductivity}\mathit{of}\mathit{fibres},{\lambda }_f={\mathit{\lambda }}_{\mathit{cotton}}+{\lambda }_{\mathit{spandex}}$(6) , ${\lambda }_f$ can be calculated as follow:

(7) ${\lambda }_f=\left[\frac{l}{\mathit{Nm}\ast \mathit{w}\ast \mathit{c}\ast \mathit{h}}\right]\left[\frac{1000\ast {\mathit{\lambda }}_c}{{\rho }_c}+\frac{10\ast SWP\ast {\lambda }_s}{{\rho }_s}\right]$(7)

Thermal conductivity of air in one repeat

$\mathit{Inter}\mathit{air}\mathit{volume}\mathit{between}\mathit{yarns}=\mathit{Total}\mathit{volume}\mathit{of}\mathit{one}\mathit{repeat}-\left(\mathit{Cotton}\mathit{yarn}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}+\mathit{Spandex}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}\right)$

$\mathit{Inter}\mathit{air}\mathit{volume}\mathit{between}\mathit{yarns}=\mathit{w}\ast \mathit{c}\ast \mathit{h}-\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}+\frac{10\ast \mathit{l}\ast \mathit{SWP}}{Nm\ast {\rho }_s}\right)$

$\mathit{Intra}\mathit{air}\mathit{volume}\mathit{inside}\mathit{cotton}\mathit{yarn}=\mathit{Cotton}\mathit{yarn}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}-\mathit{Cotton}\mathit{fibres}\mathit{volume}\mathit{in}\mathit{one}\mathit{repeat}$

$\mathit{Intra}\mathit{air}\mathit{volume}\mathit{inside}\mathit{cotton}\mathit{yarn}=\frac{\pi }{4}\ast d^2\ast \mathit{l}-\frac{1000\ast \mathit{l}}{Nm\ast {\rho }_c}$

$\mathit{Total}\mathit{air}\mathit{volume}\mathit{inside}\mathit{one}\mathit{repeat}=\mathit{Inter}\mathit{air}\mathit{volume}\mathit{between}\mathit{yarns}+\mathit{Intra}\mathit{air}\mathit{volume}\mathit{inside}\mathit{cotton}\mathit{yarn}$

$\mathit{Total}\mathit{air}\mathit{volume}\mathit{inside}\mathit{one}\mathit{repeat}=\left(\mathit{w}\ast \mathit{c}\ast \mathit{h}-\left(\frac{1000\ast \mathit{l}}{Nm\ast {\rho }_c}+\frac{10\ast \mathit{l}\ast \mathit{SWP}}{Nm\ast {\rho }_s}\right)\right)+\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}-\frac{1000\ast \mathit{l}}{Nm\ast {\rho }_c}\right)$

$\mathit{Totalairvolumefraction},F_a=\frac{\left(w\ast c\ast h-\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}+\frac{10\ast \mathit{l}\ast \mathit{SWP}}{Nm\ast {\rho }_s}\right)\right)+\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}-\frac{1000\ast \mathit{l}}{Nm\ast {\rho }_c}\right)}{\mathit{w}\ast \mathit{c}\ast \mathit{h}}$

$\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{air}\mathit{in}\mathit{one}\mathit{repeat},{\lambda }_{\mathit{air}}=F_a\ast {\lambda }_a$

Where ${\lambda }_a$ is the thermal conductivity coefficient of air (0.026 W.m⁻¹.K⁻¹)

(8) ${\lambda }_{\mathit{air}}=\frac{\left(w\ast c\ast h-\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}+\frac{10\ast \mathit{l}\ast \mathit{SWP}}{Nm\ast {\rho }_s}\right)\right)+\left(\frac{\pi }{4}\ast d^2\ast \mathit{l}-\frac{1000\ast \mathit{l}}{Nm\ast {\rho }_c}\right)}{\mathit{w}\ast \mathit{c}\ast \mathit{h}}\ast {\lambda }_a$(8)

Thermal conductivity of fabric

In this model, $\mathit{\hspace{0.17em}}{\lambda }_f$ was divided to equal three components, one-third was in the same direction of heat flow (parallel to heat flow), and two third were in series with the heat flow direction, as shown in Figure 5.

$\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{series},{\lambda }_{\mathit{ser}}=\frac{0.333{\lambda }_f\times 0.333{{\lambda }_f}_{\mathit{\hspace{0.17em}}}}{0.333{\lambda }_f+0.333{\lambda }_f}$

(9) ${\lambda }_{\mathit{ser}}=\frac{0.333{\lambda }_f}{2}$(9)

(10) $\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{parallel},{\lambda }_p=0.333{\lambda }_f$(10)

Figure 5. Fibres thermal conductivity components to heat flow direction.

(11) $\mathit{Total}\mathit{thermal}\mathit{conductivity}\mathit{of}\mathit{fabric},{\lambda }_{\mathit{fab}}={\mathit{\lambda }}_{\mathrm{ser}}+{\lambda }_p+{\lambda }_a$(11)

Validation of the new model

A new model, Schuhmeister, Militky, and ME2 were applied on elastic SJKF to compare between predicted values from a new model, Schuhmeister, Militky, ME2 and experimental values then evaluate if the new model can express the thermal conductivity of elastic SJKF.

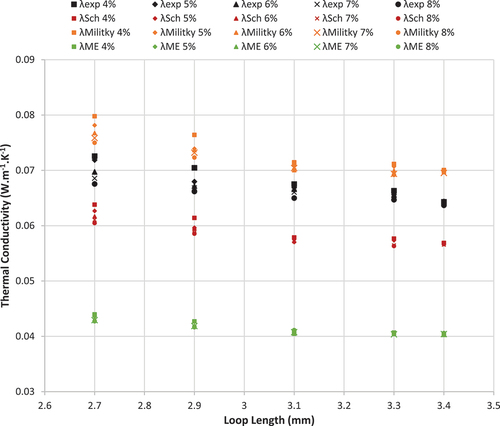
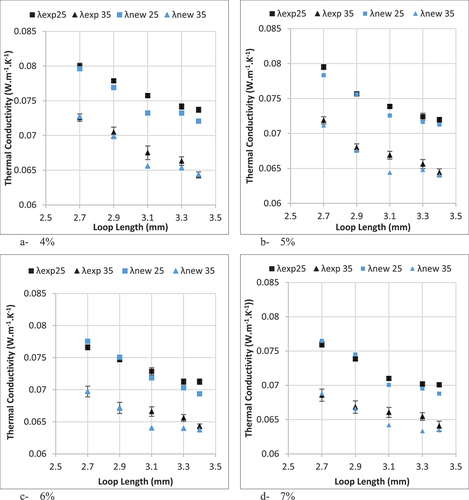
Figure 6 shows the experimental and predicted values of thermal conductivity of elastic knitted fabric produced from yarn count 35 Ne. The predicted values from a new model were very close to the experimental values of thermal conductivity at most points compared to the predicted values from Schuhmeister, Militky, and ME2 models. For the elastic SJKF samples produced from yarn count 25 Ne, the predicted values of thermal conductivity from a new model were also closed to the experimental values, as shown in Figure 7.

Figure 6. Experimental and predicted values of thermal conductivity of elastic knitted fabric produced from yarn count 35 Ne.

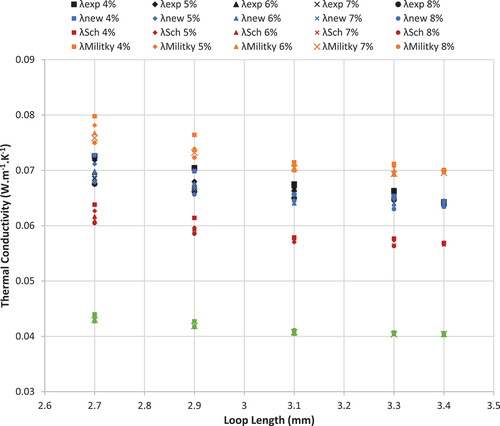
Figure 7. Experimental and predicted values of thermal conductivity of elastic knitted fabric produced from yarn count 25 Ne.

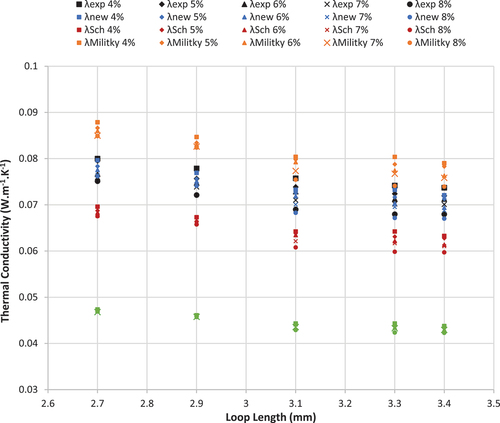
For more clear presentation, the predicted values from the new model of elastic SJKF produced from yarn count 25 and 35 Ne vs experimental values were represented as shown in Figure 8. Therefore, it can be concluded that the new model can be used to predict the thermal conductivity of the elastic SJKF compared to Schuhmeister, Militky, and ME2 models.

Figure 8. Predicted thermal conductivity values from the new model vs experimental values at different levels of SWP and yarn count.

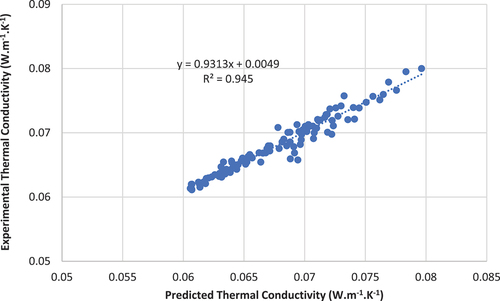
Figure 9 shows the coefficient of determination (R² = 0.95) between the predicted values from the new model and experimental results of the thermal conductivity of elastic SJKF samples produced from yarn count 25 and 35 Ne with slope of 0.93 and intercept of 0.0049.

Figure 9. Experimental thermal conductivity vs predicted thermal conductivity from a new model.

An attempt to determine structural parameters to obtain a desired thermal conductivity

When designing textiles, construction parameters are chosen in order to reach the appropriate physical properties for the specific end-use. Practically, these parameters are chosen based on previous experience in this field with the required adjustment within the competitive cost limitation. In this field, there are few mathematical models and equations that start with the desired property and end with the selection of the appropriate construction parameters, especially with the interference of the required properties.

In this part, an attempt to determine one property, which is thermal conductivity by selecting the appropriate structural parameters, namely (yarn count, SWP, and the loop length) as independent structural parameters are proposed, and vice versa. So that, the designers of elastic knitted fabric could choose the construction parameters for these fabrics based on knowing their thermal conductivity values.

To achieve this purpose, the Equations 7(10) $\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{parallel},{\lambda }_p=0.333{\lambda }_f$(10) , 8(10) $\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{parallel},{\lambda }_p=0.333{\lambda }_f$(10) , 9(10) $\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{parallel},{\lambda }_p=0.333{\lambda }_f$(10) , 10(10) $\mathit{Thermal}\mathit{conductivity}\mathit{of}\mathit{fibres}\mathit{in}\mathit{parallel},{\lambda }_p=0.333{\lambda }_f$(10) , and 11(11) $\mathit{Total}\mathit{thermal}\mathit{conductivity}\mathit{of}\mathit{fabric},{\lambda }_{\mathit{fab}}={\mathit{\lambda }}_{\mathrm{ser}}+{\lambda }_p+{\lambda }_a$(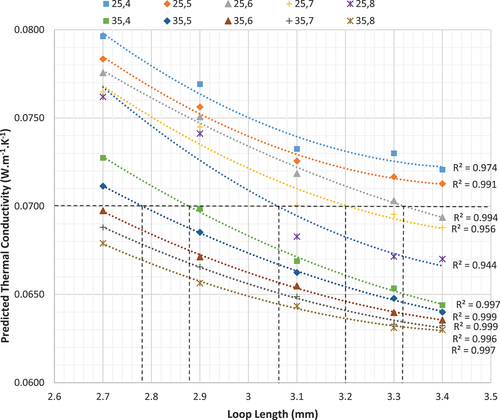11) were used to obtain the predicted value of thermal conductivity, which is the dependent variable, considering that the yarn count, SWP, and the loop length are independent variables, and (the wales spacing, courses spacing, and the fabric thickness are considered) as dependent variables. The predicted values of thermal conductivity of elastic SJKF produced from yarn count 25 and 35 Ne versus loop length are illustrated in Figure 10. The relation between thermal conductivity (y) and loop length (x) was presented by using polynomial equations, as listed in Table 2, at different levels of SWP and yarn count. This figure could be used to determine the structural parameters of elastic SJKF by knowing the desired value of the thermal conductivity.

Figure 10. The predicted values of thermal conductivity of elastic SJKF versus loop length.

Table 2. Curve fitting equations for the relation between thermal conductivity and loop length.

Yarn count (Ne)	SWP (%)	Coefficient of determination (R^2)	Curve equation
25	4	0.974	y = 0.013x^2 − 0.089× + 0.226
	5	0.991	y = 0.012x^2 − 0.082× + 0.215
	6	0.994	y = 0.006x^2 − 0.048× + 0.165
	7	0.956	y = 0.010x^2 − 0.073× + 0.200
	8	0.944	y = 0.013x^2 − 0.091× + 0.231
35	4	0.997	y = 0.008x^2 − 0.058× + 0.174
	5	0.999	y = 0.006x^2 − 0.049× + 0.157
	6	0.999	y = 0.007x^2 − 0.051× + 0.157
	7	0.996	y = 0.006x^2 − 0.047× + 0.150
	8	0.997	y = 0.007x^2 − 0.051× + 0.153

For example, if the desired value of thermal conductivity of elastic SJKF is 0.07 W.m⁻¹.K⁻¹, this value could be achieved in case of:

1. Yarn count 35 Ne, loop length 2.78 mm, and SWP 5%.

2. Yarn count 35 Ne, loop length 2.88 mm, and SWP 4%.

3. Yarn count 25 Ne, loop length 3.06 mm, and SWP 8%.

4. Yarn count 25 Ne, loop length 3.2 mm, and SWP 7%.

5. Yarn count 25 Ne, loop length 3.32 mm, and SWP 6%.

These results are related to the used material (cotton), yarn count range 25–35 Ne, and SWP 4–8%, however, this attempt can be generalized and achieved practically and industrially by expanding the range of the yarn count, SWP and the type of raw material.

Conclusion

A new model to predict thermal conductivity of elastic SJKF was derived based on geometrical parameters of loop and the fibers direction to the direction of heat flow. The elastic knitted fabric samples were produced with different yarn counts, loop length, and spandex weight percent to verify the model. Then the predicted values from a new model, three theoretical models, and experimental values were compared.

The results show that the predicted values from the new model were approximately similar to experimental values. Therefore, the new model could be generalized to investigate the thermal conductivity of elastic SJKF from the construction parameters and vice versa.

An attempt to insert structural parameters to obtain a desired thermal conductivity from the fabric construction parameters and vice versa was introduced. This attempt could be a guide to the manufacturers of elastic knitted fabric. The selection criteria of fabrics are related to material used, the range of yarn count, loop length, and spandex weight percent.

Highlights

In this work:

1. A new model to predict the thermal conductivity of elastic single jersey knitted fabric was derived based on fabric construction parameters and yarn and fibers inclination on the direction of heat flow

2. Full plaited knitted fabric samples with two different yarn count and five levels of loop length and spandex weight percent were produced.

3. To validate the new model, the thermal conductivity of these samples was measured and compared to the predicted values from a new model and previous three models.

4. the results show that the values of thermal conductivity from the new model are very closed to the experimental values; therefore, the new model could be used to predict the thermal conductivity of elastic single jersey knitted fabric.

5. The new model can assist the manufactures of elastic single jersey knitted fabric to predict the thermal conductivity from the fabric construction parameters before production process.

Disclosure statement

No potential conflict of interest was reported by the author(s).