Total and Secure Domination for Corona Product of Two Fuzzy Soft Graphs

Abstract

Fuzzy sets and soft sets are two different soft computing models for representing vagueness and uncertainty. On the other domination is a rapidly developing area of research in graph theory, and its various applications to ad hoc networks, distributed computing, social networks and web graphs partly explain the increased interest. This concept was introduced by [Benecke S, Cockayne EJ, Mynhardt CM. Secure total domination in graphs. Util Math. 2007;74:247–259.] in 2007 and Go and Canoy continue the study of these notions [Canoy RS, Go CE. Domination in the corona and join of graphs. Int Math Forum. 2011;6(16):763–771.] and afterward introduce total dominating and secure total dominating sets. Also graph operations like corona product play a very important role in mathematical chemistry, since some chemically interesting graphs can be obtained from some simpler graphs by different graph operations. In this paper, we characterised the dominating, total dominating, and secure total dominating sets in the corona of two fuzzy soft connected.

KEYWORDS:

• Soft graph
• total domination
• secure domination
• corona product

Subject classification codes:

• 05C72

1. Introduction

Molodtsov [1] introduced the concept of soft set that can be seen as a new mathematical theory for dealing with uncertainties. Molodtsov applied this theory to several directions [1–3] and then formulated the notions of soft number, soft derivative, soft integral, etc. in Molodtsov et al. [4]. The soft set theory has been applied to many different fields with greatness. Maji [5] worked on theoretical study of soft sets in detail. The algebraic structure of soft set theory dealing with uncertainties has also been studied in more detail. Aktas and Cagman [6] introduced definition of soft groups, and derived their basic properties. The most appreciate theory to deal with uncertainties is the theory of fuzzy sets, developed by Zadeh in 1965. But it has an inherent difficulty to set the membership function in each particular case.

Maji et al. [7] presented the concept of fuzzy soft sets by embedding ideas of fuzzy set in Zadeh [8]. In fact the notion of fuzzy soft set is more generalised than fuzzy set and soft set. Thereafter many papers devoted to fuzzify the concept of soft set theory which leads to a series of mathematical models such as fuzzy soft set [9–12], generalised fuzzy soft set [1,13], possibility fuzzy soft set [14] and so on. Thereafter Maji and his coauthor [15] introduced the notion of intuitionistic fuzzy soft set which is based on a combination of intuitionistic fuzzy sets and soft set models and they studied the properties of intuitionistic fuzzy soft set.

The first definition of fuzzy graphs was proposed by Kauffman [16] in 1973, from Zadeh’s fuzzy relations [8]. But Rosenfeld [17] introduced another elaborated definition including fuzzy vertex and fuzzy edges and several fuzzy analogs of notions of graph theory.

Soft graph was introduced by Thumbakara and George [18]. In 2015, Mohinta and Samanta [19] introduced the concept of fuzzy soft graph and A. Somasundram and S. Somasundram discussed domination in fuzzy graph.

Domination is a rapidly developing area of research in graph theory, and its various applications to networks, distributed computing, social networks and web graphs partly explain the increased interest.

There are other types of domination in graphs which are being studied such as total and secure domination. This concept was introduced by Benecke et al. [20] in 2007 and Go and Canoy continue the study of these notions [21].

In this paper, we characterised the dominating, total dominating and secure total dominating sets in the corona of two fuzzy soft connected graphs.

2. Preliminaries

First, we review some definitions which can be found in [8,21–29]. By a graph, we mean a pair $G^{\ast }=(V,E)$, where V is the set and E is a relation on V. The elements of V are vertices of $G^{\ast }$ and the elements of E are edges of G*. We call $V\left(G^{\ast }\right)$ the vertex set and $E\left(G^{\ast }\right)$ the edge set of $G^{\ast }$. A fuzzy set A on a set V is characterised by its membership function ${\sigma }_A:V\to [0,1]$, where ${\sigma }_A\left(u\right)$ is degree of membership of element u in fuzzy set A for each $u\in V.$ A fuzzy relation on V is a fuzzy subset of $V\times V.$ A fuzzy relation $\mu$ on V is a fuzzy relation on $\sigma$ if $\mu (u,v)\le \sigma \left(u\right)\wedge \sigma \left(v\right)$ for all u,v in V. A fuzzy graph $G=(\sigma ,\mu )$ is a pair of function $\sigma :V\to [0,1]$ and $\mu :V\times V\to [0,1]$, where for all $u,v\in V$, we have $\mu (u,v)\le \sigma \left(u\right)\wedge \sigma \left(v\right)$. The underlying crisp graph of a fuzzy graph $G=(\sigma ,\mu )$ is denoted by $G^{\ast }=({\sigma }^{\ast },{\mu }^{\ast })$, where ${\sigma }^{\ast }=\left\{u\in V:\sigma \left(u\right)>0\right\}$ and ${\mu }^{\ast }=\left\{(u,v)\in V\times V:\sigma (u,v)>0\right\}$ The strength of connectedness between two nodes u,v is defined as the maximum of strengths of all paths between u and v and is denoted by CONNG(u, v). A fuzzy graphs G is connected if CONNG(u,v) > 0 for all $u,v\in V.$ The fuzzy graph $G^{\mathrm{\prime }}=({\sigma }^{\mathrm{\prime }},{\mu }^{\mathrm{\prime }})$ is called a fuzzy subgraph of $G=(\sigma ,\mu )$, if ${\sigma }^{\mathrm{\prime }}\left(u\right)\le \sigma \left(u\right)$ and ${\mu }^{\mathrm{\prime }}(u,v)\le \mu (u,v)$ for all $u,v\in V$. A fuzzy graph $G=(\sigma ,\mu )$ is strong if $\mu (u,v)=\sigma \left(u\right)\wedge \sigma \left(v\right)$ for all $(u,v)\in E$ and is a complete fuzzy graph if $\mu (u,v)=\sigma \left(u\right)\wedge \sigma \left(v\right)$ for all $u,v\in V$. The order of fuzzy graph G is $O\left(G\right)={\sum }_{u\in V}\sigma \left(u\right)$. The size of fuzzy graph G is $S\left(G\right)={\sum }_{(u,v)\in E}\mu (u,v)$. The complement of a fuzzy graph $G=(\sigma ,\mu )$ is a fuzzy graph $\overline{G}=(\overline{\sigma },\overline{\mu })$ where $\overline{\sigma }=\sigma$ and $\overline{\mu }(u,v)=\sigma \left(u\right)\wedge \sigma \left(v\right)-\mu (u,v)$ for all $u,v\in V$. The degree of a vertex u in fuzzy graph $G=(\sigma ,\mu )$ is ${\mathrm{deg}}_G\left(u\right)={\sum }_{u\ne v}\mu (u,v)={\sum }_{uv\in E}\mu (u,v)$. A fuzzy graph $G=(\sigma ,\mu )$ is said to be a regular if every vertex which is adjacent to vertices having same degrees.

The neighbourhood of v is the set $N_G\left(v\right)=N\left(v\right)=\left\{u\in V\left(G\right):uv\in E\left(G\right)\right\}$. If $X\subseteq V\left(G\right)$, then the open neighbourhood of X is the set $N_G\left(X\right)=N\left(X\right)=\bigcup {}_{v\in X}{N}_G\left(v\right)$. The closed neighbourhood of X is $N_G\left[X\right]=X\cup N\left(X\right)$. A subset X of V(G) is a dominating set of G if for every $v\in \left(V\right(G\left)\mathrm{\setminus }X\right)$, there exists $x\in X$ such that $xv\in E\left(G\right)$, i.e. N[X] = V(G). It is a total dominating set if N(X)=V(G).

A total dominating set X is a secure total set if for every $u\in V\left(G\right)\mathrm{\setminus }X$, there exists $v\in X$ such that $uv\in E\left(G\right)$ and $\left[X\mathrm{\setminus }\right\{v\left\}\right]\cup \left\{u\right\}$ is a total dominating set. The domination number $\gamma \left(G\right)$, total domination number ${\gamma }_t\left(G\right)$ or secure total domination ${\gamma }_{st}\left(G\right)$ of G is the cardinality of a minimum dominating set of G.

3. Basic Definitions of Fuzzy Soft Graph

Let U be an initial universal set and E be a set of parameters. Let $I^U$ denotes the collection of all fuzzy subsets of U and $A\subseteq E$.

Definition 3.1:

Let $A\subseteq E$. Then the mapping $F_A:E\to I^U$, defined by $F_A\left(e\right)={\mu }_{F_A}^e$ (a fuzzy subset of U), is called fuzzy soft set over(U, E) , where ${\mu }_{F_A}^e=\overline{0}$ if $e\in E\mathrm{\setminus }A$ and${\mu }_{F_A}^e\ne \overline{0}$ if $e\in A$ and 0 denotes the null fuzzy set. The set of all fuzzy soft sets over (U, E) is denoted by FS(U,E).

Definition 3.2:

Let $V=\{x_1,x_2,\dots ,x_n\}$(non-empty set), E (parameters set) and $A\subseteq E$. Also let

1. $\sigma :A\to F\left(V\right)$ (Collection of all fuzzy subsets in V)

$e\mapsto \sigma \left(e\right)={\sigma }_e$ (say)

and ${\sigma }_e:V\to [0,1]$

$x_i\mapsto {\sigma }_x\left(x_i\right)$

$(A,\sigma )$: fuzzy soft vertex.

• (ii) $\mu :A\to F(V\times V)$ (collection of all fuzzy subsets in $V\times V$)

$e\to \mu \left(e\right)={\mu }_e$ (say)

and ${\mu }_e:V\times V\to [0,1]$

$(x_i,x_j)\mapsto {\mu }_e(x_i,x_j)$

$(A,\mu )$: fuzzy soft edge.

and $H\left(e\right)=\left(\sigma \right(e),\mu (e\left)\right)$ is a subgraph of G then $G=\left((A,\sigma ),(A,\mu )\right)=\left\{H\left(e\right)|e\in A\right\}$ is called fuzzy soft graph if and only if ${\mu }_e(x_i,x_j)\le {\sigma }_e\left(x_i\right)\wedge {\sigma }_e\left(x_j\right)$, $\mathrm{\forall }e\in A$ and $\mathrm{\forall }i,j=1,2,\dots ,n,$ and this fuzzy soft graph is denoted by $G_{A,V}$.

Definition 3.3:

The Order of a fuzzy soft graph is defined by $\text{Ord}\left(G\right)={\sum }_{e_i\in A}\left({\sum }_{a\in V}\sigma \left(e_i\right)\left(a\right)\right)$.

Definition 3.4:

The size of a fuzzy soft graph is $\text{Siz}\left(G\right)={\sum }_{e_i\in A}\left({\sum }_{ab\in E}\mu \left(e_i\right)\left(ab\right)\right)$.

Definition 3.5:

A fuzzy soft graph G is a strong fuzzy soft graph if H(e) is a strong fuzzy graph for all $e\in A$, i.e. $\mu \left(e\right)\left(ab\right)=min\left\{\sigma \left(e\right)\left(a\right),\sigma \left(e\right)\left(b\right)\right\}$ for all $ab\in E$.

A fuzzy soft graph G is a complete fuzzy soft graph if H(e) is complete fuzzy graph for all $e\in A$. That is $\mu \left(e\right)\left(ab\right)=min\left\{\sigma \left(e\right)\left(a\right),\sigma \left(e\right)\left(b\right)\right\}$ for all $a,b\in V$.

Definition 3.6:

Let $G^{\ast }=(V,E)$ be a crisp graph and G be a fuzzy soft graph of $G^{\ast }$.Then G is said to be a regular fuzzy soft graph if H(e) is a regular fuzzy graph for all $e\in A$. If H(e) is a regular fuzzy graph of degree r for all $e\in A$, then G is a r-regular fuzzy soft graph.

Definition 3.7:

Let $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ and $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two fuzzy soft graphs of $G^{\ast }$. The union of $G_1$ and $G_2$ is defined as $G_1\cup G_2=G=\left((C,\sigma ),(C,\mu )\right)$ Where

1. $C=A\cup B$.

2. for all $e\in C$, $\sigma \left(e\right)=\left\{\begin{array}{c}{\sigma }_1\left(e\right),\\ {\sigma }_2\left(e\right),\\ {\sigma }_1\left(e\right)\cup {\sigma }_2\left(e\right),\end{array}\begin{array}{c}\text{if}\\ \text{if}\\ \text{if}\end{array}\begin{array}{l}e\in A\mathrm{\setminus }B\\ e\in B\mathrm{\setminus }A\\ e\in A\cap B\end{array}\right.$

and $\mu \left(e\right)=\left\{\begin{array}{c}{\mu }_1\left(e\right),\\ {\mu }_2\left(e\right),\\ {\mu }_1\left(e\right)\cup {\mu }_2\left(e\right),\end{array}\begin{array}{c}\text{if}\\ \text{if}\\ \text{if}\end{array}\begin{array}{l}e\in A\mathrm{\setminus }B\\ e\in B\mathrm{\setminus }A\\ e\in A\cap B\end{array}\right.$ That is $G_1\cup G_2=\left\{H\left(e\right)=\left(\sigma \left(e\right),\mu \left(e\right)\right)|e\in C\right\}$.

Theorem 3.8:

[26] Let $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ and $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two fuzzy soft graphs of $G^{\ast }$ with $C=A\cup B$. Then their union $G_1\cup G_2=\left\{H\left(e\right)=\left(\sigma \left(e\right),\mu \left(e\right)\right)|e\in C\right\}$ is a soft graph.

Definition 3.9:

Let $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ and $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two soft graphs. The extended intersection of $G_1$ and $G_2$ is defined as $G_1\cap G_2=G=\left((C,\sigma ),(C,\mu )\right)$ where

1. $C=A\cup B$

2. for all $e\in C$ $\sigma \left(e\right)=\left\{\begin{array}{c}{\sigma }_1\left(e\right),\\ {\sigma }_2\left(e\right),\\ {\sigma }_1\left(e\right)\cap {\sigma }_2\left(e\right),\end{array}\begin{array}{c}\text{if}\\ \text{if}\\ \text{if}\end{array}\begin{array}{l}e\in A\mathrm{\setminus }B\\ e\in B\mathrm{\setminus }A\\ e\in A\cap B\end{array}\right.$ $\mu \left(e\right)=\left\{\begin{array}{c}{\mu }_1\left(e\right),\\ {\mu }_2\left(e\right),\\ {\mu }_1\left(e\right)\cap {\mu }_2\left(e\right),\end{array}\begin{array}{c}\text{if}\\ \text{if}\\ \text{if}\end{array}\begin{array}{l}e\in A\mathrm{\setminus }B\\ e\in B\mathrm{\setminus }A\\ e\in A\cap B\end{array}\right.$

That is $G_1\cap G_2=\left\{H\left(e\right)=\left(\sigma \left(e\right),\mu \left(e\right)\right)|e\in C\right\}$.

Theorem 3.10:

[26] Let $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ and $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two fuzzy soft graphs and $C=A\cup B$. Then their intersection $G_1\cap G_2=\left\{H\left(e\right)=\left(\sigma \left(e\right),\mu \left(e\right)\right)|e\in C\right\}$ is a soft graph.

Definition 3.11:

Let $G_1$ and $G_2$ be two soft graphs of $G_1^{\ast }$ and $G_2^{\ast }$, respectively such that $A\cap B\ne set$. Their restricted products is defined by $G_1\otimes G_2$ and is defined by $G_1\otimes G_1=(H,A\cap B)$, where $H\left(e\right)=H_1\left(e\right)\times H_2\left(e\right),$ for all $e\in A\cap B$ where H₁ (e) × H₂ (e) is the Cartesian product of two graphs, that is $G_1\times G_2=\left\{H\left(e\right)|e\in A\cap B\right\}$.

Definition 3.12:

[26] Let $L^{\ast }$ be the Cartesian product of two simple graphs $G_1^{\ast }$ and $G_2^{\ast }$. Let $G_1$ and $G_2$ be, respectively, soft graphs of $G_i^{\ast },i=1,2$. Then $G_1\times G_2=(H,A\times B)$ is a soft graphs of $L^{\ast }$

Definition 3.13:

Let $G_1$ and $G_2$ be two soft graphs of $G_1^{\ast }$ and $G_2^{\ast }$, respectively such that $A\cap B\ne set$. The composition of $G_1$ and $G_2$ denoted by $G_1\left[G_2\right]$ and is defined by $G_1\left[G_2\right]=\left(H,A\times B\right)$ where for all $(e,e^{\mathrm{\prime }})\in A\times B$, $H(e,e^{\mathrm{\prime }})=H_1\left(e\right)\left[H_2\right(e\left)\right]$. Note that $H_1\left(e\right)\odot H_2\left(e^{\mathrm{\prime }}\right)$ denotes the ordinary composition of two crisp subgraphs. That is $G_1\odot G_2=\left\{H(e,e^{\mathrm{\prime }})|(e,e^{\mathrm{\prime }})\in A\times B\right\}.$

Theorem 3.14:

[26] Let $M^{\ast }$ be the composition of two simple graphs $G_1^{\ast }$ and $G_2^{\ast }$. Let $G_1$ and $G_2$ be, respectively, soft graphs of $G_i^{\ast }$, i=1,2.Then $G_1\odot G_2=\left(H,A\times B\right)$ is a soft graph of $M^{\ast }$.

Definition 3.15:

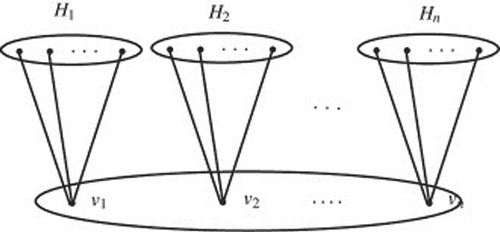
The corona product $G=G_1\circ G_2=\left(V\left(G\right),E\left(G\right),\sigma ,\mu \right)$ of two fuzzy graphs $G_1$ and $G_2$ is obtained by taking one copy of $G_1$ and $|V\left(G\right)|$ copies of $G_2$; and by joining each vertex of the ith copy $G_2$ to the ith vertex of $G_1$, where 1<i<|V(G)| , for every $v\in V\left(G\right)$ denote by $H^v$ the copy of H whose vertices are attached one by one to the vertex v. Subsequently, denote by $v+H^v$ the sub graph of the corona $G\circ H$ corresponding to the join $〈\left\{v\right\}〉+H^v,v\in V\left(G\right),$ and $\sigma \left(u\right)=\left\{\begin{array}{l}{\sigma }_1\left(u\right),\\ {\sigma }_2\left(u\right),\end{array}\begin{array}{l}u\in V\left(G\right)\\ u\in V\left(G_2\right)\end{array}\right.$ $\mu (u,v)=\left\{\begin{array}{l}{\mu }_1(u,v),\\ {\mu }_2(u,v),\\ {\sigma }_1\left(u\right)\wedge {\sigma }_2\left(v\right),\end{array}\begin{array}{l}uv\in E\left(G_1\right)\\ uv\in E\left(G_2\right)\\ u\in V\left(G_1\right),v\in V\left(G_2\right)\end{array}\right.$

Lemma 3.16:

[26] If $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ be a fuzzy soft graph of $G_1^{\ast }$. Then $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ is a soft fuzzy sub graph of $G_1$ if and only if ${\sigma }_2\subseteq {\sigma }_1$ and ${\mu }_2\subseteq {\mu }_1$ for all $e\in B$.

Theorem 3.17:

Let $K^{\ast }$ be the Corona product of two simple graphs $G_1^{\ast }$ and $G_2^{\ast }$. Let $G_1=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$ and $G_2=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two fuzzy soft graphs of $G_i^{\ast }$, i=1,2, respectively, then $G_1\circ G_2=\left((C,\sigma ),(C,\mu )\right)$ by under definition is a soft graphs of $K^{\ast }$. ${\sigma }_e=\left\{\begin{array}{l}{\sigma }_{e1}\left(v\right),\\ {\sigma }_{e2}\left(v\right),\end{array}\begin{array}{l}v\in V\left(G_1\right),e\in A\\ v\in V\left(G_2\right),e\in B\end{array}\right.$ ${\mu }_e(u,v)=\left\{\begin{array}{l}{\mu }_{e1}(u,v),\\ {\mu }_{e,2}(u,v),\\ min\left\{{\sigma }_{e1}\right(u),{\sigma }_{e2}(v\left)\right\},\end{array}\begin{array}{l}uv\in E\left(G_1\right),e_1\in A\\ uv\in E\left(G_2\right),e_2\in B\\ u\in V\left(G_1\right),v\in V\left(G_2\right),e_1\in A,e_2\in B\end{array}\right.$

Proof:

By definition of corona product, $H\left(e\right)=\left(H\left(e_1\right)\circ H\left(e_2\right)\right)$ then sub graph H(e) for all $e\in C$ by Lemma 3.16 is a fuzzy soft graphs, then the corona product $G_1\circ G_2=\left(H\left(e\right),C\right)$ is a fuzzy soft graphs of $K^{\ast }$.

Definition 3.18:

Let $G=(\sigma ,\mu )$, the vertex x dominates y in G if $\mu \left(\right\{x,y\left\}\right)=min\left\{\sigma \right(x),\sigma (y\left)\right\}$. A subset S of V(G) is called a dominating set in G if for every $v\notin S,$ there exists $u\in S$ such that u dominates v. The fuzzy cardinality of S is defined as ${\sum }_{v\in S}\sigma \left(v\right).$ The minimum fuzzy cardinality of a dominating set in G is called the domination number of G and denoted by $\gamma \left(G\right)$.

A subset T of V(G) is said to be a total dominating set if every vertex in V(G) is dominated by a vertex in T. The minimum fuzzy cardinality of a total dominating set is called the total domination number and denoted by ${\gamma }_t\left(G\right)$. Such a dominating set with minimum fuzzy cardinality is called a minimal dominating set of G.

4. Main Results

Theorem 4.1:

Let $G=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$, $H=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two connected fuzzy soft graphs and $C=A\cup B$, then$D\subseteq V\left(G\left(e_i\right)\circ H\left({e^{\mathrm{\prime }}}_i\right)\right)$ for all $e_i,e_i^{\mathrm{\prime }}\in C$, is a dominating set in $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, if and only if $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ for every $v\in V\left(G\right)$.

Proof:

Let D be a dominating set in $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ and let $v\in V\left(G\right(e_i\left)\right)$. If $v\in D$, then {v} is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$.It follows that $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$. Suppose that $v\notin D$ and let $x\in V(v+H(e^{\mathrm{\prime }}i{)}^v)\mathrm{\setminus }D$ with $x\ne v$. Since D is a dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, there exists $y\in D$ such that $xy\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$. Then $y\in V\left(H^v\right)\cap D$ and $xy\in E(v+H(e_i^{\mathrm{\prime }}{)}^v)$. This proves that $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$.

For the converse, suppose that $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ for every $v\in V\left(G\right)$. Then, clearly, D is a dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$.

Corollary 4.2:

Let $G=\left((A,{\sigma }_1),(A,{\mu }_1)\right)$, $H=\left((B,{\sigma }_2),(B,{\mu }_2)\right)$ be two connected fuzzy soft graphs and $C=A\cup B$, Then $\gamma \left(G\left(e_i\right)\circ H\left({e^{\mathrm{\prime }}}_i\right)\right)=Ord\left(G\right(e_i\left)\right)$.

Proof:

Let $D=V\left(G\left(e_i\right)\right)$. Then $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D=\left\{v\right\}$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ for every $v\in V\left(G\right(e_i\left)\right)$. By Theorem 4.1, D is a dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$; hence, $\gamma \left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)\le |D|=Ord\left(G\right(e_i\left)\right)$

Next, let $D^{\ast }$ be a minimum dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$. Then, by Theorem 4.1, $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D^{\ast }$ is a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ for every $v\in V\left(G\right(e_i\left)\right)$. It follows that $\gamma \left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=|D^{\ast }|\ge Ord\left(G\right(e_i\left)\right)$. Therefore, $\gamma \left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=Ord\left(G\right(e_i\left)\right)$.

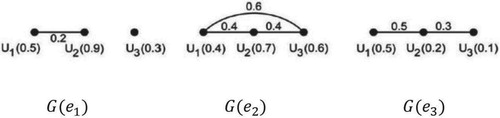
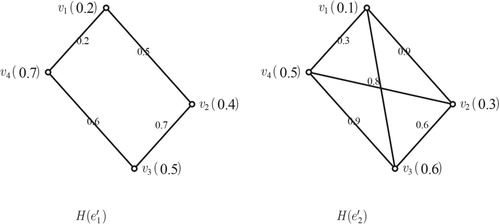
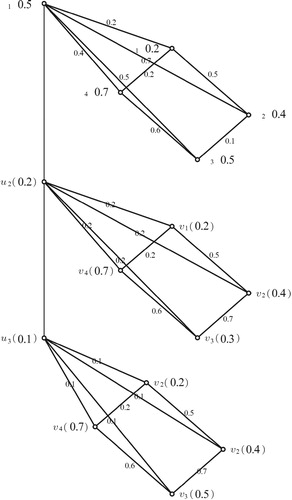
Example 4.3:

Consider two fuzzy soft graph $G_{A,V_1}$ where $V_1=\left\{u_1,u_2,u_3\right\}$ and $A=\left\{e_1,e_2,e_3\right\}$. Here $G_{\left\{A,V_1\right\}}$ described by Table 1 and is shown in Figure 1 and $H_{B,V_2}$ where $V_2=\left\{v_1,v_2,v_3,v_4\right\}$ and described by Table 2 and is shown in Figure 2.

Table 1. Tabular representation of a fuzzy soft graph $G_{A,V_1}$.

$\mathit{\mu }$	($u_1$,$u_2$)	($u_2$,$u_3$)	($u_1$,$u_3$)
${\mathit{e}}_1$	0.2	0	0
${\mathit{e}}_2$	0.4	0.4	0.6
${\mathit{e}}_3$	0.5	0.3	0
$\mathit{\sigma }$	$u_1$	$u_2$	$u_3$
${\mathit{e}}_1$	0.5	0.9	0.3
${\mathit{e}}_2$	0.4	0.7	0.6
${\mathit{e}}_3$	0.5	0.2	0.1

Table 2. Tabular representation of fuzzy soft graph $H_{B,V_2}$.

$\mathit{\sigma }$	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	${\mathit{v}}_4$
$e_1^{\mathrm{\prime }}$	0.2	0.4	0.5	0.7
$e_2^{\mathrm{\prime }}$	0.1	0.3	0.6	0.5
$\mathit{\mu }$	(${\mathit{v}}_1,{\mathit{v}}_2$)	(${\mathit{v}}_1,{\mathit{v}}_3$)	(${\mathit{v}}_1,{\mathit{v}}_4$)	(${\mathit{v}}_2,{\mathit{v}}_3$)	(${\mathit{v}}_2,{\mathit{v}}_4$)	(${\mathit{v}}_3,{\mathit{v}}_4$)
$e_1^{\mathrm{\prime }}$	0.5	0	0.2	0.7	0	0.6
$e_2^{\mathrm{\prime }}$	0.4	0.8	0.3	0.6	0.8	0.9

Figure 1. G○H.

Figure 2. Fuzzy soft graph $G_{A,V_1}$.

Thus, $G=\left\{G\left(e_1\right),G\left(e_2\right),G\left(e_3\right)\right\}$ and $H=\left\{H\left(e{}_1^{\mathrm{\prime }}\right),\left(e{}_2^{\mathrm{\prime }}\right)\right\}$ are two fuzzy soft graphs and $G\left(e_3\right)\circ H\left(e_1^{\mathrm{\prime }}\right)$ it was shown in Figures 3 and 4. Then $D=\left\{u_1,u_2,u_3\right\}$ and $\gamma \left(G\left(e_i\right)\circ H\left({e^{\mathrm{\prime }}}_i\right)\right)=0.8$.

Figure 3. Fuzzy soft graph $H_{B,V_2}.$

Figure 4. G($e_3$)○H($e_1^{\mathrm{\prime }}$).

Theorem 4.4:

Let $G=\left(\right(A,{\sigma }_1),(A,{\mu }_1\left)\right),H=\left(\right(B,{\sigma }_2),(B,{\mu }_2\left)\right)$ be two connected fuzzy soft graphs and $C=A\cup B$ Then $D\subseteq V\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$ is a total dominating set in $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ if and only if for every $v\in V\left(G\right(e_i\left)\right)$, either

• (i) $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a total dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ or

• (ii) $v\in D$ and $N_{G\left(e_i\right)}\left(v\right)\cap D\ne set$.

Proof:

Let D be a total dominating set in $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ and let $v\in V\left(G\right(e_i\left)\right)$. If $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is a total dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$, then we are done. So, suppose that $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D$ is not a total dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$. Suppose further that $v\notin D$. Since D is a dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right),V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ must be a dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$ Now, since $V(v+H(e_i^{\mathrm{\prime }}{)}^v)\cap D=V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is not a total dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$, there exists $u\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\mathrm{\setminus }D$ such that $N_{G\left(e_i{)}^{\circ }H\right({e^{\mathrm{\prime }}}_i)}\left(u\right)\cap D=set.$ This contradicts the fact that D is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, Thus, $v\in D$. By assumption $V(v+H(e_i^{\mathrm{\prime }}\left)v\right)\cap D=\left\{v\right\}$ (otherwise the set is total dominating set). Since D is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, it follows that $N_{G\left(e_i\right)}\left(v\right)\cap D\ne set$.

For the converse, suppose that the condition holds for D. Let $x\in V\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$ and let $v\in V\left(G\right(e_i\left)\right)$ such that $x\in V(v+H(e_i^{\mathrm{\prime }}{)}^v)$. Consider the following cases:

• Case 1. x = v

If $x\in D$, then there exists $u\in V\left(G\right(e_i\left)\right)\cap \left(D\mathrm{\setminus }\right\{x\left\}\right)$ such that $xu\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$.

If $x\notin D$, then $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a total dominating set of $v+H(e_i^{\mathrm{\prime }}{)}^v$.

Hence, there exists $y\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ such that $xy\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$.

• Case 2. $x\ne v$

If $x\in D$, then .$xv\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$ If $v\notin D$, then there exists $w\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ such that $xw\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$.

In both cases, we have $N_{G\left(e_i{)}^{\circ }H\right({e^{\mathrm{\prime }}}_i)}\left(u\right)\cap D\ne set$. Therefore, D is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)\text{■}$

Corollary 4.5:

Let $G=\left(\right(A,{\sigma }_1),(A,{\mu }_1\left)\right),H=\left(\right(B,{\sigma }_2),(B,{\mu }_2\left)\right)$, be two connected fuzzy soft graphs and $C=A\cup B$ then ${\gamma }_t\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=Ord\left(G\right(e_i\left)\right).$

Proof:

Let $D=V\left(G\left(e_i\right)\right)$. Then D is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, by Theorem 4.4. Thus, ${\gamma }_t(G\circ H)\le |D|=Ord\left(G\right(e_i\left)\right)$.

Next, let D* be a minimum total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$. Then, by Theorem 4.4, $|V(v+H(e_i^{\mathrm{\prime }})v\cap D^{\ast }|\ge 1$ for every $v\in V\left(G\right(e_i\left)\right)$. It follows that ${\gamma }_t\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=|D^{\ast }|\ge Ord\left(G\right(e_i\left)\right).$ Therefore, ${\gamma }_t\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=Ord\left(G\right(e_i\left)\right).$

Lemma 4.6:

Let G be a connected fuzzy soft graph and let S be a secure total dominating set of G. Then the set $S\mathrm{\setminus }\left\{v\right\}$ is a dominating set of G for every $v\in S$. In particular, $\sigma \left(v\right)+\gamma \left(G\right)\le {\gamma }_{st}\left(G\right)$.

Proof:

Let $v\in S$ and let $S^{\ast }=S\mathrm{\setminus }\left\{v\right\}$. Suppose $S^{\ast }$ is not a dominating set of G. Then there exists $z\in V\left(G\right)\mathrm{\setminus }{S}^{\ast }$ such that $zw\notin E\left(G\right)$ for all $w\in S^{\ast }$.Then $z\ne v$ and v is the only element of S with $zw\notin E\left(G\right)$ However, the set $D\mathrm{\setminus }\left\{v\right\}\cup \left\{z\right\}$ cannot be a total dominating set because $zw\notin E\left(G\right)$ for all $w\in S^{\ast }.$ This contradicts the fact that S is a secure total dominating set of G. Therefore, $S\mathrm{\setminus }\left\{v\right\}$ is a dominating set of G. Moreover, if S is a minimum secure total dominating set of G, then the result implies that $\gamma \left(G\right)\le {\gamma }_{st}\left(G\right)-\sigma \left(v\right)$.

Theorem 4.7:

Let $G=\left(\right(A,{\sigma }_1),(A,{\mu }_1\left)\right),H=\left(\right(B,{\sigma }_2),(B,{\mu }_2\left)\right)$, be two connected fuzzy soft graphs and $C=A\cup B$. Then $D\subseteq V\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$ is a secure total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ if and only if for every $v\in V\left(G\right(e_i\left)\right)$, either

• (i) $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a secure total dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$ or

• (ii) $v\in D$ and $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$.

Proof:

Let D be a secure total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ and let $v\in V\left(G\right(e_i\left)\right)$. If $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a secure total dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$, then we are done. So suppose that $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is not a secure total dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$. Suppose further that $v\notin D$. Since D is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ must be a total dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$.

By our assumption, there exists $x\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\mathrm{\setminus }D$ such that $\left[\right(V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D\left)\right\{y\left\}\right]\cup \left\{x\right\}$ is not a total dominating set for every $y\in V\left(H(e_{i^{\mathrm{\prime }}}{)}^v\right)\cap D$ with $xy\in E\left(H(e_i^{\mathrm{\prime }}{)}^v\right)$. This implies that$\left(D\mathrm{\setminus }\right\{y\left\}\right)\cup \left\{x\right\})$ is not a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$ for every $y\in D$ with $xy\in E\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)$ contrary to our assumption of the set D. Therefore, $v\in D$ If $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D=set$ and $w\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)$, then $\left(D\mathrm{\setminus }\right\{v\left\}\right)\cup \left\{w\right\}$ is not a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$, contrary to our assumption. Thus $\left(V\right(H(e_i^{\mathrm{\prime }}{)}^v)\cap D\ne set$. Using a similar argument, it can be shown that $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$.

Suppose the condition holds for D. Then D is clearly a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$. Let $x\in V\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)\mathrm{\setminus }D$ and $v\in V\left(G\right(e_i\left)\right)$ let such that $x\in V(v+H(e_i^{\mathrm{\prime }}{)}^v).$ Consider the following cases:

• Case1. x = v

By assumption $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a secure total dominating of $H(e_i^{\mathrm{\prime }}{)}^v$. Pick $y\in \left(V\right(H(e_i^{\mathrm{\prime }}{)}^v)\cap D)$ then $\left(D\mathrm{\setminus }\right\{y\left\}\right)\cup \left\{x\right\}$ is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$.

• Case 2. $x\ne v$

Then $x\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)$. If $v\notin C$, then $\left(V\right(H(e_i^{\mathrm{\prime }}{)}^v)\cap D)$ is a secure total dominating set of $H\left(e_i^{\mathrm{\prime }}\right),$ and so there exists $u\in v\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ such that $\left[V\right(H(e_i^{\mathrm{\prime }}{)}^v)\cap D)\mathrm{\setminus }\left\{u\right\}]\cup \{x\}$ is a total dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$. It follows that $D\mathrm{\setminus }\left\{u\right\}\cup \left\{x\right\}$ is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$. If $v\in D$, then $V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ is a dominating set of $H(e_i^{\mathrm{\prime }}{)}^v$.

Pick $w\in V\left(H(e_i^{\mathrm{\prime }}{)}^v\right)\cap D$ such that $wx\in E\left(H(e_i^{\mathrm{\prime }}{)}^v\right).$ Then $\left(D\mathrm{\setminus }\right\{w\left\}\right)\cup \left\{x\right\}$ is a total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$.

Therefore, D is a secure total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$.

Corollary 4.8:

Let $G=\left(\right(A,{\sigma }_1),(A,{\mu }_1\left)\right),H=\left(\right(B,{\sigma }_2),(B,{\mu }_2\left)\right)$ be two connected fuzzy soft graphs and $C=A\cup B$. Then ${\gamma }_{st}\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)={\sum }_{v\in V}\left(\sigma \right(v)+\gamma (H\left)\right).$

Proof:

For each $v\in V\left(G\right(e_i\left)\right)$, let $S_v$ be a minimum dominating set of $H^v$ and set $D={\bigcup }_{v\in V\left(G\right)}(S_v\cup \{v\left\}\right)$ then D is a secure total dominating set of $G\left(e_i\right)\circ h\left(e_i^{\mathrm{\prime }}\right)$ by Theorem 4.7. Thus ${\gamma }_{st}\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)\le |D|={\sum }_{v\in V\left(G\right)}\left(\sigma \right(v)+\gamma (H\left)\right)$.

Next, let $D^{\ast }$ be a minimum secure total dominating set of $G\left(e_i\right)\circ H\left(e_i^{\mathrm{\prime }}\right)$. Then, by Theorem 4.7, $|V(H(e_i^{\mathrm{\prime }}{)}^v\cap D^{\ast }|\ge {\gamma }_{st}(H)$ or $|\left(V\right(H\left(e_i^{\mathrm{\prime }}\right)v)\cup \{v\left\}\right)\cap D^{\ast }|\ge \left(\sigma \right(v)+\gamma (H)$ for every $v\in V\left(G\right(e_i\left)\right)$.

With Lemma 4.6, it follows that ${\gamma }_{st}\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=|D^{\ast }|\ge {\sum }_{v\in V\left(G\right)}\left(\sigma \right(v)+\gamma (H\left)\right)$.Therefore, ${\gamma }_{st}\left(G\right(e_i)\circ H(e_i^{\mathrm{\prime }}\left)\right)=|D^{\ast }|={\sum }_{v\in V\left(G\right)}\left(\sigma \right(v)+\gamma (H\left)\right)$.

5. Conclusion

Graph products that allow the mathematical design of a network in terms of small sub graphs that directly express many problems. The result is a flexible algebraic description of networks suitable for manipulation and proof. For graphical research the fuzzy total domination and secure domination are very useful for solving wide range of problems. In this paper we have studied the concepts of fuzzy total domination number and fuzzy secure total domination number for corona product of two fuzzy graphs.

Acknowledgements

The authors are thankful to the reviewers and editor of this journal for their valuable suggestions and comments which have improved this work.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Asefeh Karbasioun

Asefeh Karbasioun is a Ph.D. student in Mathematics, Payame Noor University of Tehran, Tehran, Iran. She is working on Nano Computation and has published 9 papers in mathematical journals. Her orientation in course of Ph.D. is fuzzy sets and systems and her research interest is fuzzy graphs and discrete mathematics.

Reza Ameri

Reza Ameri received the B.Sc. degree from Bahonar University of Kerman of Iran in 1989. He received Master and Ph.D. degrees in Mathematics from Bahonar University of Kerman of Iran in 1993 and 1997, respectively. Currently, he is a professor in the Department of Mathematics of School of Mathematics, Statistics and Computer Science, College of Sciences, University of Tehran, Tehran, Iran. He has published more than 100 research papers in international journals in area of fuzzy algebra, algebra and (fuzzy) hyperalgebric structures and His current research interests are in the field of fuzzy foundation and their applications of fuzzy sets and fuzzy logic in mathematics and other sciences.