http://orcid.org/0000-0003-4181-6279
ABSTRACT
This paper investigates the order statistics based on the moment-generating function for the Generalized Power Function Distribution for the two different forms of this distribution. In this paper, we continue our investigation on the distribution of order statistics assuming that the original sample of size n is taken from a population that follows the Generalized Power Function Distribution. Two different forms of the Generalized Power Function Distribution with its special cases are presented and some order statistics related to these different forms are discussed. The main technique is the consideration of the moment-generating function.
MATHEMATICS SUBJECT CLASSIFICATION:
1. Introduction
The Generalized Power Function Distribution (GPFD) is one of the useful lifetime distribution models which offers a good fit to various sets of failure data. This paper investigates the moment generating function and moments for the special cases of the order statistics for the GPFD by the classical method of moment generating functions [Citation1].
The GPFD [Citation2] is defined as(1) where
, and
and
are defined as:
(2)
It is well known that the GPFD is a special case of Beta when
distribution [Citation2].
The following is the alternative parametrization of the GPFD [Citation3]:(3) In the following, we will always assume that parameter
, and we will not specify this anymore.
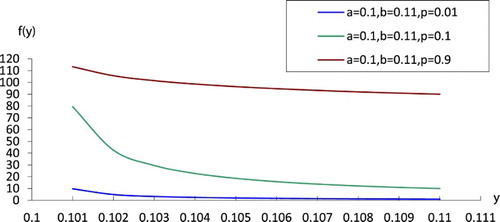
shows the probability density function for the GPFD for the parametrization (3) for different values for the shape , scale
and location
parameters.
Figure 1. Probability density functions for the GPFD of the form (3).
2. Parametrization (3)
Let be a random sample of size
from a population which follows the GPFD with the probability density function (3). Al Mutairi [Citation4] derived the probability density function of the
-th order statistic
, obtained from this random sample in the following form:
In addition, Al Mutairi [Citation4] derived the moment generating function for the order statistic as follows:
(4) where
Hence the -th moment of the order statistic
is given as:
(5)
In particular, the first moment of the order statistics is obtained by setting
in Equation (5) and this leads to
The second non-central moment is obtained by setting
in Equation (5). The same as in Al Mutairi [Citation4], we obtain
2.1. Special case
Let and
in Equation (3) to get one of the most important special cases which is known as a standard Power Function distribution that has many applications. For example, see ref. [Citation3] where data representing the failure time in minutes of an electrical insulation device are considered and have been modelled as a standard Power Function distribution.
To derive some properties for this special case, we consider the moment generating function of the order statistic (Equation (4)) as follows:
(6)
Then, by differentiating Equation (6) and setting , the first moment (mean)
of the order statistic
for the GPFD with
and
is obtained as
In the same way, the second non-central moment for the order statistic for the Standard Power Function Distribution is computed as
The variance
of the order statistic
for the GPFD with
and
can be obtained as follows:
3. Alternative parametrization (1)
A special case of the alternative parametrization of the GPFD can be obtained by setting in Equation (1). Then we obtain
(7) where
is the shape parameter,
is the scale parameter and
is the location parameter [Citation3]. Moreover, a special case of Equation (7) can be obtained by setting
and
which leads to the same formula of Standard GPFD that is discussed in Section 2.1.
The probability density function of the -th order statistic
is given [Citation4] as follows:
(8)
See refs. [Citation5] and [Citation6].
With preliminaries accounted for, we can now formulate and prove the following theorem.
Theorem 1:
If is the
-th order statistic for a sample from the population with GPFD of the form (7), then:
(i) The moment generating function
of the order statistic
(ii) The first moment(mean)
(iii) The
Proof : (i)
The moment generating function of the order statistic can be obtained by the considering the probability density function
(14)
This leads towhere
is given by
(15)
Then using the following substitution:The limits of integration become as follows:
Thus, the previous equation becomes(16)
This formula proves Equation (9) in Theorem 1, which provides the moment generating function of the order statistic
.
(ii) The first moment (mean) for the order statistic
is calculated by differentiating Equation (9) with respect to
and setting
:
Then, by setting , we obtain
which represents the first moment (mean)
for the order statistic
.
The second non-central moment of the order statistics is calculated as:
Then, by setting , we obtain
which represents the second non-central moment
of the order statistic
.
In addition, the variance of the order statistic
can be calculated as follows:
which represents the variance
for the order statistic
.
(iii) Finally, the -th moment
for the order statistic is
Using the binomial expansion, we obtain the following:
This result proves Equation (13) in Theorem 1, which represents the -th moment
of the order statistic
.
Now we consider first two moments for (7). We can obtain the first moment (mean) of the order statistic
by setting
in Equation (13) as follows:
Similarly, by setting in Equation (13), we get:
(17)
This gives the second non-central moment for GPFD.
4. Conclusion
In this paper, two different forms of the GPFD with its special cases are presented and some order statistics related to these different forms are discussed. The main technique is the consideration of the moment generating function.
Acknowledgements
The authors thank the referees for constructive comments.
Disclosure statement
No potential conflict of interest was reported by the authors.
ORCID
Andrei Volodin http://orcid.org/0000-0002-9771-846X
Additional information
Funding
References
- Hogg RV, Craig AT. Introduction to mathematical statistics. 4th ed. New York (NY): Macmillan Publishing Co., Inc., Collier Macmillan Publishers; 1978.
- Johnson NL, Kotz S, Balakrishnan N. Practical statistical process control – A tool for quality manufacturing. J R Stat Soc Ser A Stat Soc. 1996;159(2):343. doi: 10.2307/2983179
- Sultan KS, Moshref ME, Childs A. Record values from generalized power function distribution and associated inference. J Appl Stat Sci. 2002;11(2):145–157.
- Al Mutairi AO. Distribution of the order statistics of the generalized power function. Adv Appl Stat. 2016;49(2):87–104.
- Allam SM, Datta TK. Response spectrum analysis of suspension bridges for random ground motion. J Bridge Eng. 2002;7(6):325–337. doi: 10.1061/(ASCE)1084-0702(2002)7:6(325)
- Saluja GS, Postolache M, Kurdi A. Convergence of three-step iterations for nearly asymptotically nonexpansive mappings in CAT (k) spaces. J Inequal Appl. 2015;(1):1–18. doi: 10.1186/s13660-015-0670-z
- Maiti R, Biswas A. Coherent forecasting for over-dispersed time series of count data. Braz J Probab Statistics. 2015;29(4):747–766. doi: 10.1214/14-BJPS244