On types of generalized closed sets

ABSTRACT

The paper studies relations between types of generalized closed sets in topological spaces. It also answers an open question posed by Erdal.

KEYWORDS:

• wg-closed
• pg-closed
• gp-closed
• sg-closed
• gs-closed
• bg-closed
• gb-closed
• αg-closed
• gα-closed
• βg-closed
• gβ-closed set

1. Introduction and preliminaries

The concept of g-closedness of sets in topological spaces was first initiated by Levine [1] using the closure operator. Since then this concept has been investigated extensively by many topologists. They have started defining new types of generalized closed sets without paying attention that those sets happen to be equivalent. In this note, we work on those types of generalized closed sets that are equivalent. We also give answer to question of Erdal in [2, p. 265].

Throughout this paper, spaces mean topological spaces on which no any other property is assumed. For a subset A of a space X, the closure and interior of A with respect to X, respectively, are denoted by and (or simply and).

Definition 1.1:

A subset A of a space X is said to be

1. nowhere dense if ,

2. preopen [3] if ,

3. semi-open [4] if ,

4. α-open [5] if ,

5. β-open [6] if ,

6. b-open [7] or sp-open [8] or γ-open [9] if .

The complement of a preopen (resp. semiopen, α-open, β-open, b-open) set is preclosed (resp. semi-closed, α-closed, β-closed, b-closed).

The intersection of all preclosed (resp. semiclosed, α-closed, β-closed, b-closed) sets of X containing A is called the preclosure (resp. semi-closure, α-closure, β-closure, b-closure) of A, and is denoted by p- (resp. s-, α-, β-, b-).

The union of all preopen (resp. semiopen, α-open, β-open, b-open) sets of X contained in A is called the preinterior (resp. semi-interior, α-interior, β-interior, b-interior) of A, and is denoted by p- (resp. s-, α-, β-, b-).

The family of all preopen (resp. semiopen, α-open, β-open, b-open) set of X is denoted by (resp. , , , ).

Remark 1.2:

It is known that for any topological space , .

Definition 1.3:

Let X be a topological space and . A point is said to be in the preclosure (resp. semi-closure, α-closure, β-closure, b-closure) of A if for every preopen (resp. semiopen, α-open, β-open, b-open) set U containing x such that .

Fact 1.4:

A subset A of a space X is preclosed (resp. semiclosed, α-closed, β-closed, b-closed) iff A = p- (resp. A = s-, -, -, A = b-).

From Remark 1.2 and Definition 1.3, we have the following well-known lemma:

Lemma 1.5:

For any subset A of a space X, the following statements hold:

1. β----,

2. β----.

Definition 1.6:

A subset A of a space is said to be

1. generalized preclosed (briefly, gp-closed) [10] if p- whenever and ,

2. generalized semiclosed (briefly, gs-closed) [11] if s- whenever and ,

3. α-generalized closed (briefly, -closed) [12] if α- whenever and ,

4. generalized β-closed (briefly, -closed) [13] if β- whenever and ,

5. generalized b-closed (briefly, gb-closed) [2] if b- whenever and ,

6. pre-generalized closed (briefly, pg-closed) [14] if p- whenever and ,

7. semi-generalized closed (briefly, sg-closed) [15] if s- whenever and ,

8. generalized α-closed (briefly, -closed) [16] if α- whenever and ,

9. β-generalized closed (briefly, -closed) [17] if β- whenever and ,

10. b-generalized closed (briefly, bg-closed) [2] if b- whenever and ,

11. generalized -closed (briefly, -closed) [18] if b- whenever and ,

12. -generalized closed (briefly, -closed) [19] if whenever and ,

13. weakly generalized closed (briefly, wg-closed) [20] if whenever and .

2. The results

In this section, we start with the following lemma which will be used in the sequel.

Lemma 2.1 ([21]):

For a topological space , the singleton set is either preopen or nowhere dense.

Proof:

If is not nowhere dense, then . So it should contains x itself. Therefore, , which is preopen.

If is not preopen, then . Therefore . Hence is nowhere dense.▪

Remark 2.2:

The following diagram is an enlargement of Remark 1.2, Remark 22 in [2] and Remark 5.3 in [17] that hold for any subset of any topological space: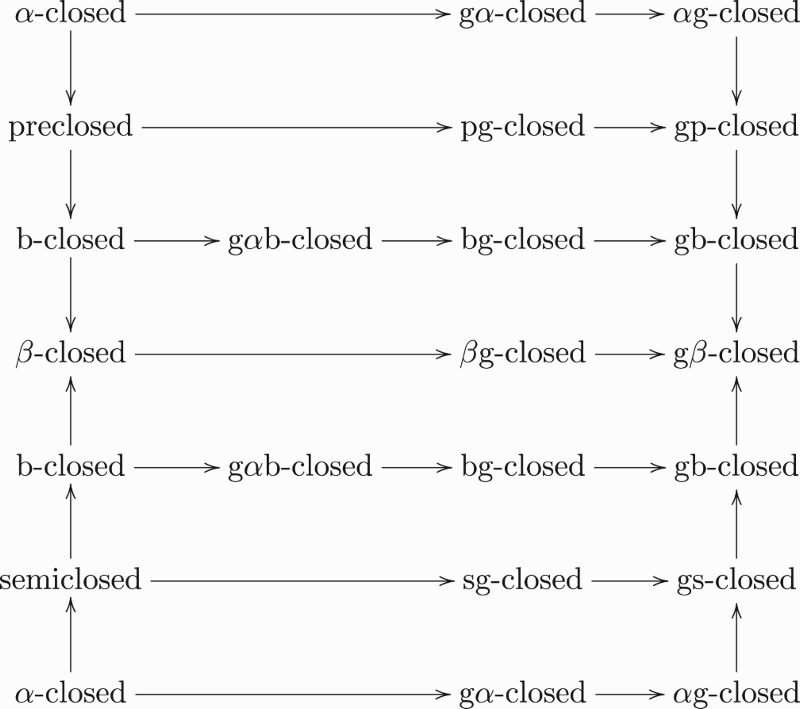

All the authors who have introduced and defined sets in the above diagram claimed that none of the implications is reversible. But this turns to be false. Before giving the answer to what we have just said, we recall the following question posed by Erdal in [2].

Question 2.3:

Does there exist a subset of a space which is

1. bg-closed but not b-closed,

2. pg-closed or sg-closed but not bg-closed.

The next result provides the answer to above question and our claim.

Theorem 2.4:

Let A be a subset of a space X. Then

1. A is preclosed if and only if it is pg-closed,

2. A is b-closed if and only if it is bg-closed,

3. A is β-closed if and only if it is -closed.

Proof:

(1) (Only if part). If A is preclosed, then A = p-. By Definition 1.6 (1), for all preopen set U with , we have p-. Thus, A is pg-closed.

(If part). Let A be pg-closed. To show that A is preclosed, it is enough to prove that p- as the other side of the inclusion is always true. Let -. By Lemma 2.1, either is preopen or nowhere dense. We consider two cases:

1. If is preopen, by Definition 1.3, . So .

2. If is nowhere dense, then . Its complement is dense in X. That is . Therefore , since and , then is preopen. Suppose for contraction that . This implies that . By assumption, A is pg-closed, so p-. Therefore -, which is a contradiction. Hence, . From (i) and (ii), we obtain that p-. Thus, A = p-. This shows that A is preclosed.

Note that the same construction (as in (1)) can be applied to (2) and (3) with few modifications. But for the sake of completeness, we try to give these modifications to (2) and leave (3).

(2) (Only if part). Let A be a b-closed set. Then follow the same steps as in ((1); only if part) and apply Fact 1.4 and Definition 1.6 (2). Hence A be bg-closed.

(If part). Let A be bg-closed. Since - in general, it is enough to prove that b-. Let -. By Lemma 2.1 , either is preopen or nowhere dense. We have the following cases:

1. If is preopen, so it is b-open. By Definition 1.3, . So .

2. If is nowhere dense, then . Its complement, , is preopen in X and so it b-open. Suppose for contraction that . Then . By assumption, A is bg-closed, so b-. Therefore -. From contradiction we have . From (i) and (ii) we get b-. Thus A = b-, which is b-closed.

(3) The proof is similar to above one.▪

From (2) we have the following corollary:

Corollary 2.5:

For any topological space, b-closed and -closed sets are equivalent.

Note that the above result has been proved by Mohammed et al. in [22]

Lemma 2.6:

Let be a space. The following hold:

1. every -closed set is sg-closed, [23, p.184–185] .

2. every sg-closed set is b-closed, [24, Proposition 2.1].

3. every -closed set is preclosed, [25, Theorem 2.4].

Theorem 2.7:

In a topological space ,

1. every -closed set is pg-closed,

2. every sg-closed set is bg-closed,

3. every pg-closed set is bg-closed,

4. every bg-closed set is -closed.

Proof:

(1) By Theorem 2.4 (1), pg-closed and preclosed are the same. By Lemma 2.6 (3), the claim follows.

(2) By Lemma 2.6 (2), every sg-closed set is b-closed and by Theorem 2.4 (2) b-closed set and bg-closed set are identical, hence the result.

(3) It is known that every preclosed set is b-closed. By Theorem 2.4 (1) and (2), every pg-closed set is bg-closed.

(4) Follows from the fact that every b-closed is β-closed and Theorem 2.4 (2) and (3).

Now, we are ready to give the answer to a big part of the Question 2.3▪

Answer (Question 2.3.):

(a) No, bg-closed set and b-closed set are equivalent. This follows from Theorem 2.4 (2).

(b) No, by Theorem 2.7 (2) and (3), every sg-closed set is bg-closed and every pg-closed set is bg-closed. ▪

Definition 2.8 ([15]):

A topological space is semi- if every singleton is either semi-open or semi-closed.

Definition 2.9 ([26]):

A topological space is semi- if every singleton is either open or nowhere dense.

Lemma 2.10 ([27])

A topological space is semi- iff it is semi-.

Proposition 2.11:

Let be a semi- space. Then

1. α-closed and -closed sets are equivalent,

2. semiclosed and sg-closed sets are equivalent.

Proof:

Since every singleton is either open or nowhere dense in semi- space, by the construction given in Theorem 2.4, the proof can be obtained.▪

Lemma 2.12 ([21]):

For a subset A of a space ,

1. p-,

2. s-,

3. α-,

4. β-.

Theorem 2.13:

For any subset A of a topological space ,

1. -closed and -closed sets are equivalent,

2. wg-closed and gp-closed sets are equivalent.

Proof:

(1) Let A be -closed, and let with . By assumption, . This implies that . But - (see Lemma 2.12 (3)). Thus α-. Since U was taken arbitrarily, so A is -closed.

On the other hand, if A is -closed, then α- whenever and . By Lemma 2.12, -. Therefore, and so A is -closed.

(2) By the same way above using Lemma 2.12 (1) one can prove this.▪

From all the above results, we try to give the final version of the diagram stated in Remark 2.2:

Finally, we shall recall that Examples 23, 24 and 25 in [2], Example 2.5 in [25] and Example 3.21 in [19] show that none of the implications (in the middle column) are reversible.

Disclosure statement

No potential conflict of interest was reported by the authors.