http://orcid.org/0000-0003-3809-2521
ABSTRACT
Elsonbaty and Daoud introduced a new type of labelling of a graph G with p vertices and q edges called an edge even graceful labelling if there is a bijection f from the edges of the graph to the set such that, when each vertex is assigned the sum of all edges incident to it mod
, where
, the resulting vertex labels are distinct. They proved necessary and sufficient conditions for some path and cycle-related graphs to be edge even graceful. In this paper we proved that triangular book graphs and quadrilateral book graphs admit edge even graceful labelling.
MATHEMATICS SUBJECT CLASSIFICATION:
1. Introduction
The field of Graph Theory plays an important role in various areas of pure and applied sciences. Labelling of a graph G is an assignment of integers either to the vertices or edges or both subject to certain conditions. Graph labelling is a very powerful tool that eventually makes things in different fields very easy to be handled in the mathematical way. Nowadays graph labelling has received much attention from different brilliant researches in different disciplines, as communication networks, coding theory, optimal circuits layouts, astronomy, radar and graph decomposition problems. See [Citation1–3] for some details and concerning applications.
In 1967, Rosa [Citation4] introduced a labelling of G called β- valuation, later on Golomb [Citation5] called as graceful labelling which is an injection f from the set of vertices to the set
such that when each edge e=uv is assigned the label
, the resulting edge labels are distinct. A graph which admits a graceful labelling is called a graceful graph.
In 1991, Gnanajothi [Citation6] introduced a labelling of G called odd graceful labelling which is an injection f from the set of vertices to the set
such that when each edge e=uv is assigned the label
, the resulting edge labels are
. A graph which admits an odd graceful labelling is called an odd graceful graph.
In 1985, Lo [Citation7] introduced a labelling of G called edge graceful labelling, which is a bijection f from the set of edges to the set
such that the induced map
from the set of vertices
to
given by
(mod p) is a bijection. A graph which admits edge graceful labelling is called an edge graceful graph.
In 2009, Solairaju and Chithra [Citation8] introduced a labelling of G called edge odd graceful labelling, which is a bijection f from the set of edges to the set
such that the induced map
from the set of vertices
to
given by
(mod
) is an injection. A graph which admits edge odd graceful labelling is called an edge odd graceful graph.
Recently, Daoud [Citation9] introduced edge odd graceful labelling of some path and cycle-related graphs. Later, Elsonbaty and Daoud [Citation10] introduced a new type of labelling of a graph G with p vertices and q edges called edge even graceful labelling, which is a bijection f from the set of edges to the set
such that the induced map
from the set of vertices
to
given by
(mod
), where
is an injection. A graph which admits edge even graceful labelling is called an edge even graceful graph. The authors in [Citation10] introduced a necessary and sufficient condition for edge even graceful labelling of path graphs
, cycle graphs
, and star graphs
. They also proved some necessary and sufficient conditions for some path and cycle-related graphs, namely, Friendship, Wheel, Double wheel and Fan graphs.
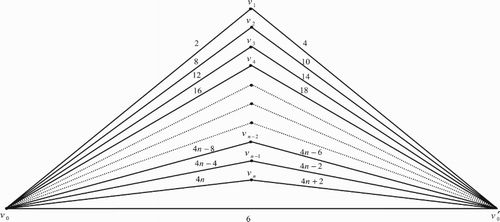
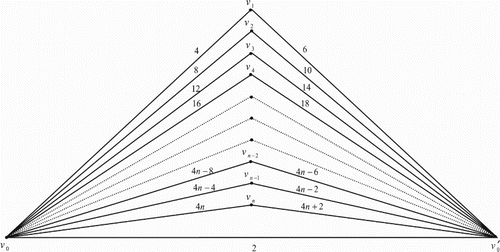
2. Edge even graceful labelling of triangular book graph
The triangular book graph for
is a planar undirected graph with n+2 vertices
and 2n+1 edges constructed by n triangles sharing a common edge
. In other words the triangular book graph
is the complete tripartite graph
Theorem 2.1:
The triangular book graph is an edge even graceful graph.
Proof:
Using standard notationthere are eight cases:
Case 1
:
(mod 8)
Let be defined by
;
; and
, as in . Therefore the corresponding labels of vertices mod 4n+2 will be:
.
, that is
.
.
.
Figure 1. Case (1) (mod 8).
Since for some positive integer m. Therefore, 4n + 2 = 32m + 2. So
, and
.
Case 2
:
(mod 8)
Let be defined by
;
; and
, as in .
Figure 2. Case (2), (3), and (4) , or 3 (mod 8).
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, that is
.
.
.
Since for
. Therefore, 4n + 2 = 32m + 6. So
, and
.
Case 3
:
(mod 8)
Let be defined exactly as in Case (2), see .
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, and
.
Since for
. Therefore, 4n + 2 = 32m + 10. So
, and
.
Case 4
:
(mod 8)
Let be defined exactly as in Case (2), see .
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, and
.
Since for
. Therefore, 4n + 2 = 32m + 14. So
, and
.
Case 5
:
(mod 8)
Let be defined by
;
; and
, as in .
Figure 3. Case (5) (mod 8).
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, that is
.
.
.
Since for
. Therefore, 4n + 2 = 32m + 18. So
, and
.
Case 6
:
(mod 8)
Let be defined by
, r is odd;
, r is even;
, r is odd;
, r is even and
, as in .
Figure 4. Case (6) (mod 8).
Therefore the corresponding labels of vertices mod 4n+2 will be:
, that is
.
.
.
Since for
. Therefore, 4n + 2 = 32m + 22. So
, and
.
Case 7
:
(mod 8)
Let be defined by
, r is odd;
, r is even;
;
, r is odd;
, r is even;
; and
, as in .
Figure 5. Case (7) (mod 8).
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, that is
.
.
.
Since for
. Therefore, 4n + 2 = 32m + 26. So
, and
.
Case 8
:
(mod 8)
Let be defined by
;
; and
, as in .
Figure 6. Case (8) (mod 8).
Therefore, the corresponding labels of vertices mod 4n+2 will be:
, that is
.
.
.
Since for
. Therefore, 4n + 2 = 32m + 30. So
, and
.
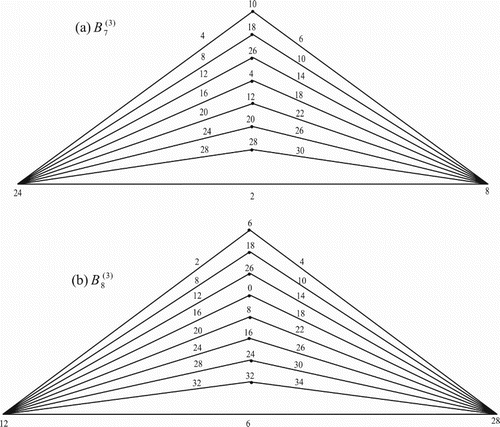
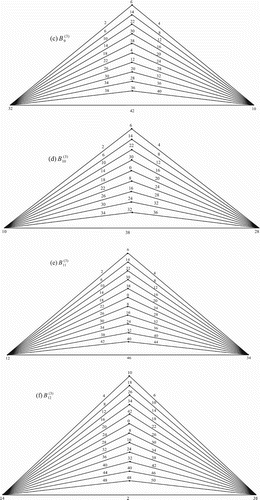
Illustration: The edge even graceful labelling of the triangular graphs are shown in .
Figure 7. .
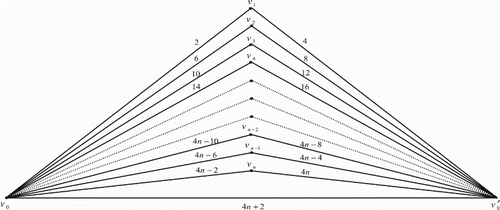
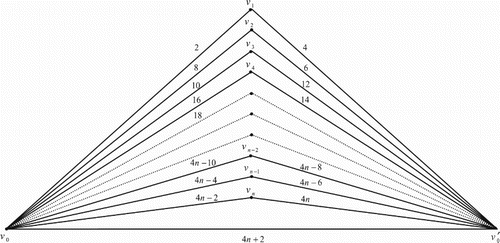
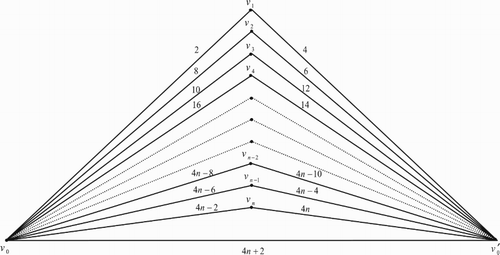
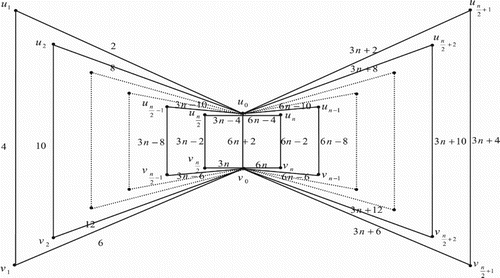
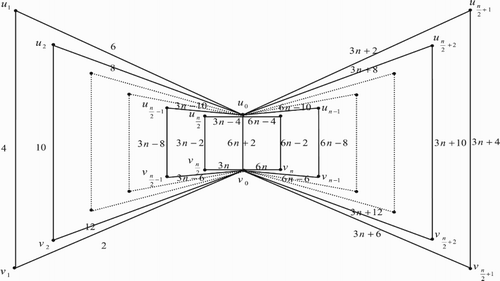
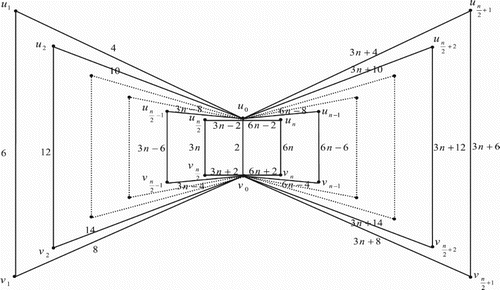
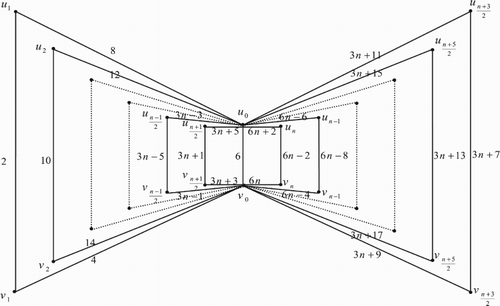
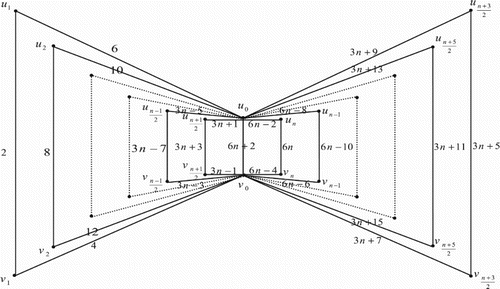
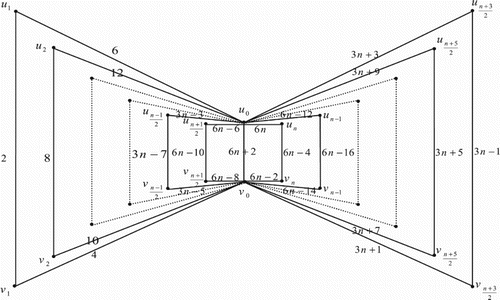
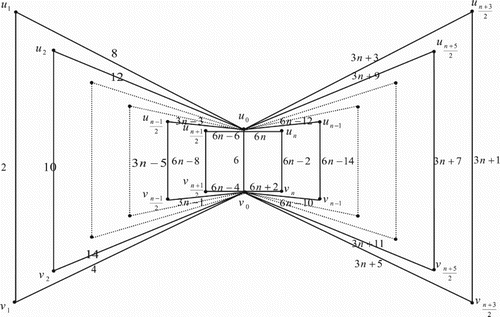
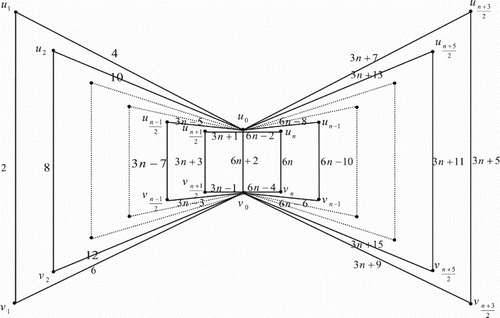
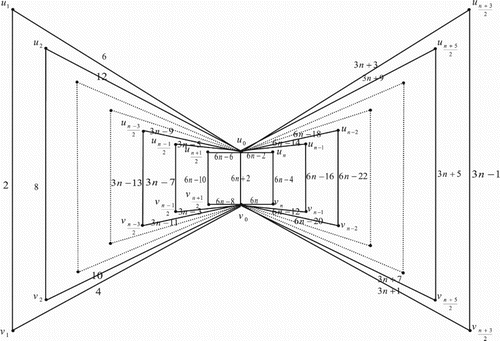
3. Edge even graceful labelling of quadrilateral book graph
The quadrilateral book graph , for
, is a planar undirected graph with
vertices
and
and 3n+1 edges constructed by n quadrilaterals sharing a common edge
. In other words the quadrilateral book graph
is the cartesian product of a star graph
and
.
Theorem 3.1:
Let n be an even positive integer, then the quadrilateral book graph is an edge even graceful graph.
Proof:
Using standard notationthere are three cases:
Case 1
:
mod 6
Let be defined by
;
;
; and
, as in .
Figure 8. Case (1) mod 6.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
, that is
.
, that is
.
.
.
Since for some positive integer m. Therefore, 6n + 2 = 36m+2. So
, and
.
Case 2
:
mod 6
Let be defined by
;
;
; and
, as in .
Figure 9. Case (2) mod 6.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
, that is
.
, that is
.
.
.
Since for
. Therefore, 6n + 2 = 36m + 14. So
, and
.
Case 3
:
mod 6
Let be defined by
;
;
; and
, as in .
Figure 10. Case (3) mod 6.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
, that is
.
, that is
.
.
.
Since for
. Therefore, 6n + 2 = 36m + 26. So
, and
.
Theorem 3.2:
Let n be an odd positive integer, then the quadrilateral book graph is an edge even graceful graph.
Proof:
Using standard notationthere are six cases:
Case 1
:
mod 12
Let be defined by
.
.
, as in .
Figure 11. Case (1) mod 12.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
.
.
.
.
Since for
. Therefore, 6n + 2 = 72m + 8. So
, and
.
Case 2
:
mod 12
Let be defined by
.
;
.
. See .
Figure 12. Case (2) mod 12.
Therefore the corresponding labels of vertices mod 6n+2 will be:
,
.
.
.
.
Since for
. Therefore, 6n + 2 = 72m + 20. So
, and
.
Case (3): mod 12
Let be defined by
.
.
. See .
Figure 13. Case (3) mod 12.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
.
.
.
.
Since for
. Therefore, 6n + 2 = 72m + 32. So
, and
.
Case 4
:
mod 12
Let be defined by
.
.
;
. See .
Figure 14. Case (4) mod 12.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
.
.
.
.
Since for
. Therefore, 6n+2=72m+44. So
, and
.
Case 5
:
mod 12
Let be defined by
.
.
;
. See .
Figure 15. Case(5) mod 12.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
.
.
.
.
Since for
. Therefore, 6n + 2 = 72m + 56. So
, and
.
Case 6
:
mod 12
Let be defined by
.
.
;
. See .
Figure 16. Case(6) mod 12.
Therefore, the corresponding labels of vertices mod 6n+2 will be:
.
.
.
.
Since for
. Therefore, 6n+2=72m+68. So
, and
.
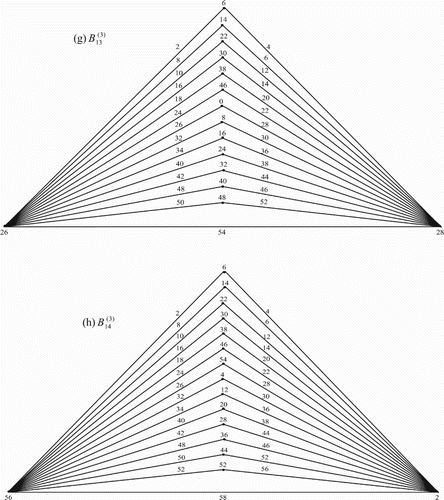
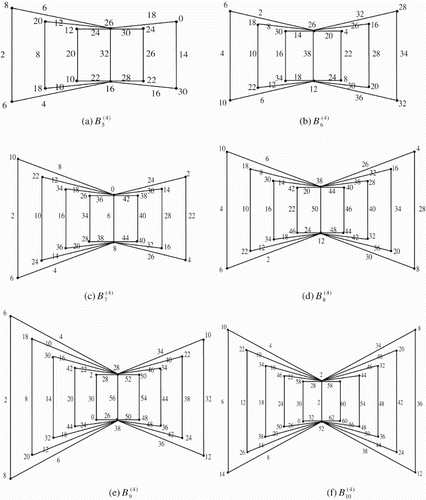
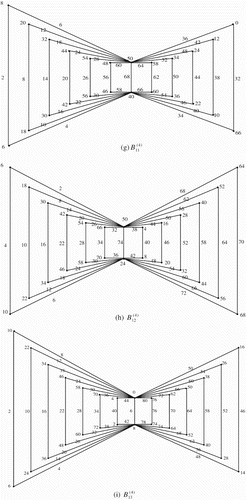
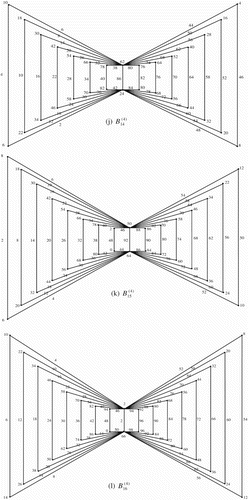
Illustration: The edge even graceful labelling of the quadrilateral graphs are shown in .
Figure 17. .
Illustration: The edge even graceful labeling of some quadrilateral graphs are shown in .
4. Conclusion
Graph labelling is the assignment of some integers for vertices, edges or both of the graphs, respectively, with certain conditions. Graph labelling is used in many applications such as coding theory, radar, astronomy, circuit design, missile guidance and communication network addressing. We introduced a new method for labelling edges and vertices using modular arithmetic. We proved that triangular and quadrilateral book graphs are edge even graceful graphs. Edge even graceful labelling is still open for more extensive studies.
Disclosure statement
No potential conflict of interest was reported by the authors.
ORCID
S.N. Daoud http://orcid.org/0000-0003-3809-2521
Ahmed N. Elsawy http://orcid.org/0000-0002-3918-5343
References
- Bloom GS, Golomb SW. Applications of numbered undirected graphs. Proc IEEE. 1977;65(4):562–570. doi: 10.1109/PROC.1977.10517
- Bloom GS, Golomb SW. Numbered complete graphs, unusual rulers, and assorted applications. In: Theory and Applications of Graphs, Proc. Internat Conf., Western Mich. Univ., Kalamazoo, Mich., 1976, Lecture Notes in Math., Volume 642. Berlin: Springer; 1978, p. 53–65.
- Sutton M. Summable graphs labellings and their applications [PhD Thesis]. Callaghan: Department of Computer Science, The University of Newcastle; 2001.
- Rosa A. On certain valuations of the vertices of a graph. Theory of graphs (Internat. Symp, Rome, July 1966), Paris: Gordon and Breach; 1967. p. 349–355.
- Golomb SW. How to number a graph. In: Read RC, editor. Graph theory and computing. New York (NY): Academic Press; 1972. p. 23–37.
- Gnanajothi RB. Topics in graph theory [PhD Thesis]. Madurai: Madurai Kamaraj University; 1991.
- Lo SP. On edge-graceful1abelings of graphs. Congr Numer. 1985;50:231–241.
- Solairaju A, Chithra K. Edge-Odd graceful graphs. Electronic Notes Discrete Math. 2009;33:15–20. doi: 10.1016/j.endm.2009.03.003
- Daoud SN. Edge odd graceful labeling of some path and cycle related graphs. AKCE Int J Graphs Comb. 2017;14(2):178–203. doi: 10.1016/j.akcej.2017.03.001
- Elsonbaty A, Daoud SN. Edge even graceful labeling of some path and cycle related graphs. Ars Comb. 2017;CXXX:79–96.