Almost soft compact and approximately soft Lindelöf spaces

ABSTRACT

The concepts of almost soft compact (almost soft Lindelöf), approximately soft Lindelöf and mildly soft compact (mildly soft Lindelöf) spaces are initiated and investigated in this work. Their characterizations and main properties are established and the relationships among them are illustrated with the help of examples. The sufficient conditions for the equivalent between almost soft Lindelöf and approximately soft Lindelöf spaces; and for the equivalent among soft Lindelöf, almost soft Lindelöf, approximately soft Lindelöf and mildly soft Lindelöf spaces are given. The image of the introduced types of soft compact and soft Lindelöf spaces under soft continuous mappings are studied; and the mutual relations between them and their parametric topological spaces are probed. Some results which associate soft hyperconnectedness and soft connectedness, respectively with almost soft compactness and mildly soft compactness are verified. This study is concluded by providing an illustrative diagram for the interrelations among the initiated soft compact and soft Lindelöf spaces.

KEYWORDS:

• Almost soft compactness
• approximately soft Lindelöfness
• mildly soft compactness
• soft locally finite and soft partition topological spaces

2010 AMS:

• 54A05
• 54D20
• 54D30

1. Introduction

Many practical problems in physics, engineering, medical and social science and economic suffer from data that involve uncertainties. For this reason, Molodtsov [1] proposed soft sets as a new mathematical tool to deal with uncertainties. He showed the advantages of soft sets compared to fuzzy sets and he successfully applied soft sets in several directions such as game theory and operations research. Maji et al. [2,3] gave an application of soft sets and initiated some operators on soft sets in 2002 and 2003, respectively. Later on, many researches related to the soft set theory and its applications appeared rapidly (see, for example, [4–8]). A novel idea of soft topological spaces was introduced in 2011 by Shabir and Naz [9]. They presented the notions of soft open and soft closed sets, soft neighbourhoods and soft separation axioms; and investigated their fundamental features. In 2012, Aygünolu and Aygün [10] introduced a concept of soft compact spaces and derived main properties. They also presented a notion of enriched soft topological spaces and illuminated its role to verified some results related to constant soft mappings and soft compact spaces. Zorlutuna et al. [11] came up with an idea of soft points and employed it to study some properties of soft interior points and soft neighbourhood systems. In [12,13], the authors simultaneously modified a concept of soft point for studying soft metric spaces and soft neighbourhood systems. Karaaslan [14], in 2016, defined the concepts of lower and upper approximations of a soft set based on soft class operations introduced therein. He ended his study by constructing a decision making method utilizing soft rough class; and providing an example to demonstrate that the suggested method can successfully work. In [15–17], the authors carried out three studies to correct some alleged results via soft topologies. Recently, we [18] introduced the notions of partial belong and total non belong relations and investigated main properties. Also, we [19] initiated a concept of soft topological ordered spaces and introduced the concepts of monotone soft sets and p-soft $T_i$-ordered spaces $(i=0,1,2,3,4)$.

In this article, we first formulate the concepts of almost soft compact and almost soft Lindelöf spaces; and deduce their main properties. Also, we verify that $(X,\tau ,K)$ is an enriched almost soft compact space if and only if $(X,{\tau }_k)$ is almost compact, for each $k\in K$. Second, we define approximately soft Lindelöf spaces and point out their equivalent with almost soft Lindelöf spaces if the space is soft locally finite. Also, we give an answer of why do not define approximately soft compact spaces. Finally, we present the notions of mildly soft compact and mildly soft Lindelöf spaces; and derive their basic properties. One of important results, in the last section, is Theorem 5.14, which illustrates the equivalent among soft Lindelöf, almost soft Lindelöff, approximately soft Lindelöf and mildly soft Lindelöf spaces if the space is soft partition. In general, we give a completely description for each type of the soft compact and soft Lindelöf spaces introduced herein; and conclude that all of them are preserved under soft continuous mappings. We proved some results related to enriched soft topological spaces; and we explore some results which associate soft hyperconnected and soft connected spaces, respectively with almost soft compact and mildly soft compact spaces.

2. Preliminaries

In this section, we mention some definitions and preliminaries results which will be needed in the sequels.

Definition 2.1

[1]

A pair $(G,K)$ is called a soft set over a non-empty set X provided that G is a mapping of a set of parameters K into the family of all subsets of X. It can be written as follows: $(G,K)=\left\{\right(k,G\left(k\right)):k\in K$ and $G\left(k\right)\in 2^X\}$.

Definition 2.2

[3]

A soft set $(G,K)$ over X is called:

1. An absolute soft set if $G\left(k\right)=X$, for each $k\in K$. It is denoted by $\tilde{X}$.

2. A null soft set if $G\left(k\right)=\mathrm{\varnothing }$, for each $k\in K$. It is denoted by $\tilde{\mathrm{\varnothing }}$.

Definition 2.3

[5]

The relative complement of a soft set $(G,K)$, denoted by $(G,K{)}^c$, is given by $(G,K{)}^c=(G^c,K)$, where a mapping $G^c:K\to 2^X$ is defined by $G^c\left(k\right)=X-G\left(k\right)$, for each $k\in K$.

We draw the attention of the readers to the existence of another definition of complement of a soft set given in [3]. With regard to this definition, the De Morgan's laws do not keep via the soft set theory.

Definition 2.4

[5,20]

The soft union and intersection of two soft sets $(G,K),(F,K)$ are defined, respectively, as follows:

1. $(G,K)\bigcup ^{~}(F,K)=(H,K),$ where $H\left(k\right)=G\left(k\right)\bigcup F\left(k\right)$, for each $k\in K$.

2. $(G,K)\bigcap ^{~}(F,K)=(H,K),$ where $H\left(k\right)=G\left(k\right)\bigcap F\left(k\right)$, for each $k\in K$.

It worthily noting that the soft union and intersection of an arbitrary family of soft sets were given in [21,22], respectively.

Definition 2.5

[23]

We say that $(G,K)$ is a soft subset of $(H,K)$, denoted by $(G,K)\tilde{\subseteq }(H,K)$, provided that $G\left(k\right)\subseteq H\left(k\right)$, for each $k\in K$.

A collection of all soft subsets of $\tilde{X}$ is denoted by $S\left(X_K\right)$.

Definition 2.6

[12,13]

A soft set $(P,K)$ over X is called soft point if there is $k\in K$ and there is $x\in X$ satisfies that $P\left(k\right)=\left\{x\right\}$ and $P\left(e\right)=\mathrm{\varnothing }$, for each $e\in K\setminus \left\{k\right\}$.

A soft point will be shortly denoted by $P_k^x$.

Definition 2.7

[12]

A soft set $(H,K)$ over X is called countable (resp. finite) if $H\left(k\right)$ is countable (resp. finite) for each $k\in K$. Otherwise, it is called uncountable (resp. infinite).

Definition 2.8

[9]

For a soft set $(G,K)$ over X and $x\in X$, we say that $x\in (G,K)$ if $x\in G\left(k\right)$, for each $k\in K$; and we say that $x\notin (G,K)$ if $x\notin G\left(k\right)$, for some $k\in K$.

Definition 2.9

[9]

A collection τ of soft sets over X with a fixed set of parameters K is called a soft topology on X if it satisfies the following two conditions:

1. τ contains the null and absolute soft sets.

2. τ is closed under arbitrary soft union and finite soft intersection.

The triple $(X,\tau ,K)$ is called a soft topological space (briefly, STS). Each member of τ is called a soft open set and its relative complement is called a soft closed set.

Definition 2.10

[9]

The soft interior and soft closure operators of a soft subset $(H,K)$ of $(X,\tau ,K)$ are defined, respectively, as follows:

1. $(H,K{)}^{\circ }$ is the largest soft open set contained in $(H,K)$.

2. $(H,K)$ is the smallest soft closed set containing $(H,K)$.

Proposition 2.11

[9]

Let $(X,\tau ,K)$ be an STS. Then a collection of ${\tau }_k=\left\{G\right(k):(G,K)\in \tau \}$ defines a topology on X, for each $k\in K$.

We term ${\tau }_k$ a parametric topology.

Definition 2.12

[9]

Let $(F,K)$ be a soft subset of $(X,\tau ,K)$. Then $(\overline{F},K)$ is defined as $\overline{F}\left(k\right)=\overline{F\left(k\right)}$, where $\overline{F\left(k\right)}$ is the closure of $F\left(k\right)$ in $(X,{\tau }_k)$ for each $k\in K$.

Proposition 2.13

[9]

Let $(L,K)$ be a soft subset of $(X,\tau ,K)$. Then:

1. $(\overline{L},K)\tilde{\subseteq }\overline{(L,K)}$.

2. $(\overline{L},K)=\overline{(L,K)}$ if and only if $(\overline{L},K)$ is soft closed.

In the literature, there are many different notions of a soft Hausdorff space. In this study, we investigate two types of them and distinguish between them by writing $T_2$ and $T_2^{\mathrm{\prime }}$. They are defined as follows:

Definition 2.14

An STS $(X,\tau ,K)$ is said to be:

1. Soft $T_2$-space [9] if for every $x\ne y\in X$, there are two disjoint soft open sets $(G,K)$ and $(F,K)$ such that $x\in (G,K)$ and $y\in (F,K)$.

2. Soft $T_2^{\mathrm{\prime }}$-space [24] if for every two soft points $P_k^x,P_e^y$ such that $x\ne y$, there are two disjoint soft open sets $(G,K)$ and $(F,K)$ such that $P_k^x\in (G,K)$ and $P_e^y\in (F,K)$.

Definition 2.15

[25]

Let $(X,\tau ,K)$ be an STS and $(Y,K)$ be a non-null soft subset of $\tilde{X}$. Then ${\tau }_{(Y,K)}=\left\{\right(Y,K\left)\bigcap ^{~}\right(G,K):(G,K)\in \tau \}$ is said to be a relative soft topology on $(Y,K)$ and $\left(\right(Y,K),{\tau }_{(Y,K)},K)$ is called a soft subspace of $(X,\tau ,K)$.

Definition 2.16

[25]

A soft set $(F,K)$ over X is said to be pseudo constant provided that $F\left(k\right)=X$ or ∅, for each $k\in K$.

A family of all pseudo constant soft sets is briefly denoted by $CS(X,K)$.

Theorem 2.17

[26]

An STS $(X,\tau ,K)$ is soft connected if and only if the only soft open and soft closed subsets of $(X,\tau ,K)$ are $\tilde{\mathrm{\varnothing }}$ and $\tilde{X}$.

Definition 2.18

[27]

An STS $(X,\tau ,K)$ is said to be soft hyperconnected if it does not contain disjoint soft open sets.

Definition 2.19

[10]

A soft topology τ on X is said to be enriched if a condition (i) of Definition 2.9 is replaced by the following condition: $(G,K)\in \tau$, for all $(G,K)\in CS(X,K)$. In this case, we term the triple $(X,\tau ,K)$ an enriched STS.

Definition 2.20

[10]

A sub-collection $\mathcal{B}$ of $(X,\tau ,K)$ is called a soft base of τ if any member of τ can be expressed as a union of members of $\mathcal{B}$.

Definition 2.21

[10,18]

1. A collection $\left\{\right(G_i,K):i\in I\}$ of soft open sets is called a soft open cover of $(X,\tau ,K)$ if $\tilde{X}={\bigcup ^{~}}_{i\in I}(G_i,K)$.

2. An STS $(X,\tau ,K)$ is called soft compact (resp. soft Lindelöf) if every soft open cover of $\tilde{X}$ has a finite (resp. countable) soft sub-collection which cover $\tilde{X}$.

Proposition 2.22

[10,18]

Every soft closed subset of a soft compact $($resp. soft Lindelöf) space is soft compact $($resp. soft Lindelöf).

Definition 2.23

[11]

A collection $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ of soft sets is said to have the finite intersection property if ${\bigcap ^{~}}_{i=1}^{i=n}(F_i,K)\ne \tilde{\mathrm{\varnothing }}$.

Theorem 2.24

[11]

An STS $(X,\tau ,K)$ is soft compact if and only if every collection of soft closed subsets of $(X,\tau ,K),$ satisfying the finite intersection property, has, itself, a non-null soft intersection.

By analogy with the above definition and theorem, we introduce the following definition and result.

Definition 2.25

A collection $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ of soft sets is said to have the countable intersection property if ${\bigcap ^{~}}_{s\in S}(F_s,K)\ne \tilde{\mathrm{\varnothing }}$, for any countable subset S of I.

Theorem 2.26

An STS $(X,\tau ,K)$ is soft Lindelöf if and only if every collection of soft closed subsets of $(X,\tau ,K),$ satisfying the countable intersection property, has, itself, a non-null soft intersection.

Definition 2.27

[11]

A soft mapping between $S\left(X_A\right)$ and $S\left(Y_B\right)$ is a pair $(f,\phi )$, denoted also by $f_{\phi }$, of mappings such that $f:X\to Y$, $\phi :A\to B$. Let $(G,K)$ and $(H,L)$ be soft subsets of $S\left(X_A\right)$ and $S\left(Y_B\right)$, respectively. Then the image of $(G,K)$ and pre-image of $(H,L)$ are defined by:

1. $f_{\phi }(G,K)=\left(f_{\phi }\right(G){)}_B$ is a soft subset of $S\left(Y_B\right)$ such that $f_{\phi }\left(G\right)\left(b\right)=\left\{\begin{array}{l}\bigcup _{a\in {\phi }^{-1}\left(b\right)\bigcap K}f\left(G\right(a\left)\right):{\phi }^{-1}\left(b\right)\bigcap K\ne \mathrm{\varnothing }\\ \mathrm{\varnothing }:{\phi }^{-1}\left(b\right)\bigcap K=\mathrm{\varnothing }\end{array}\right.$ for each $b\in B$.

2. $f_{\phi }^{-1}(H,L)=\left(f_{\phi }^{-1}\right(H){)}_A$ is a soft subset of $S\left(X_A\right)$ such that $f_{\phi }^{-1}\left(H\right)\left(a\right)=\left\{\begin{array}{l}{f}^{-1}\left(H\right(\phi \left(a\right)\left)\right):\phi \left(a\right)\in L\\ \mathrm{\varnothing }:\phi \left(a\right)\notin L\end{array}\right.$ for each $a\in A$.

Definition 2.28

[11]

A soft mapping $f_{\phi }:S\left(X_A\right)\to S\left(Y_B\right)$ is said to be surjective (resp. injective, bijective) if f and φ are surjective (resp. injective, bijective).

Proposition 2.29

[13]

Let $f_{\phi }:S\left(X_A\right)\to S\left(Y_B\right)$ be a soft mapping. Then for each soft subsets $G_A$ and $H_B$ of $S\left(X_A\right)$ and $S\left(Y_B\right),$ respectively, we have the following results:

1. $(G,A)\tilde{\subseteq }{f}_{\phi }^{-1}{f}_{\phi }(G,A)$ and $(G,A)=f_{\phi }^{-1}{f}_{\phi }(G,A)$ if $f_{\phi }$ is injective.

2. $f_{\phi }{f}_{\phi }^{-1}(H,B)\tilde{\subseteq }(H,B)$ and $f_{\phi }{f}_{\phi }^{-1}(H,B)=(H,B)$ if $f_{\phi }$ is surjective.

Definition 2.30

[11,13]

A soft mapping $f_{\phi }:(X,\tau ,K)\to (Y,\theta ,K)$ is said to be:

1. Soft continuous if the inverse image of each soft open subset of $(Y,\theta ,K)$ is a soft open subset of $(X,\tau ,K)$.

2. Soft open (resp. soft closed) if the image of each soft open (resp. soft closed) subset of $(X,\tau ,K)$ is a soft open (resp. soft closed) subset of $(Y,\theta ,K)$.

3. Soft homeomorphism if it is bijective, soft continuous and soft open.

Definition 2.31

[11,13]

Let $f_{\phi }:(X,\tau ,K)\to (Y,\theta ,K)$ be a soft mapping. Then the following properties are equivalent:

1. $f_{\phi }$ is soft continuous;

2. The inverse image of each soft open (resp. soft closed) set is soft open (resp. soft closed);

3. $f_{\phi }\overline{(L,K)}\tilde{\subseteq }\overline{f_{\phi }(L,K)}$, for each $(L,K)\tilde{\subseteq }\tilde{X}$.

Definition 2.32

[18]

A soft set $(G,K)$ over X is called stable if there is a subset S of X such that $G\left(k\right)=S$, for each $k\in K$.

Definition 2.33

[18]

For a soft set $(G,K)$ over X and $x\in X$, we say that $x⋐(G,K)$ if $x\in G\left(k\right)$, for some $k\in K$; and we say that $x⋐̸(G,K)$ if $x\notin G\left(k\right)$, for each $k\in K$.

Lemma 2.34

[28]

$(A,K)\bigcap ^{~}\overline{(B,K)}\tilde{\subseteq }\overline{(A,K)\bigcap ^{~}(B,K)},$ for each soft open set $(A,K)$ and soft set $(B,K)$ in $(X,\tau ,K)$.

Throughout this paper, we utilize the following notations:

1. $(X,\tau ,K)$ or $(Y,\theta ,K)$ to indicate to the soft topological spaces.

2. S to indicate to a countable set.

3. $\mathcal{R}$ and $\mathcal{N}$ to indicate to the set of real numbers and the set of natural numbers, respectively.

3. Almost soft compact and almost soft Lindelöf spaces

In this section, the notions of almost soft compact and almost soft Lindelöf spaces are formulated and several properties of them are given. Some interesting results which associate almost soft compact spaces with the two concepts of enriched STSs and soft $T_2^{\mathrm{\prime }}$-spaces are presented and discussed.

Definition 3.1

An STS $(X,\tau ,K)$ is called almost soft compact (resp. almost soft Lindelöf) if every soft open cover of $\tilde{X}$ has a finite (resp. countable) soft sub-cover the soft closure of whose members cover $\tilde{X}$.

For the sake of economy, the proofs of the following four propositions will be omitted.

Proposition 3.2

Every soft compact space is soft Lindelöf.

Proposition 3.3

Every almost soft compact space is almost soft Lindelöf.

Proposition 3.4

A finite $($resp. countable) union of almost soft compact $($resp. almost soft Lindelöf) subsets of $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf).

Proposition 3.5

Every soft compact $($resp. soft Lindelöf) space is almost soft compact $($resp. almost soft Lindelöf).

In general, the converse of Propositions 3.2, 3.3 and 3.5 is not true as evidenced by the two examples below.

Example 3.6

Consider $(\mathcal{N},\tau ,K)$ is a soft topological space such that $K=\{k_1,k_2\}$ and τ is the discrete soft topology. Obviously, $(\mathcal{N},\tau ,K)$ is soft Lindelöf but it is not almost soft compact.

Example 3.7

Consider $(\mathcal{R},\tau ,K)$ is a soft topological space such that $K=\{k_1,k_2\}$ and $\tau =\{\tilde{\mathrm{\varnothing }},(G,K)\tilde{\subseteq }\tilde{\mathcal{R}}$ such that $1\in (G,K)\}$. Obviously, $(\mathcal{R},\tau ,K)$ is almost soft compact but it is not soft Lindelöf.

Definition 3.8

A soft subset $(D,K)$ of $(X,\tau ,K)$ is called soft clopen provided that it is both soft open and soft closed.

Proposition 3.9

Every soft clopen subset $(D,K)$ of an almost soft compact $($resp. almost soft Lindelöf) space $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf).

Proof.

We prove the proposition when $(X,\tau ,K)$ is almost soft compact.

Let $(D,K)$ be a soft clopen subset of $\tilde{X}$ and $\left\{\right(H_i,K):i\in I\}$ be a soft open cover of $(D,K)$. Then $(D^c,K)$ is soft clopen and $(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}(H_i,K)$. Therefore $\tilde{X}={\bigcup ^{~}}_{i\in I}(H_i,K)\bigcup ^{~}(D^c,K)$. Since $\tilde{X}$ is almost soft compact, then $\tilde{X}={\bigcup ^{~}}_{i=1}^{i=n}\overline{(H_i,K)\bigcup ^{~}(D^c,K)}={\bigcup ^{~}}_{i=1}^{i=n}\overline{(H_i,K)}\bigcup ^{~}(D^c,K)$. This implies that $(D,K)\tilde{\subseteq }$ ${\bigcup ^{~}}_{i=1}^{i=n}\overline{(H_i,K)}$. Hence $(D,K)$ is almost soft compact.

A similar proof is given in the case of an almost soft Lindelöf space.

Corollary 3.10

If $(G,K)$ is an almost soft compact $($resp. almost soft Lindelöf) set and $(D,K)$ is a soft clopen set in $(X,\tau ,K),$ then $(G,K)\bigcap ^{~}(D,K)$ is almost soft compact $($resp. almost soft Lindelöf).

In Example 3.7, let $(H,K)$ be a soft subset of $(\mathcal{R},\tau ,K)$, where $H\left(k_1\right)=\{1,4\}$ and $H\left(k_2\right)=\{4,5\}$. Then the soft set $(H,K)$ is almost soft compact, but it is neither soft open nor soft closed. So the converse of the above proposition is not necessarily true.

Definition 3.11

A collection $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ of soft sets is said to have the first type of finite (resp. countable) intersection property if ${\bigcap ^{~}}_{i=1}^{i=n}(F_i,K{)}^{\circ }\ne \tilde{\mathrm{\varnothing }}$ (resp. ${\bigcap ^{~}}_{i\in S}(F_i,K{)}^{\circ }\ne \tilde{\mathrm{\varnothing }}$).

It is clear that a collection satisfies the first type of finite (resp. countable) intersection property, it also satisfies the finite (resp. countable) intersection property.

Theorem 3.12

An STS $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf) if and only if every collection of soft closed subsets of $(X,\tau ,K),$ satisfying the first type of finite $($resp. countable) intersection property, has, itself, a non-null soft intersection.

Proof.

We will start with the proof for almost soft compactness, because the proof for almost soft Lindelöfness is analogous.

Let $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ be a collection of soft closed subsets of $\tilde{X}$. Suppose that ${\bigcap ^{~}}_{i\in I}(F_i,K)=\tilde{\mathrm{\varnothing }}$. Then $\tilde{X}={\bigcup ^{~}}_{i\in I}(F_i^c,K)$. As $(X,\tau ,K)$ is almost soft compact, then $\tilde{X}={\bigcup ^{~}}_{i=1}^{i=n}\overline{(F_i^c,K)}$. Therefore $\tilde{\mathrm{\varnothing }}=({\bigcup ^{~}}_{i=1}^{i=n}\overline{(F_i^c,K)}{)}^c={\bigcap ^{~}}_{i=1}^{i=n}(F_i,K{)}^{\circ }$. Hence the necessary condition holds.

Conversely, let Λ be a collection of soft closed subsets of $\tilde{X}$ which satisfies the first type of finite intersection property. Then it also satisfies the finite intersection property. Since Λ has a non-null soft intersection, then $(X,\tau ,K)$ is a soft compact space. It follows, by Proposition 3.5, that $(X,\tau ,K)$ is almost soft compact.

Proposition 3.13

The soft continuous image of an almost soft compact $($resp. almost soft Lindelöf$)$ set is almost soft compact $($resp. almost soft Lindelöf$)$.

Proof.

For the proof, consider $g_{\phi }:(X,\tau ,K)\to (Y,\theta ,K)$ is a soft continuous mapping and let $(D,K)$ be an almost soft Lindelöf subset of $\tilde{X}$. Suppose that $\left\{\right(H_i,K):i\in I\}$ is a soft open cover of $g_{\phi }(D,K)$. Then $g_{\phi }(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}(H_i,K)$. Now, $(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}{g}_{\phi }^{-1}(H_i,K)$ and $g_{\phi }^{-1}(H_i,K)$ is soft open, for each $i\in I$. By hypotheses, $(D,K)$ is almost soft Lindelöf, then there exists S such that $(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}\overline{g_{\phi }^{-1}(H_i,K)}$. So $g_{\phi }(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}{g}_{\phi }\left(\overline{g_{\phi }^{-1}(H_i,K)}\right)$. Since $g_{\phi }$ is soft continuous, then $g_{\phi }\left(\overline{g_{\phi }^{-1}(H_i,K)}\right)\tilde{\subseteq }\overline{g_{\phi }\left(g_{\phi }^{-1}\right(H_i,K\left)\right)}\tilde{\subseteq }\overline{(H_i,K)}$. Therefore $g_{\phi }(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}\overline{(H_i,K)}$. Thus $g_{\phi }(D,K)$ is almost soft Lindelöf, as desired.

A similar proof is given in the case of an almost soft compact space.

Definition 3.14

A soft subset $(D,K)$ of $(X,\tau ,K)$ is said to be dense if $\overline{(D,K)}=\tilde{X}$.

Proposition 3.15

Every soft hyperconnected space $(X,\tau ,K)$ is almost soft compact.

Proof.

Since every soft open subset of a soft hyperconnected space $(X,\tau ,K)$ is soft dense, then $(X,\tau ,K)$ is almost soft compact.

In the following, we construct an example to show that the converse of the above proposition is not true in general.

Example 3.16

Let $K=\{k_1,k_2\}$ be a set of parameters and $\tau =\left\{\right(G,K)\tilde{\subseteq }\tilde{\mathcal{R}}:$ either $[1\in (G,K)$ and $(G^c,K)$ is finite$]$ or $1⋐̸(G,K)\}$ be a soft topology on $\mathcal{R}$. On the one hand, the relative complement of any soft open set containing $\left\{1\right\}$ is finite. Then $(\mathcal{R},\tau ,K)$ is almost soft compact. On the other hand, $(G,K)$ and $(H,K)$, where $G\left(k_1\right)=G\left(k_2\right)=\mathcal{R}\setminus \{5,6\}$ and $H\left(k_1\right)=H\left(k_2\right)=\left\{5\right\}$ are two disjoint soft open sets. Hence $(\mathcal{R},\tau ,K)$ is not soft hyperconnected.

Lemma 3.17

Let $(H,K)$ be a soft subset of an enriched STS $(X,\tau ,K)$. If $H\left(k\right)$ is a non-empty subset of $(X,{\tau }_k)$ and $H\left(k_j\right)=\mathrm{\varnothing },$ for each $k_j\ne k,$ then $(\overline{H},K)$ is a soft closed set.

Proof.

Assume that $(H,K)$ is a given soft set above. Then $(\overline{H},K)$ is defined as $\overline{H}\left(k\right)=\overline{H\left(k\right)}$ and $\overline{H}\left(k_j\right)=\mathrm{\varnothing }$, for each $k_j\ne k$. Let $P_e^x\in \overline{(H,K)}$. As $(X,\tau ,K)$ is enriched, then e=k. Now, for each soft open set $(W,K)$ containing $P_k^x$, we have $(W,K)\bigcap ^{~}(H,K)\ne \tilde{\mathrm{\varnothing }}$. Therefore $W\left(k\right)\bigcap H\left(k\right)\ne \mathrm{\varnothing }$, for each open set $W\left(k\right)$ in $(X,{\tau }_k)$ containing x. This implies that $x\in \overline{H\left(k\right)}$. Thus $P_k^x\in (\overline{H},K)$. Hence $\overline{(H,K)}\tilde{\subseteq }(\overline{H},K)$. From Proposition 2.13, we obtain $\overline{(H,K)}=(\overline{H},K)$. Hence the desired result is proved.

Remark 3.18

It can be seen that an enriched almost soft Lindelöf (resp. enriched almost soft compact) space $(X,\tau ,K)$ implies that a set of parameters K is countable (resp. finite).

Proposition 3.19

If $(X,{\tau }_k)$ is almost compact $($resp. almost Lindelöf$)$ for each $k\in K$ such that K is finite $($resp. countable$),$ then $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf$)$.

Proof.

To prove the proposition in the case of $(X,{\tau }_k)$ is almost Lindelöf, let $\left\{\right(G_j,K):j\in J\}$ be a soft open cover of $(X,\tau ,K)$ such that K is countable. Say, $\mid E\mid =\mathrm{\aleph }$, where ℵ is the cardinal number of the natural numbers set. Then $X=\bigcup _{j\in J}{G}_j\left(k\right)$ for each $k\in K$. As $(X,{\tau }_k)$ is almost Lindelöf for each $k\in K$, then there exist countable sets $M_n$ such that $X=\bigcup _{j\in M_1}\overline{G_j\left(k_1\right)}$, $X=\bigcup _{j\in M_2}\overline{G_j\left(k_2\right)}$,…, $X=\bigcup _{j\in M_m}\overline{G_j\left(k_m\right)}$,…. Therefore $\tilde{X}={\bigcup ^{~}}_{j\in \bigcup _{n\in \mathrm{\aleph }}{M}_n}\overline{(G_j,K)}$. Thus $(X,\tau ,K)$ is almost soft Lindelöf.

A similar proof is made in the case of an almost compact space.

Theorem 3.20

Let $(X,\tau ,K)$ be an enriched STS. Then $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf$)$ if and only if $(X,{\tau }_k)$ is almost compact $($resp. almost Lindelöf$),$ for each $k\in K$.

Proof.

We prove the theorem in the case of an enriched almost soft compact space and the case between parenthesis is made similarly.

$[\Rightarrow ]$ Let $\left\{H_j\right(k):j\in J\}$ be an open cover for $(X,{\tau }_k)$. By hypothesis, $(X,\tau ,K)$ is enriched, so we can construct a soft open cover of $(X,\tau ,K)$ consisting of the following soft sets:

1. All soft open sets $(F_j,K)$ in which $F_j\left(k\right)=H_j\left(k\right)$ and $F_j\left(k_i\right)=\mathrm{\varnothing }$, for all $k_i\ne k$.

2. Since $(X,\tau ,K)$ is enriched, then we take a soft open set $(G,K)$ which satisfies that $G_j\left(k\right)=\mathrm{\varnothing }$ and $G_j\left(k_i\right)=X$, for all $k_i\ne k$.

Obviously, $\left\{\right(F_j,K\left)\bigcup ^{~}\right(G,K):j\in J\}$ is a soft open cover of $(X,\tau ,K)$. As $(X,\tau ,K)$ is almost soft compact, then $\tilde{X}={\bigcup ^{~}}_{j=1}^{j=n}\overline{(F_j,K)\bigcup ^{~}(G,K)}\tilde{\subseteq }{\bigcup ^{~}}_{j=1}^{j=n}(\overline{F_j},K)\bigcup ^{~}(\overline{G},K)=(W,K)$, where $W\left(k\right)=\bigcup _{j=1}^{j=n}\overline{F_j\left(k\right)}$ and $W\left(k_i\right)=X$, for each $k_i\ne k$. Thus $X=\bigcup _{j=1}^{j=n}\overline{F_j\left(k\right)}=\bigcup _{j=1}^{j=n}\overline{H_j\left(k\right)}$. Hence $(X,{\tau }_k)$ is almost compact.

$[\Leftarrow ]$ The proof of the sufficient part comes immediately from Remark 3.18 and Proposition 3.19.

Lemma 3.21

Consider $\left(\right(A,K),{\tau }_{(A,K)},K)$ is a soft subspace of $(X,\tau ,K)$ and let ${\overline{(G,K)}}^A$ and $(G,K{)}^{\circ A}$ stand for the soft closure and soft interior operators, respectively, in $\left(\right(A,K),{\tau }_{(A,K)},K)$. Then:

1. ${\overline{(G,K)}}^A=\overline{(G,K)}\bigcap ^{~}(A,K),$ for each $(G,K)\tilde{\subseteq }(A,K)$.

2. $(G,K{)}^{\circ }=(G,K{)}^{\circ A}\bigcap ^{~}(A,K{)}^{\circ },$ for each $(G,K)\tilde{\subseteq }(A,K)$.

Proposition 3.22

A soft open subset $(A,K)$ of $(X,\tau ,K)$ is almost soft compact $($resp. almost soft Lindelöf$)$ if and only if a soft subspace $\left(\right(A,K),{\tau }_{(A,K)},K)$ is almost soft compact $($resp. almost soft Lindelöf$)$.

Proof.

We only give a proof for the proposition in the case of almost soft Lindelöfness and the other case can be made similarly.

Necessity: Let $\left\{\right(H_i,K)\in {\tau }_{(A,K)}:i\in I\}$ be a soft open cover of $\left(\right(A,K),{\tau }_{(A,K)},K)$. Then for each $(H_i,K)$, there is $(G_i,K)\in \tau$ such that $(H_i,K)=(A,K)\bigcap ^{~}(G_i,K)$. Therefore $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}(G_i,K)$. As $(A,K)$ is an almost soft Lindelöf subset of $(X,\tau ,K)$, then $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}\overline{(G_i,K)}$. So $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}\overline{(G_i,K)}\bigcap ^{~}(A,K)$. As $(A,K)$ is soft open, then $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}\overline{(H_i,K)}$. Thus $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}{\overline{(H_i,K)}}^A$. Hence a soft subspace $\left(\right(A,K),{\tau }_{(A,K)},K)$ is almost soft Lindelöf.

Sufficiency: Let $\left\{\right(G_i,K)\in \tau :i\in I\}$ be a soft open cover of $(A,K)$ in $(X,\tau ,K)$. Then $\left\{\right(A,K\left)\bigcap ^{~}\right(G_i,K):i\in I\}$ is a soft open cover of $\left(\right(A,K),{\tau }_{(A,K)},K)$. As a soft subspace $\left(\right(A,K),{\tau }_{(A,K)},K)$ is almost soft Lindelöf, then $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in S}{\overline{(A,K)\bigcap ^{~}(G_i,K)}}^A$. Therefore $(A,K)\tilde{\subseteq }$ ${\bigcup ^{~}}_{i\in S}\overline{(G_i,K)}$. Thus $(A,K)$ is an almost soft Lindelöf subset of $(X,\tau ,K)$.

Proposition 3.23

If $(A,K)$ is an almost soft compact subset of a soft $T_2^{\mathrm{\prime }}$-space $(X,\tau ,K),$ then $(A,K)$ is soft closed.

Proof.

Let the given conditions be satisfied and let $P_k^x\in (A,K{)}^c$. Then for each $P_e^{y_i}\in (A,K)$, there are two disjoint soft open sets $(G_i,K)$ and $(W_i,K)$ such that $P_k^x\in (G_i,K)$ and $P_e^{y_i}\in (W_i,K)$. It follows that $\left\{\right(W_i,K):i\in I\}$ forms a soft open cover of $(A,K)$. Consequently, $(A,K)\tilde{\subseteq }{\bigcup ^{~}}_{i=1}^{i=n}\overline{(W_i,K)}$. Putting ${\bigcap ^{~}}_{i=1}^{i=n}(G_i,K)=(H,K)$ and ${\bigcup ^{~}}_{i=1}^{i=n}\overline{(W_i,K)}=(V,K)$. By Lemma 2.34, we get $(H,K)\bigcap ^{~}(V,K)=\tilde{\mathrm{\varnothing }}$. Therefore $(H,K)\bigcap ^{~}(A,K)=\tilde{\mathrm{\varnothing }}$. This means that $P_k^x\in (H,K)\tilde{\subseteq }(A,K{)}^c$. Thus $(A,K{)}^c$ is a soft open set. Hence we find that $(A,K)$ is soft closed, as required.

Corollary 3.24

If $(A,K)$ is an almost soft compact stable subset of asoft $T_2$-space $(X,\tau ,K),$ then $(A,K)$ is soft closed.

Proof.

Since $(A,K)$ is stable, then $P_k^x\in (A,K)$ if and only if $x\in (A,K)$. So by using a similar technique of the above proof, the corollary holds.

Definition 3.25

An STS $(X,\tau ,K)$ is said to be soft partition provided that every soft open set is soft closed.

Proposition 3.26

Every bijective soft continuous mapping $g_{\phi }$ of an almost soft compact partition space $(X,\tau ,K)$ onto a soft $T_2^{\mathrm{\prime }}$-space $(Y,\theta ,K)$ is soft homeomorphism.

Proof.

It is enough to prove that $g_{\phi }$ is soft closed.

Obviously, every almost soft compact partition space $(X,\tau ,K)$ is soft compact. Let $(A,K)$ be a soft closed subset of $(X,\tau ,K)$. Then $(A,K)$ is soft compact. So $g_{\phi }(A,K)$ is soft compact subset of a soft $T_2^{\mathrm{\prime }}$-space $(Y,\theta ,K)$. Thus $g_{\phi }(A,K)$ is soft closed. Hence $g_{\phi }$ is soft homeomorphism.

Proposition 3.27

If there exists a finite soft dense subset of $(X,\tau ,K)$ such that K is finite, then $(X,\tau ,K)$ is almost soft compact.

Proof.

Let $\mathrm{\Lambda }=\left\{\right(G_i,K):i\in I\}$ be a soft open cover of $(X,\tau ,K)$ and let $(D,K)$ be a soft dense subset of $(X,\tau ,K)$. Then for each $P_{k_s}^{x_s}\in (D,K)$, there exists $(G_{x_s},K)\in \mathrm{\Lambda }$ containing $P_{k_s}^{x_s}$. This implies that $(D,K)\tilde{\subseteq }\bigcup ^{~}(G_{x_s},K)$. So $\tilde{X}=\overline{(D,K)}\tilde{\subseteq }\overline{\bigcup ^{~}(G_{x_s},K)}$. Since K is a finite set and $(D,K)$ is a finite soft set, then a collection $\left\{\right(G_{x_s},K\left)\right\}$ is finite. Thus $\tilde{X}=\bigcup ^{~}\overline{(G_{x_s},K)}$. Hence the proof is complete.

4. Approximately soft Lindelöf spaces

We define in this section an approximately soft Lindelöf spaces concept which is wider than an almost soft Lindelöf spaces concept and illustrate under what conditions almost soft Lindelöf and approximately soft Lindelöf spaces are equivalent. Also, we study several properties concerning approximately soft Lindelöf and soft locally finite spaces.

Definition 4.1

An STS $(X,\tau ,K)$ is called approximately soft Lindelöf space if every soft open cover of $\tilde{X}$ has a countable soft sub-cover in which its soft closure cover $\tilde{X}$.

Remark 4.2

If we replace a word ”countable” in the above definition by ”finite”, then we obtain a definition of an almost soft compact space because ${\bigcup ^{~}}_{i=1}^{i=n}\overline{(G,K)}=\overline{{\bigcup ^{~}}_{i=1}^{i=n}(G,K)}$. For this reason, we do not define approximately soft compact spaces.

Proposition 4.3

Every almost soft Lindelöf space is approximately soft Lindelöf.

Proof.

Since ${\bigcup ^{~}}_{i\in I}\overline{(G_i,K)}\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in I}(G_i,K)}$, then the proposition is satisfied.

Corollary 4.4

Every soft hyperconnected space is approximately soft Lindelöf.

The next example shows that the converse of Proposition 4.3 is not true in general.

Example 4.5

Let $\{V_i:i\in I\}$ be a collection of all open subsets of the usual topological space $(\mathcal{R},\mathcal{U})$ and let $K=\{k_1,k_2\}$ be a set of parameters. We construct a soft topology τ on $\mathcal{R}$ as follows: $\tau =\left\{\right(G_i,K):i\in I\}$, where $G_i\left(k_1\right)=G_i\left(k_2\right)=V_i$, for each $i\in I$. Since a soft set $(H,K)$ which is given by $H\left(k_1\right)=H\left(k_2\right)=\mathcal{Q}$ is countable soft dense, then it follows from Proposition 4.7, that $(\mathcal{R},\tau ,K)$ is approximately soft Lindelöf. On the other hand, a soft collection $\mathrm{\Lambda }=\left\{\right(H_i,K):H_i(k_1)=H_i(k_1)=(-\mathrm{\infty },i):i\in \mathcal{R}\}$ is a soft open cover of $\tilde{\mathcal{R}}$. Since this collection has not a countable soft sub-collection such that the soft closure of whose members cover $\tilde{\mathcal{R}}$, then $(\mathcal{R},\tau ,K)$ is not almost soft Lindelöf.

Proposition 4.6

A countable union of approximately soft Lindelöf subsets of $(X,\tau ,K)$ is approximately soft Lindelöf.

Proof.

Let $\left\{\right(A_s,K):s\in S\}$ be a collection of approximately soft Lindelöf subsets of $(X,\tau ,K)$ and let $\left\{\right(G_i,K):i\in I\}$ be a soft open cover of ${\bigcup ^{~}}_{s\in S}(A_s,K)$. Then there exist countable sets $M_s$ such that $(A_1,K)\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in M_1}(G_i,K)}$, …, $(A_n,K)\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in M_n}(G_i,K)}$,…. Therefore ${\bigcup ^{~}}_{s\in S}(A_s,K)\tilde{\subseteq }$ $\overline{{\bigcup ^{~}}_{i\in M_1}(G_i,K)}\bigcup ^{~}\dots \bigcup ^{~}\overline{{\bigcup ^{~}}_{i\in M_n}(G_i,K)}\bigcup ^{~}\dots$ $\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in \bigcup _{s\in S}{M}_s}(G_i,K)}$. Hence the desired result is proved.

Proposition 4.7

If there exists a countable soft dense subset of $(X,\tau ,K)$ such that K is countable, then $(X,\tau ,K)$ is approximately soft Lindelöf.

Proof.

The proof is similar of that Proposition 3.27.

Proposition 4.8

Every soft clopen subset $(D,K)$ of an approximately soft Lindelöf space $(X,\tau ,K)$ is approximately soft Lindelöf.

Proof.

Let $(D,K)$ be a soft clopen subset of $\tilde{X}$ and let $\left\{\right(H_i,K):i\in I\}$ be a soft open cover of $(D,K)$. Then $(D^c,K)$ is soft clopen and $(D,K)\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}(H_i,K)$. Therefore $\tilde{X}={\bigcup ^{~}}_{i\in I}(H_i,K)\bigcup ^{~}(D^c,K)$. Since $\tilde{X}$ is approximately soft Lindelöf, then $\tilde{X}=\overline{{\bigcup ^{~}}_{i\in S}(H_i,K)\bigcup ^{~}(D^c,K)}=\overline{{\bigcup ^{~}}_{i\in S}(H_i,K)}\bigcup ^{~}(D^c,K)$. Hence we have $(D,K)\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in S}(H_i,K)}$, as required.

Corollary 4.9

If $(G,K)$ is an approximately soft Lindelöf set and $(D,K)$ is a soft clopen set in $(X,\tau ,K),$ then $(G,K)\bigcap ^{~}(D,K)$ is approximately soft Lindelöf.

Definition 4.10

A collection $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ of soft sets is said to have the second type of countable intersection property if $\left({\bigcap ^{~}}_{i\in S}\right(F_i,K){)}^{\circ }\ne \tilde{\mathrm{\varnothing }}$.

It is clear that any collection satisfies the second type of countable intersection property, it also satisfies the first type of countable intersection property.

Theorem 4.11

An STS $(X,\tau ,K)$ is approximately soft Lindelöf if and only if every collection of soft closed subsets of $(X,\tau ,K),$ satisfying the second type of countable intersection property, has, itself, a non-null soft intersection.

Proof.

Necessity: Let $\mathrm{\Lambda }=\left\{\right(F_i,K):i\in I\}$ be a collection of soft closed subsets of $\tilde{X}$. Suppose that ${\bigcap ^{~}}_{i\in I}(F_i,K)=\tilde{\mathrm{\varnothing }}$. Then $\tilde{X}={\bigcup ^{~}}_{i\in I}(F_i^c,K)$. As $(X,\tau ,K)$ is approximately soft Lindelöf, then $\tilde{X}=\overline{{\bigcup ^{~}}_{i\in S}(F_i^c,K)}$. Therefore $\tilde{\mathrm{\varnothing }}=(\overline{{\bigcup ^{~}}_{i\in S}(F_i^c,K)}{)}^c=({\bigcap ^{~}}_{i\in S}(F_i,K){)}^{\circ }$, as required.

Sufficiency: Let Λ be a collection of soft closed subsets of $\tilde{X}$ which satisfies the second type of countable intersection property. Then it also satisfies the first type of countable intersection property. Since Λ has a non-null soft intersection, then $(X,\tau ,K)$ is an almost soft Lindelöf space. It follows, by Proposition 4.3, that $(X,\tau ,K)$ is approximately soft Lindelöf.

Proposition 4.12

The soft continuous image of an approximately soft Lindelöf set is approximately soft Lindelöf.

Proof.

By using a similar technique of the proof of Proposition 3.13, we obtain the proof.

Definition 4.13

A topological space $(X,\tau )$ is called approximately Lindelöf if every open cover of X has a countable sub-cover in which its closure cover X.

Proposition 4.14

If $(X,{\tau }_k)$ is approximately Lindelöf for each $k\in K$ such that K is countable, then $(X,\tau ,K)$ is approximately soft Lindelöf.

Proof.

The proof is similar of that Proposition 3.19.

Theorem 4.15

Let $(X,\tau ,K)$ be an enriched STS. Then $(X,\tau ,K)$ is approximately soft Lindelöf if and only if $(X,{\tau }_k)$ is approximately Lindelöf, for each $k\in K$.

Proof.

We construct a soft open cover for $\tilde{X}$ like the soft open cover initiated in the proof of Theorem 3.20. Now, $(X,\tau ,K)$ is approximately soft Lindelöf implies that $\tilde{X}=\overline{\widetilde{\bigcup _{j\in S}}(F_j,K)\bigcup ^{~}(G_j,K)}=\overline{\widetilde{\bigcup _{j\in S}}(W_j,K)}$, where $W_j\left(k\right)=F_j\left(k\right)$ and $W_j\left(k_i\right)=X$, for each $k_i\ne k$. Putting $\widetilde{\bigcup _{j\in S}}(W_j,K)=(H_j,K)$. As $(\overline{H_j},K)$ is soft closed, then $\tilde{X}=(\overline{H_j},K)$. Therefore $X=\overline{\bigcup _{j\in S}{F}_j\left(k\right)}=\overline{\bigcup _{j\in S}{H}_j\left(k\right)}$. Thus $(X,{\tau }_k)$ is approximately Lindelöf.

Proposition 4.16

A soft open subset $(A,K)$ is approximately soft Lindelöf of $(X,\tau ,K)$ if and only if a soft subspace $\left(\right(A,K),{\tau }_{(A,K)},K)$ is approximately soft Lindelöf.

Proof.

The proof is similar of that Proposition 3.22.

Definition 4.17

A collection $\left\{\right(G_i,K):i\in I\}$ of $(X,\tau ,K)$ is called soft locally finite if for each $P_k^x\in \tilde{X}$, there is a soft open set $(W,K)$ satisfies that $P_k^x\in (W,K)$ and a set $\{m:(W,K\left)\bigcap ^{~}\right(G_m,K)\ne \tilde{\mathrm{\varnothing }}\}$ is finite.

Proposition 4.18

If a collection $\left\{\right(G_i,K):i\in I\}$ of $(X,\tau ,K)$ is soft locally finite, then $\{\overline{(G_i,K)}:i\in I\}$ is also soft locally finite.

Proof.

The proof is immediately obtained from Lemma 2.34 and Definition 4.17.

Proposition 4.19

If a collection $\left\{\right(G_i,K):i\in I\}$ of $(X,\tau ,K)$ is soft locally finite, then ${\bigcap ^{~}}_{j\in J}(G_j,K)=\tilde{\mathrm{\varnothing }},$ for any infinite set $J\subseteq I$.

Proof.

Suppose, to the contrary, that ${\bigcap ^{~}}_{j\in J}(G_j,K)\ne \tilde{\mathrm{\varnothing }}$, for some infinite set $J\subseteq I$. Then there exists $P_k^x\in {\bigcap ^{~}}_{j\in J}(G_j,K)$. By taking a soft open set $(W,K)$ containing $P_k^x$, we have $\{j:(W,K\left)\bigcap ^{~}\right(G_j,K)\ne \tilde{\mathrm{\varnothing }}\}$ is an infinite set. But this contradicts that $\left\{\right(G_i,K):i\in I\}$ is soft locally finite. Hence the desired result is proved.

Definition 4.20

An STS $(X,\tau ,K)$ is called soft locally finite if the soft collection of all soft open sets is, itself, soft locally finite.

Theorem 4.21

If a collection $\left\{\right(G_i,K):i\in I\}$ of $(X,\tau ,K)$ is soft locally finite, then $\overline{{\bigcup ^{~}}_{i\in I}(G_i,K)}={\bigcup ^{~}}_{i\in I}\overline{(G_i,K)}$.

Proof.

Obviously, ${\bigcup ^{~}}_{i\in I}\overline{(G_i,K)}\tilde{\subseteq }\overline{{\bigcup ^{~}}_{i\in I}(G_i,K)}$.

Conversely, let $P_k^x\in \overline{{\bigcup ^{~}}_{i\in I}(G_i,K)}$. Then we can find a finite set $M\subseteq I$ satisfies that $P_k^x\in (G_m,K)$, for each $m\in M$. Therefore $P_k^x\in \overline{{\bigcup ^{~}}_{i\in M}(G_i,K)\bigcup ^{~}{\bigcup ^{~}}_{i\in I\setminus M}(G_i,K)}=\overline{{\bigcup ^{~}}_{i\in M}(G_i,K)}\bigcup ^{~}\overline{{\bigcup ^{~}}_{i\in I\setminus M}(G_i,K)}$. It follows that $P_k^x\in \overline{{\bigcup ^{~}}_{i\in M}(G_i,K)}={\bigcup ^{~}}_{i\in M}\overline{(G_i,K)}$. Consequently, $\overline{{\bigcup ^{~}}_{i\in I}(G_i,K)}\tilde{\subseteq }{\bigcup ^{~}}_{i\in I}\overline{(G_i,K)}$. This completes the proof.

Corollary 4.22

Let a collection $\left\{\right(F_i,K):i\in I\}$ be soft locally finite. If all members are soft closed $($resp. soft open and soft closed$),$ then ${\bigcup ^{~}}_{i\in I}(F_i,K)$ is soft closed $($resp. soft open and soft closed$)$.

Theorem 4.23

A soft locally finite space $(X,\tau ,K)$ is almost soft Lindelöf if and only if it is approximately soft Lindelöf.

Proof.

The necessary condition is proved in Proposition 4.3.

To prove the sufficient condition, let $(X,\tau ,K)$ be approximately soft Lindelöf and consider $\left\{\right(G_i,K):i\in I\}$ is a soft open cover of $\tilde{X}$. By hypothesis, $\tilde{X}\tilde{\subseteq }\overline{{\bigcup ^{~}}_{s\in S}(G_i,K)}$. As $(X,\tau ,K)$ is a soft locally finite space, then $\overline{{\bigcup ^{~}}_{s\in S}(G_i,K)}={\bigcup ^{~}}_{s\in S}\overline{(G_i,K)}$. Hence the desired result is proved.

5. Mildly soft compact and mildly soft Lindelöf spaces

The concepts of mildly soft compact and mildly soft Lindelöf spaces are presented and their basic features are studied. The necessary and sufficient conditions for them are given. A sufficient condition for the equivalent among soft Lindelöf, almost soft Lindelöf, approximately soft Lindelöf and mildly soft Lindelöf spaces is investigated.

Definition 5.1

An STS $(X,\tau ,K)$ is called mildly soft compact (resp. mildly soft Lindelöf) if every soft clopen cover of $\tilde{X}$ has a finite (resp. countable) soft sub-cover.

The proofs of the following two propositions are easy and thus omitted.

Proposition 5.2

A finite $($resp. countable$)$ union of mildly soft compact $($resp. mildly soft Lindelöf$)$ subsets of $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Proposition 5.3

Every mildly soft compact space is mildly soft Lindelöf.

Example 5.4

In Example 3.16, we replace a word ”finite” by ”countable”. It is clear that any soft open set containing 1 is soft closed as well. Consequently, a new STS $(\mathcal{R},\tau ,K)$ is mildly soft Lindelöf. However it is not mildly soft compact. Hence the converse of Proposition 5.3 fails.

Proposition 5.5

Every almost soft compact $($resp. almost soft Lindelöf$)$ space $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Proof.

Consider $(X,\tau ,K)$ is almost soft compact (resp. almost soft Lindelöf) and let $\mathrm{\Lambda }=\left\{\right(H_i,K):i\in I\}$ be a soft clopen cover of $(X,\tau ,K)$. Then $\tilde{X}={\bigcup ^{~}}_{i=1}^{i=n}\overline{(H_i,K)}($resp. $\tilde{X}={\bigcup ^{~}}_{i\in S}\overline{(H_i,K)})$. Now, $\overline{(H_i,K)}=(H_i,K)$. Hence $(X,\tau ,K)$ is mildly soft compact (resp. mildly soft Lindelöf).

Corollary 5.6

Every soft compact $($resp. soft Lindelöf$)$ space is mildly soft compact $($resp. mildly soft Lindelöf$)$.

By the next example, we illuminate that the converse of the above proposition is not true.

Example 5.7

Assume that $(\mathcal{R},\tau ,K)$ is the same as in Example 4.5. We show that $(\mathcal{R},\tau ,K)$ is not almost soft Lindelöf. It can be observed that the only soft clopen subsets of $(\mathcal{R},\tau ,K)$ are $\tilde{\mathcal{R}}$ and $\tilde{\mathrm{\varnothing }}$. So $(\mathcal{R},\tau ,K)$ is mildly soft compact.

For the sake of economy, the proofs of the following three results will be omitted.

Proposition 5.8

If $(D,K)$ is a soft clopen subset of a mildly soft compact $($resp. mildly soft Lindelöf$)$ space $(X,\tau ,K)$, then $(D,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Corollary 5.9

If $(G,K)$ is a mildly soft compact $($resp. mildly soft Lindelöf$)$ set and $(D,K)$ is a soft clopen set in $(X,\tau ,K),$ then $(G,K)\bigcap ^{~}(D,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Theorem 5.10

An STS $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$ if and only if every collection of soft clopen subsets of $(X,\tau ,K),$ satisfying the finite $($resp. countable$)$ intersection property, has, itself, a non-null soft intersection.

Proposition 5.11

Every soft connected space $(X,\tau ,K)$ is mildly soft compact.

Proof.

In view of $(X,\tau ,K)$ is soft connected, then the only soft clopen subsets of $(X,\tau ,K)$ are $\tilde{X}$ and $\tilde{\mathrm{\varnothing }}$. Hence $(X,\tau ,K)$ is mildly soft compact.

The next example illustrates that the converse of the above proposition fails.

Example 5.12

Let the STS $(X,\tau ,K)$ be the same as in Example 3.16. On the one hand, $(X,\tau ,K)$ is mildly soft compact. On the other hand, $(G,K)$ and $(H,K)$, where $G\left(k_1\right)=G\left(k_2\right)=\mathcal{R}\setminus \left\{5\right\}$ and $H\left(k_1\right)=H\left(k_2\right)=\left\{5\right\}$ are two disjoint soft open sets and their soft union is $\tilde{\mathcal{R}}$, hence $(\mathcal{R},\tau ,K)$ is soft disconnected.

Theorem 5.13

The soft continuous image of a mildly soft compact $($resp. mildly soft Lindelöf$)$ set is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Proof.

By using a similar technique of the proof of Theorem 3.13, the desired result is proved.

Theorem 5.14

Let $(X,\tau ,K)$ be a soft partition topological space. Then the following four statements are equivalent.

1. $(X,\tau ,K)$ is soft Lindelöf;

2. $(X,\tau ,K)$ is almost soft Lindelöf;

3. $(X,\tau ,K)$ is approximately soft Lindelöf;

4. $(X,\tau ,K)$ is mildly soft Lindelöf.

Proof.

$\left(i\right)\to \left(ii\right)$: It follows from Proposition 3.5.

$\left(ii\right)\to \left(iii\right)$: It follows from Proposition 4.3.

$\left(iii\right)\to \left(iv\right)$: Let $\left\{\right(G_i,K):i\in I\}$ be a clopen cover of $\tilde{X}$. As $(X,\tau ,K)$ is approximately soft Lindelöf, then $\tilde{X}\tilde{\subseteq }\overline{{\bigcup ^{~}}_{s\in S}(G_i,K)}$ and as $(X,\tau ,K)$ is soft partition, then $\overline{{\bigcup ^{~}}_{s\in S}(G_i,K)}={\bigcup ^{~}}_{s\in S}(G_i,K)$. Therefore $(X,\tau ,K)$ is mildly soft Lindelöf.

$\left(iv\right)\to \left(i\right)$: Let $\left\{\right(G_i,K):i\in I\}$ be a soft open cover of $\tilde{X}$. As $(X,\tau ,K)$ is soft partition, then $\left\{\right(G_i,K):i\in I\}$ is a clopen cover of $\tilde{X}$ and as $(X,\tau ,K)$ is mildly soft Lindelöf, then $\tilde{X}={\bigcup ^{~}}_{s\in S}(G_i,K)$. This completes the proof.

Corollary 5.15

Let $(X,\tau ,K)$ be a soft partition topological space. Then the following three statements are equivalent.

1. $(X,\tau ,K)$ is soft compact;

2. $(X,\tau ,K)$ is almost soft compact;

3. $(X,\tau ,K)$ is mildly soft compact.

Theorem 5.16

Consider $(X,\tau ,K)$ has a soft base consists of soft clopen sets. Then $(X,\tau ,K)$ is soft compact $($resp. soft Lindelöf$)$ if and only if it is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Proof.

The necessary condition is obvious.

To verify the sufficient condition, assume that Λ is a soft open cover of a mildly soft compact space $(X,\tau ,K)$. Since $\tilde{X}$ is a soft union of members of the soft base and $\tilde{X}$ is mildly soft compact, then we can find a finite member $(H_s,K)$ of the soft base satisfies that $\tilde{X}={\bigcup ^{~}}_{s=1}^{s=n}(H_s,K)$. So for each member $(G_s,K)$ of Λ, there exists a member $(H_s,K)$ of the soft base such that $(H_s,K)\tilde{\subseteq }(G_s,K)$. Thus $\tilde{X}={\bigcup ^{~}}_{s=1}^{s=n}(G_s,K)$. Hence $(X,\tau ,K)$ is mildly soft compact.

The proof for mildly soft Lindelöf spaces is achieved similarly.

Lemma 5.17

If H is a clopen subset of $(X,{\tau }_k),$ then there exists a soft clopen subset $(F,K)$ of an enriched STS $(X,\tau ,K)$ such that $F\left(k\right)=H$.

Proof.

Since H is an open subset of $(X,{\tau }_k)$, then there exists a soft open subset $(G,K)$ of $(X,\tau ,K)$ such that $G\left(k\right)=H$ and since $(X,\tau ,K)$ is enriched, then a soft set $(W,K)$, where $W\left(k\right)=\mathrm{\varnothing }$ and for each $k_i\ne k$, $W\left(k_i\right)=X$, is a soft clopen set. So $(F,K)=(G,K)\bigcup ^{~}(W,K)$ is a soft open set. Also, since H is a closed subset of $(X,{\tau }_k)$, then there exists a soft closed subset $(L,K)$ of $(X,\tau ,K)$ such that $L\left(k\right)=H$. So $(F,K)=(L,K)\bigcup ^{~}(W,K)$ is a soft closed set as well. Thus $(F,K)$ is a soft clopen set such that $F\left(k\right)=H$.

Theorem 5.18

Let $(X,\tau ,K)$ be an enriched STS. Then $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$ if and only if $(X,{\tau }_k)$ is mildly compact $($resp. mildly soft Lindelöf$),$ for each $k\in K$.

Proof.

We only prove the theorem in the case of enriched mildly soft Lindelöfness, and the other case can be made similarly.

Necessity: Let $\left\{H_j\right(k):j\in J\}$ be a clopen cover for $(X,{\tau }_k)$. By the above lemma, we can construct a soft clopen cover of $(X,\tau ,K)$ consisting of the following soft sets, all soft clopen sets $(F_j,K)$ in which $F_j\left(k\right)=H_j\left(k\right)$ and $F_j\left(k_i\right)=X$, for each $k_i\ne k$. Obviously, $\left\{\right(F_j,K):j\in J\}$ is a soft clopen cover of $(X,\tau ,K)$. As $(X,\tau ,K)$ is mildly soft Lindelöf, then $\tilde{X}={\bigcup ^{~}}_{j\in S}(F_j,K)$. Thus $X=\bigcup _{j\in S}{F}_j\left(k\right)=\bigcup _{j\in S}{H}_j\left(k\right)$. Hence $(X,{\tau }_k)$ is mildly Lindelöf.

Sufficiency: Let $\left\{\right(G_j,K):j\in J\}$ be a soft clopen cover of $(X,\tau ,K)$. Since $(X,\tau ,K)$ is enriched, then K is countable. Say, $\mid E\mid =\mathrm{\aleph }$, where ℵ is the cardinal number of the natural numbers set. Then $X=\bigcup _{j\in J}{G}_j\left(k\right)$ for each $k\in K$. As $(X,{\tau }_k)$ is mildly Lindelöf for each $k\in K$, then there exist countable sets $M_n$ such that $X=\bigcup _{j\in M_1}{G}_j\left(k_1\right)$, $X=\bigcup _{j\in M_2}{G}_j\left(k_2\right)$,…, $X=\bigcup _{j\in M_m}{G}_j\left(k_m\right)$,…. Therefore $\tilde{X}={\bigcup ^{~}}_{j\in \bigcup _{n\in \mathrm{\aleph }}{M}_n}(G_j,K)$. Thus $(X,\tau ,K)$ is mildly soft Lindelöf.

In the following, the proofs of Proposition 5.19 and Proposition 5.20 are similar to the proofs of Proposition 3.19 and Proposition 3.22, respectively.

Proposition 5.19

If $(X,{\tau }_k)$ is mildly compact $($resp. mildly Lindelöf$),$ for each $k\in K$ such that K is finite $($resp. countable$),$ then $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

Proposition 5.20

A soft subset $(A,K)$ of $(X,\tau ,K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$ if and only if a soft subspace $\left(\right(A,K),{\tau }_{(A,K)},K)$ is mildly soft compact $($resp. mildly soft Lindelöf$)$.

We demonstrate in the next example that an approximately soft Lindelöf need not be a mildly soft Lindelöf space.

Example 5.21

Let $\{V_i:i\in I\}$ be a collection of all open subsets of the upper limit topological space and let $K=\{k_1,k_2\}$ be a set of parameters. We construct a soft topology τ on $\mathcal{R}$ as follows: $\tau =\left\{\right(G_i,K):i\in I\}$, where $G_i\left(k_1\right)=G_i\left(k_2\right)=V_i$, for each $i\in I$. Since a soft set $(H,K)$ which is given by $H\left(k_1\right)=H\left(k_2\right)=\mathcal{Q}$ is countable soft dense, then it follows from Proposition 4.7, that $(\mathcal{R},\tau ,K)$ is approximately soft Lindelöf. On the other hand, a collection $\mathrm{\Lambda }=\left\{\right(H_i,K):H_i(k_1)=H_i(k_1)=(-\mathrm{\infty },i]:i\in \mathcal{R}\}$ is a soft clopen cover of $\tilde{\mathcal{R}}$. Since this collection has not a countable soft sub-collection of $\tilde{\mathcal{R}}$, then $(\mathcal{R},\tau ,K)$ is not mildly soft Lindelöf.

Question 5.22

Is a mildly soft Lindelöf space an approximately soft Lindelöf space?

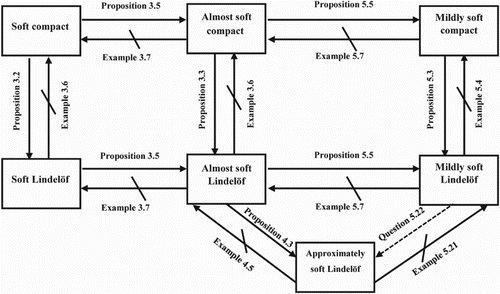
We complete this work by illustrating the relationships among the various kinds of soft compact and soft Lindelöf spaces in Figure 1.

Figure 1. The relationships among some types of soft compact and soft Lindelöf spaces.

6. Conclusion

In this work, the concepts of almost soft compact (almost soft Lindelöf), approximately soft Lindelöf and mildly soft compact (mildly soft Lindelöf) spaces are introduced and studied. The relationships among these introduced concepts are illustrated and their relationships with some soft topological notions such as soft connected and soft hyperconnected spaces are shown with the help of examples. The notions of soft locally finite and soft partition spaces are presented and then they are used to verify some important results such as Theorem 4.23 and Theorem 5.14. As well as, the given concepts of the first type of finite (countable) intersection property and the second type of countable intersection property are utilized to characterize almost soft compact (almost soft Lindelöf) and approximately soft Lindelöf spaces, respectively. Some findings concerning soft subspaces and enriched soft topological spaces are investigated in detail. The presented concepts in this study are elementary and fundamental for further researches and will open a way to improve more applications on soft topology.

Acknowledgments

The author express their sincere thanks to the reviewers for their valuable suggestions which helped to improve the presentation of the paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

M. E. El-Shafei  http://orcid.org/0000-0002-1562-505X

M. Abo-Elhamayel  http://orcid.org/0000-0003-0351-4341