Left-m-filter, Right-n-filter and (m,n)-filter on Ordered Semigroup

Abstract

In this paper, as a generalization of the concepts of left filters, right filters and filters of ordered semigroups, the concepts, for any positive integers m and n, of left-m-filters, right-n-filters and $(m,n)$-filters in ordered semigroups have been introduced and some properties of these generalized notions have been investigated. Finally left-m-filters (resp. right-n-filters, $(m,n)$-filters) of $(m,0)$-regular (resp. $(0,n)$-regular, $(m,n)$-regular) ordered semigroups have been characterized in terms of its prime generalized $(m,0)$-ideals (resp. $(0,n)$-ideals, $(m,n)$-ideals).

Keywords:

• Ordered semigroup
• left-m-filter
• right-n-filter
• $(m,n)$-filter

1. Introduction and preliminaries

In 1987, Kehayopulu [1] introduced the concept of a filter on a poe-semigroup. Later on in 1990, Kehayopulu [2] defined the relation $\mathcal{N}$ on a po-semigroup as follows: Let S be a po-semigroup. Then $\mathcal{N}=\left\{\right(a,b)\in S\times S\mid N(a)=N(b\left)\right\}$, where $N\left(a\right)$ denotes the filter of S generated by an element a of S. He showed that the relation $\mathcal{N}$ was the least semilattice congruence on S and was equal to the intersection of the semilattice congruences ${\sigma }_P=\left\{\right(a,b)\in S\times S\mid a,b\in Pora,b\notin P\}$ on S, where P is a prime ideal of S. The study of the left (resp. right) filters on a po-semigroup was initiated by S. K. Lee and S. S. Lee [3]. They proved some characterizations of these left (resp. right) filters on a po-semigroup in terms of its leftt (resp. right) prime ideals.

The notion of an $(m,n)$-ideal of a semigroup was introduced by Lajos [4] as a generalization of a one-sided ideal of a semigroup (see also [5–8] for related notions and results on $(m,n)$-ideals in semigroups). Thereafter the notion of $(m,n)$-ideals was introduced in various algebraic structures and had been studied by many authors, for instance, Akram et al. [9], Bussaban and Changphas [10], Changphas [11], Tilidetzke [12], Yaqoob and Chinram [13], and many others.

Let S be a non-empty set. The triplet $(S,\cdot ,\le )$ is called an ordered semigroup (or a po-semigroup) if $(S,\cdot )$ is a semigroup and $(S,\le )$ is a partially ordered set such that $a\le b\Rightarrow ac\le bc\text{and}ca\le cb$ for all $a,b,c\in S$.

For any non-empty subset A of an ordered semigroup S, we denote $\left(A\right]=\{t\in S\mid t\le a\text{for some}a\in A\}.$ If $A=\left\{a\right\}$, we shall be writing, in whatever follows, $\left(a\right]$ instead of $\left(\right\{a\left\}\right]$. For any non-empty subsets A and B of an ordered semigroup S, it is easy to verify that: (1) $A\subseteq \left(A\right]$; (2) $\left(\right(A\left]\right]=\left(A\right]$; (3) If $A\subseteq B$, then $\left(A\right]\subseteq \left(B\right]$; (4) $\left(A\right]\left(B\right]\subseteq \left(AB\right]$ and (5) $\left(\right(A\left]\right(B\left]\right]=\left(AB\right]$, where the product of A and B is defined as usual by $AB=\{ab\mid a\in A\text{and}b\in B\}$.

Let S be an ordered semigroup. Then a non-empty subset A of S is called

1. a subsemigroup of S if $A^2\subseteq A$;

2. a left (resp. right) ideal of S if $SA\subseteq A(\text{resp}.AS\subseteq A)$ and $\left(A\right]\subseteq A$;

3. an ideal of S if it is both a left and a right ideal of S.

Further a subsemigroup F of an ordered semigroup S is called

1. a left filter (resp. right filter) of S if for any $a,b\in S$, $ab\in F$ implies $a\in F$ (resp. $b\in S$) and $a\in F,a\le b\in S$ implies $b\in F$;

2. a filter if it is both a left filter and a right filter of S.

Throughout this paper, S will always stand for an ordered semigroup and $m,n$ for positive integers, unless and otherwise specified.

2. Main results

Definition 2.1

A subsemigroup F of an ordered semigroup S is called a left-m-filter (resp. right-n-filter) if

1. for any $a,b\in S$, $ab\in F$ implies $a^m\in F$ (resp. $b^n\in S$);

2. $a\in F,a\le b\in S$ implies $b\in F$.

Further a subsemigroup F of an ordered semigroup S is called an $(m,n)$-filter if it is both a left-m-filter and a right-n-filter of S.

Remark 1

In particular for $m=1(\text{resp.}n=1)$, F is a left filter (resp. right filter). Clearly each left filter (resp. right filter, filter) of an ordered semigroup S is a left-m-filter (resp. a right-n-filter, an $(m,n)$-filter) for each positive integers m and n. Indeed; For any left filter F of S and $a,b\in S$ such that $ab\in F$, as F is a left filter, $a\in F$. Therefore $a^m\in F$. Thus, the concept of a left-m-filter (resp. right-n-filter, $(m,n)$-filter) is a generalization of the concept of a left filter (resp. right-filter, filter). Conversely a left-m-filter (resp. right-n-filter, an $(m,n)$-filter) need not always be a left filter (resp. right filter, filter) which has been shown by the following example:

Example 2.2

Let $S=\{a,b,c,d\}$. Define an operation ○ and an order ≤ on S as follows: $\begin{array}{rl}& \begin{array}{ccccc}\circ & a& b& c& d\\ a& a& a& a& a\\ b& a& a& a& a\\ c& a& a& a& b\\ d& a& a& b& c\end{array}\\ & \le =\left\{\right(a,a),(b,b),(c,c),(d,d),(a,b\left)\right\}.\end{array}$ The covering relation ≺ and the figure of S are as follows; $\prec =\left\{\right(a,b\left)\right\}$

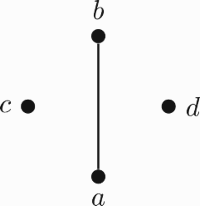
Then S is an ordered semigroup. Let $F=\{a,b\}$. Since F is subsemigroup, $d\circ c\in \{a,b\}$, $d^3\in \{a,b\}$ and $d\notin \{a,b\}$, we have that F is a left-3-filter of S but not a left filter of S.

Lemma 2.3

Let S be an ordered semigroup and T be a subsemigroup of S. Then for each left-m-filter (resp. right-n-filter) F of S, either $F\cap T=\mathrm{\varnothing }$ or $F\cap T$ is a left-m-filter (resp. right-n-filter) of T.

Proof.

Suppose that $F\cap T\ne \mathrm{\varnothing }$. Now $(F\cap T{)}^2\subseteq F^2\subseteq F$ and $(F\cap T{)}^2\subseteq T^2\subseteq T$. Therefore $(F\cap T{)}^2\subseteq F\cap T$. So $F\cap T$ is a subsemegroup of T. Next suppose that, for any $x,y\in T$, $xy\in F\cap T$. Therefore $xy\in F$. Since $x,y\in S$ and F is a left-m-filter of S, $x^m\in F$. Also $x^m\in T$. Thus $x^m\in T\cap F$. Finally take any $x\in T\cap F$ and $y\in T$ such that $x\le y$. As F is a left-m-filter of S and $F\ni x\le y\in S$, $y\in F$. Therefore $y\in T\cap F$. Hence $F\cap T$ is a left-m-filter of T.

Corollary 2.4

Let S be an ordered semigroup and T be a subsemigroup of S. Then for every $(m,n)$-filter F of S, either $F\cap T=\mathrm{\varnothing }$ or $F\cap T$ is an $(m,n)$-filter of T.

Lemma 2.5

Let S be an ordered semigroup and $\{F_i,i\in I\}$ be a family of left-m-filters (resp. right-n-filters) of S. If $\bigcap _{i\in I}{F}_i\ne \mathrm{\varnothing },$ then $\bigcap _{i\in I}{F}_i$ is a left-m-filter (resp. right-n-filter) of S.

Proof.

Assume that $\bigcap _{i\in I}{F}_i\ne \mathrm{\varnothing }$ and let $x,y\in \bigcap _{i\in I}{F}_i.$ Then $x,y\in F_i$ for each $i\in I$. As, for each $i\in I$, $F_i$ is left-m-filter, $xy\in F_i$. Therefore $xy\in \bigcap _{i\in I}{F}_i.$ Thus $\bigcap _{i\in I}{F}_i$ is a subsemigroup of S. Next take any $x,y\in S$ such that $xy\in \bigcap _{i\in I}{F}_i$. This implies that $xy\in F_i$ for each $i\in I$. As $F_i$'s are left-m-filters, $x^m\in F_i$ for each $i\in F_i$. So $x^m\in \bigcap _{i\in I}{F}_i$. Finally take any element $a\in \bigcap _{i\in I}{F}_i$ and $b\in S$ such that $a\le b$. Then $a\in F_i$ for each $i\in I$. Since $F_i$'s are left-m-filters, $b\in F_i$ for each $i\in I$ and, therefore, $b\in \bigcap _{i\in I}{F}_i$. Thus $\bigcap _{i\in I}{F}_i$ is a left-m-filter.

Corollary 2.6

Let S be an ordered semigroup and $\{F_i,i\in I\}$ be a family of $(m,n)$-filters of S. If $\bigcap _{i\in I}{F}_i\ne \mathrm{\varnothing },$ then $\bigcap _{i\in I}{F}_i$ is an $(m,n)$-filter of S.

Remark 2

Union of left-m-filters (resp. right-n-filters, $(m,n)$-filters) of an ordered semigroup need not be a left-m-filter (resp. right-n-filter, $(m,n)$-filter) in general.

The following example shows that, in general, the union of left-m-filters (resp. right-n-filters, $(m,n)$-filters) of an ordered semigroup is not always a left-m-filter (resp. right-n-filter, $(m,n)$-filter).

Example 2.7

Let $S=\{a,b,c,d\}$. Define a binary operation ○ and an order relation ≤ on S as follows: $\begin{array}{rl}& \begin{array}{cccccc}\circ & a& b& c& d& e\\ a& b& b& d& d& d\\ b& b& b& d& d& d\\ c& d& d& c& d& c\\ d& d& d& d& d& d\\ e& d& d& c& d& c\end{array}\\ & \le =\left\{\right(a,a),(b,b),(c,c),(d,d),(a,b),(c,e\left)\right\}.\end{array}$ The covering relation ≺ and the figure of S are as follows; $\prec =\left\{\right(a,b),(c,e\left)\right\}$

Then S is an ordered semigroup. The subset $F_1=\left\{b\right\}$ of S is a left-2-filter of S because $F_1\circ F_1\subseteq F_1$ and $a\circ a\in F_1$ implies $a^2\in F_1$. Thus $F_1$ is a left-2-filter of S and, as, $a\notin F_1$, F₁ is not a left-filter of S. Similarly $F_2=\{c,e\}$ is a left-2-filter of S. Now $F_1\cup F_2=\{b,c,e\}$. Since $b\circ c=\left\{d\right\}\notin F_1\cup F_2$, $F_1\cup F_2$ is not a subsemigroup of S and, hence, $F_1\cup F_2$ is not a left-2-filter of S.

Let $(S_{\lambda },{\circ }_{\lambda },{\le }_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}$ be any family of ordered semigroups. Then the cartesian product $S=\prod _{\lambda \in \mathrm{\Lambda }}{S}_{\lambda }=\left\{\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}|x_{\lambda }\in S_{\lambda }\}$ is an ordered semigroup [14] under the operation $``{\circ }^{″}$ $\left(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\circ \right(y_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}=(x_{\lambda }{\circ }_{\lambda }{y}_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}$ and order $``{\le }^{″}$ $\begin{array}{rl}\left(\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }})& \le \left(\right(y_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }})\text{if and only if}\\ & x_{\lambda }{\le }_{\lambda }{y}_{\lambda }\text{for each}\lambda \in \mathrm{\Lambda }.\end{array}$

Theorem 2.8

Let $(S_{\lambda },{\circ }_{\lambda },{\le }_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}$ be a family of ordered semigroups and $F_{\lambda },$ for each $\lambda \in \mathrm{\Lambda },$ be a left-m-filter (right-n-filters) of $S_{\lambda }$. Then $F=\prod _{\lambda \in \mathrm{\Lambda }}{F}_{\lambda }=\left\{\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\mid x_{\lambda }\in F_{\lambda }\}$ is a left-m-filter (right-n-filter) of the ordered semigroup $S=\prod _{\lambda \in \mathrm{\Lambda }}{S}_{\lambda }=\left\{\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\mid x_{\lambda }\in S_{\lambda }\}$.

Proof.

First we show that F is a subsemigroup of S. To show this, assume that $(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }},(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in F$. Then $a_{\lambda },b_{\lambda }\in F_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. As each $F_{\lambda }$ is a left-m-filter, $a_{\lambda }{\circ }_{\lambda }{b}_{\lambda }\in F_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. Therefore $\left(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\circ \right(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}=(a_{\lambda }{\circ }_{\lambda }{b}_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in F$. Thus F is a subsemigroup of S.

Next assume that, for any $(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }},(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in S$, $\left(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\circ \right(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in F.$ Therefore $a_{\lambda }{\circ }_{\lambda }{b}_{\lambda }\in F_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. As each $F_{\lambda }$ is a left-m-filter for each $\lambda \in \mathrm{\Lambda }$, $(a_{\lambda }{)}^m\in F_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. Thus $(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}^m\in F$.

Finally, take any $(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in F$ and $(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in S$ such that $(a_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\le (b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}$. Therefore $a_{\lambda }{\le }_{\lambda }{b}_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. As for each $\lambda \in \mathrm{\Lambda }$, $F_{\lambda }$ is a left-m-filter and $a_{\lambda }\in F_{\lambda }$, we have $b_{\lambda }\in F_{\lambda }$ for each $\lambda \in \mathrm{\Lambda }$. Thus $(b_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\in F$. Hence F is a left-m-filter of S.

Corollary 2.9

Let $(S_{\lambda },{\circ }_{\lambda },{\le }_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}$ be a family of ordered semigroups and $F_{\lambda },$ for each $\lambda \in \mathrm{\Lambda },$ be an $(m,n)$-filter of $S_{\lambda }$. Then $F=\prod _{\lambda \in \mathrm{\Lambda }}{F}_{\lambda }=\left\{\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\mid x_{\lambda }\in F_{\lambda }\}$ is an $(m,n)$-filter of the ordered semigroup $S=\prod _{\lambda \in \mathrm{\Lambda }}{S}_{\lambda }=\left\{\right(x_{\lambda }{)}_{\lambda \in \mathrm{\Lambda }}\mid x_{\lambda }\in S_{\lambda }\}$.

Definition 2.10

Let S be an ordered semigroup and $m,n$ be positive integers. Then a subsemigroup A of S is said to be an $(m,n)$-ideal of S if

1. $A^{m}S{A}^n\subseteq A$; and

2. $\left(A\right]\subseteq A$.

Similarly we may define a $(m,0)$-ideal and a $(0,n)$-ideal of S.

If we drop the subsemigroup condition from the above definition, then A is called a generalized $(m,n)$-ideal of S. Similarly a generalized $(m,0)$-ideal and a generalized $(0,n)$-ideal are defined.

Remark 3

It is easy to check that each $(m,n)$-ideal (resp. $(m,0)$-ideal, $(0,n)$-ideal) of any ordered semigroup is always a generalized $(m,n)$-ideal (resp. $(m,0)$-ideal, $(0,n)$-ideal), but the converse is not true in general. This has been shown by the following example.

Example 2.11

Let $S$ be an ordered semigroup of Example 2.2. Then the subset $A=\{a,d\}$ of $S$ is a generalized $(m,n)$-ideal of $S$ for all integers $m,n\ge 2$ and not an $(m,n)$-ideal of $S$. Further $A$ is a generalized $(m,0)$-ideal and a generalized $(0,n)$-ideal of $S$ for all integers $m,n\ge 3$, but not an $(m,0)$-ideal and $(0,n)$-ideal of $S$.

A generalized $(m,0)$-ideal (resp. $(0,n)$-ideal, $(m,n)$-ideal) A of an ordered semigroup S is called prime if for any $a,b\in S$ such that $ab\in A$, either $a\in A$ or $b\in A$.

Let S be an ordered semigroup and $m,n$ be non-negative integers. Then S is said to be $(m,n)$-regular if for each $a\in S$, there exists $x\in S$ such that $a\le a^{m}x{a}^n$ i.e., if $a\in \left(a^{m}S{a}^n\right]$ or equivalently for each non-empty subset A of S, $A\subseteq \left(A^{m}S{A}^n\right]$ with the convention that $A^{0}S=S{A}^0=A$.

Lemma 2.12

Let S be an $(m,0)$-regular (resp. $(0,n)$-regular) ordered semigroup and F be a non-empty subset of S. Then the following are equivalent:

1. F is a left-m-filter ( resp. right-n-filter) of S;

2. $S\setminus F=\mathrm{\varnothing }$ or $S\setminus F$ is a prime generalized $(m,0)$-ideal (resp. $(0,n)$-ideal) of S, where $S\setminus F$ is the complement of F in S.

Proof.

$\left(1\right)\Rightarrow \left(2\right)$. Assume that $S\setminus F\ne \mathrm{\varnothing }$. If $(S\setminus F{)}^{m}S\subseteq F$, then, as S is $(m,0)$-regular, $S\setminus F\subseteq (S\setminus F{)}^{m}S\subseteq F$, a contradiction. Therefore $(S\setminus F{)}^{m}S\subseteq S\setminus F.$ Let $S\ni a\le b\in S\setminus F$. If $a\in F$, then, as F is a left-m-filter, we have $b\in F$. Thus $a\in S\setminus F$. Therefore $S\setminus F$ is a generalized $(m,0)$-ideal of S. Now to show that $S\setminus F$ is a prime generalized $(m,0)$-ideal of S, take any $a,b\in S$ such that $ab\in S\setminus F$. If $a\in F$ and $b\in F$, then $ab\in F$, a contradiction. Therefore either $a\in S\setminus F$ or $b\in S\setminus F$. Hence $S\setminus F$ is a prime generalized $(m,0)$-ideal of S.

$\left(2\right)\Rightarrow \left(1\right)$. Let $S\setminus F$ is a prime generalized $(m,0)$-ideal of S. To show that F is a left-m-filter of S, take any $a,b\in F$. If $ab\in S\setminus F$, by hypothesis, either $a\in S\setminus F$ or $b\in S\setminus F$, a contradiction. Thus $ab\in F$ and, so, F is a subsemigroup of S. Next suppose that for any $a,b\in S,ab\in F$. If $a^m\in S\setminus F$, then, by $(m,0)$-regularity of S, $ab\le a^m{s}_{1}b\le (a^m{)}^m{s}_2{s}_{1}b\subseteq (S\setminus F{)}^{m}S\subseteq S\setminus F$ for some $s_1,s_2\in S$. So $ab\in S\setminus F$, a contradiction. Thus $a^m\in S\setminus F$. Finally take any element $a\in F$ and $b\in S$ such that $a\le b$. If $b\in S\setminus F$, then $a\in S\setminus F$ which is a contradiction. Thus $b\in F$. Hence $F$ is a left-m-filter of $S$.

Corollary 2.13

Let S be an $(m,n)$-regular ordered semigroup and F be any non-empty subset of S. Then the following are equivalent:

1. F is $(m,n)$-filter of S;

2. $S\setminus F=\mathrm{\varnothing }$ or $S\setminus F$ is prime generalized $(m,n)$-ideal of S, where $S\setminus F$ is the complement of F in S.

Lemma 2.14

A $(m,0)$-regular (resp. $(0,n)$-regular) ordered semigroup S does not contain proper left-m-filters (resp. right-n-filters) if and only if S does not contain proper prime generalized $(m,0)$-ideals (resp. $(0,n)$-ideals).

Proof.

Assume that S does not contain a proper left-m-filters. Let A be any proper prime generalized $(m,0)$-ideal of S. Then, by Lemma 2.12, $S\setminus F$ is a proper left-m-filter of S which is a contradiction. Therefore S does not contain any proper prime generalized $(m,0)$-ideal.

Conversely assume that S does not contain proper prime generalized $(m,0)$-ideals. Let F be any proper left-m-filter of S. Then, by Lemma 2.12, $S\setminus F$ is a proper prime generalized $(m,0)$-ideal of S which is a contradiction. Hence S does not contain proper left-m-filters.

Corollary 2.15

An $(m,n)$-regular ordered semigroup S does not contain proper $(m,n)$-filters if and only if S does not contain proper prime generalized $(m,n)$-ideals.

Let $(S,\star ,{\le }_S)$ and $(T,\diamond ,{\le }_T)$ be two ordered semigroups respectively and $\phi :S\to T$ be a mapping from S into T. Then φ is called an isotone if for all $x,y\in S,x{\le }_{S}y$ implies $\phi \left(x\right){\le }_T\phi \left(y\right)$. Further φ is called a reverse isotone if $x,y\in S,\phi \left(x\right){\le }_T\phi \left(y\right)$ implies $x{\le }_{S}y$. A mapping $\phi :S\to T$ is called a homomorphism if φ is an isotone and $\phi (x\star y)=\phi \left(x\right)\diamond \phi \left(y\right)\text{for all}x,y\in S.$ Each reverse isotone mapping $\phi :S\to T$ is clearly one-one. Further φ is called an isomorphism if

1. φ is homomorphism;

2. φ is a reverse isotone; and

3. φ is onto.

Lemma 2.16

Let $(S,\star ,{\le }_S)$ and $(T,\diamond ,{\le }_T)$ be ordered semigroups, $\phi :S⟶T$ any homomorphism and F a left-m-filter (resp. right-n-filter) of T. Then ${\phi }^{-1}\left(F\right)$ is a left-m-filter (resp. right-n-filter) of S.

Proof.

First we show that ${\phi }^{-1}\left(F\right)$ is a subsemigroup of S. If $a,b\in {\phi }^{-1}\left(F\right)$, then $\phi \left(a\right),\phi \left(b\right)\in F$. As φ is a homomorphism and F is a left-m-filter of T, $\phi (a\star b)=\phi \left(a\right)\diamond \phi \left(b\right)\in F$. So $a\star b\in {\phi }^{-1}\left(F\right)$ and, thus, ${\phi }^{-1}\left(F\right)$ is a subsemigroup of S. Next take any $a,b\in S$ such that $a\star b\in {\phi }^{-1}\left(F\right)$. Then $\begin{array}{rl}\phi (a\star b)\in F& \Rightarrow \left(\phi \right(a)\diamond \phi (b\left)\right)\in F\\ & \Rightarrow \left(\phi \right(a){)}^m\in F\\ & \Rightarrow \phi \left(a\right)\diamond \phi \left(a\right)\cdots \phi \left(a\right)\in F\\ & \Rightarrow \phi (a\star a\star \cdots \star a)\in F\\ & \Rightarrow \phi \left(a^m\right)\in F\\ & \Rightarrow a^m\in {\phi }^{-1}\left(F\right).\end{array}$ If $a\in {\phi }^{-1}\left(F\right)$ and $b\in S$ be such that $a{\le }_{S}b$, then $\phi \left(a\right)\in F$ and $\phi \left(a\right){\le }_T\phi \left(b\right)$. Therefore $\phi \left(b\right)\in F$ and, so, $b\in {\phi }^{-1}\left(F\right).$ Hence ${\phi }^{-1}\left(F\right)$ is a left-m-filter of S.

Corollary 2.17

Let $(S,\star ,{\le }_S)$ and $(T,\diamond ,{\le }_T)$ be ordered semigroups, $\phi :S⟶T$ a homomorphism, F an $(m,n)$-filter of T. Then ${\phi }^{-1}\left(F\right)$ is an $(m,n)$-filter of S.

Application: Since an ordered-Γ-semigroup is a generalization of an ordered semigroup, all the above results hold true for an ordered-Γ-semigroup.

Problems: $\left(1\right)$. Let $(S,\star ,{\le }_S)$ and $(T,\diamond ,{\le }_T)$ be two ordered semigroups, $\phi :S⟶T$ an onto homomorphism, F a left-m-filter (resp. a right-n-filter, an $(m,n)$-filter) of S. Does $\phi \left(F\right)$ is a left-m-filter (resp. a right-n-filter, an $(m,n)$-filter) of T?

$\left(2\right)$. Under what conditions, the concept of a left-m-filter (a right-n-filter, an $(m,n)$-filter) of an ordered semigroup coincides with the concept of a left-filter (a right-filter, a filter)?

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Ahsan Mahboob http://orcid.org/0000-0003-3305-2029