Effects of viscous dissipation on convective rotatory chemically reacting Rivlin–Ericksen flow past a porous vertical plate

ABSTRACT

Viscous dissipation effects on an unsteady convective rotatory Rivlin–Ericksen flow of an incompressible electrically conducting fluid under time-dependence suction is considered. The entire system rotates through the angular velocity by the axis perpendicular to the plate. The governing equations comprising of continuity, momentum, energy and concentration equations were non-dimensionalized and reduced to ordinary differential equations using perturbation technique. The resultant coupled ordinary differential equations were solved using the Adomian decomposition method. The effects of various fluid parameters on velocity, temperature and concentration were presented in tabular and graphical forms. The results revealed that resultant fluid velocity is enhanced with an increase in rotation, viscoelastic and viscous dissipation parameter while an increase in chemical reaction retards both velocity and concentration distributions of the fluid.

KEYWORDS:

• Viscous dissipation
• Rivlin–Ericksen fluid
• diffusion-thermo
• thermal-diffusion
• rotatory
• chemical reaction
• thermal radiation

Nomenclature

$x^{\ast }$	=	dimensional distance upward the plate (m)
$y^{\ast }$	=	dimensional distance normal to the plate (m)
$u^{\ast },v^{\ast },w^{\ast }$	=	dimensional velocity components in the $x^{\ast },y^{\ast },{\eta }^{\ast }$ directions respectively ($\text{m}\text{s}{}^{-\text{1}}$)
$t^{\ast }$	=	dimensional time (s)
$C_p$	=	specific heat at constant pressure ($\text{J}\text{kg}{}^{-\text{1}}\text{K}{}^{-\text{1}}$)
$B_0$	=	magnetic induction (tesla)
$T^{\ast }$	=	dimensional temperature (K)
$C^{\ast }$	=	dimensional concentration ($\text{kmol / m}{}^{\text{3}}$)
$P^{\ast }$	=	dimensional pressure ($\text{N / m}{}^{\text{2}}$)
$D$	=	chemical molecular diffusivity
$g$	=	gravitational acceleration ($\text{m / s}{}^{\text{2}}$)
$T_{\delta }^{\ast }$	=	plate dimensional temperature (K)
$C_{\delta }^{\ast }$	=	plate dimensional concentration ($\text{kmol / m}{}^{\text{3}}$)
$k_m$	=	non-dimensional permeability of the porous medium ($\text{m}{}^{\text{2}}$)
$k^{\mathrm{\prime }}$	=	mean absorption coefficient
$W_o$	=	scale of suction velocity contain non-zero positive constant
$T_m$	=	mean fluid temperature
$K_T$	=	thermal-diffusion ratio
$C_s$	=	concentration susceptibility
$T_0$	=	temperature at the left plate (K)
$C_0$	=	concentration at the left plate ($\text{kmol / m}{}^{\text{3}}$)
$Q_o$	=	dimensional heat absorption coefficient ($\text{(j / kg)}$

Greek symbols

${\eta }^{\ast }$	=	dimensional distance perpendicular to the planes of the plates (m)
$\delta$	=	distance of the plate (m)
$\rho$	=	fluid density ($\text{kg}\text{m}{}^{-\text{3}}$)
${\nu }^{\ast }$	=	kinematic viscosity ($\text{m}{}^{\text{2}}\text{s}{}^{-\text{1}}$)
$\sigma$	=	Stefan-Boltzman constant ($\text{W/m}{}^{\text{2}}\times \text{K}{}^{\text{4}}$)
$\alpha$	=	thermal diffusivity ($\text{s}{}^{\text{2}}\text{/ m)}$
${\beta }_T$,${\beta }_C$	=	thermal, concentration expansion coefficient
${\beta }_1$	=	kinematic viscoelasticity ($\text{m}{}^{\text{2}}\text{/ s)}$
$\epsilon$	=	scalar constant

1. Introduction

Rivlin–Ericksen fluid is a non-Newtonian model proposed theoretically by Rivlin and Ericksen in 1955. This kind of fluid exhibits both viscous and elastic characteristics, hence it is categorized as viscoelastic fluid. It has received attentions from many researchers across the globe due to its numerous applications in the field of engineering, science, oceanography, just to mention but a few. Hence, Ravikumar et al. [1] examined MHD and heat absorption effects on convective Rivlin–Ericksen fluid flow via a semi-infinite permeable plate in the presence of variable suction. Dada and Agunbiade [2] studied the effects of thermal radiation on convective Rivlin–Ericksen fluid flow via a permeable vertical plate in the presence of chemical reaction. It was reported that both temperature and velocity profiles decelerated with an increase in thermal radiation. Effects of Double diffusion and transverse magnetic field on free convective Rivlin–Ericksen fluid flow in the permeable medium through a vertical plate was investigated by Malleswari [3]. Hussaini et al. [4] considered MHD Rivlin–Ericksen fluid flow past permeable medium with slip condition. In all these studies, the effect of viscous dissipation was ignored.

Moreover, rotatory medium has significant applications, for instance in rotating machinery. The study on the effects of rotatory on fluid flow has attracted the interest of many researchers. Sreenadh and Reddappa [5] considered rotatory Jeffrey fluid in relation to couette flow. It was reported that an increase in Eckert number enhanced temperature profiles. The effects of rotation and Soret on mixed convective magneto-hydrodynamic viscoelastic fluid flow in the presence of heat absorption past a permeable channel was investigated by Reddy et al. [6]. Gaur and Jha [7] studied rotatory viscoelastic fluid through a porous channel with heat and mass transfer. The result showed that the effect of rotation was highly felt closed to the wall. The effects of thermal radiation, thermal-diffusion and viscous dissipation on Rivlin–Ericksen fluid were not considered in these studies.

Dissipation resulted from an irreversible process that is evident in the homogeneous thermodynamic system. The process of transformation of energy from initial to final form where the capacity of the final form to perform mechanical work is less compare to initial form, is known as a dissipative process. An example of dissipative process is heat transfer. That is transfer of energy from hotter to the colder body. The effect of viscous dissipation on fluid flow is significant due to its application in controlling the rate of cooling. Thus, the effects of viscous dissipation on Rivlin–Ericksen fluid flow have become a subject of consideration by many researchers. Gilbert et al. [8] examined viscous dissipation and radiation effects on free convective MHD Casson fluid in the non-Darcy permeable medium. Carreau fluid in non-linear radiative heat transfer with viscous dissipation and non-uniform heat source over a stretching sheet was considered by Umeshaiah et al. [9]. Malik et al. [10] investigated viscous dissipation effects on boundary layer MHD Sisko fluid past a stretching cylinder. It was reported that kinetic energy of the fluid improved with an increase in the value of Eckert number. Joint influence of radiation and viscous dissipation on free convective non-Newtonian fluid through vertically continuous moving stretched surface in the presence of no-slip condition was carried out by Fahad et al. [11]. The above studies neglected the effects of chemical reaction and the influence of viscous dissipation was not considered for Rivlin–Ericksen fluids.

Moreover, the combined effects of thermal radiation and viscous dissipation on flow distribution can not be overemphasized due to its significance in controlling the rate of cooling. Mabood and Ibrahim [12] investigated non-uniform heat source and Soret effects on convective Non-Darcian MHD Micropolar fluid flow with radiation. The effect of dissipation was considered and the result showed that temperature increased with an increase in Eckert number. Unsteady free convective MHD flow of a viscoelastic fluid past an inclined infinite porous plate with dissipation, heat source and ohmic heating was studied by Umamaheswar et al. [13]. The result revealed that an increase in Grashof number for heat transfer made the Skin friction to increase. Dada and Adefolaju [14] considered the influence of radiation, dissipation and MHD on convective heat and mass transfer past Darcy-forcheimer permeable channel. The result showed that the value of Eckert number enhances velocity profiles. Sarma and Govardhan [15] considered the effects of Diffusion-thermo and thermo-diffusion on free convection with heat and mass transfer past a permeable vertical surface in the presence of dissipation and radiation. Newtonian fluid was studied in this work and it was acknowledged that Eckert number enhanced velocity profiles. Pal and Samad [16] examined radiation and viscous dissipation effects on Non-Newtonian fluid past a surface with heat flux and generation. The result showed that increasing Eckert number led to an increase in both velocity and temperature fields. Dada et al. [17] studied the effects of Dufour and Soret on convective rotatory Rivlin–Ericksen fluid flow through vertical porous plate. They reported that the skin friction was enhanced by Soret parameter, while it was slowed down by Dufour parameter.

Alamri et al. [18] considered poiseuille nanofluid flow past a permeable medium with slip condition. The analysis was carried out using Homotopy analysis method. Zeeshan et al. [19] examined the nanofluid of hydromagnetic flow through a porous media lodged in non-Darcian Forchheimer. They reported that temperature profiles were enhanced with an increase in Eckert number. Pulsatile flow of hydromagnetic solid-liquid past permeable concentric cylinders medium was investigated by Maskeen et al. [20] and reported that the magnetic field parameter had the tendency of the decelerating velocity distribution. Hassaan et al. [21] studied convective nanofluid flow through permeable medium. It was observed that nanoparticles concentration improved convection heat transfer. Ellahi et al. [22] discussed nanofluid peristaltic flow in the presence of entropy generation past a permeable medium. The equations of their model were solved analytically. Effects of transverse magnetic field and electric double layer as a result of peristaltic propulsion of two-phase flow with mass and heat transfer were carried out by Bhatti et al. [23].

Furthermore, Riaz et al. [24] presented mass transport of Synovial fluid in the presence of asymmetric peristaltic propulsion and reported that velocity was enhanced with an increase in weissenberg number. Effects of thermal radiation and entropy generation in boundary layer MHD flow was investigated by Bhatti et al. [25]. Khan et al. [26] considered magnetic effects and mass transport of fourth grade fluid past a curved channel. Regular perturbation method was employed for solving the differential equations. Majeed et al. [27] studied the activation energy of slip model momentum second order flow with MHD in the presence of chemical reaction. This study revealed that increasing chemical reaction decelerated concentration profiles. Sheikholeslami et al. [28] examined heat transport of nanofluid flow through the non-Darcy medium with a magnetic field. The result showed that the rate of heat transfer was low at higher values of Hartmann number. As impressive as these studies were, they were not on Rivlin–Ericksen fluids.

Therefore, combined effects of thermal radiation, thermal-diffusion, diffusion-thermo, viscous dissipation, time-dependence suction, heat absorption and pressure gradient on convective rotatory Rivlin–Ericksen fluid have received little or no attention. The physical reality of the combined effects and the dearth of knowledge on the effects of viscous dissipation with above mentioned fluid properties on Rivlin–Ericksen flow are the motivation for the study. Hence, this study examines the interaction effects of viscous dissipation, rotatory, Dufour and Soret on Rivlin–Ericksen fluid flow using Adomian Decomposition method (ADM) which could handle non-linear differential equations associated with this problem.

2. Mathematical analysis

A non-Newtonian, two-dimensional incompressible free convective Rivlin–Ericksen flow of an electrically conducting fluid through a rotating vertical channel with a periodic suction is Considered. In $x$-direction, the channel is taken to be infinite, as a result of this, all physical quantities apart from pressure are functions of ${\eta }^{\ast }$ and $t^{\ast }$. Here, the fluid is bounded by two infinite vertical plates with distance $\delta$ apart. Along the mid line of the channel is the $x$-axis which is upward oriented, while $\eta$-axis is perpendicular to the plane of the plate. The fluid and the plates rotate about $\eta$-axis with a constant angular velocity $\mathrm{\Omega }$. The uniform magnetic field of strength $B_o$ is applied normal to $\eta$-axis. It is assumed that magnetic Reynolds number is much less than unity and as such the induced magnetic field is insignificant in comparison with an applied magnetic field. The Hall effect is also assumed to be negligible.

The Cauchy stress tensor $\phi$ for third-grade fluid (Chauhan and Kumar [29]) is given by (1) $\phi =-\mathit{p}\mathit{I}+\mathit{\mu }{\mathit{A}}_1+{\mathit{\lambda }}_1{\mathit{A}}_2+{\mathit{\lambda }}_2{{\mathit{A}}_1}^2+{\mathit{\alpha }}_3\left(tr{{\mathit{A}}_1}^2\right){\mathit{A}}_1,$(1) where $\mathit{\mu }$ represent viscosity coefficient, p is the pressure and ${\mathit{\lambda }}_1$, ${\mathit{\lambda }}_2$ and ${\mathit{\alpha }}_3$ are material constants related to the non-linear terms. ${\mathit{A}}_{\mathit{n}}$ are Rivlin–Ericksen tensor defined as: ${\mathit{A}}_0=\mathit{I}$is the identity tensor, ${\mathit{A}}_{\mathit{n}}=\frac{D{\mathit{A}}_{\mathit{n}-1}}{Dt}+{\mathit{A}}_{\mathit{n}-1}\left(\mathrm{\nabla }\mathit{V}\right)+(\mathrm{\nabla }\mathit{V}{)}^T{\mathit{A}}_{\mathit{n}-1}.n\ge 1$and $D/Dt$ is the material derivative. For this unsteady rotatory flow problem (Figure 1), the velosity field takes the form (2) $\mathit{V}=\left(u^{\ast }\left(\eta ,t\right),v{}^{\ast }\left(\eta ,t\right),0\right).$(2)

Figure 1. Physical configuration of the flow.

By applying Equations (1) and (2) into continuity, momentum, energy and concentration equations of the problem under consideration, one obtains a modified form of the equations (Ravikumar et al. [1] and Garg et al. [30]) as (3) $\frac{\mathrm{\partial }{w}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}=0,$(3) (4) $\begin{array}{rl}\frac{\mathrm{\partial }{u}^{\ast }}{\mathrm{\partial }{t}^{\ast }}+{\nu }^{\ast }\frac{\mathrm{\partial }{u}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}& =-\frac{1}{\rho }\frac{\mathrm{\partial }{p}^{\ast }}{\mathrm{\partial }{x}^{\ast }}+\nu \frac{{\mathrm{\partial }}^2{u}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 2}}+2{\mathrm{\Omega }}^{\ast }{v}^{\ast }\\ & +g{\beta }_T\left(T^{\ast }-T_{\delta }^{\ast }\right)+g{\beta }_C\left(C^{\ast }-C_{\delta }^{\ast }\right)-\nu \frac{u^{\ast }}{k_m^{\ast }}\\ & -\frac{\sigma B_o^2{u}^{\ast }}{\rho }-{\beta }_1\left(\frac{{\mathrm{\partial }}^3{u}^{\ast }}{\mathrm{\partial }{t}^{\ast }\mathrm{\partial }{\eta }^{\ast 2}}+{\nu }^{\ast }\frac{{\mathrm{\partial }}^3{u}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 3}}\right),\end{array}$(4) (5) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}^{\ast }}{\mathrm{\partial }{t}^{\ast }}+{\nu }^{\ast }\frac{\mathrm{\partial }{v}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}=-\frac{1}{\rho }\frac{\mathrm{\partial }{p}^{\ast }}{\mathrm{\partial }{y}^{\ast }}+\nu \frac{{\mathrm{\partial }}^2{v}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 2}}-2{\mathrm{\Omega }}^{\ast }{u}^{\ast }\\ & -\nu \frac{v^{\ast }}{k_m^{\ast }}-\frac{\sigma B_o^2{v}^{\ast }}{\rho }-{\beta }_1\left(\frac{{\mathrm{\partial }}^3{v}^{\ast }}{\mathrm{\partial }{t}^{\ast }\mathrm{\partial }{\eta }^{\ast 2}}+{\nu }^{\ast }\frac{{\mathrm{\partial }}^3{v}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 3}}\right),\end{array}$(5) (6) $\begin{array}{rl}& \frac{\mathrm{\partial }{T}^{\ast }}{\mathrm{\partial }{t}^{\ast }}+{\nu }^{\ast }\frac{\mathrm{\partial }{T}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}=\alpha \frac{{\mathrm{\partial }}^2{T}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 2}}-\frac{Q_o}{\rho c_p}\left(T^{\ast }-T_{\delta }^{\ast }\right)-\frac{1}{\rho C_p}\frac{\mathrm{\partial }{q}_r}{\mathrm{\partial }{\eta }^{\ast }}\\ & +\frac{D{K}_T{\mathrm{\partial }}^2{C}^{\ast }}{C_p{C}_s\mathrm{\partial }{\eta }^{\ast 2}}+\frac{\nu }{c_p}\left({\left(\frac{\mathrm{\partial }{u}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}\right)}^2+{\left(\frac{\mathrm{\partial }{v}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}\right)}^2\right),\end{array}$(6) (7) $\frac{\mathrm{\partial }{C}^{\ast }}{\mathrm{\partial }{t}^{\ast }}+{\nu }^{\ast }\frac{\mathrm{\partial }{C}^{\ast }}{\mathrm{\partial }{\eta }^{\ast }}=D\frac{{\mathrm{\partial }}^2{C}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 2}}-K_1^{\ast }\left(C^{\ast }-C_{\delta }^{\ast }\right)+\frac{D{K}_T}{T_m}\frac{{\mathrm{\partial }}^2{T}^{\ast }}{\mathrm{\partial }{\eta }^{\ast 2}}.$(7)

The corresponding boundary conditions are: (8) $\left.\begin{array}{l}{\eta }^{\ast }=0;u^{\ast }=v^{\ast }=0,T^{\ast }=T_{\delta }+\epsilon \left(T_o-T_{\delta }\right)\text{cos}{\omega }^{\ast }{t}^{\ast },\\ C^{\ast }=C_{\delta }+\epsilon \left(C_o-C_{\delta }\right)\text{cos}{\omega }^{\ast }{t}^{\ast }\\ {\eta }^{\ast }=\delta ;u^{\ast }=W_o\left(1+\epsilon \text{cos}{\omega }^{\ast }{t}^{\ast }\right),\\ v^{\ast }=0,T^{\ast }=T_{\delta },C^{\ast }=C_{\delta },\end{array}\right\}$(8) (9) $-\frac{1}{\rho }\frac{\mathrm{\partial }{P}^{\ast }}{\mathrm{\partial }{y}^{\ast }}=0\text{and}-\frac{1}{\rho }\frac{\mathrm{\partial }{P}^{\ast }}{\mathrm{\partial }{x}^{\ast }}=A\epsilon \text{cos}\omega t,$(9) $q_r$ is the radiative heat flux and is defined, based on Rosseland approximation (Brewster [31]), as: (10) $q_r=-\frac{4\sigma }{3k^{\mathrm{\prime }}}\frac{\mathrm{\partial }{T}^{\ast 4}}{\mathrm{\partial }{\eta }^{\ast }}.$(10) Considering the temperature differences within the flow to be sufficiently small, $T^{\ast 4}$ in Equation (10) can be expanded using Taylor series expansion and neglecting higher order terms gives; (11) $T^{\ast 4}\approx 4T_{\delta }^{\ast 3}{T}^{\ast }-3T_{\delta }^{\ast 4}.$(11) The non-dimensional variables below are used to transform the governing equations to non-dimensional form. (12) $\left.\begin{array}{c}\xi =\frac{u^{\ast }}{W_o},v=\frac{v^{\ast }}{W_o},t=\frac{t^{\ast }{W}_o^2}{\nu },\eta =\frac{W_o{\eta }^{\ast }}{\nu }=\frac{{\eta }^{\ast }}{\delta },k_m=\frac{k_m^{\ast }{W}_o^2}{{\nu }^2},x=\frac{W_o{x}^{\ast }}{\nu },\\ \vartheta =\frac{T^{\ast }-T_{\delta }^{\ast }}{T_o^{\ast }-T_{\delta }^{\ast }},\omega =\frac{{\omega }^{\ast }\nu }{W_o^2},P_r=\frac{\nu \rho C_p}{k_m}=\frac{\nu }{\alpha },M=\frac{\sigma B_0^2\nu }{\rho W_o^2},\\ G_h=\frac{\nu g{\beta }_T\left(T_o^{\ast }-T_{\delta }^{\ast }\right)}{W_o^3},Q=\frac{\nu Q_0}{\rho C_p{W}_o^2},R_n=\frac{{\beta }_1{W}_o^2}{{\nu }^2},G_m=\frac{\nu g{\beta }_c\left(C_o^{\ast }-C_{\delta }^{\ast }\right)}{W_o^3},\\ y=\frac{W_o{y}^{\ast }}{\nu },P=\frac{P^{\ast }}{\rho W_o^2},\varphi =\frac{C^{\ast }-C_{\delta }}{C_o^{\ast }-C_{\delta }^{\ast }},S_C=\frac{\nu }{D},R=\frac{k^1{k}_m}{4\sigma T_{\delta }^{\ast 3}},\\ \mathrm{\Omega }=\frac{{\mathrm{\Omega }}^{\ast }\nu }{W_o^2},K_r=\frac{K_1\nu }{W_o^2},E_c=\frac{W_o^2}{C_p\left(T_o^{\ast }-T_{\delta }^{\ast }\right)},S_t=\frac{D{K}_T\left(T_o^{\ast }-T_{\delta }^{\ast }\right)}{\nu T_m\left(C_o^{\ast }-C_{\delta }^{\ast }\right)},\\ D_t=\frac{D{K}_T\left(C_o^{\ast }-C_{\delta }^{\ast }\right)}{C_s{C}_p\nu \left(T_o^{\ast }-T_{\delta }^{\ast }\right)}\end{array}\right\}$(12)

Substituting the simplified Equation (10) into (6) and applying the non-dimensional variables (12) in the governing Equations (4)–(7), we have (13) $\begin{array}{rl}& \frac{\mathrm{\partial }\xi }{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }\xi }{\mathrm{\partial }\eta }\\ & =A\epsilon \text{cos}\omega t+\frac{{\mathrm{\partial }}^2\xi }{\mathrm{\partial }{\eta }^2}+2\mathrm{\Omega }v-\left(M+\frac{1}{k_m}\right)\xi +G_h\vartheta \\ & +G_m\varphi -R_n\left(\frac{{\mathrm{\partial }}^3\xi }{\mathrm{\partial }t\mathrm{\partial }{\eta }^2}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{{\mathrm{\partial }}^3\xi }{\mathrm{\partial }{\eta }^3}\right)\text{,}\end{array}$(13) (14) $\begin{array}{rl}& \frac{\mathrm{\partial }v}{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }v}{\mathrm{\partial }\eta }\\ & =\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{\eta }^2}-2\mathrm{\Omega }\xi -\left(M+\frac{1}{k_m}\right)v\\ & -R_n\left(\frac{{\mathrm{\partial }}^{3}v}{\mathrm{\partial }t\mathrm{\partial }{\eta }^2}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{{\mathrm{\partial }}^{3}v}{\mathrm{\partial }{\eta }^3}\right),\end{array}$(14) (15) $\begin{array}{rl}& \frac{\mathrm{\partial }\vartheta }{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }\vartheta }{\mathrm{\partial }\eta }=\left(\frac{1}{P_r}+\frac{4}{3R{P}_r}\right)\frac{{\mathrm{\partial }}^2\vartheta }{\mathrm{\partial }{\eta }^2}-Q\vartheta \\ & +D_t\frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{\eta }^2}+E_c\left({\left(\frac{\mathrm{\partial }\xi }{\mathrm{\partial }\eta }\right)}^2+{\left(\frac{\mathrm{\partial }v}{\mathrm{\partial }\eta }\right)}^2\right),\end{array}$(15) (16) $\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\eta }=\frac{1}{S_c}\frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{\eta }^2}-K_r\varphi +S_t\frac{{\mathrm{\partial }}^2\vartheta }{\mathrm{\partial }{\eta }^2}.$(16) Equations (13) and (14) can be combined by taking $\psi =\xi +iv$, hence Equations (13), (14) and (15) become (17) $\begin{array}{rl}& \frac{\mathrm{\partial }\psi }{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\eta }\\ & =A\epsilon \text{cos}\omega t+\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\eta }^2}-\left(2i\mathrm{\Omega }+N\right)\psi +G_h\vartheta \\ & +G_m\varphi -R_n\left(\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }t\mathrm{\partial }{\eta }^2}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\eta }^3}\right),\end{array}$(17) (18) $\begin{array}{rl}& \frac{\mathrm{\partial }\vartheta }{\mathrm{\partial }t}-\left(1+\epsilon B{e}^{i\omega t}\right)\frac{\mathrm{\partial }\vartheta }{\mathrm{\partial }\eta }\\ & =\left(\frac{1}{P_r}+\frac{4}{3R{P}_r}\right)\frac{{\mathrm{\partial }}^2\vartheta }{\mathrm{\partial }{\eta }^2}-Q\vartheta +D_t\frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{\eta }^2}+E_c\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\eta }\frac{\mathrm{\partial }\overline{\psi }}{\mathrm{\partial }\eta },\end{array}$(18) where $N=M+\frac{1}{k_m}.$The boundary conditions are: (19) $\left.\begin{array}{c}\psi =0,\vartheta =1+\frac{\epsilon }{2}\left({\text{e}}^{i\omega t}+{\text{e}}^{-i\omega t}\right),\varphi =1+\frac{\epsilon }{2}\left({\text{e}}^{i\omega t}+{\text{e}}^{-i\omega t}\right)\\ at\eta =0\\ \psi =1+\frac{\epsilon }{2}\left({\text{e}}^{i\omega t}+{\text{e}}^{-i\omega t}\right),\vartheta =0,\varphi =0at\eta =1\end{array}\right\}$(19) where $\varphi$, $\vartheta$, $\xi$, $M$, $R$, $R_n$, $\mathrm{\Omega }$, $Sc$, $B$, $S_t$, $k_r$, $D_t$, $Pr$, $G_h$, $Gm$, are concentration, temperature, velocity, magnetic parameter, radiation parameter, viscoelasticity parameter, rotation parameter, Schmidt number, suction velocity parameter, Soret number, chemical reaction parameter, Dufour number, Prandtl number, Grashof number for heat and mass transfer, respectively.

3. Method of solution

3.1. Perturbation and Adomian decomposition method

Perturbation technique is used to reduced the partial differential Equations (16), (17) and (18) to ordinary differential equations. Since the ordinary differential equations involve coupled non-linear differential equations and ADM is flexible in handling both linear and non-linear differential equations (Chen and Lu [32]), ADM is applied in solving the equations. With reference to the boundary conditions, the assumed solutions (Garg et al. [30]) can be expressed as follows. (20) $\left.\begin{array}{c}\psi \left(\eta ,t\right)={\psi }_0\left(\eta \right)+\frac{\epsilon }{2}\left({\psi }_1\left(\eta \right)e^{i\omega t}+{\psi }_2\left(\eta \right)e^{-i\omega t}\right)\\ \vartheta \left(\eta ,t\right)={\vartheta }_0\left(\eta \right)+\frac{\epsilon }{2}\left({\vartheta }_1\left(\eta \right)e^{i\omega t}+{\vartheta }_2\left(\eta \right)e^{-i\omega t}\right)\\ \varphi \left(\eta ,t\right)={\varphi }_0\left(\eta \right)+\frac{\epsilon }{2}\left({\varphi }_1\left(\eta \right)e^{i\omega t}+{\varphi }_2\left(\eta \right)e^{-i\omega t}\right)\end{array}\right\}$(20) Applying assumed solutions set (20) to Equations (16), (17) and (18), we have (21) $\begin{array}{r}{R}_n{\psi }_0^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}+{\psi }_0^{\mathrm{\prime \prime }}+{\psi }_0^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N\right){\psi }_0=-G_h{\vartheta }_0-G_m{\varphi }_0,\end{array}$(21) (22) $\begin{array}{rl}& R_n{\psi }_1^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}+\left(1-R_{n}i\omega \right){\psi }_1^{\mathrm{\prime \prime }}+{\psi }_1^{\mathrm{\prime }}-\left(i\omega +2i\mathrm{\Omega }+N\right){\psi }_1\\ & =-A-2B{\psi }_0^{\mathrm{\prime }}-G_h{\vartheta }_1\omega -G_m{\varphi }_1-2R_{n}B{\psi }_0^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}},\end{array}$(22) (23) $\begin{array}{rl}& R_n{\psi }_2^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}+\left(1+R_{n}i\omega \right){\psi }_2^{\mathrm{\prime \prime }}+{\psi }_2^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N-i\omega \right){\psi }_2\\ & =-A-G_h{\vartheta }_2-G_m{\varphi }_2,\end{array}$(23) (24) $F{\vartheta }_0^{\mathrm{\prime \prime }}+{\vartheta }_0^{\mathrm{\prime }}-Q{\vartheta }_0=-E_c{\psi }_0^{\mathrm{\prime }}{\overline{\psi }}_0^{\mathrm{\prime }}-D_t{\varphi }_o^{\mathrm{\prime \prime }},$(24) (25) $\begin{array}{rl}& F{\vartheta }_1^{\mathrm{\prime \prime }}+{\vartheta }_1^{\mathrm{\prime }}-\left(Q+i\omega \right){\vartheta }_1=-2B{\vartheta }_0^{\mathrm{\prime }}-E_c{\psi }_0^{\mathrm{\prime }}{\overline{\psi }}_1^{\mathrm{\prime }}\\ & -E_c{\psi }_1^{\mathrm{\prime }}{\overline{\psi }}_0^{\mathrm{\prime }}-D_t{\varphi }_1^{\mathrm{\prime \prime }},\end{array}$(25) (26) $\begin{array}{r}F{\vartheta }_2^{\mathrm{\prime \prime }}+{\vartheta }_2^{\mathrm{\prime }}-\left(Q-i\omega \right){\vartheta }_2=-E_c{\psi }_0^{\mathrm{\prime }}{\overline{\psi }}_2^{\mathrm{\prime }}-E_c{\psi }_2^{\mathrm{\prime }}{\overline{\psi }}_0^{\mathrm{\prime }}-D_t{\varphi }_2^{\mathrm{\prime \prime }},\end{array}$(26) (27) ${\varphi }_0^{\mathrm{\prime \prime }}+S_c{\varphi }_0^{\mathrm{\prime }}-S_c{K}_r{\varphi }_0=-S_c{S}_t{\vartheta }_0^{\mathrm{\prime \prime }},$(27) (28) ${\varphi }_1^{\mathrm{\prime \prime }}+S_c{\varphi }_1^{\mathrm{\prime }}-S_c\left(K_r+i\omega \right){\varphi }_1=-2B{S}_c{\varphi }_0^{\mathrm{\prime }}-S_c{S}_t{\vartheta }_1^{\mathrm{\prime \prime }},$(28) (29) ${\varphi }_2^{\mathrm{\prime \prime }}+S_c{\varphi }_2^{\mathrm{\prime }}-S_c\left(K_r-i\omega \right){\varphi }_2=-S_c{S}_t{\vartheta }_2^{\mathrm{\prime \prime }},$(29) where $F=\frac{1}{P_r}+\frac{4}{3R{P}_r}.$The boundary conditions reduce to: (30) $\begin{array}{rl}{\psi }_0& ={\psi }_1={\psi }_2=0,{\vartheta }_0={\vartheta }_1={\vartheta }_2=1,{\varphi }_0\\ & ={\varphi }_1={\varphi }_2=1at\eta =0,\end{array}$(30) (31) $\begin{array}{rl}{\psi }_0& ={\psi }_1={\psi }_2=1,{\vartheta }_0\\ & ={\vartheta }_1={\vartheta }_2=0,{\varphi }_0={\varphi }_1={\varphi }_2=0at\eta =1.\end{array}$(31) The third order ordinary differential equations (21), (22) and (23) are of only two boundary conditions. Therefore, to makeup for sufficient and necessary boundary conditions (Garg et al. [30] and Beard and walters [33]), the solutions can be expressed as: (32) $\left.\begin{array}{cc}{\psi }_0\left(\eta \right)& ={\psi }_{01}\left(\eta \right)+R_n{\psi }_{02}\left(\eta \right)+0\left(R_n^2\right)\\ {\psi }_1\left(\eta \right)& ={\psi }_{11}\left(\eta \right)+R_n{\psi }_{12}\left(\eta \right)+0\left(R_n^2\right)\\ {\psi }_2\left(\eta \right)& ={\psi }_{21}\left(\eta \right)+R_n{\psi }_{22}\left(\eta \right)+0\left(R_n^2\right)\\ {\vartheta }_0\left(\eta \right)& ={\vartheta }_{01}\left(\eta \right)+R_n{\vartheta }_{02}\left(\eta \right)+0\left(R_n^2\right)\\ {\vartheta }_1\left(\eta \right)& ={\vartheta }_{11}\left(\eta \right)+R_n{\vartheta }_{12}\left(\eta \right)+0\left(R_n^2\right)\\ {\vartheta }_2\left(\eta \right)& ={\vartheta }_{21}\left(\eta \right)+R_n{\vartheta }_{22}\left(\eta \right)+0\left(R_n^2\right)\\ {\varphi }_0\left(\eta \right)& ={\varphi }_{01}\left(\eta \right)+R_n{\varphi }_{02}\left(\eta \right)+0\left(R_n^2\right)\\ {\varphi }_1\left(\eta \right)& ={\varphi }_{11}\left(\eta \right)+R_n{\varphi }_{12}\left(\eta \right)+0\left(R_n^2\right)\\ {\varphi }_2\left(\eta \right)& ={\varphi }_{21}\left(\eta \right)+R_n{\varphi }_{22}\left(\eta \right)+0\left(R_n^2\right)\end{array}\right\}$(32) Applying equation (32) to equations (21)–(29), we obtain (33) ${\psi }_{01}^{\mathrm{\prime \prime }}+{\psi }_{01}^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N\right){\psi }_{01}=-G_h{\vartheta }_{01}-G_m{\varphi }_{01},$(33) (34) $\begin{array}{r}{\psi }_{02}^{\mathrm{\prime \prime }}+{\psi }_{02}^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N\right){\psi }_{02}=-{\psi }_{01}^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}-G_h{\vartheta }_{02}-G_m{\varphi }_{02},\end{array}$(34) (35) $\begin{array}{rl}& {\psi }_{11}^{\mathrm{\prime \prime }}+{\psi }_{11}^{\mathrm{\prime }}-\left(i\omega +2i\mathrm{\Omega }+N\right){\psi }_{11}\\ & =-A-2B{\psi }_{01}^{\mathrm{\prime }}-G_h{\vartheta }_{11}-G_m{\varphi }_{11},\end{array}$(35) (36) $\begin{array}{rl}& {\psi }_{12}^{\mathrm{\prime \prime }}+{\psi }_{12}^{\mathrm{\prime }}-\left(i\omega +2i\mathrm{\Omega }+N\right){\psi }_{12}\\ & =i\omega {\psi }_{11}^{\mathrm{\prime \prime }}-{\psi }_{11}^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}-2B{\psi }_{02}^{\mathrm{\prime }}\\ & -2B{\psi }_{01}^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}-G_h{\vartheta }_{12}-G_m{\varphi }_{12},\end{array}$(36) (37) $\begin{array}{rl}& {\psi }_{21}^{\mathrm{\prime \prime }}+{\psi }_{21}^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N-i\omega \right){\psi }_{21}\\ & =-A-G_h{\vartheta }_{21}-G_m{\varphi }_{21},\end{array}$(37) (38) $\begin{array}{rl}& {\psi }_{22}^{\mathrm{\prime \prime }}+{\psi }_{22}^{\mathrm{\prime }}-\left(2i\mathrm{\Omega }+N-i\omega \right){\psi }_{22}\\ & =-{\psi }_{21}^{{\mathrm{\prime \prime }}^{\mathrm{\prime }}}-i\omega {\psi }_{21}^{\mathrm{\prime \prime }}-G_h{\vartheta }_{22}-G_m{\varphi }_{22},\end{array}$(38) (39) $F{\vartheta }_{01}^{\mathrm{\prime \prime }}+{\vartheta }_{01}^{\mathrm{\prime }}-Q{\vartheta }_{01}=-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{01}^{\mathrm{\prime \prime }},$(39) (40) $\begin{array}{r}F{\vartheta }_{02}^{\mathrm{\prime \prime }}+{\vartheta }_{02}^{\mathrm{\prime }}-Q{\vartheta }_{02}=-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{02}^{\mathrm{\prime }}-E_c{\psi }_{02}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{02}^{\mathrm{\prime \prime }},\end{array}$(40) (41) $\begin{array}{rl}& F{\vartheta }_{11}^{\mathrm{\prime \prime }}+{\vartheta }_{11}^{\mathrm{\prime }}-\left(Q+i\omega \right){\vartheta }_{11}\\ & =-2B{\vartheta }_{01}^{\mathrm{\prime }}-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{11}^{\mathrm{\prime }}-E_c{\psi }_{11}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{11}^{\mathrm{\prime \prime }},\end{array}$(41) (42) $\begin{array}{rl}& F{\vartheta }_{12}^{\mathrm{\prime \prime }}+{\vartheta }_{12}^{\mathrm{\prime }}-\left(Q+i\omega \right){\vartheta }_{12}\\ & =-2B{\vartheta }_{02}^{\mathrm{\prime }}-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{12}^{\mathrm{\prime }}-E_c{\psi }_{02}^{\mathrm{\prime }}{\overline{\psi }}_{11}^{\mathrm{\prime }}\\ & -E_c{\psi }_{11}^{\mathrm{\prime }}{\overline{\psi }}_{02}^{\mathrm{\prime }}-E_c{\psi }_{12}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{12}^{\mathrm{\prime \prime }},\end{array}$(42) (43) $\begin{array}{rl}& F{\vartheta }_{21}^{\mathrm{\prime \prime }}+{\vartheta }_{21}^{\mathrm{\prime }}-\left(Q-i\omega \right){\vartheta }_{21}\\ & =-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{21}^{\mathrm{\prime }}-E_c{\psi }_{21}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{21}^{\mathrm{\prime \prime }},\end{array}$(43) (44) $\begin{array}{rl}& F{\vartheta }_{22}^{\mathrm{\prime \prime }}+{\vartheta }_{22}^{\mathrm{\prime }}-\left(Q-i\omega \right){\vartheta }_{22}\\ & =-E_c{\psi }_{01}^{\mathrm{\prime }}{\overline{\psi }}_{22}^{\mathrm{\prime }}-E_c{\psi }_{02}^{\mathrm{\prime }}{\overline{\psi }}_{21}^{\mathrm{\prime }}-E_c{\psi }_{21}^{\mathrm{\prime }}{\overline{\psi }}_{02}^{\mathrm{\prime }}\\ & -E_c{\psi }_{22}^{\mathrm{\prime }}{\overline{\psi }}_{01}^{\mathrm{\prime }}-D_t{\varphi }_{22}^{\mathrm{\prime \prime }},\end{array}$(44) (45) ${\varphi }_{01}^{\mathrm{\prime \prime }}+S_c{\varphi }_{01}^{\mathrm{\prime }}-S_c{K}_r{\varphi }_{01}=-S_c{S}_t{\vartheta }_{01}^{\mathrm{\prime \prime }},$(45) (46) ${\varphi }_{02}^{\mathrm{\prime \prime }}+S_c{\varphi }_{02}^{\mathrm{\prime }}-S_c{K}_r{\varphi }_{02}=-S_c{S}_t{\vartheta }_{02}^{\mathrm{\prime \prime }},$(46) (47) ${\varphi }_{11}^{\mathrm{\prime \prime }}+S_c{\varphi }_{11}^{\mathrm{\prime }}-S_c\left(K_r+i\omega \right){\varphi }_{11}=-2B{S}_c{\varphi }_{01}^{\mathrm{\prime }}-S_c{S}_t{\vartheta }_{11}^{\mathrm{\prime \prime }},$(47) (48) ${\varphi }_{12}^{\mathrm{\prime \prime }}+S_c{\varphi }_{12}^{\mathrm{\prime }}-S_c\left(K_r+i\omega \right){\varphi }_{12}=-2B{S}_c{\varphi }_{02}^{\mathrm{\prime }}-S_c{S}_t{\vartheta }_{12}^{\mathrm{\prime \prime }},$(48) (49) ${\varphi }_{21}^{\mathrm{\prime \prime }}+S_c{\varphi }_{21}^{\mathrm{\prime }}-S_c\left(K_r-i\omega \right){\varphi }_{21}=-S_c{S}_t{\vartheta }_{21}^{\mathrm{\prime \prime }},$(49) (50) ${\varphi }_{22}^{\mathrm{\prime \prime }}+S_c{\varphi }_{22}^{\mathrm{\prime }}-S_c\left(K_r-i\omega \right){\varphi }_{22}=-S_c{S}_t{\vartheta }_{22}^{\mathrm{\prime \prime }}$(50) subject to the following boundary conditions: (51) $\left.\begin{array}{cc}{\psi }_{01}& ={\psi }_{02}={\psi }_{11}={\psi }_{12}={\psi }_{21}={\psi }_{22}=0at\eta =0\\ {\psi }_{01}& ={\psi }_{11}={\psi }_{21}=1,{\psi }_{02}={\psi }_{12}={\psi }_{22}=0at\eta =1\\ {\vartheta }_{01}& ={\vartheta }_{11}={\vartheta }_{21}=1,{\vartheta }_{02}={\vartheta }_{12}={\vartheta }_{22}=0at\eta =0\\ {\vartheta }_{01}& ={\vartheta }_{11}={\vartheta }_{21}=0,{\vartheta }_{02}={\vartheta }_{12}={\vartheta }_{22}=0at\eta =1\\ {\varphi }_{01}& ={\varphi }_{11}={\varphi }_{21}=1,{\varphi }_{02}={\varphi }_{12}={\varphi }_{22}=0at\eta =0\\ {\varphi }_{01}& ={\varphi }_{11}={\varphi }_{21}=0,{\varphi }_{02}={\varphi }_{12}={\varphi }_{22}=0at\eta =1\end{array}\right\}$(51) Using ADM, the approximate solutions for Equations (33)–(50), which converges at $b=5$, can be written as: (52) $\left.\begin{array}{c}{\varphi }_{01}=\sum _{b=0}^5{\varphi }_{01}\left[b\right],{\vartheta }_{01}=\sum _{b=0}^5{\vartheta }_{01}\left[b\right];{\psi }_{01}=\sum _{b=0}^5{\psi }_{01}\left[b\right],\\ {\varphi }_{02}=\sum _{b=0}^5{\varphi }_{02}\left[b\right],{\vartheta }_{02}=\sum _{b=0}^5{\vartheta }_{02}\left[b\right];{\psi }_{02}=\sum _{b=0}^5{\psi }_{02}\left[b\right],\\ {\varphi }_{11}=\sum _{b=0}^5{\varphi }_{11}\left[b\right],{\vartheta }_{11}=\sum _{b=0}^5{\vartheta }_{11}\left[b\right];{\psi }_{11}=\sum _{b=0}^5{\psi }_{11}\left[b\right],\\ {\varphi }_{12}=\sum _{b=0}^5{\varphi }_{12}\left[b\right],{\vartheta }_{12}=\sum _{b=0}^5{\vartheta }_{12}\left[b\right];{\psi }_{12}=\sum _{b=0}^5{\psi }_{12}\left[b\right],\\ {\varphi }_{21}=\sum _{b=0}^5{\varphi }_{21}\left[b\right],{\vartheta }_{21}=\sum _{b=0}^5{\vartheta }_{21}\left[b\right];{\psi }_{21}=\sum _{b=0}^5{\psi }_{21}\left[b\right],\\ {\varphi }_{22}=\sum _{b=0}^5{\varphi }_{22}\left[b\right],{\vartheta }_{22}=\sum _{b=0}^5{\vartheta }_{22}\left[b\right];{\psi }_{22}=\sum _{b=0}^5{\psi }_{22}\left[b\right]\end{array}\right\}$(52) Using the series solutions (52) in Equations (20) and (32), the final solutions for velocity, temperature and concentration distributions are (53) $\begin{array}{rl}\psi \left(\eta ,t\right)& =\sum _{b=0}^5{\psi }_{01}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\psi }_{02}\left[b\right]\left(\eta \right)\\ & +\frac{\epsilon }{2}\left(\left(\sum _{b=0}^5{\psi }_{11}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\psi }_{12}\left[b\right]\left(\eta \right)\right)e^{i\omega t}\right.\\ & \left.+\left(\sum _{b=0}^5{\psi }_{21}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\psi }_{22}\left[b\right]\left(\eta \right)\right)e^{-i\omega t},\right)\end{array}$(53) (54) $\begin{array}{rl}\vartheta \left(\eta ,t\right)& =\sum _{b=0}^5{\vartheta }_{01}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\vartheta }_{02}\left[b\right]\left(\eta \right)\\ & +\frac{\epsilon }{2}\left(\left(\sum _{b=0}^5{\vartheta }_{11}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\vartheta }_{12}\left[b\right]\left(\eta \right)\right)e^{i\omega t}\right.\\ & \left.+\left(\sum _{b=0}^5{\vartheta }_{21}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\vartheta }_{22}\left[b\right]\left(\eta \right)\right)e^{-i\omega t}\right),\end{array}$(54) (55) $\begin{array}{rl}\varphi \left(\eta ,t\right)& =\sum _{b=0}^5{\varphi }_{01}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\varphi }_{02}\left[b\right]\left(\eta \right)\\ & +\frac{\epsilon }{2}\left(\left(\sum _{b=0}^5{\varphi }_{11}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\varphi }_{12}\left[b\right]\left(\eta \right)\right)e^{i\omega t}\right.\\ & \left.+\left(\sum _{b=0}^5{\varphi }_{21}\left[b\right]\left(\eta \right)+R_n\sum _{b=0}^5{\varphi }_{22}\left[b\right]\left(\eta \right)\right)e^{-i\omega t}\right).\end{array}$(55)

3.2. Skin friction, Nusselt and Sherwood number in term of amplitude

With reference to the boundary conditions, the amplitude is defined in terms of primary and secondary velocities for steady and unsteady flow. Therefore, total resultant velocity can be written as; (56) $R_v=\sqrt{c^2+d^2},$(56) where velocity is defined as (57) $\psi \left(\eta ,t\right)=c+id.$(57)

The Skin friction is given as; (58) $\tau \left(\eta \right)={\left(\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\eta }\right)}_{\eta =0,1}={\tau }_a+i{\tau }_b,$(58) (59) ${\beta }_1=\sqrt{{\tau }_a^2+{\tau }_b^2}.$(59)

Nusselt number (Heat transfer coefficient) is defined as; (60) $Nu\left(\eta \right)=-\left(1+\frac{4}{3R}\right){\left(\frac{\mathrm{\partial }\vartheta }{\mathrm{\partial }\eta }\right)}_{\eta =0,1}={\beta }_a+i{\beta }_b,$(60) (61) ${\beta }_2=\sqrt{{\beta }_a^2+{\beta }_b^2}.$(61)

Sherwood Number(Mass transfer coefficient) is expressed as: (62) $Sh\left(\eta \right)={\left(\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\eta }\right)}_{\eta =0,1}={\delta }_a+i{\delta }_b,$(62) (63) ${\beta }_3=\sqrt{{\delta }_a^2+{\delta }_b^2}.$(63)

4. Discussion of results

The partial differential equations (16), (17) and (18) with the boundary conditions (19) are solved using ADM with the aid of MATHEMATICA software. The computations for various parameters in the governing equations are examined for velocity, temperature and concentration profiles and the effects are presented graphically. Some of the parameters considered are: Suction velocity parameter $B$, dimensionless viscoelasticity parameter of the Rivlin–Ericksen fluid $R_n$, magnetic parameter $M$, radiation parameter $R$, Prandtl number $P_r$, Schmidt number $S_c$, dimensionless heat absorption coefficient $Q$, Grashof number for heat transfer $G_h$, Grashof number for mass transfer $G_m$, scalar constant $\epsilon$, permeability of the porous medium $k_m$, chemical reaction parameter $K_r$, rotation parameter $\mathrm{\Omega }$, dissipation parameter $E_c$, Dufour parameter $D_t$ and Soret parameter $S_t$. The default values for the computations are: $G_h=G_m=M=5,t=1,R_n=0.05,P_r=0.71,Q=0.005,R=3$, $B=k_m=0.5,kr=2,n=0.9,$ $S_c=1.002$, $\epsilon =0.01$, $\mathrm{\Omega }=10$, $S_t=2$, $D_t=0.1$ and $E_c=0.002$.

In order to validate the current ADM method, the numerical results are compared with fourth order Runge-Kutta method with shooting technique for skin friction at $\eta =0$ as shown in Table 1, where D is the difference between ADM and 4th Order R–K.

Table 1. Comparison of Skin friction for various values of $S_c$, $P_r$, $M$, $G_h$, $G_m$, $Q$, $K_r$ and $R$.

$S_c$	$P_r$	$M$	$G_h$	$G_m$	$Q$	$K_r$	$R$	ADM	4th Order R–K	$\left|D\right|$
1.5	0.71	5	5	5	0.005	2	3	3.02608	3.02607	0.00001
1.0	0.71	5	5	5	0.005	2	3	2.90833	2.90847	0.00014
1.5	0.71	5	5	5	0.005	2	3	2.80761	2.80914	0.00153
1.002	0.5	5	5	5	0.005	2	3	2.92964	2.92977	0.00013
1.002	0.9	5	5	5	0.005	2	3	2.88813	2.88828	0.00015
1.002	1.3	5	5	5	0.005	2	3	2.84626	2.84656	0.0003
1.002	0.71	1.5	5	5	0.005	2	3	3.57819	3.57872	0.00053
1.002	0.71	2.5	5	5	0.005	2	3	3.35114	3.35153	0.00039
1.002	0.71	3.5	5	5	0.005	2	3	3.15537	3.15563	0.00026
1.002	0.71	5	2	5	0.005	2	3	2.16128	2.16142	0.00014
1.002	0.71	5	4	5	0.005	2	3	3.65903	3.65916	0.00013
1.002	0.71	5	6	5	0.005	2	3	3.15677	3.15691	0.00014
1.002	0.71	5	5	2	0.005	2	3	2.27213	2.27218	0.00005
1.002	0.71	5	5	4	0.005	2	3	2.69598	2.69608	0.0001
1.002	0.71	5	5	6	0.005	2	3	3.11983	3.12000	0.00017
1.002	0.71	5	5	5	0.003	2	3	2.90797	2.90811	0.00014
1.002	0.71	5	5	5	0.03	2	3	2.90702	2.90716	0.00014
1.002	0.71	5	5	5	0.3	2	3	2.89766	2.89779	0.00013
1.002	0.71	5	5	5	0.005	0.5	3	2.98536	2.98566	0.0003
1.002	0.71	5	5	5	0.005	1.5	3	2.93171	2.93191	0.0002
1.002	0.71	5	5	5	0.005	2.5	3	2.88578	2.88586	0.00008
1.002	0.71	5	5	5	0.005	2	2	2.91772	2.91785	0.00013
1.002	0.71	5	5	5	0.005	2	4	2.90175	2.90189	0.00014
1.002	0.71	5	5	5	0.005	2	6	2.89448	2.89462	0.00014

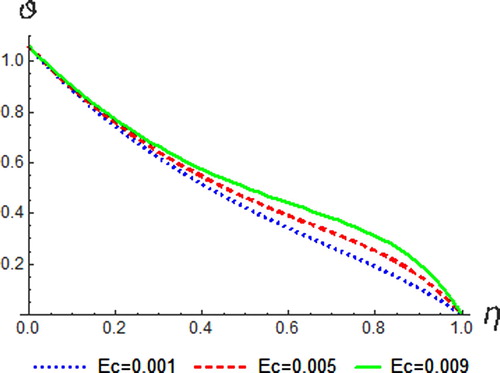
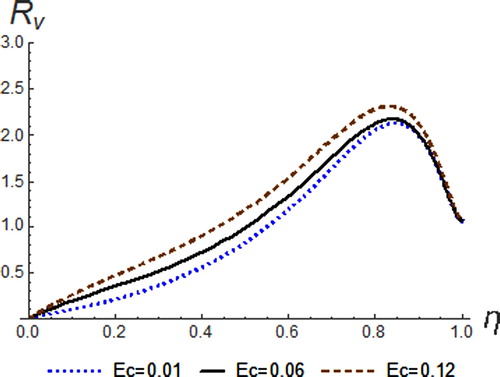
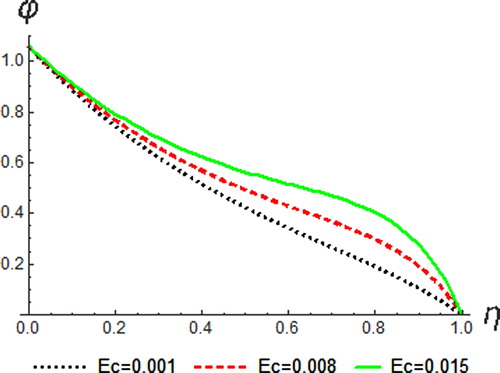
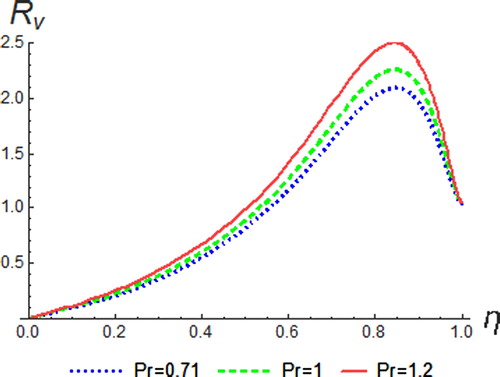
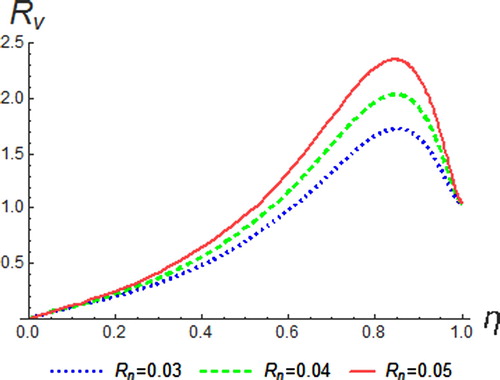
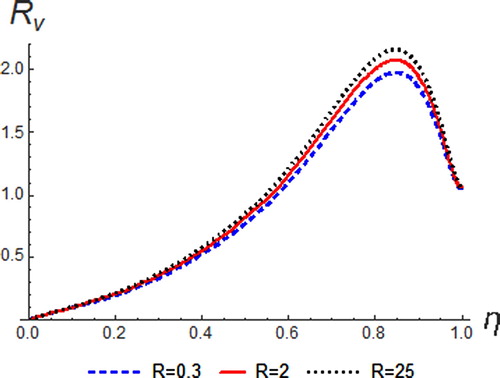
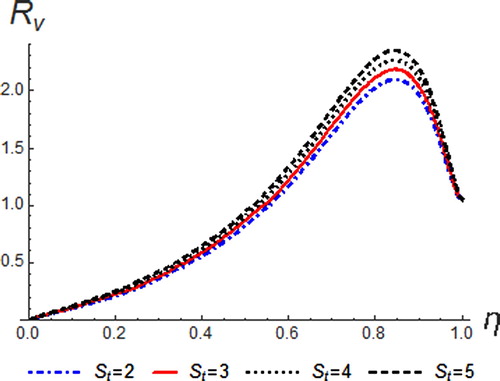
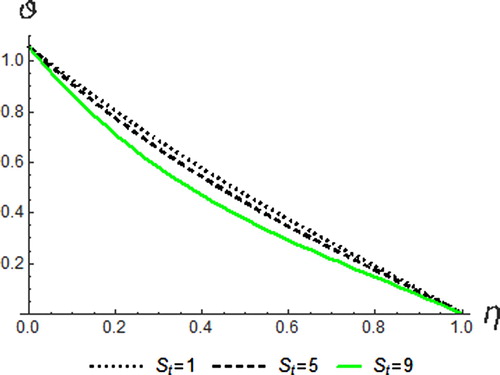
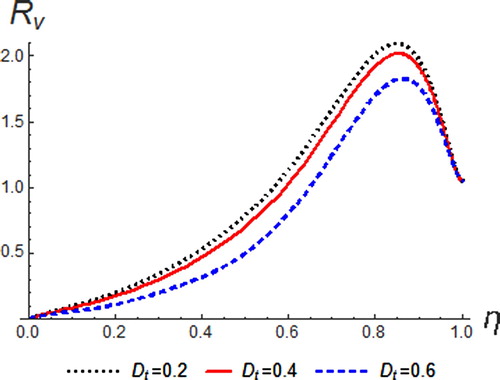
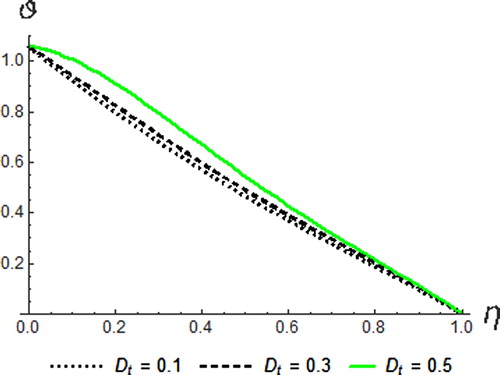
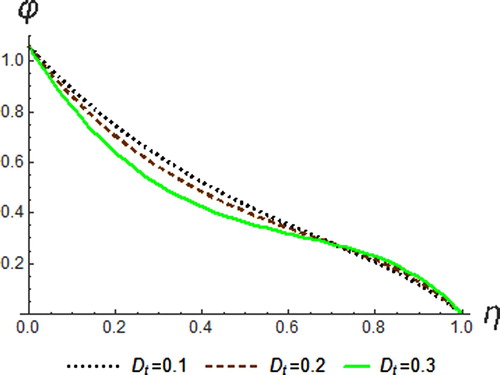
The variation of Eckert number on the temperature, velocity and concentration profile is shown in Figures 2–4. Eckert number $E_c$ is the ratio of the kinetic energy of the fluid flow to enthalpy. Thus, energy increases due to the dissipation effect on the flow leading to higher fluid temperature and increase in buoyancy force. This effectually enhances the temperature profile. Physically, dissipative heat as a result of elastic and viscosity deformation resulted in energy storage within the region of the fluid. Therefore, it can be seen that an increase in the values of $E_c$ enhances temperature, resultant velocity and concentration profiles.

Figure 2. Temperature profiles for different values of $Ec$.

Figure 3. Resultant velocity profiles for different values of $Ec$.

Figure 4. Concentration profiles for different values of $Ec$.

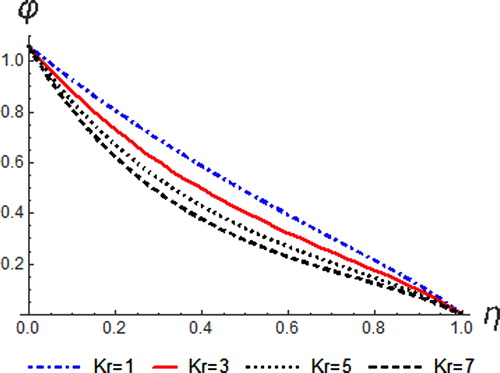
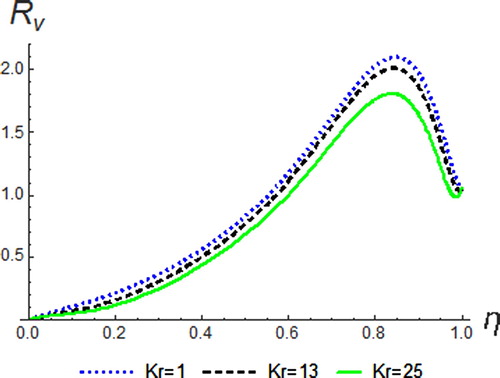
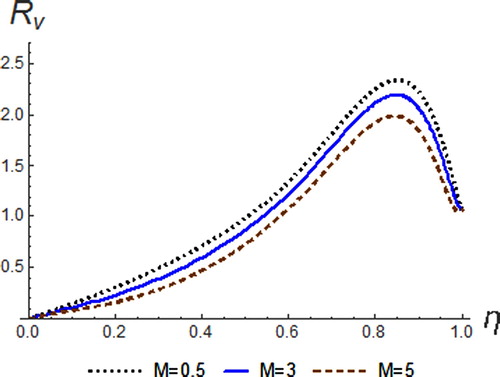
Figures 5 and 6 reveal the variation of $K_r$ on concentration and velocity. It is noticed that increasing values of $K_r$ tends to reduce both velocity and concentration distributions. The effect of $M$ on velocity is shown in Figure 7. It is noticed that an increase in the $M$ resulted in a significant decrease in the flow velocity throughout the domain of the fluid. A drag force called Lorentz force is produced in electrically conducting fluid where the magnetic field is applied. There is a reduction in the velocity of the fluid due to this force, because fluid transport is opposed as a result of the magnetic field.

Figure 5. Concentration profiles for different values of $K_r$.

Figure 6. Resultant velocity profiles for different values of $K_r$.

Figure 7. Resultant velocity profiles for different values of $M$.

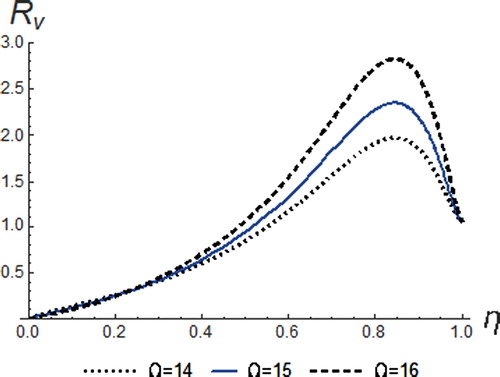
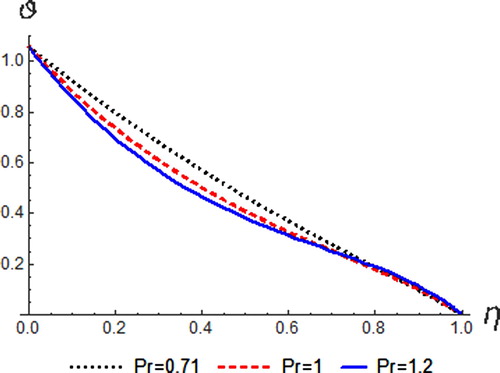
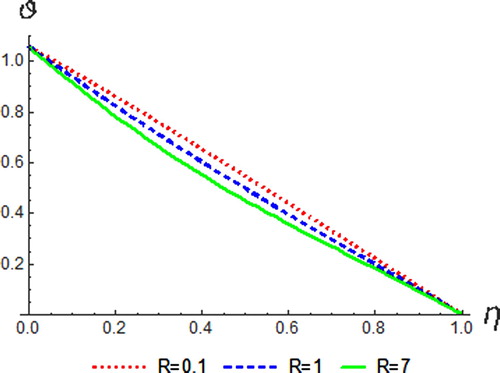
Figure 8 depicts the effect of rotation parameter $\mathrm{\Omega }$ on resultant velocity. Resultant velocity profiles are enhanced with the increasing values of the rotation parameter. Furthermore, the effects of Prandtl number $P_r$ on temperature and resultant velocity are observed in Figures 9 and 10, respectively. An increase in Prandtl number results in an increase in resultant velocity and a decline of the temperature distribution profiles. At $\eta =0.77$, a rise in fluid temperature is noticed. This is based on the fact that fluids with high Prandtl is of low thermal diffusivity and resulted to low heat penetration, hence the thermal boundary layer is reduced.

Figure 8. Resultant velocity profiles for different values of $\mathrm{\Omega }$.

Figure 9. Temperature profiles for different values of $Pr$.

Figure 10. Resultant velocity profiles for different values of $Pr$.

The effect of viscoelastic parameter $R_n$ and radiation parameter $R$ on resultant velocity is illustrated in Figures 11 and 12 respectively. It is observed that resultant velocity is enhanced by an increase in viscoelastic parameter $R_n$ and radiation parameter $R$, while the reverse effect of $R$ on temperature is shown in Figure 13. This implies that an increase in radiation parameter $R$ makes temperature profile to decrease.

Figure 11. Resultant velocity profiles for different values of $R_n$.

Figure 12. Resultant velocity profiles for different values of $R$.

Figure 13. Temperature profiles for different values of $R$.

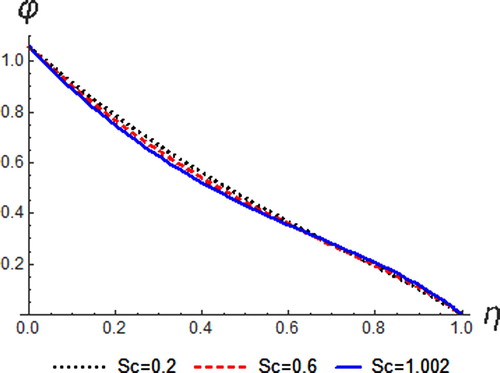
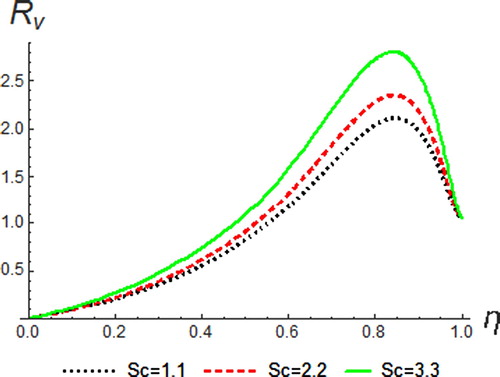
Variation of $S_c$ on concentration and resultant velocity profiles is depicted in Figures 14 and 15 respectively. The Schmidt number $S_c$ characterizes momentum diffusivity and mass diffusivity. Species diffusivity rate transcend momentum diffusivity for higher values of $S_c,$ thus decreases the concentration distribution. Physically, increasing $Sc$ makes the concentration boundary layer to become relatively thinner compared to the momentum boundary layer. Therefore, species concentration for low values of $S_c$ is higher while resultant velocity is enhanced with the increase in the values of Sc.

Figure 14. Concentration profiles for different values of $Sc$.

Figure 15. Resultant velocity profiles for different values of $Sc$.

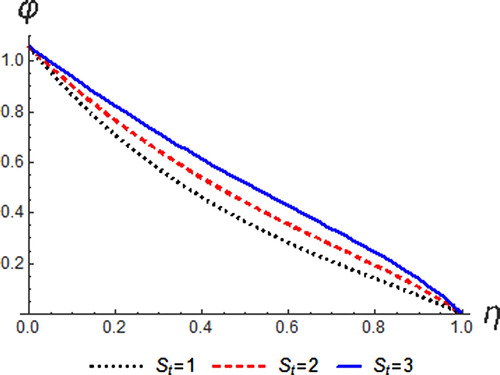
Effects of Soret on concentration, resultant velocity and temperature profiles are shown in Figures 16–18 respectively. It is noted that increasing the values of Soret parameter tend to increase both concentration and resultant velocity of the fluid. The fluid temperature reduces with a rise in Soret parameter $S_t.$

Figure 16. Concentration profiles for different values of $S_t$.

Figure 17. Resultant velocity profiles for different values of $S_t$.

Figure 18. Temperature profiles for different values of $S_t$.

The effect of Dufour parameter $D_t$ on resultant velocity, temperature and concentration profiles is presented in Figures 19–21 respectively. Diffusion-thermo expresses the contribution of concentration gradient to energy flux within the fluid. Resultant velocity profiles decelerated with an increase in Dufour parameter $D_t$, while temperature profiles are enhanced. This is due to the fact that generation of energy flux increased the fluid temperature. A rise in Dufour parameter $D_t$ resulted in the decrease in the concentration profiles; a different trend is noticed at $\eta =0.73$.

Figure 19. Resultant velocity profiles for different values of $D_t$.

Figure 20. Temperature profiles for different values of $D_t$.

Figure 21. Concentration profiles for different values of $D_t$.

The variation of fluid parameters ($K_r$, $R$, $\mathrm{\Omega }$, $S_t$, $D_t$, $R_n$ and $E_c$) on Skin friction, Nusselt number and Sherwood number is presented in Table 2. At $\eta =0$, it is observed that an increase in $K_r$, $\mathrm{\Omega }$, $D_t$ and $R_n$ resulted in decreasing the skin friction. While, $R$, $S_t$ and $E_c$ enhance the value of the skin friction. Nusselt number decelerated with an increase in $K_r$, $R$, $\mathrm{\Omega }$, $D_t$ and $E_c$. While an increase in the values of $S_t$ and $R_n$ makes Nusselt number to increase. Sherwood number increases with an increase in $K_r$ and $D_t$. On the other hand, increasing $R$, $\mathrm{\Omega }$, $S_t$, $R_n$ and $E_c$ decrease the Sherwood number. Likewise at $\eta =1$, Skin friction is reduced by increasing $D_t$ and increases with an increase in $K_r$, $R$, $\mathrm{\Omega }$, $S_t$, $R_n$ and $E_c$. Nusselt number is enhanced with an increase in $K_r$, $\mathrm{\Omega }$, $E_c$ and $D_t$ but decreases with an increase in the values of $R$, $S_t$ and $R_n$. Consequently, increase in $R$, $S_t$, $E_c$ and $\mathrm{\Omega }$ accelerate Sherwood number, while it is reduced by the values of $K_r$ and $R_n$.

Table 2. Values of skin friction, Nusselt number and Sherwood number for different parameters at $\eta =0$ and $\eta =1$.

$K_r$	$R$	$\mathrm{\Omega }$	$S_t$	$D_t$	$E_c$	$R_n$	$\tau \left(\eta =0\right)$	$Nu\left(\eta =0\right)$	$Sh\left(\eta =0\right)$	$\tau \left(\eta =1\right)$	$Nu\left(\eta =1\right)$	$Sh\left(\eta =1\right)$
1	3	15	2		0.002	0.05	1.28158	2.06081	1.48037	31.08480	1.39350	1.43100
2	3	15	2	0.1	0.002	0.05	1.24665	1.99652	1.85324	31.19390	1.42954	1.40590
3	3	15	2	0.1	0.002	0.05	1.21614	1.93783	2.18230	31.31120	1.46313	1.38315
2	2	15	2	0.1	0.002	0.05	1.24178	2.19274	1.98868	30.94580	1.66172	1.27095
2	3	15	2	0.1	0.002	0.05	1.24665	1.99652	1.85324	31.19390	1.42954	1.40590
2	4	15	2	0.1	0.002	0.05	1.24970	1.89784	1.76868	31.35560	1.31711	1.49187
2	3	10	2	0.1	0.002	0.05	2.32384	2.01221	1.86317	10.02990	1.45777	1.29769
2	3	12	2	0.1	0.002	0.05	1.93356	1.99753	1.85481	15.87190	1.50358	1.38090
2	3	14	2	0.1	0.002	0.05	1.49398	1.99173	1.85117	24.89770	1.53651	1.41584
2	3	15	0.5	0.1	0.002	0.05	1.16736	1.91194	2.38356	30.57180	1.44613	0.61153
2	3	15	1	0.1	0.002	0.05	1.19455	1.93549	2.21733	30.74620	1.44597	0.85306
2	3	15	1.5	0.1	0.002	0.05	1.22109	1.96384	2.03993	30.95440	1.44017	1.11887
2	3	15	2	0.2	0.002	0.05	1.25449	1.84645	2.21936	30.66590	1.51392	1.60648
2	3	15	2	0.3	0.002	0.05	1.23724	1.60984	2.81811	30.08070	1.60264	1.60648
2	3	15	2	0.4	0.002	0.05	1.19540	1.19349	3.76191	29.37610	1.67770	2.32727
2	3	15	2	0.1	0.001	0.05	1.23903	2.02584	1.87006	31.18790	1.47918	1.20417
2	3	15	2	0.1	0.002	0.05	1.24665	1.99652	1.85324	31.19390	1.67770	1.40590
2	3	15	2	0.1	0.003	0.05	1.25430	1.96722	1.83656	31.19950	1.88337	1.60709
2	3	15	2	0.1	0.002	0.03	1.28689	1.99421	1.85354	22.57930	1.68641	1.42355
2	3	15	2	0.1	0.002	0.04	1.26364	1.99536	1.85338	26.85770	1.68201	1.41390
2	3	15	2	0.1	0.002	0.05	1.24665	1.99652	1.85324	31.19390	1.67770	1.40590

5. Conclusion

An analysis of the combined effects of chemical reaction, thermal radiation, rotatory, thermal-diffusion (Soret), diffusion-thermo (Dufour) and viscous dissipation on convective Rivlin–Ericksen flow of an incompressible and electrically conducting fluids past a porous vertical plate with a time-dependence suction is studied. The governing equations are non-dimensionalised and the solutions are obtained using Adomian decomposition method. The impacts of different parameters on velocity, temperature, concentration, skin friction, Nusselt number and Sherwood number are illustrated both in tabular and graphical form. The results revealed that both resultant velocity and temperature of the fluid are enhanced with an increase in viscous dissipation parameter. Skin friction is strengthened with an increase in Eckert number, while both Nusselt and Sherwood numbers are weakened with an increase in dissipation parameter at $\eta =0$. Also, Skin friction, Nusselt number and Sherwood number are enhanced at $\eta =1$ with increase in viscous dissipation. The result is useful due to its application in controlling the rate of cooling of advanced energy convection systems which operate at high temperature.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

S. A. Agunbiade http://orcid.org/0000-0003-3882-0357

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.