Number of spanning trees of some families of graphs generated by a triangle

ABSTRACT

In mathematics, one always tries to get new structures from given ones. This also applies to the realm of graphs, where one can generate many new graphs from a given set of graphs. In this paper, we derive simple formulas of spanning trees of some families of graphs generated by triangle using linear algebra and the knowledge of difference equations. Finally, we compare the entropy of our graphs with other studied graphs with the average degree being 4 and 6.

KEYWORDS:

• Number of spanning trees
• matrix tree theorem
• recurrence relation

MATHEMATICS SUBJECT CLASSIFICATIONS:

• 05C05
• 05C50

1. Introduction

The problem of calculating the number of spanning trees on the graph $G$ is an important, well-studied problem in graph theory. Deriving formulas for different types of graphs can be proved to be helpful in identifying those graphs that contain the maximum number of spanning trees. Such an investigation has practical consequences related to the network. Thus for both theoretical and practical purpose, we interested to deriving formulas for the number of spanning trees of a graph based on its time complexity in order to calculate the formula. Many cases have been examined depending on the choice of $G$. It has been studied when $G$ is labelled molecular graph [1], when $G$ is a circulant graph [2], when $G$ is a complete multipartite graph [3], when $G$ is a cubic cycle and quadruple cycle graph [4], when $G$ is a threshold graph [5] and so on. A spanning tree of $G$ is a minimal connected subgraph of $G$ that has the same vertex set as $G$. The number of spanning trees in $G$, also called, the complexity of the graph, denoted by $\tau \left(G\right)$. A classical result of Kirchhoff [6] can be used to determine the number of spanning trees for $G=(V,E)$. Let $V=\{v_1,v_2,\dots ..,v_n\}$, then the Kirchhoff matrix $H$ defined as $n\times n$ characteristic matrix $H=D-A$, where $D$ is the diagonal matrix of the degrees of $G$ and $A$ is the adjacency matrix of $G$, $H=\left[a_{ij}\right]$ defined as follows: (i) $a_{ij}=-1,$ $v_i$ and $v_j$ are adjacent and $i\ne j$, (ii) $a_{ij}$ equals the degree of vertex $v_i$ if $i=j$, and (iii) $a_{ij}=0$ otherwise. All of cofactors of $H$ are equal to $\tau \left(G\right)$.

There are other methods for calculating $\tau \left(G\right)$. Let ${\mu }_1\ge {\mu }_1\ge \dots \dots .\ge {\mu }_p$ denote the eignvalues of $H$ matrix of a $p$ point graph. Then, it is easily shown that ${\mu }_p=0$. Furthermore, Kelmans and Chelnokov [7] shown that $\tau \left(G\right)=\frac{1}{p}\prod _{k=1}^{p-1}{\mu }_k$. The formula for the number of spanning trees in a $d$-regular graph $G$ can be expressed as $\tau \left(G\right)=\frac{1}{p}\prod _{k=1}^{p-1}(d-{\lambda }_k)$, where ${\lambda }_0=d,{\lambda }_1,{\lambda }_2,\dots \dots .,{\lambda }_{p-1}$ are the eigenvalues of the corresponding adjacency matrix of the graph. However, for a few special families of graphs, there exist simple formulas that make it much easier to calculate and determine the number of corresponding spanning trees, especially when these numbers are very large.

One of the first such results is due to Cayley [8] showed that complete graph on $n$ vertices, $K_n$, has $n^{n-2},n\ge 2$ spanning trees. Another result, the complete bipartite graph $K_{p,q}$ with bipartite sets containing $p$ and $q$ vertices has $p^{q-1}{q}^{p-1},p,q\ge 1$ spanning trees [9,10]. Another result is due to Sedlacek [11] derived a formula for the wheel with $n+1$ vertices, $W_{n+1}$, has $(\frac{3+\sqrt{5}}{2}{)}^n+(\frac{3-\sqrt{5}}{2}{)}^n-2,n\ge 2$ spanning trees. Sedlacek [12] also later derived a formula for the number of spanning trees in a Mobius ladder with $n$ vertices,$M_n$, has $\frac{n}{2}[(2+\sqrt{3}{)}^n+(2-\sqrt{3}{)}^n+2],n\ge 2$ spanning trees.

Another class of graphs for which an explicit formula has been derived is based on a prism [13,14].

Many works have conceived techniques to derive the number of spanning tree of a graph, which can be found at [15–23].

Now we introduce following Lemma which describes a way to calculate the number of spanning trees by an extension of Kirchhoff formula.

Lemma 1.1

[24]

Let $G$ be a graph with $n$ vertices. Then $\tau \left(G\right)=\frac{1}{n^2}det(nI-\overline{D}+\overline{A})$where $\overline{A},\overline{D}$ are the adjacency and degree matrices of $\overline{G}$, the complement of $G$, respectively, and $I$ is the $n\times n$ unit matrix.

The advantage of this formula in Lemma1.1 is to express $\tau \left(G\right)$ directly as a determinant rather than in terms of cofactors as in Kirchhoff theorem or eigenvalues as in Kelmans and Chelnokov formula.

2. Main results

In mathematics, one always tries to get new structures from given ones. This also applies to the realm of graphs, where one can generate many new graphs from a given set of graphs. In this section, we derive simple formulas of the complexity, number of spanning trees, of four families of graphs generated by a triangle say $G_n,H_n,X_n$ and $Y_n$.

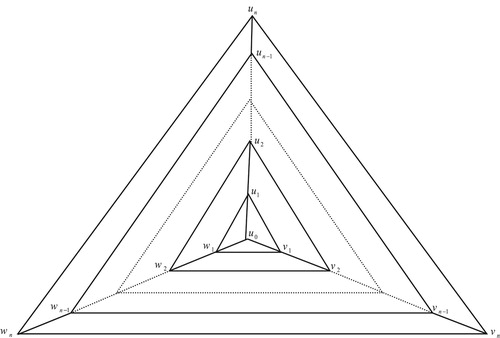
Consider the family of graphs $G_n$ generated by triangle and constructed as shown in Figure 1.

Figure 1. The graph $G_n$.

According to the construction, the number of total vertices $|V\left(G_n\right)|$ and edges $|E\left(G_n\right)|$ are $|V\left(G_n\right)|=3n+1$ and $|E\left(G_n\right)|=6n,n=1,2,\dots$.

It is clear that the average degree of $G_n$ is in the large $n$ limit is $4$.

Theorem 2.1:

For $n\ge 1$, the number of spanning trees of the graph $G_n$ is given by $\begin{array}{rl}& \left[\left(\frac{7+\sqrt{21}}{14}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^n+\left(\frac{7-\sqrt{21}}{14}\right)\right.\\ & {\left.{\left(\frac{5-\sqrt{21}}{2}\right)}^n\right]}^2.\end{array}$Proof: The Kirchhoff matrix associated to the graph $G_n$ is

$\begin{array}{r}H=\left(\begin{array}{ccccccccc}3& -1& 0& \cdots & \cdots & 0& -1& 0& \cdots \\ -1& 4& -1& 0& \cdots & 0& -1& 0& \cdots \\ 0& -1& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ ⋮& 0& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ ⋮& ⋮& \ddots & \ddots & 4& -1& ⋮& \ddots & \ddots \\ 0& 0& \cdots & 0& -1& 3& 0& \cdots & \cdots \\ -1& -1& 0& \cdots & \cdots & 0& 4& -1& 0\\ 0& 0& \ddots & \ddots & \ddots & ⋮& -1& \ddots & \ddots \\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ ⋮& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ 0& 0& \cdots & \cdots & 0& -1& 0& \cdots & 0\\ -1& -1& 0& \cdots & \cdots & 0& -1& 0& \cdots \\ 0& 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮& ⋮& \ddots & \ddots \\ ⋮& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ 0& 0& \cdots & \cdots & 0& -1& 0& \cdots & \cdots \end{array}\right.\\ \left.\begin{array}{ccccccc}\cdots & 0& -1& 0& \cdots & \cdots & 0\\ \cdots & 0& -1& 0& \cdots & \cdots & 0\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0\\ \cdots & -1& 0& \cdots & \cdots & 0& -1\\ \cdots & 0& -1& 0& \cdots & \cdots & 0\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& \ddots & \ddots & \ddots & ⋮\\ 4& -1& ⋮& \ddots & \ddots & \ddots & 0\\ -1& 3& 0& \cdots & \cdots & 0& -1\\ \cdots & 0& 4& -1& 0& \cdots & 0\\ \ddots & ⋮& -1& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & 0\\ \ddots & 0& ⋮& \ddots & \ddots & 4& -1\\ 0& -1& 0& \cdots & 0& -1& 3\end{array}\right)\end{array}$

Thus, we get: $\begin{array}{r}\tau \left(G_n\right)=\left(\begin{array}{cccccccc}4& -1& 0& \cdots & 0& -1& 0& \cdots \\ -1& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ 0& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ ⋮& \ddots & \ddots & 4& -1& ⋮& \ddots & \ddots \\ 0& \cdots & 0& -1& 3& 0& \cdots & \cdots \\ -1& 0& \cdots & \cdots & 0& 4& -1& 0\\ 0& \ddots & \ddots & \ddots & ⋮& -1& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ 0& \cdots & \cdots & 0& -1& 0& \cdots & 0\\ -1& 0& \cdots & \cdots & 0& -1& 0& \cdots \\ 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & ⋮& ⋮& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots \\ 0& \cdots & \cdots & 0& -1& 0& \cdots & \cdots \end{array}\right.\\ \left.\begin{array}{cccccc}0& -1& 0& \cdots & \cdots & 0\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0\\ \cdots & -1& 0& \cdots & \cdots & 0& -1\\ \cdots & 0& -1& 0& \cdots & \cdots & 0\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ \ddots & 0& ⋮& \ddots & \ddots & \ddots & ⋮\\ 4& -1& ⋮& \ddots & \ddots & \ddots & 0\\ -1& 3& 0& \cdots & \cdots & 0& -1\\ \cdots & 0& 4& -1& 0& \cdots & 0\\ \ddots & ⋮& -1& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& 0& \ddots & \ddots & \ddots & 0\\ \ddots & 0& ⋮& \ddots & \ddots & 4& -1\\ 0& -1& 0& \cdots & 0& -1& 3\end{array}\right)\end{array}$

Then we have $\tau \left(G_n\right)=det\left(\begin{array}{ccc}A& B& B\\ B& A& B\\ B& B& A\end{array}\right)=[det(A-B){]}^2[det(A+2B\left)\right]$ $\begin{array}{rl}& =(det\left(\begin{array}{ccccc}5& -1& 0& \cdots & 0\\ -1& 5& \ddots & \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & 5& -1\\ 0& \cdots & 0& -1& 4\end{array}\right){)}^2\\ & \times det\left(\begin{array}{ccccc}2& -1& 0& \cdots & 0\\ -1& 2& \ddots & \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & 2& -1\\ 0& \cdots & 0& -1& 1\end{array}\right)\end{array}$Straightforward induction using properties of determinants, we have $det(A+2B)=1$, and by expanding the first five determinants of the matrix $A-B$, yields

$det(A-B)$ has the values $4,19,91,436,2089,\dots$ for $n=1,2,3,4,5,\dots$

These values can be written in the form: $\begin{array}{rl}& 4=5\times 1-1,\\ & 19=5\times 4-1,\\ & 91=5\times 19-4,\\ & 436=5\times 91-19,\\ & 2089=5\times 436-91,\dots \dots .\end{array}$Thus we have the following recurrence relation (1) $a_{n+2}=5a_{n+1}-a_n.$(1) Its characteristic Equation is $r^2-5r+1=0$ with two roots being $\frac{5+\sqrt{21}}{2}$ and $\frac{5-\sqrt{21}}{2}$.

The general solution of the recurrence relation (1) is $det(A-B)=\alpha {\left(\frac{5+\sqrt{21}}{2}\right)}^n+\beta {\left(\frac{5-\sqrt{21}}{2}\right)}^n$Using the initial condition $det(A-B)=4$ and $det(A-B)=19$ at $n=1\text{and}2$, respectively. We have $4=\alpha \left(\frac{5+\sqrt{21}}{2}\right)+\beta \left(\frac{5-\sqrt{21}}{2}\right),$ $19=\alpha {\left(\frac{5+\sqrt{21}}{2}\right)}^2+\beta {\left(\frac{5-\sqrt{21}}{2}\right)}^2$Solving these equations, we get $\alpha =\frac{7+\sqrt{21}}{14}$ and $\beta =\frac{7-\sqrt{21}}{14}$, therefore $\begin{array}{rl}det(A-B)& =\left(\frac{7+\sqrt{21}}{14}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^n\\ & +\left(\frac{7-\sqrt{21}}{14}\right){\left(\frac{5-\sqrt{21}}{2}\right)}^n.\end{array}$Thus $\begin{array}{rl}\tau \left(G_n\right)& =\left[\left(\frac{7+\sqrt{21}}{14}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^n\right.\\ & {\left.+\left(\frac{7-\sqrt{21}}{14}\right){\left(\frac{5-\sqrt{21}}{2}\right)}^n\right]}^2.\end{array}$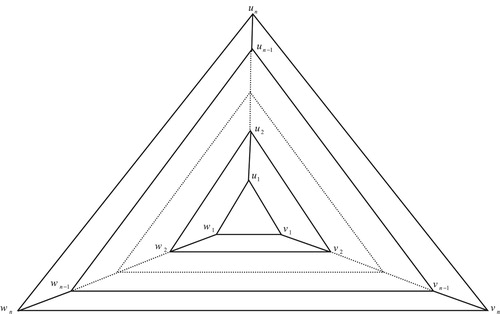Consider the family of graphs $H_n$ generated by a triangle and constructed as shown in Figure 2.

Figure 2. The graph $H_n$.

According to the construction, the number of total vertices $|V\left(H_n\right)|$ and edges $|E\left(H_n\right)|$ are $|V\left(H_n\right)|=3n$ and $|E\left(H_n\right)|=6n-3,n=1,2,\dots$.

It is clear that the average degree of $H_n$ is in the large $n$ limit is $4$.

Theorem 2.2:

For $n\ge 1$, the number of spanning trees of the graph $H_n$ is given by $\begin{array}{rl}& 3\left[\left(\frac{21+5\sqrt{21}}{42}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^{n-1}\right.\\ & {\left.+\left(\frac{21-5\sqrt{21}}{42}\right){\left(\frac{5-\sqrt{21}}{2}\right)}^{n-1}\right]}^2.\end{array}$Proof: Applying Lemma 1.1, we have: $\tau \left(H_n\right)=\frac{1}{{\left(3n\right)}^2}det(3nI-\overline{D}+\overline{A})$

$\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}det\left(\begin{array}{cccccccc}4& 0& 1& \cdots & 1& 0& 1& \cdots \\ 0& 5& \ddots & \ddots & ⋮& 1& \ddots & \ddots \\ 1& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots \\ ⋮& \ddots & \ddots & 5& 0& ⋮& \ddots & \ddots \\ 1& \cdots & 1& 0& 4& 1& \cdots & \cdots \\ 0& 1& \cdots & \cdots & 1& 4& 0& 1\\ 1& \ddots & \ddots & \ddots & ⋮& 0& 5& \ddots \\ ⋮& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots \\ 1& \cdots & \cdots & 1& 0& 1& \cdots & 1\\ 0& 1& \cdots & \cdots & 1& 0& 1& \cdots \\ 1& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & ⋮& ⋮& \ddots & \ddots \\ ⋮& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots \\ 1& \cdots & \cdots & 1& 0& 1& \cdots & \cdots \end{array}\right.\\ & \left.\begin{array}{ccccccc}\cdots & 1& 0& 1& \cdots & \cdots & 1\\ \ddots & ⋮& 1& \ddots & \ddots & \ddots & ⋮\\ \ddots & ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ \ddots & 1& ⋮& \ddots & \ddots & \ddots & 1\\ \cdots & 0& 1& \cdots & \cdots & 1& 0\\ \cdots & 1& 0& 1& \cdots & \cdots & 1\\ \ddots & ⋮& 1& \ddots & \ddots & \ddots & ⋮\\ \ddots & 1& ⋮& \ddots & \ddots & \ddots & ⋮\\ 5& 0& ⋮& \ddots & \ddots & \ddots & 1\\ 0& 4& 1& \cdots & \cdots & 1& 0\\ \cdots & 1& 4& 0& 1& \cdots & 1\\ \ddots & ⋮& 0& 5& \ddots & \ddots & ⋮\\ \ddots & ⋮& 1& \ddots & \ddots & \ddots & 1\\ \ddots & 1& ⋮& \ddots & \ddots & 5& 0\\ 1& 0& 1& \cdots & 1& 0& 4\end{array}\right)\end{array}$

Thus, we get: $\begin{array}{rl}\tau \left(H_n\right)& =\frac{1}{{\left(3n\right)}^2}det\left(\begin{array}{ccc}A& B& B\\ B& A& B\\ B& B& A\end{array}\right)\\ & =\frac{1}{{\left(3n\right)}^2}[det(A-B){]}^2[det(A+2B\left)\right]\end{array}$ $\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}{\left(det\left(\begin{array}{ccccc}4& -1& 0& \cdots & 0\\ -1& 5& \ddots & \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & 5& -1\\ 0& \cdots & 0& -1& 4\end{array}\right)\right)}^2\\ & \times det\left(\begin{array}{ccccc}4& 2& 3& \cdots & 3\\ 2& 5& \ddots & \ddots & ⋮\\ 3& \ddots & \ddots & \ddots & 3\\ ⋮& \ddots & \ddots & 5& 2\\ 3& \cdots & 3& 2& 4\end{array}\right)\end{array}$Straightforward induction using properties of determinants, we have $det(A+2B)=3n^2$, and by expanding the first six determinants, yields

$det(A-B)$ has the values $15,72,345,1653,7920,12649\dots$ for $n=2,3,4,5,6,7,\dots$

These values can be written in the form: $\begin{array}{rl}& 15=5\times 3,\\ & 72=5\times 15-3,\\ & 345=5\times 72-15,\\ & 1653=5\times 345-72,\\ & 7920=5\times 1653-345,\dots \dots .\end{array}$Thus we have the following recurrence relation (2) $a_{n+2}=5a_{n+1}-a_n.$(2) Its characteristic Equation is $r^2-5r+1=0$ with two roots being $\frac{5+\sqrt{2}}{2}$ and $\frac{5+\sqrt{2}}{2}$.

The general solution of the recurrence relation (2) is $det(A-B)=\alpha {\left(\frac{5+\sqrt{21}}{2}\right)}^{n-1}+\beta {\left(\frac{5-\sqrt{21}}{2}\right)}^{n-1}$Using the initial condition $det(A-B)=15$ and $det(A-B)=75$ at $n=2\text{and}3$, respectively. We have $5=\alpha \left(\frac{5+\sqrt{21}}{2}\right)+\beta \left(\frac{5-\sqrt{21}}{2}\right),$ $24=\alpha (\frac{5+\sqrt{21}}{2}{)}^2+\beta (\frac{5-\sqrt{21}}{2}{)}^2$Solving these equations, we get $\alpha =\frac{21+5\sqrt{21}}{42}$ and $\beta =\frac{21-5\sqrt{21}}{42}$, therefore

$\begin{array}{rl}det(A-B)& =3\left[\left(\frac{21+5\sqrt{21}}{42}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^{n-1}\right.\\ & \left.+\left(\frac{21-5\sqrt{21}}{42}\right){\left(\frac{5-\sqrt{21}}{2}\right)}^{n-1}\right].\end{array}$Thus $\begin{array}{rl}\tau \left(H_n\right)& =3\left[\left(\frac{21+5\sqrt{21}}{42}\right){\left(\frac{5+\sqrt{21}}{2}\right)}^{n-1}\right.\\ & {\left.+\left(\frac{21-5\sqrt{21}}{42}\right){\left(\frac{5-\sqrt{21}}{2}\right)}^{n-1}\right]}^2.\end{array}$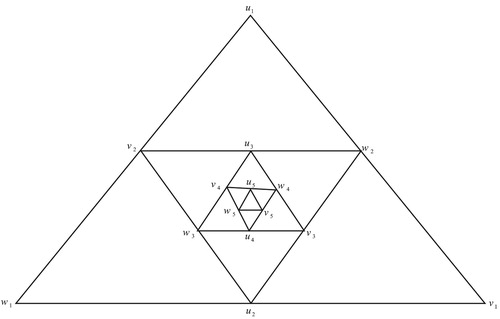Consider the family of graphs $X_n$ generated by the triangle and constructed as shown in Figure 3.

Figure 3. The graph $X_n$.

According to the construction, the number of total vertices $|V\left(X_n\right)|$ and edges $|E\left(X_n\right)|$ are $|V\left(X_n\right)|=3n$ and $|E\left(X_n\right)|=6n-3,n=1,2,\dots$.

It is clear that the average degree of $X_n$ is in the large $n$ limit is $4$.

Theorem 2.3: For $n\ge 1$, the number of spanning trees of the graph $X_n$ is given by $\frac{2^{n-1}}{12}{\left[\left(3-\sqrt{3}\right){\left(2+\sqrt{3}\right)}^n+\left(3+\sqrt{3}\right){\left(2-\sqrt{3}\right)}^n\right]}^2.$Proof: Applying Lemma 1.1, we have: $\tau \left(X_n\right)=\frac{1}{{\left(3n\right)}^2}det(3nI-\overline{D}+\overline{A})$ $\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}det\\ & \times \left(\begin{array}{ccccccccccccccc}3& 1& \cdots & \cdots & 1& 1& 0& 1& \cdots & 1& 1& 0& 1& \cdots & 1\\ 1& 5& \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots & \ddots & 1& 1& \ddots & \ddots & \ddots & 1\\ ⋮& \ddots & \ddots & 5& 1& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0\\ 1& \cdots & \cdots & 1& 3& 1& \cdots & 1& 0& 1& 1& \cdots & 1& 0& 1\\ 1& 0& 1& \cdots & 1& 3& 1& \cdots & \cdots & 1& 1& 0& 1& \cdots & 1\\ 0& \ddots & \ddots & \ddots & ⋮& 1& 5& \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ 1& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots & \ddots & 1\\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & 5& 1& ⋮& \ddots & \ddots & \ddots & 0\\ 1& \cdots & 1& 0& 1& 1& \cdots & \cdots & 1& 3& 1& \cdots & 1& 0& 1\\ 1& 0& 1& \cdots & 1& 1& 0& 1& \cdots & 1& 3& 1& \cdots & \cdots & 1\\ 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮& 1& 5& \ddots & \ddots & ⋮\\ 1& \ddots & \ddots & \ddots & 1& 1& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & 5& 1\\ 1& \cdots & 1& 0& 1& 1& \cdots & 1& 0& 1& 1& \cdots & \cdots & 1& 3\end{array}\right)\end{array}$Thus, we get: $\begin{array}{rl}\tau \left(X_n\right)& =\frac{1}{{\left(3n\right)}^2}det\left(\begin{array}{ccc}A& B& B\\ B& A& B\\ B& B& A\end{array}\right)\\ & =\frac{1}{{\left(3n\right)}^2}[det(A-B){]}^2[det(A+2B\left)\right]\end{array}$ $\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}{\left(det\left(\begin{array}{ccccc}2& 1& 0& \cdots & 0\\ 1& 4& \ddots & \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & 4& 1\\ 0& \cdots & 0& 1& 5\end{array}\right)\right)}^2\\ & \times det\left(\begin{array}{ccccc}5& 1& 3& \cdots & 3\\ 1& 7& \ddots & \ddots & ⋮\\ 3& \ddots & \ddots & \ddots & 3\\ ⋮& \ddots & \ddots & 7& 1\\ 3& \cdots & 3& 1& 5\end{array}\right)\end{array}$Straightforward induction using properties of determinants, we have $det(A+2B)=3n^2\times 2^{n-1}$, and by expanding the first five determinants, yields

$det(A-B)$ has the values $9,33,123,459,1713,\dots$ for $n=2,3,4,5,6,\dots$

These values can be written in the form: $\begin{array}{rl}& 9=3(4\times 1-1),\\ & 33=3(4\times 3-1),\\ & 123=3(4\times 11-3),\\ & 459=3(4\times 41-11),\\ & 1713=3(4\times 153-41),\dots \end{array}$Thus we have the following recurrence relation (3) $a_{n+2}=4a_{n+1}-a_n.$(3) Its characteristic Equation is $r^2-4r+1=0$ with two roots being $2+\sqrt{3}$ and $2-\sqrt{3}$.

The general solution of the recurrence relation (3) is $det(A-B)=3[\alpha (2+\sqrt{3}{)}^n+\beta (2-\sqrt{3}{)}^n]$Using the initial condition $det(A-B)=9$ and $det(A-B)=33$ at $n=2\text{and}3$, respectively. We have $\begin{array}{rl}3& =\alpha (2+\sqrt{3})+\beta (2-\sqrt{3}),\end{array}$ $\begin{array}{rl}11& =\alpha (2+\sqrt{3}{)}^2+\beta (2-\sqrt{3}{)}^2\end{array}$Solving these equations, we get $\alpha =\frac{3-\sqrt{3}}{6}$ and $\beta =\frac{3+\sqrt{3}}{6}$, therefore

$\begin{array}{rl}det(A-B)& =3\left[\left(\frac{3-\sqrt{3}}{6}\right){\left(2+\sqrt{3}\right)}^n\right.\\ & \left.+\left(\frac{3+\sqrt{3}}{6}\right){\left(2-\sqrt{3}\right)}^n\right].\end{array}$Thus $\begin{array}{rl}\tau \left(X_n\right)& =\frac{1}{{\left(3n\right)}^2}\times 3n^2\times 2^{n-1}\\ & \times \left[\left(\frac{3-\sqrt{3}}{6}\right){(2+\sqrt{3})}^n\right.\\ & {\left.+\left(\frac{3+\sqrt{3}}{6}\right){(2-\sqrt{3})}^n\right]}^2\\ & =\frac{2^{n-1}}{12}\left[\right(3-\sqrt{3})(2+\sqrt{3}{)}^n\\ & +(3+\sqrt{3})(2-\sqrt{3}{)}^n{]}^2.\end{array}$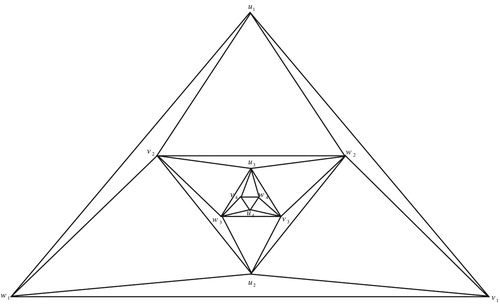Consider the family of graphs $Y_n$ generated by triangle and constructed as shown in Figure 4.

Figure 4. The graph $Y_n$.

According to the construction, the number of total vertices $|V\left(Y_n\right)|$ and edges $|E\left(Y_n\right)|$ are $|V\left(Y_n\right)|=3n$ and $|E\left(Y_n\right)|=9n-6,n=1,2,\dots$.

It is clear that the average degree of $Y_n$ is in the large $n$ limit is $6$.

Theorem 2.4:

For $n\ge 1$, the number of spanning trees of the graph $Y_n$ is given by $3\times 2^{n-1}{\left[\left(\frac{5+3\sqrt{5}}{10}\right){\left(\frac{7+3\sqrt{5}}{2}\right)}^{n-1}+\left(\frac{5-3\sqrt{5}}{10}\right){\left(\frac{7-3\sqrt{5}}{2}\right)}^{n-1}\right]}^2.$

Proof: Applying Lemma 1.1, we have: $\tau \left(Y_n\right)=\frac{1}{{\left(3n\right)}^2}det(3nI-\overline{D}+\overline{A})$ $\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}det\\ & \left(\begin{array}{ccccccccccccccc}5& 1& \cdots & \cdots & 1& 0& 0& 1& \cdots & 1& 0& 0& 1& \cdots & 1\\ 1& 7& \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots & \ddots & 1& 1& \ddots & \ddots & \ddots & 1\\ ⋮& \ddots & \ddots & 7& 1& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0\\ 1& \cdots & \cdots & 1& 5& 1& \cdots & 1& 0& 0& 1& \cdots & 1& 0& 0\\ 0& 0& 1& \cdots & 1& 5& 1& \cdots & \cdots & 1& 0& 0& 1& \cdots & 1\\ 0& \ddots & \ddots & \ddots & ⋮& 1& 7& \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮\\ 1& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots & \ddots & ⋮& 1& \ddots & \ddots & \ddots & 1\\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & 7& 1& ⋮& \ddots & \ddots & \ddots & 0\\ 1& \cdots & 1& 0& 0& 1& \cdots & \cdots & 1& 5& 1& \cdots & 1& 0& 0\\ 0& 0& 1& \cdots & 1& 0& 0& 1& \cdots & 1& 5& 1& \cdots & \cdots & 1\\ 0& \ddots & \ddots & \ddots & ⋮& 0& \ddots & \ddots & \ddots & ⋮& 1& 7& \ddots & \ddots & ⋮\\ 1& \ddots & \ddots & \ddots & 1& 1& \ddots & \ddots & \ddots & 1& ⋮& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & \ddots & 0& ⋮& \ddots & \ddots & 7& 1\\ 1& \cdots & 1& 0& 0& 1& \cdots & 1& 0& 0& 1& \cdots & \cdots & 1& 5\end{array}\right)\end{array}$Thus, we get: $\begin{array}{rl}\tau \left(Y_n\right)& =\frac{1}{{\left(3n\right)}^2}det\left(\begin{array}{ccc}A& B& B\\ B& A& B\\ B& B& A\end{array}\right)\\ & =\frac{1}{{\left(3n\right)}^2}[det(A-B){]}^2[det(A+2B\left)\right]\end{array}$ $\begin{array}{rl}& =\frac{1}{{\left(3n\right)}^2}{\left(det\left(\begin{array}{ccccc}5& 1& 0& \cdots & 0\\ 1& 7& \ddots & \ddots & ⋮\\ 0& \ddots & \ddots & \ddots & 0\\ ⋮& \ddots & \ddots & 7& 1\\ 0& \cdots & 0& 1& 5\end{array}\right)\right)}^2\\ & \times det\left(\begin{array}{ccccc}5& 1& 3& \cdots & 3\\ 1& 7& \ddots & \ddots & ⋮\\ 3& \ddots & \ddots & \ddots & 3\\ ⋮& \ddots & \ddots & 7& 1\\ 3& \cdots & 3& 1& 5\end{array}\right)\end{array}$Straightforward induction using properties of determinants, we have $det(A+2B)=3n^2\times 2^{n-1}$, and by expanding the first six determinants, yields

$det(A-B)$ has the values $24,165,1131,7752,53133,364179,\dots$ for $n=2,3,4,5,6,7,\dots$

These values can be written in the form: $\begin{array}{rl}& 24=3\times 8,\\ & 165=3\times 55=3(7\times 8-1),\\ & 1131=3\times 377=3(7\times 55-8),\\ & 7752=3\times 2584=3(7\times 377-55),\\ & 53133=3\times 17711=3(7\times 2584-377),\\ & 364179=3\times 121393=3(7\times 17711-2584),\dots \end{array}$Thus we have the following recurrence relation (4) $a_{n+2}=7a_{n+1}-a_n.$(4) Its characteristic Equation is $r^2-7r+1=0$ with two roots being $\frac{7+3\sqrt{5}}{2}$ and $\frac{7-3\sqrt{5}}{2}$.

The general solution of the recurrence relation (4) is $\begin{array}{rl}& det(A-B)\\ & =3\left[\alpha {\left(\frac{7+3\sqrt{5}}{2}\right)}^{n-1}+\beta {\left(\frac{7-3\sqrt{5}}{2}\right)}^{n-1}\right]\end{array}$Using the initial condition $det(A-B)=24$ and $det(A-B)=165$ at $n=2\text{and}3$respectively. We have $8=\alpha \left(\frac{7+3\sqrt{5}}{2}\right)+\beta \left(\frac{7-3\sqrt{5}}{2}\right),$ $55=\alpha {\left(\frac{7+3\sqrt{5}}{2}\right)}^2+\beta {\left(\frac{7-3\sqrt{5}}{2}\right)}^2$Solving these equations, we get $\alpha =\frac{5+3\sqrt{5}}{10}$ and $\beta =\frac{5-3\sqrt{5}}{10}$, therefore

$\begin{array}{rl}& det(A-B)=3\left[\left(\frac{5+3\sqrt{5}}{10}\right){\left(\frac{7+3\sqrt{5}}{2}\right)}^{n-1}\right.\\ & \left.+\left(\frac{5-3\sqrt{5}}{10}\right){\left(\frac{7-3\sqrt{5}}{2}\right)}^{n-1}\right].\end{array}$Thus $\begin{array}{rl}& \tau \left(Y_n\right)=\frac{1}{{\left(3n\right)}^2}\times 3n^2\times 2^{n-1}\times 9\\ & \times \left[\left(\frac{5+3\sqrt{5}}{10}\right){\left(\frac{7+3\sqrt{5}}{2}\right)}^{n-1}\right.\\ & {\left.+\left(\frac{5-3\sqrt{5}}{10}\right){\left(\frac{7-3\sqrt{5}}{2}\right)}^{n-1}\right]}^2\\ & =3\times 2^{n-1}\left[\left(\frac{5+3\sqrt{5}}{10}\right){\left(\frac{7+3\sqrt{5}}{2}\right)}^{n-1}\right.\\ & {\left.+\left(\frac{5-3\sqrt{5}}{10}\right){\left(\frac{7-3\sqrt{5}}{2}\right)}^{n-1}\right]}^2.\end{array}$

3. Numerical results

The following table illustrates some of the values of the number of spanning trees in the graphs $G_n,H_n,X_n$ and $Y_n$ (Table 1)_.

Table 1. Some values of $\tau \left(G_n\right),\tau \left(H_n\right),\tau \left(X_n\right)$ and $\tau \left(Y_n\right)$_.

$n$	$G_n$	$H_n$	$X_n$	$Y_n$
$1$	$16$	$3$	$3$	$3$
$2$	$361$	$75$	$54$	$384$
$3$	$8281$	$1728$	$1452$	$36,300$
$4$	$190,096$	$39,675$	$40,344$	$3,411,096$
$5$	$4,363,921$	$910,803$	$1,123,632$	$320,498,688$
$6$	$100,180,081$	$20,908,800$	$31,299,936$	$30,113,234,016$
$7$	$2,299,777,936$	$479,991,603$	$871,902,912$	$2,829,362,006,208$
$8$	$52,794,712,441$	$11,018,898,075$	$24,288,080,256$	$265,839,575,654,400$
$9$	$1,211,978,608,201$	$252,954,664,128$	$676,578,632,448$	$24,977,602,663,502,592$
$10$	$27,822,713,276,176$	$5,806,938,376,875$	$18,847,049,381,376$	$2,346,831,292,066,653,696$

It is clear from the table that the number of the graph $Y_n$ of average degree $6$ is larger than the other three graphs $G_n,H_n,X_n$ of average degree $4$ at different values of $n\ge 2.$

In addition, the number of spanning trees of the graph $G_n$ is larger than the number of spanning trees of the graphs $H_n$ and $X_n$ of the same average degree $4$ at different values of $n\ge 2.$

4. Spanning tree entropy

The spanning tree entropy is a quantitative measure of the robustness of a network based on its complexity.

After having explicit Formulas for the number of spanning trees of the sequence of the four graphs $G_n,H_n,X_n$ and $Y_n$, we can calculate its spanning tree entropy $Z$ which is a finite number and a very interesting quantity characterizing the network structure, defined as in [4,12] as: For a graph $G$, (5) $Z\left(G\right)=\underset{n\to \mathrm{\infty }}{lim}\frac{\ln \tau \left(G\right)}{|V\left(G\right)|}.$(5) $Z\left(G_n\right)=-\frac{2}{3}\left(\ln \left[\frac{2}{5+\sqrt{21}}\right]\right)=\mathrm{1.044532825.}$ $Z\left(H_n\right)=-\frac{2}{3}\left(\ln \left[\frac{2}{5+\sqrt{21}}\right]\right)=\mathrm{1.044532825.}$ $Z\left(X_n\right)=\frac{1}{3}\left(\ln \left[2\right]+2\ln \left[2+\sqrt{3}\right]\right)=\mathrm{1.109020991.}$ $Z\left(Y_n\right)=\frac{1}{3}\left(-\ln \left[2\right]+2\ln \left[7+3\sqrt{5}\right]\right)=\mathrm{1.514280594.}$

Now we compare the value of entropy in our graphs with other graphs. It is clear that the entropy of the graph $Y_n$ of average degree $6$ is larger than the entropy of the other three graphs $G_n,H_n,X_n$ of average degree $4$. In addition, the entropy of the graph $X_n$ is larger than the entropy of the two graphs $G_n$ and $H_n$ of the same average degree 4. Also the entropy of the graph $Y_n$ is larger than the entropy of the Apollonian graph [25] which has the entropy $1.3540$ of the same average degree 6. Finally, the entropy of our first three graphs $G_n,H_n,X_n$ is larger than the entropy of fractal scale-free lattice [26] which has the entropy $\mathrm{1.040.}$

5. Conclusions

The number of spanning trees in graphs (networks) is an important invariant. The evaluation of this number is not only interesting from a mathematical (computational) perspective, but also, it is an important measure of reliability of a network and designing electrical circuits. Some computationally hard problems such as the travelling salesman problem can be solved approximately by using spanning trees. In this work, we compute the number of spanning trees of some families of graphs generated by triangle using linear algebra and knowledge of difference equations.

Acknowledgments

The author is grateful to the anonymous reviewers for their helpful comments and suggestions toward improving the original version of the paper.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

S. N. Daoud http://orcid.org/0000-0003-3809-2521