Global dynamical properties of two discrete-time exponential systems

Abstract

We explore the global dynamics of following three directional discrete-time exponential systems of difference equations: $x_{n+1}=\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-y_n}}{{\gamma }_{19}+z_{n-1}},y_{n+1}=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-z_n}}{{\gamma }_{20}+x_{n-1}},z_{n+1}=\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-x_n}}{{\gamma }_{21}+y_{n-1}},$ $x_{n+1}=\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-z_n}}{{\gamma }_{22}+x_{n-1}},y_{n+1}=\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-x_n}}{{\gamma }_{23}+y_{n-1}},z_{n+1}=\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-y_n}}{{\gamma }_{24}+z_{n-1}},$where ${\alpha }_i,{\beta }_i,{\gamma }_i$, $i=19,20,\cdots ,24$ and $x_i,y_i,z_i,i=0,-1$ are belonging to ${\text{R}}^{\ge 0}$. Precisely, we explore the boundedness and persistence of positive solution, existence of invariant rectangle, existence and uniqueness of positive equilibrium point, local and global dynamics about the unique positive equilibrium, and rate of convergence of these discrete-time exponential systems. Finally, theoretical results are verified numerically.

KEYWORDS:

• Difference equations
• stability
• numerical simulations

Mathematics Subject Classifications:

• 39A10
• 40A05

1. Introduction

Global dynamical properties of discrete-time exponential difference equations or systems of difference equations have widely investigated in the recent years. For instance, Ozturk et al. [1] have explored the dynamical properties of following exponential difference equation: (1) $x_{n+1}=\frac{{\alpha }_1+{\alpha }_2{e}^{-x_n}}{{\alpha }_3+x_{n-1}},n=0,1,\cdots ,$(1)

where ${\alpha }_i,i=1,2,3$ and $x_i,i=0,-1$ are belonging to ${\mathbb{R}}^{\ge 0}$. Papaschinopoulos et al. [2] have explored the dynamical properties of following discrete-time exponential systems: (2) $\left.\begin{array}{c}{x}_{n+1}=\frac{{\alpha }_1+{\alpha }_2{e}^{-y_n}}{{\alpha }_3+y_{n-1}},y_{n+1}=\frac{{\alpha }_4+{\alpha }_5{e}^{-x_n}}{{\alpha }_6+x_{n-1}}\\ x_{n+1}=\frac{{\alpha }_1+{\alpha }_2{e}^{-y_n}}{{\alpha }_3+x_{n-1}},y_{n+1}=\frac{{\alpha }_4+{\alpha }_5{e}^{-x_n}}{{\alpha }_6+y_{n-1}}\\ x_{n+1}=\frac{{\alpha }_1+{\alpha }_2{e}^{-x_n}}{{\alpha }_3+y_{n-1}},y_{n+1}=\frac{{\alpha }_4+{\alpha }_5{e}^{-y_n}}{{\alpha }_6+x_{n-1}}\end{array}\right\},$(2)

where ${\alpha }_i,i=1,2,\cdots ,6$ and $x_i,y_i,i=0,-1$ are belonging to ${\mathbb{R}}^{\ge 0}$. Motivated from above studies, we explore the global dynamics of following two three-species discrete-time models which are extension of the work of [1,2]: (3) $\begin{array}{rl}{x}_{n+1}& =\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-y_n}}{{\gamma }_{19}+z_{n-1}},y_{n+1}=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-z_n}}{{\gamma }_{20}+x_{n-1}},\\ z_{n+1}& =\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-x_n}}{{\gamma }_{21}+y_{n-1}},\end{array}$(3) (4) $\begin{array}{rl}{x}_{n+1}& =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-z_n}}{{\gamma }_{22}+x_{n-1}},y_{n+1}=\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-x_n}}{{\gamma }_{23}+y_{n-1}},\\ z_{n+1}& =\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-y_n}}{{\gamma }_{24}+z_{n-1}},\end{array}$(4) where ${\alpha }_i,{\beta }_i,{\gamma }_i$, $i=19,20,\cdots ,24$ and $x_i,y_i,z_i,i=0,-1$ are belonging to ${\text{R}}^{\ge 0}$. Discrete-time systems (3) and (4) viewed as models in mathematical biology where biological interpretation of parameters ${\alpha }_i,{\beta }_i,{\gamma }_i$, $i=19,20,\cdots ,24$ are depicted in Table 1:

Table 1. Parameters of the discrete-time models (3) and (4) along their Biological interpretations.

Parameters	Biological interpretations
${\alpha }_{19},{\alpha }_{22}$	Immigration rate of species $x_n$
${\alpha }_{20},{\alpha }_{23}$	Immigration rate of $y_n$
${\alpha }_{21},{\alpha }_{24}$	Immigration rate of $z_n$
${\beta }_{19},{\beta }_{22}$	Growth rate of $x_n$
${\beta }_{20},{\beta }_{23}$	Growth rate of $y_n$
${\beta }_{21},{\beta }_{24}$	Growth rate of $z_n$
${\gamma }_{19},{\gamma }_{22}$	Carrying capacity of $x_n$
${\gamma }_{20},{\gamma }_{23}$	Carrying capacity of $y_n$
${\gamma }_{21},{\gamma }_{24}$	Carrying capacity of $z_n$

Our main contribution in this paper is to explore the global dynamical properties for discrete-time systems (3) and (4). Global dynamics and rate of convergence of (3) are explored in Section 2. This includes the study of boundedness and persistence, existence of invariant rectangle, existence of the unique $+\text{ve}$ equilibrium, global dynamics, and Rate of convergence. Same analysis for system (4) is explored in Section 3. Theoretical results are verified numerically in Section 4. Conclusion is given in Section 5.

2. Dynamics of the system (3)

2.1. Boundedness and persistence

In the following theorem, we explore that every $+ve$ solution $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ of (3) is bounded and persists (see [3,4]).

Theorem 2.1:

The $+ve$ solution $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ of (3) is bounded and persists.

Proof:

If the $+ve$ solution of (3) is $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ then (5) $\begin{array}{rl}{x}_n\le \frac{{\alpha }_{19+}{\beta }_{19}}{{\gamma }_{19}}& =U_{19},y_n\le \frac{{\alpha }_{20+}{\beta }_{20}}{{\gamma }_{20}}\\ & =U_{20},z_n\le \frac{{\alpha }_{21+}{\beta }_{21}}{{\gamma }_{21}}\\ & =U_{21},n=0,1,\cdots .\end{array}$(5) From (3) and (5), one gets (6) $\left.\begin{array}{c}{x}_n\ge \frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}}{{\gamma }_{19}+{\displaystyle \frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}}}=L_{19}\\ y_n\ge \frac{{\alpha }_{20+}{\beta }_{20}{e}^{-{\displaystyle \frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}}}}{{\gamma }_{20}+{\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}}}=L_{20}\\ z_n\ge \frac{{\alpha }_{21}+{\beta }_{21}{e}^{-{\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}}}}{{\gamma }_{21}+{\displaystyle \frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}}=L_{21}\end{array}\right\},$(6) $n=2,3,\cdots$. Finally from (5) and (6), one gets

$L_{19}\le x_n\le U_{19},L_{20}\le y_n\le U_{20},L_{21}\le z_n\le U_{21},\text{n}=3,4,\cdots$.

2.2. Existence of invariant rectangle

Theorem 2.2:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (3) then its corresponding invariant rectangle is $\left[L_{19},U_{19}\right]\times [L_{20},U_{20}\left]\times \right[L_{21},U_{21}]$ where $\begin{array}{rl}{L}_{19}& =\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}}{{\gamma }_{19}+\frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}},U_{19}=\frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}},\\ L_{20}& =\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}}}{{\gamma }_{20}+\frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}},U_{20}=\frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}},\\ L_{21}& =\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}}}{{\gamma }_{21}+\frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}\mathrm{a}\mathrm{n}\mathrm{d}{U}_{21}=\frac{{\alpha }_{21+}{\beta }_{21}}{{\gamma }_{21}}.\end{array}$

Proof:

Follows by induction.

2.3. Existence of unique $+\text{ve}$ equilibrium, global and local dynamics

Hereafter we will study existence of the $+\text{ve}$ equilibrium, global and local dynamics of (3). It is worthwhile to mentioned that in more general setting, system (3) can also be written as (7) $\begin{array}{rl}{x}_{n+1}& =f\left(y_n,z_{n-1}\right)y_{n+1}=g\left(z_n,x_{n-1}\right),\\ z_{n+1}& =h\left(x_n,y_{n-1}\right).\end{array}$(7)

Lemma 2.1:

Let $\left[a_1,b_1\right],\left[a_2,b_2\right],$ and $\left[a_3,b_3\right]$ be intervals of real numbers, s.t., (8) $\left.\begin{array}{c}f:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_1,b_1\right]\\ g:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_2,b_2\right]\\ h:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_3,b_3\right]\end{array}\right\},$(8) where $f,g$ and $h$ are continuous functions that satisfy the following conditions:

1. Let $f\left(y,z\right)$ is non-increasing $w.r.t.$ $y$(resp.$z$) $\mathrm{\forall }z$(resp.$y$); $g\left(z,x\right)$ is non-increasing $w.r.t$. $z$(resp.$x$) $\mathrm{\forall }x$(resp.$z$) and $h\left(x,y\right)$ is non-increasing $w.r.t.$ $x$(resp.$y$) $\mathrm{\forall }y$(resp.$x$).

2. If$\left(m_1,M_1,m_2,M_2,m_3,M_3\right)\in [a_1,b_1{]}^2\times [a_2,b_2{]}^2\times [a_3,b_3{]}^2$ is a solution of (9) $\left.\begin{array}{cc}{m}_1=f\left(M_2,M_3\right)& M_1=f\left(m_2,m_3\right)\\ m_2=g\left(M_1,M_3\right)& M_2=g\left(m_1,m_3\right)\\ m_3=h\left(M_1,M_2\right)& M_3=h\left(m_1,m_2\right)\end{array}\right\},$(9)

then $m_1=M_1,m_2=M_2,m_3=M_3$. Then (7) has a unique $+ve$ equilibrium $\left(\overline{x},\overline{y},\overline{z}\right)\in \left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]$ and every $+ve$ solution of (7) satisfies (10) $\left.\begin{array}{c}{x}_{n_0}\in \left[a_1,b_1\right],x_{n_0+1}\in \left[a_1,b_1\right]\\ y_{n_0}\in \left[a_2,b_2\right],y_{n_0+1}\in \left[a_2,b_2\right]\\ z_{n_0}\in \left[a_3,b_3\right],z_{n_0+1}\in \left[a_3,b_3\right]\end{array}\right\},$(10) $n_0\in \mathbb{N}$ tends to unique $+ve$ equilibrium $\left(\overline{x},\overline{y},\overline{z}\right)\in \left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]$.

Proof:

Set (11) $\left.\begin{array}{c}{m}_1^{\left(0\right)}=a_1,m_2^{\left(0\right)}=a_2,m_3^{\left(0\right)}=a_3\\ M_1^{\left(0\right)}=b_1,M_2^{\left(0\right)}=b_2,M_3^{\left(0\right)}=b_3\end{array}\right\}.$(11) And for $i=1,2,3,\cdots$, define (12) $\left.\begin{array}{c}{m}_1^{\left(i\right)}=f\left(M_2^{\left(i-1\right)},M_3^{\left(i-1\right)}\right),M_1^{\left(i\right)}\\ =f\left(m_2^{\left(i-1\right)},m_3^{\left(i-1\right)}\right)\\ m_2^{\left(i\right)}=g\left(M_1^{\left(i-1\right)},M_3^{\left(i-1\right)}\right),M_2^{\left(i\right)}\\ =g\left(m_1^{\left(i-1\right)},m_3^{\left(i-1\right)}\right)\\ m_3^{\left(i\right)}=h\left(M_1^{\left(i-1\right)},M_2^{\left(i-1\right)}\right),M_3^{\left(i\right)}\\ =h\left(m_1^{\left(i-1\right)},m_2^{\left(i-1\right)}\right)\end{array}\right\}.$(12) Clearly (13) $\left.\begin{array}{c}{m}_1^{\left(0\right)}\le m_1^{\left(1\right)},m_2^{\left(0\right)}\le m_2^{\left(1\right)},m_3^{\left(0\right)}\le m_3^{\left(1\right)}\\ M_1^{\left(0\right)}\ge M_1^{\left(1\right)},M_2^{\left(0\right)}\ge M_2^{\left(1\right)},M_3^{\left(0\right)}\ge M_3^{\left(1\right)}\end{array}\right\}.$(13) Using the monotonicity of $f,g$ and $h$ one gets (14) $\left.\begin{array}{c}{m}_1^{\left(1\right)}=f\left(M_2^{\left(0\right)},M_3^{\left(0\right)}\right)\le f\left(M_2^{\left(1\right)},M_3^{\left(1\right)}\right)=m_1^{\left(2\right)}\\ m_2^{\left(1\right)}=g\left(M_1^{\left(0\right)},M_3^{\left(0\right)}\right)\le g\left(M_1^{\left(1\right)},M_3^{\left(1\right)}\right)=m_2^{\left(2\right)}\\ m_3^{\left(1\right)}=h\left(M_1^{\left(0\right)},M_2^{\left(0\right)}\right)\le h\left(M_1^{\left(1\right)},M_2^{\left(1\right)}\right)=m_3^{\left(2\right)}\\ M_1^{\left(1\right)}=f\left(m_2^{\left(0\right)},m_3^{\left(0\right)}\right)\ge f\left(m_2^{\left(1\right)},m_3^{\left(1\right)}\right)=M_1^{\left(2\right)}\\ M_2^{\left(1\right)}=g\left(m_1^{\left(0\right)},m_3^{\left(0\right)}\right)\ge g\left(m_1^{\left(1\right)},m_3^{\left(1\right)}\right)=M_2^{\left(2\right)}\\ M_3^{\left(1\right)}=h\left(m_1^{\left(0\right)},m_2^{\left(0\right)}\right)\ge h\left(m_1^{\left(1\right)},m_2^{\left(1\right)}\right)=M_3^{\left(2\right)}\end{array}\right\}.$(14) By induction, we obtain for $i=1,2,3,\cdots$, (15) $\left.\begin{array}{c}{a}_1=m_1^{\left(0\right)}\le m_1^{\left(1\right)}\le \cdots \le m_1^{\left(i\right)}\le \cdots \le \\ M_1^{\left(i\right)}\le \cdots \le M_1^{\left(1\right)}\le M_1^{\left(0\right)}=b_1\\ a_2=m_2^{\left(0\right)}\le m_2^{\left(1\right)}\le \cdots \le m_2^{\left(i\right)}\le \cdots \le \\ M_2^{\left(i\right)}\le \cdots \le M_2^{\left(1\right)}\le M_2^{\left(0\right)}=b_2\\ a_3=m_3^{\left(0\right)}\le m_3^{\left(1\right)}\le \cdots \le m_3^{\left(i\right)}\le \cdots \le \\ M_3^{\left(i\right)}\le \cdots \le M_3^{\left(1\right)}\le M_3^{\left(0\right)}=b_3\end{array}\right\}.$(15) Clearly (16) $\left.\begin{array}{c}{m}_1^{\left(0\right)}\le x_{n_0}\le M_1^{\left(0\right)}\\ m_2^{\left(0\right)}\le y_{n_0}\le M_2^{\left(0\right)}\\ m_3^{\left(0\right)}\le z_{n_0}\le M_3^{\left(0\right)}\end{array}\right\},$(16) which by the monotonicity of $f,g$ and $h$ Implies (17) $\left.\begin{array}{c}{m}_1^{\left(1\right)}=f\left(M_2^{\left(0\right)},M_3^{\left(0\right)}\right)\le x_{n_0+1}=f\left(y_0,z_0\right)\\ \le f\left(m_2^{\left(0\right)},m_3^{\left(0\right)}\right)=M_1^{\left(1\right)}\\ m_2^{\left(1\right)}=g\left(M_1^{\left(0\right)},M_3^{\left(0\right)}\right)\le y_{n_0+1}=g\left(x_0,z_0\right)\\ \le g\left(m_1^{\left(0\right)},m_3^{\left(0\right)}\right)=M_2^{\left(1\right)}\\ m_3^{\left(1\right)}=h\left(M_1^{\left(0\right)},M_2^{\left(0\right)}\right)\le z_{n_0+1}=h\left(x_0,y_0\right)\\ \le h\left(m_1^{\left(0\right)},m_2^{\left(0\right)}\right)=M_3^{\left(1\right)}\\ m_1^{\left(2\right)}=f\left(M_2^{\left(1\right)},M_3^{\left(1\right)}\right)\le x_{n_0+2}=f\left(y_1,z_1\right)\\ \le f\left(m_2^{\left(1\right)},m_3^{\left(1\right)}\right)=M_1^{\left(2\right)}\\ m_2^{\left(2\right)}=g\left(M_1^{\left(1\right)},M_3^{\left(1\right)}\right)\le y_{n_0+2}=g\left(x_1,z_1\right)\\ \le g\left(m_1^{\left(1\right)},m_3^{\left(1\right)}\right)=M_2^{\left(2\right)}\\ m_3^{\left(2\right)}=h\left(M_1^{\left(1\right)},M_2^{\left(1\right)}\right)\le z_{n_0+2}=h\left(x_1,y_1\right)\\ \le h\left(m_1^{\left(1\right)},m_2^{\left(1\right)}\right)=M_3^{\left(2\right)}\end{array}\right\}.$(17) By induction it follows that (18) $\left.\begin{array}{c}{m}_1^{\left(k\right)}\le x_k\le M_1^{\left(k\right)}\\ m_2^{\left(k\right)}\le y_k\le M_2^{\left(k\right)}\\ m_3^{\left(k\right)}\le z_k\le M_3^{\left(k\right)}\end{array}\right\}.$(18) Thus for every $k=0,1,\cdots$, there exist numbers $m_1,m_2,m_3,M_1,M_2,M_3$, $s.t.$, (19) $\left.\begin{array}{c}{m}_1=\underset{k\to \mathrm{\infty }}{lim}{m}_1^{\left(k\right)},m_2=\underset{k\to \mathrm{\infty }}{lim}{m}_2^{\left(k\right)},\\ m_3=\underset{k\to \mathrm{\infty }}{lim}{m}_3^{\left(k\right)}\\ M_1=\underset{k\to \mathrm{\infty }}{lim}{M}_1^{\left(k\right)},M_2=\underset{k\to \mathrm{\infty }}{lim}{M}_2^{\left(k\right)},\\ M_3=\underset{k\to \mathrm{\infty }}{lim}{M}_3^{\left(k\right)}\end{array}\right\}.$(19) Clearly (20) $\left.\begin{array}{c}{m}_1\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{x}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{x}_k\le M_1\\ m_2\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{y}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{y}_k\le M_2\\ m_3\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{z}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{z}_k\le M_3\end{array}\right\}.$(20) Using the continuity of $f,g$ and $h$, equation (12) then implies that (21) $\left.\begin{array}{c}{m}_1=f\left(M_2,M_3\right),M_1=f\left(m_2,m_3\right)\\ m_2=g\left(M_1,M_3\right),M_2=g\left(m_1,m_3\right)\\ m_3=h\left(M_1,M_2\right),M_3=h(m_1,m_2\end{array}\right\}.$(21) By assumption (b) one gets: $m_1=M_1=\overline{x},m_2=M_2=\overline{y},m_3=M_3=\overline{z}$.

Hereafter based on Lemma 2.1, we will prove the following Theorem:

Theorem 2.3:

If (22) ${\beta }_{19}{\beta }_{20}{\beta }_{21}<{\gamma }_{19}{\gamma }_{20}{\gamma }_{21},$(22) then ${\mathrm{\Gamma }}_1=\left(\overline{x},\overline{y},\overline{z}\right)\in \left[L_{19},U_{19}\right]\times [L_{20},U_{20}\left]\times \right[L_{21},U_{21}]$ is the unique $+ve$ equilibrium of (3) and every $+ve$ solution of (3) tends to ${\mathrm{\Gamma }}_1$ of (3) as $n\to \mathrm{\infty }$.

Proof:

From (3) one has (23) $\begin{array}{rl}f\left(y,z\right)& =\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-y}}{{\gamma }_{19}+z},g\left(x,z\right)=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-z}}{{\gamma }_{20}+x},\\ h\left(x,y\right)& =\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-x}}{{\gamma }_{21}+y}.\end{array}$(23) It is clear that $f,g$ and $h$ satisfies the hypothesis of Lemma 2.1 and let $m_1,m_2,m_3,M_1,M_2,M_3$ be positive numbers, s.t., (24) $\left.\begin{array}{c}{m}_1=\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-M_2}}{{\gamma }_{19}+M_3},M_1=\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-m_2}}{{\gamma }_{19}+m_3}\\ m_2=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-M_3}}{{\gamma }_{20}+M_1},M_2=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-m_3}}{{\gamma }_{20}+m_1}\\ m_3=\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-M_1}}{{\gamma }_{21}+M_2},M_3=\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-m_1}}{{\gamma }_{21}+m_2}\end{array}\right\}.$(24) From (24) one gets (25) $\left.\begin{array}{cc}{e}^{-M_2}& =\frac{m_1\left({\gamma }_{19}+M_3\right)-{\alpha }_{19}}{{\beta }_{19}},e^{-m_2}\\ & =\frac{M_1\left({\gamma }_{19}+m_3\right)-{\alpha }_{19}}{{\beta }_{19}}\\ e^{-M_3}& =\frac{m_2\left({\gamma }_{20}+M_1\right)-{\alpha }_{20}}{{\beta }_{20}},e^{-m_3}\\ & =\frac{M_2\left({\gamma }_{20}+m_1\right)-{\alpha }_{20}}{{\beta }_{20}}\\ e^{-M_1}& =\frac{m_3\left({\gamma }_{21}+M_2\right)-{\alpha }_{21}}{{\beta }_{21}},e^{-m_1}\\ & =\frac{M_3\left({\gamma }_{21}+m_2\right)-{\alpha }_{21}}{{\beta }_{21}}\end{array}\right\},$(25) which implies that (26) $\left.\begin{array}{c}{m}_1-M_1=\frac{{\beta }_{19}}{{\gamma }_{19}}\left(e^{-M_2}-e^{-m_2}\right)\\ =\frac{{\beta }_{19}}{{\gamma }_{19}}{e}^{-M_2-m_2}\left(e^{m_2}-e^{M_2}\right)\\ m_2-M_2=\frac{{\beta }_{20}}{{\gamma }_{20}}\left(e^{-M_3}-e^{-m_3}\right)\\ =\frac{{\beta }_{20}}{{\gamma }_{20}}{e}^{-M_3-m_3}\left(e^{m_3}-e^{M_3}\right)\\ m_3-M_3=\frac{{\beta }_{21}}{{\gamma }_{21}}\left(e^{-M_1}-e^{-m_1}\right)\\ =\frac{{\beta }_{21}}{{\gamma }_{21}}{e}^{-M_1-m_1}\left(e^{m_1}-e^{M_1}\right)\end{array}\right\}.$(26) Moreover one gets (27) $\left.\begin{array}{c}{e}^{m_2}-e^{M_2}=e^{\zeta }\left(m_2-M_2\right),\\ \text{min}\left\{m_2,M_2\right\}\le \zeta \le max\left\{m_2,M_2\right\}\\ e^{m_3}-e^{M_3}=e^{\theta }\left(m_3-M_3\right),\\ \text{min}\left\{m_3,M_3\right\}\le \theta \le max\left\{m_3,M_3\right\}\\ e^{m_1}-e^{M_1}=e^{\eta }\left(m_1-M_1\right),\\ \text{min}\left\{m_1,M_1\right\}\le \eta \le max\left\{m_1,M_1\right\}\end{array}\right\}.$(27) In view of (27), equation (26) then implies that (28) $\left.\begin{array}{c}{m}_1-M_1=\frac{{\beta }_{19}}{{\gamma }_{19}}{e}^{-M_2-m_2+\zeta }\left(m_2-M_2\right)\\ m_2-M_2=\frac{{\beta }_{20}}{{\gamma }_{20}}{e}^{-M_3-m_3+\theta }\left(m_3-M_3\right)\\ m_3-M_3=\frac{{\beta }_{21}}{{\gamma }_{21}}{e}^{-M_1-m_1+\eta }\left(m_1-M_1\right)\end{array}\right\}.$(28) From (28) one gets (29) $\left.\begin{array}{c}|m_1-M_1|\le \frac{{\beta }_{19}}{{\gamma }_{19}}|m_2-M_2|\\ |m_2-M_2|\le \frac{{\beta }_{20}}{{\gamma }_{20}}|m_3-M_3|\\ |m_3-M_3|\le \frac{{\beta }_{21}}{{\gamma }_{21}}|m_1-M_1|\end{array}\right\}.$(29) From (22) and (29) one gets (30) $\left.\begin{array}{c}\left(1-\frac{{\beta }_{19}{\beta }_{20}{\beta }_{21}}{{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}}\right)|m_1-M_1|\le 0\\ \left(1-\frac{{\beta }_{19}{\beta }_{20}{\beta }_{21}}{{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}}\right)|m_2-M_2|\le 0\\ \left(1-\frac{{\beta }_{19}{\beta }_{20}{\beta }_{21}}{{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}}\right)|m_3-M_3|\le 0\end{array}\right\}.$(30) Finally equation (30) then implies that $m_1=M_1,m_2=M_2$ and $m_3=M_3$. Therefore from (5) and (6) and statement (b) of Lemma 2.1, (3) has a unique $+ve$ equilibrium ${\mathrm{\Gamma }}_1$ and every $+ve$ solution of (3) tends to ${\mathrm{\Gamma }}_1$ as $n\to \mathrm{\infty }$.

Hereafter global dynamics of (3) about ${\mathrm{\Gamma }}_1$ is investigated.

Theorem 2.4:

Assume that (22) hold and if (31) $\begin{array}{rl}& \frac{1}{{\gamma }_{19}+L_{21}}\left(\frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{{({\gamma }_{20}+L_{19})}^2}\right.\\ & \left.+\frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{21}+L_{20}\right)}\right)\\ & +\frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}\\ & +\frac{1}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\\ & \left(\begin{array}{c}{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}+\\ \times \frac{\begin{array}{c}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\\ \left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)\end{array}}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\end{array}\right)<1,\end{array}$(31) then ${\mathrm{\Gamma }}_1$ of (3) is globally asymptotically stable.

Proof:

Jacobian matrix $J_{{\mathrm{\Gamma }}_1}$ about ${\mathrm{\Gamma }}_1$ is (32) $J_{{\mathrm{\Gamma }}_1}=\left(\begin{array}{cccccc}0& 0& A_1& 0& 0& A_2\\ 1& 0& 0& 0& 0& 0\\ 0& B_1& 0& 0& B_2& 0\\ 0& 0& 1& 0& 0& 0\\ C_1& 0& 0& C_2& 0& 0\\ 0& 0& 0& 0& 1& 0\end{array}\right),$(32) where (33) $\left.\begin{array}{c}{A}_1=\frac{-{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}},A_2=-\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{({\gamma }_{19}+\overline{z})}^2},\\ B_1=-\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{({\gamma }_{20}+\overline{x})}^2},B_2=-\frac{{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}},\\ C_1=-\frac{{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}},C_2=-\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{({\gamma }_{21}+\overline{y})}^2}\end{array}\right\}.$(33) Moreover Characteristic equation of $J_{{\mathrm{\Gamma }}_1}$ about ${\mathrm{\Gamma }}_1$ is given by (34) ${\lambda }^6+{\mu }_1{\lambda }^3+{\mu }_2=0,$(34) where (35) $\begin{array}{rl}{\mu }_1& =-\left(A_1{B}_1+A_2{C}_1+A_1{B}_2{C}_1+B_2{C}_2\right),\\ {\mu }_2& =-A_2{B}_1{C}_2.\end{array}$(35) Now (36) $\begin{array}{rl}& \sum _{i=1}^2|{\mu }_i|\\ & =\frac{{\beta }_{19}{e}^{-\overline{y}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}\right)}{\left({\gamma }_{19}+\overline{z}\right){({\gamma }_{20}+\overline{x})}^2}\\ & +\frac{{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-\overline{x}-\overline{y}-\overline{z}}}{\left({\gamma }_{19}+\overline{z}\right)\left({\gamma }_{20}+\overline{x}\right)\left({\gamma }_{21}+\overline{y}\right)}\\ & +\frac{{\beta }_{21}{e}^{-\overline{x}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}\right)}{{({\gamma }_{19}+\overline{z})}^2\left({\gamma }_{21}+\overline{y}\right)}\\ & +\frac{{\beta }_{20}{e}^{-\overline{z}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}\right)}{\left({\gamma }_{20}+\overline{x}\right){({\gamma }_{21}+\overline{y})}^2}\\ & \times \frac{\begin{array}{c}\left({\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}\right)\\ \left({\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}\right)\end{array}}{{({\gamma }_{19}+\overline{z})}^2{({\gamma }_{20}+\overline{x})}^2{({\gamma }_{21}+\overline{y})}^2},\\ & \le \frac{{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\\ & +\frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{\left({\gamma }_{19}+L_{21}\right){({\gamma }_{20}+L_{19})}^2}\\ & +\frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{{({\gamma }_{19}+L_{21})}^2\left({\gamma }_{21}+L_{20}\right)}\\ & +\frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}\\ & \times \frac{\begin{array}{c}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\\ \left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)\end{array}}{{({\gamma }_{19}+L_{21})}^2{({\gamma }_{20}+L_{19})}^2{({\gamma }_{21}+L_{20})}^2},\\ & =\frac{1}{{\gamma }_{19}+L_{21}}\left(\frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{{({\gamma }_{20}+L_{19})}^2}\right.\\ & \left.+\frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{21}+L_{20}\right)}\right)\\ & +\frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}\\ & +\frac{1}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\\ & \times \left(\begin{array}{c}{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}+\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\\ \frac{\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\end{array}\right).\end{array}$(36) Assuming condition (31) holds then from (36) one get ${\sum }_{i=1}^2|{\mu }_i|<1$ and hence Theorem 1.5 of [5] implies that ${\mathrm{\Gamma }}_1$ of (3) is locally asymptotically stable. Moreover by Theorem 2.3, ${\mathrm{\Gamma }}_1$ of (3) is globally asymptotically stable.

Hereafter Rate of convergence about ${\mathrm{\Gamma }}_1$ of (3) is investigated motivated from the work of [6].

2.4. Rate of convergence

Theorem 2.5:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (3), s.t.,. (37) $\left.\begin{array}{c}\underset{n\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{x}_n=\overline{x}\\ \underset{n\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{y}_n=\overline{y}\\ \underset{n\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{z}_n=\overline{z}\end{array}\right\},$(37) where (38) $\left.\begin{array}{c}\overline{x}\in \left[L_{19},U_{19}\right]\\ \overline{y}\in \left[L_{20},U_{20}\right]\\ \overline{z}\in \left[L_{21},U_{21}\right]\end{array}\right\}.$(38) Then error vector $e_n=(e_n^{19},e_{n-1}^{19},e_n^{20},e_{n-1}^{20},e_n^{21},e_{n-1}^{21}{)}^T$ of every $+ve$ solution of (3) satisfying (39) $\left.\begin{array}{c}\underset{n\to \mathrm{\infty }}{\text{lim}}(\parallel e_n\parallel {)}^{\frac{1}{n}}=|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_1}|\\ \underset{n\to \mathrm{\infty }}{\text{lim}}\frac{\parallel e_{n+1}\parallel }{\parallel e_n\parallel }=|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_1}|\end{array}\right\},$(39) where $|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_1}|$ are the Characteristic Root of $J_{{\mathrm{\Gamma }}_1}$.

Proof:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (3), s.t., (37) along with (38) hold. For error terms one has (40) $\begin{array}{r}\left.\begin{array}{c}{x}_{n+1}-\overline{x}=\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-y_n}}{{\gamma }_{19}+z_{n-1}}-\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}}\\ =\frac{{\beta }_{19}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{19}+z_{n-1}\right)\left(y_n-\overline{y}\right)}\left(y_n-\overline{y}\right)\\ -\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{\left({\gamma }_{19}+z_{n-1}\right)\left({\gamma }_{19}+\overline{z}\right)}\left(z_{n-1}-\overline{z}\right)\\ y_{n+1}-\overline{y}=\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-z_n}}{{\gamma }_{20}+x_{n-1}}-\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}}\\ =\frac{{\beta }_{20}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{20}+x_{n-1}\right)\left(z_n-\overline{z}\right)}\left(z_n-\overline{z}\right)\\ -\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{\left({\gamma }_{20}+x_{n-1}\right)\left({\gamma }_{20}+\overline{x}\right)}\left(x_{n-1}-\overline{x}\right)\\ z_{n+1}-\overline{z}=\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-x_n}}{{\gamma }_{21}+y_{n-1}}-\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}}\\ =\frac{{\beta }_{21}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{21}+y_{n-1}\right)\left(x_n-\overline{x}\right)}\left(x_n-\overline{x}\right)\\ -\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{\left({\gamma }_{21}+y_{n-1}\right)\left({\gamma }_{21}+\overline{y}\right)}\left(y_{n-1}-\overline{y}\right)\end{array}\right\},\end{array}$(40) that is (41) $\left.\begin{array}{c}{x}_{n+1}-\overline{x}=\frac{{\beta }_{19}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{19}+z_{n-1}\right)\left(y_n-\overline{y}\right)}\left(y_n-\overline{y}\right)\\ -\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{\left({\gamma }_{19}+z_{n-1}\right)\left({\gamma }_{19}+\overline{z}\right)}\left(z_{n-1}-\overline{z}\right)\\ y_{n+1}-\overline{y}=\frac{{\beta }_{20}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{20}+x_{n-1}\right)\left(z_n-\overline{z}\right)}\left(z_n-\overline{z}\right)\\ -\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{\left({\gamma }_{20}+x_{n-1}\right)\left({\gamma }_{20}+\overline{x}\right)}\left(x_{n-1}-\overline{x}\right)\\ z_{n+1}-\overline{z}=\frac{{\beta }_{21}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{21}+y_{n-1}\right)\left(x_n-\overline{x}\right)}\left(x_n-\overline{x}\right)\\ -\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{\left({\gamma }_{21}+y_{n-1}\right)\left({\gamma }_{21}+\overline{y}\right)}\left(y_{n-1}-\overline{y}\right)\end{array}\right\}.$(41) Set (42) $\left.\begin{array}{c}{e}_n^{19}=x_n-\overline{x}\\ e_n^{20}=y_n-\overline{y}\\ e_n^{21}=z_n-\overline{z}\end{array}\right\}.$(42) By (42), (41) gives (43) $\left.\begin{array}{c}{e}_{n+1}^{19}=a_n{e}_n^{20}+b_n{e}_{n-1}^{21}\\ e_{n+1}^{20}=c_n{e}_{n-1}^{19}+d_n{e}_n^{21}\\ e_{n+1}^{21}=e_n{e}_n^{19}+f_n{e}_{n-1}^{20}\end{array}\right\},$(43) where (44) $\left.\begin{array}{c}{a}_n=\frac{{\beta }_{19}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{19}+z_{n-1}\right)\left(y_n-\overline{y}\right)},\\ b_n=-\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{\left({\gamma }_{19}+z_{n-1}\right)\left({\gamma }_{19}+\overline{z}\right)},\\ c_n=-\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{\left({\gamma }_{20}+x_{n-1}\right)\left({\gamma }_{20}+\overline{x}\right)},\\ d_n=\frac{{\beta }_{20}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{20}+x_{n-1}\right)\left(z_n-\overline{z}\right)},\\ e_n=\frac{{\beta }_{21}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{21}+y_{n-1}\right)\left(x_n-\overline{x}\right)},\\ f_n=-\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{\left({\gamma }_{21}+y_{n-1}\right)\left({\gamma }_{21}+\overline{y}\right)}\end{array}\right\}.$(44) Taking the limits of $a_n,b_n,c_n,d_n,e_{n}and{f}_n$ one gets (45) $\left.\begin{array}{c}\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=-\frac{{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}},\underset{n\to \mathrm{\infty }}{\text{lim}}{b}_n=-\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{\left({\gamma }_{19}+\overline{z}\right)}^2},\\ \underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=-\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{\left({\gamma }_{20}+\overline{x}\right)}^2},\underset{n\to \mathrm{\infty }}{\text{lim}}{d}_n=-\frac{{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}},\\ \underset{n\to \mathrm{\infty }}{\text{lim}}{e}_n=-\frac{{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}},\underset{n\to \mathrm{\infty }}{\text{lim}}{f}_n=-\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{\left({\gamma }_{21}+\overline{y}\right)}^2}\end{array}\right\},$(45) that is (46) $\left.\begin{array}{c}{a}_n=-\frac{{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}}+\alpha {20}_n,b_n=-\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{\left({\gamma }_{19}+\overline{z}\right)}^2}\\ +\alpha {21}_{n-1},c_n=-\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{\left({\gamma }_{20}+\overline{x}\right)}^2}+\alpha {19}_{n-1}\\ d_n=-\frac{{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}}+\alpha {21}_n,e_n=-\frac{{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}}\\ +\alpha {19}_n,f_n=-\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{\left({\gamma }_{21}+\overline{y}\right)}^2}+\alpha {20}_{n-1}\end{array}\right\},$(46) where $\alpha {19}_n,\alpha {19}_{n-1},\alpha {20}_n,\alpha {20}_{n-1},\alpha {21}_n,\alpha {21}_{n-1}\to 0$ as $n\to \mathrm{\infty }$. Now we have system (1.10) of [7], where (47) $\begin{array}{r}A=\left(\begin{array}{ccc}0& 0& -\frac{{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}}\\ 1& 0& 0\\ 0& -\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{\left({\gamma }_{20}+\overline{x}\right)}^2}& 0\\ 0& 0& 1\\ -\frac{{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}}& 0& 0\\ 0& 0& 0\end{array}\right.\\ \left.\begin{array}{ccc}0& 0& -\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{\left({\gamma }_{19}+\overline{z}\right)}^2}\\ 0& 0& 0\\ 0& -\frac{{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}}& 0\\ 0& 0& 0\\ -\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{\left({\gamma }_{21}+\overline{y}\right)}^2}& 0& 0\\ 0& 1& 0\end{array}\right),\end{array}$(47) and (48) $B\left(n\right)=\left(\begin{array}{cccccc}0& 0& \alpha {20}_n& 0& 0& \alpha {21}_{n-1}\\ 1& 0& 0& 0& 0& 0\\ 0& \alpha {19}_{n-1}& 0& 0& \alpha {21}_n& 0\\ 0& 0& 1& 0& 0& 0\\ \alpha {19}_n& 0& 0& \alpha {20}_{n-1}& 0& 0\\ 0& 0& 0& 0& 1& 0\end{array}\right),$(48)

and $B\left(n\right)\to 0$, $n\to \mathrm{\infty }$. Thus error terms about ${\mathrm{\Gamma }}_1$ similar to (32) is (49) $\begin{array}{rl}& \left(\begin{array}{c}\begin{array}{c}{e}_{n+1}^{19}\\ e_n^{19}\\ e_{n+1}^{20}\end{array}\\ \begin{array}{c}{e}_n^{20}\\ e_{n+1}^{21}\\ e_n^{21}\end{array}\end{array}\right)=\left(\begin{array}{ccc}0& 0& -\frac{{\beta }_{19}{e}^{-\overline{y}}}{{\gamma }_{19}+\overline{z}}\\ 1& 0& 0\\ 0& -\frac{{\alpha }_{20}+{\beta }_{20}{e}^{-\overline{z}}}{{\left({\gamma }_{20}+\overline{x}\right)}^2}& 0\\ 0& 0& 1\\ -\frac{{\beta }_{21}{e}^{-\overline{x}}}{{\gamma }_{21}+\overline{y}}& 0& 0\\ 0& 0& 0\end{array}\right.\\ & =\left.\begin{array}{ccc}0& 0& -\frac{{\alpha }_{19}+{\beta }_{19}{e}^{-\overline{y}}}{{\left({\gamma }_{19}+\overline{z}\right)}^2}\\ 0& 0& 0\\ & 0& -\frac{{\beta }_{20}{e}^{-\overline{z}}}{{\gamma }_{20}+\overline{x}}& 0\\ 0& 0& 0\\ -\frac{{\alpha }_{21}+{\beta }_{21}{e}^{-\overline{x}}}{{\left({\gamma }_{21}+\overline{y}\right)}^2}& 0& 0\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}\begin{array}{c}{e}_n^{19}\\ e_{n-1}^{19}\\ e_n^{20}\end{array}\\ \begin{array}{c}{e}_{n-1}^{20}\\ e_n^{21}\\ e_{n-1}^{21}\end{array}\end{array}\right).\end{array}$(49)

3. Dynamics of the system (4)

3.1. Boundedness and persistence

Theorem 3.1:

The $+ve$ solution $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ of (4) is bounded and persists.

Proof:

If the $+ve$ solution of (4) is $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$then (50) $\begin{array}{rl}{x}_n& \le \frac{{\alpha }_{22+}{\beta }_{22}}{{\gamma }_{22}}=U_{22},y_n\le \frac{{\alpha }_{23+}{\beta }_{23}}{{\gamma }_{23}}\\ & =U_{23},z_n\le \frac{{\alpha }_{24+}{\beta }_{24}}{{\gamma }_{24}}=U_{24},n=0,1,\cdots .\end{array}$(50) In addition from (4) and (50), one gets (51) $\left.\begin{array}{c}{x}_n\ge \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}}}{{\gamma }_{22}+{\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}}}=L_{22}\\ y_n\ge \frac{{\alpha }_{23+}{\beta }_{23}{e}^{-{\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}}}}{{\gamma }_{23}+{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}}}=L_{23}\\ z_n\ge \frac{{\alpha }_{24}+{\beta }_{24}{e}^{-{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}}}}{{\gamma }_{24}+{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}}=L_{24}\end{array}\right\},$(51) $n=2,3,\cdots$. Finally from (50) and (51), one gets $\begin{array}{rl}{L}_{22}& \le x_n\le U_{22},L_{23}\le y_n\le U_{23},L_{24}\le z_n\\ & \le U_{24},\text{n}=3,4,\cdots .\end{array}$

3.2. Existence of invariant rectangle

Theorem 3.2:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (4) then its corresponding invariant rectangle is $\left[L_{22},U_{22}\right]\times [L_{23},U_{23}\left]\times \right[L_{24},U_{24}]$ where $\begin{array}{rl}{L}_{22}& =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}}{{\gamma }_{22}+\frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}},U_{22}=\frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}},\\ L_{23}& =\frac{{\alpha }_{23+}{\beta }_{23}{e}^{-\frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}}}{{\gamma }_{23}+\frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}},U_{23}=\frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}},\\ L_{24}& =\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}}}{{\gamma }_{24}+\frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}\text{and}{U}_{24}=\frac{{\alpha }_{24+}{\beta }_{24}}{{\gamma }_{24}}.\end{array}$

3.3. Existence of the unique $+\mathit{v}\mathit{e}$ equilibrium, global and local dynamics

We will study existence of the $+\text{ve}$ equilibrium, local and global dynamics of (4). It is also noted that in more general notation (4) can also be written as (52) $\begin{array}{rl}{x}_{n+1}& =f\left(x_{n-1},z_n\right),y_{n+1}=g\left(x_n,y_{n-1}\right),\\ z_{n+1}& =h\left(y_n,z_{n-1}\right).\end{array}$(52)

Lemma 3.1:

Let $\left[a_1,b_1\right],\left[a_2,b_2\right]$ and $\left[a_3,b_3\right]$ be intervals of real numbers, s.t., (53) $\left.\begin{array}{c}f:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_1,b_1\right]\\ g:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_2,b_2\right]\\ h:\left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]\to \left[a_3,b_3\right]\end{array}\right\},$(53) where $f,g$ and $h$ are differentiable functions that satisfy the following conditions:

1. Let $f\left(x,z\right)$ is non-increasing $w.r.t.$ $x$(resp.$z$) $\mathrm{\forall }z$(resp.$x$); $g\left(x,y\right)$ is non-increasing $w.r.t.$ $x$(resp.$y$) $\mathrm{\forall }y$(resp.$x$) and $h\left(y,z\right)$ is non-increasing $w.r.t.y$(resp.$z$) $\mathrm{\forall }z$(resp.$y$.);

2. If $\left(m_1,M_1,m_2,M_2,m_3,M_3\right)\in [a_1,b_1{]}^2\times [a_2,b_2{]}^2\times [a_3,b_3{]}^2$ is a solution of (54) $\left.\begin{array}{cc}{m}_1=f\left(M_1,M_3\right),& M_1=f\left(m_1,m_3\right)\\ m_2=g\left(M_1,M_2\right),& M_2=g\left(m_1,m_2\right)\\ m_3=h\left(M_2,M_3\right),& M_3=h\left(m_2,m_3\right)\end{array}\right\},$(54)

then $m_1=M_1,m_2=M_2,m_3=M_3$. Then $\left(\overline{x},\overline{y},\overline{z}\right)\in \left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]$ is the unique $+ve$ equilibrium of (52) and $+ve$ solution of (52) satisfies (55) $\left.\begin{array}{c}{x}_{n_0}\in \left[a_1,b_1\right],x_{n_0+1}\in \left[a_1,b_1\right]\\ y_{n_0}\in \left[a_2,b_2\right],y_{n_0+1}\in \left[a_2,b_2\right]\\ z_{n_0}\in \left[a_3,b_3\right],z_{n_0+1}\in \left[a_3,b_3\right]\end{array}\right\},$(55) $n_0\in \mathbb{N}$ tends to $\left(\overline{x},\overline{y},\overline{z}\right)\in \left[a_1,b_1\right]\times \left[a_2,b_2\right]\times \left[a_3,b_3\right]$.

Proof:

Set (56) $\left.\begin{array}{c}{m}_1^{\left(0\right)}=a_1,m_2^{\left(0\right)}=a_2,m_3^{\left(0\right)}=a_3\\ M_1^{\left(0\right)}=b_1,M_2^{\left(0\right)}=b_2,M_3^{\left(0\right)}=b_3\end{array}\right\}.$(56) And for $i=1,2,3,\cdots ,$ define (57) $\left.\begin{array}{c}{m}_1^{\left(i\right)}=f\left(M_1^{\left(i-1\right)},M_3^{\left(i-1\right)}\right),M_1^{\left(i\right)}\\ =f\left(m_1^{\left(i-1\right)},m_3^{\left(i-1\right)}\right)\\ m_2^{\left(i\right)}=g\left(M_1^{\left(i-1\right)},M_2^{\left(i-1\right)}\right),M_2^{\left(i\right)}\\ =g\left(m_1^{\left(i-1\right)},m_2^{\left(i-1\right)}\right)\\ m_3^{\left(i\right)}=h\left(M_2^{\left(i-1\right)},M_3^{\left(i-1\right)}\right),M_3^{\left(i\right)}\\ =h\left(m_2^{\left(i-1\right)},m_3^{\left(i-1\right)}\right)\end{array}\right\}.$(57) Clearly (58) $\left.\begin{array}{c}{m}_1^{\left(0\right)}\le m_1^{\left(1\right)},m_2^{\left(0\right)}\le m_2^{\left(1\right)},m_3^{\left(0\right)}\le m_3^{\left(1\right)}\\ M_1^{\left(0\right)}\ge M_1^{\left(1\right)},M_2^{\left(0\right)}\ge M_2^{\left(1\right)},M_3^{\left(0\right)}\ge M_3^{\left(1\right)}\end{array}\right\}.$(58) Using the monotonicity of $f,g$ and $h$ one gets: (59) $\left.\begin{array}{c}{m}_1^{\left(1\right)}=f\left(M_1^{\left(0\right)},M_3^{\left(0\right)}\right)\le f\left(M_1^{\left(1\right)},M_3^{\left(1\right)}\right)=m_1^{\left(2\right)}\\ m_2^{\left(1\right)}=g\left(M_1^{\left(0\right)},M_2^{\left(0\right)}\right)\le g\left(M_1^{\left(1\right)},M_2^{\left(1\right)}\right)=m_2^{\left(2\right)}\\ m_3^{\left(1\right)}=h\left(M_2^{\left(0\right)},M_3^{\left(0\right)}\right)\le h\left(M_2^{\left(1\right)},M_3^{\left(1\right)}\right)=m_3^{\left(2\right)}\\ M_1^{\left(1\right)}=f\left(m_1^{\left(0\right)},m_3^{\left(0\right)}\right)\ge f\left(m_1^{\left(1\right)},m_3^{\left(1\right)}\right)=M_1^{\left(2\right)}\\ M_2^{\left(1\right)}=g\left(m_1^{\left(0\right)},m_2^{\left(0\right)}\right)\ge g\left(m_1^{\left(1\right)},m_2^{\left(1\right)}\right)=M_2^{\left(2\right)}\\ M_3^{\left(1\right)}=h\left(m_2^{\left(0\right)},m_3^{\left(0\right)}\right)\ge h\left(m_2^{\left(1\right)},m_3^{\left(1\right)}\right)=M_3^{\left(2\right)}\end{array}\right\}.$(59) By induction, we obtain for $i=1,2,3,\cdots ,$ (60) $\left.\begin{array}{c}{a}_1=m_1^{\left(0\right)}\le m_1^{\left(1\right)}\le \cdots \le m_1^{\left(i\right)}\le \cdots \le M_1^{\left(i\right)}\\ \le \cdots \le M_1^{\left(1\right)}\le M_1^{\left(0\right)}=b_1\\ a_2=m_2^{\left(0\right)}\le m_2^{\left(1\right)}\le \cdots \le m_2^{\left(i\right)}\le \cdots \le M_2^{\left(i\right)}\\ \le \cdots \le M_2^{\left(1\right)}\le M_2^{\left(0\right)}=b_2\\ a_3=m_3^{\left(0\right)}\le m_3^{\left(1\right)}\le \cdots \le m_3^{\left(i\right)}\le \cdots \le M_3^{\left(i\right)}\\ \le \cdots \le M_3^{\left(1\right)}\le M_3^{\left(0\right)}=b_3\end{array}\right\}.$(60) Moreover it is clear that (61) $\left.\begin{array}{c}{m}_1^{\left(0\right)}\le x_{n_0}\le M_1^{\left(0\right)}\\ m_2^{\left(0\right)}\le y_{n_0}\le M_2^{\left(0\right)}\\ m_3^{\left(0\right)}\le z_{n_0}\le M_3^{\left(0\right)}\end{array}\right\}.$(61) Now monotonicity of $f,g$ and $h$ then implies that (62) $\left.\begin{array}{c}{m}_1^{\left(1\right)}=f\left(M_1^{\left(0\right)},M_3^{\left(0\right)}\right)\le x_{n_0+1}=f\left(x_0,z_0\right)\\ \le f\left(m_1^{\left(0\right)},m_3^{\left(0\right)}\right)=M_1^{\left(1\right)}\\ m_2^{\left(1\right)}=g\left(M_1^{\left(0\right)},M_2^{\left(0\right)}\right)\le y_{n_0+1}=g\left(x_0,y_0\right)\\ \le g\left(m_1^{\left(0\right)},m_2^{\left(0\right)}\right)=M_2^{\left(1\right)}\\ m_3^{\left(1\right)}=h\left(M_2^{\left(0\right)},M_3^{\left(0\right)}\right)\le z_{n_0+1}=h\left(y_0,z_0\right)\\ \le h\left(m_2^{\left(0\right)},m_3^{\left(0\right)}\right)=M_3^{\left(1\right)}\\ m_1^{\left(2\right)}=f\left(M_1^{\left(1\right)},M_3^{\left(1\right)}\right)\le x_{n_0+2}=f\left(x_1,z_1\right)\\ \le f\left(m_1^{\left(1\right)},m_3^{\left(1\right)}\right)=M_1^{\left(2\right)}\\ m_2^{\left(2\right)}=g\left(M_1^{\left(1\right)},M_2^{\left(1\right)}\right)\le y_{n_0+2}=g\left(x_1,y_1\right)\\ \le g\left(m_1^{\left(1\right)},m_2^{\left(1\right)}\right)=M_2^{\left(2\right)}\\ m_3^{\left(2\right)}=h\left(M_2^{\left(1\right)},M_3^{\left(1\right)}\right)\le z_{n_0+2}=h\left(y_1,z_1\right)\\ \le h\left(m_2^{\left(1\right)},m_3^{\left(1\right)}\right)=M_3^{\left(2\right)}\end{array}\right\}.$(62) By induction it follows that (63) $\left.\begin{array}{c}{m}_1^{\left(k\right)}\le x_k\le M_1^{\left(k\right)}\\ m_2^{\left(k\right)}\le y_k\le M_2^{\left(k\right)}\\ m_3^{\left(k\right)}\le z_k\le M_3^{\left(k\right)}\end{array}\right\}.$(63) Thus for every $k=0,1,\cdots ,$ there exist numbers $m_1,m_2,m_3,M_1,M_2,M_3,$ s.t., (64) $\left.\begin{array}{c}{m}_1=\underset{k\to \mathrm{\infty }}{lim}{m}_1^{\left(k\right)},m_2=\underset{k\to \mathrm{\infty }}{lim}{m}_2^{\left(k\right)},\\ m_3=\underset{k\to \mathrm{\infty }}{lim}{m}_3^{\left(k\right)}\\ M_1=\underset{k\to \mathrm{\infty }}{lim}{M}_1^{\left(k\right)},M_2=\underset{k\to \mathrm{\infty }}{lim}{M}_2^{\left(k\right)},\\ M_3=\underset{k\to \mathrm{\infty }}{lim}{M}_3^{\left(k\right)}\end{array}\right\}.$(64) Clearly, (65) $\left.\begin{array}{c}{m}_1\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{x}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{x}_k\le M_1\\ m_2\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{y}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{y}_k\le M_2\\ m_3\le \underset{k\to \mathrm{\infty }}{\underset{\_}{\text{lim}}}{z}_k\le \underset{k\to \mathrm{\infty }}{\overline{\text{lim}}}{z}_k\le M_3\end{array}\right\}.$(65) Using the continuity of $f,g$ and $h$, equation (57) then implies that (66) $\left.\begin{array}{c}{m}_1=f\left(M_1,M_3\right),M_1=f\left(m_1,m_3\right)\\ m_2=g\left(M_1,M_2\right),M_2=g\left(m_1,m_2\right)\\ m_3=h\left(M_2,M_3\right),M_3=h\left(m_2,m_3\right)\end{array}\right\}.$(66) By assumption (b) one gets (67) $\left.\begin{array}{c}{m}_1=M_1=\overline{x}\\ m_2=M_2=\overline{y}\\ m_3=M_3=\overline{z}\end{array}\right\}.$(67)

Theorem 3.3:

If (68) ${\beta }_{22}{\beta }_{23}{\beta }_{24}<{\gamma }_{22}{\gamma }_{23}{\gamma }_{24},$(68) then ${\mathrm{\Gamma }}_2=\left(\overline{x},\overline{y},\overline{z}\right)\in )\in [L_{22},U_{22}]\times [L_{23},U_{23}\left]\times \right[L_{24},U_{24}]$  is the unique $+ve$ equilibrium and $+ve$ solution of (4) tends to ${\mathrm{\Gamma }}_2$ of (4) as $n\to \mathrm{\infty }$.

Proof:

From (4), we have (69) $\begin{array}{rl}f\left(x,z\right)& =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-z}}{{\gamma }_{22}+x},g\left(x,y\right)=\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-x}}{{\gamma }_{23}+y},\\ h\left(y,z\right)& =\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-y}}{{\gamma }_{24}+z}.\end{array}$(69) It is clear that $f,g$ and $h$ satisfies the hypothesis of Lemma 3.1 and let $m_1,m_2,m_3,M_1,M_2,M_3$ be positive numbers such that (70) $\left.\begin{array}{c}{m}_1=\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-M_3}}{{\gamma }_{22}+M_1},M_1=\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-m_3}}{{\gamma }_{22}+m_1}\\ m_2=\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-M_1}}{{\gamma }_{23}+M_2},M_2=\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-m_1}}{{\gamma }_{23}+m_2}\\ m_3=\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-M_2}}{{\gamma }_{24}+M_3},M_3=\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-m_2}}{{\gamma }_{24}+m_3}\end{array}\right\}.$(70) From (70) one gets (71) $\left.\begin{array}{c}{e}^{-M_3}=\frac{m_1\left({\gamma }_{22}+M_1\right)-{\alpha }_{22}}{{\beta }_{22}},e^{-m_3}\\ =\frac{M_1\left({\gamma }_{22}+m_1\right)-{\alpha }_{22}}{{\beta }_{22}}\\ e^{-M_1}=\frac{m_2\left({\gamma }_{23}+M_2\right)-{\alpha }_{23}}{{\beta }_{23}},e^{-m_1}\\ =\frac{M_2\left({\gamma }_{23}+m_2\right)-{\alpha }_{23}}{{\beta }_{23}}\\ e^{-M_2}=\frac{m_3\left({\gamma }_{24}+M_3\right)-{\alpha }_{24}}{{\beta }_{24}},e^{-m_2}\\ =\frac{M_3\left({\gamma }_{24}+m_3\right)-{\alpha }_{24}}{{\beta }_{24}}\end{array}\right\},$(71) which implies that (72) $\left.\begin{array}{c}{m}_1-M_1=\frac{{\beta }_{22}}{{\gamma }_{22}}\left(e^{-M_3}-e^{-m_3}\right)\\ =\frac{{\beta }_{22}}{{\gamma }_{22}}{e}^{-M_3-m_3}\left(e^{m_3}-e^{M_3}\right)\\ m_2-M_2=\frac{{\beta }_{23}}{{\gamma }_{23}}\left(e^{-M_1}-e^{-m_1}\right)\\ =\frac{{\beta }_{23}}{{\gamma }_{23}}{e}^{-M_1-m_1}\left(e^{m_1}-e^{M_1}\right)\\ m_3-M_3=\frac{{\beta }_{24}}{{\gamma }_{24}}\left(e^{-M_2}-e^{-m_2}\right)\\ =\frac{{\beta }_{24}}{{\gamma }_{24}}{e}^{-M_2-m_2}\left(e^{m_2}-e^{M_2}\right)\end{array}\right\}.$(72) Moreover (73) $\left.\begin{array}{c}{e}^{m_3}-e^{M_3}=e^{\zeta }\left(m_3-M_3\right),\\ \text{min}\left\{m_3,M_3\right\}\le \zeta \le max\left\{m_3,M_3\right\}\\ e^{m_1}-e^{M_1}=e^{\theta }\left(m_1-M_1\right),\\ \text{min}\left\{m_1,M_1\right\}\le \theta \le max\left\{m_1,M_1\right\}\\ e^{m_2}-e^{M_2}=e^{\eta }\left(m_2-M_2\right),\\ \text{min}\left\{m_2,M_2\right\}\le \eta \le max\left\{m_2,M_2\right\}\end{array}\right\}.$(73) In view of (73), equation (72) then implies that (74) $\left.\begin{array}{c}{m}_1-M_1=\frac{{\beta }_{22}}{{\gamma }_{22}}{e}^{-M_3-m_3+\zeta }\left(m_3-M_3\right)\\ m_2-M_2=\frac{{\beta }_{23}}{{\gamma }_{23}}{e}^{-M_1-m_1+\theta }\left(m_1-M_1\right)\\ m_3-M_3=\frac{{\beta }_{24}}{{\gamma }_{24}}{e}^{-M_2-m_2+\eta }\left(m_2-M_2\right)\end{array}\right\}.$(74) And so (75) $\left.\begin{array}{c}|m_1-M_1|\le \frac{{\beta }_{22}}{{\gamma }_{22}}|m_3-M_3|\\ |m_2-M_2|\le \frac{{\beta }_{23}}{{\gamma }_{23}}|m_1-M_1|\\ |m_3-M_3|\le \frac{{\beta }_{24}}{{\gamma }_{24}}|m_2-M_2|\end{array}\right\}.$(75) In addition from (68) and (75) one gets (76) $\left.\begin{array}{c}\left(1-\frac{{\beta }_{22}{\beta }_{23}{\beta }_{24}}{{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}}\right)|m_1-M_1|\le 0\\ \left(1-\frac{{\beta }_{22}{\beta }_{23}{\beta }_{24}}{{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}}\right)|m_2-M_2|\le 0\\ \left(1-\frac{{\beta }_{22}{\beta }_{23}{\beta }_{24}}{{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}}\right)|m_3-M_3|\le 0\end{array}\right\}.$(76) From which one can see that $m_1=M_1,m_2=M_2$ and $m_3=M_3$. Therefore from (50) and (51) and statement (b) of Lemma 3.1, (4) has a unique $+ve$ equilibrium point ${\mathrm{\Gamma }}_2$ and every $+ve$ solution of (4) tends to ${\mathrm{\Gamma }}_2$ as $n\to \mathrm{\infty }$.

Theorem 3.4:

Assume that (68) hold and if (77) $\begin{array}{rl}& \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\left(1+\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\right)\\ & +\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\\ & \times \left(1+\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\right)+\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\\ & \times \left(1+\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\right)\\ & +\frac{1}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\\ & \times \left(\begin{array}{c}{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-L_{22}-L_{23}-L_{24}}+\\ \frac{\begin{array}{c}\left({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)\\ \left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)\end{array}}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\end{array}\right)<1,\end{array}$(77) then ${\mathrm{\Gamma }}_2$ of (4) is globally asymptotically stable.

Proof:

Jacobian matrix $J_{{\mathrm{\Gamma }}_2}$ about ${\mathrm{\Gamma }}_2$ is (78) $J_{{\mathrm{\Gamma }}_2}=\left(\begin{array}{cccccc}0& A_1& 0& 0& A_2& 0\\ 1& 0& 0& 0& 0& 0\\ B_1& 0& 0& B_2& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& C_1& 0& 0& C_2\\ 0& 0& 0& 0& 1& 0\end{array}\right),$(78) where (79) $\left.\begin{array}{c}{A}_1=-\frac{{\alpha }_{22+}{\beta }_{22}{e}^{-\overline{z}}}{{({\gamma }_{22}+\overline{x})}^2},A_2=-\frac{{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}\\ B_1=-\frac{{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}},B_2=-\frac{{\alpha }_{23+}{\beta }_{23}{e}^{-\overline{x}}}{{({\gamma }_{23}+\overline{y})}^2}\\ C_1=-\frac{{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}},C_2=-\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{({\gamma }_{24}+\overline{z})}^2}\end{array}\right\}.$(79) Moreover the Characteristic equation of $J_{{\mathrm{\Gamma }}_2}$ about ${\mathrm{\Gamma }}_2$ is (80) ${\lambda }^6+{\mu }_1{\lambda }^4+{\mu }_2{\lambda }^3+{\mu }_3{\lambda }^2+{\mu }_4=0,$(80) where (81) $\left.\begin{array}{c}{\mu }_1=-\left(A_1+B_2+C_2\right)\\ {\mu }_2=-A_2{B}_1{C}_1\\ {\mu }_3=A_1{B}_2+A_1{C}_2+B_2{C}_2\\ {\mu }_4=-A_1{B}_2{C}_2\end{array}\right\}.$(81) Now (82) $\begin{array}{rl}\sum _{i=1}^4|{\mu }_i|& =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{({\gamma }_{22}+\overline{x})}^2}+\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{({\gamma }_{23}+\overline{y})}^2}\\ & +\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{({\gamma }_{24}+\overline{z})}^2}+\frac{{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-\overline{x}-\overline{y}-\overline{z}}}{\left({\gamma }_{22}+\overline{x}\right)\left({\gamma }_{23}+\overline{y}\right)\left({\gamma }_{24}+\overline{z}\right)}\\ & +\frac{\left({\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}\right)}{{({\gamma }_{22}+\overline{x})}^2{({\gamma }_{23}+\overline{y})}^2}\\ & +\frac{\left({\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}\right)\left({\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}\right)}{{({\gamma }_{22}+\overline{x})}^2{({\gamma }_{24}+\overline{z})}^2}\\ & +\frac{\left({\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}\right)\left({\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}\right)}{{({\gamma }_{23}+\overline{y})}^2{({\gamma }_{24}+\overline{z})}^2}\\ & +\frac{\left({\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}\right)({\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}})}{{({\gamma }_{22}+\overline{x})}^2{({\gamma }_{23}+\overline{y})}^2{({\gamma }_{24}+\overline{z})}^2},\\ & \le \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}+\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\\ & +\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\\ & +\frac{{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-L_{22}-L_{23}-L_{24}}}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\\ & +\frac{({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}})\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)}{{({\gamma }_{22}+L_{22})}^2{({\gamma }_{23}+L_{23})}^2}\\ & +\frac{({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}})\left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)}{{({\gamma }_{22}+L_{22})}^2{({\gamma }_{24}+L_{24})}^2}\\ & +\frac{({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}})\left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)}{{({\gamma }_{23}+L_{23})}^2{({\gamma }_{24}+L_{24})}^2}\\ & +\frac{\begin{array}{c}({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}})\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)\\ ({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\end{array}}{{({\gamma }_{22}+L_{22})}^2{({\gamma }_{23}+L_{23})}^2{({\gamma }_{24}+L_{24})}^2},\\ & =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\left(1+\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\right)\\ & +\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\left(1+\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\right)\\ & +\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\left(1+\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\right)\\ & +\frac{1}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\\ & \cdot \left(\begin{array}{c}{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-L_{22}-L_{23}-L_{24}}+\\ \frac{\begin{array}{c}\left({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)\\ \left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)\end{array}}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\end{array}\right).\end{array}$(82) Assuming condition (77) holds then from (82) one get ${\sum }_{i=1}^4|{\mu }_i|<1$ and hence Theorem 1.5 of [5] implies that ${\mathrm{\Gamma }}_2$ of (4) is locally asymptotically stable. Moreover by Theorem 3.3, one can see that ${\mathrm{\Gamma }}_2$ of (4) is globally asymptotically stable.

3.4. Rate of convergence

Theorem 3.5:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (4) such that (37) along with following relation hold: (83) $\left.\begin{array}{c}\overline{x}\in \left[L_{22},U_{22}\right]\\ \overline{y}\in \left[L_{23},U_{23}\right]\\ \overline{z}\in \left[L_{24},U_{24}\right]\end{array}\right\}.$(83) Then $e_n=(e_n^{22},e_{n-1}^{22},e_n^{23},e_{n-1}^{23},e_n^{24},e_{n-1}^{24}{)}^T$ of every $+ve$ solution of (4) satisfying (84) $\left.\begin{array}{c}\underset{n\to \mathrm{\infty }}{\text{lim}}(\parallel e_n\parallel {)}^{\frac{1}{n}}=|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_2}|\\ \underset{n\to \mathrm{\infty }}{\text{lim}}\frac{\parallel e_{n+1}\parallel }{\parallel e_n\parallel }=|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_2}|\end{array}\right\},$(84) where $|{\lambda }_{1,2,3,4,5,6}{J}_{{\mathrm{\Gamma }}_2}|$ are Characteristic root of $J_{{\mathrm{\Gamma }}_2}$.

Proof:

If $\{\left(x_n,y_n,z_n\right){\}}_{n=-1}^{\mathrm{\infty }}$ is a $+ve$ solution of (4), s.t., (37) along with (83) hold. For error terms, one has (85) $\left.\begin{array}{cc}{x}_{n+1}-\overline{x}& =\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-z_n}}{{\gamma }_{22}+x_{n-1}}-\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}\\ & =\frac{{\beta }_{22}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{22}+x_{n-1}\right)\left(z_n-\overline{z}\right)}\left(z_n-\overline{z}\right)\\ & -\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{\left({\gamma }_{22}+x_{n-1}\right)\left({\gamma }_{22}+\overline{x}\right)}\left(x_{n-1}-\overline{x}\right)\\ y_{n+1}-\overline{y}& =\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-x_n}}{{\gamma }_{23}+y_{n-1}}-\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}}\\ & =\frac{{\beta }_{23}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{23}+y_{n-1}\right)\left(x_n-\overline{x}\right)}\left(x_n-\overline{x}\right)\\ & -\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{\left({\gamma }_{23}+y_{n-1}\right)\left({\gamma }_{23}+\overline{y}\right)}\left(y_{n-1}-\overline{y}\right)\\ z_{n+1}-\overline{z}& =\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-y_n}}{{\gamma }_{24}+z_{n-1}}-\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}}\\ & =\frac{{\beta }_{24}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{24}+z_{n-1}\right)\left(y_n-\overline{y}\right)}\left(y_n-\overline{y}\right)\\ & -\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{\left({\gamma }_{24}+z_{n-1}\right)\left({\gamma }_{24}+\overline{z}\right)}\left(z_{n-1}-\overline{z}\right)\end{array}\right\},$(85) that is (86) $\left.\begin{array}{cc}{x}_{n+1}-\overline{x}& =\frac{{\beta }_{22}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{22}+x_{n-1}\right)\left(z_n-\overline{z}\right)}\left(z_n-\overline{z}\right)\\ & -\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{\left({\gamma }_{22}+x_{n-1}\right)\left({\gamma }_{22}+\overline{x}\right)}\left(x_{n-1}-\overline{x}\right)\\ y_{n+1}-\overline{y}& =\frac{{\beta }_{23}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{23}+y_{n-1}\right)\left(x_n-\overline{x}\right)}\left(x_n-\overline{x}\right)\\ & -\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{\left({\gamma }_{23}+y_{n-1}\right)\left({\gamma }_{23}+\overline{y}\right)}\left(y_{n-1}-\overline{y}\right)\\ z_{n+1}-\overline{z}& =\frac{{\beta }_{24}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{24}+z_{n-1}\right)\left(y_n-\overline{y}\right)}\left(y_n-\overline{y}\right)\\ & -\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{\left({\gamma }_{24}+z_{n-1}\right)\left({\gamma }_{24}+\overline{z}\right)}\left(z_{n-1}-\overline{z}\right)\end{array}\right\}.$(86) Set (87) $\left.\begin{array}{c}{e}_n^{22}=x_n-\overline{x}\\ e_n^{23}=y_n-\overline{y}\\ e_n^{24}=z_n-\overline{z}\end{array}\right\}.$(87) By (87), (86) gives (88) $\left.\begin{array}{c}{e}_{n+1}^{22}=a_n{e}_{n-1}^{22}+b_n{e}_n^{24}\\ e_{n+1}^{23}=c_n{e}_n^{22}+d_n{e}_{n-1}^{23}\\ e_{n+1}^{24}=e_n{e}_n^{23}+f_n{e}_{n-1}^{24}\end{array}\right\},$(88) where (89) $\left.\begin{array}{c}{a}_n=-\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{\left({\gamma }_{22}+x_{n-1}\right)\left({\gamma }_{22}+\overline{x}\right)}\\ b_n=\frac{{\beta }_{22}\left(e^{-z_n}-e^{-\overline{z}}\right)}{\left({\gamma }_{22}+x_{n-1}\right)\left(z_n-\overline{z}\right)}\\ c_n=\frac{{\beta }_{23}\left(e^{-x_n}-e^{-\overline{x}}\right)}{\left({\gamma }_{23}+y_{n-1}\right)\left(x_n-\overline{x}\right)}\\ d_n=-\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{\left({\gamma }_{23}+y_{n-1}\right)\left({\gamma }_{23}+\overline{y}\right)}\\ e_n=\frac{{\beta }_{24}\left(e^{-y_n}-e^{-\overline{y}}\right)}{\left({\gamma }_{24}+z_{n-1}\right)\left(y_n-\overline{y}\right)}\\ f_n=-\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{\left({\gamma }_{24}+z_{n-1}\right)\left({\gamma }_{24}+\overline{z}\right)}\end{array}\right\}.$(89) Taking the limits of $a_n,b_n,c_n,d_n,e_n$ and $f_n$ one gets (90) $\left.\begin{array}{c}\underset{n\to \mathrm{\infty }}{\text{lim}}{a}_n=-\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{\left({\gamma }_{22}+\overline{x}\right)}^2},\underset{n\to \mathrm{\infty }}{\text{lim}}{b}_n=-\frac{{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}\\ \underset{n\to \mathrm{\infty }}{\text{lim}}{c}_n=-\frac{{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}},\underset{n\to \mathrm{\infty }}{\text{lim}}{d}_n=-\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{\left({\gamma }_{23}+\overline{y}\right)}^2}\\ \underset{n\to \mathrm{\infty }}{\text{lim}}{e}_n=-\frac{{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}},\underset{n\to \mathrm{\infty }}{\text{lim}}{f}_n=-\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{\left({\gamma }_{24}+\overline{z}\right)}^2}\end{array}\right\},$(90) that is (91) $\left.\begin{array}{c}{a}_n=-\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{\left({\gamma }_{22}+\overline{x}\right)}^2}+\alpha {22}_{n-1},\\ b_n=-\frac{{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}+\alpha {24}_n,c_n=-\frac{{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}}+\alpha {22}_n\\ d_n=-\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{\left({\gamma }_{23}+\overline{y}\right)}^2}+\alpha {23}_{n-1},e_n=-\frac{{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}}\\ +\alpha {23}_n,f_n=-\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{\left({\gamma }_{24}+\overline{z}\right)}^2}+\alpha {24}_{n-1}\end{array}\right\},$(91) where $\alpha {22}_n,\alpha {22}_{n-1},\alpha {23}_n,\alpha {23}_{n-1},\alpha {24}_n,\alpha {24}_{n-1}\to 0$ as $n\to \mathrm{\infty }$. Now we have system (1.10) of [7], where (92) $\begin{array}{rl}A& =\left(\begin{array}{ccc}0& -\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{\left({\gamma }_{22}+\overline{x}\right)}^2}& 0\\ 1& 0& 0\\ -\frac{{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}}& 0& 0\\ 0& 0& 1\\ 0& 0& -\frac{{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}}\\ 0& 0& 0\end{array}\right.\\ & \left.\begin{array}{ccc}0& -\frac{{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}& 0\\ 0& 0& 0\\ -\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{\left({\gamma }_{23}+\overline{y}\right)}^2}& 0& 0\\ 0& 0& 0\\ 0& 0& -\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{\left({\gamma }_{24}+\overline{z}\right)}^2}\\ 0& 1& 0\end{array}\right),\end{array}$(92) and (93) $\begin{array}{rl}& B\left(n\right)=\left(\begin{array}{cccc}0& \alpha {22}_{n-1}& 0& 0\\ 1& 0& 0& 0\\ \alpha {22}_n& 0& 0& \alpha {23}_{n-1}\\ 0& 0& 1& 0\\ 0& 0& \alpha {23}_n& 0& \\ 0& 0& 0& 0\end{array}\right.\\ & \left.\begin{array}{cc}\alpha {24}_n& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& \alpha {24}_{n-1}\\ 1& 0\end{array}\right),\end{array}$(93) and $B\left(n\right)\to 0$, $n\to \mathrm{\infty }$. Thus error terms about ${\mathrm{\Gamma }}_2$ similar to Linearized system of (4) is (94) $\begin{array}{rl}& \left(\begin{array}{c}\begin{array}{c}{e}_{n+1}^{22}\\ e_n^{22}\\ e_{n+1}^{23}\end{array}\\ \begin{array}{c}{e}_n^{23}\\ e_{n+1}^{24}\\ e_n^{24}\end{array}\end{array}\right)=\left(\begin{array}{ccc}0& -\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-\overline{z}}}{{\left({\gamma }_{22}+\overline{x}\right)}^2}& 0\\ 1& 0& 0\\ -\frac{{\beta }_{23}{e}^{-\overline{x}}}{{\gamma }_{23}+\overline{y}}& 0& 0\\ 0& 0& 1\\ 0& 0& -\frac{{\beta }_{24}{e}^{-\overline{y}}}{{\gamma }_{24}+\overline{z}}\\ 0& 0& 0\end{array}\right.\\ & \left.\begin{array}{ccc}0& -\frac{{\beta }_{22}{e}^{-\overline{z}}}{{\gamma }_{22}+\overline{x}}& 0\\ 0& 0& 0\\ -\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-\overline{x}}}{{\left({\gamma }_{23}+\overline{y}\right)}^2}& 0& 0\\ 0& 0& 0\\ 0& 0& -\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-\overline{y}}}{{\left({\gamma }_{24}+\overline{z}\right)}^2}\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}\begin{array}{c}{e}_n^{22}\\ e_{n-1}^{22}\\ e_n^{23}\end{array}\\ \begin{array}{c}{e}_{n-1}^{23}\\ e_n^{24}\\ e_{n-1}^{24}\end{array}\end{array}\right).\end{array}$(94)

4. Numerical simulations

Here we will verify theoretical results obtain in Section 2–3 numerically. If ${\alpha }_{19}=45,{\beta }_{19}=4,{\gamma }_{19}=7.0,{\alpha }_{20}=39,{\beta }_{20}=3,{\gamma }_{20}=4,{\alpha }_{21}=59,{\beta }_{21}=2,{\gamma }_{21}=4$ then (3) with $x_0=0.2,x_{-1}=0.7,y_0=0.4,y_{-1}=1.9,z_0=0.4,z_{-1}=0.9$ can be written as (95) $\begin{array}{rl}{x}_{n+1}& =\frac{45+4e^{-y_n}}{7.0+z_{n-1}},y_{n+1}=\frac{39+3e^{-z_n}}{4+x_{n-1}},\\ z_{n+1}& =\frac{59+2e^{-x_n}}{48+y_{n-1}}.\end{array}$(95)

From computations it is easy to confirm that for above chosen values of parameters ${\alpha }_{19}=45,{\beta }_{19}=4,{\gamma }_{19}=7.0,{\alpha }_{20}=39,{\beta }_{20}=3,{\gamma }_{20}=4,{\alpha }_{21}=59,{\beta }_{21}=2,{\gamma }_{21}=4$ conditions under which ${\mathrm{\Gamma }}_1$ is globally asymptotically stable hold, i.e. $\begin{array}{rl}& {\beta }_{19}{\beta }_{20}{\beta }_{21}\\ & =24<{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}=112\text{and}\\ & \frac{1}{{\gamma }_{19}+L_{21}}\left(\frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{{({\gamma }_{20}+L_{19})}^2}\right.\\ & \left.+\frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{21}+L_{20}\right)}\right)\\ & +\frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}\\ & +\frac{1}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}.\end{array}$ $\begin{array}{rl}& \left(\frac{\begin{array}{c}{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}\\ +\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\\ \left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)\end{array}}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\right)\\ & =0.0909986005619405595473877796<1.\end{array}$

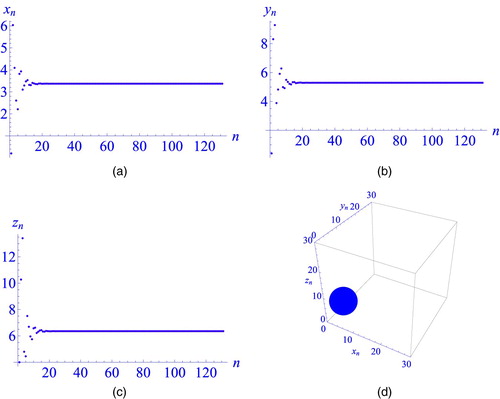
Moreover, plot of $nvs{x}_n,nvs{y}_n,nvs{z}_n$ and its Global attractor is shown in Figure 1(a–d), respectively. Now if ${\alpha }_{19}=45,{\beta }_{19}=4,{\gamma }_{19}=27,{\alpha }_{20}=39,{\beta }_{20}=3,{\gamma }_{20}=14,{\alpha }_{21}=59,{\beta }_{21}=2,{\gamma }_{21}=4$ then (3) with $x_0=0.002,x_{-1}=0.07,y_0=0.004,y_{-1}=1.9,z_0=4,z_{-1}=0.9$ can be written as (96) $\begin{array}{rl}{x}_{n+1}& =\frac{45+4e^{-y_n}}{27+z_{n-1}},y_{n+1}=\frac{39+3e^{-z_n}}{14+x_{n-1}},\\ z_{n+1}& =\frac{59+2e^{-x_n}}{4+y_{n-1}}.\end{array}$(96) Computations show that if ${\alpha }_{19}=45,{\beta }_{19}=4,{\gamma }_{19}=27,{\alpha }_{20}=39,{\beta }_{20}=3,{\gamma }_{20}=14,{\alpha }_{21}=59,{\beta }_{21}=2,{\gamma }_{21}=4$ then conditions under which ${\mathrm{\Gamma }}_1$ 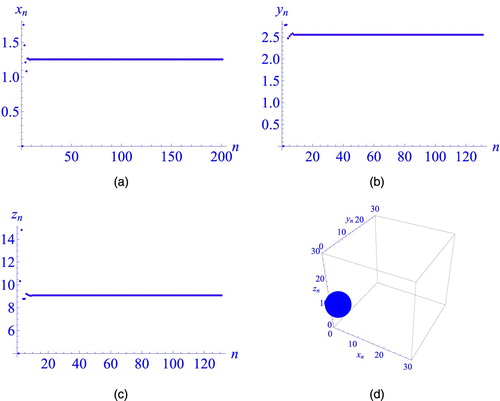is globally asymptotically stable hold, i.e. $\begin{array}{rl}{\beta }_{19}{\beta }_{20}{\beta }_{21}& =24<{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}=1512\text{and}\frac{1}{{\gamma }_{19}+L_{21}}\\ & \times \left(\frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{{({\gamma }_{20}+L_{19})}^2}\right.\\ & \left.+\frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{21}+L_{20}\right)}\right)\\ & +\frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}\\ & +\frac{1}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}.\end{array}$ $\begin{array}{rl}& \left(\begin{array}{c}{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}+\\ \frac{\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}\end{array}\right)\\ & =0.0856704522853635631846346627<1.\end{array}$

Figure 1. Graph for (95).

Moreover, plot of $nvs{x}_n,nvs{y}_n,nvs{z}_n$ and Global attractor is shown in Figure 2(a–d), respectively. For system (4), if we choose ${\alpha }_{22}=315,{\beta }_{22}=1.4,{\gamma }_{22}=1.7,{\alpha }_{23}=222,{\beta }_{23}=123,{\gamma }_{23}=124,{\alpha }_{24}=222,{\beta }_{24}=112,{\gamma }_{24}=114$ with $x_0=0.2,x_{-1}=0.1,y_0=0.4,y_{-1}=0.29,z_0=2,z_{-1}=0.9$ can be written as (97) $\begin{array}{rl}{x}_{n+1}& =\frac{315+1.4e^{-z_n}}{1.7+x_{n-1}},y_{n+1}=\frac{222+123e^{-x_n}}{124+y_{n-1}},\\ z_{n+1}& =\frac{222+1129e^{-y_n}}{114+z_{n-1}}.\end{array}$(97) For these values ${\alpha }_{22}=315,{\beta }_{22}=1.4,{\gamma }_{22}=1.7,{\alpha }_{23}=222,{\beta }_{23}=123,{\gamma }_{23}=124,{\alpha }_{24}=222,{\beta }_{24}=112,{\gamma }_{24}=114$ 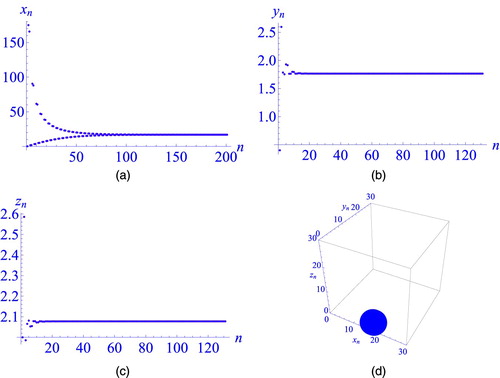the conditions under which ${\mathrm{\Gamma }}_2$ is globally asymptotically stable satisfied, i.e. ${\beta }_{22}{\beta }_{23}{\beta }_{24}=19286.399999999998<{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}=24031.199999999997$ and $\begin{array}{rl}& \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\left(1+\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\right)\\ & +\frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}\left(1+\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\right)\\ & +\frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}\left(1+\frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}\right)\\ & +\frac{1}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}.\end{array}$ $\begin{array}{rl}& \left(\begin{array}{c}{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-L_{22}-L_{23}-L_{24}}+\\ \frac{\left({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)\left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}\end{array}\right)\\ & =0.2351437011808576519431082194520031<1.\end{array}$Moreover, plot of $nvs{x}_n,nvs{y}_n,nvs{z}_n$ and its attractor is shown in Figure 3(a–d), respectively.

Figure 2. Graph for (96).

Figure 3. Graph for (97).

5. Conclusions

We have explored the global properties of exponential systems of difference equations. For both systems, we have studied the dynamics including boundedness and persistence, existence of invariant rectangle, existence of the unique $+\text{ve}$ equilibrium, global and local dynamics about the unique $+\text{ve}$ equilibrium point and conclusion are presented in Tables 2–4. Furthermore rate of convergence for each system is also demonstrated. Finally, theoretical results are verified numerically.

Table 2. Existence of invariant rectangle corresponding to system (3) and (4).

Systems	Existence of invariant rectangle
(3)	$\left[L_{19},U_{19}\right]\times [L_{20},U_{20}\left]\times \right[L_{21},U_{21}]$ where
	$L_{19}={\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}{e}^{-{\displaystyle \frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}}}{{\gamma }_{19}+{\displaystyle \frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}}}},U_{19}={\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}},L_{20}={\displaystyle \frac{{\alpha }_{20}+{\beta }_{20}{e}^{-{\displaystyle \frac{{\alpha }_{21}+{\beta }_{21}}{{\gamma }_{21}}}}}{{\gamma }_{20}+{\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}}}},U_{20}={\displaystyle \frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}},$
	$L_{21}={\displaystyle \frac{{\alpha }_{21}+{\beta }_{21}{e}^{-{\displaystyle \frac{{\alpha }_{19}+{\beta }_{19}}{{\gamma }_{19}}}}}{{\gamma }_{21}+{\displaystyle \frac{{\alpha }_{20}+{\beta }_{20}}{{\gamma }_{20}}}}},U_{21}={\displaystyle \frac{{\alpha }_{21+}{\beta }_{21}}{{\gamma }_{21}}}.$
(4)	$[L_{22},U_{22}]\times [L_{23},U_{23}]\times [L_{24},U_{24}]$ where
	$L_{22}={\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}}}{{\gamma }_{22}+{\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}}}},U_{22}={\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}},L_{23}={\displaystyle \frac{{\alpha }_{23+}{\beta }_{23}{e}^{-{\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}}{{\gamma }_{22}}}}}{{\gamma }_{23}+{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}}}},U_{23}={\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}},$
	$L_{24}={\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}{e}^{-{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}}{{\gamma }_{23}}}}}{{\gamma }_{24}+{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}}{{\gamma }_{24}}}}},U_{24}={\displaystyle \frac{{\alpha }_{24+}{\beta }_{24}}{{\gamma }_{24}}}.$

Table 3. Existence of the uniqueness $+\text{ve}$ equilibrium of system (3) and (4).

Systems	Existence of the uniqueness $+\text{ve}$ equilibrium
(3)	${\beta }_{19}{\beta }_{20}{\beta }_{21}<{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}.$
(4)	${\beta }_{22}{\beta }_{23}{\beta }_{24}<{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}.$

Table 4. Existence of parametric conditions under which the $+\text{ve}$ equilibrium of system (3) and (4) is globally asymptotically stable.

Systems	Existence of parametric conditions under which the $+\text{ve}$ equilibrium point is GAS
(3)	$\left(\overline{x},\overline{y},\overline{z}\right)\in \left[L_{19},U_{19}\right]\times [L_{20},U_{20}\left]\times \right[L_{21},U_{21}]$ is GAS if
	${\beta }_{19}{\beta }_{20}{\beta }_{21}<{\gamma }_{19}{\gamma }_{20}{\gamma }_{21}$ and
	${\displaystyle \frac{1}{{\gamma }_{19}+L_{21}}}\left({\displaystyle \frac{{\beta }_{19}{e}^{-L_{20}}\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)}{{({\gamma }_{20}+L_{19})}^2}}+{\displaystyle \frac{{\beta }_{21}{e}^{-L_{19}}\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{21}+L_{20}\right)}}\right)+{\displaystyle \frac{{\beta }_{20}{e}^{-L_{21}}\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{20}+L_{19}\right){({\gamma }_{21}+L_{20})}^2}}+{\displaystyle \frac{1}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}}\left(\begin{array}{c}{\beta }_{19}{\beta }_{20}{\beta }_{21}{e}^{-L_{19}-L_{20}-L_{21}}+\\ {\displaystyle \frac{\left({\alpha }_{19}+{\beta }_{19}{e}^{-L_{20}}\right)\left({\alpha }_{20}+{\beta }_{20}{e}^{-L_{21}}\right)\left({\alpha }_{21}+{\beta }_{21}{e}^{-L_{19}}\right)}{\left({\gamma }_{19}+L_{21}\right)\left({\gamma }_{20}+L_{19}\right)\left({\gamma }_{21}+L_{20}\right)}}\end{array}\right)<1.$
(4)	$\left(\overline{x},\overline{y},\overline{z}\right)\in \left[L_{22},U_{22}\right]\times [L_{23},U_{23}\left]\times \right[L_{24},U_{24}]$ is GAS if ${\beta }_{22}{\beta }_{23}{\beta }_{24}<{\gamma }_{22}{\gamma }_{23}{\gamma }_{24}$ and
	${\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}}\left(1+{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}}\right)+{\displaystyle \frac{{\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}}{{({\gamma }_{23}+L_{23})}^2}}\left(1+{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}}\right)+{\displaystyle \frac{{\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}}{{({\gamma }_{24}+L_{24})}^2}}\left(1+{\displaystyle \frac{{\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}}{{({\gamma }_{22}+L_{22})}^2}}\right)$
	$+{\displaystyle \frac{1}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}}\left(\begin{array}{c}{\beta }_{22}{\beta }_{23}{\beta }_{24}{e}^{-L_{22}-L_{23}-L_{24}}+\\ {\displaystyle \frac{\left({\alpha }_{22}+{\beta }_{22}{e}^{-L_{24}}\right)\left({\alpha }_{23}+{\beta }_{23}{e}^{-L_{22}}\right)\left({\alpha }_{24}+{\beta }_{24}{e}^{-L_{23}}\right)}{\left({\gamma }_{22}+L_{22}\right)\left({\gamma }_{23}+L_{23}\right)\left({\gamma }_{24}+L_{24}\right)}}\end{array}\right)<1.$

Acknowledgement

The author declares that he got no funding on any part of this research.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

A. Q. Khan http://orcid.org/0000-0002-0278-1352