Cut vertex and cut edge problem for topological graph indices

Abstract

The symmetric figure of a molecule and the fact that the bond polarities are equal imply that the polarities of the bonds cancel each other out and the molecule would be nonpolar. Many molecules are nonpolar, but have polar bonds. A chemical bond is polar if the atoms on either end of its molecular diagram are different. Therefore, the notion of symmetry plays an important role in chemical as well as the mathematical study of molecular graphs. By means of graph pieces such as cut vertices, cut edges and bridges, it is possible to separate a large graph into smaller pieces which we can handle easily. Using this new combinatorial technique for graphs, we obtain several formulae for some important topological graph indices of symmetrical graphs by means of smaller ones.

Keywords:

• Cut-vertex
• cut-edge
• bridge
• topological graph index

MSC Numbers:

• 05C07
• 05C30
• 37F20
• 14J80
• 11F23

1. Introduction

Let $G=(V,E)$ be a simple $(n,m)$ graph with $\mid V\left(G\right)\mid =n$ vertices and $\mid E\left(G\right)\mid =m$ edges. That is, we do not allow loops or multiple edges. For a vertex $v\in V\left(G\right)$, we denote the degree of v by $d_G\left(v\right)$.

Topological graph indices have been used in a lot of areas to study required properties of different objects such as atoms and molecules. Such indices have been described and studied by many mathematicians and chemists since most graphs are generated from molecules by replacing each atom with a vertex and each chemical bond with an edge. These indices are also topological graph invariants measuring several chemical, physical, biological, pharmacological, pharmaceutical, etc. properties of graphs corresponding to real life situations. They are grouped mainly into three classes according to their definition: by vertex degrees, by distances or by matrices.

Two of the most popular topological graph indices are called the first and second Zagreb indices denoted by $M_1\left(G\right)$ and $M_2\left(G\right)$, respectively: $\begin{array}{rl}{M}_1\left(G\right)& =\sum _{u\in V\left(G\right)}\left(d_G\right(u){)}^2\mathrm{a}\mathrm{n}\mathrm{d}\\ M_2\left(G\right)& =\sum _{uv\in E\left(G\right)}{d}_G\left(u\right)d_G\left(v\right).\end{array}$ They were defined in 1972 by Gutman and Trinajstic [1] and are mostly referred to due to their advantages in QSAR and QSPR studies. In Das et al. [2], some results on the first Zagreb index together with some other indices are given. In Das et al. [3], multiplicative Zagreb indices of graph operations were studied. In Ranjini et al. [4], Zagreb indices of subdivision graphs were considered and in Ranjini et al. [5], Zagreb indices of the line graphs of the subdivision graphs are found.

There is a large number of results on these indices for several graphs, or sometimes for a general graph. In Bell [6], some irregularity indices are considered. The Albertson irregularity index is defined by $Irr\left(G\right)=\sum _{uv\in E\left(G\right)}\mid d_G\left(u\right)-d_G\left(v\right)\mid ,$ see [7]. There are other irregularity indices in the literature. For one of these indices, there was no investigation until some time after it was mentioned that it may have several useful properties [8]. Motivated by this fact, the authors studied this index denoted by σ in resemblance with the standard deviation in statistics and defined by $\sigma \left(G\right)=\sum _{uv\in E\left(G\right)}\left(d_G\right(u)-d_G(v){)}^2.$ The hyper-Zagreb index is defined by $HM\left(G\right)=\sum _{uv\in E\left(G\right)}\left(d_G\right(u)+d_G(v){)}^2.$ The forgotten index is defined by $F\left(G\right)=\sum _{u\in V\left(G\right)}\left(d_G\right(u){)}^3.$ The first entire-Zagreb index is defined by $M_1^{ϵ}\left(G\right)=\sum _{u\in V\left(G\right)}\left(d_G\right(u){)}^2+\sum _{uv\in E\left(G\right)}{d}_G(u\left)d_G\right(v).$ 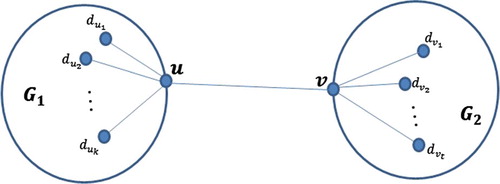A vertex v in a graph G is called a cut-vertex if deleting v from G increases the number of components of G. An edge e = uv in a graph G is called a bridge if deleting e from G increases the number of components in G. Similarly an edge e = uv in a graph G is called a cut-edge if deleting e together with end vertices u and v from G increases the number of components in G. We shall denote the two parts of a graph G which are separated from each other by a cut-vertex, a bridge or a cut-edge by $G_1$ and $G_2$. In this paper, we study the effect of deleting a cut-vertex, a bridge and a cut-edge from a graph G on first and second Zagreb indices, forgotten index, hyper-Zagreb index, irregularity index, σ index and first entire Zagreb index. Knowing the result of these three operations will help us to calculate this indices for a large graph without doing a lot of calculations. It will be necessary and sufficient to calculate this indices for some smaller graphs such as cycles, paths and complete graphs.

In molecular chemistry, a bond is called polar if the two atoms on either ends are different. Many molecules in chemistry are nonpolar with polar bonds. The symmetry of a given molecule is determined by means of some symmetry operations around some symmetry elements. A symmetry element could be a line, a point or a plane. A rotation or reflection around such an element leaves the object in an orientation indistinguishable from the original. Most of the molecules have certain symmetries. Symmetry means that the polarities of the chemical bonds are exactly the same and hence the polarities of these bonds cancel out each other. This leaves a nonpolar molecule. In Figure 1, the first three members of the class of alkanes which are examples of symmetrical molecules are shown.

Figure 1. Symmetry in alkanes.

A molecule is called chiral if it is not superimposable on its mirror image. Most chiral molecules can be identified by their lack of a plane of symmetry or a centre of symmetry. An inversion centre is a point in the molecule through which all other atoms can be reflected 180 degrees into another identical atom. Rarely, the inversion centre could be between two atoms. Algebraically, an inversion through a centre is equivalent to a rotation by 180 degrees followed by a reflection through a plane perpendicular to the rotation axis. This type of symmetry is more common in inorganic molecules. Whenever there are asymmetric atoms in a molecule, there is the possibility of stereo-isomers and chiral molecules are very important in biochemistry as many organisms could react to stereo-isomers differently. As seen, the notion of symmetry in a molecule gives important clues about the molecule and therefore is an essential subject. See the symmetry in an acetic anhydride molecule in Figure 2.

Figure 2. Acetic anhydride.

In Section 2, we describe the methods we shall be using to obtain our results in later parts of the paper. In Section 3, we study three problems which are called as cut-vertex, cut-edge and bridge problem and calculate the topological indices in each of these cases. In Section 4, a brief discussion of the results obtained in Section 3 is given. In Section 5, some conclusions that are reached by the given results that are mentioned and also some open problems are given.

2. Materials and methods

A bond in a chemical molecule is polar if the atoms on either end of its molecular diagram are different. If a molecule has a symmetric shape and the bond polarities are equal, then the polarities of the bonds cancel each other out and the molecule becomes nonpolar which is a desirable property. Many molecules are nonpolar, but have polar bonds. Therefore, the notion of symmetry plays an important role in the mathematical study of molecular graphs.

The symmetry that a molecule has could be around a vertex or an edge. For example, the symmetry in a water molecule is around a vertex, and the symmetry in an ethane molecule is around an edge, see Figure 1. If a graph G is symmetric at a vertex v, or at an edge e, then both sides of G separated by v or e are mirror images of each other. Let us denote each of these two parts by $G_1$. In the former case where v is a symmetry point for G, G−v has two symmetrical $G_1$'s and this case is denoted by $G=Sy{m}_2^v{G}_1$. An arbitrary (molecular) graph G could sometimes have more than two symmetrical $G_1$'s. If G has n symmetrical $G_1$'s, we shall write $G=Sy{m}_n^v{G}_1$. If G is symmetrical at a bridge b = uv (or a cut-edge e = uv), then we use the notation $G=Sy{m}_n^b{G}_1$ (or $G=Sy{m}_n^e{G}_1$) similarly. Here, we shall do calculations for n = 2. They can easily be generalized to any $n\ge 3$.

The above-mentioned symmetries occur around some graph pieces such as cut vertices, cut edges and bridges. By means of these graph pieces, it is possible to separate a large graph into smaller pieces which we can handle easily. Using this method, we obtain several formulae for some of the important topological graph indices for symmetrical graphs by means of smaller ones. In particular, we calculate these topological graph indices for symmetrical graphs with symmetry being around a cut vertex, cut edge or a bridge.

3. Results

3.1. Effect of cut-vertices on topological indices

In this subsection, we give some results on the cut-vertex problem for topological indices such as first and second Zagreb indices, forgotten index, sigma index, irregularity index, hyper-Zagreb index and first entire-Zagreb index.

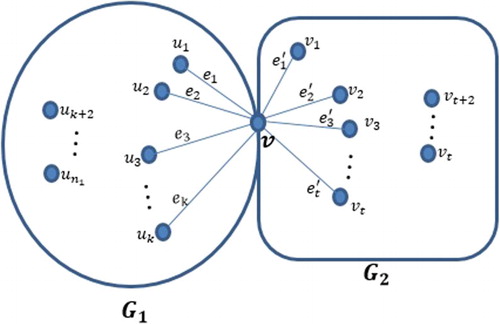
Theorem 3.1

Let $G_1$ and $G_2$ be two simple connected $(n_1,m_1)$ and $(n_2,m_2)$ graphs, respectively, and let G be a graph which consists of two components $G_1$ and $G_2$ having only a common vertex v. Let $k=d_{G_1}\left(v\right)$ and $t=d_{G_2}\left(v\right),$ see Figure  3. Then $M_1\left(G\right)=M_1\left(G_1\right)+M_1\left(G_2\right)+2d_{G_1}\left(v\right)d_{G_2}\left(v\right).$

Figure 3. A cut-vertex v.

Proof.

Since $M_1\left(G\right)=\sum _{u\in V\left(G\right)}{d}_G\left(u\right)$, then $M_1\left(G_1\right)=\sum _{i=1}^k\left[d_{G_1}\right(u_i){]}^2+[d_{G_1}\left(v\right){]}^2+\sum _{i=k+2}^{n_1}\left[d_{G_1}\right(u_i){]}^2$ and $M_1\left(G_2\right)=\sum _{j=1}^t\left[d_{G_2}\right(v_j){]}^2+[d_{G_2}\left(v\right){]}^2+\sum _{j=t+2}^{n_2}\left[d_{G_2}\right(v_j){]}^2,$ where for $i=1,2,\dots ,k$, $u_i$'s are the neighbours of v in $G_1$ and for $j=1,2,\dots ,t$, $v_j$'s are the neighbours of v in $G_2$. So $\begin{array}{rl}{M}_1\left(G\right)& =\sum _{i=1}^k\left[d_{G_1}\right(u_i){]}^2+\sum _{j=1}^t[d_{G_2}\left(v_j\right){]}^2+\left[d_G\right(v){]}^2\\ & +\sum _{i=k+2}^{n_1}\left[d_{G_1}\right(u_i){]}^2+\sum _{j=t+2}^{n_2}[d_{G_2}\left(v_j\right){]}^2\\ & =\sum _{i=1}^k\left[d_{G_1}\right(u_i){]}^2+\sum _{j=1}^t[d_{G_2}\left(v_j\right){]}^2+(k+t{)}^2\\ & +\sum _{i=k+2}^{n_1}\left[d_{G_1}\right(u_i){]}^2+\sum _{j=t+2}^{n_2}[d_{G_2}\left(v_j\right){]}^2\\ & =M_1\left(G_1\right)+M_1\left(G_2\right)+2d_{G_1}\left(v\right)d_{G_2}\left(v\right).\end{array}$ Hence the result is obtained.

Corollary 3.2

Let G be a graph as given in Theorem 3.1 with $G_1=G_2$. Then the first Zagreb index of G in terms of the first Zagreb index of $G_1$ is $M_1\left(G\right)=M_1\left(Sy{m}_2^v{G}_1\right)=2M_1\left(G_1\right)+2d_{G_1}(v{)}^2.$

Theorem 3.3

Let G be a graph as given in Theorem 3.1. Then $\begin{array}{rl}{M}_2\left(G\right)& =M_2\left(G_1\right)+M_2\left(G_2\right)+t\cdot \sum _{i=1}^k{d}_{G_1}\left(u_i\right)\\ & +k\cdot \sum _{j=1}^t{d}_{G_2}\left(v_j\right).\end{array}$

Proof.

It follows by the definition of $M_2\left(G\right)$.

Example 3.4

Let $G_1=G_2=K_{r,s}$. Then, $M_1\left(K_{r,s}\right)=r{s}^2+s{r}^2=rs(r+s).$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v{K}_{r,s}\right)& =2r{s}^2+(2s-2)r^2+(2r{)}^2\\ & =2r{s}^2+2s{r}^2-2r^2+4r^2\\ & =2rs(r+s)+2r^2\\ & =2M_1\left(K_{r,s}\right)+2r^2.\end{array}$ Let secondly $G_1=G_2=P_n$. Then, $M_1\left(P_n\right)=4n-6.$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v{P}_n\right)& =(2n-3)2^2+2\cdot 1^2\\ & =2M_1\left(P_n\right)+2.\end{array}$ Let thirdly $G_1=G_2=K_n$. Then, $M_1\left(K_n\right)=n(n-1{)}^2.$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v\right(K_n\left)\right)& =2(n-1)(n-1{)}^2\\ & +(2n-2{)}^2\\ & =\frac{2(n+1)}{n}{M}_1\left(K_n\right).\end{array}$ Let now $G_1=G_2=T_{r,s}$. Then, $M_1\left(T_{r,s}\right)=4(r+s)+2.$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v\right(T_{r,s}\left)\right)& =(2s-1)\cdot 2^2+2\cdot 3^2\\ & +(2r-2)\cdot 2^2\\ & =2M_1\left(Tr,s\right)+2.\end{array}$ Let $G_1=G_2=C_n$. Then, $M_1\left(K_n\right)=4n.$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v\right(C_n\left)\right)& =8(n+1)\\ & =2M_1\left(C_n\right)+8.\end{array}$ Let finally $G_1=G_2=S_n$. Then, $M_1\left(S_n\right)=n(n-1).$ So $\begin{array}{rl}{M}_1\left(G\right)=M_1\left(Sy{m}_2^v\right(S_n\left)\right)& =2(n-2)\cdot 1^2\\ & +2(n-1{)}^2+2^2\\ & =2M_1\left(S_n\right)+2.\end{array}$

Theorem 3.5

Let G be a graph as given in Theorem 3.1. Then $Irr\left(G\right)\le Irr\left(G_1\right)+Irr\left(G_2\right)+2d_{G_1}\left(v\right)d_{G_2}\left(v\right).$

Proof.

Since $Irr\left(G\right)=\sum _{uv\in E\left(G\right)}\mid d_G\left(u\right)-d_G\left(v\right)\mid$, we can write $\begin{array}{rl}Irr\left(G_1\right)& =\sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-d_{G_1}\left(v\right)\mid \\ & +\sum _{\begin{array}{c}w,q\in V\left(G_1\right)\\ w,q\ne v\\ w\sim q\end{array}}\mid d_{G_1}\left(w\right)-d_{G_1}\left(q\right)\mid \\ & =\sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-k\mid +A,\end{array}$ and $\begin{array}{rl}Irr\left(G_2\right)& =\sum _{j=1}^t\mid d_{G_2}\left(u_j\right)-d_{G_2}\left(v\right)\mid \\ & +\sum _{\begin{array}{c}w,q\in V\left(G_2\right)\\ w,q\ne v\\ w\sim q\end{array}}\mid d_{G_2}\left(w\right)-d_{G_2}\left(q\right)\mid \\ & =\sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-k\mid +B,\end{array}$ where $A=\sum _{\begin{array}{c}w,q\in V\left(G_1\right)\\ w,q\ne v\\ w\sim q\end{array}}\mid d_{G_1}\left(w\right)-d_{G_1}\left(q\right)\mid$ and $B=\sum _{\begin{array}{c}w,q\in V\left(G_2\right)\\ w,q\ne v\\ w\sim q\end{array}}\mid d_{G_2}\left(w\right)-d_{G_2}\left(q\right)\mid$. So $\begin{array}{rl}Irr\left(G\right)& =\sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-d_G\left(v\right)\mid \\ & +\sum _{j=1}^t\mid d_{G_2}\left(u_j\right)-d_G\left(v\right)\mid +A+B\\ & =\sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-k-t\mid \\ & +\sum _{j=1}^t\mid d_{G_2}\left(u_j\right)-k-t\mid +A+B\\ & \le \sum _{i=1}^k\mid d_{G_1}\left(u_i\right)-k\mid +\sum _{i=1}^{k}t\\ & +\sum _{j=1}^t\mid d_{G_2}\left(u_j\right)-t\mid +\sum _{j=1}^{t}k+A+B\\ & =Irr\left(G_1\right)+Irr\left(G_2\right)+2d_{G_1}\left(v\right)d_{G_2}\left(v\right).\end{array}$ This gives the desired result.

Corollary 3.6

Let G be a graph as given in Theorem 3.1 with $G_1=G_2$. Then $Irr\left(G\right)\le 2Irr\left(G_1\right)+2\left(d_{G_1}\right(v){)}^2.$

The following three results follow from definitions as in previous results.

Theorem 3.7

Let G be a graph as given in Theorem 3.1. Then $\begin{array}{rl}\sigma \left(G\right)& =\sigma \left(G_1\right)+\sigma \left(G_2\right)\\ & +3d_{G_1}\left(v\right)d_{G_2}\left(v\right)\left(d_{G_1}\left(v\right)+d_{G_2}\left(v\right)\right)\\ & -2\left[d_{G_2}\left(v\right)\sum _{i=1}^k{d}_{G_1}\left(u_i\right)+d_{G_1}\left(v\right)\sum _{j=1}^t{d}_{G_2}\left(v_j\right)\right].\end{array}$

Theorem 3.8

Let G be a graph as given in Theorem 3.1. Then $\begin{array}{rl}F\left(G\right)& =F\left(G_1\right)+F\left(G_2\right)+3d_{G_1}\left(v\right)d_{G_2}\left(v\right)\left(d_{G_1}\right(v)\\ & +d_{G_2}\left(v\right)).\end{array}$

Theorem 3.9

Let G be a graph as given in Theorem 3.1. Then $\begin{array}{rl}HM\left(G\right)& =HM\left(G_1\right)+HM\left(G_2\right)\\ & +3d_{G_1}\left(v\right)d_{G_2}\left(v\right)\left(d_{G_1}\right(v)+d_{G_2}(v\left)\right)\\ & +2\left[d_{G_2}\left(v\right)\sum _{i=1}^k{d}_{G_1}\left(u_i\right)+d_{G_1}\left(v\right)\sum _{j=1}^t{d}_{G_2}\left(v_j\right)\right].\end{array}$

Theorem 3.10

Let G be a graph as given in Theorem 3.1. Then $\begin{array}{rl}{M}_1^{ϵ}\left(G\right)& =M_1^{ϵ}\left(G_1\right)+M_1^{ϵ}\left(G_2\right)\\ & +d_{G_1}\left(v\right)d_{G_2}\left(v\right)\left(d_{G_1}\right(v)+d_{G_2}(v)+2)\\ & +\left[d_{G_2}\left(v\right)\sum _{i=1}^k{d}_{e_i}+d_{G_1}\left(v\right)\sum _{j=1}^t{d}_{e_j}\right].\end{array}$

Proof.

Since $M_1^{ϵ}\left(G\right)=\sum _{i\in V\left(G\right)}{d}_i^2+\sum _{e\in E\left(G\right)}{d}_e^2,$ then $\begin{array}{rl}{M}_1^{ϵ}\left(G_1\right)& =\sum _{i=1}^k\left(d_{G_1}\right(u_i){)}^2+(d_{G_1}\left(v\right){)}^2\\ & +\sum _{i=k+2}^{n_1}\left(d_{G_1}\right(u_i){)}^2+\sum _{i=1}^k{d}_{e_i}^2+\sum _{i=k+2}^{m_1}{d}_{e_i}^2,\end{array}$ and $\begin{array}{rl}{M}_1^{ϵ}\left(G_2\right)& =\sum _{j=1}^t\left(d_{G_2}\right(v_j){)}^2+(d_{G_2}\left(v\right){)}^2\\ & +\sum _{j=t+2}^{n_2}\left(d_{G_2}\right(v_j){)}^2+\sum _{j=1}^t{d}_{e_j^{\mathrm{\prime }}}^2\\ & +\sum _{j=t+2}^{m_2}{d}_{e_j^{\mathrm{\prime }}}^2.\end{array}$ So $\begin{array}{rl}{M}_1^{ϵ}\left(G\right)& =\sum _{i=1}^k\left(d_{G_1}\right(u_i){)}^2+\sum _{j=1}^t(d_{G_2}\left(v_j\right){)}^2\\ & +\sum _{i=k+2}^{n_1}\left(d_{G_1}\right(u_i){)}^2+\sum _{i=k+2}^{m_1}{d}_{e_i}^2+(k+t{)}^2\\ & +\sum _{j=t+2}^{n_2}\left(d_{G_2}\right(v_j){)}^2+\sum _{j=t+2}^{m_2}{d}_{e_j^{\mathrm{\prime }}}^2+\sum _{i=1}^k(d_{e_i}+t{)}^2\\ & +\sum _{j=1}^t(d_{e_j^{\mathrm{\prime }}}+k{)}^2.\end{array}$ Hence, the result follows.

Corollary 3.11

Let G be a graph as given in Theorem 3.1 with $G_1=G_2$. Then $\begin{array}{rl}{M}_1^{ϵ}\left(G\right)& =2M_1^{ϵ}\left(G_1\right)+2\left(\right(d_{G_1}\left(v\right){)}^2\\ & +\left(d_{G_1}\right(v\left){)}^3\right)+4d_{G_1}\left(v\right)\sum _{i=1}^k{d}_{e_i}.\end{array}$

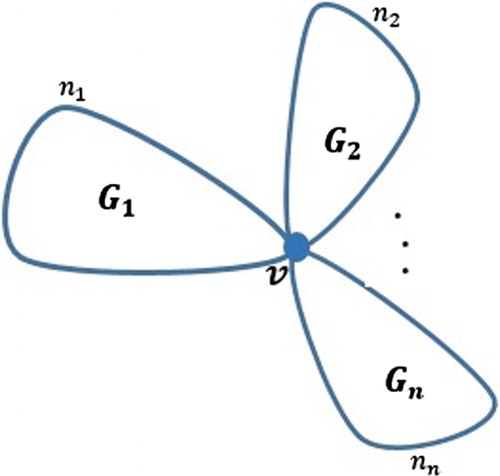
We can generalize this result to a graph with n parts meeting at a common vertex:

Corollary 3.12

For a graph G consisting of graphs $G_1,G_2,\cdots ,G_n$ all meeting at a common vertex v, see Figure 4, we have $M_1\left(G\right)=\sum _{i=1}^n{M}_1\left(G_i\right)+2\left[\sum _{\begin{array}{c}i,j=1\\ i<j\end{array}}^n{d}_{G_i}\left(v\right)d_{G_j}\left(v\right)\right].$

Figure 4. n graphs meeting at v.

Corollary 3.13

If all $G_i$ in Corollary 3.12 are the same, then $M_1\left(G\right)=M_1\left(Sy{m}_n^v{G}_1\right)=n{M}_1\left(G_1\right)+(n^2-n)\left(d_{G_1}\right(v){)}^2.$

3.2. Effect of bridges on topological indices

Secondly, we shall search for the topological graph indices of the graphs which have components connected to each other by bridges. In Theorem 3.14, we calculate the first Zagreb index of G in terms of $G_1$ and $G_2$:

Theorem 3.14

Let $G_1$ and $G_2$ be two simple connected $(n_1,m_1)$ and $(n_2,m_2)$ graphs, respectively, and let G be a graph which consists of two components $G_1$ and $G_2$ which are connected by a bridge uv between $u\in V\left(G_1\right)$ and $v\in V\left(G_2\right),$ see Figure 5. Then $M_1\left(G\right)=M_1\left(G_1\right)+M_1\left(G_2\right)+2\left(d_{G_1}\right(u)+d_{G_2}(v)+1).$

Figure 5. Two graphs $G_1$ and $G_2$ connected by a bridge.

Proof.

Since $d_G\left(u\right)=d_{G_1}\left(u\right)+1$, $d_G\left(v\right)=d_{G_1}\left(v\right)+1$, then $\begin{array}{rl}{M}_1\left(G_1\right)& =\sum _{w\in V\left(G_1\right),w\notin N\left[u\right]}(d_w{)}^2\\ & +\sum _{i=1}^k\left(d_{G_1}\right(u_i){)}^2+(d_{G_1}\left(u\right){)}^2,\end{array}$ and $\begin{array}{rl}{M}_1\left(G_2\right)& =\sum _{w\in V\left(G_2\right),w\notin N\left[v\right]}(d_w{)}^2\\ & +\sum _{j=1}^t\left(d_{G_2}\right(v_j){)}^2+(d_{G_2}\left(v\right){)}^2.\end{array}$ So $\begin{array}{rl}{M}_1^e\left(G\right)& =\sum _{w\in V\left(G_1\right),w\notin N\left[u\right]}(d_w{)}^2+\sum _{i=1}^k(d_{G_1}\left(u_i\right){)}^2\\ & +\sum _{w\in V\left(G_2\right),w\notin N\left[v\right]}(d_w{)}^2+\sum _{j=1}^t(d_{G_2}\left(v_j\right){)}^2\\ & +\left(d_{G_1}\right(u)+1{)}^2+(d_{G_2}\left(v\right)+1{)}^2\\ & =M_1\left(G_1\right)+M_1\left(G_2\right)+2\left(d_{G_1}\right(u)+d_{G_2}(v)+1).\end{array}$ Hence the proof follows.

Corollary 3.15

Let G be a graph as given in Theorem 3.14 with $G_1=G_2$. Then $M_1\left(G\right)=2M_1\left(G_1\right)+2\left(2d_{G_1}\right(u)+1).$

We can give some new upper and lower bounds for the first Zagreb index of a graph if the graph is separated into two parts by a bridge:

Corollary 3.16

Let $G_1$ and $G_2$ be two $(n_1,m_1)$ and $(n_2,m_2)$ graphs, respectively, and let G be a graph which consists of two components $G_1$ and $G_2$ which are connected by a bridge. Let also $\mathrm{\Delta }=\underset{v\in G}{max}{d}_G\left(v\right)$ and $\delta =\underset{v\in G}{min}{d}_G\left(v\right)$. Then $\begin{array}{rl}& (n_1+n_2){\delta }^2+2(2\delta +1)\le M_1\left(G\right)\\ & \le (n_1+n_2){\mathrm{\Delta }}^2+2(2\mathrm{\Delta }+1).\end{array}$ In particular, if $G_1=G_2$, then $2(n_1\cdot {\delta }^2+2\delta +1)\le M_1\left(G\right)\le 2(n_1\cdot {\mathrm{\Delta }}^2+2\mathrm{\Delta }+1).$

Corollary 3.17

Let $G_1$ and $G_2$ be two $(n_1,m_1)$ and $(n_2,m_2)$ graphs, respectively, and let G be an r-regular graph which consists of two components $G_1$ and $G_2$ which are connected by a bridge. Then $M_1\left(G\right)=(n_1+n_2)r^2+2(2r+1).$ In particular, if $G_1=G_2,$ then $M_1\left(G\right)=2(n_1{r}^2+2r+1).$

Now we study the second Zagreb, hyper-Zagreb, sigma and irregularity indices for the same graphs above. The proofs uses the similar reasoning and will hence be skipped.

Theorem 3.18

Let G be a graph as given in Theorem 3.1. Let $k=d_{G_1}\left(u\right)$ and $t=d_{G_2}\left(v\right)$. Then $\begin{array}{rl}{M}_2\left(G\right)& =M_2\left(G_1\right)+M_2\left(G_2\right)+(k+1)(t+1)\\ & +\sum _{i=1}^k{d}_{G_1}\left(u_i\right)+\sum _{j=1}^t{d}_{G_2}\left(v_j\right).\end{array}$

Theorem 3.19

Let G be a graph as given in Theorem 3.1. Let $k=d_{G_1}\left(u\right)$ and $t=d_{G_2}\left(v\right)$. Then $\begin{array}{rl}HM\left(G\right)& =HM\left(G_1\right)+HM\left(G_2\right)+3k(k+1)+3t(t+1)\\ & +2\left[\sum _{i=1}^k{d}_{G_1}\left(u_i\right)+\sum _{j=1}^t{d}_{G_2}\left(v_j\right)\right.\\ & +\left.\phantom{\sum _{i=1}^k}(k+1)(t+1)\right].\end{array}$

Theorem 3.20

Let G be a graph as given in Theorem 3.1. Let $k=d_{G_1}\left(u\right)$ and $t=d_{G_2}\left(v\right)$. Then $\begin{array}{rl}\sigma \left(G\right)& =\sigma \left(G_1\right)+\sigma \left(G_2\right)+3k(k+1)+3t(t+1)\\ & -2\left[\sum _{i=1}^k{d}_{G_1}\left(u_i\right)+\sum _{j=1}^t{d}_{G_2}\left(v_j\right)\right.\\ & +\left.\phantom{\sum _{j=1}^t}(k+1)(t+1)\right].\end{array}$

Theorem 3.21

Let G be a graph as given in Theorem 3.1. Let $k=d_{G_1}\left(u\right)$ and $t=d_{G_2}\left(v\right)$. Then $Irr\left(G\right)=Irr\left(G_1\right)+Irr\left(G_2\right)+k+t+|k-t|.$

3.3. Effect of cut-edges on topological indices

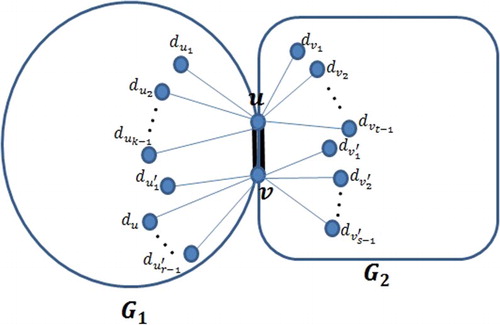
Finally in this section, we shall consider the effect of cut-edges on some important topological graph indices, see Figure 6.

Figure 6. Two graphs meeting at a cut-edge uv.

Theorem 3.22

Let $G_1$ and $G_2$ be two simple connected graphs and let G be a graph which consists of two components $G_1$ and $G_2$ connected by a common edge e = uv where u and v are the only vertices lying both in $G_1$ and $G_2$. Then $\begin{array}{rl}{M}_1\left(G\right)& =M_1\left(G_1\right)+M_1\left(G_2\right)+2\left[\right(d_{G_1}\left(u\right)-1)\\ & \times \left(d_{G_2}\right(u)-1)+\left(d_{G_1}\right(v)-1)\\ & \times \left(d_{G_2}\right(v)-1)-1].\end{array}$

Proof.

Let us say $d_{G_1}\left(u\right)=k,d_{G_2}\left(u\right)=t$ and $d_{G_1}\left(v\right)=r,d_{G_2}\left(v\right)=s$. So $\begin{array}{rl}{M}_1\left(G_1\right)& =\sum _{\begin{array}{c}w\in V\left(G_1\right)\\ w\notin N_u\cup N_v\end{array}}\left(d_{G_1}\right(w){)}^2+\sum _{i=1}^{k-1}(d_{G_1}\left(u_i\right){)}^2\\ & +\sum _{j=1}^{r-1}\left(d_{G_1}\right(v_j^{\prime }){)}^2\\ & +\left(d_{G_1}\right(u){)}^2+(d_{G_1}\left(v\right){)}^2\end{array}$ and $\begin{array}{rl}{M}_1\left(G_2\right)& =\sum _{\begin{array}{c}w\in V\left(G_2\right)\\ w\notin N_u\cup N_v\end{array}}\left(d_{G_2}\right(w){)}^2+\sum _{i=1}^{t-1}(d_{G_2}\left(v_i\right){)}^2\\ & +\sum _{j=1}^{s-1}\left(d_{G_2}\right(v_j^{\prime }){)}^2\\ & +\left(d_{G_2}\right(u){)}^2+(d_{G_2}\left(v\right){)}^2.\end{array}$ Now calculating $M_1\left(G\right)$, we get $\begin{array}{rl}{M}_1\left(G\right)& =\sum _{\begin{array}{c}w\in V\left(G_1\right)\\ w\notin N_u\cup N_v\end{array}}\left(d_{G_1}\right(w){)}^2+\sum _{i=1}^{k-1}(d_{G_1}\left(u_i\right){)}^2\\ & +\sum _{j=1}^{r-1}\left(d_{G_2}\right(v_j^{\prime }){)}^2+\sum _{\begin{array}{c}w\in V\left(G_2\right)\\ w\notin N_u\cup N_v\end{array}}(d_{G_2}\left(w\right){)}^2\\ & +\sum _{i=1}^{t-1}\left(d_{G_2}\right(v_i){)}^2+\sum _{j=1}^{s-1}(d_{G_2}\left(v_j^{\prime }\right){)}^2\\ & +\left(d_{G_1}\right(u)+d_{G_2}(u)-1{)}^2\\ & +\left(d_{G_1}\right(v)+d_{G_2}(v)-1{)}^2.\\ M_1\left(G\right)& =\sum _{\begin{array}{c}w\in V\left(G_1\right)\\ w\notin N_u\cup N_v\end{array}}\left(d_{G_1}\right(w){)}^2+\sum _{i=1}^{k-1}\left(d_{G_1}\right(u_i){)}^2\\ & +\sum _{j=1}^{r-1}\left(d_{G_2}\right(v_j^{\prime }){)}^2+\sum _{\begin{array}{c}w\in V\left(G_2\right)\\ w\notin N_u\cup N_v\end{array}}(d_{G_2}\left(w\right){)}^2\\ & +\sum _{i=1}^{t-1}\left(d_{G_2}\right(v_i){)}^2+\sum _{j=1}^{s-1}(d_{G_2}\left(v_j^{\prime }\right){)}^2\\ & +\left(d_{G_1}\right(u){)}^2+(d_{G_2}\left(u\right){)}^2+1\\ & +\left(d_{G_1}\right(v){)}^2+(d_{G_2}\left(v\right){)}^2+1\\ & +2\left[d_{G_1}\right(u\left)d_{G_2}\right(u)-d_{G_1}(u)-d_{G_2}(u)\\ & +d_{G_1}\left(v\right)d_{G_2}\left(v\right)-d_{G_1}\left(v\right)-d_{G_2}\left(v\right)]\end{array}$ and hence $\begin{array}{rl}{M}_1\left(G\right)& =M_1\left(G_1\right)+M_1\left(G_2\right)+2\left[\right(d_{G_1}\left(u\right)-1)\\ & \times \left(d_{G_2}\right(u)-1)+\left(d_{G_1}\right(v)-1)\\ & \times \left(d_{G_2}\right(v)-1)-1].\end{array}$

Corollary 3.23

Let G be a graph as given in Theorem 3.22 with $G_1=G_2$. Then $\begin{array}{rl}{M}_1\left(G\right)& =2M_1\left(G_1\right)+2\left[\right(d_{G_1}\left(u\right)-1{)}^2\\ & +\left(d_{G_1}\right(v)-1{)}^2-1].\end{array}$

Proof.

The result can easily be seen by Theorem 3.22.

Corollary 3.24

Let G be a graph as given in Theorem 3.22 with $G_1=G_2$. Then $\begin{array}{rl}& 2M_1\left(G_1\right)+2\left[\right(\delta -1{)}^2-1]\le M_1^e(G)\le 2M_1(G_1)\\ & +2\left[\right(\mathrm{\Delta }-1{)}^2-1].\end{array}$

Corollary 3.25

Let G be an r-regular graph as given in Theorem 3.22 with $G_1=G_2$. Then $M_1\left(G\right)=2\left[\right(n_1+2)r^2-4r+1].$

Example 3.26

Let G be a graph constructed by the tadpole graph $T_{3,5}$ and the cycle graph $C_7$ having a common cut-edge between them as in Figure 7. $M_1\left(T_{3,5}\right)=34$ and $M_1\left(C_7\right)=28$. So $\begin{array}{rl}{M}_1\left(G\right)& =34+28+2\left[\right(2-1\left)\right(2-1)\\ & +(2-1)(2-1)-1]=64.\end{array}$

Figure 7. A graph having two neighbour faces.

Theorem 3.27

Let G be a graph as given in Theorem 3.22. Then $\begin{array}{rl}{M}_2\left(G\right)& =M_2\left(G_1\right)+M_2\left(G_2\right)+(t-1)\sum _{i=1}^{k-1}{d}_{G_1}\left(u_i\right)\\ & +(s-1)\sum _{i=1}^{r-1}{d}_{G_1}\left(u_i^{\mathrm{\prime }}\right)+(k-1)\sum _{j=1}^{t-1}{d}_{G_2}\left(v_j\right)\\ & +(r-1)\sum _{j=1}^{s-1}{d}_{G_2}\left(v_j^{\mathrm{\prime }}\right)+ks-k\\ & +tr-t-r-s+1.\end{array}$

Theorem 3.28

Let G be a graph as given in Theorem 3.22. Then $\begin{array}{rl}HM\left(G\right)& =HM\left(G_1\right)+HM\left(G_2\right)+2M_2\left(G\right)\\ & +3\left[\right(k+t\left)\right(kt+1)-(k^2+t^2)\\ & +(r+s)(rs+1)-(r^2+s^2)].\end{array}$

Proof.

From the definition of hyper-Zagreb index we get $\begin{array}{rl}HM\left(G_1\right)& =\sum _{i=1}^{k-1}\left(d_{G_1}\right(u_i){)}^3+\sum _{i=1}^{r-1}(d_{G_1}\left(u_i^{\mathrm{\prime }}\right){)}^3+\left(d_{G_1}\right(u){)}^3\\ & +\left(d_{G_1}\right(v){)}^3+2M_2(G_1)\\ & +\sum _{\begin{array}{c}w\notin N\left[u\right]\cup N\left[v\right]\\ w\in V\left(G_1\right)\end{array}}{d}_{G_1}(w{)}^2,\end{array}$ and $\begin{array}{rl}HM\left(G_2\right)& =\sum _{j=1}^{t-1}\left(d_{G_2}\right(v_j){)}^3+\sum _{j=1}^{s-1}(d_{G_2}\left(v_j^{\mathrm{\prime }}\right){)}^3\\ & +\left(d_{G_2}\right(u){)}^3+(d_{G_2}\left(v\right){)}^3+2M_2\left(G_2\right)\\ & +\sum _{\begin{array}{c}w\notin N\left[u\right]\cup N\left[v\right]\\ w\in V\left(G_2\right)\end{array}}{d}_{G_2}(w{)}^2.\end{array}$ So $\begin{array}{rl}HM\left(G\right)& =HM\left(G_1\right)+HM\left(G_2\right)+2M_2\left(G\right)\\ & +3\left[\right(k+t\left)\right(kt+1)-(k^2+t^2)\\ & +(r+s)(rs+1)-(r^2+s^2)].\end{array}$

Theorem 3.29

Let G be a graph as given in Theorem 3.22. Then $\begin{array}{rl}{\sigma }^e\left(G\right)& =\sigma \left(G_1\right)+\sigma \left(G_2\right)-2M_2\left(G\right)\\ & +3\left[\right(k+t\left)\right(kt+1)-(k^2+t^2)\\ & +(r+s)(rs+1)-(r^2+s^2)].\end{array}$

Proof.

Since $\sigma \left(G\right)=\sum _{u,v\in E\left(G\right)}\left[d_G\right(u)-d_G(v){]}^2$, the proof is similar to the proof of the previous theorem.

Theorem 3.30

Let $G_1$ and $G_2$ are simple connected graphs and G be a graph which consists of components $G_1$ and $G_2$ by a common edge e = uv. Then $\begin{array}{rl}Irr\left(G\right)& \le Irr\left(G_1\right)+Irr\left(G_2\right)+2\left[\right(k-1\left)\right(t-1)\\ & +(s-1)(r-1)].\end{array}$

Theorem 3.31

Let G be a graph as given in Theorem 3.22. Then $\begin{array}{rl}{M}_1^{ϵ}\left(G\right)& =M_1^{ϵ}\left(G_1\right)+M_1^{ϵ}\left(G_2\right)+2+2kt-2k-2t\\ & +2rs-2r-2s+2(t-1)\sum _{i=1}^{k-1}{d}_{G_1}\left(e_i\right)\\ & +(t-1{)}^2(k-1)+2(s-1\left)\sum _{i=1}^{r-1}{d}_{G_1}\right(e_i^{\mathrm{\prime }})\\ & +(s-1{)}^2(r-1)+2(k-1\left)\sum _{j=1}^{t-1}{d}_{G_2}\right(f_j)\\ & +(k-1{)}^2(t-1)+2(r-1\left)\sum _{j=1}^{s-1}{d}_{G_2}\right(f_j^{\mathrm{\prime }})\\ & +(r-1{)}^2(s-1)+2(k+r-2\left)\right(t+s-2).\end{array}$

Proof.

The proof can be done by using the definition of first entire-Zagreb index.

4. Discussion

Topological indices have been defined and calculated for either all graphs whenever possible or for some graph classes since 1947. There is a large number of papers dealing with such calculations in the literature. But no one yet has considered the symmetrical graphs and their topological indices. In this paper, as a result of all the calculations in Section 3, we had determined the topological indices of some large (chemical) graphs showing point-wise or edge-wise symmetry in terms of the topological indices of smaller identical subpieces and also in terms of the degrees of the vertices in the symmetry center.

5. Conclusions

Starting with the distance-based topological index called the Wiener index defined by H. Wiener in 1947, a large number of topological indices have been defined and used in chemical applications. In this paper, three problems called the cut-vertex, cut-edge and bridge problems for symmetrical graphs have been solved. In each of these problems, topological indices such as first and second Zagreb indices, forgotten index, sigma index, irregularity index, hyper-Zagreb index and first entire-Zagreb index have been calculated for a large symmetrical (molecular) graph and formalized for such molecular graphs. Such a method helps to reduce the computation time of these topological indices by means of the symmetric structures of molecular graphs.

The same method can be applied to the derived graphs such as the line, total, subdivision and middle graphs and also to graph operations.

Acknowledgments

The authors acknowledge that they all equally contributed to the paper. No part of it has been published or simultaneously submitted to any other journals. The authors also thank to the anonymous referees who helped to improve the submitted material by their valuable suggestions.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Muge Togan http://orcid.org/0000-0001-5349-3978

Feriha Celik http://orcid.org/0000-0002-0791-9293

Ismail Naci Cangul http://orcid.org/0000-0002-0700-5774