On certain prime cordial families of graphs

Abstract

Graph labelling is an important tool in modelling real life problems. In the present paper, different graph families are studied for prime cordial labelling. In this work, we show that the double comb graph $P_n\odot 2K_1$, for $n\ge 2$, as well as sunflower planar graph $S{f}_n$ for $n\ge 3$, admit prime cordial labelling. We also prove that if we join two copies of sunflower planar graph by a path of arbitrary length then the resultant graph is also prime cordial.

KEYWORDS:

• Double comb graph
• sunflower graph
• cordial labelling
• prime cordial labelling

1. Introduction

A relation between numbers and structure of graphs is called graph labelling. Graph labelings have broad range of applications in various areas of science and technology such as radar, astronomy, computer science and communication networks. Gallian [1] gave a comprehensive survey of graph labelings. Cahit introduced the concept of cordial labelling [2]. Many other researchers [3–6] have a great contribution for deriving various results on cordial labelling.

Different labelling schemes have been introduced with minor changes in cordial labelling conditions. Motivated through the concept of prime labelling and cordial labelling, Sundaram et al. introduced prime cordial labelling [7]. Prime cordial labelling contains blend of both the labelings. The present work is focused on prime cordial labelling of certain graph families.Vaidya and Vihol investigated the prime cordial labelling of graphs obtained by various graph operations [8]. They also investigated prime cordial behaviour of some cycle related graphs [9].

Vaidya and Shah have proved that the wheel graph and some wheel related graphs like gear, helm and closed helm graphs admit prime cordial labelling [10]. Babitha and Baskar gave certain characterizations of prime cordial graphs [11]. In addition to this many other researchers [12–14] have great contribution for deriving characterization results on prime cordial labelling. For other studies which use similar techniques include [15], [16].

Every graph is not prime cordial. In this paper, we add new families of graphs to Prime cordial graphs.

These graphs correspond to many electrical, protein or communication network, and prime cordiality can help in solving the problems in different areas like coding theory, artificial intelligence, clinical psychology, radio networks and many more. In this paper we prove that double comb graph, sunflower graph and two copies of sunflower graph are prime cordial. These prime cordial graphs can, in turn, help to construct new families of prime cordial graphs by certain graph transformations.

2. Materials and methods

In this work we investigate some families of graphs for prime cordial labelling. We consider finite, simple connected graphs. Let the graph $G$ has $p$ vertices and $q$ edges, denoted as $G\left(p,q\right)$. $V\left(G\right)$ denotes the set of vertices of graph $G$ and $E\left(G\right)$ denotes the set of edges of $G$. We follow Gross and Yellen [17] for basic graph theoretic concepts, symbols and terminology. We provide brief summary of definitions which are necessary for the present investigations.

Definition 1:

The labelling of graph is the allocation of numbers to the vertices or edges or both under certain conditions. If we assign numbers to the vertices, then the labelling is called a vertex labelling an is called an edge labelling if we assign numbers to the set of edges.

Definition 2:

A labelling is called binary vertex labelling if we assign only $0$ and $1$ to the vertices of $G$ i.e the range of mapping $p$ is the set $\left\{0,1\right\}$.

Notation 1. Let $v$ be a vertex of $G$ then $p\left(v\right)$is called the label of the vertex $v$ under $p$.

Notation 2. If $p:V\left(G\right)\to \left\{0,1\right\}$ is binary vertex labelling. Then $v_p\left(i\right)=|\{v\in V(G\left)|p\right(v)=i\}|$ where $i\in \left\{0,1\right\}$.

Notation 3. Consider the induced edge labelling $p^{\mathrm{\prime }}:E\left(G\right)\to \left\{0,1\right\}$ defined as $p^{\mathrm{\prime }}\left(e\right)=|p\left(u\right)-p\left(v\right)|$, where $e=uv$ is an edge. Then $e_p\left(i\right)=|\{e\in E(G\left)|p^{\mathrm{\prime }}\right(e)=i\}|$ where $i\in \left\{0,1\right\}$.

Definition 3:

Let $p:V\left(G\right)\to \left\{0,1\right\}$ be a binary vertex labelling of $G$ then it is called cordial labelling if it satisfies the following conditions. $\begin{array}{c}|v_p\left(0\right)-v_p\left(1\right)|\le 1\\ |e_p\left(0\right)-e_p\left(1\right)|\le 1\end{array}$A graph $G$ which satisfies the above conditions is called a cordial graph.

Definition 4:

An injective mapping $p:V\left(G\right)\to \left\{1,2,\dots ,|V\left(G\right)|\right\}$ is called prime labelling of $G$ if, $gcd\left(p\right(u),p(v\left)\right)=1$, for every pair of adjacent vertices $u,v$. A graph $G$ is termed as prime graph if it satisfies the condition of prime labelling.

Definition 5:

A bijection $p:V\left(G\right)\to \left\{1,2,...,|V|\right\}$ is called a prime cordial labelling of $G$ if the induced edge function $p^{\mathrm{\prime }}:E\left(G\right)\to \left\{0,1\right\}$ defined by $p^{\mathrm{\prime }}\left(e=uv\right)=\left\{\begin{array}{ll}1ifgcd\left(p\left(u\right),p\left(v\right)\right)=1& \\ 0otherwise& \end{array}\right.$such that $\text{|}{e}_p\left(0\right)\text{--}{e}_p\left(1\right)\text{|}\le 1$.

A graph with labelling satisfying above conditions is termed as prime cordial graph.

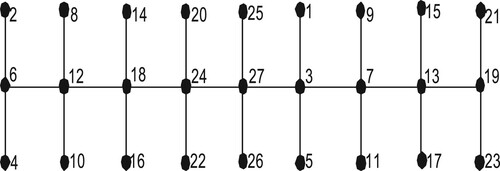
Definition 6:

A double comb graph is a graph obtained from a path $P_n$ by attaching two pendant vertices at each vertex of $P_n$ denoted by $P_n\odot 2K_1$.

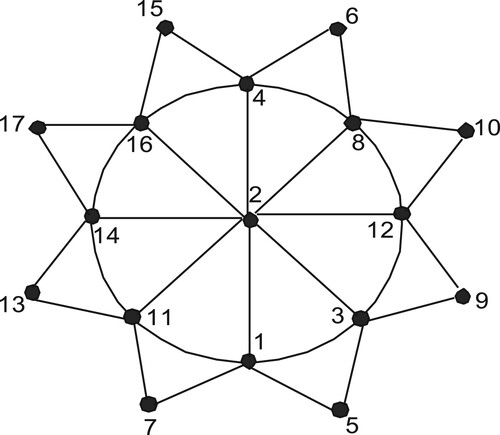
Definition 7:

A sunflower planar graph $S{f}_n$ is obtained from a wheel graph with vertices $v_0,v_1,v_2,\dots ,v_n$ ($v_0$ is central vertex and $v_1,v_2,\dots ,v_n$ are rim vertices) and additional vertices $u_1,u_2,\dots ,u_n$ such that $u_j$ is joined to $v_j$ and $v_{j+1}$, where $v_{j+1}$ is taken modulo $n$.

3. Main results

Theorem 1:

Double comb graph admits prime cordial labeling for. admits prime cordial labeling for.

Proof: Let $H$ denotes double comb graph $\begin{array}{rl}& P_n\odot 2K_1\text{with}V\left(H\right)=\left\{v_i,u_{ij},1\le i\le n,j=1,2\right\}\text{and}\\ & E\left(H\right)=\left\{\left[\left(v_i{v}_{i+1}\right):i=1,2,\dots ,n-1\right]\cup \right.\\ & \left.\left[\left(v_i{u}_{ij}\right):i=1,2,\dots ,n;j=1,2\right]\right\}.\end{array}$Then $\text{|}V\left(H\right)\text{|}=3n\text{|}E\left(H\right)\text{|}=3n-1\text{|}V\left(H\right)\text{|}=3n\text{|}E\left(H\right)\text{|}=3n-1$.

We define $p:V\left(H\right)\to \left\{1,2,3,\dots ,3n\right\}$ according to the following cases.

Case 1: $n\ge 2n1:n\ge 2n$ is even. $p\left(v_i\right)=6i;1\le i\le \frac{n}{2}\text{and}p\left(v_{\frac{n+2}{2}}\right)=1,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+6;\frac{n}{2}+1\le i\le n-1$ $p\left(u_{i1}\right)=p\left(v_i\right)-4;1\le i\le \frac{n}{2}$ $p\left(u_{i1}\right)=p\left(v_i\right)+2;\frac{n}{2}+1\le i\le n$ $p\left(u_{i2}\right)=p\left(v_i\right)-2;1\le i\le \frac{n}{2}$ $p\left(u_{i2}\right)=p\left(v_i\right)+4;\frac{n}{2}+1\le i\le n.$

According to the labelling scheme we have $e_p\left(0\right)+1=e_p\left(1\right)=\left(3n/2\right)$.

Case 2: $n\ge 3n2:n\ge 3n$ is odd. $p\left(v_i\right)=6i;1\le i\le \frac{n}{2}$ $p\left(v_{\frac{n}{2}}\right)=3n,p\left(v_{\frac{n+3}{2}}\right)=3,p\left(v_{\frac{n+5}{2}}\right)=7,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+6;\frac{n+5}{2}\le i\le n-1$ $p\left(u_{i1}\right)=p\left(v_i\right)-4;1\le i\le \frac{n}{2}$ $p\left(u_{i1}\right)=p\left(v_i\right)-2;i=\frac{n}{2}$ $p\left(u_{i1}\right)=1;i=\frac{n+3}{2},p\left(u_{i1}\right)=9;i=\frac{n+5}{2}$ $p\left(u_{i1}\right)=p\left(v_i\right)+2;\frac{n+5}{2}\le i\le n$ $p\left(u_{i2}\right)=p\left(v_i\right)-2;1\le i\le \frac{n}{2}$ $p\left(u_{i2}\right)=p\left(v_i\right)-1;i=\frac{n}{2}$ $p\left(u_{i2}\right)=5;i=\frac{n+3}{2},p\left(u_{i2}\right)=11;i=\frac{n+5}{2}$ $p\left(u_{i2}\right)=p\left(v_i\right)+4;\frac{n+5}{2}\le i\le n.$

Here, we have $e_p\left(0\right)=e_p\left(1\right)=(3n-1/2)$.

So, in the two cases discussed above it can be observed that $\text{|}{e}_p\left(0\right)-e_p\left(1\right)\text{|}\le 1$.

As a result, we can say that $\begin{array}{l}{P}_n\odot 2K_1\\ n\ge 2P_n\odot 2K_1\\ n\ge 2\end{array}$, labeling is elaborated in Figure 1.

Figure 1. Prime cordial labelling of $P_9\odot 2K_1$.

Theorem 2:

The sunflower planar graph $S{f}_{n}n\ge 6.S{f}_{n}n\ge 6$.

Proof: Let $\left\{v_0,v_1,v_2,\dots ,v_n,w_1,w_2,\dots ,w_n\right\}$ be the vertices of $S{f}_n\left\{e_1,e_2,e_3,\dots ,e_{4n}\right\}S{f}_n\left\{e_1,e_2,e_3,\dots ,e_{4n}\right\}$ be the edges of $\begin{array}{l}S{f}_n|V\left(S{f}_n\right)|=2n+1\\ |E\left(S{f}_n\right)|=4nS{f}_n|V\left(S{f}_n\right)|=2n+1\\ |E\left(S{f}_n\right)|=4nS{f}_n|V\left(S{f}_n\right)|=2n+1\\ |E\left(S{f}_n\right)|=4n\end{array}$

We define $p:V\left(S{f}_n\right)\to \left\{1,2,3,\dots ,2n+1\right\}$ as follows Figure 2,

Figure 2. Prime cordial labelling of Sf_8.

Case 1: $n\text{is even,}n\equiv 0\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_i\right)=4i;1\le i\le \frac{n}{2}$ $p\left(v_{\frac{n}{2}+1}\right)=3,p\left(v_{\frac{n}{2}+2}\right)=1,p\left(v_{\frac{n}{2}+3}\right)=11,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+3\le i\le n-1$ $p\left(w_1\right)=6,p\left(w_{\frac{n}{2}}\right)=9,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\text{ for}1\le i\le \frac{n}{2}-1$ $p\left(w_{\frac{n}{2}+1}\right)=5,p\left(w_{\frac{n}{2}+2}\right)=7,p\left(w_{\frac{n}{2}+3}\right)=13,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+3\le i\le n-1$

In this case, we have $e_p\left(0\right)=e_p\left(1\right)=2n$.

Case 2: $n\text{is even,}n\equiv 1\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_i\right)=4i;1\le i\le \frac{n}{2}-1$ $p\left(v_{\frac{n}{2}}\right)=2n-2,p\left(v_{\frac{n}{2}+1}\right)=3,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+1\le i\le n-1$ $p\left(w_1\right)=6,p\left(w_{\frac{n}{2}-1}\right)=2n,p\left(w_{\frac{n}{2}}\right)=9,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le \frac{n}{2}-3$ $p\left(w_{\frac{n}{2}+1}\right)=1,p\left(w_{\frac{n}{2}+2}\right)=5,p\left(w_{\frac{n}{2}+3}\right)=13,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+3\le i\le n-1$

We can see that $e_p\left(0\right)=e_p\left(1\right)=2n$ in this case.

Case 3: $n\text{is even,}n\equiv 2\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_i\right)=4i;1\le i\le \frac{n}{2}-1$ $p\left(v_{\frac{n}{2}}\right)=3,p\left(v_{\frac{n}{2}+1}\right)=1,p\left(v_{\frac{n}{2}+2}\right)=11,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+2\le i\le n-3$ $\begin{array}{rl}p\left(v_{n-1}\right)& =2n-2,p\left(v_n\right)=2n,p\left(w_1\right)=6,\\ p\left(w_n\right)& =2n-1\end{array}$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le \frac{n}{2}-3$ $\begin{array}{rl}& p\left(w_{\frac{n}{2}-1}\right)=9,p\left(w_{\frac{n}{2}}\right)=5,p\left(w_{\frac{n}{2}+1}\right)=7,\\ & p\left(w_{\frac{n}{2}+2}\right)=13,\end{array}$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+2\le i\le n-2$

According to this labelling scheme, $e_p\left(0\right)=e_p\left(1\right)=2n$.

Case 4: $n\text{is odd},n\equiv 0\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_i\right)=4i;1\le i\le \frac{n}{2}$ $\begin{array}{rl}p\left(v_{\frac{n}{2}}\right)& =2n,p\left(v_{\frac{n}{2}+1}\right)=3,p\left(v_{\frac{n}{2}+2}\right)=5,\\ p\left(v_{\frac{n}{2}+3}\right)& =13,\end{array}$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+3\le i\le n-1$ $p\left(w_1\right)=6,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le \frac{n}{2}-2$ $p\left(w_{\frac{n}{2}}\right)=1,p\left(w_{\frac{n}{2}}\right)=9,p\left(w_{\frac{n}{2}+1}\right)=7,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+1\le i\le n-1$

Here, $e_p\left(0\right)=e_p\left(1\right)=2n$.

Case 5: $n\text{is odd},n\equiv 1\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_i\right)=4i;1\le i\le \frac{n}{2}$ $p\left(v_{\frac{n}{2}}\right)=3,p\left(v_{\frac{n}{2}+1}\right)=1,$ $p\left(v_{\frac{n}{2}+2}\right)=5,p\left(v_{\frac{n}{2}+3}\right)=13,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+3\le i\le n-2$ $p\left(v_n\right)=2n,p\left(w_1\right)=6,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le \frac{n}{2}-2$ $p\left(w_{\frac{n}{2}-1}\right)=9,p\left(w_{\frac{n}{2}}\right)=2n-1,p\left(w_{\frac{n}{2}+1}\right)=7,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+1\le i\le n-1$

This labelling scheme gives $e_p\left(0\right)=e_p\left(1\right)=2n$.

Case 6: $n\text{is odd},n\equiv 2\left(mod3\right)$ $p\left(v_0\right)=2,p\left(v_1\right)=2n,p\left(v_2\right)=6,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;2\le i\le \frac{n}{2}-1$ $p\left(v_{\frac{n}{2}}\right)=3,p\left(v_{\frac{n}{2}+1}\right)=9,p\left(v_{\frac{n}{2}+2}\right)=7,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;\frac{n}{2}+2\le i\le n-1$ $p\left(w_i\right)=4i;1\le i<\frac{n}{2}$ $p\left(w_{\frac{n}{2}}\right)=2n-1,p\left(w_{\frac{n}{2}+1}\right)=1,$ $p\left(w_{\frac{n}{2}+2}\right)=5,p\left(w_{\frac{n}{2}+3}\right)=13,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;\frac{n}{2}+3\le i\le n-2$ $p\left(w_n\right)=2n+1$

By this labelling scheme, we get $e_p\left(0\right)=e_p\left(1\right)=2n$. So, in all the cases discussed above, it can be observed that$\text{|}{e}_p\left(0\right)-e_p\left(1\right)\text{|}\le 1$. Consequently, we can say that $S{f}_n$ is prime cordial for $n\ge 6$.

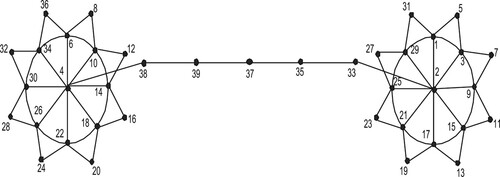
Theorem 3:

The graph obtained by joining two copies of sunflower planar graph $S{f}_n$ by a path of finite length is prime cordial.

Proof: Let.

Here we define the labelling function $p:V\left(G\right)\to \left\{1,2,3,\dots ,4n+k+2\right\}$ as follows.

Case 1: $k=2$ $p\left(v_0=u_1\right)=2,p\left(v_1\right)=4,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;1\le i\le n-1$ $p\left(w_1\right)=6,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le n-1$ $p\left(v_0^{\mathrm{\prime }}=u_2\right)=1,p\left(v_1^{\mathrm{\prime }}\right)=3,$ $p\left(v_{i+1}^{\mathrm{\prime }}\right)=p\left(v_i^{\mathrm{\prime }}\right)+4;1\le i\le n-1$ $p\left(w_1^{\mathrm{\prime }}\right)=5,$ $p\left(w_{i+1}^{\mathrm{\prime }}\right)=p\left(w_i^{\mathrm{\prime }}\right)+4;1\le i\le n-1$

Case 2: $k=3$ $\begin{array}{rl}& p\left(u_1=v_0\right)=4,p\left(u_3=v_0^{\mathrm{\prime }}\right)=2,\\ & p\left(u_2\right)=4n+3,p\left(v_1\right)=6,\end{array}$ $p\left(v_2\right)=12,p\left(v_3\right)=8,p\left(v_4\right)=16,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;4\le i\le n-1$ $p\left(w_1\right)=9,p\left(w_2\right)=10,p\left(w_3\right)=14,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;3\le i\le n-1$ $\begin{array}{rl}& p\left(v_1^{\mathrm{\prime }}\right)=1,p\left(v_2^{\mathrm{\prime }}\right)=3,p\left(v_3^{\mathrm{\prime }}\right)=1,\\ & p\left(v_4^{\mathrm{\prime }}\right)=13,p\left(v_5^{\mathrm{\prime }}\right)=19,\end{array}$ $p\left(v_{i+1}^{\mathrm{\prime }}\right)=p\left(v_i^{\mathrm{\prime }}\right)+4;5\le i\le n-1$ $p\left(w_1^{\mathrm{\prime }}\right)=5,p\left(w_2^{\mathrm{\prime }}\right)=7,p\left(w_3^{\mathrm{\prime }}\right)=11,p\left(w_4^{\mathrm{\prime }}\right)=17,$ $p\left(w_{i+1}^{\mathrm{\prime }}\right)=p\left(w_i^{\mathrm{\prime }}\right)+4;4\le i\le n-1$

Case 3: $k\text{is even,}k\ge 4$ $p\left(v_0=u_1\right)=4,p\left(v_1\right)=6,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;1\le i\le n-1$ $p\left(w_1\right)=8,$ $p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le n-1$ $p\left(v_0^{\mathrm{\prime }}=u_k\right)=2,p\left(v_1^{\mathrm{\prime }}\right)=1,$ $p\left(v_2^{\mathrm{\prime }}\right)=3,p\left(v_3^{\mathrm{\prime }}\right)=9,p\left(v_4^{\mathrm{\prime }}\right)=13,$ $p\left(v_{i+1}^{\mathrm{\prime }}\right)=p\left(v_i^{\mathrm{\prime }}\right)+4;4\le i\le n-1$ $p\left(w_1^{\mathrm{\prime }}\right)=5,p\left(w_2^{\mathrm{\prime }}\right)=7$ $p\left(w_{i+1}^{\mathrm{\prime }}\right)=p\left(w_i^{\mathrm{\prime }}\right)+4;2\le i\le n-1$ $p\left(u_i\right)=4n+2i+2;2\le i\le \frac{k}{2}-1$ $p\left(u_{\frac{k}{2}}\right)=4n+k-1$ $p\left(u_{i+1}\right)=p\left(u_i\right)-2;\frac{k}{2}\le i\le k-2$

Case 4: $k\text{is odd,}k\ge 5$ $p\left(v_0=u_1\right)=4,p\left(v_1\right)=6,$ $p\left(v_{i+1}\right)=p\left(v_i\right)+4;1\le i\le n-1$ $p\left(w_1\right)=8,p\left(w_{i+1}\right)=p\left(w_i\right)+4;1\le i\le n-1$ $\begin{array}{rl}& p\left(v_0^{\mathrm{\prime }}=u_k\right)=2,p\left(v_1^{\mathrm{\prime }}\right)=1,p\left(v_2^{\mathrm{\prime }}\right)=3,p\left(v_3^{\mathrm{\prime }}\right)=9,\\ & p\left(v_4^{\mathrm{\prime }}\right)=15,p\left(v_5^{\mathrm{\prime }}\right)=17,\end{array}$ $p\left(v_{i+1}^{\mathrm{\prime }}\right)=p\left(v_i^{\mathrm{\prime }}\right)+4;5\le i\le n-1$ $\begin{array}{rl}& p\left(w_1^{\mathrm{\prime }}\right)=5,p\left(w_2^{\mathrm{\prime }}\right)=7,p\left(w_3^{\mathrm{\prime }}\right)=11,\\ & p\left(w_4^{\mathrm{\prime }}\right)=13,p\left(w_5^{\mathrm{\prime }}\right)=19,\end{array}$ $p\left(w_{i+1}^{\mathrm{\prime }}\right)=p\left(w_i^{\mathrm{\prime }}\right)+4;5\le i\le n-1$ $p\left(u_i\right)=4n+2i+2;2\le i\le \frac{k}{2}-1$ $p\left(u_{\frac{k}{2}}\right)=4n+k,$ $p\left(u_{i+1}\right)=p\left(u_i\right)-2;\frac{k}{2}\le i\le k-2.$

According to the labelling scheme defined above we have $e_p\left(0\right)=e_p\left(1\right)=2n+\left(k/2\right)$.

It can be easily observed that the labelling scheme defined in each case is according to the criteria of prime cordial labelling. So, the graph is prime cordial Figure 3.

Figure 3. Prime cordial labelling of graph having two copies of $S{f}_8{P}_{7}S{f}_8{P}_7$.

4. Conclusion

It is very challenging and captivating to examine whether a graph is prime cordial or not. In this paper we have contributed some new families of graphs to the family of prime cordial graphs like sunflower graph, double comb graph, sunflower graph and duplication of sunflower graph. The defined labelling schemes are demonstrated by illustrations for better perception of derived results.

It would be interesting to investigate the prime cordiality of other families of graphs by using graphical transformations of the present studied graphs.

Acknowledgement

Authors are highly grateful to reviewers for their valuable comments which helped in improvement of the article.

Disclosure statement

No potential conflict of interest was reported by the author(s).