Nonlinearity contributions on critical MKP equation

Abstract

The mathematical new plasma wave solutions are specified in the compose of trigonometric, rational, hyperbolic, periodic and explosive kinds that are realistic for Modified-Kadomtsev-Petviashvili (MKP) equation. Also, numeral studies for the acquired solutions have been reveals that periodic, shock and explosive new forms may applicable in D-F Earth's ionosphere plasma. The used method is influential and robust in comparison applications in plasma fluids. To depict the propagating soliton profiles in a plasma medium, it is needful to solve MKP equation at a critical mass ratio. The Riccati–Bernoulli sub-ODE technique has been utilized to introduce some new important and applicable solutions. The number of these MKP solutions give a leading deed in applied ion acoustics in ionosphere.

Keywords:

• MKP equation
• explosive solutions
• RB sub-ODE method
• plasma applications

AMS Subject Classifications:

• 35A20
• 35A99
• 35C07
• 35Q51
• 65Z05

1. Introduction

The existence of the ion-acoustic solitary excitations (IAs) in plasmas has been spotted in laboratory [1–5]. Different observations in space assured the IAs propagations in magnetospheres and ionosphere [6–10]. The ion pairs electrostatic oscillations were conceived by Oohara and Hatakeyama by using fullerenes [11,12]. Saleem studied the plasma quasineutrality in pair ion-acoustic nonlinear dynamical properties [13]. Sabry et al. [14] used nonthermal properties of electron to discuss the ion wave formation characteristics in pair plasma. On the other hand, the progress of rogue ion-acoustic behaviours in many distributed electrons have been investigated [15,16]. Generally, many theoretical studies in solitary applications in natural science and space have been reported [16–26].

Consider the nonlinear partial differential equation (1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) for an unknown function $\psi (x,t)$. Utilizing the wave transformation (2) $\psi (x,t)=\psi \left(\xi \right),\xi =kx-\omega t.$(2) Equation (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ) converted to the following ODE: (3) $E(\psi ,{\psi }^{\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }},\dots )=0.$(3) There are so many models in physics, fluid mechanics and engineering fields in forms of partial differential Equation (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ) are transformed into the following ODE: (4) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(4) see for example [27–39]. This observation gives this equation special and important feature. Due to the importance of Equation (3(3) $E(\psi ,{\psi }^{\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }},\dots )=0.$(3) ), we pose the robust and unified solver for the widely used NPDEs, utilizing RB sub-ODE method [40]. Namely, RB sub-ODE method [40] is the basic ingredient for this solver. This solver can be used as a box solver for solving so many equations arising in applied science. This solver will be so helpful for engineers, physicists and mathematicians in order to emphasis some interesting phenomena in real-life problems.

2. The RB sub-ODE method

According to RB sub-ODE method [40], the solution of Equation (3(3) $E(\psi ,{\psi }^{\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }},{\psi }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }},\dots )=0.$(3) ) is (5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) where a, b, c and n are constants determined later. Equation (5(5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) ) gives (6) $\begin{array}{rl}{\psi }^{\mathrm{\prime }\mathrm{\prime }}& =ab(3-m){\psi }^{2-m}+a^2(2-m){\psi }^{3-2m}\\ & +m{c}^2{\psi }^{2m-1}+bc(m+1){\psi }^m+(2ac+b^2)\psi ,\end{array}$(6) (7) $\begin{array}{rl}{\psi }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}& ={\psi }^{\mathrm{\prime }}\left[ab\right(3-m\left)\right(2-m){\psi }^{1-m}\\ & +a^2(2-m)(3-2m){\psi }^{2-2m}\\ & +m(2m-1)c^2{\psi }^{2m-2}\\ & +bcn(m+1){\psi }^{m-1}+(2ac+b^2)].\end{array}$(7) The solitary solutions ${\psi }_i\left(\xi \right)$ of Equation (5(5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) ) are

1. For m = 1 (8) $\psi \left(\xi \right)=\varsigma e^{(a+b+c)\xi }.$(8)

2. For $m\ne 1$, b = 0 and c = 0 (9) $\psi \left(\xi \right)={\left(a(m-1)(\xi +\varsigma )\right)}^{1/m-1}.$(9)

3. For $m\ne 1$, $b\ne 0$ and c = 0 (10) $\psi \left(\xi \right)={\left(\frac{-a}{b}+\varsigma e^{b(m-1)\xi }\right)}^{1/m-1}.$(10)

4. For $m\ne 1$,$a\ne 0$ and $b^2-4ac<0$ (11) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}+\frac{\sqrt{4ac-b^2}}{2a}\right.\\ & \times {\left.\tan \left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}\end{array}$(11) and (12) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{4ac-b^2}}{2a}\right.\\ & \times {\left.\cot \left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}.\end{array}$(12)

5. For $m\ne 1$, $a\ne 0$ and $b^2-4ac>0$ (13) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right.\\ & \times {\left.\coth \left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}\end{array}$(13) and (14) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right.\\ & \times {\left.\tanh \left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}.\end{array}$(14)

6. For $m\ne 1$, $a\ne 0$ and $b^2-4ac=0$ (15) $\psi \left(\xi \right)={\left(\frac{1}{a(m-1)(\xi +\varsigma )}-\frac{b}{2a}\right)}^{1/1-m}.$(15)

2.0.1. Bäcklund transformation

If ${\psi }_{r-1}\left(\xi \right)$ and ${\psi }_r\left(\xi \right)\left({\psi }_r\right(\xi )={\psi }_r({\psi }_{r-1}\left(\xi \right)\left)\right)$ are the solutions of Equation (5(5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) ), we have $\begin{array}{rl}\frac{\mathrm{d}{\psi }_r\left(\xi \right)}{\mathrm{d}\xi }& =\frac{\mathrm{d}{\psi }_r\left(\xi \right)}{\mathrm{d}{\psi }_{r-1}\left(\xi \right)}\frac{\mathrm{d}{\psi }_{r-1}\left(\xi \right)}{\mathrm{d}\xi }\\ & =\frac{\mathrm{d}{\psi }_r\left(\xi \right)}{\mathrm{d}{\psi }_{r-1}\left(\xi \right)}(a{\psi }_{r-1}^{2-m}+b{\psi }_{r-1}+c{\psi }_{r-1}^m),\end{array}$ namely (16) $\frac{d{\psi }_r\left(\xi \right)}{a{\psi }_r^{2-m}+b{\psi }_r+c{\psi }_r^m}=\frac{d{\psi }_{r-1}\left(\xi \right)}{a{\varphi }_{r-1}^{2-m}+b{\psi }_{r-1}+c{\psi }_{r-1}^m}.$(16) Integrating Equation (16(16) $\frac{d{\psi }_r\left(\xi \right)}{a{\psi }_r^{2-m}+b{\psi }_r+c{\psi }_r^m}=\frac{d{\psi }_{r-1}\left(\xi \right)}{a{\varphi }_{r-1}^{2-m}+b{\psi }_{r-1}+c{\psi }_{r-1}^m}.$(16) ) once with respect to ξ, yields a Bäcklund transformation of Equation (5(5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) ) as follows: (17) ${\psi }_r\left(\xi \right)={\left(\frac{-c{\mathrm{\Lambda }}_1+a{\mathrm{\Lambda }}_2{\left({\psi }_{r-1}\left(\xi \right)\right)}^{1-m}}{b{\mathrm{\Lambda }}_1+a{\mathrm{\Lambda }}_2+a{\mathrm{\Lambda }}_1{\left({\psi }_{r-1}\left(\xi \right)\right)}^{1-m}}\right)}^{1/1-m},$(17) where ${\mathrm{\Lambda }}_1$ and ${\mathrm{\Lambda }}_2$ are arbitrary constants. Equation (17(17) ${\psi }_r\left(\xi \right)={\left(\frac{-c{\mathrm{\Lambda }}_1+a{\mathrm{\Lambda }}_2{\left({\psi }_{r-1}\left(\xi \right)\right)}^{1-m}}{b{\mathrm{\Lambda }}_1+a{\mathrm{\Lambda }}_2+a{\mathrm{\Lambda }}_1{\left({\psi }_{r-1}\left(\xi \right)\right)}^{1-m}}\right)}^{1/1-m},$(17) ) gives the infinite solutions of Equation (5(5) ${\psi }^{\prime }=a{\psi }^{2-m}+b\psi +c{\psi }^m,$(5) ), as well of Equation (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ).

3. Unified solver

In this section, we will see how the concept of a unified solver is in practice implemented. (18) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(18) using RB sub-ODE method. Substituting Equations (6(6) $\begin{array}{rl}{\psi }^{\mathrm{\prime }\mathrm{\prime }}& =ab(3-m){\psi }^{2-m}+a^2(2-m){\psi }^{3-2m}\\ & +m{c}^2{\psi }^{2m-1}+bc(m+1){\psi }^m+(2ac+b^2)\psi ,\end{array}$(6) ) into Equation (18(18) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(18) ), we obtain (19) $\begin{array}{rl}& {\alpha }_1\left(ab(3-m){\psi }^{2-m}+a^2(2-m){\psi }^{3-2m}\right.\\ & +\left.m{c}^2{\psi }^{2n-1}+bc(m+1){\psi }^m+(2ac+b^2)\psi \right)\\ & +{\alpha }_2{\psi }^3+{\alpha }_3\psi =0.\end{array}$(19) Putting m = 0, Equation (19(19) $\begin{array}{rl}& {\alpha }_1\left(ab(3-m){\psi }^{2-m}+a^2(2-m){\psi }^{3-2m}\right.\\ & +\left.m{c}^2{\psi }^{2n-1}+bc(m+1){\psi }^m+(2ac+b^2)\psi \right)\\ & +{\alpha }_2{\psi }^3+{\alpha }_3\psi =0.\end{array}$(19) ) is reduced to (20) $\begin{array}{rl}& {\alpha }_1(3ab{u}^2+2a^2{\psi }^3+bc+(2ac+b^2\left)\psi \right)\\ & +{\alpha }_2{\psi }^3+{\alpha }_3\psi =0.\end{array}$(20) Setting each coefficient of ${\psi }^i(i=0,1,2,3)$ to zero, we get (21) $\begin{array}{rl}{\alpha }_{1}bc& =0,\end{array}$(21) (22) $\begin{array}{rl}{\alpha }_1(2ac+b^2)+{\alpha }_3& =0,\end{array}$(22) (23) $\begin{array}{rl}3{\alpha }_{1}ab& =0,\end{array}$(23) (24) $\begin{array}{rl}2{\alpha }_1{a}^2+{\alpha }_2& =0.\end{array}$(24) Solving Equations (21(21) $\begin{array}{rl}{\alpha }_{1}bc& =0,\end{array}$(21) )–(24(24) $\begin{array}{rl}2{\alpha }_1{a}^2+{\alpha }_2& =0.\end{array}$(24) ), yields (25) $\begin{array}{rl}b& =0,\end{array}$(25) (26) $\begin{array}{rl}c& =\mp \frac{{\alpha }_3}{\sqrt{-2{\alpha }_1{\alpha }_2}},\end{array}$(26) (27) $\begin{array}{rl}a& =\pm \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}.\end{array}$(27) Hence, we give the cases of solutions for Equations (18(18) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(18) ) and (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ), respectively

1. When b = 0 and $c=0({\alpha }_3=0)$, the solution of Equation (18(18) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(18) ) is (28) ${\psi }_1(x,t)={\left(\mp \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}\left(\xi +\varsigma \right)\right)}^{-1},$(28) where ς is arbitrary constant.

2. When ${\alpha }_3/{\alpha }_1<0$, substituting Equations (25(25) $\begin{array}{rl}b& =0,\end{array}$(25) )– (27(27) $\begin{array}{rl}a& =\pm \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}.\end{array}$(27) ) and (2(2) $\psi (x,t)=\psi \left(\xi \right),\xi =kx-\omega t.$(2) ) into Equations (11(11) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}+\frac{\sqrt{4ac-b^2}}{2a}\right.\\ & \times {\left.\tan \left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}\end{array}$(11) ) and (12(12) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{4ac-b^2}}{2a}\right.\\ & \times {\left.\cot \left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}.\end{array}$(12) ), then the trigonometric function solutions of Equation (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ) are (29) ${\psi }_{2,3}(x,t)=\pm \sqrt{\frac{{\alpha }_3}{{\alpha }_2}}\tan \left(\sqrt{\frac{-{\alpha }_3}{2{\alpha }_1}}\left(\xi +\varsigma \right)\right)$(29) and (30) ${\psi }_{4,5}(x,t)=\pm \sqrt{\frac{{\alpha }_3}{{\alpha }_2}}\cot \left(\sqrt{\frac{-{\alpha }_3}{2{\alpha }_1}}\left(\xi +\varsigma \right)\right),$(30) where ς is arbitrary constant.

3. When ${\alpha }_3/{\alpha }_1>0$, substituting Equations (25(25) $\begin{array}{rl}b& =0,\end{array}$(25) )–(27(27) $\begin{array}{rl}a& =\pm \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}.\end{array}$(27) ) and (2(2) $\psi (x,t)=\psi \left(\xi \right),\xi =kx-\omega t.$(2) ) into Equations (13(13) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right.\\ & \times {\left.\coth \left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}\end{array}$(13) ) and (14(14) $\begin{array}{rl}& \psi \left(\xi \right)\\ & =\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right.\\ & \times {\left.\tanh \left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{1/1-m}.\end{array}$(14) ), then the hyperbolic function solutions of Equation (1(1) $H(\psi ,{\psi }_x,{\psi }_t,{\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots )=0$(1) ) are, (31) ${\psi }_{6,7}(x,t)=\pm \sqrt{\frac{-{\alpha }_3}{{\alpha }_2}}\tanh \left(\sqrt{\frac{{\alpha }_3}{2{\alpha }_1}}\left(\xi +\varsigma \right)\right)$(31) and (32) ${\psi }_{8,9}(x,t)=\pm \sqrt{\frac{-{\alpha }_3}{{\alpha }_2}}\coth \left(\sqrt{\frac{{\alpha }_3}{2{\alpha }_1}}\left(\xi +\varsigma \right)\right),$(32) where ς is arbitrary constant.

4. Mathematical model

Using stretched $\tau ={ϵ}^{3}t,\xi =ϵ(x-\lambda t),\eta ={ϵ}^{2}y,$ where ε is a very small value and λ is the IA speed. Sabry et al. [17] examined the propagating IAWs in plasma having negative and positive fluids in addition to electrons. In the case of Maxwillian electrons, Poisson's equation reads, (33) $\frac{{\mathrm{\partial }}^2\mathit{\phi }}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^2\mathit{\phi }}{\mathrm{\partial }{y}^2}={\mu }_{-}{n}_{-}-n_{+}+{\mu }_e\exp \left(\phi \right).$(33) Where $n_{-,+}$ is the number density of heavy negative ions, light positive ions normalized by its equilibrium value $n_{-0,+0}$, $u_{-},v_{-}(u_{+},v_{+})$ is the negative (positive) ion fluid velocity, the electrostatic potential φ. With ${\mu }_{-}=Z_{-}{n}_{-0}/Z_{+}{n}_{+0}$ and ${\mu }_e=n_{e0}/Z_{+}{n}_{+0}$ are the unperturbed negative ion and electron to positive ion ratio, respectively. Thus, the equilibrium condition implies ${\mu }_{-}+{\mu }_e=1,Q=m_{+}/m_{-}$ is the mass ratio, where $m_{-}\left(m_{+}\right)$ is the heavy (light) ion fluid mass, $\alpha =Z_{-}/Z_{+}$ where $Z_{\mp }$ is charge numbers. The obtained results support that the system becomes at critical at $Q=Q_c$, the modified KP equation was given: (34) $\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\left(\frac{\mathrm{\partial }}{\mathrm{\partial }\tau }\phi +G{\phi }^2\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\phi +R\frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{\xi }^3}\phi \right)+P\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\eta }^2}\phi =0$(34) with (35) $\begin{array}{rl}{Q}_c& =\pm \frac{\sqrt{3-{\lambda }^4{\mu }_e}}{\alpha \sqrt{3\left(1-{\mu }_e\right)}},\end{array}$(35) (36) $\begin{array}{rl}G& =\frac{15-{\lambda }^6{\mu }_e+15{\alpha }^3{Q}^3{\mu }_n+}{4{\lambda }^5{\mu }_e}\\ R& =\frac{\lambda }{2{\mu }_e},P=\frac{\lambda }{2}.\end{array}$(36) By using a similarity transformation given in the form: (37) $\begin{array}{rl}\chi & =L\xi +M\eta -\tau ({\upsilon }_1+{\upsilon }_2),\end{array}$(37) (38) $\begin{array}{rl}\phi \left(\chi \right)& =\phi (x,y,t)\end{array}$(38) (39) $\begin{array}{rl}\tau & =t,\end{array}$(39) where L and M are the directional cosines of x- and y -axes.

The modified KP form transformed into the ODE in the form: (40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) Equation (40(40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) ) gives stationary soliton in the form (41) $\begin{array}{rl}{\phi }_c& =\sqrt{6\left(\frac{v-S}{h}\right)}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(\frac{\sqrt{\frac{v-S}{h}}}{\sqrt{\frac{\theta }{h}}}\chi \right),\end{array}$(41) (42) $\begin{array}{rl}S& =\frac{M^{2}P}{L}-u,\end{array}$(42) (43) $\begin{array}{rl}h& =GL,\theta =R{L}^3,\end{array}$(43) where u and v are the travelling speed in the two directions.

5. Results and discussion

Comparing Equation (40(40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) ) with the general form (18(18) ${\alpha }_1{\psi }^{\mathrm{\prime }\mathrm{\prime }}+{\alpha }_2{\psi }^3+{\alpha }_3\psi =0,$(18) ), gives ${\alpha }_1=3\theta$, ${\alpha }_2=h$ and ${\alpha }_3=-3(\upsilon -s)$. According to the unified solver given in Section 3, the solutions of Equation (40(40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) ) are:

Rational function solutions: (when $\upsilon =s$)

The rational solutions of Equation (40(40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) ) are (44) ${\phi }_{1,2}(x,t)={\left(\mp \sqrt{\frac{-h}{6\theta }}\left(\chi +\varsigma \right)\right)}^{-1}.$(44) Trigonometric function solution: (When $\upsilon -s/\theta >0$)

The trigonometric solutions of Equation (40(40) $\mathbf{-}\mathbf{3}\mathbf{(}\mathbf{v}\mathbf{-}\mathbf{s}\mathbf{)}\phi \mathbf{+}\mathbf{h}{\phi }^3\mathbf{+}\mathbf{3}\theta \frac{{\mathrm{d}}^2\phi }{\mathrm{d}{\chi }^2}\mathbf{=}\mathbf{0.}$(40) ) are (45) ${\phi }_{3,4}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{h}}\tan \left(\sqrt{\frac{\upsilon -s}{2\theta }}(\chi +\varsigma )\right)$(45) and (46) ${\phi }_{5,6}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{h}}\cot \left(\sqrt{\frac{\upsilon -s}{2\theta }}(\chi +\varsigma )\right).$(46) Hyperbolic function solution : (When $\upsilon -s/\theta <0$)

The hyperbolic solutions of Equation (41(41) $\begin{array}{rl}{\phi }_c& =\sqrt{6\left(\frac{v-S}{h}\right)}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(\frac{\sqrt{\frac{v-S}{h}}}{\sqrt{\frac{\theta }{h}}}\chi \right),\end{array}$(41) ) are (47) ${\phi }_{7,8}(x,t)=\pm \sqrt{\frac{3(\upsilon -s)}{h}}\tanh \left(\sqrt{\frac{s-\upsilon )}{2\theta }}(\chi +\varsigma )\right)$(47) and (48) ${\phi }_{9,10}(x,t)=\pm \sqrt{\frac{3(\upsilon -s)}{h}}\coth \left(\sqrt{\frac{s-\upsilon }{2\theta }}(\chi +\varsigma )\right).$(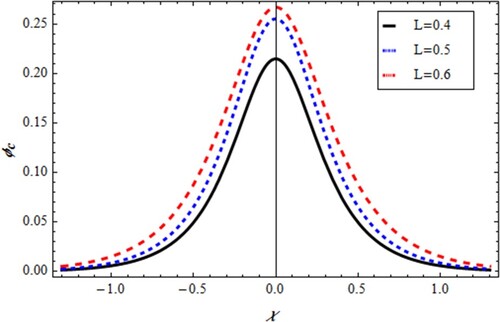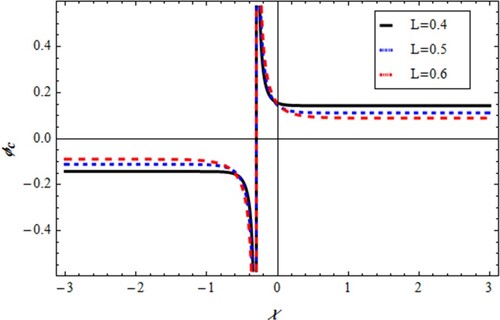48) Two-dimensional propagation of MKP solitary nonlinear IAs have been examined in a plasma mode using parameters related to the plasmas of Earth's ionosphere [16,17]. At certain mass ratio value called the criticality value, the obtained equation cannot describe mode. So, new stretching produced MKP equation which describes critical system under investigation. Equation (42(42) $\begin{array}{rl}S& =\frac{M^{2}P}{L}-u,\end{array}$(42) ) represents soliton with stationary behaviour at different directionalcosine in x-axis (L) as shown in Figure 1. At a critical point, many solitary forms were expected to discuss the IAs behaviour using Riccati–Bernoulli solver for MKP equation. 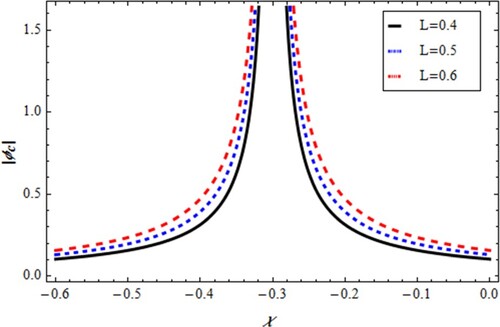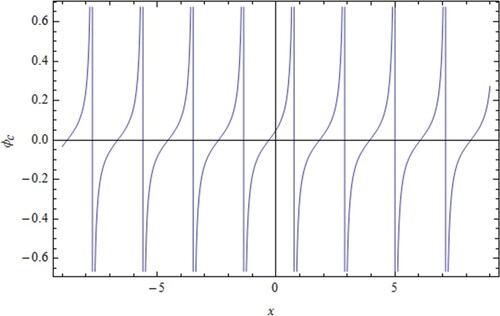Solution (45(45) ${\phi }_{3,4}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{h}}\tan \left(\sqrt{\frac{\upsilon -s}{2\theta }}(\chi +\varsigma )\right)$(45) ) is solitonic wave type called explosive type with rapid increasing amplitude as depicted in Figure 2. 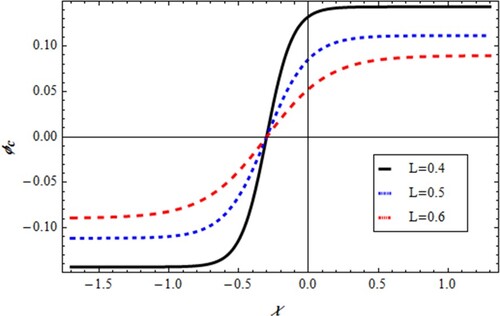Solution (46(46) ${\phi }_{5,6}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{h}}\cot \left(\sqrt{\frac{\upsilon -s}{2\theta }}(\chi +\varsigma )\right).$(46) ) is blow-up periodic shape as in Figure 3. On the other hand, the dissipative behaviours are also produced in Figures 4 and 5. In the solution of (48(48) ${\phi }_{9,10}(x,t)=\pm \sqrt{\frac{3(\upsilon -s)}{h}}\coth \left(\sqrt{\frac{s-\upsilon }{2\theta }}(\chi +\varsigma )\right).$(48) ), the shock wave is propagated in the medium as shown in Figure 4. Finally, the explosive shock profile is obtained for solution (49) as shown in Figure 5.

Figure 1. Variation ${\phi }_c$ of against $\chi ,L$ for $u=0.5,\alpha =1.0,{\mu }_e=0.8,\upsilon =0.01$.

Figure 2. Variation of ${\phi }_c$ against $\chi ,L$ for $u=0.2,\alpha =1.0,{\mu }_e=0.8,\upsilon =0.3$.

Figure 3. Plot of ${\phi }_c$ against χ for $u=0.02,\alpha =1.0,{\mu }_e=0.8,\upsilon =0.3,L=0.6$.

Figure 4. Variation of periodic ${\phi }_c$ against χ for $u=0.02,\alpha =1.0,{\mu }_e=0.8,\upsilon =0.3$, L = 0.92.

Figure 5. Variation of shock ${\phi }_c$ against $\chi ,L$ for $u=0.02,\alpha =1.0,{\mu }_e=0.8,\upsilon =0.03$.

6. Conclusions

Riccati–Bernoulli solver gives new solitary excitations for MKP equation such as periodic, explosive, shock and new explosive shocks which represent the pictures of wave motion of plasma solitons. It was reported that the obtained forms can be used in verify the broadband and magnetotail electrostatic waves observations.

Acknowledgements

This project was supported by the deanship of scientific research at Prince Sattam Bin Abdulaziz University under the research project No. 10259/01/2019.

Disclosure statement

No potential conflict of interest was reported by the author(s).