Bifurcation analysis of ion-acoustic waves in an adiabatic trapped electron and warm ion plasma

Abstract

Bifurcation analysis of ion-acoustic waves in complex plasmas in the presence of adiabatic trapped electrons and warm ions is studied. Using bifurcation theory of dynamical structure, the Hamiltonian system inculpated electrostatic potential is derived. Effects of physical parameters, such as T and ${\sigma }_i$, are shown on the analytical solitary wave solution. The numerical results show that parameters T and ${\sigma }_i$ affect significantly on nonlinear electrostatic solitary waves. By adding an external periodic perturbation to unperturbed Hamiltonian system, we investigate quasiperiodic structure of the perturbed Hamiltonian system.

Keywords:

• Ion-acoustic solitary wave
• adiabatic trapped electron
• phase plot
• bifurcation theory

1. Introduction

Excitations and propagations of the nonlinear electrostatic and electromagnetic waves in plasmas have been explored both experimentally and theoretically in the last five decades [1–3,4–6]. Since these types of nonlinear structures are one of the fundamental research in mentioned media, different kinds of waves, like vortices, solitons, shocks, etc. have been studied in various nonlinear environments [7–9]. One of the interesting attention in nonlinear features is the ion-acoustic (IA) drift wave reported by a good number of authors [9–11]. The IA wave is a wave with low frequency and can exist owing to the restoring force providing by the electron thermal pressure, whereas inertia comes from the ion mass [12,13]. The observations have been reported by Viking spacecraft [14] and Freja satellite [15] emphasizing that the characteristic of IA waves can be modified by varying the particle distributions in plasmas. Cairns et al. [16] have reported the effects of the temperature of ions, exterior static magnetic field, and obliqueness on IA solitons in a magnetized plasma with hot adiabatic ions and electrons following non-thermal distribution. The influence of trapping electrons on the IA solitary waves have been studied by Schamel [17]. The soliton or the solitary wave is the result of a delicate balance between nonlinearity and dispersion. The standard reductive perturbation technique (RPT) is one of the famous methods which can help researchers to investigate various nonlinear evolution equations and soliton solutions [7,18–20]. Esfandyari-Kalejahi et al. [8] have reported via RPT the nonlinear IA solitary waves with finite amplitude in a plasma with adiabatic hot ions, non-isothermal electrons in the presence of weakly relativistic electron beam. Numerically, it is concluded that the phase speed of IA modes might be complex-valued, solitary wave will not exist for these modes. The results have demonstrated that the phase speed is highly affected by the density ratio of beam-to- background electron, velocity of electron beam and partially on the temperature ratio of ion to free-electron. Very recently, Farooq et al. [21] have reported the propagation of dissipative IA waves in a magneto-rotating collisional plasma with cold inertial ions and hybrid (kappa and Cairn's) non-thermally distributed electrons and positrons. The obliquely propagating IA solitary waves in a non-thermal collisional magnetized dusty plasma with κ-distributed electrons, stationary dusts and inertial ions have been studied by Sultana [22]. Via RPT, the damped KdV equation has been derived and shown that the polarity of the wave changes due to the variation of density ratios of dusts and ions and also due to the variation of the super-thermally index in the plasma system. Another method by which the behaviour of the nonlinear wave has been studied is the bifurcation of phase portraits. By means of this method, researchers can investigate all possible nonlinear wave solutions, viz. the solitary wave solution and periodic wave solution [23]. For instance, the nonlinear behaviour of dust ion acoustic (DIA) waves in a nonextensive plasma has been explored by Saha et al. [24]. They have found that the effects of plasma parameters significantly alter the characteristics of nonlinear DIA solitary and periodic structures. Employing RPT, Saha et al. [25] have derived the Kadomtsev–Petviashili equation in magnetoplasmas with considering the Cairns–Tsallis distribution for electrons. Using the bifurcation theory, the existence of solitary wave solution sand periodic wave solution of the KP equation have been discussed. Recently, nonlinear and supernonlinear IA periodic waves in an unmagnetized plasma with cold mobile ions and the q-nonextensive hot electrons have been studied [26] and effects of plasma parameters on all probable phase plots consisting of nonlinear homoclinic trajectory, nonlinear periodic trajectory, superhomoclinic trajectory and superperiodic trajectory have been presented by analysis of planar dynamical systems. After pioneering work on the IA wave by Sagdeev [27], many researchers tended to use this approach widely to analysis the impacts of various plasma parameters on the nonlinear propagation [28–30]. For instance, by applying the pseudopotential method, the nonlinear wave features of large amplitude IA waves have been reported in a plasma with electron beams by Nejoh et al. [28]. The authors have also reported that temperature and density of electron beam have a great influence on the region and condition of the existence of large amplitude IA waves. Recently, Mahmood et al. [30] have explored the linear and nonlinear IA waves in unmagnetized e-i quantum plasmas by Sagdeev potential approach. The authors have found that the density dips structures have been formed in the subsonic region and the nonlinear wave amplitude has been reduced with the growth of Mach number in an e-i quantum plasma media. Recently, M. Akbari-Moghanjoughi [31,32] has applied the Sagdeev pseudopotential approach to nonlinear plasma excitations and autoresonance effect. On the other hand, a famous concept, existed in the space plasma and laboratory plasma, is the particle trapping and it may be owing to the hot electrons trapped in the wave potentials [33,34]. The conceptual idea of “trapping” predominantly deals with to a condition in which few particles in plasma are confined in a limited phase space region, where they both bounce back and show the closed orbits. Since the pioneering work by Bernstein et al. [35], the idea of trapping in the plasma system has been introduced. The authors have pointed out that, by addition of an appropriate number of plasma particles trapped in the potential-energy troughs, fundamentally arbitrary travelling waves can be established. Gurevich [36] and Crains et al. [37] have proposed to a 3/2 power nonlinearity substituted for the habitual quadratic in adiabatic trapping problems. Many researchers have tried to find effects of trapped particles in plasma on the genesis and propagation of solitary wave features [38–40]. Very recently, by applying the RPT and hydrodynamic model equations for the ion fluid, Abdikian [41] has studied the nonlinear DIA solitary waves in magnetized dusty plasmas with negative and positive ions, and stationary opposite polarity dust particles. By considering the Cairns–Gurevich distribution for electrons, the author has derived the modified ZK equation and discussed how the different plasma parameters have an influence on the solitary wave features. Using the bifurcation theory of dynamical systems, the centres and saddle points have been reported. Waves are basic structures in laboratory and space plasma physics. By studying wave dynamics accompanied by the parameters of the medium, one can extract the information about the oscillations linked to the transported and transformed energy due to various physical processes. In the present study, we have investigated the propagation of solitary structures and its quasiperiodic motion in an unmagnetized complex plasma involving adiabatic trapped electrons and warm ions in the presence of an external periodic force and it has been found that although the first one has solitary wave, the second one has the quasiperiodic motion. This media may be found in the space environments where trapped populations of electrons [1,42–44] have been observed.

The paper has been decomposed in the following manner. In Section 2, theoretical formulation of a dense e-i plasma has been presented. Section 3 has been devoted to the planner dynamical systems and corresponding phase portraits. We have investigated quasiperiodic behaviours of the perturbed Hamiltonian system in Section 4, and finally, the conclusion is shown in Section 5.

2. Theoretical formulation

We suppose a confined homogeneous e-i plasma system including to species of particles which are warm positive non-degenerate ions owing to their mass as collated to degenerate electrons and temperature adiabatic trapped electrons. The normalized dynamic equations of the IA waves are [28,29,46–49]. (1) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_i}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}(n_i{u}_i)=0,\end{array}$(1) (2) $\begin{array}{rl}& \frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }t}+u_i\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }x}=-\frac{\mathrm{\partial }\mathrm{\Phi }}{\mathrm{\partial }x}-\frac{{\sigma }_i}{n_i}\frac{\mathrm{\partial }{P}_i}{\mathrm{\partial }x},\end{array}$(2) (3) $\begin{array}{rl}& \frac{\mathrm{\partial }{P}_i}{\mathrm{\partial }t}+u_i\frac{\mathrm{\partial }{P}_i}{\mathrm{\partial }x}+3P_i\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }x}=0,\end{array}$(3) (4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2\mathrm{\Phi }}{{\mathrm{\partial }}^{2}x}=n_e-n_i,\end{array}$(4) where ${\sigma }_i$ is the ratio of ion temperature. We adopt the adiabatic trapped degenerate for electrons. Thus, the normalized electron number density is given by [1,42–44] (5) $n_e=(1+\mathrm{\Phi }{)}^{3/2}+T^2(1+\mathrm{\Phi }{)}^{-1/2},$(5) where T determines the normalized degenerate electron temperature. We choose some of the typical plasma parameters found in ultra-dense astrophysical environments (such as neutron stars and white dwarfs) in which the relativistic effects are important [45] $n_{e0}={10}^{27}{\mathrm{cm}}^{-3}$ and ${\sigma }_i=T_i/T_e=0.03$.

3. Dynamical structure and phase portrait analysis

In this section, by considering an independent variable $\xi =x-Mt$, where M is the velocity of the travelling wave, one may transform the above model equations into a dynamical system and shall consider all possible phase plots of the system. Now, under the suitable boundary conditions, viz., $\mathrm{\Phi }\to 0,u_i\to 0,P_i\to 1$, and $n_i\to 1$ as $\xi \to \pm \mathrm{\infty }$, Equations (1(1) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_i}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}(n_i{u}_i)=0,\end{array}$(1) )–(3(3) $\begin{array}{rl}& \frac{\mathrm{\partial }{P}_i}{\mathrm{\partial }t}+u_i\frac{\mathrm{\partial }{P}_i}{\mathrm{\partial }x}+3P_i\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }x}=0,\end{array}$(3) ) provide, (6) $\begin{array}{rl}{n}_i& ={\displaystyle \frac{1}{1-u_i/M}},\end{array}$(6) (7) $\begin{array}{rl}{P}_i& =n_i^3,\end{array}$(7) (8) $\begin{array}{rl}{n}_i& ={\displaystyle \frac{{\sigma }_1}{\sqrt{2}{\sigma }_0}}\\ & \times {[1-{\displaystyle \frac{2\mathrm{\Phi }}{M^2{\sigma }_1^2}}-\sqrt{{(1-{\displaystyle \frac{2\mathrm{\Phi }}{M^2{\sigma }_1^2}})}^2-4\frac{{\sigma }_0^2}{{\sigma }_1^4}}]}^{1/2},\end{array}$(8) where ${\sigma }_0=\sqrt{3{\sigma }_i/M^2}$ and ${\sigma }_1=\sqrt{1+{\sigma }_0^2}$.

Using Equations (5(5) $n_e=(1+\mathrm{\Phi }{)}^{3/2}+T^2(1+\mathrm{\Phi }{)}^{-1/2},$(5) ) and (8(8) $\begin{array}{rl}{n}_i& ={\displaystyle \frac{{\sigma }_1}{\sqrt{2}{\sigma }_0}}\\ & \times {[1-{\displaystyle \frac{2\mathrm{\Phi }}{M^2{\sigma }_1^2}}-\sqrt{{(1-{\displaystyle \frac{2\mathrm{\Phi }}{M^2{\sigma }_1^2}})}^2-4\frac{{\sigma }_0^2}{{\sigma }_1^4}}]}^{1/2},\end{array}$(8) ) in Equation (4(4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2\mathrm{\Phi }}{{\mathrm{\partial }}^{2}x}=n_e-n_i,\end{array}$(4) ), and using Taylor's series expansion, one can obtain (9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) where ${\alpha }_1=\frac{3}{2}-\frac{T^2}{2}$, ${\alpha }_2=\frac{3}{8}(1+T^2)$, $\begin{array}{rl}{\beta }_1& =\frac{4{\sigma }_0^2+(s-1){\sigma }_1^4}{M^2{s}^2{\sigma }_0{\sigma }_1^5\sqrt{2-2s}}\mathrm{and}\\ {\beta }_2& =-{\displaystyle \frac{8{\sigma }_0^4+2{\sigma }_0^2{\sigma }_1^4+(s-1){\sigma }_1^8}{M^2(s-1)s^4{\sigma }_0{\sigma }_1^{11}\sqrt{2-2s}}}\end{array}$ with $s=\sqrt{({\sigma }_1^4-4{\sigma }_0^2)/{\sigma }_1^4}$.

Then Equation (9(9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) ) is analogue to the Hamiltonian structure: (10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) One can find all possible travelling wave solutions of Equation (9(9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) ) by definition of the phase plots and by showing the vector fields of 10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) . The system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) is a dynamical structure that involves parameters ${\sigma }_i$, T and M, and the related Hamiltonian function is obtained as: (11) $H(\varphi ,z)=\frac{z^2}{2}-({\alpha }_1-{\beta }_1)\frac{{\mathrm{\Phi }}^2}{2}-({\alpha }_2-{\beta }_2)\frac{{\mathrm{\Phi }}^3}{3}.$(11) When the plasma parameters are altered, one can study the effects of them on the bifurcations of phase portraits of system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) in the $(\mathrm{\Phi },z)$ phase plane. According to the bifurcation theory, a homoclinic orbit of system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) corresponds to a solitary wave solution of Equation (9(9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) ). A periodic orbit of system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) refers to a periodic travelling wave solution of Equation (9(9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) ) [50–52]. By applying the bifurcation theory [50–52] of phase portraits of system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ), it is proven that the two equilibrium points can be seen at $E_0({\mathrm{\Phi }}_0,0)$ and $E_1({\mathrm{\Phi }}_1,0)$, where ${\mathrm{\Phi }}_0=0$ and ${\mathrm{\Phi }}_1=({\alpha }_1-{\beta }_1)/({\beta }_2-{\alpha }_2)$. If we take into account $M({\mathrm{\Phi }}_i,0)$ to be the coefficient matrix of the linearized system of system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) at an equilibrium point $E_i({\mathrm{\Phi }}_i,0)$, then we have (12) $J=detM({\mathrm{\Phi }}_i,0)=-({\alpha }_1-{\beta }_1)-2({\alpha }_2-{\beta }_2){\mathrm{\Phi }}_i.$(12) Using the theory of dynamical systems [50–52], it is known as the equilibrium point $E_i({\mathrm{\Phi }}_i,0)$ of the Hamiltonian system to be a saddle point or to be a centre if J<0 or J>0, respectively. Using systematic analysis, one can show the effects of T and ${\sigma }_i$ on phase portraits of 10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) plotted in Figures 1 and 2. For plotting the phase portrait of Figures 1 and 2, values of T and ${\sigma }_i$ should be chosen with the relations ${\beta }_2>{\alpha }_2$ and ${\alpha }_1>{\beta }_1$. Figure 1 illustrates phase portrait of Equation 10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) for various values of T with fixed value of ${\sigma }_i=0.03$. It is clear from the Figure 2(a) that $E_0({\mathrm{\Phi }}_0,0)$ is saddle point and $E_1({\mathrm{\Phi }}_1,0)$ is centre point but for the Figure 2(b) they are vice versa i.e. $E_0({\mathrm{\Phi }}_0,0)$ is centre point and $E_1({\mathrm{\Phi }}_1,0)$ is a saddle point.

3.1. Solitary wave solution

The solitary wave solution of the system 9(9) $\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}{\xi }^2}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2,$(9) for the ion-acoustic wave is compressive and is proportional to the following relation (13) $\mathrm{\Phi }=\frac{-3({\alpha }_1-{\beta }_1)}{2({\alpha }_2-{\beta }_2)}{\mathrm{sech}}^2\left(\frac{\sqrt{{\alpha }_1-{\beta }_1}}{2}\xi \right).$(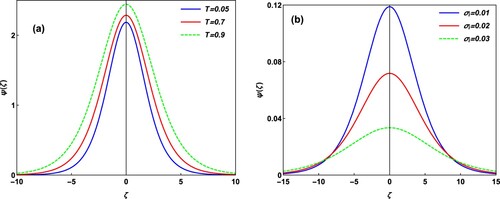13) In Figure 3(a,b), we have presented variations of ion-acoustic solitary wave profile for various values of T and ${\sigma }_i$, respectively. In Figure 3(a), Φ has been depicted as a function of ξ for various values of T with M = 1.2 and ${\sigma }_i=0.03$. Obviously, from Figure 3(a), we get that amplitude and width of ion-acoustic solitary wave increase while the value of T increases. Thus, the ion-acoustic solitary wave flourishes as T increases. Conversely, in Figure 3(b), Φ has been shown as a function of ξ for different values of parameters ${\sigma }_i$ with M = 0.9 and T = 0.3. It is clear that although the amplitude of ion-acoustic solitary wave decreases, the width of this structure increases when the value of ${\sigma }_i$ increases. As a result, the ion-acoustic solitary wave becomes smooth.

Figure 1. Phase plots of the system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) for: (a) $M=1.2,{\sigma }_i=0.03$; (b) $M=0.8,{\sigma }_i=0.03$.

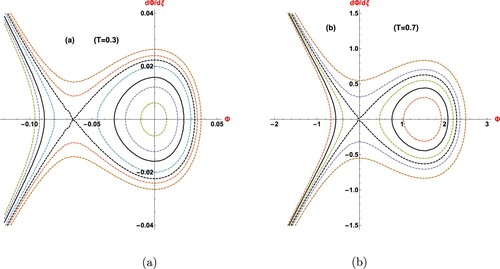
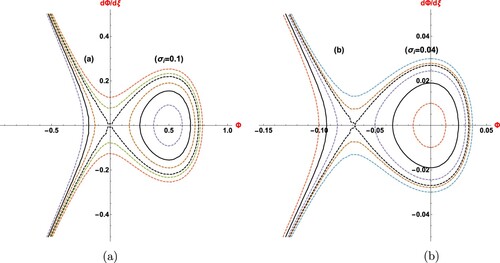
Figure 2. Phase plots of the system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) for: (a) M = 1.2, T = 0.3; (b) M = 0.8, T = 0.3.

Figure 3. Illustrates ion-acoustic solitary waves for: (a) different values of T with M = 1.2 and ${\sigma }_i=0.03$, (b) different values ${\sigma }_i$ with M = 0.9 and T = 0.3.

4. Quasiperiodic behaviour

Quasiperiodic behaviour of a dynamical system exhibits irregular periodicity. Quasiperiodic feature is the kind of motion performed by a dynamical system composing of incommensurable two frequencies, i.e. ratio of these frequencies takes an irrational number. The root of many nonlinear characteristics of unlimited dynamical systems such as pondermotive force [53,54], period doubling [55,56], harmonic generation [57,58] soliton and shock wave generation [59] lies on the fact that there is a connection between the amplitude and frequency of oscillations in these systems. By adding an external sinusoidal force i.e. $f_0\cos ({\omega }_0\xi )$ to the Hamiltonian structure (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ), one can investigate the autoresonance phenomenon, where $f_0$ and ${\omega }_0$ are strength and frequency of the periodic perturbation. In fact, the autoresonance is a phenomenon of excitation of a nonlinear dynamical system to higher amplitudes by phase-locking with the external periodic force oscillations with small drive amplitude and chirped frequency [60]. In this case, we explore the quasiperiodic feature of the perturbed Hamiltonian system: (14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) where $f_0$ and ${\omega }_0$ are strength and frequency of the periodic perturbation, respectively. The last term in second equation of the system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ), i.e. $f_0\cos ({\omega }_0\xi )$, is the exterior periodic force that causes the difference between the system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) and the system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ).

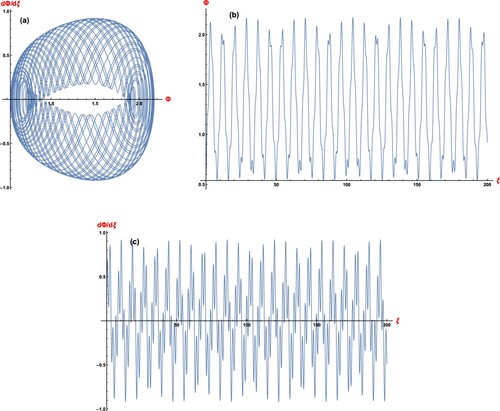
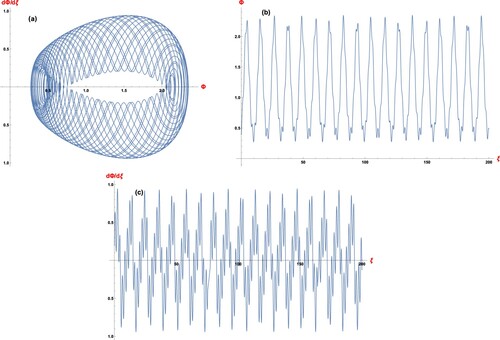
In Figure 4(a), we have depicted the phase plot and in Figure 4( b,c), we have presented time series plots for Φ and $\mathrm{d}\mathrm{\Phi }/\mathrm{d}\xi$ against ξ of the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) for specific values of $M=1.2,{\sigma }_i=0.03,T=0.3,f_0=1.11$ and $\omega =3.16$ with initial condition $({\mathrm{\Phi }}_0,\mathrm{d}\mathrm{\Phi }/{\mathrm{d}\xi }_0)=(0.6,0.2)$. It is concluded that the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) bears irregular periodicity with ratio of the frequencies as an irrational number. Thus, the perturbed system 14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) performs a quasiperiodic behaviour.

Figure 4. (a) Phase plot, (b) Φ vs ξ and (c) $\mathrm{d}\mathrm{\Phi }/\mathrm{d}\xi$ vs ξ of the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) for $M=1.2,$ ${\sigma }_i=0.03,T=0.3,f_0=1.11$ and $\omega =3.16$ with initial condition $({\mathrm{\Phi }}_0,\mathrm{d}\mathrm{\Phi }/{\mathrm{d}\xi }_0)=(0.6,0.2)$.

On the other hand in Figure 5(a), we have depicted phase plot of system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) with specific values $M=1.5,{\sigma }_i=0.03,T=0.5,f_0=1.4$ and $\omega =3.6$ with initial condition $({\mathrm{\Phi }}_0,z_0)=(0.1,0.4)$. Variations of Φ and $\mathrm{d}\mathrm{\Phi }/\mathrm{d}\xi$ with respect to ξ of perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) are shown in Figure 5( a,b), respectively, with same values of parameters. It is seen that the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) makes irregular periodicity with ratio of the frequencies as an irrational number. Thus, in this case the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) also performs a quasiperiodic behaviour. It is clear that, from Figures 4 and 5, by adding the external periodic perturbation to the system (10(10) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2.\end{array}$(10) ) to have the quasi-periodic behaviour, however not to have chaotic motion. It is depicted that the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) shows irregular periodic motion with ratio of the frequencies as an irrational number. Therefore, in this case, the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) also shows a quasiperiodic motion.

Figure 5. (a) Phase plot, (b) Φ vs ξ and (c) $\mathrm{d}\mathrm{\Phi }/\mathrm{d}\xi$ vs ξ of the perturbed system (14(14) $\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\xi }}=z\\ & {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}\xi }}=({\alpha }_1-{\beta }_1)\mathrm{\Phi }+({\alpha }_2-{\beta }_2){\mathrm{\Phi }}^2+f_0\cos ({\omega }_0\xi )\end{array}$(14) ) for $M=1.5,$ ${\sigma }_i=0.03,T=0.5,f_0=1.4$ and $\omega =3.6$ with initial condition $({\mathrm{\Phi }}_0,\mathrm{d}\mathrm{\Phi }/{\mathrm{d}\xi }_0)=(0.1,0.4)$.

5. Conclusion

In this paper, by means of the bifurcation theory of dynamical systems, various wave features (solitonic and quasiperiodic) for ion-acoustic waves have been examined in an unmagnetized complex plasma involving adiabatic trapped electrons and warm ions. The fundamental equations including hydrodynamic equations and Poisson equation have been used, based on the pseudopotential approach, to obtain a nonlinear equation for an unmagnetized complex plasma involving adiabatic trapped electrons and warm ions. Classically, this equation shows the motion of a pseudoparticle in the presence of damping and the external drive. By reducing the nonlinear equation to a Hamiltonian system with electrostatic potential and using the bifurcation theory of dynamical systems, various wave features (solitonic and quasiperiodic) for ion-acoustic waves have been examined. It has been obviously shown that the physical parameters, such as, T and ${\sigma }_i$ affect signicantly on the analytical solitary wave solution. It is found although the ion-acoustic solitary wave flourishes as T increases, the amplitude of ion-acoustic solitary wave decreases, width of this structure increases when the value of ${\sigma }_i$ increases. By combining an external periodic perturbation to unperturbed Hamiltonian system, the perturbed Hamiltonian system has been derived and tried to study the quasiperiodic behaviour. It has been found that although the first one has the solitary wave, the second has quasiperiodic motion. The present investigation may be beneficial in understanding the propagation of solitary structures in different space environments [45] (neutron stars and white dwarfs), where trapped populations of electrons have been observed.

Disclosure statement

No potential conflict of interest was reported by the authors.