Fractional anisotropic diffusion equation in cylindrical brush model

Abstract

In this work, we have suggested a neat method of obtaining the fractional diffusion equation for an anomalous anisotropic diffusion process using fractal brush structure as a background medium. For the sake of completeness, we intend to present an analytical solution in the case of the Dirichlet boundary condition. Finally, some notes and remarks are represented to show the vital role of a physical or biological system that exhibits a multiple trapping process.

KEYWORDS:

• Anomalous diffusion
• fractional derivative
• fractal brush structure

1. Introduction

In the well-known phenomenon of normal diffusion, the mean square displacement (MSD) is linearly proportional to time, $⟨x^2\left(t\right)⟩\sim t$, i.g. Brownian motion. But in many physical systems, it has been observed that this linearity does not hold. This diffusive process is called anomalous diffusion where the behaviour of MSD can be written as $⟨x^2\left(t\right)⟩\sim t^{\gamma }$ with $\gamma \ne 1$. For $0<\gamma <1$, the variance of particles' position is slower than linearly with time, this case is called subdiffusion. While for $\gamma >1$, MSD grows faster than linearly with time and it is called superdiffusion. Anomalous diffusion (both sub- and superdiffusion) occurs in the mathematics of numerous application fields that see recent developments as financial systems [1], transport of fluids in porous media [2], optical lattices [3] and in epidemiology [4–6]. There exist many methods for dealing with anomalous diffusion in different cases: in the presence or the absence of an external velocity or force field we can use methods such as continuous time random walk (CTRW) theory [7,8] which has become as a standard tool to model anomalous diffusion, i.e. diffusion is modelled by a sequence of jumps interrupted by periods of waiting. Another approach is to use differential fractional operators to these processes which are more suitable for handling external fields and boundary value problems.

Fractional diffusion equation for anomalous diffusion, composed of an extended Laplacian operator and a fractal time derivative, is proposed in [9] and the solution is achieved exactly in terms of Fox's H-function. Also in [10,11], the fractional radial diffusion in cylindrical symmetry is suggested $p(r,t)={}_0{D}_t^{-\gamma }\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}rD\left(r\right)\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right)p(r,t),$

where $p(r,t)$ is the probability density and ${}_0{D}_t^{-\gamma }$ is the Riemann–Liouville fractional integral operator with order $0<\gamma <1$ [12]. The solution of this equation has been obtained in [10] for the isotropic case. It is worth mentioning that the fractional diffusion equation in one dimension has been well studied for its solutions and derivation either by CTRW theory or fractional differential operators [13]. There have been numerous studies to investigate the analytical methods, for instance, the recent developments [14–16]. However, few studies have devoted to deriving the diffusion equation in anisotropic cylindrical geometry [17]. For this study, it was of interest to obtain and investigate the fractional diffusion equation for anomalous anisotropic diffusion processes in a cylindrical structure. We have suggested in previous work [17] a toy model that extends the comb-like structure to cylindrical coordinate, so-called fractal brush structure.

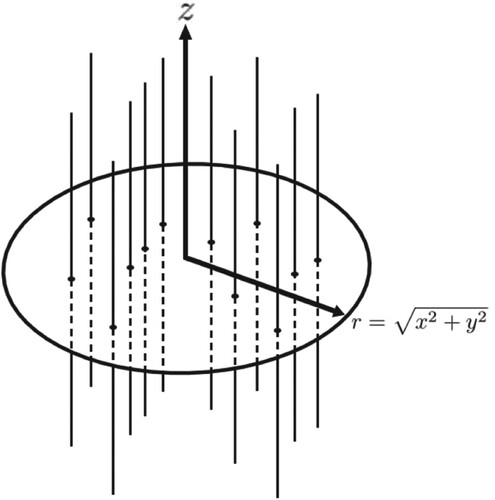
In this model, the base is a two-dimensional structure (circular sector), $r=\sqrt{x^2+y^2}$, at which the random walk particles diffuse. The trapping process occurs in fingers along the z-direction. This toy model is an idealization for the structures that may be used in various applications, for instance in biological systems and semiconductors. This work aims to develop an analytic derivation of the anisotropic fractional diffusion equation in the cylindrical model using fractal brush structure.

2. The derivation

Based on the brush structure in Figure 1, let us consider the current density components along the base of the structure (1) $J_r=-\delta \left(z\right)D_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}p(r,\varphi ,z,t)$(1) and (2) $J_{\varphi }=-\frac{\delta \left(z\right)}{r}{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }\varphi }p(r,\varphi ,z,t),$(2) where $D_{r,\varphi }$ is the diffusion coefficient along the backbone and $\delta \left(z\right)$ is the delta function, while the z-component of the current is (3) $J_z=-D_0\frac{\mathrm{\partial }}{\mathrm{\partial }z}p(r,\varphi ,z,t),$(3) where $D_0$, the diffusion coefficient along the z-direction, is assumed to be constant. From the continuity equation (4) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}p(r,\varphi ,z,t)=-{\mathrm{\nabla }}_{\mathrm{c}\mathrm{y}\mathrm{l}.}\mathbf{\cdot }\mathbf{J}(r,\varphi ,z,t).$(4) By applying Fick's law in (4(4) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}p(r,\varphi ,z,t)=-{\mathrm{\nabla }}_{\mathrm{c}\mathrm{y}\mathrm{l}.}\mathbf{\cdot }\mathbf{J}(r,\varphi ,z,t).$(4) ) and using Equations (1(1) $J_r=-\delta \left(z\right)D_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}p(r,\varphi ,z,t)$(1) )–(3(3) $J_z=-D_0\frac{\mathrm{\partial }}{\mathrm{\partial }z}p(r,\varphi ,z,t),$(3) ), one gets (5) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}p(r,\varphi ,z,t)\\ & =\left(\delta \left(z\right)\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\delta \left(z\right)\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }+D_0\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\right)\\ & p(r,\varphi ,z,t).\end{array}$(5) If we rearrange the equation to get a diffusion equation with elementary source (6) $\begin{array}{rl}& \left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}-D_0\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\right)p(r,\varphi ,z,t)\\ & =\delta \left(z\right)\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,z,t).\end{array}$(6) Therefore, the fundamental solution of the homogeneous part of Equation (6(6) $\begin{array}{rl}& \left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}-D_0\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\right)p(r,\varphi ,z,t)\\ & =\delta \left(z\right)\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,z,t).\end{array}$(6) ) at initial condition $G(z,0)=\delta \left(z\right)$ admits the well-known Gaussian distribution (7) $G(z,t)=\frac{1}{\sqrt{4\pi D_{0}t}}\exp \left(\frac{-z^2}{4D_{0}t}\right).$(7) Then the general solution of Equation (6(6) $\begin{array}{rl}& \left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}-D_0\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\right)p(r,\varphi ,z,t)\\ & =\delta \left(z\right)\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,z,t).\end{array}$(6) ) in the form superposition integral becomes (8) $\begin{array}{rl}p(r,\varphi ,z,t)& =\int \mathrm{d}{t}^{\prime }\int \mathrm{d}{z}^{\prime }G(z-z^{\prime },t-t^{\prime })\delta \left(z\right)\\ & \times \left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)\\ & \times p(r,\varphi ,z^{\prime },t^{\prime }).\end{array}$(8) As we concern at the diffusion along the backbone, putting z = 0 (9) $\begin{array}{rl}p(r,\varphi ,t)& =\frac{1}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)\\ & \times \int \mathrm{d}{t}^{\prime }\frac{1}{\sqrt{t-t^{\prime }}}p(r,\varphi ,t^{\prime }).\end{array}$(9) Now, from Riemann–Liouville fractional integral operator (10) ${}_0{D}_t^{-1/2}p(r,\varphi ,t)=\frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\int }_0^t\mathrm{d}{t}^{\prime }\frac{1}{\sqrt{t-t^{\prime }}}p(r,\varphi ,t^{\prime }),$(10) by comparing (9(9) $\begin{array}{rl}p(r,\varphi ,t)& =\frac{1}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)\\ & \times \int \mathrm{d}{t}^{\prime }\frac{1}{\sqrt{t-t^{\prime }}}p(r,\varphi ,t^{\prime }).\end{array}$(9) ) with Riemann–Liouville fractional integral we can write it as (11) $\begin{array}{rl}& p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right){}_0{D}_t^{-1/2}p(r,\varphi ,t).\end{array}$(11) Acting on both sides with the temporal derivative of the first order (12) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right){}_0{D}_t^{1/2}p(r,\varphi ,t),\end{array}$(12) which is equivalent to the known Caputo fractional operator (13) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{\frac{1}{2}}}{\mathrm{\partial }{t}^{\frac{1}{2}}}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,t),\end{array}$(13) where Caputo fractional derivative is defined as $\begin{array}{rl}{D}_C^{\alpha }& \equiv \frac{{\mathrm{d}}^{\alpha }f\left(t\right)}{\mathrm{d}{t}^{\alpha }}=I^{m-\alpha }{D}^{m}f\left(t\right)\\ & =\frac{1}{\mathrm{\Gamma }(m-\alpha )}{\int }_0^t(t-\tau {)}^{m-\alpha -1}\frac{{\mathrm{d}}^{m}f\left(\tau \right)}{\mathrm{d}{\tau }^m}\mathrm{d}\tau ,\\ & m-1<\alpha <m.\end{array}$ Equation (13(13) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{\frac{1}{2}}}{\mathrm{\partial }{t}^{\frac{1}{2}}}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,t),\end{array}$(13) ) is the time-fractional diffusion equation. The fractional order derivative arises due to the trapping along with the fingers along the z-direction. Moreover, the casualty and non-locality is encoded in the dependence on past time in the integral of (10(10) ${}_0{D}_t^{-1/2}p(r,\varphi ,t)=\frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\int }_0^t\mathrm{d}{t}^{\prime }\frac{1}{\sqrt{t-t^{\prime }}}p(r,\varphi ,t^{\prime }),$(10) ).

Figure 1. The brush structure.

3. Mathematical solution

It is obvious that (13(13) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{\frac{1}{2}}}{\mathrm{\partial }{t}^{\frac{1}{2}}}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,t),\end{array}$(13) ) is an example of a time-fractional diffusion wave equation (14) $\frac{{\mathrm{\partial }}^{\gamma }p}{\mathrm{\partial }{t}^{\gamma }}=a\mathrm{\Delta }p.$(14) In [17–19], they have shown an interest in solutions to time-fractional diffusion wave equation. Also in [20–23], they have studied problems in polar or cylindrical coordinates. The time-fractional diffusion wave equation with the Caputo derivative in a circular sector is considered in [24] under different boundary conditions.

Let us consider (13(13) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{\frac{1}{2}}}{\mathrm{\partial }{t}^{\frac{1}{2}}}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,t),\end{array}$(13) ) for general fractional order derivative α in domain $0\le r<R$, $0<\varphi <{\varphi }_0$ in the case of $D_{r,\varphi }=D=const$. For the first Cauchy problem where the initial condition $t=0:p(r,\varphi ,0)=\frac{\delta (r-r_0)}{r}\delta (\varphi -\phi ).$ Under zero Dirichlet boundary condition, by using Laplace transform with time t (15) $\begin{array}{rl}& s^{\alpha }{p}^{\ast }-s^{\alpha -1}\cdot \frac{\delta (r-r_0)}{r}\cdot \delta (\varphi -\phi )\\ & =\frac{\mathrm{\Gamma }\left(\alpha \right)D}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}\right)p^{\ast }(r,\varphi ,s).\end{array}$(15) Using the finite sin-Fourier transform with respect to the angular coordinate ϕ, with ${\xi }_n=n\pi /{\varphi }_0$ (16) $\begin{array}{rl}& s^{\alpha }\widetilde{p^{\ast }}-s^{\alpha -1}\cdot \frac{\delta (r-r_0)}{r}\cdot \sin \left({\xi }_n\phi \right)\\ & =\frac{\mathrm{\Gamma }\left(\alpha \right)D}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{{\xi }_n^2}{r^2}\right)\widetilde{p^{\ast }}(r,{\xi }_n,s).\end{array}$(16) And using finite Hankel transform with respect to the radial variable r (17) $\widehat{{\stackrel{~}{p}}^{\ast }}({\xi }_{{\xi }_n,m},{\xi }_n,s)=J_{{\xi }_n}\left(r_0{\xi }_{{\xi }_n,m}\right)\cdot \sin \left({\xi }_n\phi \right)\cdot \frac{s^{\alpha -1}}{s^{\alpha }+b{\xi }_{{\xi }_n,m}},$(17) where $b=\frac{\mathrm{\Gamma }\left(\alpha \right)}{\sqrt{4\pi D_0}}$ and ${\xi }_{{\xi }_n,m}$ are the positive roots of the transcendental equation $J_{{\xi }_n}\left(R{\xi }_{{\xi }_n,m}\right)=0.$ The inverse integral transforms result in [24] (18) $\begin{array}{rl}p(r,\varphi ,t)& =\frac{4}{{\varphi }_0{R}^2}\sum _{n=1}^{\mathrm{\infty }}\sum _{m=1}^{\mathrm{\infty }}{E}_{\alpha }(-b{\xi }_{{\xi }_n,m}^2{t}^{\alpha })\sin \left({\xi }_n\varphi \right)\\ & \times \sin \left({\xi }_n\phi \right)\cdot \frac{J_{{\xi }_n}\left(r{\xi }_{{\xi }_n,m}\right)J_{{\xi }_n}\left(r_0{\xi }_{{\xi }_n,m}\right)}{\left[J_{{\xi }_n}^{\prime }\right(R{\xi }_{{\xi }_n,m}){]}^2},\end{array}$(18) where $E_{\alpha }(-x)$ is defined as the Mittag–Leffler function which interpolates between a purely exponential law and power-like behaviour [25].

4. Fractional radial diffusion

Back to (13(13) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{\frac{1}{2}}}{\mathrm{\partial }{t}^{\frac{1}{2}}}p(r,\varphi ,t)=\\ & \frac{\mathrm{\Gamma }\left(\frac{1}{2}\right)}{\sqrt{4\pi D_0}}\left(\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r{D}_{r,\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\varphi }^2}{D}_{r,\varphi }\right)p(r,\varphi ,t),\end{array}$(13) ), in the case of independence of angular part, we get fractional radial diffusion equation (19) $\frac{{\mathrm{\partial }}^{\alpha }}{\mathrm{\partial }{t}^{\alpha }}p(r,t)=\frac{\mathrm{\Gamma }\left(\alpha \right)}{\sqrt{4\pi D_0}}\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r{D}_r\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right)p(r,t).$(19) In the case of $D_{r,\varphi }=D=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$ with initial condition $t=0:p(r,0)=\frac{\delta \left(r\right)}{2\pi r}.$ Above (19(19) $\frac{{\mathrm{\partial }}^{\alpha }}{\mathrm{\partial }{t}^{\alpha }}p(r,t)=\frac{\mathrm{\Gamma }\left(\alpha \right)}{\sqrt{4\pi D_0}}\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r{D}_r\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right)p(r,t).$(19) ) subject to the initial condition becomes in Laplace domain (20) $s^{\alpha }{p}^{\ast }-s^{\alpha -1}\cdot \frac{\delta \left(r\right)}{2\pi r}=\frac{\mathrm{\Gamma }\left(\alpha \right)D}{\sqrt{4\pi D_0}}\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right)p^{\ast }(r,s).$(20) Then applying Hankel transform of order zero with respect to the radial variable r one finds (21) $\widetilde{p^{\ast }}(k,s)=\frac{1}{2\pi }\frac{s^{\alpha -1}}{s^{\alpha }+a{k}^2},$(21) where $a=\frac{\mathrm{\Gamma }\left(\alpha \right)D}{\sqrt{4\pi D_0}}$, applying the inverse Laplace transform we have (22) $\tilde{p}(k,t)=\frac{1}{2\pi }{E}_{\alpha }(-a{k}^2{t}^{\alpha }).$(22) By taking the inverse Hankel transform we obtain (23) $p(r,t)=\frac{1}{2\pi }{\int }_0^{\mathrm{\infty }}{E}_{\alpha }(-a{k}^2{t}^{\alpha })J_0\left(kr\right)k\mathrm{d}k.$(23) Using the MATHEMATICA command NIntgrate, we obtained the numerical solution of our result as shown in Figures 2 and 3. It is worth mentioning that we can find the solution in terms of Fox's H-function but the availability of its tables will be an obstruction to find the explicit values of our solutions.

Figure 2. Time evolution of distribution function by using the expression obtained in (23(23) $p(r,t)=\frac{1}{2\pi }{\int }_0^{\mathrm{\infty }}{E}_{\alpha }(-a{k}^2{t}^{\alpha })J_0\left(kr\right)k\mathrm{d}k.$(23) ) at $\alpha =0.5$.

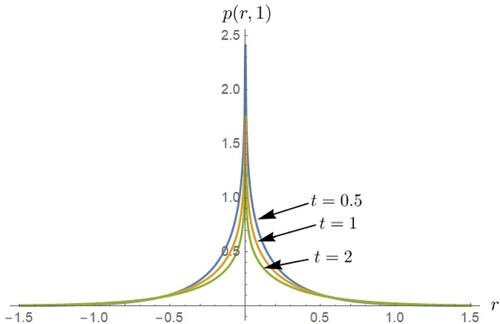
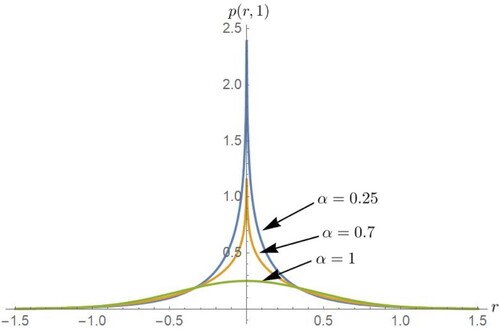
Figure 3. At t = 1, plotting the normal diffusion ($\alpha =1$) and anomalous diffusion (at $\alpha =0.25$ and $\alpha =0.7$) by using the expression obtained in (23(23) $p(r,t)=\frac{1}{2\pi }{\int }_0^{\mathrm{\infty }}{E}_{\alpha }(-a{k}^2{t}^{\alpha })J_0\left(kr\right)k\mathrm{d}k.$(23) ).

5. Conclusion

We can summarize our notes and remark as follows:

• In particular, it would be interesting to suggest that the model like brush structure gives an obvious and clear idea about the direct connection between anomalous diffusion as a physical phenomenon from one side and fractional calculus in cylindrical geometry as a mathematical approach from the other side.

• As one can inform from Figure 3 that the fractional order $\alpha =1/2$ has a compatible correlation with the density of particle in the vicinity of the origin that shows an appreciated difference between normal diffusion and subdiffusion.

• Notably, in the brush structure, the diffusion along the fingers is normal diffusion with $⟨z^2\left(t\right)⟩\sim t$ while in the base is anomalous diffusion with $⟨r^2\left(t\right)⟩\sim t^{\gamma }$.

• In essence, this suggested dentinal brush structure can be a wide range of different phenomena like for instance in charge carrier transport in amorphous semiconductor, subdiffusion in biological tissues and transport of contaminants through the soil to name a few.

Acknowledgements

We would like to express our sincere gratitude to the referee for a number of valuable criticisms and comments that have led to the improvement of the original paper. We also thank the editor for his kind cooperation.

Disclosure statement

No potential conflict of interest was reported by the author(s).