Dynamical behaviours and soliton solutions of the conformable fractional Schrödinger–Hirota equation using two different methods

Abstract

The nonlinear conformable fractional Schrödinger–Hirota (NCFSH) equation, describing the propagation of optical solitons in a dispersive optical fibre, is considered and its exact solutions are investigated. Abundant solutions including dark, bright and singular solutions have been obtained by two distinct methods, namely direct method and trial equation method. These methods provide a direct and efficient strategy for the NCFSH equation. The solutions have been simulated by graphs to check the types of solitons and their dynamical behaviours. With back substitution using Mathematica, all the solutions have been verified. Obtaining optical solutions to the proposed equation will play a fundamental role due to the applications in quantum mechanics, fluid dynamics, nonlinear optics and various other branches of mathematical physics.

KEYWORDS:

• Fractional Schrödinger–Hirota equation
• conformable derivative
• optical solutions

1. Introduction

In recent times, fractional derivatives are more preferred than classical derivatives to model real-world problems. Fractional derivatives are commonly seen in conservative and nonconservative phenomena. To model processes consisting of electromagnetic waves, electro-electrolyte polarization, diffusion wave and heat conduction, etc. fractional derivatives can be used [1].

The class of Schrödinger equations is generally modelled phenomenon, especially in quantum mechanics, energy and energy quantization. The linear Schrödinger equation represents the time evolution of wave function, whereas the nonlinear form is the most common equation for the evolution of slowly changing quasi-monochrome wave packets in weak nonlinear media with dispersion [2]. It models various nonlinearity effects in fibre such as self-phase modulation, second harmonic generation, ultrashort pulses, optical solitons, four-wave mixing, stimulated Raman scattering and so on. Laskin proposed the fractional Schrödinger equation which is an essential equation of fractional quantum mechanics [3].

In this paper, the nonlinear conformable fractional Schrödinger–Hirota (NCFSH) equation is considered as [4–7] (1) $\begin{array}{r}i{u}_t^{(\mu )}+\frac{1}{2}{u}_{xx}+|u{|}^{2}u+i\lambda u_{xxx}=0,t\ge 0,0<\mu \le 1.\end{array}$(1) The NCFSH equation describes real-world models in nonlinear optics and dispersive optical fibres [6,7]. Due to the applications in various fields, especially in optical communication systems, this equation and its solutions which enable to interperet the phenomena it represents taken much attention recently.

For the fractional operator, many approaches are known based on Gamma function. Therefore, in Equation (1), the fractional operator is considered the conformable derivative operator [8]. Most of the properties of the conformable derivative correspond to the classical derivative [9] and this definition allows to solve nonlinear partial fractional differential equations (NPFDEs) more easily [10].

The conformable derivative of order $\mu$ for the function $f$ is given by [8] (2) $T_{\mu }(f)(t)=\underset{\epsilon \to 0}{lim}\frac{f(t+\epsilon t^{1-\mu })-f(t)}{\epsilon },$(2) where $f:[0,\mathrm{\infty })\to R$, $\mathrm{\forall }t>0,\mu \in (0,1)$.

All of the classical derivative rules, such as linearity, sum, product, division, etc. are same as the conformable derivative. Additionally, if $\mu \in (0,1)$ and $f$ is differentiable, $T_{\mu }(f)(t)=t^{1-\mu }\frac{df}{dt}$can be determined [8]. Some authors [11,12] studied conformable fractional derivative and integral operators and gave geometric meaning of the conformable derivative [13]. The analysis of asymptotical stability for conformable fractional systems is given in recently published paper [14]. Recent studies [15–17] show attention to the conformable fractional derivative and its applications.

In order to find the numerical and analytical solutions of NPDEs, variety of approaches are proposed such as $G^{\mathrm{\prime }}/G$-expansion method [18,19], tanh-method [20,21], auxiliary equation method [22], simplest equation method [23], sub-equation method [24], hyperbolic function method [25], exponential rational function technique [26], ILC method [27], Picard operators method [28], invariant subspace method [29], Adomian decomposition method [30], exp-function method [31] and so on. More recently, Bernoulli approximation method and trial solution method are efficiently used in [32–36] to find exact solutions of fractional equations in physics and biology.

In this work, in addition to studies in [4–7], the TEM and the direct method are considered in the view of the definition and rules of the conformable derivative to attain the analytical solutions of the NCFSH equation.

2. Briefs of methods and results

In this section, briefs of methods and results obtained with these methods are given.

2.1. Trial equation method (TEM)

First, a nonlinear PDE, (3) $P(u,u_t,u_x,u_{xx},u_{tt},u_{xt},\dots )=0,$(3) is reduced to an ordinary differential equation, (4) $N(\xi ,z,z^{\mathrm{\prime }},z^{\mathrm{\prime }\mathrm{\prime }},\dots )=0,$(4) under the transformation $u(x,t)=z(\xi ),\xi =x-c(t^{\mu }/\mu ).$Second, consider the trial equation (5) $(z^{\mathrm{\prime }}{)}^2=\sum _{i=0}^n{a}_i{z}^i,$(5) where $a_i$ and $n$ are constants, which are derived from the solution of the system and the balancing principle, respectively.

Finally, the solution of Equation (5) can be given by the integral form (6) $\pm (\xi -{\xi }_0)=\int \frac{1}{\sqrt{\sum _{i=0}^n{a}_i{z}^i}}\text{d}z.$(6) The roots of the denominator can be classified and Equation (6) can be solved by a complete discrimination system for polynomial. Therefore, the exact solution of Equation (3) is hold [32].

Also, the trial equation can be chosen as (7) $z^{\mathrm{\prime }}=F(z)=\frac{G(z)}{H(z)}=\frac{a_r{z}^r+\dots +a_{1}z+a_0}{b_s{z}^s+\dots +b_{1}z+b_0}$(7) in the modified trial equation method [33,34], then the same procedure can be applied with the integral form solution of Equation (7) as (8) $\pm (\xi -{\xi }_0)=\int \frac{H(z)}{G(z)}\text{d}z.$(8) Similarly, one can solve integral (8) and find the exact travelling wave solutions of Equation (3).

2.1.1. Results for NCFSH Equation via the TEM

Consider the suitable wave transformation (9) $u(x,t)=z(\xi )e^{i\left(kx+\eta \frac{t^{\mu }}{\mu }\right)},\xi =x-2k\frac{t^{\mu }}{\mu },$(9) where $k$ and $\eta$ are constants. Using the above transformations and substituting the derivatives in Equation (1), and in point of the real and imaginary parts [7], $k=-1/3\lambda$ is obtained. Also, $z(\xi )$ satisfies the following ordinary differential equation: (10) $-\left(\frac{5}{54{\lambda }^2}+\eta \right)z+\frac{3}{2}{z}^{\mathrm{\prime }\mathrm{\prime }}+z^3=0.$(10)

Balancing $z^{\mathrm{\prime }\mathrm{\prime }}$ and $z^3$, we obtain $n=4$. So, trial equation is (11) $(z^{\mathrm{\prime }}{)}^2=a_0+a_{1}z+a_2{z}^2+a_3{z}^3+a_4{z}^4.$(11) Using the solution procedure of the algorithm yields a system of algebraic equations: $\begin{array}{l}81{\lambda }^2{a}_1=0,\\ -10-108\eta {\lambda }^2+162{\lambda }^2{a}_2=0,\\ 243{\lambda }^2{a}_3=0,\\ 108{\lambda }^2+324{\lambda }^2{a}_4=0.\end{array}$As a result of the system, coefficients are determined as (12) $\begin{array}{r}{a}_0=a_0,a_1=0,a_2=\frac{2\eta }{3}+\frac{5}{81{\lambda }^2},a_3=0,a_4=-\frac{1}{3}.\end{array}$(12) Equation (6) is rewritten with Equation (12), (13) $\begin{array}{r}\pm (\xi -{\xi }_0)=\int \frac{1}{\sqrt{a_0+\left(\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}\right)z^2-\frac{1}{3}{z}^4}}\text{d}z.\end{array}$(13) If we set $a_0=0$ in Equation (13) and integrate this equation, the exact solutions of Equation (1) are obtained:

If $\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}>0$, then we have bright and singular solutions, respectively: (14) $\begin{array}{rl}u(x,t)& =\pm \sqrt{2\eta +\frac{5}{27{\lambda }^2}}\\ & \times sech\left[\sqrt{\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }\right)\right]e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)},\end{array}$(14) (15) $\begin{array}{rl}u(x,t)& =\pm \sqrt{-\left(2\eta +\frac{5}{27{\lambda }^2}\right)}\\ & \times csch\left[\sqrt{\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }\right)\right]e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)}.\end{array}$(15) If $\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}<0$, the singular periodic solutions appear as (16) $\begin{array}{rl}u(x,t)& =\pm \sqrt{2\eta +\frac{5}{27{\lambda }^2}}\\ & \times \sec \left[\sqrt{-\left(\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}\right)}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)},\end{array}$(16) (17) $\begin{array}{rl}u(x,t)& =\pm \sqrt{2\eta +\frac{5}{27{\lambda }^2}}\\ & \times \csc \left[\sqrt{-\left(\frac{2\eta }{3}+\frac{5}{81{\lambda }^2}\right)}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)}.\end{array}$(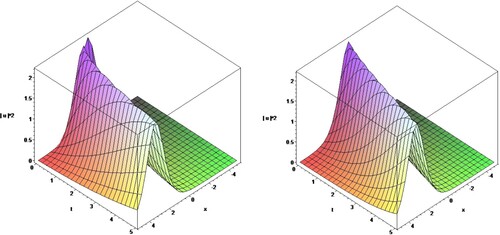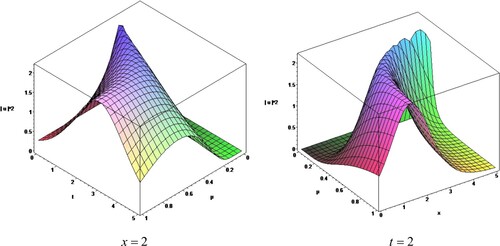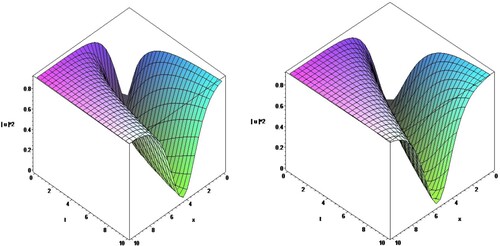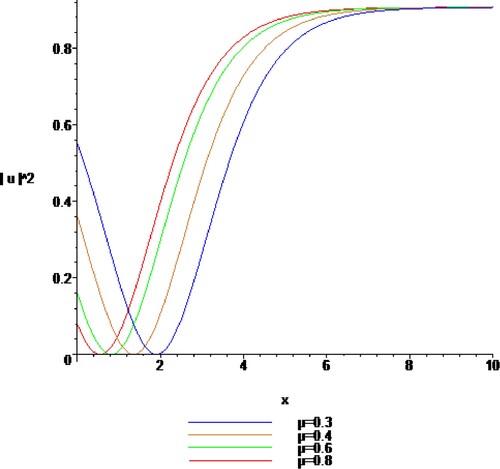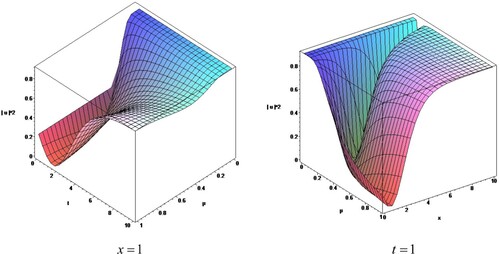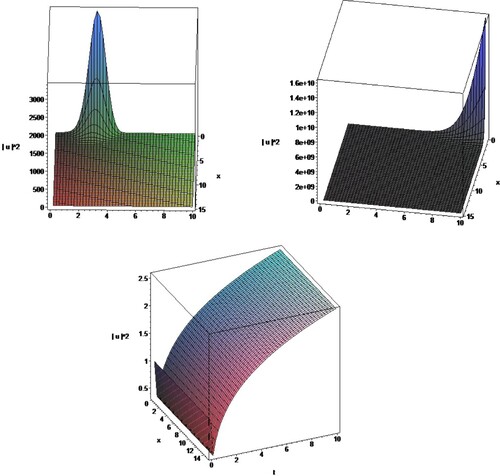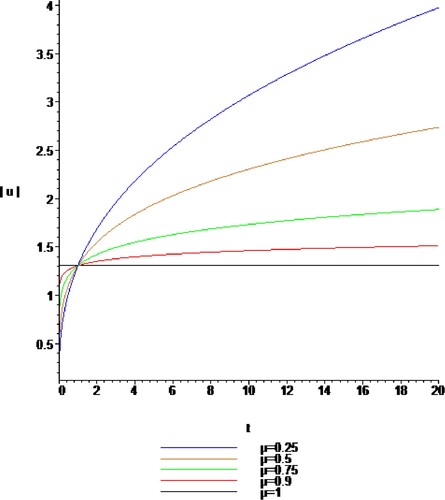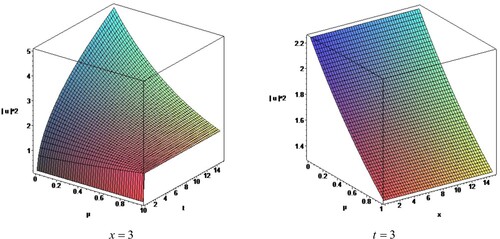17) Figures 1–3 show the nature of proposed solutions.

Figure 1. Behaviour of $|u(x,t){|}^2$ for solution (14) at $\lambda =-1,\eta =1$ and $\mu =0.4,0.8$, respectively.

Figure 2. The solution (14) for different values of $\mu$ at $t=0.6$.

Figure 3. The solution (14) for fixed values of $x$ and $t$, respectively.

We now consider the modified form of the method to solve Equation (1).

If we now use the trial Equation (7) in Equation (10) for balancing procedure, we get $r-s=2$. Choosing $r=2$ and $s=0$, the trial equation is (18) $z^{\mathrm{\prime }}=\frac{a_0+a_{1}z+a_2{z}^2}{b_0}$(18) The corresponding system is: $\begin{array}{l}81{\lambda }^2{a}_0{a}_1=0,\\ 81{\lambda }^2{a}_1^2+162{\lambda }^2{a}_0{a}_2-5b_0^2-54\eta {\lambda }^2{b}_0^2=0,\\ 243{\lambda }^2{a}_1{a}_2=0,\\ 162{\lambda }^2{a}_2^2+54{\lambda }^2{b}_0^2=0.\end{array}$Solving the corresponding system, we obtain (19) $\begin{array}{r}{a}_0=\pm \frac{i{b}_0(5+54\eta {\lambda }^2)}{54\sqrt{3}{\lambda }^2},a_1=0,a_2=\mp \frac{i{b}_0}{\sqrt{3}},b_0=b_0.\end{array}$(19) Using these coefficients in Equation (8), we get (20) $\pm (\xi -{\xi }_0)=\int \frac{b_0}{\pm \frac{i{b}_0(5+54\eta {\lambda }^2)}{54\sqrt{3}{\lambda }^2}\mp \frac{i{b}_0}{\sqrt{3}}{z}^2}\text{d}z.$(20) When we integrate this equation and use the wave transformation, the exact travelling wave solutions of Equation (1) are obtained as follows:

If $\frac{5}{2}+27\eta {\lambda }^2<0$, then we have dark optical solutions: (21) $\begin{array}{rl}u(x,t)& =\pm \frac{i}{3\lambda }\sqrt{-\frac{5}{6}-9\eta {\lambda }^2}\\ & \times \tanh \left[\frac{1}{9\lambda }\sqrt{-\frac{5}{2}-27\eta {\lambda }^2}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }+{\xi }_0\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)},\end{array}$(21) (22) $\begin{array}{rl}u(x,t)& =\pm \frac{i}{3\lambda }\sqrt{-\frac{5}{6}-9\eta {\lambda }^2}\\ & \times \coth \left[\frac{1}{9\lambda }\sqrt{-\frac{5}{2}-27\eta {\lambda }^2}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }+{\xi }_0\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)}.\end{array}$(22) If $\frac{5}{2}+27\eta {\lambda }^2>0$, then the solutions purport periodic solutions: (23) $\begin{array}{rl}u(x,t)& =\pm \frac{i}{3\lambda }\sqrt{\frac{5}{6}+9\eta {\lambda }^2}\\ & \times \tan \left[\frac{1}{9\lambda }\sqrt{\frac{5}{2}+27\eta {\lambda }^2}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }+{\xi }_0\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)},\end{array}$(23) (24) $\begin{array}{rl}u(x,t)& =\pm \frac{i}{3\lambda }\sqrt{\frac{5}{6}+9\eta {\lambda }^2}\\ & \times \cot \left[\frac{1}{9\lambda }\sqrt{\frac{5}{2}+27\eta {\lambda }^2}\left(x+\frac{2}{3\lambda }\frac{t^{\mu }}{\mu }+{\xi }_0\right)\right]\\ & \times e^{i\left(\frac{-1}{3\lambda }x+\eta \frac{t^{\mu }}{\mu }\right)}.\end{array}$(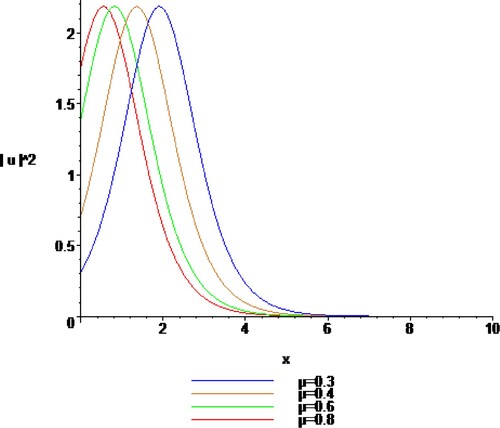24) Figures 4–6 show the graph of the corresponding solutions for the proposed equation.

Figure 4. Behaviour of $|u(x,t){|}^2$ for solution (21) at $\lambda =-1,\eta =1$, and $\mu =0.4,0.8$ respectively.

Figure 5. The solution (21) for different values of $\mu$ at $t=0.6$.

Figure 6. The solution (21) for fixed values of $x$ and $t$, respectively.

2.2. Direct method

If $f$ is differentiable, to reduce NPFDEs, the following rule of conformable fractional derivative, $T_{\alpha }(f)(t)=t^{1-\alpha }\frac{df}{dt},$can be used with the transformation $u(x,t)=z(\xi )e^{i(\sigma (\xi )-ct)},\xi =x-mt.$As a result, the reduced equation is nonlinear ordinary differential equation.

The reduced equation can be solved via analytical, semi-analytical and numerical methods.

2.2.1. Results for NCFSH equation via the direct method

Now, we consider the direct method to obtain analytical solutions of the NCFSH equation.

With conformable fractional derivative property, from Equation(1), (25) $\begin{array}{r}i{t}^{1-\mu }{u}_t+\frac{1}{2}{u}_{xx}+|u{|}^{2}u+i\lambda u_{xxx}=0,t\ge 0,0<\mu \le 1,\end{array}$(25) is obtained.

Case 1: With the transformation $u(x,t)=z(\xi )e^{i(x-ct)},\xi =x-mt,$the following equations are attained due to imaginary and real parts, respectively: (26) $\begin{array}{rl}\lambda z^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}-(m{t}^{1-\mu }+3\lambda -1)z^{\mathrm{\prime }}& =0,\end{array}$(26) (27) $\begin{array}{rl}\left(\frac{1}{2}-3\lambda \right)z^{\mathrm{\prime }\mathrm{\prime }}-\frac{1}{2}{z}^{\mathrm{\prime }}+(c{t}^{1-\mu }+\lambda )z+z^3& =0.\end{array}$(27) The analytical solution of the first equation is (28) $\begin{array}{rl}z(\xi )& =C_1+C_2\exp \left(\frac{\xi \sqrt{m{t}^{1-\mu }+3\lambda -1}}{\sqrt{\lambda }}\right)\\ & +C_3\exp \left(-\frac{\xi \sqrt{m{t}^{1-\mu }+3\lambda -1}}{\sqrt{\lambda }}\right).\end{array}$(28) Substituting the analytical solution $z(\xi )$ into the second equation and setting the coefficients of exponential function to zero gives the following system: $\begin{array}{rl}& 3{C_1}^2{C}_2\sqrt{\lambda }+C_2{\lambda }^{3/2}+3{C_2}^2{C}_3\sqrt{\lambda }+c{C}_2{t}^{1-\mu }\sqrt{\lambda }\\ & -3C_2\lambda \sqrt{m{t}^{1-\mu }+3\lambda -1}=0,\\ & 3{C_3}^2{C}_2\sqrt{\lambda }+C_3{\lambda }^{3/2}+3{C_1}^2{C}_3\sqrt{\lambda }+c{C}_3{t}^{1-\mu }\sqrt{\lambda }\\ & -3C_3\lambda \sqrt{m{t}^{1-\mu }+3\lambda -1}=0,\\ & {C_1}^3\sqrt{\lambda }+C_1{\lambda }^{3/2}+6C_1{C}_2{C}_3\sqrt{\lambda }+c{C}_1{t}^{1-\mu }\sqrt{\lambda }=0.\end{array}$Using Maple, the above system has 18 solutions. However, some of the results are trivial solutions and some of them do not match up to our aim. One of them satisfies all conditions, which is (29) $C_1=\sqrt{-\lambda -c{t}^{1-\mu }},C_2=0,C_3=0.$(29)

Therefore, the exact solution of the considered Equation (1) is (30) $u(x,t)=\sqrt{-\lambda -c{t}^{1-\mu }}{e}^{i(x-ct)},0<\mu \le 1.$(30) Figures 7–9 show the graph of the corresponding solutions for the proposed equation.

Figure 7. The solution (30) for $\mu =0.25,0.6,0.75$, respectively.

Figure 8. The solution (35) for various values of $\mu$ at $x=1$.

Figure 9. The solution (35) for fixed values of $x$ and $t$, respectively.

Case 2: Using the general transformation $u(x,t)=z(\xi )e^{i(\sigma (\xi )-ct)},\xi =x-mt,$the following equations are attained due to imaginary and real parts, respectively. (31) $\begin{array}{rl}& \lambda z^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}+({\sigma }^{\mathrm{\prime }}-m{t}^{1-\mu }+3\lambda {({\sigma }^{\mathrm{\prime }})}^2)z^{\mathrm{\prime }}\\ & +\left(\frac{1}{2}-3\lambda {\sigma }^{\mathrm{\prime }}\right){\sigma }^{\mathrm{\prime }\mathrm{\prime }}z=0,\end{array}$(31) (32) $\begin{array}{rl}& \left(\frac{1}{2}-3\lambda {\sigma }^{\mathrm{\prime }}\right)z^{\mathrm{\prime }\mathrm{\prime }}-3\lambda {\sigma }^{\mathrm{\prime }\mathrm{\prime }}{z}^{\mathrm{\prime }}\\ & +\left(c{t}^{1-\mu }+m{\sigma }^{\mathrm{\prime }}{t}^{1-\mu }-\frac{1}{2}{({\sigma }^{\mathrm{\prime }})}^2-\lambda {\sigma }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}+\lambda {({\sigma }^{\mathrm{\prime }})}^3\right)z\\ & +z^3=0.\end{array}$(32) Considering $\sigma (\xi )=\frac{\xi }{6\lambda }+C_1$, the analytical solution of the first equation is (33) $\begin{array}{rl}z(\xi )& =C_2+C_3\sin \left(\frac{\xi \sqrt{-36m\lambda t^{1-\mu }+3}}{6\lambda }\right)\\ & +C_4\cos \left(\frac{\xi \sqrt{-36m\lambda t^{1-\mu }+3}}{6\lambda }\right).\end{array}$(33) Substituting the analytical solution $z(\xi )$ into the second equation, (34) $C_2=\left(\begin{array}{l}-\lambda C_3\sin \left(\frac{\zeta \sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right)\\ -\lambda C_4\cos \left(\frac{\zeta \sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right)\\ +\frac{1}{18}{\left(\begin{array}{l}324{\lambda }^2{C_4}^2\cos {\left(\frac{\zeta \sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right)}^2\\ -54t^{(1-\mu )}m\lambda \\ -324t^{(1-\mu )}c{\lambda }^2+3-324{\lambda }^2{C_4}^2\\ +324{\lambda }^2{C_4}^2\sin {\left(\frac{\zeta \sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right)}^2\end{array}\right)}^{1/2}\end{array}\right)/\lambda$(34) is obtained.

Therefore, the exact solution of the considered Equation (1) with general transformation is (35) $\begin{array}{rl}u(x,t)& =(C_2+C_3\sin \left(\frac{(x-mt)\sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right)\\ & +C_4\sin \left(\frac{(x-mt)\sqrt{-36t^{(1-\mu )}m\lambda +3}}{6\lambda }\right))\\ & \times \exp \left(\left(\frac{x-mt}{6\lambda }+C_1-ct\right)I\right),\end{array}$(35) where $C_2$ is given above.

3. Conclusion

In this work, TEM and the direct method are considered to investigate exact solutions of the NCFSH equation. To this purpose, NCFSH equation is converted into an integer order ordinary differential equation by using the rules of the conformable derivative and the considered transformations. Using these methods, Maple and Mathematica, the optical wave solutions including various types of solitons that can be useful in nonlinear optics and telecommunication industry are obtained. Physical meanings and dynamical behaviours of the solutions are exhibited by using figures. Results indicate that these methods are powerful tools for NPDEs. Obtained solutions represent some real-life situations. Additionally, as seen in the proposed results, these suggested methods can be implemented to various fractional models arising in other areas of physics and science.

Disclosure statement

No potential conflict of interest was reported by the author(s).