Entropy generation of nanofluid flow in hexagonal microchannel

Abstract

A new model for entropy generation number in hexagonal microchannel is developed going from the equation proposed by Bejan. The effect of Cu, CuO, Al2O3 and TiO2 mixed with pure water inside the microchannel is evaluated via entropy generation analysis. To show the contribution of entropy heat-transfer generation, Bejan number is also investigated. The effects of heat flux in the range of [2000–12000] W/m², and volume fraction and nanoparticles size, respectively, on entropy generation numbers and Bejan number are all evaluated. The results demonstrate that increasing heat flux increases both thermal entropy generation and Bejan number but decreases the frictional entropy production. The results also show that thermal and friction entropy generation numbers exhibit an inverse variation trend when varying volume percentage and nanoparticle diameter.

KEYWORDS:

• Entropy generation
• hexagonal microchannel
• nanofluid
• heat flux
• thermophysical properties
• thermodynamic optimization

1. Introduction

The global expansion of energy necessitates the improvement of heat transmission and the decrease of energy losses. Optimizing the design of new energetic gadgets and developing sophisticated technological systems may effectively increase energy contribution to create rising demand. The necessity of understanding the comportment of flow in microsystems is an important step for technological application [1]. Furthermore, recent advancements have shown that microfluidic devices have a variety of advantageous features [2,3]. The concept of microchannel and nanosize equipment has attracted the attention of many researchers because of its ability to advance the heat transfer in industrial systems and remove the generation of high heat flux within electronic components [4]. Therefore, scientists [5–9] studied different shapes of microchannels in order to predict the best configuration to improve heat transfer and fluid flow in small equipment.

In addition to heat-exchanger geometrical design, the utilization of nanofluids becomes an interesting way of heat transfer enhancement [10]. Nanofluids are suspensions of solid particles of nanometric size in a base fluid. The suspension of small solid particles in energy transmission fluids can enhance their thermal conductivity and supplies an efficient and innovative way to improve their heat transfer characteristics significantly. Abollahi et al. [11] evaluated the effects of using different nanofluids on heat transfer and performance of microchannel heat sink. They found that Al₂O₃, SiO₂, CuO and ZnO in water had better heat transfer enhancement in comparison with pure water, and that SiO₂ nanofluid with nanoparticle concentration of 2% and size of 30 nm had the greatest performance compared to other nanofluids. Alkasmoul et al. [12] studied the performance of this discovered fluid, and proved that nanofluids are beneficial. They reported experimentally a comprehensive evaluation of heat transfer for Al₂O₃, TiO₂ and CuO–water nanofluids for cooling configuration. Vasefi et al. [13] studied the turbulent forced convection of CuO–water nanofluid through a horizontal channel. They investigated the effect of adding CuO nanoparticles to the base fluid on the dimensioness mean and fluctuations of velocity and temperature profiles. Jung and Park [14] analysed the heat transfer of Al₂O₃–water nanofluid in microchannel heat sink. They evaluated flow behaviours and compared the flow velocity, circulation and Reynold’s shear stress. They found, as a result, that those properties exposed higher values for Al₂O₃ nanofluid rather than water.

Increasing the number of fins particles or shrinking the size of the system is the best approach to increase heat transmission in thermal systems [15].

In reality, increasing entropy or decreasing thermal efficiency always has an impact on energy devices. As a result, it is critical to reduce entropy creation, which explains why systems’ capacity to generate work is decreasing. As a result, assessing entropy creation or exergy destruction due to heat or friction entropy is critical for optimization. As a result, entropy generation minimization is used as a design criterion for optimal thermal systems [16]. According to the thermodynamics second law, Bahiraei et al. [17] investigated the impact of water–Al2O3 nanofluid with different nanoparticles’ shapes in microchannel, on thermal, friction, total entropy generation and Bejan number at various Reynold’s numbers. Torabi et al. [18] looked into the processes that control the rate of entropy generation in micro-energy systems. They conducted an extensive literature review on the analysis of the second law in microthermal and thermochemical systems. They covered essential entropy generation equations, the entropy production idea in single-phase and multiphase flow, and research on the rate of entropy development within microchannels and nanofluid flows. Manay et al. [19] conducted experiments to determine the effect of nanofluid and microchannel heat sink height on entropy production. They also tested the influence of TiO2 nanoparticles volume fraction. Bazdidi-Tehrani et al. [20] studied the turbulent mixed convection of CuO–water nanofluid in a vertical square duct. They explored influence of nanoparticles on thermal and fractional entropy generation. They found that increasing the nanoparticle volume fraction decreases the ratio of thermal entropy generation and the frictional entropy generation. Hosseini et al. [21] analytically studied the nanofluid entropy production in a porous horizontal microchannel under MHD field. In another analytical investigation, Sheikhzadeh et al. [22] studied parameters that influence entropy generation such as volume fraction, Reynold’s number and diameter of the microchannel. Based on the second law of thermodynamics, Khlifi et al. [23] theoretically examined the creation of entropy in two various microchannels. They developed mathematical models to predict entropy generation in rectangular and elliptical microchannel and used different type of nanofluids. Shah et al. [24] also used a theoretical method and analysed mathematically entropy generation of nanofluid flow.

Different research on entropy production and exergy analysis in nanofluid within microchannels have also been conducted [25–27]. As far as is known, the entropy generation in hexagonal microchannel has not been studied much. The purpose of this research is to develop a new model for estimating entropy production rate in regular hexagon microchannel and to investigate entropy generation using nanofluids. Four nanofluids are used and compared with pure water. The heat flux effects imposed on the microchannel surface, as well as on the volume fraction and size of nanoparticles, are investigated in terms of entropy generation numbers and Bejan number.

2. Methodology

2.1. Problem of the issue

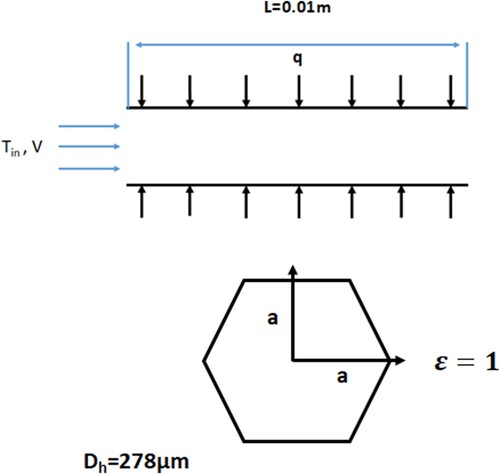
The issues addressed in this study include an examination of entropy generation using nanofluid flow in hexagonal microchannel cross sections. The considered configuration is displayed in Figure 1 which describes a fully developed steady-state microchannel laminar flow in arbitrary regular hexagonal cross section with hydraulic diameter equal to 278 µm, with a perimeter P, a cross-sectional area A and length of 0.01 m.

Figure 1. Arbitrary hexagonal constant cross-section microchannel.

A uniform wall heat flux in the range 2000–12000 W/m² heats the hexagonal channel, where $\begin{array}{rl}{T}_{\text{in}}& =290\text{K}\\ u_{\text{in}}& =2\text{m/s}\\ D_{\text{h}}& =278\mu \mathrm{m}\end{array}$$\epsilon$ is the aspect ratio of the regular hexagonal: $\epsilon =(a/a)$

This work proposes a development of a model for entropy generation number in arbitrary hexagonal microchannel in the first section. The mathematical formulation is described in the second section. Important results as well as comparative study, influence of working fluids, nanoparticles volume fraction and size are analysed in the third section.

2.2. Entropy generation formulation

Based on the analytical formula derived by Bejan [28], the development of the present model started. (1) $S_{gen,T}^{\mathrm{\prime }}=S_{gen,t}^{\mathrm{\prime }}+S_{gen,f}^{\mathrm{\prime }}$(1) In Equation (1), the entropy generation is composed of two contributions, entropy generation resultant of heat transfer and friction losses, which is formulated by Bejan as [23]: (2) $S_{gen,T}^{\mathrm{\prime }}=\frac{q^{\mathrm{\prime }}.\mathrm{\Delta }T(x)}{T^2}+\frac{\dot{m}}{{\rho }^{2}T}\left(-\frac{dp}{dx}\right)$(2) After integrating (Equation (2)), the expression obtained is independent of the form of cross section of the channel [29]: (3) $S_{gen,T}=\frac{q^{2}P{D}_{h}L}{{T^2}_{ave}kNu}+\frac{2{\dot{m}}^{3}L}{{\rho }^2{T}_{ave}{D}_h{A}^{2}Re}fRe$(3) In order to get a dimensionless formula of entropy generation rate, the following expression presents the entropy generation number N_s (4) $N_{s,T}=\frac{T_{ave}}{q{A}_w}(S_{gen,t}+S_{gen,f})$(4) Consequently, thermal and frictional entropy generation numbers are (4a) $\begin{array}{rl}{N}_{s,t}& =\frac{q{D}_h}{T_{ave}kNu}\end{array}$(4a) (4b) $\begin{array}{rl}{N}_{s,f}& =\frac{2\dot{m^3}}{{\rho }^{2}qP{D}_h{A}^{2}Re}fRe\end{array}$(4b) where T_ave, Nu and f are, respectively, the fluid temperature, the Nusselt number and the friction factor that are estimated as follows:

The average temperature is given by (5) $T_{ave}=\frac{T_{in}-T_{out}}{ln\left(\frac{T_{in}}{T_{out}}\right)}$(5) Using the energy balance of the outlet and inlet section of the channel, T_out can be estimated as (6) $T_{out}=T_{in}+\frac{q{A}_w}{\dot{m}Cp}$(6) Substituting (Equation (6)) into (Equation (5)), to get the expression of T_ave, the following equation can be used: (7) $T_{ave}=\frac{q{A}_w}{\dot{m}Cp\ln \left(1+\frac{q{A}_w}{\dot{m}CpTin}\right)}$(7) To estimate Nusselt number and Poiseuille number, two compact models were proposed, respectively, by [30], and [31], which investigates $N{u}_{\sqrt{A}}$ and $fR{e}_{\sqrt{A}}$ of a laminar flow in microchannel of regular polygonal cross section as (8) $\begin{array}{rl}N{u}_{\sqrt{A}}& =58.375(I{p}^{\ast }{)}^{0.71}{\left(\frac{\sqrt{A}}{P}\right)}^{0.62}\end{array}$(8) (9) $\begin{array}{rl}fR{e}_{\sqrt{A}}& =32{\pi }^2\frac{\sqrt{A}}{P}I{p}^{\ast }\end{array}$(9) Equations (8) and (9) are the functions of the perimeter P, the area A of the regular polygonal cross-section and the dimensionless inertia polar moment from the cross-section centre ${I_p}^{\ast }$.

Besides, the length characteristic of Nusselt number and Poiseuille number is the square root of cross-sectional area. In the present work, Nu and f_Re are related to the hydraulic diameter of the cross section.

So, they are converted as follows: (10) $\begin{array}{rl}N{u}_{D_h}& =\frac{4\sqrt{A}}{P}N{u}_{\sqrt{A}}\end{array}$(10) (11) $\begin{array}{rl}fR{e}_{D_h}& =\frac{4\sqrt{A}}{P}fR{e}_{\sqrt{A}}\end{array}$(11) As a result, Nu and Re in Equation (4a) and Equation (4b) are used with the following expressions: (12) $\begin{array}{rl}N{u}_{D_h}& =233.5(I{p}^{\ast }{)}^{0.71}{\left(\frac{\sqrt{A}}{P}\right)}^{1.62}\end{array}$(12) (13) $\begin{array}{rl}fR{e}_{D_h}& =128{\pi }^{2}I{p}^{\ast }{\left(\frac{\sqrt{A}}{P}\right)}^2\end{array}$(13) The parameters A, P and ${I_p}^{\ast }$ are illustrated, respectively, as follows. A, P and ${I_p}^{\ast }$ are expressed as functions of the side number (n) in regular polygons.

For regular hexagon, n is 6. (14) $\begin{array}{rl}A& =\frac{n{a}^2}{4\tan \left(\frac{\pi }{n}\right)}\end{array}$(14) (15) $\begin{array}{rl}\text{P}& =\text{n a }\end{array}$(15) (16) $\begin{array}{rl}{I}_P^{\ast }& =\frac{1}{6n}\left(\tan \left(\frac{\pi }{n}\right)+\frac{3}{\tan \left(\frac{\pi }{n}\right)}\right)\end{array}$(16)

After having replaced the previous formulas in Equations (12) and (13), the Nusselt and Poiseuille numbers obtained are (17) $\begin{array}{rl}N{u}_{Dh}& =21.288\frac{{\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]}^{0.71}}{n^{1.52}{\left[\tan \left(\frac{\pi }{n}\right)\right]}^{0.1}}\end{array}$(17) (18) $\begin{array}{rl}fR{e}_{Dh}& =\frac{16{\pi }^2}{3n^2}\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]\end{array}$(18) Afterwards, by using the following formulas of hydraulic diameter, Reynold’s number and the mass flow rate, a theoretical development is done for Equation (4) as follows: (19) $\begin{array}{rl}{D}_h& =\frac{4A}{P}\end{array}$(19) (20) $\begin{array}{rl}Re& =\frac{D_h\dot{m}}{A\mu }\end{array}$(20) (21) $\begin{array}{rl}\dot{m}& =\rho vA\end{array}$(21) As a result, a dimensionless expression of the total entropy generation number inside hexagonal microchannel of laminar fluid flow is obtained as (22) $\begin{array}{rl}{N}_{s,T}& =\frac{1}{85.152}\frac{{\rho }_{nf}C{p}_{nf}v}{K_{nf}L}{D_h}^2\ln \left(1+\frac{4qL}{{\rho }_{nf}v{D}_{h}C{p}_{nf}Tin}\right)\\ & \times \frac{n^{1.52}{\left[\tan \left(\frac{\pi }{n}\right)\right]}^{0.1}}{{\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]}^{0.71}}\\ & +\frac{32{\pi }^2{v}^2{\mu }_{nf}}{3q{D}_h}\frac{\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]}{n^2}\end{array}$(22) where (22a) $\begin{array}{rl}{N}_{s,t}& =\frac{1}{85.152}\frac{{\rho }_{nf}C{p}_{nf}v}{K_{nf}L}{D_h}^2\ln \left(1+\frac{4qL}{{\rho }_{nf}v{D}_{h}C{p}_{nf}Tin}\right)\\ & \times \frac{n^{1.52}{\left[\tan \left(\frac{\pi }{n}\right)\right]}^{0.1}}{\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]}\end{array}$(22a) (22b) $\begin{array}{rl}{N}_{s,f}& =\frac{8{\pi }^2{v}^2{\mu }_{nf}}{3q{D}_h}\frac{\left[1+\frac{3}{{\tan }^2\left(\frac{\pi }{n}\right)}\right]}{n^2}\end{array}$(22b) In order to estimate the contribution of the heat transfer component’s entropy creation, the Bejan number [32] is determined as follows: (23) $Be=\frac{{S^{\mathrm{\prime }}}_{gen,t}}{{S^{\mathrm{\prime }}}_{gen,t}+{S^{\mathrm{\prime }}}_{gen,f}}$(23)

2.3. Thermophysical properties

The identification of thermophysical properties is essential for understanding the nanofluid behaviour. For that, various formulas have been used to evaluate nanofluid properties, namely, specific heat, density, dynamic viscosity and thermal conductivity.

The correlations used to evaluate the density and specific heat are given in, respectively, (Equation (24)) and (Equation (25)) as [33] (24) $\begin{array}{rl}{\rho }_{nf}& =(1-\phi ){\rho }_{bf}+\phi {\rho }_s\end{array}$(24) (25) $\begin{array}{rl}C{p}_{nf}& =\frac{[{(\rho Cp)}_s-{(\rho Cp)}_{bf}]\phi +{(\rho Cp)}_{bf}}{{\rho }_{nf}}\end{array}$(25) The thermal conductivity of nanofluids is calculated using the Hamilton–Crosser [34] model depending on volume fraction and the Corione [35] depending on diameter nanoparticle. (26) $\begin{array}{rl}{k}_{nf}& =\frac{k_s+2k_{bf}-2(k_{bf}-k_s)\phi }{k_s+2k_{bf}+(k_{bf}-k_s)\phi }{k}_{bf}\end{array}$(26) (27) $\begin{array}{rl}\frac{k_{nf}}{k_{bf}}& =1+4.4R{e}^{0.4}\stackrel{0.66}{Pr}(\frac{T}{T_{fr}}{)}^{10}{\left(\frac{k_s}{k_{bf}}\right)}^{0.03}{\phi }^{0.66}\end{array}$(27) where $Re=\frac{{\rho }_f{v}_B{d}_p}{{\mu }_{bf}}$. The dynamic viscosity is evaluated using Corcione [35] model depending on nanoparticles volume fraction and size. (28) ${\mu }_{nf}=\frac{{\mu }_f}{1-34.87{\left(\frac{dp}{d_{bf}}\right)}^{-0.3}{\phi }^{1.03}}$(28) where $d_{bf}=0.1{\left[\frac{6M}{N\pi {\rho }_{f0}}\right]}^{1/3}$

The nanoparticle properties and base fluid are indicated in Table 1.

Table 1. Nanoparticle and base fluid properties.

Nanoparticles	$\rho (\text{Kg}{\text{m}}^{-3})$	$Cp(\text{J}\text{K}{\text{g}}^{-1}{\text{k}}^{-1})$	$\text{k}(\text{W}{\text{m}}^{-1}{\text{K}}^{-1})$	$\mu (\text{N}\text{s}{\text{m}}^{-2})$
CuO	6320	551	76.500	–
AL2O3	3970	765	40	–
TiO2	4230	692	8.400	–
Cu	8954	383.10	386	_
H2O	998.203	4182.20	0.613	0.00101

3. Results and discussion

3.1. Comparative research

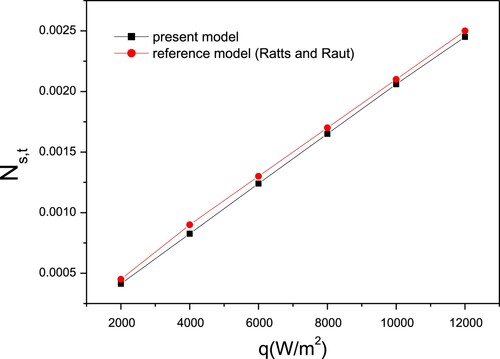
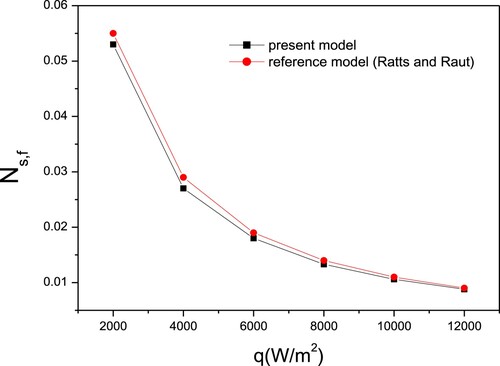
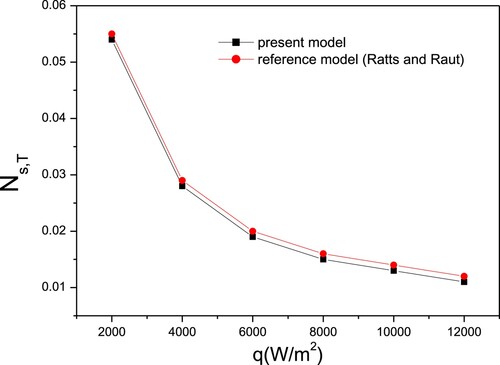
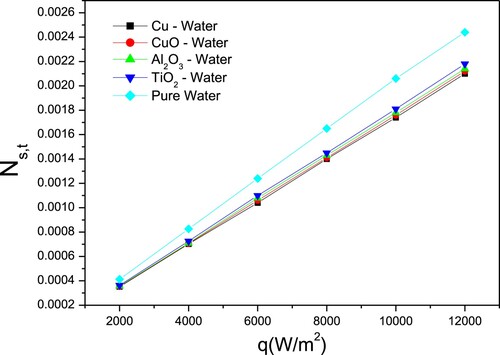
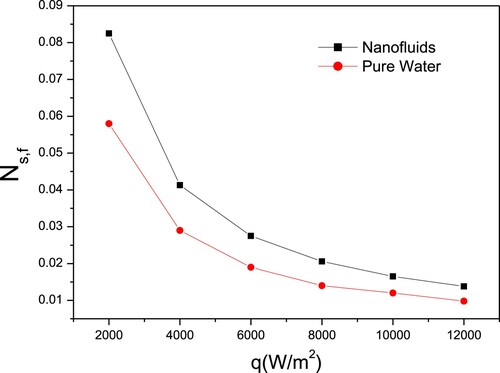
To validate the present model of entropy generation number (i.e. Equation (22)), developed for a regular hexagon microchannel, and to show its accuracy, the general model derived by Ratts and Raut [36] have been used. Figures 2–4 indicate, respectively, frictional, thermal and total entropy generation numbers when varying the imposed heat flux.

Figure 2. Comparative studies: thermal entropy generation number vs. heat flux.

Figure 3. Comparative studies: frictional entropy generation number vs. heat flux.

Figure 4. Comparative studies: total entropy generation number vs. heat flux.

So far, only pure water is considered. Clearly, the current model gives results similar to the past results published from the reference model. Furthermore, the results show that increasing the heat flux led to thermal entropy generation number increase, owing to the considerable influence on fluid temperature. Figure 3 shows a decreasing frictional entropy generation number, because of the existence of a heat flow term in the denominator of Equation 22b. Simultaneously, an increase in heat flux resulted in a decrease in total entropy generation number, indicating that in this case, entropy generation due to friction losses is the dominant part of the total number, as presented in Figure 4.

3.2. Effect of different nanofluids

This section demonstrates how heat flow influences the thermal, frictional and total entropy generation numbers of various nanofluids consisting of Cu, CuO, Al2O₃ and TiO₂ nanoparticles mixed with pure water. The volume concentration of nanoparticles is 4% in all cases, and the nanoparticle size is 25 nm.

Figure 5 depicts the relationship between the thermal entropy generation number and the heat flow for various nanofluids. It is evident that all forms of nanofluids have lower thermal entropy generation numbers than pure water, because of the nanofluids’ higher thermal conductivity, where the Hamilton crosser model was used to compute thermal conductivity in this section. It is also worth noting that Cu has the lowest thermal entropy generation number.

Figure 5. Thermal entropy generation number as a function of heat flux for various nanofluids.

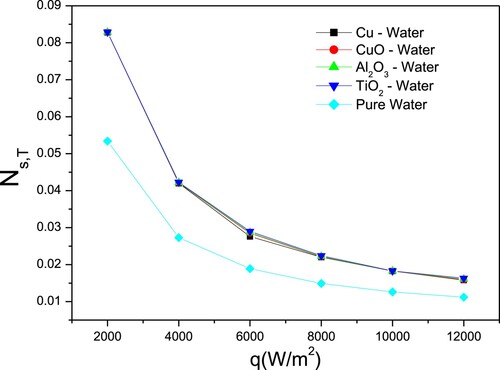
While this is true, the nanofluids viscosity is larger than that of pure water, resulting in a drop in frictional entropy production number three times more than that one of pure water, as seen in Figure 6. This figure indicates that all considered nanofluids have the same amount of frictional entropy production number. This behaviour is the resultant of the fact that Equation (22b) highly depends on the dynamic viscosity, and that the Corcione model calculates the viscosity by considering the base fluid properties and nanoparticles concentration.

Figure 6. Frictional entropy generation number vs. heat flux for various nanofluids.

Furthermore, as illustrated in Figures 5 and 6, the frictional entropy generation number is bigger than that of the thermal entropy generation. Consequently, the total entropy generation number is determined by friction irreversibility, as shown in Figure 7. Total entropy generation follows the same variation pattern as frictional entropy in all nanofluids, up to the heat flux interval between 4000 and 8000 W/m², where the Cu–water nanofluid has the lowest total entropy values.

Figure 7. Total entropy generation number as a function of heat flux for various nanofluids.

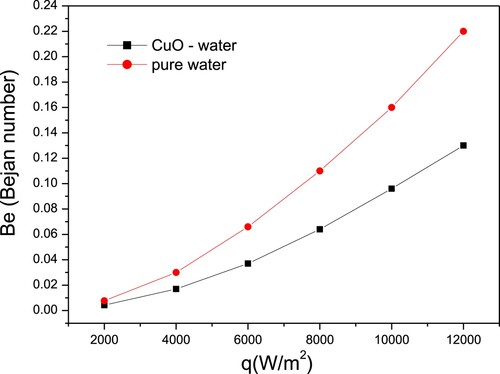
Figure 8 presents the change of the Bejan number function of heat flux. To track the variation of the Bejan number, copper oxide was combined with water at 4% volume and measured at 25 nm.

Figure 8. Variation of Bejan number vs. heat flux.

A Bejan number close to zero indicates that the fluid viscous contribution to entropy generation is greater, whereas a Bejan number close to 1 indicates that the fluid friction contribution is minimal. The Bejan number rises with increasing heat flux and is lower in CuO–water nanofluid than in pure water. This phenomenon is derived from the data obtained for the thermal entropy generation number, which demonstrates that this number increases with heat flux augmentation and exhibits the least amount of irreversibility in the case of nanofluids.

3.3. Effect of volume fraction

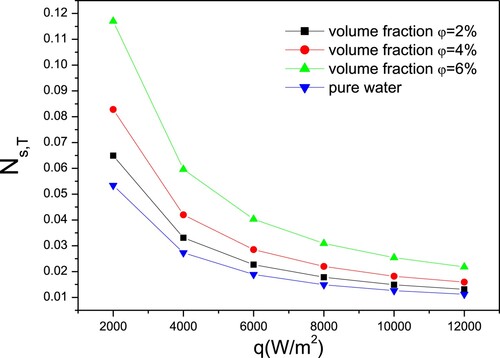
The CuO–water nanofluid is the working fluid in order to investigate the influence of nanoparticle concentration on entropy generation numbers. In this paragraph, CuO volume fraction is varied between 2%, 4% and 6%, and the nanoparticle diameter is fixed at 25 nm.

The results show that the thermal and frictional entropy production numbers always vary with heat flux in the same way.

Figures 9 and 10 illustrate that the heat flux increase leads to rising the thermal entropy generation number and fulling the frictional entropy generation number simultaneously. Furthermore, Figure 9 indicates that increasing the particle fraction results in decreasing the thermal entropy generation number. This is related to the addition of nanoparticles to the base fluid, from 2% to 6%, increased thermal conductivity and consequently ameliorate the heat exchange and decrease the temperature difference. In addition, in Figure 10, the frictional entropy generation number is the consequence of increasing the volume fraction. This is because raising the volume percentage of nanoparticles induced an increase in dynamic viscosity.

Figure 9. Variation of thermal entropy generation number vs. heat flux for different volume fraction of CuO–water.

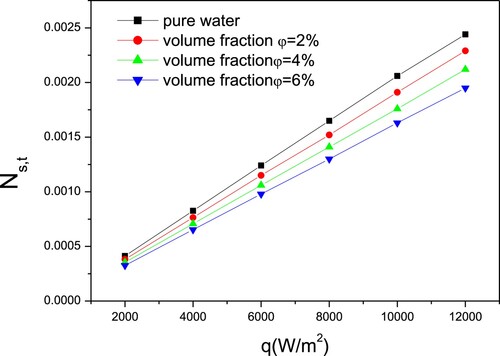
Figure 10. Variation of frictional entropy generation number vs. heat flux for different volume fraction of CuO–water.

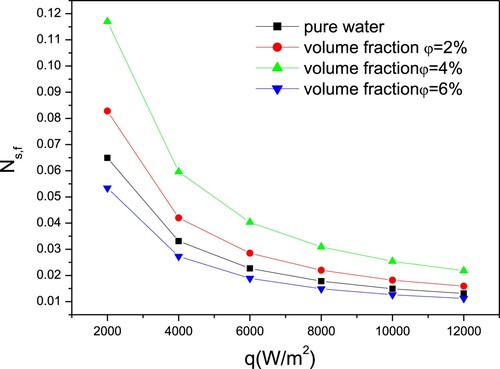
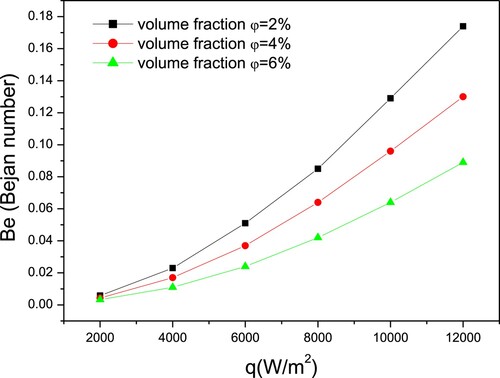
Figure 11 presents the overall entropy generation number variation vs. heat flow for various volume fraction. It has the same tendency as the frictional entropy generation number, which continues to be the most important contribution. As a result, increasing the volume percentage of nanoparticles preceded with an increase in the overall entropy generation number.

Figure 11. Total entropy generation number vs. heat flux for various volume fraction of CuO–water.

Figure 12 indicates that the volume fraction grows jointly with the Bejan number. This is coming as a result that introducing tiny particles into the base fluid resulted in thermal entropy generation number decrease.

Figure 12. Variation of Bejan number vs. heat flux for different volume fraction of CuO–water.

3.4. Nanoparticle diameter effect

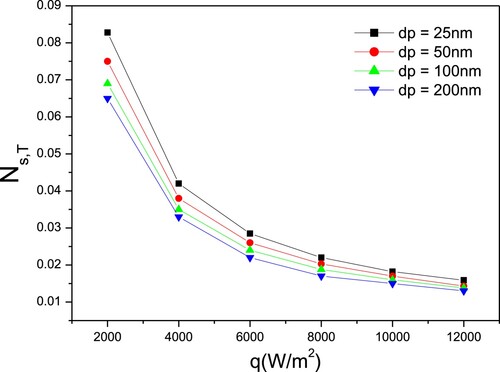
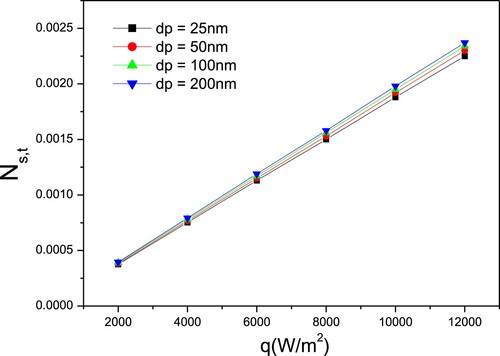
Rarely is the influence of the diameter of nanoparticle on entropy generation studied. This paragraph introduces the effect of heat flux and nanoparticle size on entropy generation numbers and Bejan number.

Figure 13 shows the thermal entropy generation number vs. heat flux for CuO–water nanofluid as its diameter varies. The volume fraction of CuO–water is 4% and the diameter varied from 25 to 200 nm. Consequently, the variation vs. heat flux is the same. The number of thermal entropy production increases as the nanoparticles’ diameter increases, which is explained by the statement that increasing the nanoparticles size decreases the thermal conductivity of nanoparticles of nanofluids, which is estimated in this instance using the Corcione model.

Figure 13. Variation of thermal entropy generation number vs. heat flux for various nanoparticles diameter of CuO–water.

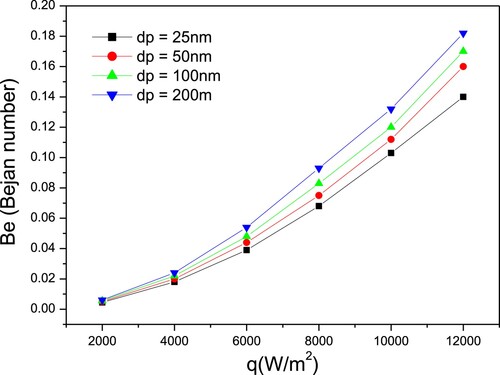
Furthermore, Figure 14 revealed that the number of frictional entropy production decreases as nanoparticle diameter increases, since increasing the size of nanoparticles decreases the dynamic viscosity of nanofluids.

Figure 14. Variation of frictional entropy generation number vs. heat flux for various nanoparticles diameter of CuO–water.

Figure 15 exhibits similar results to the frictional entropy production number, indicating that when the size of CuO nanoparticles increases, the overall entropy generation number decreases. Figure 16 depicts the change of the Bejan number vs. heat flux for various nanoparticle sizes. It has been discovered that as the diameter of nanoparticles decreases, so does the Bejan number.

Figure 15. Variation of total entropy generation number vs. heat flux for different nanoparticles diameter of CuO–water.

Figure 16. Variation of Bejan number vs. heat flux for different nanoparticles diameter of CuO–water.

4. Conclusion

An analytical analysis was provided in this work in order to decrease irreversibility and achieve thermodynamic optimization. A theoretical model for calculating the entropy generation number in hexagonal microchannels has been created.

Various working fluids are utilized to demonstrate their impact on the entropy generation number. The effects of heat flow, volume fraction and nanoparticle size on thermal, frictional and total entropy production numbers and the Bejan number were studied. The following are the crucial points:

• Increasing the heat flux imposed on the channel results in increasing the thermal entropy generation number and reducing the entropy caused by the viscous dissipation.

• Since the thermal entropy generation number is small by reference to the frictional entropy generation number, it has less influence on the total entropy generation number.

• The nanoparticles addition in the base fluid results in increasing the thermal conductivity and decreasing the thermal entropy generation number. Therefore, the increase in volume fraction is effective in improving heat transfer and minimizing thermal irreversibility.

• Smaller nanoparticles led to minimizing the frictional entropy generation number.

• Rising the heat flux, the nanoparticles size and the volume fraction results in decreasing the Bejan number.

Acknowledgements

This Project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (G: 21-305-1442). The authors, therefore, acknowledge with thanks DSR for technical and financial support.

Disclosure statement

No potential conflict of interest was reported by the author(s).