Comparison of radiation shielding and elastic properties of germinate tellurite glasses with the addition of Ga₂O₃

Abstract

The current research elucidates the nuclear shielding capacity of germinate tellurite glasses: 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 37.5GeO₂–62.5TeO₂, 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 12.5GeO₂–87.5TeO₂. Gamma-ray photon, fast neutron and electron shielding parameters of the present glassy materials were evaluated and studied via the Geant4 Monte Carlo, Phy-X/PSD software, ESTAR and analytic computations. In addition, Makishima–Mackenzie’s theory was applied to assess the elastic properties of the studied tellurite glass system containing Ga₂O₃ and/or GeO₂. The effective atomic number of the glasses varies from 19.14 to 44.08 for 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 20.63–48.02 for 37.5GeO₂–62.5TeO₂, 21.15–48.15 for 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 22.42–50.29 for 12.5GeO₂–87.5TeO₂. The obtained fast neutron removal cross sections of the glasses were 0.0991, 0.0966, 0.1024 and 0.1021 cm⁻¹, respectively, for 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 37.5GeO₂–62.5TeO₂, 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 12.5GeO₂–87.5TeO₂. Also, an equilibrium is reached between total stopping power (TSP) due to radiation and collision for electrons at energy T = 1.0 MeV where the TSP was minimum in the investigated glasses. Computed Young’s modulus for 37.5GeO₂–62.5TeO₂ was the lowest with a value of 0.218 GPa while the other three glass samples have almost equal value of 0.226 GPa. The present glasses’ shielding ability outclassed some conventional shields, hence have potential for radiation safety/shielding purposes in nuclear facilities.

KEYWORDS:

• Germinate tellurite glass
• radiation
• nuclear shielding
• Monte Carlo

1. Introduction

The nineteenth century witnessed a lot of milestones in the scientific community. The discovery of radioactivity and X-rays are some of these astonishing discoveries [1]. Since Roentgen described the essential features of X-rays in 1895, this discovery has been of great benefit to human beings and the environment. Nowadays, X and gamma rays are utilized in academics, medicine (e.g. diagnostic X-rays or radiation therapy), nuclear power plants (e.g. production of electricity) and industry (e.g. irradiation of foods). Exposure to radiation, even at low doses, is very dangerous for human beings of all ages and the surrounding environment. Thus, the use of suitable shields is an urgent demand to guarantee the safety of nuclear radiation technology.

Over the years, concrete and lead (Pb) are used as shields against damaging radiation in various nuclear and medical facilities. However, these traditional shielding materials have many drawbacks in terms of their lack of mobility, toxicity and tendency to crack [2]. Therefore, finding alternative and outstanding candidates for shielding applications became a basic research topic among a wide set of scientists. In this regard, different materials and composites including polymers, alloys, rocks and glass systems were reported by means of their radiation attenuation features and nuclear shielding properties for different types of radiation fields such as X-ray, gamma-ray, neutron beam, electron/proton beam, alpha particle and carbon ion [3–9]. After a large scale of extensive studies, it was concluded that glassy materials (glass systems) are a promising candidate to develop effective, reliable and economical radiation shields especially in circumstances where the optical transparency of the shield is required [10–12]. This fact is due to the unique physical, chemical and mechanical glass systems. For example, glass systems can be prepared and modified using numerous oxides that are commercially available. Moreover, glass systems can work as transparent radiation shields that are very important when radiation exposure control is required whether this is for building windows, walls or doors in nuclear and medical facilities. We can frankly say that glasses, as radiation shields, become preferable for protection against radiation whether this is in a hospital or nuclear power plants where the high energy radiation is used.

For providing superior glassy shielding material, the glass composition has to contain at least one heavy metal oxide (HMO), e.g. BaO, Bi₂O₃, TeO₂ and PbO (not preferable due to its toxicity). Glass systems containing HMO are usually dense materials which help to increase the interaction cross section leading to absorb the radiation energy [7–12]. The effect/impact of Bi₂O₃ (as HMO) on the shielding properties of lithium/zinc/borate glass systems is investigated using PSD programme and Monte Carlo method (via Geant4 simulation) for energies up to 15 MeV [9]. Divina et al. studied the impact of different HMO on gamma shielding ability and on the optical parameters and mechanical features of lithium–borate glass systems [10]. Al-Buriahi et al. provided an extensive study on the influence/impact of Gd₂O₃ addition on the shielding competence against beta and gamma radiations of TeO₂–ZnO–Nb₂O₅ glasses using Geant4 simulation toolkit [12]. Also, Alrowaili et al. evaluated and compared the shielding parameters of different glasses containing Li₂O, P₂O₅ and B₂O₃ [13]. The photon and fast neutron shielding parameters of the glasses showed strong dependence on the chemical composition. These glassy specimens showed higher photon and fast neutron absorbing capacity compared to other investigated glasses. In another study, the photon and fast neutron shielding properties of some of Ge–Se–Te bulk glasses containing varying amounts of Cu content were theoretically and systematically investigated [14]. It was found that the increase in the concentration of _V2O₅ reduced the photon shielding ability of the binary TeO₂–V₂O₅ glasses. Also, the addition of TiO₂ in TeO₂–V₂O₅–TiO₂ was found to increase the half value layer (HVL) of the glasses while CeO₂ improved the shielding ability of TeO₂–V₂O₅–CeO₂ glasses. It was revealed in the report that the photon absorbing competence of TeO₂–V₂O₅–CeO₂ glasses were better than that of the TeO₂–V₂O₅ and TeO₂–V₂O₅–TiO₂ glasses. The glasses also showed exceptional shielding efficiency when compared to ordinary and basalt magnetite concrete. This superior radiation shielding ability was attributed to high radiation cross section of the chemical content of the glasses as well as their higher density. In a related report, the effect of chemical content and density of another set of binary tellurite-based glasses was shown to have profound effect in their gamma-ray shielding competence [15]. Recent research on the radiation attenuating efficiency of other tellurite glass systems has also been conducted by wide spectrum of research groups [16–19]. These may not be unconnected to the outstanding properties of tellurite-based glasses and the outstanding results which the previous study have presented. The need to have environmentally friendly, cheap and transparent shields would always warrant research into glasses as potential radiation absorbers.

The current research work aims to study the role of Ga₂O₃ addition on the nuclear radiation shielding properties of germinate tellurite glass systems such as 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 37.5GeO₂–62.5TeO₂, 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 12.5GeO₂–87.5TeO₂. For this purpose, Geant4 simulation toolkit was employed to design both the investigated glass systems and the radiation transmission geometry (RTG). Then, some empirical equations were used to obtain all of the radiation transmission factors such as mass attenuation coefficient (MAC), mean free path (MFP), HVL and effective atomic number (EAN). As tellurite glasses, the present glass systems are attractive for radiation shielding consideration due to the attractive features of tellurite glass systems. The high mass density that is usually associated with tellurite-based glasses due to their high density of TeO₂ makes them potentially attractive for photon and charged particles such as electron attenuation. In fact, glasses containing GeO₂ and TeO₂ are referred to as HMO glasses. Second, the combination of these two HMO can produce a beautiful combination of the unique properties inherent in both GeO₂ and TeO₂ glasses. Previous studies [20] have shown that such a combination produces a more stable glass system with attractive optical and structural properties. This research thus attempts to expand available knowledge about the properties and functionality of the present glass system.

2. Materials and methods

The chemical composition and density of the studied glasses such as 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 37.5GeO₂–62.5TeO₂, 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 12.5GeO₂–87.5TeO₂ coded as GTG1, GTG2, GTG3 and GTG4, respectively, can be found in Table 1. These glass samples were prepared by Środa et al. [20]. The elastic features of these glassy specimens are assessed based on the Makishima–Mackenzie’s theory [21,22]. All the theoretical expressions, for all the studied elastic parameters such as elastic moduli (Young’s modulus, etc.), hardness and Poisson’s ratio, of this theory are summarized in Table 2.

Table 1. Sample code, chemical composition (in mol.%), density (in g/cm³) and GeO₂/TeO₂ ratio for the present glasses.

	Chemical composition (mol.%)
Sample code	GeO2	TeO2	Ga2O3	Density (g/cm^3)	GeO2/TeO2 ratio
GTG1	41.7	41.7	16.6	4.57	1.0
GTG2	37.5	62.5	0.0	4.72	0.6
GTG3	10.4	72.9	16.7	5.07	0.14
GTG4	12.5	87.5	0.0	5.28	0.14

Table 2. The equations for evaluating the mechanical factors and elastic moduli.

No.	Parameter	Equation
1	Packing factor (Vt, cm^3/mol)	$V_t={\displaystyle \frac{1}{V_m}}\sum _i{x}_i{V}_i$
2	Dissociation energy (Gt, kJ/cm^3)	$G_t=\sum _i{x}_i{G}_i$
3	Young’s modulus (Eth, GPa)	$E_{th}=8.36V_t{G}_t$
4	Bulk modulus (Kth, GPa)	$K_{th}=10.0V_t^2{G}_t$
5	Shear modulus (Sth, GPa)	$S_{th}={\displaystyle \frac{3K_{th}}{10.2V_t-1}}$
6	Longitudinal modulus (Lth, GPa)	$L_{th}=K_{th}+{\displaystyle \frac{4S_{th}}{3}}$
7	Poisson’s ratio (P)	$P=0.5-{\displaystyle \frac{1}{7V_t}}$
8	Hardness (H)	$H={\displaystyle \frac{(1-2P)E_{th}}{6(1+P)}}$
9	Fractal bond connectivity (d)	$d=4{\displaystyle \frac{S_{th}}{K_{th}}}$

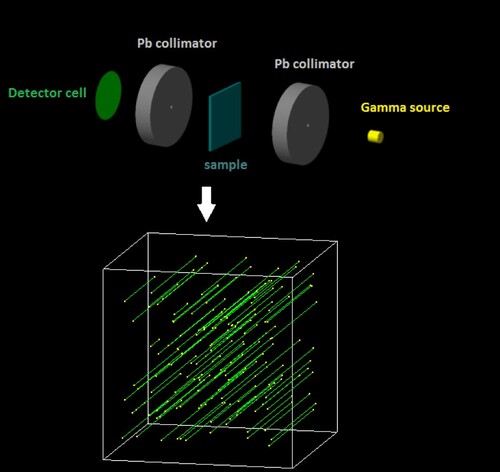
The linear attenuation coefficient (LAC or µ) is a measure of photon transmittance through a length of an absorbing material. The µ of the present glassy samples was obtained through the RTG via Geant4 simulation toolkit [23]. The simulation setup for studying gamma interaction with different glass systems is described in detail in our previous publications elsewhere [24–30]. Briefly, we defined the gamma source, detector, dimensions, materials (as described in Table 1) and Pb shields in the input file of Geant4 simulation. The simulation geometry in Geant4 is as shown in Figure 1.

Figure 1. 3D representation of the simulation setup in FLUKA.

From Geant4 output file, one can obtain the number of transmitted photons (I) using the relation below [31]: (1) $\mu (\text{c}{\text{m}}^{-1})=\frac{1}{x}\ln \left(\frac{I_0}{I}\right),$(1) where I₀ is the original number (one million photons) and x is the thickness of glass as described in Ref. [32].

The µ factor was also evaluated directly via Phy-X/PSD, a free online platform available at https://phy-x.net/PSD for photon energy in the range of 0.015–15 MeV [33]. The Phy-X/PSD platform is a free-user friendly online software which may be used to obtain the photon shielding parameters of a medium once the density and chemical composition of the medium are previously known. On the platform, photon interaction parameters like $\mu /\rho$, µ, HVL and TVL, EAN or Z_eff, MFP, buildup factor, etc. can be determined for materials at standard photon energy grid and for common radioactive sources. Results from this platform have been previously validated and found to be reliable by comparing them with those obtained via XCOM, experimental procedures and numerical simulations [33,34]. To obtain photon shielding parameters for the present glasses, the chemical composition of the glasses in molar concentration and glass densities were used as input parameters on the platform.

The values of µ factor obtained by the Geant4 simulation toolkit were compared with those calculated by Phy-X/PSD for the data validation process. Then, the percentage difference (Dev %) between the values of µ factor calculated via Geant4 simulation (${\mu }_{\text{Geant4}}$) and Phy-X calculation (${\mu }_{\text{PhyX}}$) was evaluated by the relation below: (2) $\text{Dev}(\mathrm{\%})=\frac{{\mu }_{\text{PhyX}}-{\mu }_{\text{Geant4}}}{{\mu }_{\text{PhyX}}}\times 100.$(2)

Using the calculated LAC (${\mu }_{\text{Geant4}}$) values at each energy and the density ($\rho$) of the glasses, other photon shielding parameters (MFP, HVL and Z_eff) were given for each glass according to the equations: (3) $\text{HVL}=\frac{\ln 2}{\mu },\text{MFP}=\frac{1}{\mu }\text{and}{Z}_{eff}=\frac{{\sum }_i{w}_i{A}_i{({\mu }_m)}_i}{{\sum }_i{w}_i\frac{A_i}{Z_i}{({\mu }_m)}_i},$(3) where the fractional weight, molar mass and atomic number of the ith constituent element are represented by w_i, A_i and Z_i, respectively.

3. Results and discussion

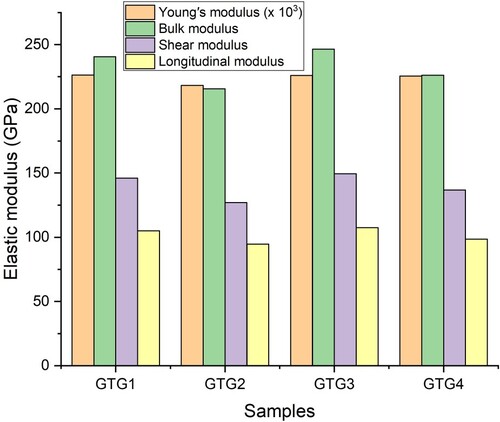
Table 1 gives the chemical composition and mass densities of the GTG glasses. The density assumes the value of 4.57, 4.72, 5.07 and 5.28 g cm⁻³ for GTG1, GTG2, GTG3 and GTG4 accordingly. The density clearly is affected by the chemical composition of the glasses; it increases linearly with the molar concentration of TeO₂. Also, the density of glasses without Ga₂O₃ (GTG2 and GTG4), an increase in molar concentration of TeO₂ and GeO₂ precipitated an increase in the density as observed for GTG1 and GTG3. The increase in the molar concentration of TeO₂ and GeO₂ is obviously responsible for the observed elevation in the glasses’ densities despite having individually lower density compared to Ga₂O₃. Table 3 presents the elastic moduli and other mechanical parameters of GTG1, GTG2, GTG3 and GTG4. The elastic moduli are important mechanical parameters that macroscopically define the stiffness/rigidity of the glass to distortion. The packing pacing of GTG1 and GTG4 are highest and equal while that of GTG3 > GTG2. Hypothetically, the packing factor should be directly related to the molar volume of the chemical constituents and density of the glasses. The packing factor, however, appears to follow the trend of the molar volume of the components of the GTG glasses. The dissociation energy G_t depends on the constituent molecules and their corresponding dissociation energies. The trend of G_t is such that the least value was obtained for the glasses without Ga₂O₃ (GTG2 and GTG4). This is attributed to the low level of G_t for Ga₂O₃ compared to the other two chemical species in the GTG glasses. The introduction of Ga₂O₃ thus reduces the glass bond network leading to weaker glass network. This could be due to the formation of Ga–O–Ga bonds which weaken the glass connectivity, thus the Ga₂O₃ plays the role of a glass modifier. GTG3 had the highest G_t, packing fraction as well as GeO₂/TeO₂ ratio; this clearly shows its higher rigidity and stability. The quantitative relationship between the elastic moduli of the glasses is presented in Figure 2. Clearly, the moduli vary as the chemical composition of the glasses changes. GTG2 possessed the lowest Young’s modulus with the values of 0.218 GPa while all the other glass samples, namely GTG1, GTG3 and GTG4, have a similar value (0.226 GPa). Moreover, the most interesting observation in the elastic properties is that both GTG1 and GTG3 samples have the highest bulk, shear and longitudinal modulus. The absence of Ga₂O₃ in these samples shows that its introduction increases the number of non-bridging oxygen (NBO). This could be attributed to the breakage of the Te–OTe bonds and the formation of Ga₂O₃ units with NBO, thus leading to weakening glass network and increase in molar volume. All these could result in the trend of the elastic moduli observed among the glasses. This is affirmed by the trend of Poisson’s ratio (P), hardness (H) and fractal bond connectivity (d). Highest P and H and lowest d shows that GTG3 is the most mechanically stable among the studied glasses.

Figure 2. Elastic moduli of the tellurite glass system containing Ga₂O₃ and/or GeO₂.

Table 3. Mechanical factors and elastic moduli of the tellurite glass system containing Ga₂O₃ and/or GeO₂ using Makishima–Mackenzie’s theory.

Property/glass code	GTG1	GTG2	GTG3	GTG4
Packing factor (Vt, cm^3/mol)	0.507	0.493	0.507	0.506
Dissociation energy (Gt, kJ/cm^3)	56.722	52.313	58.158	53.438
Young’s modulus (Eth, GPa)	0.226	0.218	0.226	0.226
Bulk modulus (Kth, GPa)	240.605	215.555	246.465	226.072
Shear modulus (Sth, GPa)	146.031	127.086	149.448	136.846
Longitudinal modulus (Lth, GPa)	104.921	94.665	107.501	98.647
Poisson’s ratio (P)	285.926	253.306	292.782	268.375
Hardness (H)	17.903	16.620	18.360	16.876
Fractal bond connectivity (d)	2.874	2.980	2.877	2.883

The LACs (µ) of the glasses, as a fundamental parameter for describing photon interaction/shielding properties, evaluated via Geant4 simulation procedure and calculated directly via Phy-X/PSD, are presented in Tables 4 and 5. The µ factor is a photon interaction (attenuation indicator) term that measures the level of transmitted photons through an attenuating medium per unit length when a beam of photon is incident on it. As shown on the tables, µ values obtained from the two methods at individual energies are very close. The agreement between the two procedures is quantitatively evaluated and given in the tables in terms of Dev (%). Tables 4 and 5 show that the Dev. (%) at all energies and for the four GTG glasses were all less than 2%. This further validates the simulation process and the obtained results.

Table 4. LAC (μ) of the GTG1 and GTG2 glasses obtained by Geant4 simulations and Phy-X programme with different photons energies.

	GTG1			GTG2
Photon energy (MeV)	Phy-X	Geant4	Dev.%	Phy-X	Geant4	Dev.%
0.015	242.953	241.659	0.53	224.119	221.698	1.08
0.02	112.013	110.617	1.25	103.387	101.519	1.81
0.03	37.136	36.424	1.92	34.557	34.140	1.21
0.04	46.188	45.575	1.33	61.940	61.224	1.16
0.05	25.513	25.295	0.86	34.327	34.101	0.66
0.06	15.710	15.515	1.24	21.146	20.918	1.08
0.08	7.381	7.303	1.06	9.877	9.803	0.75
0.1	4.206	4.180	0.62	5.559	5.512	0.86
0.15	1.693	1.675	1.07	2.137	2.118	0.90
0.2	1.013	1.007	0.51	1.217	1.206	0.88
0.3	0.604	0.596	1.25	0.676	0.666	1.44
0.4	0.469	0.464	1.03	0.505	0.501	0.87
0.5	0.400	0.396	1.14	0.423	0.418	1.23
0.6	0.358	0.355	0.68	0.374	0.371	0.76
0.8	0.303	0.299	1.42	0.314	0.310	1.04
1	0.268	0.266	0.66	0.276	0.274	0.59
1.5	0.217	0.215	0.94	0.222	0.220	0.87
2	0.190	0.188	0.87	0.195	0.192	1.49
3	0.163	0.161	1.27	0.169	0.167	1.17
4	0.152	0.150	0.80	0.159	0.158	0.56
5	0.146	0.144	1.47	0.154	0.152	1.20
6	0.143	0.141	1.39	0.152	0.151	0.68
8	0.142	0.141	0.90	0.153	0.152	0.85
10	0.144	0.143	0.99	0.156	0.156	0.56
15	0.152	0.150	1.22	0.167	0.166	0.96

Table 5. LAC (μ) of the GTG3 and GTG4 glasses obtained by Geant4 simulations and Phy-X programme with different photons energies.

	GTG3			GTG4
Photon energy (MeV)	Phy-X	Geant4	Dev.%	Phy-X	Geant4	Dev.%
0.015	238.763	234.116	1.95	226.730	223.343	1.49
0.02	110.054	107.906	1.95	104.569	102.765	1.73
0.03	36.741	36.373	1.00	35.175	34.674	1.42
0.04	67.470	66.569	1.34	81.927	80.938	1.21
0.05	37.395	37.151	0.65	45.478	44.917	1.23
0.06	23.036	22.745	1.26	28.021	27.817	0.73
0.08	10.756	10.683	0.67	13.048	12.943	0.80
0.1	6.051	6.012	0.63	7.297	7.195	1.40
0.15	2.321	2.290	1.31	2.735	2.699	1.32
0.2	1.318	1.308	0.73	1.512	1.504	0.56
0.3	0.729	0.725	0.54	0.802	0.792	1.26
0.4	0.544	0.539	0.94	0.584	0.580	0.77
0.5	0.455	0.452	0.67	0.482	0.476	1.37
0.6	0.402	0.396	1.45	0.422	0.417	1.21
0.8	0.337	0.333	1.22	0.351	0.349	0.68
1	0.296	0.293	0.91	0.307	0.305	0.89
1.5	0.238	0.235	1.16	0.246	0.243	1.20
2	0.209	0.207	1.06	0.217	0.215	1.02
3	0.182	0.180	1.23	0.190	0.188	1.00
4	0.171	0.168	1.33	0.179	0.177	1.30
5	0.166	0.164	1.26	0.175	0.173	1.19
6	0.164	0.163	0.73	0.174	0.172	1.29
8	0.165	0.163	1.36	0.177	0.175	1.17
10	0.169	0.168	0.60	0.182	0.181	0.64
15	0.181	0.178	1.44	0.197	0.194	1.47

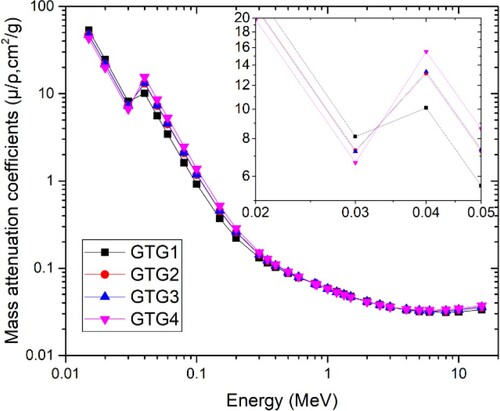
In order to compare and discuss the attenuation capacity of the glasses with one another, the MAC ($\mu /\rho$) is plotted for all the glasses as presented in Figure 3. The figure shows that $\mu /\rho$ varies with E and the glass species (chemical composition) in a way that is similar to µ in Tables 4 and 5, although differences between the $\mu /\rho$ values of the glasses at similar energy are less pronounced than that of the µ differences. This is due to the dependence of µ on density/thickness in contrast to $\mu /\rho$. Consequently, the same factors are responsible for the variation of $\mu /\rho$ and µ with chemical composition as well as photon energy of the glasses. The appearance of the $\mu /\rho$ spectrum of each glass and the differences in the value of $\mu /\rho$ at each energy within the investigated energy spectrum can be attributed to the changes in photon energy and its effect on photon interaction processes and also differences in the molar concentrations in the chemical species contained in GTG1-4. As observed in Figure 3, the $\mu /\rho$ value decreases with E smoothly for the four glasses. This decrease terminates at 8 MeV beyond which the value of $\mu /\rho$ increases steadily for the remaining part of the energy range. Hence, maximum values of 53.163, 47.483, 47.093 and 42.942 cm²/g were recorded for GTG1–GTG4, respectively, at 15 keV with a corresponding minimum value of 0.031, 0.032, 0.032 and 0.033 cm²/g at 8 MeV. The rate of $\mu /\rho$ decay was not uniform throughout; for $E\le 0.06\text{MeV}$, the decrement rate was higher compared to that at $0.06<E\le 8\text{MeV}$. The difference in the decay rate at these two energy regions can be explained by considering partial $\mu /\rho$ due to photoelectric absorption $((\mu /\rho {)}_{PE})$ and Compton scattering absorption $((\mu /\rho {)}_{CS})$ which dictate predominantly the $\mu /\rho$ values at these regions respectively. In the former energy region, $(\mu /\rho {)}_{PE}$ contribute most to the value of $\mu /\rho$ and since $(\mu /\rho {)}_{PE}\propto E^{-3}$, hence the observed rapid decline in the value of the MAC of the glasses. On the other hand, in the later energy region, $(\mu /\rho {)}_{CS}$ contributes significantly to $\mu /\rho$, however, $\mu /\rho \propto 1/E$. This accounts for the less rapid decline in the values of $\mu /\rho$ at $0.06<E\le 8\text{MeV}$ compared to the lower photon energy region. For energies above 8 MeV, the pair production (PP) with partial attenuation coefficient $(\mu /\rho {)}_{PP}\propto E$ is a significant photon absorption process that ensures that $\mu /\rho$ increases gradually with E.

Figure 3. Variation of µ/ρ of the glasses with photon energy.

An interruption of the smooth decline in $\mu /\rho$ spectra in the low energy region was observed at 40 keV (Figure 3). Such interruptions are always due to characteristic absorption at specific energies by orbital electrons of atomic species contained in the absorbing medium (GTG glasses). In this case, the spike is attributed to characteristic absorption by K shell electrons of Te atoms. This is reinforced by the increase in the intensity of the peaks from 10.107 to 15.516 cm²/g as Te weight fraction in the glasses increases from 0.3766 to 0.7311. Furthermore, at each E, the relative differences in $\mu /\rho$ values of the glasses are mostly dictated by the inconsistency in the chemical composition of the glasses and how the different partial photon absorption processes depend on such variations. The partial interaction processes (PE, CS and PP) dependence on the chemical composition is expressed according to $(\mu /\rho {)}_{PE}\propto Z^3$, $(\mu /\rho {)}_{CS}\propto Z/A$ and $(\mu /\rho {)}_{PP}\propto Z$, where Z and A are atomic number and mass number; both of which are defined by the chemical elements of the glass composition. Consequently, glasses with higher “atomic number” should possess higher $\mu /\rho$. Beyond the Te-absorption edge, the $\mu /\rho$ value follows the trend: $(\mu /\rho {)}_{\text{GTG4}}>(\mu /\rho {)}_{\text{GTG3}}>(\mu /\rho {)}_{\text{GTG2}}>(\mu /\rho {)}_{\text{GTG1}}$. This suggest that this is the trend of the EAN of the glasses. Furthermore, $\mu /\rho$ value of the glasses was very close to one another at equal energy within the CS dominated energy $(0.06<E\le 8\text{MeV}$) compared to other parts of the energy spectrum. This is as a result of independence of $(\mu /\rho {)}_{CS}$ on Z as $Z/A$ approximately vary within a thin range ($0.4\le Z/A\le 0.5$) for most materials except hydrogen [35]. It is also worthy of note that the trend of increasing mass attenuation at each energy for the glasses is also consistent with that of their mass densities. It is safe thus to conclude that higher density GTG glasses are better photon shields.

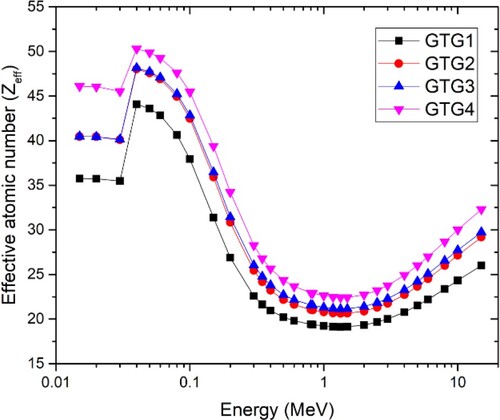
The EAN (Z_eff) value of the glasses as a function interacting photon energy is presented in Figure 4. Z_eff is a parameter that depends on the chemical composition of the interacting medium photon energy. This factor/term is used to characterize and compare the photon absorption capacity of different media such as the GTG glasses as low Z_eff implies low photon absorption capacity and vice versa. Also, equal Z_eff is an indication of similar photon interaction processes within the materials and hence comparable photon shielding ability [36]. Figure 4 shows that the trend of the Z_eff at each energy is consistent with that of mass density, $\mu /\rho$ and TeO₂ content of the glasses. The EAN of the glasses varies from 19.14 to 44.08 for GTG1, 20.63 to 48.02 for GTG2, 21.15 to 48.15 for GTG3 and 22.42 to 50.29 for GTG4.

Figure 4. Changes in Z_eff with energy for the GTG glasses.

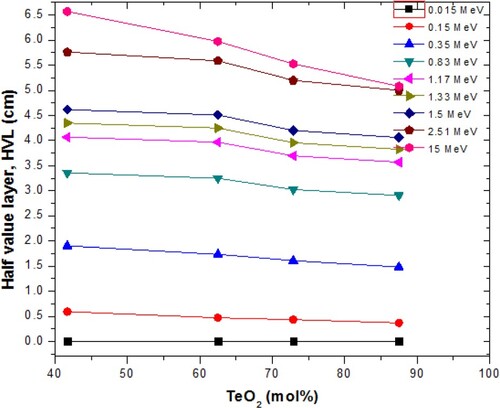
The HVL data are an easy parameter for comparing photon absorbing capacity of different potential photon shields. The thickness of a medium to reduce intensity of photons to 50% of its initial value is its HVL. The HVL is energy dependent just like $\mu /\rho$. The effect of TeO₂ content on HVL of the glasses at selected photon energies is shown in Figure 5. Obviously, the increase in the TeO₂ content of the glasses leads to reduction in HVL at each energy. This indicates that photon attenuation is improved as TeO₂ content increases in the GTG glasses. The reduction of the HVL due to TeO₂ is more pronounced at higher energies. Figure 5 also shows an increase in HVL as energy increases as expected; this is due to the decrease in photon interaction cross section as energy increases. Similar to HVL, the MFP is a responsible and reliable term to compare the shielding capacity of diverse media against radiation (say photon). The MFP is the thickness of a medium to the intensity of photons to 1/e (≈37%) of its initial value. The $MFP\propto \text{HVL}$; hence, MFP variation with energy is inverse to that of $\mu /\rho$ similarly as HVL. Figure 6 presents the MFP spectra of the investigated glasses in comparison with commercial glassy shields (these shields introduced and developed by SCHOTT Technical Glasses), namely RS-253-G18, RS-360 and RS-520 [37], as well as conventional concrete shields (ordinary (OC) and barite (BC) concretes) [38]. The figure shows that the shielding capacities of the GTG glasses are second only to that of RS-520 among the compared materials. GTG1–GTG4 are thus potential materials for radiation protection purposes in nuclear technology applications.

Figure 5. HVL at selected energies as a function of TeO₂ content (mol.%) of GTG1–GTG4.

Figure 6. MFP spectra of the investigated glasses in comparison with conventional shielding glasses and concretes.

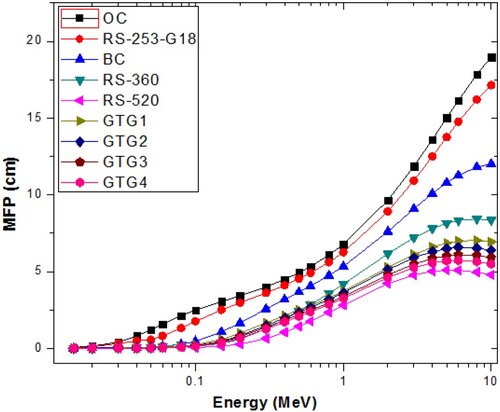
Figure 7(a–d) shows the variation of exposure buildup factor (EBF) with depth for 0.015, 0.15, 1.5 and 15 MeV photon energies. The EBF is a measure of production and transmission of secondary photons in the glasses as the primary photons interact within the absorbing glasses. Higher EBF thus implies weaker photon attenuation capacity. Generally, there is a consistent increase in EBF as glass thickness (number of MFP) increases for all the investigated glasses. For photon energies less than 15 MeV, relative values of EBF are inversely proportional to relative Z_eff values. This further proves that the increase/addition of TeO₂ content into the glasses may improve their photon absorption prowess. However, at 15 MeV, the reverse is the case as the highest EBF is recorded for the glass with the highest Z_eff (GTG4). The dominance of the PP interaction process at 15 MeV is majorly responsible for this. Since $(\mu /\rho {)}_{PP}\propto Z_{eff}$, more secondary photons are produced from the annihilation of electrons and positrons created by the PP process for GTG4. Also noticeable from Figure 7(a–d) is the close proximity between EBF GTG2 and GTG3. This is due to their close EANs. The trend in the differences between the EBF of the glasses is similar to that of the EAN and its dependence on the various partial photon interaction processes. Table 6 gives the range of the value of the equivalent atomic number ($Z_{eq})$ as well all the fitting parameters. This parameter is used for the determination of EBF for GTG1–GTG4. The $Z_{eq}$ gives the atomic number of an element with similar EBF as the absorber at specific energy. From the $Z_{eq}$ results, it is obvious that its values vary from 24.70 to 47.12 for the glasses with maximum values obtained at intermediate energies where CS dominates photon interaction. This is equivalent to elements in the range of atomic numbers 25 (Mn)–48 (Ag).

Figure 7. (a) EBF of GTG1–GTG4 as a function of glass thickness at photon energy of 0.015 MeV. (b) EBF of GTG1–GTG4 as a function of glass thickness at photon energy of 0.15 MeV. (c) EBF of GTG1–GTG4 as a function of glass thickness at photon energy of 1.5 MeV. (d) EBF of GTG1–GTG4 as a function of glass thickness at photon energy of 15 MeV.

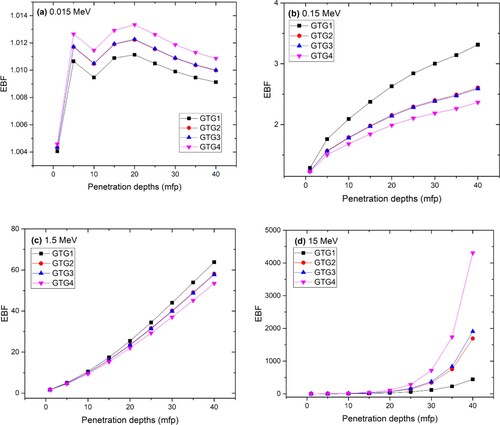
Table 6. Equivalent atomic number (Z_eq) and G-P EBFs for GTG1 and GTG4 glasses.

		GTG1						GTG4
Photon energy (MeV)	Zeq	a	b	c	d	Xk	Zeq	a	b	c	d	Xk
0.015	25.88	−0.544	1.004	1.544	0.349	5.625	24.70	−0.442	1.005	1.372	0.309	5.879
0.02	26.08	0.624	1.012	0.129	−0.628	11.373	24.82	0.542	1.013	0.185	−0.522	11.302
0.03	26.37	0.192	1.027	0.372	−0.283	27.099	25.07	0.195	1.032	0.374	−0.289	26.865
0.04	37.52	0.134	3.057	0.324	−0.052	20.651	44.72	0.091	3.809	0.645	−0.066	24.430
0.05	37.96	−0.164	2.553	0.124	0.002	12.214	45.14	−0.070	3.265	0.225	−0.065	13.959
0.06	38.30	0.887	2.084	0.094	−0.145	16.528	45.43	0.594	2.650	0.108	−0.106	11.885
0.08	38.73	0.641	1.558	0.124	−0.224	14.306	45.81	0.789	1.734	0.025	−0.204	14.923
0.1	39.01	0.265	1.184	0.341	−0.143	13.778	46.04	0.500	1.283	0.171	−0.243	13.771
0.15	39.45	0.161	1.288	0.521	−0.084	14.347	46.40	0.234	1.228	0.396	−0.127	14.151
0.2	39.71	0.155	1.508	0.563	−0.090	14.188	46.59	0.172	1.347	0.506	−0.095	14.486
0.3	40.01	0.070	1.625	0.771	−0.040	14.231	46.82	0.096	1.474	0.679	−0.047	14.328
0.4	40.10	0.031	1.735	0.920	−0.031	13.855	46.88	0.055	1.596	0.825	−0.039	14.155
0.5	40.18	0.011	1.788	1.002	−0.022	13.834	46.93	0.033	1.668	0.909	−0.031	14.156
0.6	40.29	0.000	1.806	1.045	−0.017	13.359	47.01	0.017	1.697	0.966	−0.023	13.992
0.8	40.36	−0.011	1.808	1.089	−0.013	13.298	47.06	0.003	1.724	1.024	−0.016	14.066
1	40.42	−0.015	1.787	1.103	−0.010	12.825	47.10	−0.004	1.719	1.050	−0.014	13.430
1.5	40.43	−0.031	1.645	1.166	0.003	9.254	47.11	−0.025	1.594	1.139	−0.002	11.179
2	40.45	−0.021	1.638	1.125	−0.005	11.165	47.12	−0.019	1.587	1.121	−0.006	12.771
3	39.16	−0.002	1.593	1.061	−0.020	12.466	46.35	0.000	1.557	1.065	−0.028	12.835
4	36.33	0.011	1.532	1.022	−0.032	13.068	44.37	0.016	1.508	1.023	−0.042	13.329
5	33.72	0.024	1.491	0.988	−0.043	13.359	41.89	0.043	1.515	0.949	−0.066	13.556
6	32.84	0.031	1.447	0.975	−0.049	13.392	40.93	0.052	1.488	0.930	−0.074	13.744
8	32.40	0.048	1.397	0.940	−0.066	13.661	40.40	0.073	1.503	0.891	−0.092	14.048
10	32.11	0.046	1.339	0.963	−0.063	13.980	40.05	0.056	1.466	0.964	−0.075	14.159
15	31.78	0.048	1.278	1.003	−0.063	14.407	39.63	0.038	1.505	1.091	−0.061	14.217

The fast neutron shielding effectiveness of the investigated glasses is assessed via their fast neutron removal cross section (FNRC). The FNRC is the probability that fissile neutrons will be removed from a fast neutron beam after first interaction with the glass. For GTG glasses, the FNRC $({\mathrm{\Sigma }}_R{)}_g$ can be computed and studied from the addition rule as [39] (4) $({\mathrm{\Sigma }}_R{)}_g=\sum _i{\rho }_i(\text{MRCS}{)}_i=\rho \sum w_i(\text{MRCS}{)}_i,$(4) where $\rho$, $w_i$, ${\rho }_i$ and $(\text{MRCS}{)}_i$ are the density of glass, weight fraction, partial density and fast neutron cross section for each component of glasses. $\text{MRCS}$ of the constituent elements of each glass was obtained from the literature [40–42]. FNRC of the studied glasses is presented together with partial density of elements in the glasses as given in Table 7. The result reveals that the GTG3 contains the optimum concentration of glass constituents that gives the best neutron shielding ability with FNRC of 0.1024 cm⁻¹. Compared to recently studied glass, S30 (FNRC = 0.0506) [43], graphite (FNRC = 0.077 cm⁻¹) and OC (FNRC = 0.093 cm⁻¹ calculated)) [37,44], the magnetite-limonite concrete grade FNRC value is 0.1314 cm⁻¹ (calculated) and 0.2019 cm⁻¹ (measured), ordinary–ordinary measured FNRC is 0.1083 cm⁻¹ [44], and FL2 ordinary/limonite-ordinary grade of concrete FNRC are 0.1051 cm⁻¹ (calculated) and 0.1092 cm⁻¹ (measured) (see Table 4 of Ref. [44]). Therefore, FNRC of GTG glasses is good and comparative to different types of concretes, especially those reported in Table 4 of Ref. [44].

Table 7. Partial density (ρ) and FNRC of GTG1–GTG4 glasses.

	Partial, ρ (g/cm^3)				FNRC (cm^−1)
Element	GTG1	GTG2	GTG3	GTG4	GTG1	GTG2	GTG3	GTG4
Ge	0.9793	0.9247	0.2415	0.3137	0.0172	0.0163	0.0042	0.0055
O	1.1208	1.0867	1.1088	1.1062	0.0453	0.044	0.0449	0.0448
Te	1.7210	2.7084	2.9749	3.8599	0.023	0.0363	0.0398	0.0518
Ga	0.7487	–	0.7447	–	0.0134	–	0.0133	–
Total FNRC (cm^−1)					0.0991	0.0966	0.1024	0.1021

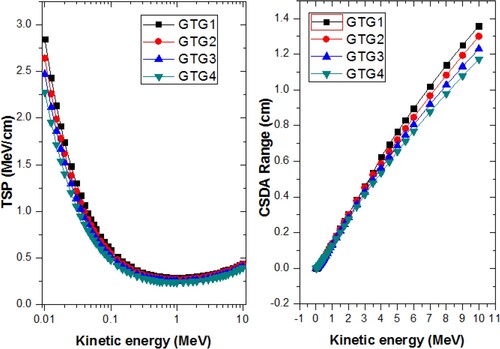
In order to assess the relative charged particles attenuation capacity of the GTG glasses, their total stopping powers (TSP) (MeV/cm) and CSDA range (cm) were evaluated for electron kinetic energy between 0.01 and 10 MeV. The ESTAR (physics.nist.gov) was employed for the calculations. Figure 8 gives the spectra of TSP and CSDA range with kinetic energy, T (MeV). As an electron traverses through a material, it loses energy through coulomb interaction and via bremsstrahlung production. The TSP accounts for the energy loss due to these two processes, however, the probability of both processes differ for a particular T. The cross section for collision (Coulomb) losses decreases with T while that of radiation production increases as T progresses. An equilibrium is reached between TSP due radiation and collision at energy T = 1.0 MeV where TSP was minimum in the GTG glasses. Below 1 MeV, collision losses dominate electron energy loses in the glasses while radiation loses dominates at energies greater than 1 MeV. The CSDA range is greater in GTG glasses with lower density and TeO₂ content.

Figure 8. TSP and CSDA range of electron as functions of electron kinetic energy for the GTG glasses.

4. Conclusion

In the current research article, we studied and discussed the role of Ga₂O₃ addition on the nuclear shielding ability of germinate tellurite glasses such as 41.7GeO₂–41.7TeO₂–16.6Ga₂O₃, 37.5GeO₂–62.5TeO₂, 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ and 12.5GeO₂–87.5TeO₂. The photon, fast neutron and electron shielding parameters of the glasses were evaluated and studied via the Geant4 simulation, Phy-X/PSD software, ESTAR and analytic computations. The gamma-ray absorbing capacity of the glasses improved with mass density and decrease in Ga₂O₃ content of the glasses. Among the glasses, 12.5GeO₂–87.5TeO₂ presented the best shielding capacity against photons and electrons. Compared to ordinary concrete and commercial glass shields, the GTG glasses were superior photon absorbers. The optimum chemical composition for fast neutron absorption was found in 10.4GeO₂–72.9TeO₂–16.7Ga₂O₃ glass sample with FNRC of 0.1024 cm⁻¹ which is comparative to different types of concretes. The investigated glasses can be adopted for radiation safety purposes in many nuclear technology facilities.

Acknowledgment

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project (grant number PNURSP2022R291), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Moreover, this work was supported by King Khalid University through a grant (RCAMS/KKU/G001/21) under the Research Center for Advanced Materials Science (RCAMS) at King Khalid University, Saudi Arabia.

Disclosure statement

No potential conflict of interest was reported by the author(s).