Mixed convective flow of Casson and Oldroyd-B fluids through a stratified stretching sheet with nonlinear thermal radiation and chemical reaction

Abstract

Non-Newtonian fluids flow with mixed convection has got the researcher’s attention due to its widespread application in engineering and manufacturing systems. Furthermore, the thermal radiation in convective thermal transmission plays a key role in regulating the thermal transmission. That’s why the authors’ interest comes to the point to present a detailed analysis of the mixed convective flow of Casson and Oldroyd-B fluids through a linearly stratified stretching sheet. Also, the flow of Casson and Oldroyd-B fluids are considered as chemically reactive, thermally radiative, and magnetized by a strong magnetic field. The mathematical model of the present analysis is presented in PDEs (partial differential equations) format which is transformed into ODEs (ordinary differential equations) by employing suitable variables. The transformed ODEs are treated with an analytical technique called HAM (Homotopy analysis method) which provides an analytical solution for both linear and nonlinear differential equations. Through the use of diagrams, the converging exploration of HAM is depicted. An interesting result has been introduced that, the streamlines of Casson liquid are highly affected by a strong magnetic field as compared to Oldroyd-B liquid. The strong magnetic field and buoyancy ratio parameter moderate the velocity profile, while an opposite trend is found in the motion of liquid by using mixed convectional factors. Additionally, the impacts of magnetic and buoyancy ratio parameters are greater for Oldroyd-B fluid as associated with Casson liquid. On the other hand, the mixed convection parameter is stronger for Casson liquid as equated to Oldroyd-B fluid. The present results have a great agreement with previously published results.

KEYWORDS:

• Casson fluid
• Oldroyd-B fluid
• Mixed convection
• Magnetic field
• Nonlinear thermal radiation
• HAM

Nomenclature

$u$, $v$	=	Components of velocity $\left[\text{m}\text{.}{\text{s}}^{-1}\right]$
$x,y$	=	Coordinate axes $\left[\text{m}\right]$
$g$	=	Gravitational force $\left[\text{m}\text{.}{\text{s}}^{-2}\right]$
${\text{β}}_T$,${\text{β}}_C$	=	Coefficients of thermal and Concentration expansion $\left[K^{-1}\right]$
$\text{β}$	=	Casson parameter $[-]$
$a,b,d$, $e$	=	Constants $[-]$
${\alpha }_1$,${\alpha }_2$	=	Deborah numbers with respect to relaxation and retardation times $[-]$
$Rd$	=	Nonlinear thermal radiation $[-]$
$M$	=	Magnetic parameter $[-]$
$Pr$	=	Prandtl number $[-]$
$Sc$	=	Schmidt number $[-]$
$Nt$	=	Thermophoresis $[-]$
$K$	=	Chemical reaction parameter $[-]$
$t$	=	Time $\left[s\right]$
$\mu$	=	Dynamic viscosity $\left[\text{Pa}\text{.s}\right]$
${\lambda }_1$	=	Relaxation time $[-]$
${\lambda }_2$	=	Retardation time $[-]$
$\rho$	=	Density $\left[\text{kg}\text{.}{\text{m}}^{-3}\right]$
$\nu$	=	Kinematic viscosity $\left[{\text{m}}^2.{\text{s}}^{-1}\right]$
$\sigma$	=	Electrical conductivity $\left[\text{S}.{\text{m}}^{-1}\right]$
$q_r$	=	Radiative heat flux $\left[\text{W}.{\text{m}}^{-2}\right]$
$D_B$, $D_T$	=	Coefficients of Brownian motion and thermophoresis $\left[{\text{m}}^2.{\text{s}}^{-1}\right]$
$\alpha$	=	Thermal diffusivity $\left[\text{W}\text{.}{\text{m}}^{-1}.{\text{K}}^{-1}\right]$
$T$	=	Temperature $\left[K\right]$
$C$	=	Concentration $\left[\text{mol}.{\left(\text{kg}\right)}^{-1}\right]$
$T_0$	=	Reference temperature $\left[K\right]$
$C_0$	=	Reference concentration $\left[\text{mol}.{\left(\text{kg}\right)}^{-1}\right]$
$T_{\mathrm{\infty }}$	=	Free stream temperature $\left[K\right]$
$C_{\mathrm{\infty }}$	=	Free stream concentration $\left[\text{mol}.{\left(\text{kg}\right)}^{-1}\right]$
${\theta }_w$	=	Temperature ratio parameter $[-]$
$Nb$	=	Brownian motion $[-]$
$S_1$	=	Thermal stratification parameter $[-]$
$S_2$	=	Concentration stratification parameter $[-]$

1. Introduction

In recent years, there have been several experiments on mixed convectional transfer of non-Newtonian liquids via thermal and solutal stratifications. This is due to their widespread use in engineering and manufacturing systems. Heat release into the atmosphere such as rivers, oceans, lakes, and solar ponds are a few examples of such processes. The accumulation or formation of layers in a liquid happens as effect of thermal fluctuations, variations in concentration, or the interaction of various fluids. The analysis of thermal and concentration stratification of hydrogen and oxygen reservoirs is significant although it openly affects the rate of increase of all cultured species. The boundary layer flow and thermal transmission through an extending surface was initially investigated by Sakiadis [1,2]. Meanwhile different properties of liquid flows through an extending surface considering diverse physical circumstances were examined by many investigators. Tsou et al. [3] presented the empirical and quantitative exploration of fluid motion through a moving sheet. Far ahead in 1970, Crane [4] introduced the boundary layer flow concept and investigated the incompressible flow of liquid through a linear extending surface. Investigating the flow properties, the steady flow in an extending cylinder and extending channel was adopted by Brady and Acrivos [5]. The stagnation point of dense liquid dynamics across an extending surface was investigated by Chaim [6]. The impression if buoyancy forces on viscous liquid through an extending surface was presented by Chamkha [7]. The stagnation movement of viscoelastic and viscid liquids past a stretched plate was explored by Mahapatra and Gupta [8,9]. The fluid flow of dime-dependent boundary layer over an extending flat surface has scrutinized by Nazar et al. [10]. The thermal profiles of a steady fluid flow through an extending surface were offered by Ishak et al. [11]. Furthermore, Ishak et al. [12] examined the heat transmission of liquid motion through a stretchable sheet. Patil et al. [13] presented the quadratic convective steam of power law liquid through a stretched surface. The numerical study of steady fluid motion through a stretched media has probed by Zaimi and Ishak [14]. Further related works can be study in [15–22].

In industrial developments where the value of the products is dependent on factors of thermal control, the thermal radiation shows an imperative character in regulating thermal transmission. Mat et al. [23] presented the analysis of magnetic effects on nanofluid flow with thermal radiation consequence. Hady et al. [24] considered the viscous nanofluid flow through a nonlinear extending sheet. The thermal transmission in a mixed convective liquid through an extending sheet was probed by Aldawody and Elbashbeshy [25]. The stagnation point flow with thermal radiation consequence on a mixed convective flow was studied by Makinde [26]. The influence of radiation on chemically reactive steam of fluid over an spreading surface was investigated by Kahar et al. [27]. The effect of temperature transformation in a nanofluid over a stretchable surface has evaluated by Shankar and Ibrahim [28]. Kumar et al. [29] have explored Casson liquid motion over an expanding plate. Yusuf et al. [30] addressed the entropy production in MHD Williamson motion over a permeable wall and impact of chemical interaction. Mabood et al. [31] used asymmetric radiant heat and exergy destruction modelling to study the water-based Cu-Al₂O₃ hybrid nanofluid movement. Yusuf et al. [32] investigated the 3D motion of Cu-TiO₂/H₂O hybrid nanoliquid through an extending medium. Ferdows et al. [33] studied the H₂O -based nanofluid flow under the influence of an applied magnetic field quantitatively. The H₂O -based CNTs nanofluid across rotatory discs was studied by Mabood et al. [34].

Krishna et al. [35] examined the magnetohydrodynamic Casson hybrid nanofluid movement past an infinite exponentially stretching medium. Entropy production in micropolar liquid dynamics including slip condition was demonstrated by Yusuf et al. [36]. Magnetohydrodynamics Oldroyd 8-constant flow pattern in a channel having irregular convective and chemical processes consequences was explored by Yusuf et al. [37]. The entropy study in MHD couple stress flow of nanofluid including melt heat transmission, thermal radiation, and slip condition was presented by Mabood et al. [38]. Ali et al. [39] examined the magnetohydrodynamic Maxwell and tangent hyperbolic nanofluids flow through a bi-directional spreading medium. Yusuf et al. [40] used activation energy to explore the Magnetohydrodynamic stagnation steam of Casson nanofluid. Krishna et al. [41] presented the radiated MHD convectional nanofluids motion through a vertically extending surface. Mabood et al. [42] examined the energy and mass transformation analysis of nanofluid flow over a rotating frame with MHD and entropy generation. Ahamad et al. [43] analysed the Dufour and Soret influences on magnetohydrodynamic nanofluid motion across a semi-infinite sliding surface with thermal radiation and uniform energy source. Further related studies and mathematical methods can be analyse in [44–53].

Motivated by the above literature survey, the authors have come into the point to present the heat and mass transmission in a flow of Casson and Oldroyd-B fluids through a linearly extending sheet. Also, the flow of Casson and Oldroyd-B fluids is considered as mixed convective, chemically reactive, thermally radiative, and highly magnetized by a strong magnetic field. Our focus is to present the comparative analysis of Casson and Oldroyd-B fluids via different embedded parameter. The present analysis is divided section wise as section 2 represents the problem formulation, section 3 displays the analytical solution, section 4 represents the convergence of HAM, and section 5 indicates the results and discussion. Section 6 includes the final comments. By the end of this study, the authors have to answer the following research questions:

• How do the Casson and Oldroyd-B fluids behave against a magnetic field parameter and for which fluid does the magnetic parameter have a dominant impact?

• How do the Casson and Oldroyd-B fluids behave against the buoyancy proportion and mixed convectional factors and for which fluid do the buoyancy ratio and mixed convective factors have a dominant impact?

• How does the magnetic parameter affect the streamlines of the Casson and Oldroyd-B fluids flows?

2. Formulation of problem

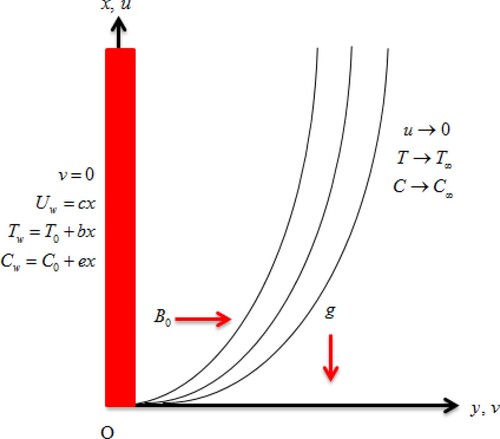
Suppose the time independent, chemically reactive, and stratified flow of Casson and Oldroyd-B fluids through a linearly stretched surface. The velocity of extending surface is $u=U_w\left(x\right)=cx$, where $c>0$ denotes the stretching rate constant. Magnetic effect with strength $B_0$ is pragmatic normal to the fluid flow. $T_w$denotes surface temperature and $C_w$ signifies surface concentration of the fluids flow. The ambient temperature and concentration of the fluids flow are signified by $T_{\mathrm{\infty }}$ and $C_{\mathrm{\infty }}$, respectively. Furthermore, the nonlinear thermal radiation, Brownian motion coefficient, thermophoresis coefficient, and mixed convection are also considered. The flow geometry of the modelled problem is exhibited in Figure 1.

Figure 1. Geometry of the flow problem.

The basic equations for Oldroyd-B fluid are: (1) $\begin{array}{rl}& T=S-pI,\end{array}$(1) (2) $\begin{array}{rl}& S+{\lambda }_1\left[\frac{dS}{dt}-\left(S{L}^T+LS\right)\right]\\ & =\mu \left[A_1+{\lambda }_2\left(\frac{d{A}_1}{dt}-\left(A_1{L}^T+L{A}_1\right)\right)\right],\end{array}$(2) where $A_1$ and $L$ are defined as: (3) $L=\mathrm{\nabla }V,A_1=L+L^T.$(3) The following is the rheological model for Casson fluid: (4) $\begin{array}{rl}{\tau }^{1/n}& ={\tau }_0^{1/n}+\mu {\gamma }^{1/n},\end{array}$(4) (5) $\begin{array}{rl}{\tau }_{ij}& =\{\begin{array}{l}2\left(\frac{p_y}{\sqrt{2\pi }}+{\mu }_B\right)e_{ij},\pi >{\pi }_c,\\ 2\left(\frac{p_y}{\sqrt{2{\pi }_c}}+{\mu }_B\right)e_{ij},\pi <{\pi }_c,\end{array}\end{array}$(5) Therefore, the leading equations are defined as [54–56]: (6) $\begin{array}{rl}& \frac{\mathrm{\partial }u}{\mathrm{\partial }x}+\frac{\mathrm{\partial }v}{\mathrm{\partial }y}=0,\end{array}$(6) (7) $\begin{array}{rl}& u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }u}{\mathrm{\partial }y}+{\lambda }_1\left(2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }x\mathrm{\partial }y}uv+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}{v}^2+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}{u}^2\right)\\ & =\nu \left(1+\frac{1}{\text{β}}\right)\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}-\frac{\sigma B_0^2}{\rho }u\\ & +\nu {\lambda }_2\left(\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }x\mathrm{\partial }{y}^2}u+\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{y}^3}v-\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}\frac{\mathrm{\partial }u}{\mathrm{\partial }x}-\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{y}^2}\frac{\mathrm{\partial }u}{\mathrm{\partial }y}\right)\\ & +g\left[{\text{β}}_C\left(C-C_{\mathrm{\infty }}\right)+{\text{β}}_T\left(T-T_{\mathrm{\infty }}\right)\right],\end{array}$(7) (8) $\begin{array}{rl}& u\frac{\mathrm{\partial }T}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }T}{\mathrm{\partial }y}=\alpha \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{y}^2}+\frac{16{\sigma }^{\ast }}{3k^{\ast }\rho c_p}\frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(T^3\frac{\mathrm{\partial }T}{\mathrm{\partial }y}\right)\\ & +\tau \left(D_B\frac{\mathrm{\partial }T}{\mathrm{\partial }y}\frac{\mathrm{\partial }C}{\mathrm{\partial }y}+\frac{D_T}{T_{\mathrm{\infty }}}{\left(\frac{\mathrm{\partial }T}{\mathrm{\partial }y}\right)}^2\right),\end{array}$(8) (9) $\begin{array}{rl}& u\frac{\mathrm{\partial }C}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }C}{\mathrm{\partial }y}+k_1\left(C-C_{\mathrm{\infty }}\right)=D_B\frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(\frac{\mathrm{\partial }C}{\mathrm{\partial }y}\right)+\frac{D_T}{T_{\mathrm{\infty }}}\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{y}^2},\end{array}$(9) with boundary conditions [57,58]: (10) $\begin{array}{rl}v& =0,U_w\left(x\right)=u=cx,C=C_w=C_0+dx,\\ T& =T_w=bx+T_{0}aty=0,\\ T& \to T_{\mathrm{\infty }}=ax+T_0,u\to 0,C\to C_{\mathrm{\infty }}\\ & =ex+C_{0}asy\to 0.\end{array}$(10) The similarity variables are defined as [58]: (11) $\begin{array}{rl}u& =cx{f}_{\eta }\left(\eta \right),v=-\sqrt{c\nu }f\left(\eta \right),\eta =\sqrt{\frac{c}{\nu }}y,{\theta }_w=\frac{T_w}{T_{\mathrm{\infty }}},\\ T& =T_{\mathrm{\infty }}\left(1+\left({\theta }_w-1\right)\theta \right),\varphi \left(\eta \right)\left(C_w-C_{\mathrm{\infty }}\right)=C-C_{\mathrm{\infty }}.\end{array}$(11) Continuity equation is obvious; momentum, energy, and concentration are reduced as: (12) $\begin{array}{rl}& \left(1+\frac{1}{\text{β}}\right)f_{\eta \eta \eta }+\left(2f_{\eta \eta }f{f}_{\eta }-f_{\eta \eta \eta }{f}^2\right){\alpha }_1\\ & +\left(f_{\eta \eta }-f{f}_{\eta \eta \eta \eta }\right){\alpha }_2\\ & +f{f}_{\eta \eta }-f_{\eta }^2-M{f}_{\eta }+\lambda \left(\theta +N\varphi \right)=0,\end{array}$(12) (13) $\begin{array}{rl}& {\theta }_{\eta \eta }+Rd\left[\begin{array}{c}{\theta }_{\eta \eta }(1+\left({\theta }_w-1\right)\theta {)}^3\\ +3\left({\theta }_w-1\right)(1+\left({\theta }_w-1\right)\theta {)}^2({\theta }_{\eta }{)}^2\end{array}\right]\\ & +Prf{\theta }_{\eta }+PrNt{\theta }_{\eta }^2-PrS{}_1{f}_{\eta }+PrNb{\theta }_{\eta }{\varphi }_{\eta }=0,\end{array}$(13) (14) $\begin{array}{rl}& {\varphi }_{\eta \eta }+Scf{\varphi }_{\eta }-Sc{f}_{\eta }\varphi -Sc{S}_2{f}_{\eta }-KrSc\varphi +\frac{Nt}{Nb}{\theta }_{\eta \eta }=0,\end{array}$(14) with transformed boundary conditions: (15) $\begin{array}{rl}f\left(0\right)& =0=f_{\eta }\left(\mathrm{\infty }\right),f_{\eta }\left(0\right)=1,\theta \left(0\right)=1-S_1,\\ \theta \left(\mathrm{\infty }\right)& =0,\varphi \left(0\right)=1-S_2,\varphi \left(\mathrm{\infty }\right)=0.\end{array}$(15) where (16) $\begin{array}{rl}{\alpha }_1& ={\lambda }_{1}c,{\alpha }_2={\lambda }_{2}c,M=\frac{\sigma B_0^2}{\rho c},Rd=\frac{16}{3}\frac{{\sigma }^{\ast }{T}_{\mathrm{\infty }}^3}{k{k}^{\ast }},\\ Pr& =\frac{\nu }{\alpha },{\theta }_w=\frac{T_w}{T_{\mathrm{\infty }}},Sc=\frac{\nu }{D_B},\\ Nt& =\frac{D_T\tau \left(T_w-T_{\mathrm{\infty }}\right)}{\nu T_{\mathrm{\infty }}},Nb=\frac{D_B\tau \left(C_w-C_{\mathrm{\infty }}\right)}{\nu },\\ K& =\frac{kr}{c},S_1=\frac{a}{b},S_2=\frac{e}{d}.\end{array}$(16) All of the above dimensional and non-dimensional parameters are defined in the nomenclature.

Physical quantities of interest $N{u}_x$ and $S{h}_x$, are defined as: (17) $N{u}_x=\frac{x{q}_w}{k(T_w-T_{\mathrm{\infty }})},S{h}_x=\frac{x{q}_m}{D_B(C_w-C_{\mathrm{\infty }})}.$(17) Using the similarity variables defined in Equation (11), we have (18) $\begin{array}{rl}Nu& =\frac{1}{\sqrt{{Re}_x}}N{u}_x=-\left(1+Rd{\theta }_w^3\right){\theta }^{\mathrm{\prime }}\left(0\right).\\ Sh& =\frac{1}{\sqrt{{Re}_x}}S{h}_x=-{\varphi }^{\mathrm{\prime }}\left(0\right).\end{array}$(18) where $Re=\frac{U_w\left(x\right)x}{\nu }$ is signified the local Reynolds number.

3. HAM solution

Homotopy analysis method (HAM) is a semi-analytical method capable of solving both linear and highly nonlinear differential equations. Additionally, HAM is free of variables choices. In order to present the analytical solution of the current framework, HAM is applied.

The linear operators and initial guesses are: (19) $\begin{array}{rl}{L}_f\left(f\right)& =f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}-f^{\mathrm{\prime }},L_{\theta }\left(\theta \right)={\theta }^{\mathrm{\prime }\mathrm{\prime }}-\theta ,L_{\varphi }\left(\varphi \right)={\varphi }^{\mathrm{\prime }\mathrm{\prime }}-\varphi ,\end{array}$(19) (20) $\begin{array}{rl}{f}_0\left(\eta \right)& =1-e^{-\eta },{\theta }_0\left(\eta \right)=\left(1-S_1\right)e^{-\eta },\\ {\varphi }_0\left(\eta \right)& =\left(1-S_2\right)e^{-\eta },\end{array}$(20)

with

(21) $\begin{array}{rl}& L_f\left[{\mathbb{Q}}_1+{\mathbb{Q}}_{2}exp\left(\eta \right)+{\mathbb{Q}}_{3}exp(-\eta )\right]\\ & =0,L_{\theta }\left[{\mathbb{Q}}_{4}exp\left(\eta \right)+{\mathbb{Q}}_{5}exp(-\eta )\right]=0,\\ & L_{\varphi }\left[{\mathbb{Q}}_{6}exp\left(\eta \right)+{\mathbb{Q}}_{7}exp(-\eta )\right]=0,\end{array}$(21) where ${\mathbb{Q}}_1$ to ${\mathbb{Q}}_7$ are constants.

4. HAM convergence

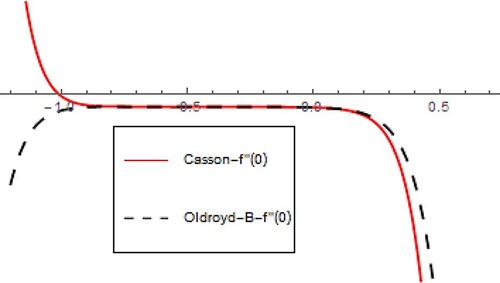
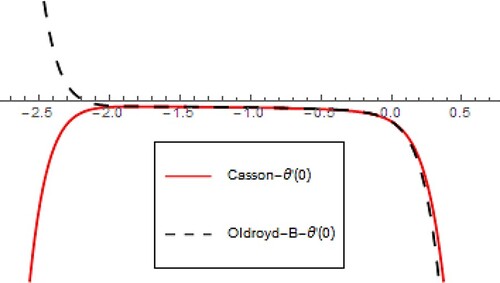
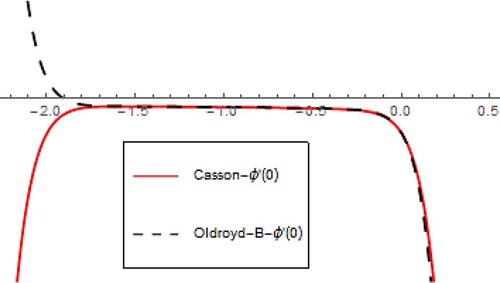
The current model is treated with an analytical approach called HAM which provides an analytical solution for equations of the modelled problem. Here, in this section, the convergence of HAM is presented. HAM has the power to govern and regulates the convergence of the problem. Figures 2–4 show the convergence areas of velocity, thermal, concentration profiles of the flow for both Casson and Oldroyd-B fluids. The convergence areas for velocity profile $f^{\mathrm{\prime }\mathrm{\prime }}\left(0\right)$ is$-1.83\le {\hslash }_f\le 0.40$, thermal profile ${\theta }^{\mathrm{\prime }}\left(0\right)$ is $-2.0\le {\hslash }_{\theta }\le 0.0$, and concentration profile ${\varphi }^{\mathrm{\prime }}\left(0\right)$ is$-2.75\le {\hslash }_{\varphi }\le -0.1$for both Casson and Oldroyd-B fluids.

Figure 2. $\hslash -$curves for $f^{\mathrm{\prime }\mathrm{\prime }}\left(0\right)$.

Figure 3. $\hslash -$curves for ${\theta }^{\mathrm{\prime }}\left(0\right)$.

Figure 4. $\hslash -$curves for ${\varphi }^{\mathrm{\prime }}\left(0\right)$.

5. Results and discussion

The present portion deals with the graphical outcomes and physical discussion of the mixed convective, thermally radiative, and chemically reactive Casson and Oldroyd-B fluids through a stratified linearly stretching sheet is presented. The analytical explanation of the present model is represented by employing HAM scheme. The flow of Casson and Oldroyd-B fluids is treated using strong magnetic field. In this regards, Figures 5–15 are displayed. The predefine setting of the embedded factors are chosen as ${\alpha }_1={\alpha }_2=0.5$, $M=5.0$, $Rd=0.3$, $Pr=6.0$, ${\theta }_w=0.5$, $Sc=1.0$, $Nt=0.4$, $Nb=0.3$, $S_1=S_2=0.2$ and $K=1.0$.

Figure 5. Influence of $M$ on $f_{\eta }$.

Figure 6. Influence of $\lambda$on $f_{\eta }$.

Figure 7. Influence of $N$on $f_{\eta }$.

Figure 8. Influence of $S_1$ on $\theta$.

Figure 9. Influence of $Rd$ on $\theta$.

Figure 10. Influence of ${\theta }_w$ on $\theta$.

Figure 11. Influence of $S_2$ on $\varphi$.

Figure 12. Influence of $Sc$ on $\varphi$.

Figure 13. Influence of $kr$ on $\varphi$.

Figure 14. (a–d) Streamlines for Casson fluid when $M=0.0$,$M=1.0$,$M=2.0$ and $M=5.0$.

Figure 15. (a–d) Streamlines for Oldroyd-B fluid when $M=0.0$, $M=1.0$, $M=2.0$ and $M=5.0$.

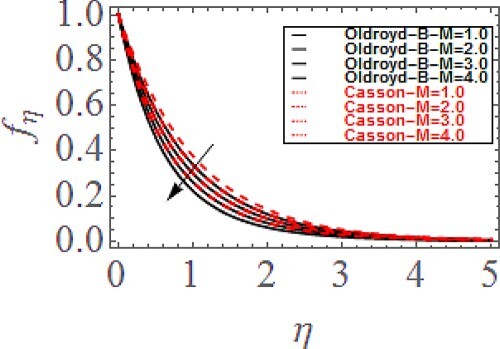
Figure 5 indicates the change in velocity profile via $M$. It is perceived that the greater $M$ reduces the velocity profile for both fluids. Physically, the fluid velocity drops with higher $M$ because of Lorentz force, which yields an opposing force to the fluid flow. Such conflicting intensity generates opposition to the velocity of the fluid particles. Thus, the fluid velocity reduces with the increasing $M$. 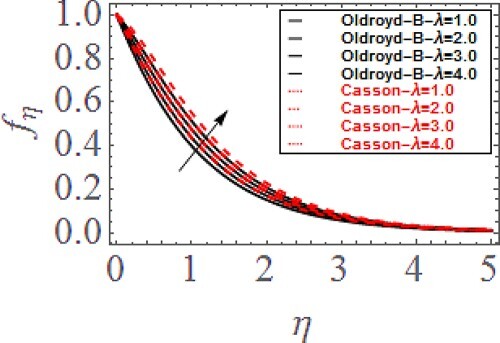Additionally, the reducing impact of magnetic parameter is superior for Oldroyd-B liquid as equated to the Casson liquid. Figure 6 exhibits the variation in $f_{\eta }$ profile via $\lambda$. Actually, the buoyancy forces heighten with higher $\lambda$. 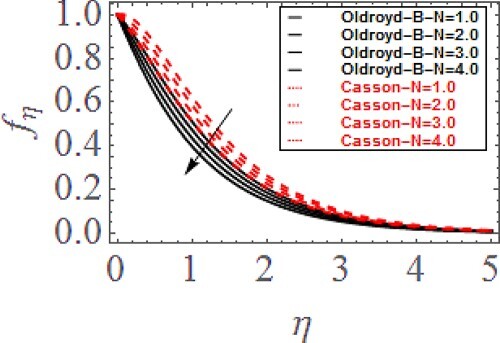This increasing buoyancy forces escalates the velocity of the fluids particles that causes the heightening influence in velocity field. Additionally, the increasing impact of mixed convection parameter is dominant for Casson fluid as compared to Oldroyd-B liquid. Figure 7 reveals the variation in $f_{\eta }$ field via buoyancy ratio factor $N$. The greater $N$ decreases the velocity profile. 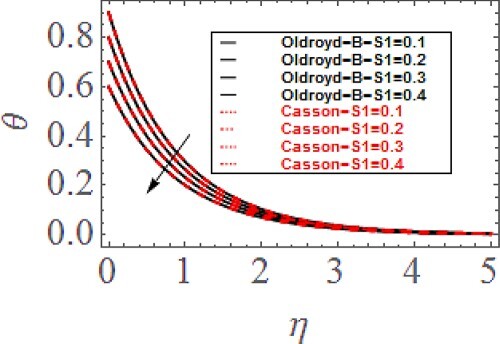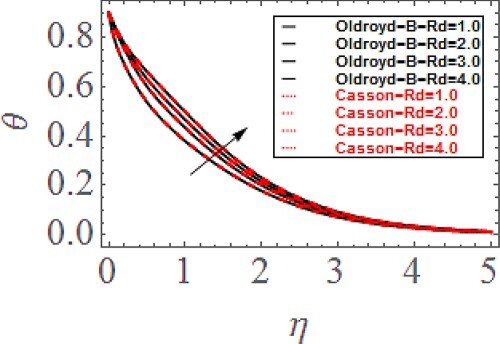Physically, the larger $N$ increases the viscosity of the fluids flow which causes to slow down the fluid’s particles movement and consequently the velocity profile reduces. Furthermore, the diminishing influence of buoyancy ratio factor is superior for Oldroyd-B fluid as equated to Casson fluid. Figure 8 displays the change in temperature profile via thermal stratification parameter $S_1$. Greater $S_1$ reduces the thermal profile. Actually, the higher $S_1$ reduces the thermal alteration between the static flow and sheet surface which results the reducing influence in thermal profile. Figure 9 exhibits the change in thermal profile via thermal radiation parameter $R$. The greater values of $R$ increases the thermal profile. Greater $R$ upsurges the heat flux forms the sheet which results the heightening effect on thermal profile. 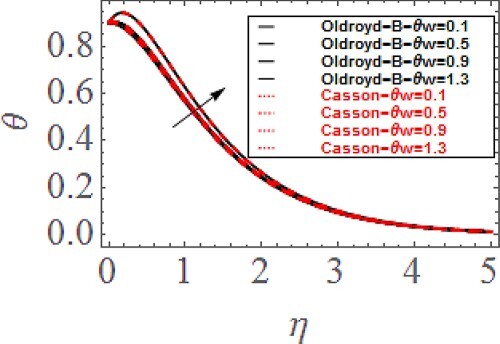That’s why the greater $R$ increases the temperature profile. Figure 10 displays the change in thermal profile via temperature ratio parameter ${\theta }_w$. Greater ${\theta }_w$ increases the thermal profile. 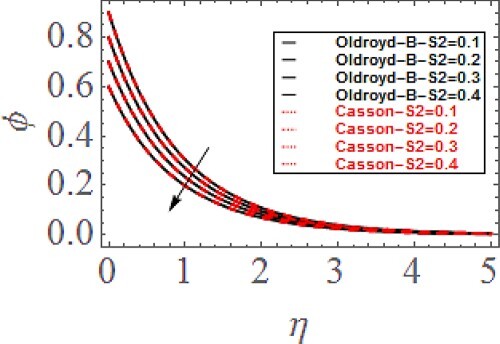The greater ${\theta }_w$ means supplementary heat will generate to the fluids flow which consequently rises the temperature of the fluids. Figure 11 indicates the variation in concentration profile via concentration stratification parameter $S_2$. 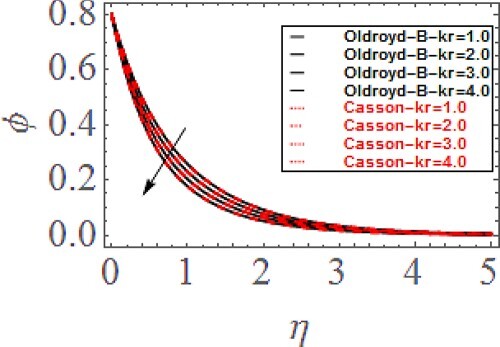It is found that the higher $S_2$ reduces the concentration profile. Figure 12 exhibits the change in concentration profile via Schmidt number $Sc$. 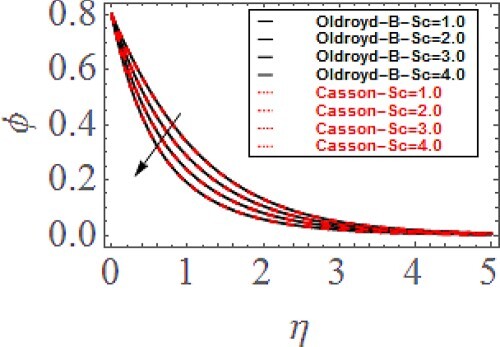Greater $Sc$ reduces the concentration profile. In fact, there is an inverse relation between molecular diffusivity and $Sc$. So, the higher $Sc$ reduces the concentration profile. Figure 13 displays the variation in concentration profile due to chemical reaction parameter $kr$. Larger $kr$ reduces the concentration profile. 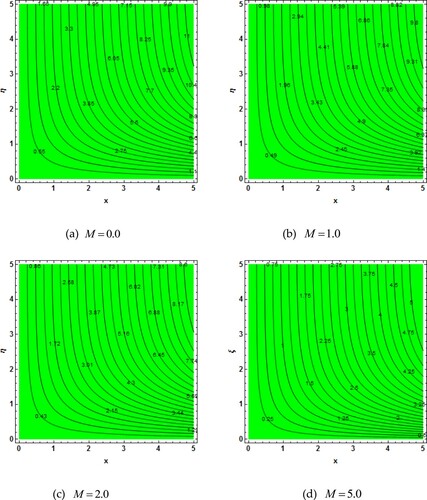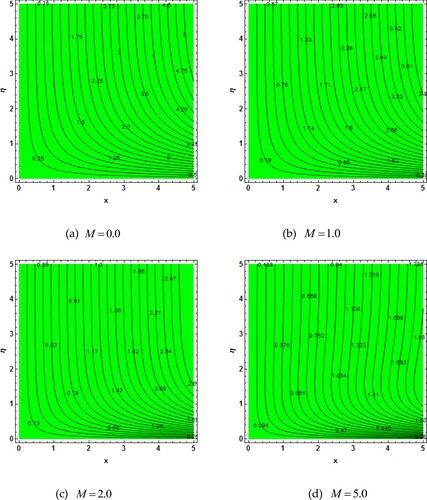Actually, the greater $kr$ creates contrasting force to the fluid flow molecules. The reduced molecular movement of the fluids diminishes the concentration profile. Figures 14(a–d) and 15(a–d) symbolize the analysis of streamlines for both Casson and Oldroyd-B fluids via magnetic field parameter, respectively. Figures 14(a) and 15(a) show the non-magnetized fluids flow. Here, we have seen that the streamlines are distinct from each other because of no magnetic field. Figures 14(b–d) and 15(b–d) represent the streamlines of magnetized Casson and Oldroy-B fluids flow respectively. Here, it is pragmatic that the higher $M$ reduces the fluids flow velocity. As $M$ increase, the streamlines become closer to each other which mean that the velocity profile reduces. This impact is actually as of Lorentz force that causes opposing force to the fluids flow. Furthermore, this impression is leading for Casson liquid as related to Oldroyd-B liquid. The relationship of the present results with the finding already reported is displayed in Table 1. Here, a great agreement with previously published is found. The influences of the common parameters on $N{u}_x$ and $S{h}_x$ numbers have depicted in Tables 2 and 3 for the Casson and Oldroyd-B fluids respectively. The outputs are the same for the Casson and Oldroyd-B fluids. The larger values of $M$, $Rd$, $Nt$, $Nb$, $N$ and $\lambda$ improving the heat transfer rate and the influence is comparatively better using the Oldroyd-B fluid. While the $N{u}_x$ number reduces with the larger values of $Sc$. Similarly, the Sherwood number upsurges with the larger amount of $Rd$, $\lambda$, $Nb$, $N$ and $Sc$, and declines with the decreasing value of $M$ and $Nt$.

Table 1. Correlation of the current and previous outcomes.

Authors	$Pr=1.0$	$Pr=10.0$
Ramesh et al. [59]	−1.33332	4.79672
Present results	−1.33333	4.7969

Table 2. Physical parameters versus $Nu$ and $Sh$ for Casson fluid.

$M$	$Rd$	$Nt$	$Nb$	$\lambda$	$N$	$Sc$	$Nu$	$Sh$
0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.5421324	0.8565421
0.2							0.5621433	0.8530563
0.3							0.5734240	0.8257342
	0.2						0.6785336	0.8226785
	0.3						0.7432120	0.8207432
		0.2					0.7802376	0.7997802
		0.3					0.8320835	0.7248320
			0.2				0.9532784	0.8895327
			0.3				0.9754699	0.9023754
				0.2			0.9896542	0.9231896
				0.3			0.9996863	0.9421996
					0.2		1.0358541	0.9780358
					0.3		1.3204865	1.1322204
						0.2	1.3204852	1.4633204
						0.3	1.3204844	1.8653432

Table 3. Physical parameters versus $Nu$ and $Sh$ for Oldroyd-B fluid.

$M$	$Rd$	$Nt$	$Nb$	$\lambda$	$N$	$Sc$	$Nu$	$Sh$
0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.5546213	0.8665654
0.2							0.5785621	0.8621530
0.3							0.5882734	0.8102257
	0.2						0.6864785	0.8113226
	0.3						0.7563432	0.8100207
		0.2					0.7932802	0.7832199
		0.3					0.8432320	0.7323248
			0.2				0.9632532	0.8994895
			0.3				0.9877546	0.9130237
				0.2			0.9978965	0.9102231
				0.3			1.0019299	0.9301421
					0.2		1.1231358	0.9887803
					0.3		1.4123204	1.1201322
						0.2	1.4323204	1.4213633
						0.3	1.410204	1.8532653

6. Final comments

The Mixed convective, thermally radiative, and chemically reactive flow of Casson and Oldroyd-B fluids through a stratified linearly stretching sheet is described in this investigation. The transformed ODEs are treated with an analytical technique called HAM (Homotopy analysis method) which provides an analytical solution for both linear and nonlinear differential equations. The convergence investigation of applied scheme HAM is portrayed using graphs. The variations in the fluids flow profiles via embedded parameters are analysed and debated in depth. The concluding remarks of the current analysis are listed as:

• The strong magnetic field and buoyancy ratio parameter moderate the velocity distribution while an opposite trend is found in velocity field via mixed convectional factors. Additionally, the impacts of magnetic and buoyancy ratio parameters are leading for Oldroyd-B liquid as equated to Casson fluid. On the other hand, the mixed convection parameter is dominant for Casson liquid as compared to Oldroyd-B liquid.

• The thermal profile reduces with thermal stratification parameter, while increase with nonlinear thermal radiation and temperature ratio parameters.

• The concentration profile reduces with concentration stratification parameter, while an opposite behaviour in concentration profile is perceived via Schmidt number and chemical reaction parameter.

• Greater reduction in streamlines is exhibited for highly magnetize fluid flows as compared to non-magnetized fluid flows. Additionally, such impact is superior for Casson liquid as associated to Oldroyd-B fluid.

• The present results have great agreement with previously published results.

Acknowledgements

The authors gratefully acknowledge the support of the University of Tabuk, Ministry of Education in Saudi Arabia.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

All data used in this manuscript have been presented within the article.