Product of spacing estimation of entropy for inverse Weibull distribution under progressive type-II censored data with applications

Abstract

This paper seeks to estimate the entropy for the inverse Weibull distribution using progressively Type-II censored data. To reach this objective, the entropy is defined through three entropy measures, namely, Rényi, q-entropy and Shannon entropy, and two estimation methods are used to estimate them. The first approach to estimate these quantities is the method of maximum likelihood. Furthermore, and for the first time, we consider the method of maximum product of spacing to estimate the mentioned entropy measures. Also, a simulation study is carried out and two real data sets are analysed. The numerical outcomes showed that the maximum likelihood provides good point estimates while the interval estimates based on the maximum product of spacing method have the shortest confidence interval lengths.

Keywords:

• Inverse Weibull distribution
• maximum likelihood estimation
• maximum product of spacing estimation
• Rényi entropy
• Shannon entropy

1. Introduction

Entropy is the expected quantity of information for the random variable. Measuring entropy is a very important role in many areas such as statistics, physics, chemicals, economics, insurance, financial analysis and biological phenomenon. More entropy is referred to less information found in a sample. Using the approaches of probability and statistics, the concept of entropy was defined by [1] as a measure of information. This concept was enhanced by numerous other entropy measures, arising from different real applications, see for complete survey [2]. In this study, we focus our attention on three of the most popular entropy measures, namely, Rényi entropy (RE) by [3], the q-entropy (QE) by [4] and Shannon entropy (SE) by [1].

Let X be a random variable with a probability density function (PDF) $f(x,\mathrm{\Omega })$, where Ω is the vector of the unknown parameters. Then, the RE, QE and SE of X are defined, respectively, as follow (1) $\begin{array}{rl}{H}_{\zeta }& =\frac{1}{1-\zeta }\log ({\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(f(x;\mathrm{\Omega }){)}^{\zeta }\mathrm{d}x),\zeta \ge 0,\zeta \ne 1,\end{array}$(1) (2) $\begin{array}{rl}{H}_q& =\frac{1}{q-1}[1-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(f(x;\mathrm{\Omega }){)}^q\mathrm{d}x].q\ge 0q\ne 1,\end{array}$(2) and (3) $H_S=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x;\mathrm{\Omega })\log (f(x;\mathrm{\Omega }))\mathrm{d}x.$(3) In most of the studies, at least Ω is unknown as well as the entropy. For this reason, estimating the parameters and the entropy has been the object of all the attention in various studies. See for example [5–13].

The inverse Weibull (IW) distribution occupies an essential place in representing the lifetime of components and investigating different extreme circumstances retaining rainfall, sea waves, wind speeds, earthquakes, floods queues in supermarkets, etc. The IW distribution furnishes a useful fit for non-monotone failure rates, such as decreasing and unimodal failure rates. The random variable X has the two-parameter IW distribution, denoted by IW$(\alpha ,\beta )$, if its PDF and cumulative distribution function (CDF), are respectively, given as (4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) and (5) $F(x;\beta ,\alpha )=e^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(5) where $\beta >0$ is the shape parameter and $\alpha >0$ is the scale parameter.

This study gives a contribution to the estimation of the RE, QE and SE for the IW distribution based on progressive Type-II censoring (PT-IIC) data. We first use the maximum likelihood (ML) estimation method to estimate the entropy measures based on the invariance property of the ML method. The approximate confidence intervals (ACIs) for these quantities are also obtained. Besides this approach and for the first time, we consider using the maximum product of spacing (MPS) estimation method to estimate the entropy measures and to construct the corresponding ACIs. To compare the performance of the different estimates, a simulation study is implemented. Finally, to show the applicability of the proposed methods, two real data sets are investigated.

The rest of this paper is organized as follows: The expressions of the three entropy measures are derived in Section 2. The ML method is investigated in Section 3. In Section 4, the estimates of the entropy measures are obtained using the MPS approach. A simulation study is conducted in Section 5, and two real data sets are studied in Section 6. Lastly, the paper is concluded in Section 7.

2. Expressions of entropies

Let X be a random variable following the IW distribution, then, using (1(1) $\begin{array}{rl}{H}_{\zeta }& =\frac{1}{1-\zeta }\log ({\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(f(x;\mathrm{\Omega }){)}^{\zeta }\mathrm{d}x),\zeta \ge 0,\zeta \ne 1,\end{array}$(1) ) and (4(4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) ) with $\mathrm{\Omega }=(\beta ,\alpha {)}^{\mathrm{\top }}$, the RE of X can be written as

(6) $\begin{array}{rl}{H}_{\zeta }& =\frac{1}{1-\zeta }\log \left({\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^{\zeta }\mathrm{d}x\right)\\ & =\log \left(\frac{1}{\beta }\right)+\frac{1}{\beta }\log \left(\zeta \alpha \right)-\frac{\zeta }{1-\zeta }\log (\zeta )\\ & +\frac{\log \left(\mathrm{\Gamma }(\frac{1}{\beta }(\zeta -1)+\zeta )\right)}{1-\zeta },\end{array}$(6) with $\zeta \ge 0$, $\zeta \ne 1$ and $\zeta \ge \frac{1}{1+\beta }$. 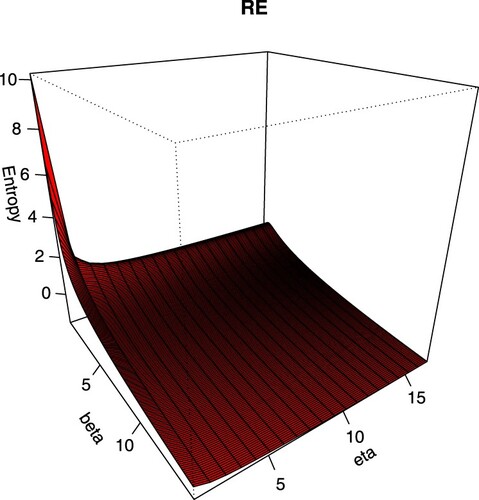Figure 1 displays the plot of the RE for the IW distribution for different values of β and ζ with $\alpha =1$. Figure 1 shows that the RE of the IW distribution is decreasing as β and ζ increase.

Figure 1. Plot of the RE for the IW distribution.

Similarly, the QE of the random variable X can be obtained based on (2(2) $\begin{array}{rl}{H}_q& =\frac{1}{q-1}[1-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(f(x;\mathrm{\Omega }){)}^q\mathrm{d}x].q\ge 0q\ne 1,\end{array}$(2) ) and (4(4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) ) as

(7) $\begin{array}{rl}{H}_q& =\frac{1}{q-1}[1-{\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^q\mathrm{d}x]\\ & =\frac{1}{q-1}[1-{\left(\frac{\beta }{{\alpha }^{\frac{1}{\beta }}}\right)}^{q-1}\frac{\mathrm{\Gamma }(\frac{1}{\beta }(q-1)+q)}{q^{(\frac{1}{\beta }(q-1)+q)}}],\end{array}$(7) with $q\ge 0$, $q\ne 1$ and $q\ge \frac{1}{1+\beta }$. 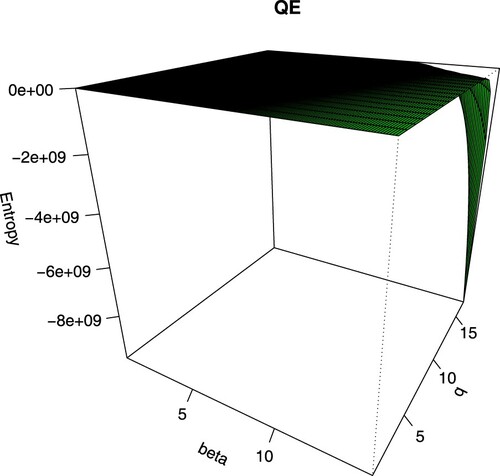Figure 2 shows the plot of the QE for the IW distribution for different values of β and q with $\alpha =1$. It is noted from Figure 2 that as β and q increase, the QE of the IW distribution decreases.

Figure 2. Plot of the QE for the IW distribution.

Also, the SE of a random variable X can be obtained from (3(3) $H_S=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x;\mathrm{\Omega })\log (f(x;\mathrm{\Omega }))\mathrm{d}x.$(3) ) and (4(4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) ) as $\begin{array}{rl}{H}_S& =-{\int }_0^{\mathrm{\infty }}\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\\ & \times \log \left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)\mathrm{d}x\\ & =-\log (\beta \alpha ){\int }_0^{\mathrm{\infty }}\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\mathrm{d}x+(\beta +1)\\ & \times {\int }_0^{\mathrm{\infty }}\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\ln (x)\mathrm{d}x\\ & +\beta {\alpha }^2{\int }_0^{\mathrm{\infty }}{x}^{-(2\beta +1)}{e}^{-\alpha x^{-\beta }}\mathrm{d}x.\end{array}$After some simplifications, the SE of IW model is given by (8) $\begin{array}{rl}{H}_S& =-\log (\beta \alpha ){\int }_0^{\mathrm{\infty }}{e}^{-y}\mathrm{d}y-(\beta +1){\int }_0^{\mathrm{\infty }}\frac{1}{\beta }{e}^{-y}\\ & \times \log \left(\frac{y}{\alpha }\right)\mathrm{d}y+{\int }_0^{\mathrm{\infty }}y{e}^{-y}\mathrm{d}y\\ & =-\log (\beta \alpha )+\frac{(\beta +1)}{\beta }(\gamma +\log (\alpha ))+1,\end{array}$(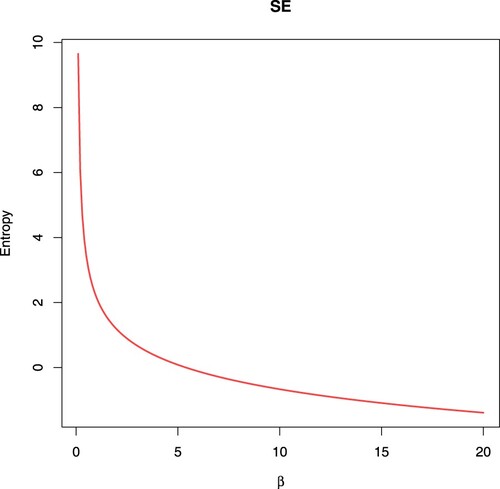8) where γ is Euler constant. Figure 3 depicts the plot of the SE for the IW distribution for different values of β with $\alpha =1$, which indicates that the SE is decreasing as β increases.

Figure 3. Plot of the SE for the IW distribution.

3. Estimation of entropies using ML method

In this section, the ML method is used to obtain the point and interval estimates of the unknown parameters of the IW distribution as well as the entropy measures based on a PT-IIC sample.

3.1. ML estimation

Due to rapid advancements in technology, researchers often want to save costs and the total time on the test. Therefore, a general censoring scheme called PT-IIC scheme can be considered. In the PT-IIC scheme, n items are put on a life test with a predetermined censoring scheme $R_1,\dots ,R_m$, where m is the effective sample size. For more details about PT-IIC scheme, see for example [14–16]. See also for more details [17–19]. Let $x=(x_1,x_2,\dots ,x_m)$ be a PT-IIC sample of size m with progressive censoring scheme $(R_1,\dots ,R_m)$. Then, the likelihood function (LF), ignoring the constant term, can be written as (9) $\ell (\mathrm{\Omega })=\prod _{i=1}^{m}f(x_i)[1-F(x_i){]}^{R_i}.$(9) From (4(4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) ), (5(5) $F(x;\beta ,\alpha )=e^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(5) ) and (9(9) $\ell (\mathrm{\Omega })=\prod _{i=1}^{m}f(x_i)[1-F(x_i){]}^{R_i}.$(9) ), the natural logarithm of the LF, $L(\mathrm{\Omega })=\log \ell (\mathrm{\Omega })$, can be given as (10) $\begin{array}{rl}L(\mathrm{\Omega })& \propto m\log (\alpha )+m\log (\beta )-(\beta +1)\sum _{i=1}^m\log (x_i)\\ & -\alpha \sum _{i=1}^m{x}_i^{-\beta }+\sum _{i=1}^m{R}_i\log [1-e^{-\alpha x_i^{-\beta }}].\end{array}$(10) The first partial derivatives of (10(10) $\begin{array}{rl}L(\mathrm{\Omega })& \propto m\log (\alpha )+m\log (\beta )-(\beta +1)\sum _{i=1}^m\log (x_i)\\ & -\alpha \sum _{i=1}^m{x}_i^{-\beta }+\sum _{i=1}^m{R}_i\log [1-e^{-\alpha x_i^{-\beta }}].\end{array}$(10) ) with respect to α and β are given, respectively, by (11) $\frac{\mathrm{\partial }L(\mathrm{\Omega })}{\mathrm{\partial }\alpha }=\frac{m}{\alpha }-\sum _{i=1}^m{x}_i^{-\beta }+\sum _{i=1}^m\frac{R_i{x}_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}$(11) and (12) $\begin{array}{rl}\frac{\mathrm{\partial }L(\mathrm{\Omega })}{\mathrm{\partial }\beta }& =\frac{m}{\beta }-\sum _{i=1}^m\log (x_i)\\ & +\alpha \sum _{i=1}^m(x_i^{-\beta }\log (x_i)-\frac{R_i{x}_i^{-\beta }\log (x_i)e^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}).\end{array}$(12) The maximum likelihood estimates (MLEs) of β and α denoted by $\hat{\beta }$ and $\hat{\alpha }$ can be computed by equating (11(11) $\frac{\mathrm{\partial }L(\mathrm{\Omega })}{\mathrm{\partial }\alpha }=\frac{m}{\alpha }-\sum _{i=1}^m{x}_i^{-\beta }+\sum _{i=1}^m\frac{R_i{x}_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}$(11) ) and (12(12) $\begin{array}{rl}\frac{\mathrm{\partial }L(\mathrm{\Omega })}{\mathrm{\partial }\beta }& =\frac{m}{\beta }-\sum _{i=1}^m\log (x_i)\\ & +\alpha \sum _{i=1}^m(x_i^{-\beta }\log (x_i)-\frac{R_i{x}_i^{-\beta }\log (x_i)e^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}).\end{array}$(12) ) to zero and solve the two normal equations simultaneously. Now, based on the invariance property of the MLEs, the MLEs of the entropies $H_{\zeta }$, $H_q$ and $H_S$ for the IW distribution can be obtained directly from (6(6) $\begin{array}{rl}{H}_{\zeta }& =\frac{1}{1-\zeta }\log \left({\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^{\zeta }\mathrm{d}x\right)\\ & =\log \left(\frac{1}{\beta }\right)+\frac{1}{\beta }\log \left(\zeta \alpha \right)-\frac{\zeta }{1-\zeta }\log (\zeta )\\ & +\frac{\log \left(\mathrm{\Gamma }(\frac{1}{\beta }(\zeta -1)+\zeta )\right)}{1-\zeta },\end{array}$(6) ), (7(7) $\begin{array}{rl}{H}_q& =\frac{1}{q-1}[1-{\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^q\mathrm{d}x]\\ & =\frac{1}{q-1}[1-{\left(\frac{\beta }{{\alpha }^{\frac{1}{\beta }}}\right)}^{q-1}\frac{\mathrm{\Gamma }(\frac{1}{\beta }(q-1)+q)}{q^{(\frac{1}{\beta }(q-1)+q)}}],\end{array}$(7) ) and (8(8) $\begin{array}{rl}{H}_S& =-\log (\beta \alpha ){\int }_0^{\mathrm{\infty }}{e}^{-y}\mathrm{d}y-(\beta +1){\int }_0^{\mathrm{\infty }}\frac{1}{\beta }{e}^{-y}\\ & \times \log \left(\frac{y}{\alpha }\right)\mathrm{d}y+{\int }_0^{\mathrm{\infty }}y{e}^{-y}\mathrm{d}y\\ & =-\log (\beta \alpha )+\frac{(\beta +1)}{\beta }(\gamma +\log (\alpha ))+1,\end{array}$(8) ), respectively, as follow $\begin{array}{rl}{\hat{H}}_{\zeta }& =\log \hat{\beta }+\frac{1}{\hat{\beta }}\log \left(\frac{\zeta }{\hat{\alpha }}\right)-\frac{\zeta }{1-\zeta }\log (\zeta )\\ & +\frac{\log \left(\mathrm{\Gamma }(\frac{1}{\hat{\beta }}(\zeta -1)+\zeta )\right)}{1-\zeta },\end{array}$with $\zeta \ge 0$, $\zeta \ne 1$ and $\zeta \ge \frac{1}{1+\hat{\beta }}$, ${\hat{H}}_q=\frac{1}{q-1}[1-{\left(\frac{\hat{\beta }}{{\hat{\alpha }}^{\frac{1}{\hat{\beta }}}}\right)}^{q-1}\frac{\mathrm{\Gamma }(\frac{1}{\hat{\beta }}(q-1)+q)}{q^{(\frac{1}{\hat{\beta }}(q-1)+q)}}],$with $q\ge 0$, $q\ne 1$ and $q\ge \frac{1}{1+\hat{\beta }}$, and ${\hat{H}}_S=-\log (\hat{\beta }\hat{\alpha })+\frac{(\hat{\beta }+1)}{\hat{\beta }}(\gamma +\log (\hat{\alpha }))+1.$

3.2. ACIs using MLEs

To construct the ACIs of the entropy measures $H_{\zeta }$, $H_q$ and $H_S$, we should first obtain the approximate asymptotic variance-covariance (VC) matrix of the MLEs. In this case, the approximate asymptotic VC can be computed through the inverse of the observed Fisher information matrix as follows (13) $J(\hat{\beta },\hat{\alpha })={\left(\begin{array}{cc}-{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\alpha }^2}}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}\\ -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\beta }^2}}\end{array}\right)}_{\alpha =\hat{\alpha },\beta =\hat{\beta }}^{-1}.$(13) The elements of (13(13) $J(\hat{\beta },\hat{\alpha })={\left(\begin{array}{cc}-{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\alpha }^2}}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}\\ -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\beta }^2}}\end{array}\right)}_{\alpha =\hat{\alpha },\beta =\hat{\beta }}^{-1}.$(13) ) are given by $\begin{array}{rl}\frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\alpha }^2}& =\frac{-m}{{\alpha }^2}-\sum _{i=1}^m\frac{R_i{x}_i^{-2\beta }{e}^{-\alpha x_i^{-\beta }}}{{(1-e^{-\alpha x_i^{-\beta }})}^2},\\ \frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }{\beta }^2}& =\frac{-m}{{\beta }^2}-\alpha \sum _{i=1}^m{x}_i^{-\beta }(\log (x_i){)}^2\\ & -\beta \sum _{i=1}^m\frac{\begin{array}{c}{R}_i{x}_i^{-\beta }(\log (x_i){)}^2{e}^{-\alpha x_i^{-\beta }}\\ [\alpha x_i^{-\beta }+e^{-\alpha x_i^{-\beta }}-1]\end{array}}{{(1-e^{-\alpha x_i^{-\beta }})}^2}\end{array}$and $\begin{array}{rl}\frac{{\mathrm{\partial }}^{2}L(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }& =\sum _{i=1}^m{x}_i^{-\beta }\log (x_i)\\ & +\sum _{i=1}^m\frac{\begin{array}{c}{R}_i{x}_i^{-\beta }\log (x_i)e^{-\alpha x_i^{-\beta }}\\ (\alpha x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}+e^{-\alpha x_i^{-\beta }}-1)\end{array}}{{(1-e^{-\alpha x_i^{-\beta }})}^2}.\end{array}$Here, we employ the delta method to get the approximate variances of the entropy measures. Let ${\mathrm{\Lambda }}_{\zeta }=(\mathrm{\partial }{H}_{\zeta }/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_{\zeta }/\mathrm{\partial }\beta )$, ${\mathrm{\Lambda }}_q=(\mathrm{\partial }{H}_q/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_q/\mathrm{\partial }\beta )$ and ${\mathrm{\Lambda }}_S=(\mathrm{\partial }{H}_S/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_S/\mathrm{\partial }\beta )$, which are obtained at the MLEs of α and β, where (14) $\begin{array}{rl}\frac{\mathrm{\partial }{H}_{\zeta }}{\mathrm{\partial }\alpha }& =-\frac{1}{\beta \alpha },\\ \frac{\mathrm{\partial }{H}_{\zeta }}{\mathrm{\partial }\beta }& =\frac{1}{\beta }-\frac{1}{{\beta }^2}[\log \left(\frac{\zeta }{\alpha }\right)-\psi (\frac{1}{\beta }(\zeta -1)+\zeta )],\end{array}$(14) (15) $\begin{array}{rl}\frac{\mathrm{\partial }{H}_q}{\mathrm{\partial }\alpha }& =\frac{\varphi }{\alpha \beta },\\ \frac{\mathrm{\partial }{H}_q}{\mathrm{\partial }\beta }& =-\frac{\varphi (\log (\alpha )-\psi (\frac{q-1}{\beta }+q)+\beta +\log (q))}{{\beta }^2}\end{array}$(15) and (16) $\begin{array}{rl}\frac{\mathrm{\partial }{H}_S}{\mathrm{\partial }\alpha }& =\frac{\beta +1}{\alpha \beta }-\frac{1}{\alpha },\\ \frac{\mathrm{\partial }{H}_S}{\mathrm{\partial }\beta }& =-\frac{(\beta +1)(\log (\alpha )+\gamma )}{{\beta }^2}+\frac{\log (\alpha )+\gamma }{\beta }-\frac{1}{\beta }\end{array}$(16) where $\psi (.)=\frac{\acute{\mathrm{\Gamma }}(.)}{\mathrm{\Gamma }(.)}$ gives the digamma function, $\acute{\mathrm{\Gamma }}(.)$ is the ordinary derivative of $\mathrm{\Gamma }(.)$ and $\varphi =q^{\frac{1-(\beta +1)q}{\beta }}(\beta {\alpha }^{-1/\beta }{)}^{q-1}\mathrm{\Gamma }(\frac{q-1}{\beta }+q)$. Now, the approximate estimates for the variances of the entropy measures $H_{\zeta }$, $H_q$ and $H_S$ can be obtained, respectively, as $\begin{array}{rl}\hat{V}({\hat{H}}_{\zeta })& \approx [{\mathrm{\Lambda }}_{\zeta }J(\hat{\beta },\hat{\alpha }){\mathrm{\Lambda }}_{\zeta }^{\mathrm{\top }}],\\ \hat{V}({\hat{H}}_q)& \approx [{\mathrm{\Lambda }}_{q}J(\hat{\beta },\hat{\alpha }){\mathrm{\Lambda }}_q^{\mathrm{\top }}]\mathrm{and}\\ \hat{V}({\hat{H}}_S)& \approx [{\mathrm{\Lambda }}_{S}J(\hat{\beta },\hat{\alpha }){\mathrm{\Lambda }}_S^{\mathrm{\top }}].\end{array}$Therefore, the two-sided ACIs for $H_{\zeta }$, $H_q$ and $H_S$ at confidence level $100(1-\tau )$, are given, respectively, by $\begin{array}{rl}{\hat{H}}_{\zeta }& \pm z_{\frac{\tau }{2}}\sqrt{\hat{V}({\hat{H}}_{\zeta })},{\hat{H}}_q\pm z_{\frac{\tau }{2}}\sqrt{\hat{V}({\hat{H}}_q)}\mathrm{and}\\ {\hat{H}}_S& \pm z_{\frac{\tau }{2}}\sqrt{\hat{V}({\hat{H}}_S)},\end{array}$where $z_{\frac{\tau }{2}}$ is the $100(1-\tau /2)$ standard normal percentile.

4. Estimation of entropies using MPS method

Cheng and Amin [20] introduced the MPS method and many other authors used this method because the MPS estimators (MPSEs) retain most of the properties of the MLEs including the invariance property, see [21,22]. For more details about the MPS method, one can refer to [23–26]. Based on a PT-IIC sample, the MPS function can be written according to [27] as follows (17) $p(\mathrm{\Omega })=\prod _{i=1}^{m+1}[F(x_i)-F(x_{i-1})]\prod _{i=1}^m{[1-F(x_i)]}^{R_i}.$(17)

4.1. MPS estimation

The MPS function of the IW distribution can be obtained from (4(4) $f(x;\beta ,\alpha )=\alpha \beta x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(4) ), (5(5) $F(x;\beta ,\alpha )=e^{-\alpha x^{-\beta }},x\ge 0,\beta ,\alpha >0,$(5) ) and (17(17) $p(\mathrm{\Omega })=\prod _{i=1}^{m+1}[F(x_i)-F(x_{i-1})]\prod _{i=1}^m{[1-F(x_i)]}^{R_i}.$(17) ) as follows (18) $p(\mathrm{\Omega })=\prod _{i=1}^{m+1}(e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }})\prod _{i=1}^m{(1-e^{-\alpha x_i^{-\beta }})}^{R_i}.$(18) The natural logarithm of (18(18) $p(\mathrm{\Omega })=\prod _{i=1}^{m+1}(e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }})\prod _{i=1}^m{(1-e^{-\alpha x_i^{-\beta }})}^{R_i}.$(18) ), denoted by $P(\mathrm{\Omega })=\log p(\mathrm{\Omega })$, takes the form (19) $\begin{array}{rl}P(\mathrm{\Omega })& =\sum _{i=1}^{m+1}\log (e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }})\\ & +\sum _{i=1}^m{R}_i\log (1-e^{-\alpha x_i^{-\beta }}).\end{array}$(19) The MPSEs of α and β, denoted by $\tilde{\alpha }$ and $\tilde{\beta }$, respectively, are obtained by solving the following normal equations simultaneously (20) $\begin{array}{rl}\frac{\mathrm{\partial }P(\mathrm{\Omega })}{\mathrm{\partial }\alpha }& =\sum _{i=1}^m\frac{R_i{x}_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}\\ & +\sum _{i=1}^{m+1}\frac{x_{i-1}^{-\beta }{e}^{-\alpha x_{i-1}^{-\beta }}-x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }}}=0\end{array}$(20) and (21) $\begin{array}{rl}\frac{\mathrm{\partial }P(\mathrm{\Omega })}{\mathrm{\partial }\beta }& =-\sum _{i=1}^m\frac{\alpha R_i{x}_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}\\ & +\alpha \sum _{i=1}^{m+1}\frac{\begin{array}{c}{x}_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}\\ -x_{i-1}^{-\beta }\log \left(x_{i-1}\right)e^{-\alpha x_{i-1}^{-\beta }}\end{array}}{e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }}}=0.\end{array}$(21) Any numerical method can be implemented to get $\tilde{\alpha }$ and $\tilde{\beta }$ from (20(20) $\begin{array}{rl}\frac{\mathrm{\partial }P(\mathrm{\Omega })}{\mathrm{\partial }\alpha }& =\sum _{i=1}^m\frac{R_i{x}_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}\\ & +\sum _{i=1}^{m+1}\frac{x_{i-1}^{-\beta }{e}^{-\alpha x_{i-1}^{-\beta }}-x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }}}=0\end{array}$(20) ) and (21(21) $\begin{array}{rl}\frac{\mathrm{\partial }P(\mathrm{\Omega })}{\mathrm{\partial }\beta }& =-\sum _{i=1}^m\frac{\alpha R_i{x}_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}}{1-e^{-\alpha x_i^{-\beta }}}\\ & +\alpha \sum _{i=1}^{m+1}\frac{\begin{array}{c}{x}_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}\\ -x_{i-1}^{-\beta }\log \left(x_{i-1}\right)e^{-\alpha x_{i-1}^{-\beta }}\end{array}}{e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }}}=0.\end{array}$(21) ), respectively. Utilizing the invariance property of the MPSEs, the MPSEs of the entropies $H_{\zeta }$, $H_q$ and $H_S$ can be acquired from (6(6) $\begin{array}{rl}{H}_{\zeta }& =\frac{1}{1-\zeta }\log \left({\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^{\zeta }\mathrm{d}x\right)\\ & =\log \left(\frac{1}{\beta }\right)+\frac{1}{\beta }\log \left(\zeta \alpha \right)-\frac{\zeta }{1-\zeta }\log (\zeta )\\ & +\frac{\log \left(\mathrm{\Gamma }(\frac{1}{\beta }(\zeta -1)+\zeta )\right)}{1-\zeta },\end{array}$(6) ), (7(7) $\begin{array}{rl}{H}_q& =\frac{1}{q-1}[1-{\int }_0^{\mathrm{\infty }}{\left(\beta \alpha x^{-(\beta +1)}{e}^{-\alpha x^{-\beta }}\right)}^q\mathrm{d}x]\\ & =\frac{1}{q-1}[1-{\left(\frac{\beta }{{\alpha }^{\frac{1}{\beta }}}\right)}^{q-1}\frac{\mathrm{\Gamma }(\frac{1}{\beta }(q-1)+q)}{q^{(\frac{1}{\beta }(q-1)+q)}}],\end{array}$(7) ) and (8(8) $\begin{array}{rl}{H}_S& =-\log (\beta \alpha ){\int }_0^{\mathrm{\infty }}{e}^{-y}\mathrm{d}y-(\beta +1){\int }_0^{\mathrm{\infty }}\frac{1}{\beta }{e}^{-y}\\ & \times \log \left(\frac{y}{\alpha }\right)\mathrm{d}y+{\int }_0^{\mathrm{\infty }}y{e}^{-y}\mathrm{d}y\\ & =-\log (\beta \alpha )+\frac{(\beta +1)}{\beta }(\gamma +\log (\alpha ))+1,\end{array}$(8) ), respectively, as $\begin{array}{rl}{\tilde{H}}_{\zeta }& =\ln \tilde{\beta }+\frac{1}{\tilde{\beta }}\log \left(\frac{\zeta }{\tilde{\alpha }}\right)-\frac{\zeta }{1-\zeta }\log (\zeta )\\ & +\frac{\log \left(\mathrm{\Gamma }(\frac{1}{\tilde{\beta }}(\zeta -1)+\zeta )\right)}{1-\zeta },\end{array}$with $\zeta \ge 0$, $\zeta \ne 1$ and $\zeta \ge \frac{1}{1+\tilde{\beta }}$, ${\tilde{H}}_q=\frac{1}{q-1}[1-{\left(\frac{\tilde{\beta }}{{\tilde{\alpha }}^{\frac{1}{\tilde{\beta }}}}\right)}^{q-1}\frac{\mathrm{\Gamma }(\frac{1}{\tilde{\beta }}(q-1)+q)}{q^{(\frac{1}{\tilde{\beta }}(q-1)+q)}}],$with $q\ge 0$, $q\ne 1$ and $q\ge \frac{1}{1+\tilde{\beta }}$, and ${\tilde{H}}_S=-\log (\tilde{\beta }\tilde{\alpha })+\frac{(\tilde{\beta }+1)}{\tilde{\beta }}(\gamma +\log (\tilde{\alpha }))+1.$

4.2. ACIs using MPSEs

In order to construct the ACIs of $H_{\zeta }$, $H_q$ and $H_S$, we first obtain the approximate asymptotic VC matrix based on the MPSEs as follows (22) $J(\tilde{\beta },\tilde{\alpha })={\left(\begin{array}{cc}-{\displaystyle \frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }{\alpha }^2}}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}\\ -{\displaystyle \frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }}& -{\displaystyle \frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }{\beta }^2}}\end{array}\right)}_{\alpha =\tilde{\alpha },\beta =\tilde{\beta }}^{-1}$(22) The second derivatives of the (19(19) $\begin{array}{rl}P(\mathrm{\Omega })& =\sum _{i=1}^{m+1}\log (e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }})\\ & +\sum _{i=1}^m{R}_i\log (1-e^{-\alpha x_i^{-\beta }}).\end{array}$(19) ) with respect to α and β are given by $\begin{array}{rl}\frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }{\alpha }^2}& =\sum _{i=1}^{m+1}[\frac{{\left({\eta }_i\right)}_{\alpha \alpha }}{{\eta }_i}-\frac{{\left({\eta }_i\right)}_{\alpha }^2}{{\eta }_i^2}]\\ & -\sum _{i=1}^m{R}_i{x}_i^{-2\beta }{e}^{-\alpha x_i^{-\beta }}\left(\frac{{\zeta }_i+e^{-\alpha x_i^{-\beta }}}{{\zeta }_i^2}\right),\\ \frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }{\beta }^2}& =\sum _{i=1}^m\alpha R_i{x}_i^{-\beta }{\log }^2\left(x_i\right)e^{-\alpha x_i^{-\beta }}\\ & \times (\frac{1-\alpha x_i^{-\beta }}{{\zeta }_i}-\frac{\alpha x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{{\zeta }_i^2})\\ & -\sum _{i=1}^{m+1}[\frac{{\left({\eta }_i\right)}_{\beta \beta }}{{\eta }_i}+{\left(\frac{\alpha {\left({\eta }_i\right)}_{\beta }}{{\eta }_i}\right)}^2]\end{array}$and $\begin{array}{rl}\frac{{\mathrm{\partial }}^{2}P(\mathrm{\Omega })}{\mathrm{\partial }\beta \mathrm{\partial }\alpha }& =\sum _{i=1}^m{R}_i{x}_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}\\ & \times (\frac{\alpha x_i^{-\beta }-1}{{\zeta }_i}+\frac{\alpha x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }}}{{\zeta }_i^2})\\ & +\sum _{i=1}^{m+1}[\frac{{\left({\eta }_i\right)}_{\alpha \beta }}{{\eta }_i}-\frac{\alpha {\left({\eta }_i\right)}_{\alpha }{\left({\eta }_i\right)}_{\beta }}{{\eta }_i^2}],\end{array}$where $\begin{array}{rl}{\eta }_i& \equiv {\eta }_i(\alpha ,\beta )=e^{-\alpha x_i^{-\beta }}-e^{-\alpha x_{i-1}^{-\beta }},\\ {\zeta }_i& \equiv {\zeta }_i(\alpha ,\beta )=1-e^{-\alpha x_i^{-\beta }},\\ {\left({\eta }_i\right)}_{\alpha }& \equiv \frac{\mathrm{\partial }{\eta }_i(\alpha ,\beta )}{\mathrm{\partial }\alpha }=x_{i-1}^{-\beta }{e}^{-\alpha x_{i-1}^{-\beta }}-x_i^{-\beta }{e}^{-\alpha x_i^{-\beta }},\\ {\left({\eta }_i\right)}_{\alpha \alpha }& \equiv \frac{{\mathrm{\partial }}^2{\eta }_i(\alpha ,\beta )}{\mathrm{\partial }{\alpha }^2}=x_i^{-2\beta }{e}^{-\alpha x_i^{-\beta }}\\ & -x_{i-1}^{-2\beta }{e}^{-\alpha x_{i-1}^{-\beta }},\\ {\left({\eta }_i\right)}_{\beta }& \equiv \frac{\mathrm{\partial }{\eta }_i(\alpha ,\beta )}{\mathrm{\partial }\beta }=x_i^{-\beta }\log \left(x_i\right)e^{-\alpha x_i^{-\beta }}\\ & -x_{i-1}^{-\beta }\log \left(x_{i-1}\right)e^{-\alpha x_{i-1}^{-\beta }},\\ {\left({\eta }_i\right)}_{\alpha \beta }& \equiv \frac{{\mathrm{\partial }}^2{\eta }_i(\alpha ,\beta )}{\mathrm{\partial }\alpha \mathrm{\partial }\beta }\\ & =x_{i-1}^{-\beta }\log \left(x_{i-1}\right)e^{-\alpha x_{i-1}^{-\beta }}(\alpha x_{i-1}^{-\beta }-1)\\ & -x_i^{-\beta }\log \left(x_i\right)(\alpha x_i^{-\beta }-1)\end{array}$and $\begin{array}{rl}{\left({\eta }_i\right)}_{\beta \beta }& \equiv \frac{{\mathrm{\partial }}^2{\eta }_i(\alpha ,\beta )}{\mathrm{\partial }{\beta }^2}\\ & =\alpha x_{i-1}^{-\beta }{\log }^2\left(x_{i-1}\right)e^{-\alpha x_{i-1}^{-\beta }}(\alpha x_{i-1}^{-\beta }-1)\\ & -\alpha x_i^{-\beta }{\log }^2\left(x_i\right)(\alpha x_i^{-\beta }-1).\end{array}$Now, we use the delta method to approximate the variances of $H_{\zeta }$, $H_q$ and $H_S$. We first obtain the quantities $\begin{array}{rl}{\mathrm{\Lambda }}_{\zeta }& =(\mathrm{\partial }{H}_{\zeta }/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_{\zeta }/\mathrm{\partial }\beta ){|}_{(\alpha ,\beta )=(\tilde{\alpha },\tilde{\beta })},\\ {\mathrm{\Lambda }}_q& =(\mathrm{\partial }{H}_q/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_q/\mathrm{\partial }\beta ){|}_{(\alpha ,\beta )=(\tilde{\alpha },\tilde{\beta })}\end{array}$and ${\mathrm{\Lambda }}_S=(\mathrm{\partial }{H}_S/\mathrm{\partial }\alpha ,\mathrm{\partial }{H}_S/\mathrm{\partial }\beta ){|}_{(\alpha ,\beta )=(\tilde{\alpha },\tilde{\beta })}$, where the elements of these quantities are given by (14(14) $\begin{array}{rl}\frac{\mathrm{\partial }{H}_{\zeta }}{\mathrm{\partial }\alpha }& =-\frac{1}{\beta \alpha },\\ \frac{\mathrm{\partial }{H}_{\zeta }}{\mathrm{\partial }\beta }& =\frac{1}{\beta }-\frac{1}{{\beta }^2}[\log \left(\frac{\zeta }{\alpha }\right)-\psi (\frac{1}{\beta }(\zeta -1)+\zeta )],\end{array}$(14) )–(16(16) $\begin{array}{rl}\frac{\mathrm{\partial }{H}_S}{\mathrm{\partial }\alpha }& =\frac{\beta +1}{\alpha \beta }-\frac{1}{\alpha },\\ \frac{\mathrm{\partial }{H}_S}{\mathrm{\partial }\beta }& =-\frac{(\beta +1)(\log (\alpha )+\gamma )}{{\beta }^2}+\frac{\log (\alpha )+\gamma }{\beta }-\frac{1}{\beta }\end{array}$(16) ). Therefore, the approximates variances of $H_{\zeta }$, $H_q$ and $H_S$ can be computed, respectively, as $\begin{array}{rl}\tilde{V}({\hat{H}}_{\zeta })& \approx [{\mathrm{\Lambda }}_{\zeta }J(\tilde{\beta },\tilde{\alpha }){\mathrm{\Lambda }}_{\zeta }^{\mathrm{\top }}],\\ \tilde{V}({\hat{H}}_q)& \approx [{\mathrm{\Lambda }}_{q}J(\tilde{\beta },\tilde{\alpha }){\mathrm{\Lambda }}_q^{\mathrm{\top }}]\mathrm{and}\\ \tilde{V}({\hat{H}}_S)& \approx [{\mathrm{\Lambda }}_{S}J(\tilde{\beta },\tilde{\alpha }){\mathrm{\Lambda }}_S^{\mathrm{\top }}].\end{array}$Several authors have elicited the asymptotic equivalence of the MPS and ML methods, Refs. [20,22,28] revealed that the MPS method also exhibits asymptotic properties like the ML method. One can also refer to [29]. Therefore, the two-sided ACIs for $H_{\zeta }$, $H_q$ and $H_S$ at confidence level $100(1-\tau )$, are given, respectively, by $\begin{array}{rl}{\tilde{H}}_{\zeta }& \pm z_{\frac{\tau }{2}}\sqrt{\tilde{V}({\tilde{H}}_{\zeta })},{\tilde{H}}_q\pm z_{\frac{\tau }{2}}\sqrt{\tilde{V}({\tilde{H}}_q)}\mathrm{and}\\ {\tilde{H}}_S& \pm z_{\frac{\tau }{2}}\sqrt{\tilde{V}({\tilde{H}}_S)}.\end{array}$

5. Monte Carlo simulation

To investigate the behaviour of $H_{\zeta }$, $H_q$ and $H_S$, an extensive Monte Carlo simulation study is conducted. Using different combinations of n, m and $R$, we generate 1,000 PT-IIC samples under two sets of the true value of $\text{IW}(\alpha ,\beta )$ such as $\text{IW}(3,3)$ (Set-1) and $\text{IW}(5,5)$ (Set-2). Further, to estimate $H_{\zeta }$ and $H_q$, two different choices of ζ and q are used namely, $\zeta =q=0.4$ and $\zeta =q=0.8$. The true values of $H_{\zeta }$ and $H_q$ based on Set-1 and 2 are $H_{\zeta }=(2.1130,1.1940)$, $H_{\zeta }=(1.0870,0.5231)$, $H_q=(4.2560,1.3490)$ and $H_q=(1.5340,0.5515)$, respectively. Also, three censoring schemes (Schs) are also considered as $\begin{array}{rl}& \text{Sch-I}:R_1=n-m,R_i=0\text{for}i\ne 1,\\ & \text{Sch-II}:R_{\frac{m}{2}}=n-m,R_i=0\text{for}i\ne m/2,\\ & \text{Sch-III}:R_m=n-m,R_i=0\text{for}i\ne m.\end{array}$For each setting, the root mean square errors (RMSEs) and relative absolute biases (RABs) are computed for each entropy measure and reported in Tables 1 and 2. Also, the confidence lengths (CLs) as well as the coverage probabilities (CPs) of these measures are also obtained and presented in Tables 3 and 4. We refer to the RE entropy as $H_{\zeta }^{\ast }$ and to QE as $H_q^{\star }$ in the simulation and real data outcomes. All numerical computations are implemented via “maxLik” package, proposed by [30], in the $\mathcal{R}$ statistical programming language software which using Newton-Raphson method of maximization in the computations.

Table 1. Average RMSEs and RABs (in parentheses) of $H_S$, $H_{\zeta }$ and $H_q$ for $(\alpha ,\beta )=(3,3)$.

			MLE			MPSE
n	m	Entropy	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
20	10	$H_S$	0.371 (0.281)	0.387 (0.292)	0.395 (0.299)	0.524 (0.407)	0.441 (0.333)	0.448 (0.340)
		$H_{0.4}^{\ast }$	0.669 (0.247)	0.691 (0.258)	0.696 (0.262)	0.837 (0.333)	0.733 (0.281)	0.746 (0.288)
		$H_{0.8}^{\ast }$	0.395 (0.260)	0.412 (0.271)	0.420 (0.277)	0.554 (0.376)	0.468 (0.308)	0.475 (0.314)
		$H_{0.4}^{\star }$	3.338 (0.446)	2.908 (0.457)	2.751 (0.452)	2.459 (0.478)	2.338 (0.435)	2.482 (0.447)
		$H_{0.8}^{\star }$	0.486 (0.286)	0.502 (0.297)	0.512 (0.303)	0.651 (0.399)	0.559 (0.331)	0.567 (0.338)
	15	$H_S$	0.298 (0.230)	0.306 (0.232)	0.291 (0.221)	0.384 (0.296)	0.328 (0.251)	0.330 (0.253)
		$H_{0.4}^{\ast }$	0.550 (0.204)	0.553 (0.208)	0.530 (0.199)	0.640 (0.249)	0.568 (0.219)	0.584 (0.224)
		$H_{0.8}^{\ast }$	0.318 (0.214)	0.327 (0.216)	0.311 (0.206)	0.408 (0.274)	0.350 (0.233)	0.353 (0.235)
		$H_{0.4}^{\star }$	3.145 (0.373)	2.103 (0.359)	1.995 (0.348)	1.879 (0.370)	1.891 (0.349)	2.070 (0.367)
		$H_{0.8}^{\star }$	0.396 (0.237)	0.404 (0.238)	0.386 (0.227)	0.490 (0.295)	0.426 (0.254)	0.431 (0.257)
40	20	$H_S$	0.243 (0.189)	0.259 (0.198)	0.256 (0.195)	0.323 (0.251)	0.335 (0.259)	0.274 (0.210)
		$H_{0.4}^{\ast }$	0.450 (0.170)	0.466 (0.177)	0.475 (0.176)	0.546 (0.213)	0.563 (0.220)	0.480 (0.185)
		$H_{0.8}^{\ast }$	0.268 (0.180)	0.274 (0.180)	0.275 (0.182)	0.344 (0.233)	0.357 (0.240)	0.292 (0.196)
		$H_{0.4}^{\star }$	1.774 (0.309)	1.670 (0.305)	1.896 (0.310)	1.658 (0.327)	1.704 (0.336)	1.602 (0.304)
		$H_{0.8}^{\star }$	0.336 (0.200)	0.342 (0.201)	0.342 (0.202)	0.417 (0.253)	0.431 (0.260)	0.359 (0.215)
	30	$H_S$	0.209 (0.161)	0.209 (0.161)	0.196 (0.150)	0.243 (0.189)	0.251 (0.193)	0.220 (0.169)
		$H_{0.4}^{\ast }$	0.381 (0.145)	0.386 (0.146)	0.368 (0.138)	0.425 (0.166)	0.439 (0.170)	0.393 (0.151)
		$H_{0.8}^{\ast }$	0.219 (0.146)	0.230 (0.152)	0.224 (0.148)	0.259 (0.176)	0.268 (0.180)	0.236 (0.158)
		$H_{0.4}^{\star }$	1.357 (0.252)	1.408 (0.256)	1.374 (0.244)	1.349 (0.265)	1.372 (0.269)	1.310 (0.250)
		$H_{0.8}^{\star }$	0.277 (0.164)	0.289 (0.170)	0.282 (0.165)	0.319 (0.193)	0.329 (0.197)	0.292 (0.174)
80	40	$H_S$	0.176 (0.134)	0.184 (0.140)	0.181 (0.136)	0.207 (0.163)	0.219 (0.169)	0.185 (0.140)
		$H_{0.4}^{\ast }$	0.325 (0.122)	0.340 (0.128)	0.340 (0.124)	0.365 (0.143)	0.381 (0.147)	0.337 (0.127)
		$H_{0.8}^{\ast }$	0.183 (0.121)	0.185 (0.123)	0.188 (0.124)	0.222 (0.151)	0.234 (0.157)	0.198 (0.131)
		$H_{0.4}^{\star }$	1.207 (0.216)	1.243 (0.225)	1.318 (0.219)	1.175 (0.231)	1.197 (0.234)	1.157 (0.214)
		$H_{0.8}^{\star }$	0.231 (0.136)	0.232 (0.138)	0.236 (0.138)	0.274 (0.167)	0.288 (0.173)	0.247 (0.145)
	60	$H_S$	0.140 (0.109)	0.144 (0.111)	0.142 (0.108)	0.160 (0.125)	0.157 (0.121)	0.140 (0.109)
		$H_{0.4}^{\ast }$	0.260 (0.099)	0.268 (0.101)	0.265 (0.099)	0.291 (0.113)	0.284 (0.109)	0.259 (0.099)
		$H_{0.8}^{\ast }$	0.148 (0.098)	0.154 (0.103)	0.153 (0.101)	0.172 (0.117)	0.169 (0.113)	0.151 (0.101)
		$H_{0.4}^{\star }$	0.946 (0.175)	0.958 (0.177)	0.978 (0.176)	0.970 (0.188)	0.938 (0.180)	0.896 (0.170)
		$H_{0.8}^{\star }$	0.187 (0.110)	0.195 (0.116)	0.193 (0.113)	0.214 (0.129)	0.210 (0.125)	0.189 (0.113)

Table 2. Average RMSEs and RABs (in parentheses) of $H_S$, $H_{\zeta }$ and $H_q$ for $(\alpha ,\beta )=(5,5)$.

			MLE			MPSE
n	m	Entropy	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
20	10	$H_S$	0.332 (0.648)	0.355 (0.689)	0.358 (0.692)	0.472 (0.946)	0.510 (1.013)	0.403 (0.786)
		$H_{0.4}^{\ast }$	0.436 (0.319)	0.462 (0.338)	0.468 (0.341)	0.594 (0.451)	0.635 (0.479)	0.517 (0.382)
		$H_{0.8}^{\ast }$	0.344 (0.520)	0.367 (0.553)	0.371 (0.556)	0.487 (0.757)	0.525 (0.810)	0.416 (0.630)
		$H_{0.4}^{\star }$	0.816 (0.436)	0.825 (0.430)	0.848 (0.437)	0.911 (0.511)	0.953 (0.534)	0.866 (0.461)
		$H_{0.8}^{\star }$	0.371 (0.537)	0.391 (0.567)	0.396 (0.570)	0.504 (0.754)	0.539 (0.803)	0.438 (0.638)
	15	$H_S$	0.282 (0.524)	0.267 (0.527)	0.265 (0.518)	0.360 (0.720)	0.309 (0.602)	0.308 (0.607)
		$H_{0.4}^{\ast }$	0.355 (0.261)	0.356 (0.263)	0.351 (0.258)	0.462 (0.350)	0.401 (0.296)	0.402 (0.298)
		$H_{0.8}^{\ast }$	0.278 (0.421)	0.227 (0.424)	0.275 (0.417)	0.372 (0.578)	0.320 (0.483)	0.319 (0.487)
		$H_{0.4}^{\star }$	0.656 (0.341)	0.664 (0.345)	0.642 (0.335)	0.749 (0.414)	0.680 (0.366)	0.693 (0.369)
		$H_{0.8}^{\star }$	0.302 (0.437)	0.301 (0.440)	0.298 (0.432)	0.392 (0.584)	0.340 (0.494)	0.341 (0.498)
40	20	$H_S$	0.210 (0.413)	0.229 (0.445)	0.224 (0.439)	0.277 (0.547)	0.305 (0.610)	0.254 (0.497)
		$H_{0.4}^{\ast }$	0.282 (0.207)	0.305 (0.222)	0.224 (0.439)	0.360 (0.268)	0.392 (0.297)	0.334 (0.246)
		$H_{0.8}^{\ast }$	0.225 (0.342)	0.244 (0.372)	0.236 (0.352)	0.287 (0.439)	0.315 (0.490)	0.263 (0.399)
		$H_{0.4}^{\star }$	0.535 (0.277)	0.570 (0.294)	0.558 (0.292)	0.607 (0.330)	0.647 (0.358)	0.584 (0.312)
		$H_{0.8}^{\star }$	0.246 (0.357)	0.266 (0.386)	0.256 (0.365)	0.306 (0.449)	0.334 (0.498)	0.283 (0.411)
	30	$H_S$	0.177 (0.347)	0.228 (0.446)	0.180 (0.352)	0.221 (0.439)	0.225 (0.445)	0.201 (0.392)
		$H_{0.4}^{\ast }$	0.240 (0.175)	0.302 (0.222)	0.241 (0.177)	0.291 (0.217)	0.296 (0.220)	0.267 (0.196)
		$H_{0.8}^{\ast }$	0.182 (0.276)	0.195 (0.290)	0.187 (0.279)	0.229 (0.353)	0.234 (0.358)	0.208 (0.316)
		$H_{0.4}^{\star }$	0.464 (0.237)	0.553 (0.290)	0.447 (0.235)	0.291 (0.217)	0.296 (0.220)	0.474 (0.251)
		$H_{0.8}^{\star }$	0.199 (0.288)	0.213 (0.302)	0.204 (0.292)	0.247 (0.363)	0.251 (0.368)	0.226 (0.326)
80	40	$H_S$	0.148 (0.288)	0.162 (0.314)	0.156 (0.304)	0.178 (0.349)	0.184 (0.360)	0.160 (0.313)
		$H_{0.4}^{\ast }$	0.199 (0.144)	0.216 (0.157)	0.210 (0.153)	0.234 (0.173)	0.243 (0.178)	0.214 (0.157)
		$H_{0.8}^{\ast }$	0.150 (0.228)	0.161 (0.246)	0.155 (0.235)	0.184 (0.281)	0.191 (0.290)	0.167 (0.252)
		$H_{0.4}^{\star }$	0.379 (0.195)	0.401 (0.208)	0.401 (0.206)	0.413 (0.221)	0.427 (0.227)	0.389 (0.205)
		$H_{0.8}^{\star }$	0.166 (0.239)	0.178 (0.257)	0.170 (0.246)	0.199 (0.290)	0.207 (0.299)	0.182 (0.262)
	60	$H_S$	0.124 (0.247)	0.132 (0.261)	0.126 (0.252)	0.140 (0.275)	0.146 (0.289)	0.131 ( 0.255)
		$H_{0.4}^{\ast }$	0.168 (0.124)	0.179 (0.132)	0.171 (0.127)	0.186 (0.138)	0.196 (0.145)	0.177 (0.128)
		$H_{0.8}^{\ast }$	0.122 (0.186)	0.132 (0.202)	0.128 (0.193)	0.145 (0.222)	0.152 (0.233)	0.137 (0.205)
		$H_{0.4}^{\star }$	0.321 (0.167)	0.340 (0.178)	0.324 (0.171)	0.333 (0.178)	0.352 (0.188)	0.324 (0.169)
		$H_{0.8}^{\star }$	0.135 (0.195)	0.145 (0.212)	0.141 (0.202)	0.158 (0.230)	0.152 (0.233)	0.149 (0.214)

Table 3. The ACLs of $H_S$, $H_{\zeta }$ and $H_q$ with their CPs in parentheses, when $(\alpha ,\beta )=(3,3)$.

			ACI-LF			ACI-MPS
n	m	Entropy	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
20	10	$H_S$	0.571 (0.794)	0.543 (0.820)	0.516 (0.852)	0.568 (0.807)	0.788 (0.803)	0.733 (0.795)
		$H_{0.4}^{\ast }$	0.668 (0.804)	0.614 (0.834)	0.558 (0.866)	0.614 (0.815)	0.860 (0.812)	0.807 (0.808)
		$H_{0.8}^{\ast }$	0.904 (0.843)	0.894 (0.847)	0.830 (0.870)	1.112 (0.835)	1.642 (0.825)	1.671 (0.818)
		$H_{0.4}^{\star }$	10.98 (0.818)	10.16 (0.825)	8.979 (0.865)	7.193 (0.825)	16.13 (0.820)	14.52 (0.814)
		$H_{0.8}^{\star }$	1.743 (0.888)	1.705 (0.863)	1.568 (0.874)	1.836 (0.832)	3.035 (0.828)	2.986 (0.819)
	15	$H_S$	0.438 (0.860)	0.425 (0.865)	0.417 (0.885)	0.362 (0.846)	0.898 (0.843)	0.897 (0.842)
		$H_{0.4}^{\ast }$	0.525 (0.845)	0.470 (0.862)	0.469 (0.892)	0.438 (0.833)	1.004 (0.829)	1.085 (0.827)
		$H_{0.8}^{\ast }$	0.746 (0.863)	0.728 (0.877)	0.705 (0.903)	0.838 (0.849)	2.302 (0.840)	2.523 (0.843)
		$H_{0.4}^{\star }$	8.944 (0.849)	7.378 (0.870)	7.359 (0.888)	5.417 (0.843)	21.20 (0.837)	21.66 (0.835)
		$H_{0.8}^{\star }$	1.464 (0.896)	1.403 (0.900)	1.379 (0.906)	1.396 (0.860)	4.266 (0.851)	4.629 (0.853)
40	20	$H_S$	0.343 (0.884)	0.325 (0.888)	0.304 (0.908)	0.312 (0.891)	0.327 (0.887)	0.512 (0.890)
		$H_{0.4}^{\ast }$	0.408 (0.885)	0.339 (0.896)	0.328 (0.916)	0.347 (0.895)	0.361 (0.890)	0.451 (0.894)
		$H_{0.8}^{\ast }$	0.640 (0.891)	0.641 (0.899)	0.598 (0.918)	0.773 (0.901)	0.892 (0.898)	1.352 (0.900)
		$H_{0.4}^{\star }$	6.814 (0.897)	6.244 (0.900)	5.990 (0.910)	5.249 (0.910)	6.478 (0.906)	11.74 (0.903)
		$H_{0.8}^{\star }$	1.267 (0.916)	1.247 (0.914)	1.154 (0.920)	1.334 (0.918)	1.568 (0.915)	2.508 (0.912)
	30	$H_S$	0.277 (0.893)	0.267 (0.901)	0.258 (0.912)	0.255 (0.904)	0.260 (0.900)	0.657 (0.901)
		$H_{0.4}^{\ast }$	0.318 (0.895)	0.296 (0.905)	0.295 (0.920)	0.269 (0.912)	0.264 (0.908)	0.607 (0.899)
		$H_{0.8}^{\ast }$	0.526 (0.898)	0.520 (0.915)	0.500 (0.922)	0.602 (0.923)	0.656 (0.916)	1.962 (0.913)
		$H_{0.4}^{\star }$	5.185 (0.903)	5.139 (0.919)	5.062 (0.925)	4.182 (0.920)	4.717 (0.915)	16.83 (0.918)
		$H_{0.8}^{\star }$	1.056 (0.922)	1.027 (0.928)	0.993 (0.929)	1.044 (0.928)	1.149 (0.921)	3.707 (0.920)
80	40	$H_S$	0.230 (0.899)	0.214 (0.908)	0.206 (0.911)	0.215 (0.914)	0.218 (0.909)	0.429 (0.912)
		$H_{0.4}^{\ast }$	0.265 (0.894)	0.212 (0.903)	0.204 (0.917)	0.204 (0.911)	0.214 (0.908)	0.295 (0.910)
		$H_{0.8}^{\ast }$	0.451 (0.902)	0.456 (0.911)	0.427 (0.921)	0.518 (0.920)	0.597 (0.913)	1.063 (0.923)
		$H_{0.4}^{\star }$	4.586 (0.910)	4.388 (0.912)	4.159 (0.913)	3.743 (0.923)	4.427 (0.919)	9.626 (0.917)
		$H_{0.8}^{\star }$	0.903 (0.924)	0.889 (0.923)	0.833 (0.926)	0.915 (0.929)	1.072 (0.924)	2.015 (0.925)
	60	$H_S$	0.187 (0.917)	0.178 (0.918)	0.174 (0.922)	0.196 (0.919)	0.198 (0.912)	0.555 (0.915)
		$H_{0.4}^{\ast }$	0.218 (0.927)	0.190 (0.925)	0.192 (0.926)	0.174 (0.925)	0.161 (0.923)	0.413 (0.918)
		$H_{0.8}^{\ast }$	0.371 (0.929)	0.368 (0.928)	0.354 (0.932)	0.419 (0.933)	0.454 (0.931)	1.680 (0.935)
		$H_{0.4}^{\star }$	3.736 (0.928)	3.557 (0.927)	3.510 (0.935)	3.100 (0.937)	3.451 (0.930)	14.91 (0.934)
		$H_{0.8}^{\star }$	0.747 (0.944)	0.728 (0.930)	0.354 (0.942)	0.743 (0.953)	0.815 (0.940)	3.246 (0.949)

Table 4. The ACLs of $H_S$, $H_{\zeta }$ and $H_q$ with their CPs in parentheses, when $(\alpha ,\beta )=(5,5)$.

			ACI-LF			ACI-MPS
n	m	Entropy	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
20	10	$H_S$	1.189 (0.877)	1.006 (0.885)	0.928 (0.905)	0.805 (0.887)	0.581 (0.908)	0.632 (0.905)
		$H_{0.4}^{\ast }$	0.550 (0.864)	0.496 (0.878)	0.455 (0.908)	0.541 (0.875)	0.462 (0.899)	0.551 (0.892)
		$H_{0.8}^{\ast }$	1.189 (0.884)	0.745 (0.900)	0.688 (0.910)	0.683 (0.883)	0.582 (0.903)	0.753 (0.893)
		$H_{0.4}^{\star }$	2.781 (0.856)	2.341 (0.883)	2.224 (0.903)	1.574 (0.880)	1.332 (0.900)	2.086 (0.896)
		$H_{0.8}^{\star }$	1.218 (0.877)	1.048 (0.897)	0.976 (0.907)	0.857 (0.904)	0.727 (0.914)	0.998 (0.909)
	15	$H_S$	1.036 (0.898)	0.923 (0.892)	0.934 (0.896)	0.502 (0.904)	1.001 (0.924)	1.006 (0.919)
		$H_{0.4}^{\ast }$	0.463 (0.874)	0.423 (0.881)	0.425 (0.889)	0.443 (0.899)	0.822 (0.930)	0.825 (0.923)
		$H_{0.8}^{\ast }$	0.727 (0.880)	0.661 (0.903)	0.662 (0.914)	0.564 (0.922)	1.157 (0.935)	1.171 (0.925)
		$H_{0.4}^{\star }$	2.370 (0.866)	2.161 (0.893)	2.128 (0.908)	1.353 (0.895)	3.287 (0.933)	3.379 (0.920)
		$H_{0.8}^{\star }$	1.053 (0.885)	0.956 (0.901)	0.953 (0.911)	0.718 (0.925)	1.569 (0.939)	1.594 (0.928)
40	20	$H_S$	0.767 (0.889)	0.597 (0.907)	0.557 (0.915)	0.414 (0.916)	0.322 (0.934)	0.326 (0.926)
		$H_{0.4}^{\ast }$	0.390 (0.902)	0.350 (0.911)	0.323 (0.922)	0.393 (0.908)	0.345 (0.932)	0.405 (0.912)
		$H_{0.8}^{\ast }$	0.618 (0.905)	0.540 (0.910)	0.497 (0.925)	0.516 (0.917)	0.448 (0.933)	0.559 (0.919)
		$H_{0.4}^{\star }$	2.039 (0.918)	1.738 (0.915)	1.621 (0.919)	1.322 (0.928)	1.112 (0.934)	1.577 (0.927)
		$H_{0.8}^{\star }$	0.897 (0.920)	0.773 (0.920)	0.710 (0.923)	0.674 (0.934)	0.579 (0.941)	0.753 (0.929)
	30	$H_S$	0.661 (0.895)	0.610 (0.909)	0.591 (0.920)	0.284 (0.921)	0.246 (0.939)	0.573 (0.931)
		$H_{0.4}^{\ast }$	0.323 (0.906)	0.352 (0.917)	0.296 (0.924)	0.323 (0.914)	0.312 (0.938)	0.580 (0.926)
		$H_{0.8}^{\ast }$	0.521 (0.914)	0.474 (0.919)	0.470 (0.927)	0.424 (0.932)	0.410 (0.942)	0.827 (0.938)
		$H_{0.4}^{\star }$	1.747 (0.922)	1.695 (0.921)	1.533 (0.930)	1.099 (0.944)	1.060 (0.948)	2.411 (0.941)
		$H_{0.8}^{\star }$	0.762 (0.929)	0.686 (0.930)	0.687 (0.936)	0.556 (0.962)	0.538 (0.949)	1.137 (0.947)
80	40	$H_S$	0.528 (0.905)	0.401 (0.913)	0.392 (0.921)	0.248 (0.929)	0.183 (0.948)	0.172 (0.937)
		$H_{0.4}^{\ast }$	0.276 (0.912)	0.249 (0.915)	0.248 (0.929)	0.283 (0.914)	0.249 (0.937)	0.285 (0.928)
		$H_{0.8}^{\ast }$	0.445 (0.927)	0.385 (0.924)	0.357 (0.946)	0.378 (0.934)	0.333 (0.943)	0.393 (0.945)
		$H_{0.4}^{\star }$	1.476 (0.945)	1.212 (0.933)	1.241 (0.947)	1.016 (0.959)	0.889 (0.952)	1.109 (0.956)
		$H_{0.8}^{\star }$	0.653 (0.951)	0.555 (0.940)	0.514 (0.950)	0.504 (0.977)	0.442 (0.966)	0.532 (0.961)
	60	$H_S$	0.455 (0.915)	0.385 (0.919)	0.394 (0.926)	0.172 (0.931)	0.149 (0.952)	0.334 (0.940)
		$H_{0.4}^{\ast }$	0.228 (0.939)	0.213 (0.938)	0.208 (0.942)	0.229 (0.942)	0.222 (0.960)	0.392 (0.936)
		$H_{0.8}^{\ast }$	0.371 (0.952)	0.337 (0.940)	0.333 (0.955)	0.306 (0.960)	0.297 (0.975)	0.557 (0.960)
		$H_{0.4}^{\star }$	1.240 (0.968)	1.101 (0.949)	1.096 (0.965)	0.824 (0.970)	0.804 (0.976)	1.624 (0.973)
		$H_{0.8}^{\star }$	0.550 (0.970)	0.492 (0.954)	0.489 (0.972)	0.407 (0.981)	0.396 (0.983)	0.768 (0.980)

For the parameter estimation, the outcomes of the simulation study showed that the ML approach provides better estimates than the MPS approach in terms of minimum RMSEs and RABs. On the other hand, the MPS approach gives more accurate interval estimates in terms of minimum ACLs. From the simulation results established in Tables 1–4, in respect of RMSEs, RABs, ACLs and CPs of the proposed estimates, we can obtain the following considerations. In general, it can be seen that the MLEs and MPSEs of $H_S$, $H_{\zeta }$ and $H_q$ are very good in terms of minimum RMSEs, RABs and ACLs as well as highest CPs. As n (or $m/n$) increases, the RMSEs, RABs and ACLs of all investigated estimates decrease while CPs increase as expected. Therefore, to get better estimation results, one may tend to increase the total (or effective) sample size. As α and β increase, the RMSEs associated with all proposed estimates decrease while the RABs increase. In most cases, when α and β increase, it is observed that the ACLs constructed based on LF and MPS approaches decrease while the corresponding CPs increase. Further, for each setting, it is evident that the RMSEs associated with MLEs decrease for both $H_{\zeta }$ and $H_q$ when ζ and q increase. Similar behaviour is observed in the case of MPSEs of $H_{\zeta }$ and $H_q$. As ζ increases, the corresponding RABs of all estimates increase when $(\alpha ,\beta )=(5,5)$. Also, as q increases, the corresponding RABs of all estimates increase when $(\alpha ,\beta )=(5,5)$ while these decrease when $(\alpha ,\beta )=(3,3)$. In addition, for each test, ζ and q increase, the CPs using both LF and MPS approaches are mostly below (or near to) the specified nominal level.

Comparing the proposed censoring schemes I, II and III, it is observed that the MLEs (based on Scheme-I) and MPSEs (based on Scheme-III) performed better than other censoring schemes in terms of the lowest RMSEs and RABs for both true value sets. Also, the interval estimates, using observed likelihood samples, performed better based on Scheme-III compared to the other censoring schemes in terms of the shortest ACLs and highest CPs. It is also noted that the ACI estimates using the MPS approach worked effectively based on censoring schemes I and II when $(\alpha ,\beta )$ taken as $(3,3)$ and $(5,5)$, respectively. To sum up, simulation results showed that the likelihood approach has performed superior to the other in the case of point estimation while the product of spacings approach has performed superior to the other in the case of interval estimation.

6. Real-life applications

To show the adaptability and flexibility of the proposed methodologies to a real phenomenon, we shall provide two numerical applications using real-life data sets in this section. The first data set (referred to as Data-I) represents the vinyl chloride data (in mg/L) obtained from clean-up-gradient monitoring wells. The data was first used by [31] and recently analysed by [32]. The second data set (referred to as Data-II) shows the times (in min) to breakdown of an insulating fluid between 19 electrodes recorded at 34 kV. The Data-II was reported by [33] and recently analysed by [34,35]. The ordered values of Data-I and -II are presented in Table 5.

Table 5. The real data sets.

Data	Size	Items
I	34	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5,
		0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2, 1.3,
		1.8, 2.0, 2.0, 2.3, 2.4, 2.5, 2.7, 2.9, 3.2, 4.0,
		5.1, 5.3, 6.8, 8.0
II	19	0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67, 4.85, 6.50,
		7.35, 8.01, 8.27, 12.06, 31.75, 32.52, 33.91, 36.71, 72.89

We first fit the IW distribution to the two data sets. For this purpose, the Kolmogorov-Smirnov (K-S) and Cramér-von Mises (CvM) goodness-of-fit test statistics with associated p-values are reported in Table 6. The MLEs and the corresponding standard errors (SErs) and the goodness of fit statistics are displayed in Table 6, which show that the IW distribution is a suitable model to fit the two data set.

Table 6. MLEs (with SEs in parentheses) and goodness of fit statistics for the real data.

	MLEs (SEs)
Data	α	β	K-S (p-value)	CvM (p-value)
I	0.6540 (0.1347)	0.8804 (0.1093)	0.1134 (0.775)	0.1065 (0.092)
II	1.9275 (0.4447)	0.6434 (0.1048)	0.1580 (0.673)	0.0933 (0.139)

Now, from Table 5, three PT-IIC samples are generated using different choices of m and R. These generated samples are provided in Table 7. In short, the censoring scheme $R=(3,0,0,3)$ is referred as $R=(3,0^{\ast }2,3)$. Using the generated sample, the MLEs and MPSEs of the unknown parameters as well as $H_S$, $H_{\zeta }$ and $H_q$ with their SErs are reported in Table 8 for the two data sets. Also, the 95% ACIs of these quantities with their lengths are listed in Table 9. From Tables 8 and 9, it is observed that the estimates of $H_S$, $H_{\zeta }$ and $H_q$ using the MPS approach performed better than those using the ML approach in terms of minimum SErs and confidence lengths. The data analysis shows that based on the MLEs, Sch-III performs better than other schemes. The estimated entropies have the smallest values in this case, which indicates that the data obtained using Sch-III provides more information than other schemes. On the other hand, using the MPSEs, we can observe that the data acquired employing Sch-I gives more information than other schemes. Based on these results and when using the PT-IIC data, one can estimate the entropy to decide which scheme gives more information.

7. Conclusion

This article considers the estimation of the Rényi, q-entropy and Shannon entropy for inverse Weibull distribution based on progressively Type-II censored data. The methods of maximum likelihood and maximum product of spacing are used. The point estimators are acquired through the invariance property and the approximate confidence intervals are also computed. To examine the efficiency of the offered estimators, a simulation study and two real data sets are investigated. The numerical analysis shows that the maximum likelihood provides an acceptable approach to estimate the entropy measures and the maximum product of spacing is a good choice when the researcher wishes to obtain confidence intervals for these measures. For future work, the Bayesian approach can be considered to estimate the entropy measures employing both maximum likelihood and maximum product of spacing methods. Another future work is to perform the bootstrap confidence intervals of the entropies using the both estimation methods.

Table 7. Different generated PT-IIC samples.

Data	$n(m)$	R	Censored Data
I	34(20)	$R_1=(14,0^{\ast }19)$	0.1, 1.0, 1.1, 1.2, 1.2, 1.3, 1.8, 2.0, 2.0, 2.3,
			2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3, 6.8, 8.0
		$R_2=(0^{\ast }9,14,0^{\ast }10)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5,
			2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3, 6.8, 8.0
		$R_3=(0^{\ast }19,14)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5,
			0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2, 1.3
II	19(10)	$R_1=(9,0^{\ast }9)$	0.19, 7.35, 8.01, 8.27, 12.06, 31.75, 32.52,
			33.91, 36.71, 72.89
		$R_2=(0^{\ast }4,9,0^{\ast }5)$	0.19, 0.78, 0.96, 1.31, 2.78, 31.75, 32.52,
			33.91, 36.71, 72.89
		$R_3=(0^{\ast }9,9)$	0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67,
			4.85, 6.50

Table 8. The MLEs and MPSEs (with their SEs in parentheses) for the real data.

		MLE (SE)			MPSE (SE)
Data	Parameter	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
I	α	1.2043 (0.2764)	0.8525 (0.1864)	0.7354 (0.1607)	2.8224 (0.8172)	0.8630 (0.1931)	0.7525 (0.1655)
	β	0.8079 (0.1145)	0.7072 (0.1155)	0.7785 (0.1268)	1.8440 (0.3564)	0.7559 (0.1279)	0.8211 (0.1396)
	$H_S$	2.7353 (0.4569)	2.5142 (0.5316)	2.1743 (0.4683)	1.8010 (0.2191)	2.4259 (0.5211)	2.1309 (0.4613)
	$H_{0.6}^{\ast }$	6.0855 (1.4338)	8.5401 (6.4094)	5.9844 (2.1553)	2.4844 (0.1315)	6.7029 (2.8537)	5.3105 (1.5559)
	$H_{0.9}^{\ast }$	3.0181 (0.2880)	2.8604 (0.2648)	2.4732 (0.2346)	1.9021 (0.1905)	2.7384 (0.2599)	2.4070 (0.2300)
	$H_{0.6}^{\star }$	26.017 (21.950)	73.621 (213.91)	24.886 (29.520)	4.2535 (1.2120)	34.006 (50.682)	18.415 (17.524)
	$H_{0.9}^{\star }$	3.5230 (0.6661)	3.3114 (0.7797)	2.8059 (0.6595)	2.0950 (0.3848)	3.1501 (0.7521)	2.7213 (0.6456)
II	α	2.2959 (0.6841)	2.1292 (0.5092)	1.9497 (0.4552)	34.426 (9.1671)	2.5691 (0.6879)	2.4335 (0.6540)
	β	0.4971 (0.1020)	0.4649 (0.1063)	0.5328 (0.1219)	1.4434 (0.1792)	0.5593 (0.1451)	0.6531 (0.1762)
	$H_S$	5.1095 (0.9897)	5.2102 (1.0329)	4.5437 (0.8867)	4.0621 (0.3723)	4.8771 (0.9822)	4.2470 (0.8395)
	$H_{0.7}^{\ast }$	10.120 (3.8556)	12.043 (8.4886)	8.4593 (2.7171)	4.6298 (0.2356)	8.2490 (2.3295)	6.4968 (1.2583)
	$H_{0.9}^{\ast }$	5.7304 (0.5980)	5.9091 (0.5115)	5.0943 (0.4351)	4.1950 (0.2958)	5.3839 (0.4544)	4.6393 (0.3759)
	$H_{0.7}^{\star }$	66.062 (100.56)	20.26 (355.04)	38.839 (45.976)	10.035 (1.9569)	36.261 (40.298)	20.073 (15.137)
	$H_{0.9}^{\star }$	7.7365 (1.9942)	8.0562 (0.2095)	6.6433 (1.7042)	5.2121 (0.6368)	7.1324 (1.9241)	5.9031 (1.5021)

Table 9. The ACIs (with confidence lengths in parentheses) for the real data.

		ACI-LF			ACI-MPS
Data	Parameter	Sch-I	Sch-II	Sch-III	Sch-I	Sch-II	Sch-III
I	α	(0.6627, 1.7460)	(0.4872, 1.2179)	(0.4204, 1.0504)	(1.2208, 4.4241)	(0.4846, 1.2414)	(0.4282, 1.0767)
		[1.0833]	[0.7307]	[0.6300]	[3.2033]	[0.7568]	[0.6486]
	β	(0.5835, 1.0322)	(0.4808, 0.9337)	(0.5299, 1.0271)	(1.1854, 2.5825)	(0.5051, 1.0066)	(0.5475, 1.0948)
		[0.4487]	[0.4529]	[0.4972]	[1.3971]	[0.5015]	[0.5472]
	$H_S$	(1.8396, 3.6309)	(1.4722, 3.5562)	(1.2564, 3.0921)	(1.3716, 2.2303)	(1.4045, 3.4473)	(1.2267, 3.0350)
		[1.7913]	[2.0840]	[1.8357]	[0.8587]	[2.0428]	[1.8083]
	$H_{0.6}^{\ast }$	(3.2752, 8.8958)	(0.0000, 21.102)	(1.7601, 10.209)	(2.2268, 2.7421)	(1.1098, 12.296)	(2.2610, 8.3600)
		[5.6206]	[21.102]	[8.4486]	[0.5154]	[11.186]	[6.0990]
	$H_{0.9}^{\ast }$	(2.4537, 3.5825)	(2.3415, 3.3793)	(2.0134, 2.9330)	(1.5288, 2.2754)	(2.2290, 3.2478)	(1.9562, 2.8577)
		[1.1288]	[1.0378]	[0.9196]	[0.7466]	[1.0188]	[0.9015]
	$H_{0.6}^{\star }$	(0.0000, 69.037)	(0.0000, 492.88)	(0.0000, 82.743)	(1.8781, 6.6289)	(0.0000, 133.34)	(0.0000, 52.762)
		[69.037]	[492.88]	[82.743]	[4.7508]	[133.34]	[52.762]
	$H_{0.9}^{\star }$	(2.2175, 4.8286)	(1.7832, 4.8397)	(1.5132, 4.0985)	(1.3408, 2.8492)	(1.6760, 4.6242)	(1.4561, 3.9866)
		[2.6111]	[3.0565]	[2.5853]	[1.5085]	[2.9482]	[2.5305]
II	α	(0.9544, 3.6374)	(1.1323, 3.1261)	(1.0574, 2.8420)	(16.459, 52.392)	(1.2209, 3.9174)	(1.1514, 3.7156)
		[2.6830]	[1.9938]	[1.7846]	[35.933]	[2.6964]	[2.5642]
	β	(0.2975, 0.6966)	(0.2573, 0.6755)	(0.2938, 0.7717)	(1.0922, 1.7944)	(0.2750, 0.8437)	(0.3084, 0.9985)
		[0.3991]	[0.4152]	[0.4779]	[0.7022]	[0.5687]	[0.6901]
	$H_S$	(3.1697, 7.0493)	(3.1858, 7.2345)	(2.8059, 6.2815)	(3.3324, 4.7917)	(2.9521, 6.8021)	(2.6016, 5.8923)
		[3.8797]	[4.0488]	[3.4756]	[1.4594]	[3.8501]	[3.2907]
	$H_{0.7}^{\ast }$	(2.5627, 17.676)	(0.0000, 28.681)	(3.1339, 13.785)	(4.1680, 5.0916)	(3.6833, 12.815)	(4.0306, 8.9630)
		[15.114]	[28.681]	[10.651]	[0.9236]	[9.1315]	[4.9324]
	$H_{0.9}^{\ast }$	(4.5583, 6.9024)	(4.9065, 6.9116)	(4.2414, 5.9471)	(3.6152, 4.7748)	(4.4934, 6.2744)	(3.9026, 5.3760)
		[2.3441]	[2.0051]	[1.7056]	[1.1597]	[1.7810]	[1.4734]
	$H_{0.7}^{\star }$	(0.0000, 263.15)	(0.0000, 816.13)	(0.0000, 128.95)	(6.2001, 13.871)	(0.0000, 115.24)	(0.0000, 49.741)
		[263.15]	[816.13]	[128.95]	[7.6708]	[115.24]	[49.741]
	$H_{0.9}^{\star }$	(3.8279, 11.645)	(3.7256, 12.387)	(3.3031, 9.9836)	(3.9639, 6.4601)	(3.3615, 10.903)	(2.9592, 8.8470)
		[7.8171]	[8.6612]	[6.6805]	[2.4962]	[7.5419]	[5.8878]

Acknowledgements

The authors would like to express their appreciation to the editor and anonymous referees for valuable guidance and useful comments.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IFPIP: 895-130-1442) and King Abdulaziz University, DSR, Jeddah, Saudi Arabia (IFPIP: 895-130-1442).