Unsteady MHD third-grade fluid past an absorbent high-temperature shrinking sheet packed with silver nanoparticles and non-linear radiation

Abstract

This investigation peruses the features of temperature and mass transport of the non-Newtonian third-order liquid over an absorbent convective temperature shrinking sheet. The sheet is packed with silver nanoparticles. The Buongiornos modelling uses a particular non-Newtonian third-order liquid with the Brownian movement and the thermophoresis consequences using the non-linear radiation. The non-linear partial differential equations are changed to the ordinary differential equations with similarity transformations. The changed system of equations is then resolved using the numerical Shooting method and the sixth-order Runge-Kutta’s method. The numerically obtained solutions of the velocity profiles, temperature distributions, and concentrations of nanoparticles are discussed graphically. Also, the non-Newtonian parameter reduced the velocity of the liquid, increased the temperature and the concentration profiles throughout the fluid. Ultimately, the qualified systematic analysis is built by the preceding study in restrictive cases and displaingy the best correlation.

KEYWORDS:

• Nanofluid
• third-grade fluid
• magnetic field
• shooting technique
• Runge–Kutta method

1. Introduction

The flows of the non-Newtonian fluids are increasing considered due to their various applications in manufacturing and industrial procedures. Examples of non-Newtonian fluids are molten plastic, blood, ketchup, grease, artificial fibre, paint certain oily liquids etc. These fluids violate Newton’s law of viscosity. They are extremely glutinous and expose their elasticity. They are essential in composite process, polymer depolarization, absorptions of bubbles, boiling points, etc. The second-grade fluids exhibit the effects of the natural stress and cannot predict the shear thin and thick phenomenon. But a model of the third-order liquids can predict together the natural stresses and the shear thin and thick phenomenon evenly, and the constitutive governing equations have more complexity.

In the taxonomy, the third-grade fluid, a secondary type of non-Newtonian fluid, is confined to the non-Newtonian impacts. These fluids are shear thin and thick and natural stress components and they have rigid boundaries. They exhibit glutinous elastic features. The second-order fluid exhibits normal stress effects and does not show the shear thinning and thickening phenomenon. Furthermore, the equations of flow in the third-grade fluids are more difficult than the consequent equations in the second-grade fluids. The non-Newtonian fluid along with temperature and mass transport is significantly very important for paper production and lubrication with the grease industry, in addition, due to those considerable practical applications.

The solutions of the specific third-grade liquid towards the stagnation points of the unstable absorbent stretched and/or shrinking surfaces were obtained by Naganthran et al. [1]. The increment of the thermally conductance of the liquid through scattering nanoparticles was studied by Masuda et al. [2]. Buongiorno [3] found that the Brownian movement and thermophoresis impacts of nanofluids incremented fluid’s thermal conductivity. The computational resolutions of nanofluids over the stretched sheets were obtained by Khan and Pop [4] using Buongiornos modelling and analysing the Brownian movement along with the thermophoretic impacts on the temperature transportation rates at the surface. Makinde and Aziz [5] studied the temperature transportation in the nanofluids past the stretched sheets to represent convection frontier conditions. Makinde and Aziz [6] inspected MHD combined convective frontier layered movement and warm transport past the warmed perpendicular plate engrossed in the permeable media. The frontier layered movements by the temperature transportations towards the warmed absorbent stretched surfaces were explored computationally by Ishak [7]. Yao et al. [8] examined a systematic resolution for the frontier layered movement over the convective warmed porous stretched and/or shrinking walls. Rahman et al. [9] deliberated the combined convection flows over the perpendicular smooth plate by representing convective frontier conditions. Mustafa et al. [10] explored the Maxwells fluids past the warmed exponential stretched surfaces engrossed in the nanofluids. Khan et al. [11] considered the effects of non-linearly radiation on MHD flows of Carreau’s liquids over the non-linearly stretched surfaces by the convection frontier conditions.

Zaib et al. [12] studied the impacts of the nanoparticle on the flows of the specially non-Newtonians third-grade liquids past the absorbent warmed shrinking sheets by the non-linear radiation. More recently, Krishna and Chamkha [13] explored the diffusion thermo, radiating absorption and, Hall and ion slips impacts on MHD free convection rotating flow of nanoliquids over the semi-infinite porous stirring plate by the invariable temperature sources. Krishna and Chamkha [14] considered the MHD squeezing flows of the H₂O-supported nanoliquid during the saturated permeable media concerning two equivalent discs, appying the Hall currents to descriptions. Hall and ion slip consequences on uneven MHD convective revolving flows of the nanoliquids were investigated by Krishna and Chamkha [15]. Krishna [16] researched the stable MHD convection flows of the gelatinous nanoliquid due to the porous exponential stretched absorbent surfaces. Krishna et al. [17] conferred the radiation and absorption on the MHD convection flows of nanoliquids over a vertically travelling porous plate. Krishna et al. [18] explored unsteady radiating MHD flow of the Casson hybrid nanoliquid past an infinite exponentially accelerated vertical absorbent surface. Ahammad and Krishna [19] discussed the chemically reacting, Soret and Dufour consequences on MHD natural convective revolving flow through a perpendicular permeable channel.

Prakash et al. [20] conducted theoretical study of laminar, stable, noncompressible bio-convection flows of tangential hyperbolically non-Newtonian nanofluids from the two path-stretching surfaces underneath a reciprocally, orthogonally and electrically magnetic field. Tripathi et al. [21] explored the computational modelling approaches to describe the peristaltic pumping of the couple stresses hybrid nanofluid standardized by the electro-osmosis system in the micro-channel. The consequences of the boron-nitride nanotube suspensions on the heat transfer performances of ethylene-glycol based nanofluid flow across the micro-channel/duct driven by peristaltically pumping and electro-osmotic pumping has been researched by Akram et al. [22]. Akram et al. [23] explored the peristaltic synchronized electro-osmotic pumping of H₂O-supported hybrid Silver–Gold nanofluid in an inclined asymmetrical micro-fluidic duct/channel into an absorbent medium. Akram et al. [24] examined hybrid Ag-Al₂O₃ nanofluids and Al₂O₃ mono-nanofluids in the convection temperature transport processes determined by electro-osmotis and peristaltic pumping. Prakash et al. [25] explored the electro-osmotic flows of hybrid nanoliquids in an asymmetrically micro-channel. This moved sinusoidally by invariable wave velocity underneath axial electrical fields and Joule heating. The consequences of the dissimilar categories of supporting fluid on carbon nanotube nanofluid flow past a spherical stretching sheet have been explored by Akbar et al. [26]. The influences of Coriolis body forces, electro-magneto hydro-dynamics and thermally radiative temperature transport on the Cassons hybrid-assorted convective nanofluids determined by an exponential accelerating plate adjoining to an absorbent media in the revolving structure have been explored by Tripathi et al. [27].

Khan et al. [28] explored a three-dimensional revolving flow of H₂O-supported nanofluid originated from infinitely revolving discs. Turkyilmazoglu [29] examined the interactions of overhanging particles by the fluid past a stretchable gyratory disc. The visible consequences of Buongiornos nanofluids modelling on the pace of temperature and accumulation transport in dissimilar fluids movement geometry have been conferred by Turkyilmazoglu [30]. Anuar et al. [31] examined the upshots of MHD on the sturdy 2D combined convective movement induced with non-linear surfaces in carbon nanotubes. Turkyilmazoglu [32] researched the frontier layered flows of movement due to a revolution with stretchable and/or shrinkable bendable cone in an immobile fluid.

The mutual consequences of MHD temperature transport flow underneath the influences of slips past an affecting smooth plate with the effect of entropy have been scrutinized by Ellahi et al. [34]. Bhatti et al. [35] explored the electro-osmotic MHD movement of non-Newtonian Jeffrey fluids in petite particles affecting the sinusoidal format in a Darcy Brinkmans Forchheimers medium.

The frontier layered movement of the particular non-Newtonian third-order liquid over the convection heated shrinking sheets by the non-linear heat radiating due to solar energies and magnetic effect with the numerical solutions, generated by the Mathematica 10.0 computational software, has not yet been investigated. Therefore, the present investigation was to consider the frontier layered movement of the particular non-Newtonian third-order liquid over the convection heated shrinking sheets by the non-linear heat radiating due to solar energies and magnetic effect. The Buongiornos modelling includes the Brownian movement and the thermophoretic effects for the third-grade liquid. The renovated non-linear equations were resolved computationally utilizing the Shooting methodology. To the best of our knowledge, this specific problem on the third-grad fluids has not been measured before; therefore, the description results are innovative and original.

2. Formulation and solution of the problem

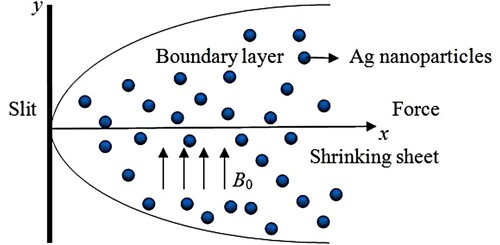
The present investigation scrutinizes the features of temperature and mass transport of the particular non-Newtonian third-order liquid over an absorbent convective temperature shrinking sheet packed with the nanoparticles. The Buongiornos modelling is used for the particular non-Newtonian third-order liquid. This included the Brownian movement and the thermophoretic consequences of non-linear radiating. The physical configuration of the problem is displayed in Figure 1.

Figure 1. Physical model of the problem.

It is assumed that the $x$-direction is taken by the side of the shrinking sheet and the $y$-direction vertical to it. The shrinking surface velocity is $U_w=ax$ for $a>0$. The lower surfaces of the sheet are warmed convectively by the temperature $T_w$, which delivers the temperature transport coefficient h_f. An invariable magnetic domain by the strength $B_0$ is applied on the transversal flow path. $T_{\mathrm{\infty }}$ and $C_{\mathrm{\infty }}$ are the heat and nanoparticle concentration at a large distance from the surface, respectively. The physical calculations , governing the steady flow were written by (Naganthran et al. [1] and Mustafa et al. [10]): (1) $\begin{array}{rl}& \frac{\mathrm{\partial }u}{\mathrm{\partial }x}+\frac{\mathrm{\partial }v}{\mathrm{\partial }y}=0\end{array}$(1) (2) $\begin{array}{rl}& u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }v}{\mathrm{\partial }y}=\upsilon \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+6\mathrm{\Gamma }\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}{\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }y}\right)}^2-\frac{\sigma {B_0}^2}{\rho }u\end{array}$(2) (3) $\begin{array}{rl}& u\frac{\mathrm{\partial }T}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }T}{\mathrm{\partial }y}=\alpha \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{y}^2}+\tau \left[D_B\frac{\mathrm{\partial }C}{\mathrm{\partial }y}\frac{\mathrm{\partial }T}{\mathrm{\partial }y}+\frac{D_T}{T_{\mathrm{\infty }}}{\left(\frac{\mathrm{\partial }T}{\mathrm{\partial }y}\right)}^2\right]\\ & -\frac{1}{\rho C_p}\frac{\mathrm{\partial }{q}_r}{\mathrm{\partial }y}\end{array}$(3) (4) $\begin{array}{rl}& u\frac{\mathrm{\partial }C}{\mathrm{\partial }x}+v\frac{\mathrm{\partial }C}{\mathrm{\partial }y}=D_B\frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{y}^2}+\frac{D_T}{T_{\mathrm{\infty }}}\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{y}^2}\end{array}$(4)

The relevant frontier stipulations were (5) $\begin{array}{rl}u& =-U_w,v=v_0,-K_1\frac{\mathrm{\partial }T}{\mathrm{\partial }y}=h\left(T_w-T\right),\\ C& =C_w\text{ at }y=0\\ u& \to 0,T\to T_{\mathrm{\infty }},C=C_{\mathrm{\infty }}\text{ at }y=\mathrm{\infty }\end{array}$(5) where u and v are the velocity constituents in the x and y axis, respectively. $\mathrm{\Gamma }$ is the non-Newtonian constraint, $B_0$ is the magnetic parameter, $T_{\mathrm{\infty }}$ is the free stream temperature, $T_w$ is the convective fluid, temperature, $C_w$ is the concentration near the surfaces, $C$ is the concentration of nanoparticle, $\alpha$ is the heat diffusivity, $\upsilon =\frac{\mu }{\rho }$ is the kinematic viscosity, $\rho$ is the density of the liquid, $\sigma$ is the electrical conductivity, $\tau$ is the ratio of effectively heat capacity of the nanoparticle materials to the heat capacity of the fluid, $K_1$ is the thermal conductivity, $D_B$ is the Brownian diffusion coefficient and $D_T$ is the thermophoresis diffusion coefficient, $\rho C_p$ is the specific heat capacitance of nanofluid. $q_r$ is radiative temperature discharge. Radiative temperature discharge $q_r$ via Rosselands approximations might be set into the following format (6) $q_r=-\frac{4{\sigma }^{\ast }}{3k^{\ast }}\frac{\mathrm{\partial }{T}^4}{\mathrm{\partial }y}=-\frac{16{\sigma }^{\ast }{T}^3}{3k^{\ast }}\frac{\mathrm{\partial }T}{\mathrm{\partial }y}$(6) where ${\sigma }^{\ast }$ is the Stefan–Boltzmann’s invariable and $k^{\ast }$ is the coefficient of the mean absorption.

Using the following transformation (7) $\begin{array}{rl}u& =ax{f}^{\mathrm{\prime }}\left(\eta \right),v=-\sqrt{a\upsilon }f\left(\eta \right),\eta =\sqrt{\frac{a}{\upsilon }}y,\\ T& =T_{\mathrm{\infty }}\left(1+\left({\theta }_w\right)\theta \left(\eta \right)\right),\phi \left(\eta \right)=\frac{C-C_{\mathrm{\infty }}}{C_w-C_{\mathrm{\infty }}}\end{array}$(7) Here ${\theta }_w=\frac{T_w}{T_{\mathrm{\infty }}}>1$ is the temperature ratio parameter. Later, using equation (7), equation (1) was satisfied identically and equations (2), (3), in addition to (4) consider the subsequent form as (9) $\begin{array}{rl}& \left(1+N_p{\left(f^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)\right)}^2\right)f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)+f\left(\eta \right)f^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)-(f\left(\eta \right){)}^2-M{f}^{\mathrm{\prime }}\left(\eta \right)\\ & =0\end{array}$(9) (10) $\begin{array}{rl}& {\theta }^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)+\frac{4}{3}R{\theta }^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)\left(\right(1+3\left({\theta }_w-1\right)\theta \left(\eta \right)\\ & +3{({\theta }_w-1)}^2{\left(\theta \left(\eta \right)\right)}^2+{({\theta }_w-1)}^3{\left(\theta \left(\eta \right)\right)}^3)\\ & +\frac{4}{3}R{\theta }^{\mathrm{\prime }}\left(\eta \right)\left(\right(3\left({\theta }_w-1\right){\theta }^{\mathrm{\prime }}\left(\eta \right)+6{({\theta }_w-1)}^2\theta \left(\eta \right){\theta }^{\mathrm{\prime }}\left(\eta \right)\\ & +{({\theta }_w-1)}^3{\left(\theta \left(\eta \right)\right)}^2{\theta }^{\mathrm{\prime }}\left(\eta \right))\\ & +P_r\left[N_b{\theta }^{\mathrm{\prime }}\left(\eta \right){\phi }^{\mathrm{\prime }}\left(\eta \right)+N_t{\left({\theta }^{\mathrm{\prime }}\left(\eta \right)\right)}^2+f\left(\eta \right){\theta }^{\mathrm{\prime }}\left(\eta \right)\right]\end{array}$(10) (11) $\begin{array}{rl}& {\phi }^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)+L_e{P}_r{\phi }^{\mathrm{\prime }}\left(\eta \right)+\frac{N_t}{N_b}{\theta }^{\mathrm{\prime }\mathrm{\prime }}\left(\eta \right)=0\end{array}$(11)

Revised boundary conditions

$f\left(0\right)=S,f^{\mathrm{\prime }}\left(0\right)=-1,\theta \left(0\right)=-\gamma \left(1-{\theta }^{\mathrm{\prime }}\left(0\right)\right),\phi \left(0\right)=1\text{at}\eta =0$ (12) $f^{\mathrm{\prime }}\left(\mathrm{\infty }\right)=0,\theta \left(\mathrm{\infty }\right)\to 0,\phi \left(\mathrm{\infty }\right)\to 0\text{at}\eta \to \mathrm{\infty }$(12) where $M=\frac{\sigma B^2}{\rho a}$ is the magnetic parameter, $\gamma =\frac{h}{K_1}\sqrt{\frac{\upsilon }{a}}$ is the thermal convective parameter, $S=v_0\sqrt{a\upsilon }$ is the suction parameter,$N_p=\frac{{\mathrm{\Gamma }}^2{b}^3{x}^2}{\upsilon }$ is the dimensionless Non-Newtonian parameter, $P_r=\frac{\upsilon }{\alpha }$ is the Prandtl number, $R=\frac{4{\sigma }^{\ast }{T_{\mathrm{\infty }}}^3}{3\alpha \rho C_p{k}^{\ast }}$ is the thermal radiation parameters $L_e=\frac{\alpha }{D_B}$ is the Lewis number, $N_b=\frac{\tau D_B\left(C_w-C_{\mathrm{\infty }}\right)}{\upsilon }$ is the Brownian motion parameter, $N_t=\frac{\tau D_T\left(T_w-T_{\mathrm{\infty }}\right)}{\upsilon }$ is the thermophoresis parameter.

The significant physical variables of interest were the local skin frictions coefficient, the locally Nusselts number and the locally Sherwoods number were designated as (13) $\begin{array}{r}{C}_{fx}=\frac{{\tau }_w}{\rho u_w^2},N{u}_x=-\frac{x{q}_w}{k\text{(}{T}_f-T_w\text{)}},S{h}_x=-\frac{x{m}_w}{D_B\text{(}{T}_f-T_w\text{)}}\end{array}$(13) where ${\tau }_w$ was the shear stress in the x-axis ((Naganthran et al. [1]), $q_w$ was the temperature flux and $m_w$ is the mass discharge specified by (14) $\begin{array}{rl}{\tau }_w& =\mu {\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }y}\right)}_{y=0},q_w=-k{\left(\frac{\mathrm{\partial }T}{\mathrm{\partial }y}\right)}_{y=0}+(q_r{)}_{y=0},\\ m_w& =-D_B{\left(\frac{\mathrm{\partial }C}{\mathrm{\partial }y}\right)}_{y=0}\end{array}$(14)

Using (7), we obtained as (15) $\begin{array}{rl}{C}_{f}R{e}_x^{1/2}& =f^{{}^{\mathrm{\prime }\mathrm{\prime }}}\left(0\right),\\ N{u}_{x}R{e}_x^{1/2}& =-\left(1+\frac{4}{3R_d}{\left\{1+\left({\theta }_w-1\right)\theta \left(0\right)\right\}}^3\right){\theta }^{\mathrm{\prime }}\left(0\right),\\ S{h}_{x}R{e}_x^{-1/2}& =-{\varphi }^{\mathrm{\prime }}\left(0\right),\end{array}$(15) where $R{e}_x=\frac{x{u}_w\left(x\right)}{\nu }$ the Reynolds quantity.

3. Numerical solution of the problem

Yang and Zhang [33] explored the existence and multiple resolutions for a non-linear system with the pertinent parameters involved in the boundary value problem. Now the reduced sets of non-linear ordinary differential equations from (9) to (11) mutually by the frontier conditions (12) are resolved computationally by the Nachtsheim-Swigert Shooting iterations methodology simultaneously by the Runge-Kutta’s sixth-order iteration technique. The numerical solutions to the non-dimensional boundary value problem are generated by the Mathematica 10.0 computational software. The relative error tolerance to ${10}^{-6}$ was deemed for the convergence, and the step size was $\mathrm{\Delta }\eta =0.001$.

For computation, the thermo-physical characteristics of the supporting fluid (water) and Silver utilized for program code validation, are given in Table 1.

Table 1. Thermophysical properties of water and Ag nanoparticles.

	$\rho /kg{m}^{-3}$	$C_p/Jk{g}^{-1}k$	$k/W{m}^{-1}k$	$\text{β}\times {10}^5/K^{-1}$
Water	997.10	4179	0.613	21.0
Silver	10500	235.0	429.0	1.89

Table 2. Skin frictions, Nusselts number and Sherwoods number.

$M$	$N_p$	$N_t$	$N_b$	$\gamma$	$Le$	$P_r$	$R$	$C_f$	$Nu$	$Sh$
0.1	1.0	0.5	0.5	0.3	1.0	3.0	2.0	2.525014	1.547887	1.854779
0.2								2.855479	1.336589	1.784452
0.3								3.114785	1.102254	1.698554
	2.0							2.255468	1.458879	1.666325
	3.0							2.986642	1.336554	1.478554
		1.0						…..	1.885452	1.966587
		1.5						…..	2.105214	2.014025
			1.0					…..	1.225489	1.658742
			1.5					…..	1.024963	1.452287
				0.4				…..	2.588749	2.988547
				0.5				…..	3.665284	3.996584
					1.5			…..	1.698554	2.001452
					2.0			…..	1.789956	2.225525
						4.0		…..	1.447855	1.669998
						5.0		…..	1.306658	1.452514
							3.0	…..	1.665245	1.996698
							4.0	…..	1.774485	2.101145

4. Results and discussion

The current research systematically found the frontier layered movement by the temperature and accumulation transport of the third-order liquid by the non-linear heat radiation and magnetic domain effect. The renovated ordinary differential equalities are computationally resolved by the Shooting technique for various quantities of the significant constraints.

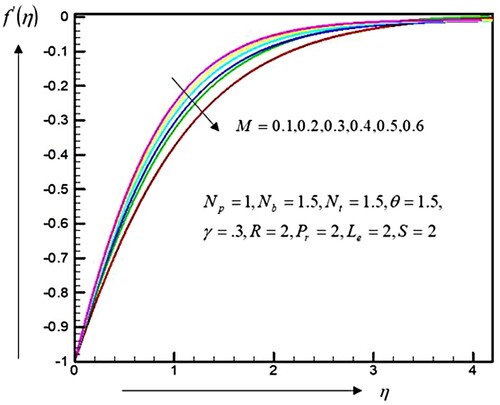
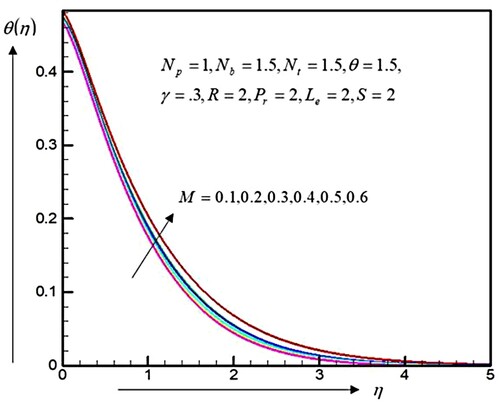
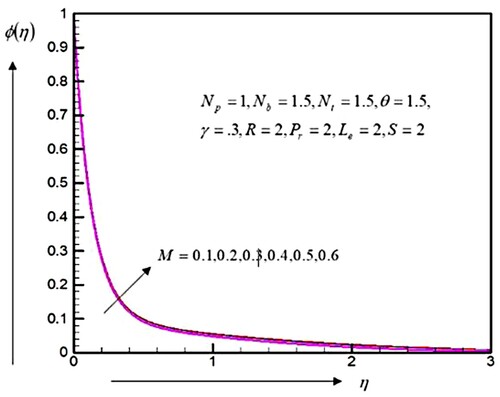
The analysis of computational results for dissimilar physically restrictions connecting into a problem were explored by the graphs. The velocities, temperature distributions, and concentrations of nanoparticles for the distinct quantities of $M$ are depicted in Figures 2–4. Figure 2 displays that the velocity profiles are decreased by the enhancing quantities of $M$. Therefore, the momentum boundary layer thickness decreased. The magnetic domain is vertical towards the movement paths. An inclination on or attraction to produce the resistances is called Lorentzs force. It shows the propensity to refuses to go together with the flow field throughout the fluids media. In contrast, the temperatures distributions and concentrations of nanoparticles are increased by the magnetic parameters $M$_, as displayed in Figures 3 and 4. As a result, the thermal and concentration of frontier layers are increased.

Figure 2. Velocity profiles with Hartmann number M.

Figure 3. Temperature profiles with Hartmann number M.

Figure 4. Concentration profiles with Hartmann number M.

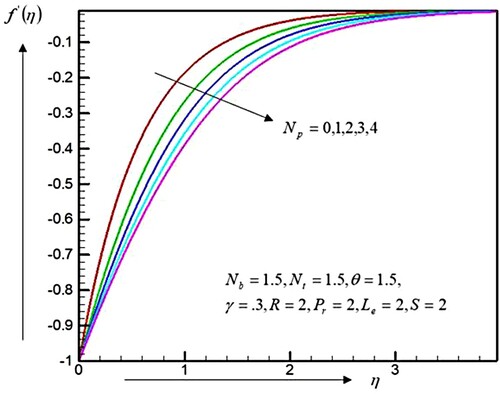
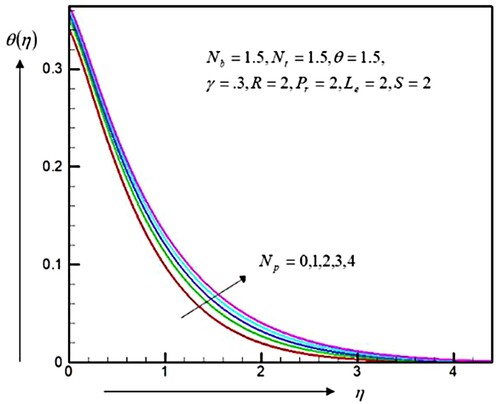
The velocities, temperature delivery, and the concentrations of nanoparticles for dissimilar quantities of the dimensionless non-Newtonians parameters $N_p$ are shown in Figures 5–7. Figure 5 displays that the velocity profiles are decreased by increasing the quantities of $N_p$. Therefore, the momentum frontier layered thickness increased. In contrast, the temperature distributions and the concentrations of nanoparticles are increased by the $N_p$, as represented in Figures 6 and 7, and therefore, the heat and concentrations frontier layers are augmented throughout the fluid region. This was also explored from those figures that the velocities, temperature delivery, and concentrations of nanoparticles were the largest for the particular third-grad liquid, as evaluated by the Newtonian fluid ($N_p$ =  0).

Figure 5. Velocity profiles with non-Newtonian parameter N_p.

Figure 6. Temperature profiles with non-Newtonian parameter N_p.

Figure 7. Concentration profiles with non-Newtonian parameter N_p.

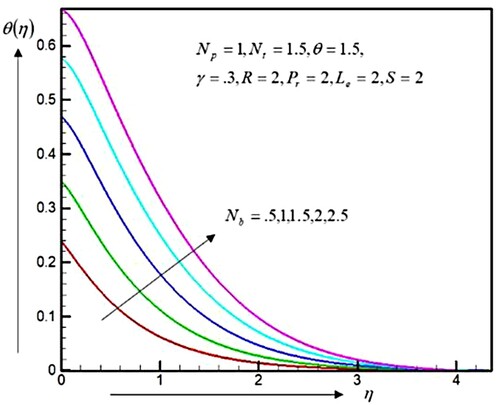
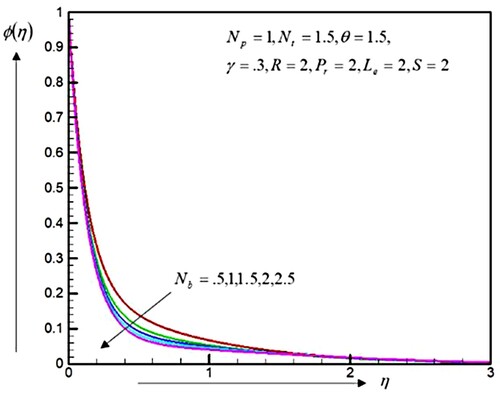
Figure 8 displays due to the growth of quantities of the Brownian movement parameter$N_b$, the temperature profiles are increased. But, the contradictory behaviour was detected for the concentrations profile, as shown in Figure 9. Hence, the thermally frontier layered thicknesses increase, whereas the concentrations of frontier layered thicknesses decrease. The kinetic energy of nanoparticles increases because the strength of the chaotic movement and the temperature of the fluid increase. The Brownians movement at the nanoscales and the molecular level are significant mechanisms of the nanoscale levels that govern the thermal behaviour. In systems using nanofluid, the Brownian movement has occurred since the sizes of nanoparticle might change the characteristics of the warm transport. As the scale sizes of the particles approached the scales of the nano-meters, the particle Brownian movement and this result on the neighbouring liquids play very important roles in the temperature transport features.

Figure 8. Temperature profiles with Brownian motion parameter N_b.

Figure 9. Concentration profiles with Brownian motion parameter N_b.

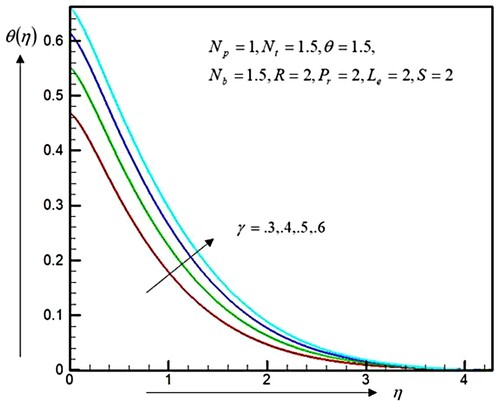
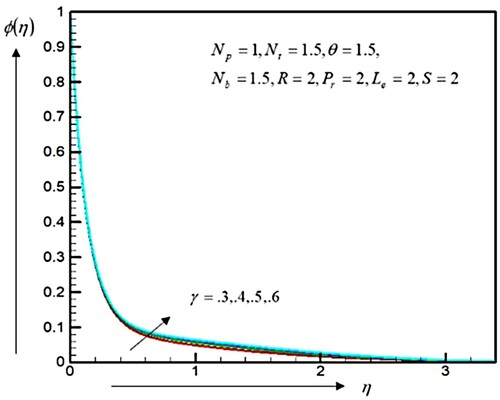
The effects of the convective parameter$\gamma$ on the temperatures delivery and concentrations of nanoparticles are inspected in Figures 10 and 11, respectively. Figure 10 shows that by increasing the values of $\gamma$ due to the stronger convection warming near the surfaces, the temperature gradients near the surfaces of the sheets are increasing. It allowed the temperature effects to penetrate cavernous into the sluggish fluids. Hence, the temperatures delivery and the thermally frontier stratum thicknesses increase by an increase in in the value of $\gamma$. Figure 11 displays that the concentrations of nanoparticles and the concentrations frontier stratum are increased by the largest quantities of $\gamma$.

Figure 10. Temperature profiles with thermal convective parameter $\gamma$.

Figure 11. Concentration profiles with thermal convective parameter $\gamma$.

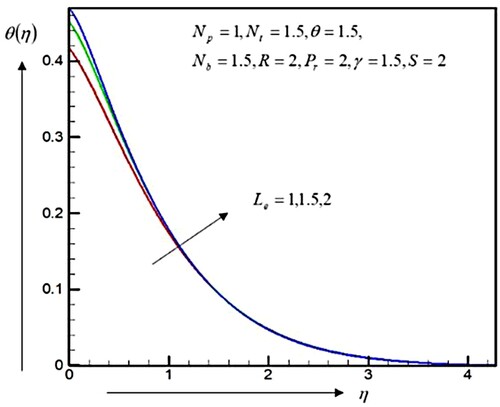
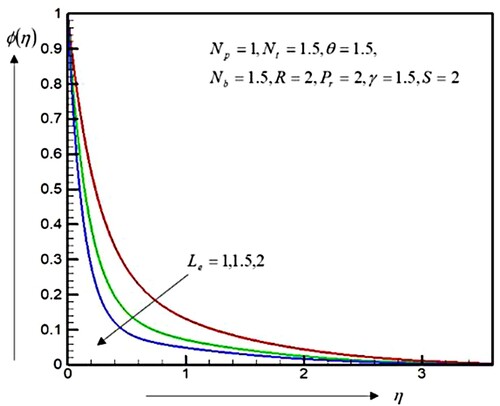
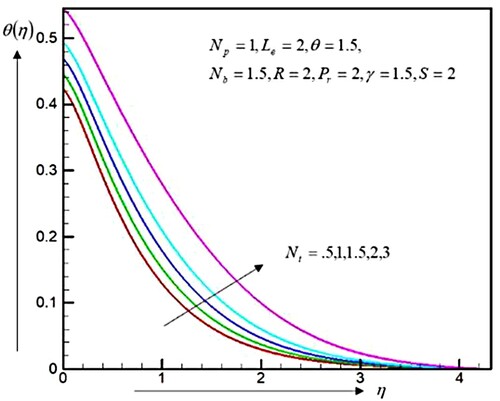
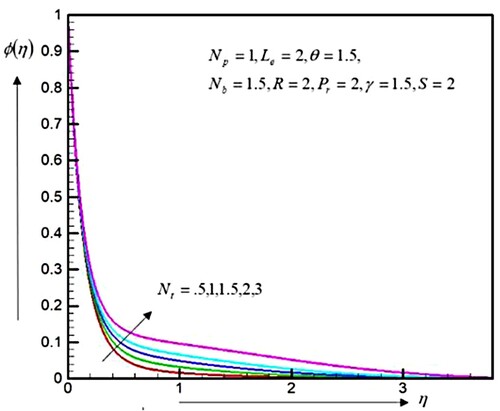
Figure 12 displays the cross-flow of the temperature with the increase of $L_e$. Figure 13 shows that the concentration profiles are decreased by an augment in the Lewis number $L_e$. Hence, the thermal and concentration frontier layer thickness became thin for the numerical solution. Figures 14 and 15 depict the outcomes of the thermophoretic restriction $N_t$ on the temperatures delivery and the concentrations of nanoparticles. These figures show that the temperatures profiles and the concentrations of nanoparticles are increased by an enhancement in $N_t$. It is since the diffusion penetrated deeply in the fluid due to an increasing quantity of $N_t$ which reasons the thickness of the thermal boundary layer and the concentration boundary layer stratum.

Figure 12. Temperature profiles with Lewis number L_e.

Figure 13. Concentration profiles with Lewis number L_e.

Figure 14. Temperature profiles with thermophoresis number N_t.

Figure 15. Concentration profiles with thermophoresis number N_t.

The Skin frictions and Nusselts numbers, in addition, to the Sherwoods numbers, are evaluated with reference to the governing parameters and are tabulated in Table 2. The skin frictions are increased by an enhancement in Hartmann number and retard with non-Newtonian fluid parameters. The local Nusselts quantity and Sherwoods numbers are increased with the growth in thermophoresis parameter, thermal convective parameter, Lewis number and thermal radiation parameter. These are also reduced with escalating in Hartmann number, non-Newtonian parameter, Brownian motion parameter and Prandtl number. Consequently, the third-order liquid accelerated the frontier layered partitions with increasing Non-Newtonian parameter.

Table 3 compares the outcomes. Here, the heat and mass transport of the third-order liquid over an absorbent convective temperature shrinking sheet packed with the Ag nanoparticles together with the Brownian movement and the thermophoresis impacts the non-linear radiating have been discussed comfortably. These results are the best concurrence by the existing outcomes of Makinde and Aziz [5] and Zaib et al. [12]. The current developments describe the features and the applications of non-Newtonian liquids in tribology and automotive industries, and so on. Lubricating oil in the machines is recurrently tested for gumminess since it could affect the performance of oils. Therefore, it influence the lifetime of the equipment. As oil utilized for elongated duration and still being utilize that factors together with defect particles as well as soot from unfinished combustion can cause them to takes on further non-Newtonian attributes even at the lowest shear rate. Thus, connected parameters engaged in addition suitable situations needed to be apply and handle to controls the non-Newtonian behaviour of the oils.

Table 3. Comparisons of outcomes for $-{\theta }^{\mathrm{\prime }}\text{(}0\text{)}$ and $-{\varphi }^{\mathrm{\prime }}\text{(}0\text{)}$ ($M=0.1,N_p=1,\gamma =0.3,Le=1,P_r=3,\text{and}R=2$).

		Zaib et al. [12]		Makinde and Aziz [5]		Current work
$N_t$	$N_b$	$-{\theta }^{\mathrm{\prime }}\text{(}0\text{)}$	$-{\varphi }^{\mathrm{\prime }}\text{(}0\text{)}$	$-{\theta }^{\mathrm{\prime }}\text{(}0\text{)}$	$-{\varphi }^{\mathrm{\prime }}\text{(}0\text{)}$	$-{\theta }^{\mathrm{\prime }}\text{(}0\text{)}$	$-{\varphi }^{\mathrm{\prime }}\text{(}0\text{)}$
0.1	0.1	0.952425	2.129478	0.952425	2.129478	0.95242585	2.12947889
0.2		0.505645	2.381956	0.505645	2.381956	0.50564544	2.38195656
0.3		0.252288	2.410085	0.252288	2.410085	0.25228849	2.41008552
0.4		0.119433	2.399796	0.119433	2.399796	0.11943356	2.39979655
0.5		0.054359	2.383678	0.054359	2.383678	0.05435922	2.38367814
	0.2	0.693220	2.274058	0.693220	2.274058	0.69322014	2.27405820
	0.3	0.520174	2.528622	0.520174	2.528622	0.52017410	2.52862245
	0.4	0.402685	2.795221	0.402685	2.795221	0.40268533	2.79522178
	0.5	0.321166	3.051850	0.321166	3.051850	0.32116663	3.05185033

5. Conclusions

The boundary layered flows with the heat and mass transportation of the third-order liquid by non-linear heat radiating and magnetic field impacts have been explored. The subsequent terminations are preserved as follows.

• The velocity deliveries are decreased , but temperature and concentration distributions are increased for magnetic field parameters.

• The temperature distributions and concentration distributions are increased by an enhancement in Brownian motion and convective parameters.

• The temperature distributions and concentration distributions are increased for the thermophoresis parameter.

• The temperature distribution increases and concentration distributions are decreased by an increase in the Lewis parameter.

• The current consequences might be utilized for displaying the non-Newtonian features of second- and third grade-fluid in addition to the relevance in the engineering field, automobile industries, etc.

• Therefore, the implicated physical constraints and appropriate circumstances, for instance, shrinking , stretching sheets, etc. required to be handled and useful to organize the non-Newtonian behaviours of the oils.

Disclosure statement

No potential conflict of interest was reported by the author(s).