n-Type narrow band gap A₃InAs₃ (A = Sr and Eu) Zintl phase semiconductors for optoelectronic and thermoelectric applications

Abstract

Optoelectronic and thermoelectric properties of A₃InAs₃ (A = Sr and Eu) Zintl compounds are investigated using FP-LAPW method with LDA, GGA and mBJ potentials for Sr₃InAs₃ in addition with Hubbard (U) for Eu₃InAs₃ based on DFT. Electronic properties reveal that both the compounds are direct bandgap semiconductors and their semiconducting nature is also supported by electrical resistivity (conductivity). The direct bandgap value is ranging from 0.50 to 0.74 and is decreasing with the replacement of Sr by Eu. The results divulge that both the compounds are optically active in the infrared region and optically anisotropic in nature and can be used as a shield for ultraviolet radiation and potential candidate for optoelectronic devices. Negative value of -383 and -411 µV/K Seebeck coefficients suggest that electrons are the majority charge carriers. Low thermal conductivity, high Seebeck coefficient and high power factor indicating that A₃InAs₃ (A = Sr and Eu) are the potential matrix for thermoelectric application.

KEYWORDS:

• Zintl phase compounds
• first principal calculations
• electronic band profiles
• optical properties
• thermoelectric properties

1. Introduction

In order to overcome the energy crises over the world, it is necessary to enhance the harvest of current energy sources. The Carnot cycle limits the effectiveness of all thermal engines; therefore, the only way to gain an advantage is to take the dissipated heat that is being expelled into the environment. It is accomplished simply by catching the released heat that would otherwise be squandered in the environment. Through thermoelectricity, this wasted heat can be converted into a valuable source of electrical energy [1,2]. The power factor (PF) is frequently used to study thermoelectric properties in materials. High power factors can be achieved in compounds that obey the phonon glass electron crystal idea (PGEC). In these substances, the charge transportation is handled similar to that which occurred in ideal crystal [2,3]. Some compounds such as skutterudites, minerals and clathrates are best-known instances of materials obeying the PGEC concept. These materials are widely examined to find their thermoelectric uses in various fields. However, some of the Zintl phases possess tremendous thermoelectric features under the normal and high-temperature ranges, i.e. 500–1200 K. Various Zintl phases have structures as zero dimension, one dimension and two dimension polyanions and they are investigated for the power generation systems like A₃BX₃ A₉B_4+δX₉, AB₂X₂, A₅B₂X₆ and A₁₄BX₁₁, etc. In these systems, “A” indicates alkali or alkaline earth metals or simply rare earth metals, “B” represents transition elements and “X” denotes the elements of group-15 from “P” to “Bi” [4]. In the aforementioned classes of Zintl pnictides, two classes A₁₄BX₁₁ and AB₂X₂ have their own special importance and they are discussed frequently. Among the best p-type Zintl materials, the A₁₄BX₁₁-class is mostly considered and performs appropriately in high-temperature range. Its figure of merit (ZT) value is greater than or equal to one [5]. For instance, the value of ZT = 1 for Yb₁₄MnSb₁₁ under 1223 K temperature. For the Yb₁₄Mn_0.2Al_0.8Sb₁₁ material, their ZT value is about 1.3 under 1223 K temperature. The values of Seebeck Coefficient (α) and thermal conductivity (κ) are 250 μV/K and 0.5 W/m/K correspondingly [6,7]. Recently the materials AB₂X₂ type are mainly focused. Some of these materials are considered to devour both n and p-type dupability [8]. There are many reports available about the structural properties of A₃BX₃ type pnictide materials, where A is alkaline earth element and nominally it is Eu divalent and B represents the elements of group 13 [9–18]. The class A₃BX₃ is known to be very unique in sense of structure as it crystallizes in five different structures [10,13,14,18]. All the known structures are centred on BX₄ tetrahedral. However, their interconnectivity is found to be very different from each other. The surprising outcomes are picked because of the difference of electro-negativities and atomic sizes. For instance, one can choose any structure among the following; Ba₃AlAs₃, Ba₃GaAs₃ and Ba₃InAs₃. In these structures, there is only variation of B atom which may vary from aluminium to Indium. The compound Ba₃AlAs₃ has orthorhombic structure and categories in Cmce-64 space group and the aspects dimeric Al₂As₆ units [14]. It is isostructure with diborane B₂H₆ molecule [16]. Two other materials Ba₃GaAs₃ and Ba₃InAs₃ also have orthorhombic structure with Pnma-62 space group. However, their structural properties are different. The first compound Ba₃GaAs₃ consists of 56 atoms per unit cell claims Ga₂As₆ fragments [16] which are analogous to formerly discussed Al₂As₆ units. On contrary, the second compound Ba₃InAs₃ has a unit cell with 28 atoms and claims InAs₄ tetrahedra are linked as infinite chains through corners [15]. Almost similar structural trend noticed for Eu₃BAs₃ phases, where B may be Al or Ga. The compound Eu₃AlAs₃ has monoclinic structure with P2_1/c-14 space group and the Eu₃GaAs₃ phase has orthorhombic structure along the space group of Cmce-64. These two structures feature Al₂As₆ as well as Ga₂As₆ units, as mentioned earlier are arranged in different ways according to one-to-one prolonged symmetries [18].

Thermoelectric properties of A₃BX₃ type materials are studied only for the p-type semiconductors like Sr₃AlSb₃ preserves p-type semiconductor nature along the higher values of α and κ, i.e. 470 μV/K and κ of 0.55 W/m/K, respectively, under 800 K temperature. The doped compounds Sr₃Ga_0.93Zn_0.07Sb₃ and Ca_2.94Na_0.06AlSb₃ of that material have gained the attraction because of their ZT values ∼0.94 and 0.78, respectively, under 1000 K temperature. However, there is no information available on the n-type nature of 3-1-3 family of Zintl classes.

Recently Rajput et al. [19] observed the unexpected n-type semiconductor Eu₃InAs₃ in A₃BX₃ family. This new A₃BX₃ composition expresses the n-type semiconductor behaviour without doping considerations. Moreover, the phase Eu₃InAs₃ is single crystalline solid having anonymously greater Seebeck coefficient, i.e. α ≈ −280 μV/K under RT (room temperature). These outcomes are found to be unprecedented showing the best-found value of n-type pnictides. The value of Mg_3.2Bi_0.49Te_0.01Sb_1.5 material is about −200 μV/K [20]. Since, the Eu₃InAs₃ compound is an arsenide, can provide new pattern and essential hints about the construction of next-generation thermoelectric substances. The current investigation may provide fundamental ground to researchers working in this field.

A₃InAs₃ (A = Sr and Eu) is reported as a narrow bandgap semiconductor when crystallized in ortho-rhombic symmetry with space group Pnma (# 62) [19]. Only Eu₃InAs₃ (A = Sr and Eu) Zintl phase compounds have been reported as n-type thermoelectric compounds based on the Seebeck Coefficient. There is no light shed on these compounds regarding their optical and thermoelectric properties, which motivate us to investigate the electronic, optical and thermoelectric performance of these materials for useful application in the framework of Density Functional Theory (DFT).

2. Computational detail

The FP-LAPW approach contained by DFT [21,22], as implemented in the WIEN2k package [23], is used to examine the electronic and optical properties of A₃InAs₃ (A = Sr and Eu) compounds. DFT is the most accurate theory for manipulative solid-state electronic structure [24–32]. For Sr₃InAs₃ and the addition of Hubbard U for Eu₃InAs₃, the exchange-correlation effects were treated  by LDA [33],  and GGA [34] while Modified Tran and Blaha Becke–Johnson (TB-mBJ) is used for enhanced calculation of optoelectronic properties having low computational cost [35].

The unit cell is separated into interstitial and atomic sphere muffin-tin regions in the FP-LAPW technique. The potential is considered a plane wave outside the sphere, whereas, inside the atomic spheres, the potential is solved using spherical harmonics. The valance atomic states are separated from core states by cut-off energy of −6 Ry, and 1000 k-points were used throughout the Brillouin zone computations. In the interstitial region, the cut-off parameter RMT/K_max were set to 8.0. The charge density is Fourier extended up to G_max = 12/a.u. The valance wave function inside the muffin-tin spheres is extended up to l_max = 10. The self-interaction corrections (SIC) technique [36] was used to calculate an approximated value of U_eff = U − J in which J = 0. In the instance of Eu₃InAs₃, different Hubbard U values were tested, and U = 7 eV/Eu was chosen for the current calculation, with the energy between iterations converging to 0.1 mRy and forces decreased to 1 mRy/Bohr. To calculate all of the transport parameters for the chemicals under investigation, the BoltzTrap algorithm is based on the Boltzmann transport semi-classical theory [37].

3. Results and discussion

3.1. Electronic properties

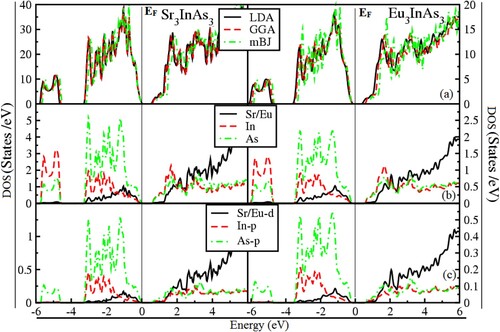
A band has several different energy states in which an array of electrons is prohibited. Many physical features are linked to a material’s band structure, which can be better understood by illustrating the band structure (BS) [38]. The BS for A₃InAs₃ (A = Sr and Eu) with Pnma space group shown in Figure 1 are calculated using LDA and GGA potentials and LDA + U and GGA + U through R-Γ-X-M-Γ integration path. Conversely, mBJ and mBJ + U is also used for the estimation of electronic properties. For the understudy compounds, the estimated band structures and total density of state are shown in Figure 1. The Fermi level (E_F) in the band structure is located between the valance and conduction bands at zero energy. Figure 2 shows that these compounds’ valance and conduction bands are separated by a gap, confirming their semiconductor nature. Due to the lower conduction band (CB) meeting with the higher valence band (VB) at Γ symmetry point, both compounds are classified as “direct bandgap semiconductors” (DBGS). The calculated values of bandgap (E_g) are 0.58, 0.61 and 0.76 eV for Sr₃InAs₃ and 0.50, 0.60 and 0.74 eV for Eu₃InAs₃. The reported results for Sr₃InAs₃ are 0.58 and 0.64 eV using atomic sphere approximation and Arrhenius equation while 0.31 and 0.55 eV for Eu₃InAs₃ through Arrhenius equation and by E_g = 2e|α_max|T_max relation [19]. The E_g for these compounds are decline going from Sr to Eu due to increasing of atomic size and also rising with change in potential from LDA → GGA → mBJ. The calculated outcome is well accordance with the experimental reported results [19] shows reliability of the present work and also comparable with results obtained for (0.78 eV) Ba₃GaAs₃, (0.5 eV) Ca₃AlSb₃ and (0.6 eV) Sr₃GaSb₃ [16,39–41]. The total density of states (TDOS) along with partial density of states (PDOS); d state of Sr/Eu and p state of In and As are also considered for these compounds to further clarify the semiconducting nature of the understudy compounds as shown in Figure 3(a–c) as 0 eV energy is taken as Fermi level (E_F). Figure 3(a) shows the computed TDOS for the understudy compounds, confirming their semiconductor character by showing that the VB and CB does not overlapping the E_F.

Figure 1. Crystal structure of A₃InAs₃ (A = Sr and Eu).

Figure 2. Electronic band structures along with total density of state up to −1 to 1 eV range of A₃InAs₃ (A = Sr and Eu).

Figure 3. (a–c) Total and partial density of states of A₃InAs₃ (A = Sr and Eu).

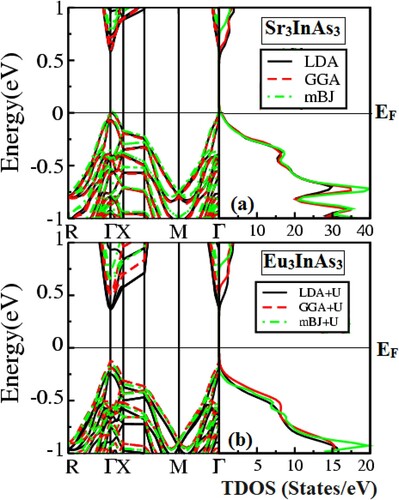
The TDOS consists of three sections in the energy range of −6 to 6 eV. The first section lies in the range of −6 to −5.33 eV, the second section lies in the range of −4.33–0 eV and the third section starts from the bang gap and reaches to 6 eV, respectively, for both compounds. From Figure 3(a,b), it is also clear that there is a variation in the density of states of both compounds going from LDA/LDA + U to mBJ/mBJ + U. In Sr base compound, the energy gap is sheeted from 0.58 to 0.61 and 0.76 eV and from 0.50 to 0.60 and 0.74 eV for Eu₃InAs₃, respectively, by LDA, GGA and mBJ without and with Hubbard U.

In order to find out the contribution to the total density of states, total densities of constituent elements of both the compounds are taken into account presented in Figure 3(b). From the figure, it is obvious that the section from −6 to −5.33 eV is contributed by In and As states while sections from −4.33 to 0 eV and from band gap to 6 eV are contributed by Sr/Eu, In and As, respectively, in both compounds with different contribution in valance and conduction band. To verify the basis of semiconducting character of A₃InAs₃ (A = Sr and Eu) compounds, their partial density of state (PDOS) is also considered shown in Figure 3(c). In Figure 3(c), it is clear that the contribution of Sr/Eu is due to d state and contribution of In and As is due to p state. The densities of both Sr/Eu-d and In/As-p states are composed of valance and conduction band. In valance band, density of As-p state shows greater contribution as compare to d and p state of Sr/Eu and In while in the conduction band density of Sr/Eu-d state shows greater contribution as compare to, p state of In and As. These compounds have an energy gap between the As-p states, as seen from the conduction and valence bands.

3.2. Optical properties

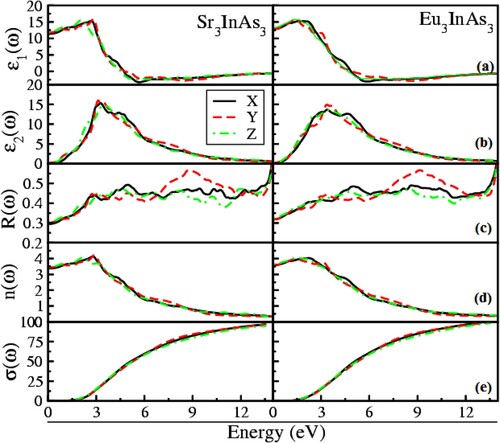
The optical response of a material to an optoelectronic application must be thoroughly examined. Therefore optical characteristics of the compounds A₃InAs₃ (A = Sr and Eu) are investigated along the three crystallographic axis (X, Y and Z), in the energy limit of 0–14 eV. In the current study, the optical parameters under investigation are real and imaginary parts of dielectric function (ϵ₁ (ω) and (ϵ₂ (ω)), reflectivity, refractive index and loss function presented in Figure 4(a–e). In Figure 4(a), the ϵ₁ (ω) demonstrates different physical characteristic of the compound. The zero-frequency limit of ϵ₁ (ω) referred to as static dielectric function (ϵ₁ (0)). Figure 4(a) shows that the ϵ₁ (0) lies in the range of 11.33–13.5, respectively, for both compounds. The static dielectric value for the X, Y and Z axis are 11.33, 11.66 and 12.0 for Sr₃InAs₃ and 12.96, 12.98 and 13.15 for Eu₃InAs₃ correspondingly as shown in Figure 5(a). Beyond the zero-frequency limit, as seen in Figure 5(a), the spectra grow and reach their highest peak at 2.32, 2.48 and 1.73 eV for Sr₃InAs₃ and 1.48, 1.3 and 1.2 eV for Eu₃InAs₃ correspondingly in crystallographic axis. For materials with dielectric properties, beyond the most significant peak, spectra begin to fall until they hit zero, at which point they become metallic.

Figure 4. (a–e) Optical parameters of A₃InAs₃ (A = Sr and Eu).

Figure 5. (a–e) Spacific part of optical parameters in spacific energy range of A₃InAs₃ (A = Sr and Eu).

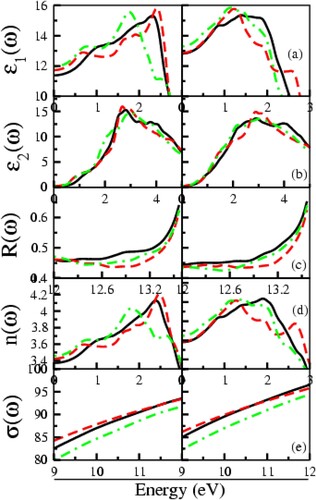
From Figure 4(b), the starting point of the ϵ₂ (ω) is a threshold point correspond to the E_g of the compounds. It is obvious that after the threshold value the gap is falling from Sr to Eu in these compounds and optical E_g lies in the boundary of infrared region of electromagnetic spectrum make these materials as potential candidate as optoelectronic materials in infrared region. When the major inter-band transition occurs, the raise in curve is observed extremely quickly and reaches its highest peak at 2.80, 2.60 and 2.90 eV for Sr₃InAs₃ and 2.80, 2.75 and 2.81 eV for Eu₃InAs₃, respectively, in the X, Y and Z direction revealed from Figure 5(b).

The determined reflectivity (R (ω)) displayed in Figure 4(c) and visualized clearly in Figure 5(c) in the energy range of 12–13.8 eV. Figure 4(c) shows that the highest reflectivity of 63%–65% corresponds to Sr₃InAs₃ at 13.7 eV and 65%–67% correspond to Eu₃InAs₃ at 13.7 eV. Intriguingly, the reflectivity increases almost as much as when the ϵ₁ (ω) decreases. In the ultraviolet, these materials’ high reflectivity can be utilized as a shield in opposition to extremely high-frequency radiations.

Figure 4(d) characterizes refractive index (n(ω)). The static value (n(0)) of n(ω) lies in the array of 3.38–3.65 correspondingly for both compounds A₃InAs₃ (A = Sr and Eu). From Figure 4(d), the value of n(0) is 3.38, 3.42 and 3.47 for Sr₃InAs₃ and 3.58 and 3.65 for Eu₃InAs₃ correspondingly in the X, Y and Z crystallographic axis. At energies between 1.0 and 2.0 eV, the real part of refractive will rise above its static value and reach its maximum value, respectively, for A₃InAs₃ (A = Sr and Eu). From Figure 5(d), it is clear that the static value of refractive index for Sr₃InAs₃ and Eu₃InAs₃ lies at 2.88, 2.97 and 1.8 eV, 1.98, 1.2 and 1.21 eV in X, Y and Z directions. The slowing of the greater number of photons when they interact with the materials causes to maximization of the refractive index of these compounds [42].

One of the essential tools for determining how many electrons are involved in a material’s optical transition is the sum rule (σ (ω)). Figure 4(e) demonstrates that the oscillator strength of the under investigation compounds increases with the increase in energy.

Since there are no unoccupied electrons at lower energies, the σ (ω)) is zero, and electrons begin to rise rapidly at higher energies when energy exceeds the bang gap. The strength of the oscillator generally increases as the bandgap narrows. From Figure 5(e), it is clear that the oscillator strength shows that 92–94 and 94–97 effective electrons are concerned with optical transition correspondingly in deferent directions of A₃InAs₃ (A = Sr and Eu).

3.3. Thermoelectric properties

The thermoelectric generators are incredibly effective at converting heat energy into electrical energy. Consequently research into thermoelectric characteristics has significantly boosted in recent years (TE). There are numerous applications for thermoelectric materials, including computer cooling and TE refrigeration, and the design of small detector components. These materials’ thermoelectric properties must be studied to determine how well they work at high temperatures. There are semiconductors known as active thermoelectric materials with a small bandgap. The BoltzTrap programme examines transport characteristics based on the density of states and band topologies [37]. Thermoelectric characteristics are examined in the current study in-between 0 and 750 K temperature range. Charges flow is measured by electrical conductivity (σ) and resistance to flow is calculated through electrical resistivity (ρ). The calculated ρ and σ are calculated by the removal of time factor of 10¹⁶ s and presented in Figure 6 for both compounds A₃InAs₃ (A = Sr and Eu). For understudy compound, curve for electrical resistivity is decreasing with increasing temperature. The ρ of Eu₃InAs₃ follows the same trend as experimental result given as inset in Figure 6. On the other hand, electrical conductivity of these compounds is very small at low temperature and rises with enhance in temperature. In addition to increasing temperature, the σ also rises with the substitution of Eu for Sr in the circuit.

Figure 6. Electrical resistivity and conductivity versus temperature plot of A₃InAs₃ (A = Sr and Eu).

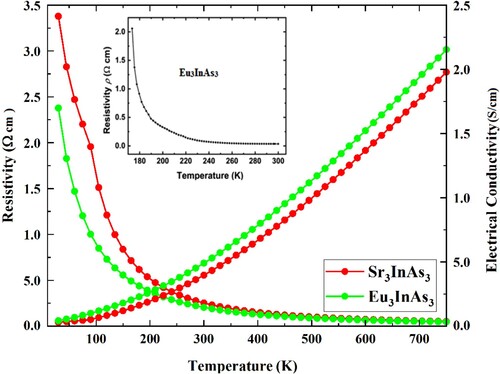
Due to the narrowing of the bandgap by cation substitution causes to increase σ. σ of these compounds are 3.96 and 4.90 S/cm at room temperature and 2.17 and 2.35 at 750 K going from Sr₃InAs₃ to Eu₃InAs₃. From both electrical resistivity and conductivity, it is also indicated that these compounds ate semiconductors in nature. Similar nature of ρ has also been reported for the iso-structural Zintl phase Eu₃InP₃ compound [17]

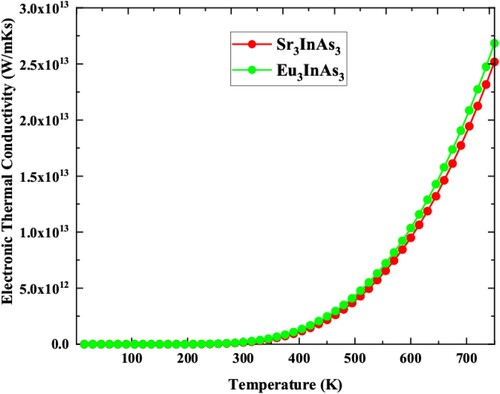
Electron conduction and lattice vibrations are two of the most common mechanisms for heat conduction in materials. The electronic part  of thermal conductivity (K_e) for the compounds under investigation is computed using the BoltzTraP package as shown in Figure 7. The increase in K_e as temperature rises as seen from the figure. The K_e of the studied compounds are almost invariable at low temperatures and fluctuate as the temperature growing. The K_e for the understudy compounds are 1.84 × 10¹¹ and 1.85 × 10¹¹ W/mKs and 3.19 × 10¹³, 3.38 × 10¹³ at 300 and 800 K, respectively, for Sr₃InAs₃ and Eu₃InAs_3. The thermal conductivity of Eu₃InAs₃ is almost same at room temperature while higher at 750 K than the Sr₃InAs₃ compound.

Figure 7. Electronic thermal conductivity versus temperature plot of A₃InAs₃ (A = Sr and Eu).

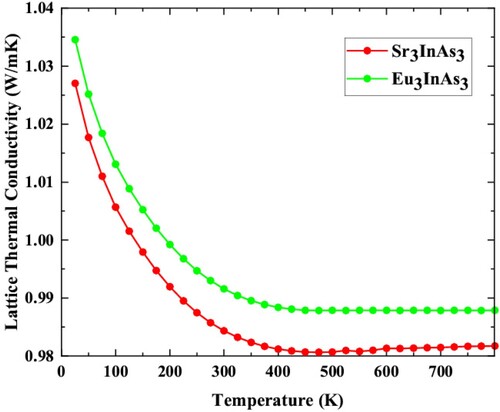
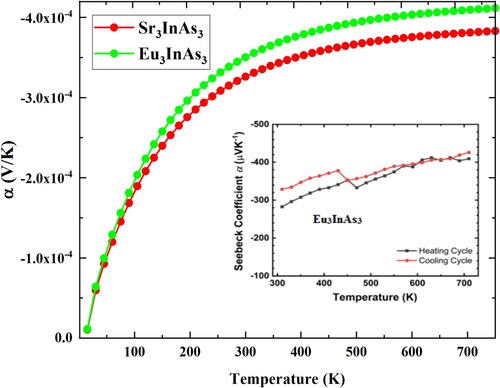
The Lattice thermal conductivity (K_L) for A₃InAs₃ (A = Sr and Eu) is calculated by famous Slack’s model [43] as shown in Figure 8. The K_L of the understudy compound is 0.981 and 0.987 W/mK at 750 K for A₃InAs₃ (A = Sr and Eu). The figure shows that the K_L of all compounds is decline with raise in temperature. This signifies that there is low phonon–phonon interaction at lesser temperatures and raises at high temperatures. Thermoelectric voltage increases when two dissimilar materials are brought together at opposed temperatures. Voltage patterns are restricted when there is a temperature differential between two materials. Increased thermoelectric voltage is a sign of higher levels of efficiency when applied to a particular temperature gradient. The α determines the thermocouple’s efficiency by comparing voltage to the temperature differential. Computed value of α for A₃InAs₃ (A = Sr and Eu) is presented in Figure 9. -ive values of the α point out that the compounds are n-type semiconductors, whereas positive values suggest that they are p-type.

Figure 8. Lattice thermal conductivity versus temperature plot of A₃InAs₃ (A = Sr and Eu).

Figure 9. Seebeck coefficient versus temperature plot of A₃InAs₃ (A = Sr and Eu).

The α for A₃InAs₃ (A = Sr and Eu) is negative, verify their n-type semiconducting nature and indicate that electrons are the majority carrier in these compounds. For both compounds, α not only rises with increase in temperature but also with the replacement of Sr by Eu. Substituting Sr for Eu improves the thermoelectric performance of the compounds under study. The absolute value of −326 and −350 µV/K at room temperature and −383 and −411 µV/K at 750 K, respectively, for A₃InAs₃ (A = Sr and Eu). The reported results for Eu₃InAs₃ are will agreement with the experimental result [19] given as inset in Figure 9 therefore the result reported for Sr₃InAs₃ is rational and logical.

Comparatively most Zintl phase compounds show p-type performance and no A₃BC₃ n-type Zintl compounds have been reported so far. The greater calculated value (−383 and −411 µV/K) for the A₃InAs₃ (A = Sr and Eu) disclose  that these compounds are potential candidate for thermoelectric applications analogous to other Zintl phase compounds having α of 180 μV/K forYb₁₄MnSb₁₁ [6], 260 μV/K for Ca_2.94Na_0.06AlSb₃ [39], 470 μV/K for Sr₃AlSb₃ [41], −310 μV/K for K_0.995Ba_0.005GaSb₄ [44], −85 μV/K for Ba₃Cd₂P₄ [45]. 200 μV/K for Ca₅Al_0.95In_0.95Zn_0.1Sb₆ [46], 185 μV/K for Eu₁₁Cd_4.5Zn_1.5Sb₁₂ [47] and 270 μV/K for Ca₉Zn_4.6Sb₉ [48].

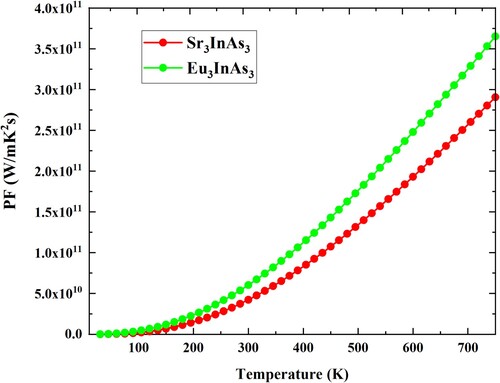
An additional thermoelectric property known as the power factor (PF) determines the ability of a material to produce power. Figure 10 shows the calculated power factor for the understudy compounds concerning temperature. With temperature increase, the carrier concentration increases, resulting in an overall increase in the Power Factor of all molecules. Highest value of PF at 300 K for A₃InAs₃ (A = Sr and Eu) compounds are 4.22 × 10¹⁰ and 6.02 × 10¹⁰ at 300 K and 2.90 × 10¹¹ and 3.65 × 10¹¹ at 800 K, respectively.

Figure 10. Power factor versus temperature plot of A₃InAs₃ (A = Sr and Eu).

4. Conclusions

The electronic, optical and thermoelectric properties of orthorhombic Sr₃InAs₃ and Eu₃InAs₃ Zintl phase compounds are studied using the FP-LAPW method, and DFT potentials such as LDA, GGA, and GGA-mBJ. According to the BS and DOS, all compounds are centrally symmetric direct bandgap semiconductors. It is estimated that the direct bandgap ranges from 0.50 to 0.74 eV and decreases with atomic replacement from Sr to Eu while increasing with the transition from LDA to mBJ. Evidence suggests that all of the compounds studied are optically active and anisotropic, indicating that they could be helpful in optoelectronic devices and UV protection. Therefore, their thermoelectric properties, such as electrical and thermal conductivity, Seebeck coefficient, and power factor, are computed. According to the Seebeck coefficient, electrons make up the majority of the charge carriers in these materials. These compounds, which have high Seebeck coefficients and power factors, are excellent candidates for use as active thermoelectrics. Its poor heat conductivity makes it an ideal starting point for developing novel thermoelectric materials.

Acknowledgement

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2022R124), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Moreover, we would like to thank Taif University Research Supporting Project number (TURSP-2020/63), Taif University, Taif, Saudi Arabia.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Data sharing is not applicable to this article as no data sets were generated during the present study.

Additional information

Funding

This work was supported by The Deanship of Scientific Research at Princess Nourah Bint Abdulrahman University [grant number PNURSP2022R124]; Taif University [grant number TURSP-2020/63].