On the nonextensivity contributions in collisional plasma damping waves

Abstract

Waves characteristic of solitary damped forms in plasmas fluids contain two polarity ions, nonextensivity positrons and electrons have been studied. The damped equation of Kadomtsev–Petviashvili (DKP) equation has been derived. The critical plasma density condition of DKP equation is introduced for parameters concerning Earth's ionosphere. The impacts of densities, ionic mass ratio, index of nonextensivity and frequencies of collision parameters on the nonlinear structures have been investigated. It is mentioned that the consequences obtained from this study may be applied in space plasmas.

Keywords:

• Damped forms
• nonextensive particles
• two fluid ions

1. Introduction

The physical phenomena description using equations with damped nonlinear structural solutions and their applications are one of the important intractable issues in the dynamics of fluid and plasmas [1–5]. Dynamical and collisional features of DIAWs have been studied in nonextensive electron dusty plasma via novel approximated analytical structures for the DKdV equation [6]. In space models and experimental labs, the damped noises observed may cause considerable puzzles in localized soliton behaviours [7–12]. The distorted and dissipated structures in soliton shapes were studied in various studies via numerous physics ways, such as particles collision [13–17], fluctuation in charges [4,18], fluids kinematics viscosity [19,20]. The assistances of strength and frequencies on the damped KdV equation with a forced term that describe dust superthermality plasma have been introduced [5]. They found that the force strength and frequency were significantly modulated the wave structures of the damped soliton. Also, the realizations in models containing pairs of ions (PI) becomes one of the motivating investigations for the propagation of ion acoustic-soliton (IAS) application in many astrophysics models and laboratories [21–28]. Abdelwahed et al. [29] inspected the effects of electron superthermal parameters and mass ratios on the waves of rogue profiles in ion pair system. However, plasma of electrons-positrons-ions (E-P-I) is observed in astrophysics, quantum hydrodynamics environments and industry of semiconductors [30–39]. Furthermore, the double-layer existence in the model with two temperature ions and superthermality electrons has been inspected [40]. The criticality state is based on the electrons index and thermal ionic ratio. Also, large soliton amplitudes in electronegative fluid have been studied by pseudo-potential technique [41]. It was noted that the positive–negative potentials were formed by nonextensively electrons. The effects of frequencies of collisions on damped 3D cylindrical solitary forms in plasma of the dust-negative-positive model have been studied [42]. They recited that the collision frequencies and radial effects substantially influenced the damped structures. On the other hand, plasmas usually contain particles having distributions in non-Maxwellian forms such as nonthermal, trapped, and nonextensive electron-ion distributions [25,43–47]. Moreover, nonextensive distribution has many applications in astrophysics, auroral plasma and galaxy clusters [46–50]. The ionization and nonextensive effects on dynamical transition and solitary excitations have been investigated in a dusty collisional plasma model [51]. El-Taibany investigated both the 3D IAWs Modulation instability and highly energetic freak IAW waves in Earth's Ionosphere model having non-Maxwellian (r,q) distributions of electrons (positrons) via 3D NLSE. It was discussed the stabe-unstabe conditions depend mainly on obliqueness angle and the (r,q) distributions parameters [52]. So, we aim to investigate the damping structure's dependence on physical parameters such as the ionic mass ratio $(Q=m_{+}/m_{-})$, the frequencies of collision parameters (${\nu }_{+},\tilde{\nu },{\nu }_{-}),$ and the index of nonextensive (q).

2. Equations of model

In this system, a collisional four-components unmagnetized plasma contains negative and positive fluids, nonextensive electrons and positrons are suggested. Normalized model is given by: (1a) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i+}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}(n_{i+}{u}_{i+})+\frac{\mathrm{\partial }}{\mathrm{\partial }y}(n_{i+}{v}_{i+})\\ & ={\nu }_{+}{N}_e,\end{array}$(1a) (1b) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left(n_{i+}{u}_{i+}\right)+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(n_{i+}{u}_{i+}^2\right)+\frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(n_{i+}{u}_{i+}{v}_{i+}\right)+n_{i+}\frac{\mathrm{\partial }\phi }{\mathrm{\partial }x}\\ & =-\tilde{\nu }{n}_{i+}{u}_{i+},\end{array}$(1b) (1c) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left(n_{i+}{v}_{i+}\right)+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(n_{i+}{u}_{i+}{v}_{i+}\right)+\frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(n_{i+}{v}_{i+}^2\right)+n_{i+}\frac{\mathrm{\partial }\phi }{\mathrm{\partial }y}\\ & =-\tilde{\nu }{n}_{i+}{v}_{i+},\end{array}$(1c) (2a) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i-}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}(n_{i-}{u}_{i-})+\frac{\mathrm{\partial }}{\mathrm{\partial }y}(n_{i-}{v}_{i-})={\nu }_{-}{N}_p,\end{array}$(2a) (2b) $\begin{array}{rl}& \frac{\mathrm{\partial }{u}_{i-}}{\mathrm{\partial }t}+u_{i-}\frac{\mathrm{\partial }{u}_{i-}}{\mathrm{\partial }x}+v_{i-}\frac{\mathrm{\partial }{u}_{i-}}{\mathrm{\partial }y}-\alpha Q\frac{\mathrm{\partial }\phi }{\mathrm{\partial }x}=0,\end{array}$(2b) (2c) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_{i-}}{\mathrm{\partial }t}+u_{i-}\frac{\mathrm{\partial }{v}_{i-}}{\mathrm{\partial }x}+v_{i-}\frac{\mathrm{\partial }{v}_{i-}}{\mathrm{\partial }y}-\alpha Q\frac{\mathrm{\partial }\phi }{\mathrm{\partial }y}=0,\end{array}$(2c) which is supplemented by Poisson's equation: (3) $(\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}^2})\phi =\mu n_{i-}-n_{i+}+n_e-n_p.$(3) Where $n_{i(-,+)}$ denotes the density of negative and positive ions normalized by $n_{i(+,-)}^{(0)};$ $u_{i-},v_{i-}(u_{i+},v_{i+})$ are the fluid velocities of ions (normalized by $C_s=(K_B{T}_e/m_{i+}{)}^{1/2}$), potential φ (normalized by$\frac{K_B{T}_e}{e{Z}_{i+}}$), $x,t$ (normalized by ${\lambda }_D=(K_B{T}_e/4\pi e^2{Z}_{i+}^2{n}_{i+}^{(0)}{)}^{1/2}$ and ${\omega }_{pi}^{-1}=(m_{i+}/4\pi e^2{Z}_{i+}^2{n}_{i+}^{(0)}{)}^{1/2}$, respectively). $\tilde{\nu }$ is the frequency for loss in positive ion momentum due to the recombination on negative one and the collisions between them, ${\nu }_{+}({\nu }_{-})$ are the ionization frequency of plasma. These collision frequencies are normalized by ${\omega }_{pe}^{-1}$. $Q=m_{i+}/m_{i-}$ is the mass ratio of positive–negative ions, $\alpha =$ $Z_{i-}/Z_{i+}$ where $Z_{i\mp }$ are charges number. Here, $T_e$ and $K_B$ are electrons temperature and Boltzmann constant. The electron and positron density ($N_e$ and $N_p$) expressions through the nonextensive velocity distribution function can be written as: (4) $\begin{array}{rl}{N}_e& ={\mu }_e{(1+(q-1)\phi )}^{\frac{q+1}{2(q-1)}},\\ N_p& ={\mu }_p{(1-\sigma (q-1)\phi )}^{\frac{q+1}{2(q-1)}},\end{array}$(4) where $\sigma =T_e/T_p$ and $T_p(T_e)$ is the positron (electron) temperature. The q-nonextensive distributed electrons and positrons are used on similar notations in [53,54] wherein the algebraic calculations are given in details.

Where q>−1. Thus, condition equilibrium reads (5) $\mu +{\mu }_e={\mu }_p+1,$(5) with $\mu =Z_{i-}{n}_{i-}^{(0)}/Z_{i+}{n}_{i+}^{(0)},$ ${\mu }_p=n_p^{(0)}/Z_{i+}{n}_{i+}^{(0)},$ and ${\mu }_e=n_e^{(0)}/Z_{i+}{n}_{i+}^{(0)}$.

3. Damped KP equation

We used the new stretched coordinates as: (6) $\tau ={ϵ}^{3}t,X=ϵ(x-\lambda t),\mathrm{and}Y={ϵ}^{2}y,$(6) where $ϵ(\lambda )$ is a small expansion value (velocity of IAWs), (we assumed that ${\nu }_{+}\sim {ϵ}^3{\nu }_{+0}$, $\tilde{\nu }$ $\sim {ϵ}^3{\tilde{\nu }}_0$ and ${\nu }_{-}\sim {ϵ}^3{\nu }_{-0})$. All dependent system variables are expanded in ϵ as: (7) $\begin{array}{r}\begin{array}{rl}{n}_{i(+,-)}& =1+{ϵ}^2{n}_{i(+,-)}^{(1)}+{ϵ}^4{n}_{i(+,-)}^{(2)}+{ϵ}^6{n}_{i(+,-)}^{(3)}+\cdots ,\\ u_{i(+,-)}& ={ϵ}^2(u_{i(+,-)}^{(1)}+{ϵ}^2{u}_{i(+,-)}^{(2)}+{ϵ}^4{u}_{i(+,-)}^{(3)}+\cdots ),\\ v_{i(+,-)}& ={ϵ}^3(v_{i(+,-)}^{(1)}+{ϵ}^2{v}_{i(+,-)}^{(2)}+{ϵ}^4{v}_{i(+,-)}^{(3)}+\cdots ),\\ \phi & ={ϵ}^2({\phi }^{(1)}+{ϵ}^2{\phi }^{(2)}+{ϵ}^4{\phi }^{(3)}+\cdots ).\end{array}\end{array}$(7) The boundary conditions are $|\xi |\to \mathrm{\infty },n_{i(+,-)}=1,u_{i(+,-)}=v_{i(+,-)}=0,\phi =0.$ By the use of Equations (6(6) $\tau ={ϵ}^{3}t,X=ϵ(x-\lambda t),\mathrm{and}Y={ϵ}^{2}y,$(6) ) and (7(7) $\begin{array}{r}\begin{array}{rl}{n}_{i(+,-)}& =1+{ϵ}^2{n}_{i(+,-)}^{(1)}+{ϵ}^4{n}_{i(+,-)}^{(2)}+{ϵ}^6{n}_{i(+,-)}^{(3)}+\cdots ,\\ u_{i(+,-)}& ={ϵ}^2(u_{i(+,-)}^{(1)}+{ϵ}^2{u}_{i(+,-)}^{(2)}+{ϵ}^4{u}_{i(+,-)}^{(3)}+\cdots ),\\ v_{i(+,-)}& ={ϵ}^3(v_{i(+,-)}^{(1)}+{ϵ}^2{v}_{i(+,-)}^{(2)}+{ϵ}^4{v}_{i(+,-)}^{(3)}+\cdots ),\\ \phi & ={ϵ}^2({\phi }^{(1)}+{ϵ}^2{\phi }^{(2)}+{ϵ}^4{\phi }^{(3)}+\cdots ).\end{array}\end{array}$(7) ) in Equations (1a(1a) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i+}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}(n_{i+}{u}_{i+})+\frac{\mathrm{\partial }}{\mathrm{\partial }y}(n_{i+}{v}_{i+})\\ & ={\nu }_{+}{N}_e,\end{array}$(1a) )–(3(3) $(\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}^2})\phi =\mu n_{i-}-n_{i+}+n_e-n_p.$(3) ), equating same coefficients of ϵ order. Lowest orders gives: (8) $\begin{array}{rl}{n}_{i+}^{(1)}& =\frac{{\phi }^{(1)}}{{\lambda }^2},u_{i+}^{(1)}=\frac{{\phi }^{(1)}}{\lambda },\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }X}=\frac{1}{\lambda }\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }Y}\end{array}$(8) (9) $\begin{array}{rl}{n}_{i-}^{(1)}& =-\frac{\alpha Q}{{\lambda }^2}{\phi }^{(1)},u_{i-}^{(1)}=-\frac{\alpha Q}{\lambda }{\phi }^{(1)},\\ \frac{\mathrm{\partial }{v}_{i-}^{(1)}}{\mathrm{\partial }X}& =-\frac{\alpha Q}{\lambda }\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }Y}.\end{array}$(9) With condition: (10) $\lambda =\sqrt{\frac{1+\alpha Q\mu }{C_1({\mu }_e+\sigma {\mu }_p)}},$(10) $C_1=\frac{(1+q)}{2}.$ The higher orders in ϵ reads: (11) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i+}^{(1)}}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{n}_{i+}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }}{\mathrm{\partial }X}(u_{i+}^{(2)}+u_{i+}^{(1)}{n}_{i+}^{(1)})+\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }Y}\\ & =C_1{\nu }_{+0}{\mu }_e{\phi }^{(1)},\\ & -\lambda \frac{\mathrm{\partial }{u}_{i+}^{(2)}}{\mathrm{\partial }X}+2u_{i+}^{(1)}\frac{\mathrm{\partial }{u}_{i+}^{(1)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{i+}^{(1)}}{\mathrm{\partial }\tau }\\ & +\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }X}-\lambda \frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(n_{i+}^{(1)}{u}_{i+}^{(1)}\right)\\ & +n_{i+}^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }X}=-{\tilde{\nu }}_0{u}_{i+}^{(1)},\\ & -\lambda \frac{\mathrm{\partial }{v}_{i+}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }\tau }+\frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(u_{i+}^{(1)}{v}_{i+}^{(1)}\right)+\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }Y}\\ & -\lambda \frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(n_{i+}^{(1)}{v}_{i+}^{(1)}\right)+n_{i+}^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }Y}\\ & =-{\tilde{\nu }}_0{v}_{i+}^{(1)},\end{array}$(11) (12) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i-}^{(1)}}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{n}_{i-}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }}{\mathrm{\partial }X}(u_{i-}^{(2)}+u_{i-}^{(1)}{n}_{i-}^{(1)})+\frac{\mathrm{\partial }{v}_{i-}^{(1)}}{\mathrm{\partial }Y}\\ & =-C_1{\nu }_{-0}{\mu }_p\sigma {\phi }^{(1)},\\ & u_{i-}^{(1)}\frac{\mathrm{\partial }{u}_{i-}^{(1)}}{\mathrm{\partial }X}-\lambda \frac{\mathrm{\partial }{u}_{i-}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{i-}^{(1)}}{\mathrm{\partial }\tau }-\alpha Q\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }X}=0,\\ & -\lambda \frac{\mathrm{\partial }{v}_{i-}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{v}_{i-}^{(1)}}{\mathrm{\partial }\tau }+u_{i-}^{(1)}\frac{\mathrm{\partial }{v}_{i-}^{(1)}}{\mathrm{\partial }X}-\alpha Q\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }Y}=0,\end{array}$(12) and (13) $\begin{array}{rl}\frac{{\mathrm{\partial }}^2{\phi }^{(1)}}{\mathrm{\partial }{X}^2}& =\mu n_{i-}^{(2)}-n_{i+}^{(2)}+C_1({\mu }_e+\sigma {\mu }_p){\varphi }^{(2)}\\ & +C_2({\mu }_e-{\sigma }^2{\mu }_p){\left({\varphi }^{(1)}\right)}^2,\end{array}$(13) where $C_2=(1+q)(3-q)/8$.

After several algebraic steps with the aids of Equations (8(8) $\begin{array}{rl}{n}_{i+}^{(1)}& =\frac{{\phi }^{(1)}}{{\lambda }^2},u_{i+}^{(1)}=\frac{{\phi }^{(1)}}{\lambda },\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }X}=\frac{1}{\lambda }\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }Y}\end{array}$(8) )–(10(10) $\lambda =\sqrt{\frac{1+\alpha Q\mu }{C_1({\mu }_e+\sigma {\mu }_p)}},$(10) ), and (11(11) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{i+}^{(1)}}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{n}_{i+}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }}{\mathrm{\partial }X}(u_{i+}^{(2)}+u_{i+}^{(1)}{n}_{i+}^{(1)})+\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }Y}\\ & =C_1{\nu }_{+0}{\mu }_e{\phi }^{(1)},\\ & -\lambda \frac{\mathrm{\partial }{u}_{i+}^{(2)}}{\mathrm{\partial }X}+2u_{i+}^{(1)}\frac{\mathrm{\partial }{u}_{i+}^{(1)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{i+}^{(1)}}{\mathrm{\partial }\tau }\\ & +\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }X}-\lambda \frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(n_{i+}^{(1)}{u}_{i+}^{(1)}\right)\\ & +n_{i+}^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }X}=-{\tilde{\nu }}_0{u}_{i+}^{(1)},\\ & -\lambda \frac{\mathrm{\partial }{v}_{i+}^{(2)}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{v}_{i+}^{(1)}}{\mathrm{\partial }\tau }+\frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(u_{i+}^{(1)}{v}_{i+}^{(1)}\right)+\frac{\mathrm{\partial }{\phi }^{(2)}}{\mathrm{\partial }Y}\\ & -\lambda \frac{\mathrm{\partial }}{\mathrm{\partial }X}\left(n_{i+}^{(1)}{v}_{i+}^{(1)}\right)+n_{i+}^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }Y}\\ & =-{\tilde{\nu }}_0{v}_{i+}^{(1)},\end{array}$(11) )–(13(13) $\begin{array}{rl}\frac{{\mathrm{\partial }}^2{\phi }^{(1)}}{\mathrm{\partial }{X}^2}& =\mu n_{i-}^{(2)}-n_{i+}^{(2)}+C_1({\mu }_e+\sigma {\mu }_p){\varphi }^{(2)}\\ & +C_2({\mu }_e-{\sigma }^2{\mu }_p){\left({\varphi }^{(1)}\right)}^2,\end{array}$(13) ) gives the DKP equation: (14) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }X}(\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }\tau }+AB{\phi }^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }X}+B\frac{{\mathrm{\partial }}^3{\phi }^{(1)}}{\mathrm{\partial }{X}^3}+RB{\phi }^{(1)})\\ & +\frac{\lambda }{2}\frac{{\mathrm{\partial }}^2{\phi }^{(1)}}{\mathrm{\partial }{Y}^2}=0.\end{array}$(14) Where $\begin{array}{rl}A& =\frac{3}{{\lambda }^4}(1-\mu {\alpha }^2{Q}^2-\frac{2C_2({\mu }_e-{\sigma }^2{\mu }_p){\lambda }^4}{3}),\\ B& =\frac{\lambda }{2C_1({\mu }_e+\sigma {\mu }_p)},\\ R& =\frac{{\tilde{\nu }}_0-C_1({\nu }_{+0}{\mu }_e+{\nu }_{-0}\mu {\mu }_p\sigma ){\lambda }^2}{{\lambda }^3}.\end{array}$ Analytically, Equation (14(14) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }X}(\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }\tau }+AB{\phi }^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }X}+B\frac{{\mathrm{\partial }}^3{\phi }^{(1)}}{\mathrm{\partial }{X}^3}+RB{\phi }^{(1)})\\ & +\frac{\lambda }{2}\frac{{\mathrm{\partial }}^2{\phi }^{(1)}}{\mathrm{\partial }{Y}^2}=0.\end{array}$(14) ) is not solved exactly. So, in a weakly dissipation using the transformation: (15) $\chi =LX+MY-(V_0-\frac{\lambda M^2}{2L})\tau ,$(15) where L and M are X and Y cosine directions, so, the approximated solution of Equation (14(14) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }X}(\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }\tau }+AB{\phi }^{(1)}\frac{\mathrm{\partial }{\phi }^{(1)}}{\mathrm{\partial }X}+B\frac{{\mathrm{\partial }}^3{\phi }^{(1)}}{\mathrm{\partial }{X}^3}+RB{\phi }^{(1)})\\ & +\frac{\lambda }{2}\frac{{\mathrm{\partial }}^2{\phi }^{(1)}}{\mathrm{\partial }{Y}^2}=0.\end{array}$(14) ) can be obtained as [42,55]: (16) $\begin{array}{rl}\mathrm{\Phi }(\chi ,\tau )& ={\varphi }_1(\tau ){\mathrm{sech}}^2\\ & \times \left(\frac{\sqrt{\frac{a}{b}{\varphi }_1(\tau )}(\chi -\frac{1}{3}a{\int }_0^T{\varphi }_1\left({\tau }^{-}\right)\mathrm{d}{\tau }^{-})}{2\sqrt{3}}\right),\\ a& =ABL,\\ b& =B{L}^3.\end{array}$(16) With (17) $\begin{array}{rl}{\varphi }_1(\tau )& ={\varphi }_0(0)e^{-\frac{4\theta \tau }{3}},\end{array}$(17) (18) $\begin{array}{rl}W(\tau )& =\frac{2\sqrt{3}b{e}^{\frac{4\theta \tau }{3}}\sqrt{\frac{a{\varphi }_0(0)e^{-\frac{4\theta \tau }{3}}}{b}}}{a{\varphi }_0(0)},\end{array}$(18) (23) $\begin{array}{rl}{\varphi }_0(0)& =\frac{3V_0}{a},\theta =RB,\end{array}$(23) where the amplitude and width ${\varphi }_1(\tau )$and $W(\tau )$ and ${\varphi }_0(0)$is the amplitude for C = 0.

4. Results and discussion

The IAW properties in our model are explained. The model equations are reduced to nonlinear DKP equations with the damped term. Using parameters corresponding to D-F-Earth's ionosphere, the damped wave properties have been examined [25,28,56]. 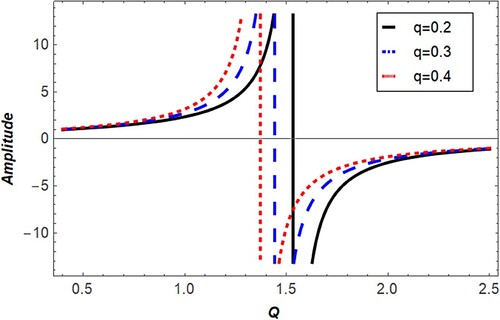Since, our intent is to check some effects of the frequencies of collision parameters (${\nu }_{+},\tilde{\nu },{\nu }_{-}),$ the ionic mass ratio $(Q=m_{+}/m_{-})$, and the index of nonextensive (q) on the IAW formation. The studied system supports the coexistence of compressive and rarefactive damped soliton kind as in Figure 1.

Figure 1. Change of the amplitude ${\varphi }_1(\tau )$ with $Q$and q for ${\mu }_e=0.4,\sigma =1.1,{\mu }_p=0.6,\alpha$ $=1.0,V_0=0.5,{\tilde{\nu }}_0=0.7,L=0.86,{\nu }_{+0}=0.3,{\nu }_{-0}=0.3,$ and $\tau =1.$

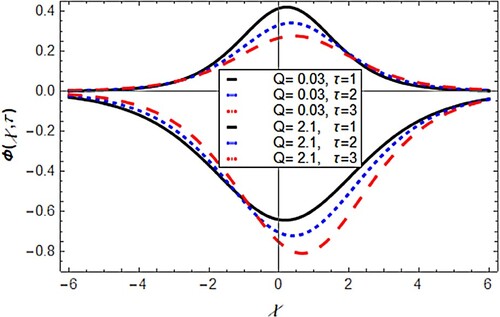
As clear in Figure 1, at value of Q $(Q=0.03)$ i.e. $(H^{+},O_2^{-})$ a positive potential is existed, whereas at $(Q=2.1)$ i.e. $(A{r}^{+},F^{-})$ a negative potential is existed. To show the potency of wave formation on Q parameter, the potential time evolutions are given in Figure 2. It was shown that the compressive potential damped with time, but rarefactive potential growing with time. 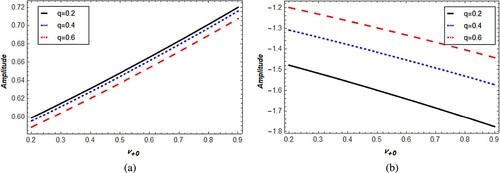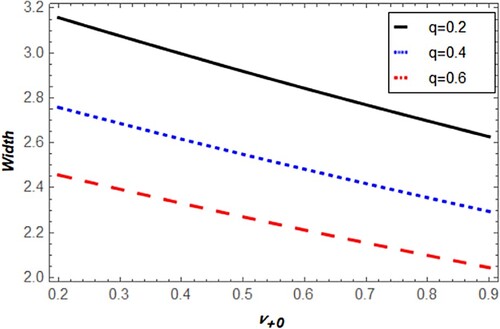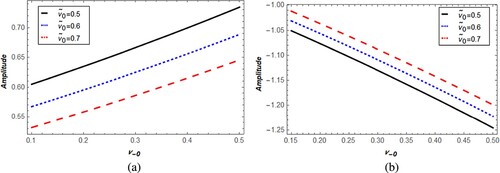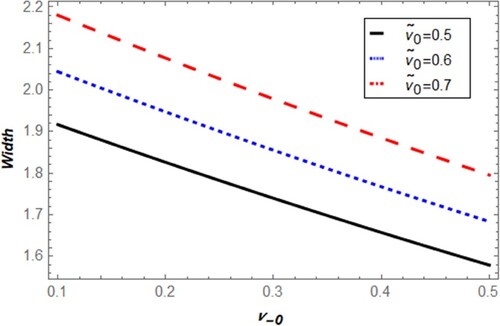The sensitivity of potential properties due to the parameters q and the model frequency parameters ${\nu }_{+0}$, ${\nu }_{-0}$ and ${\tilde{\nu }}_0$ on the potential amplitude and width are investigated in Figures 3–6. The amplitudes of both compressive and rarefactive potential decrease by q also their width decreases as depicted in Figures 3 and 4. On the other hand, it is apparent from Figures 3–6 that the potential amplitudes magnitude of compressive and rarefactive generations decreases by ${\tilde{\nu }}_0$ and increases with ${\nu }_{+0}$ and ${\nu }_{-0}$. Accordingly, the two types of width raise with ${\tilde{\nu }}_0$ and decrease by ${\nu }_{+0}$ and ${\nu }_{-0}$.

Figure 2. Variation of $\mathrm{\Phi }(\chi ,\tau )$ versus χ and for Q = 0.03 (thick lines) and Q = 2.1 (thin lines), with $L=0.86,\sigma =1.1,V_0=0.4,{\mu }_p=0.7,{\mu }_e=0.4,\alpha =1.0,{\nu }_{+0}=0.3,{\tilde{\nu }}_0=0.7,{\nu }_{-0}=0.3,$ and q = 1.5.

Figure 3. Change of ${\varphi }_1(\tau )$ with ${\nu }_{+0}$ for different q when $\alpha =1.0,\sigma =1.1,L=0.86,V_0=0.5,{\mu }_e=0.5,{\mu }_p=0.7,{\tilde{\nu }}_0=0.7,{\nu }_{-0}=0.3$, $\tau =1,$ and q = 1.0 with (a) Q = 0.03; (b) Q = 2.1.

Figure 4. Change of $W(\tau )$ with ${\nu }_{+0}$ for different q when $\sigma =1.1,L=0.86,\alpha =1.0,V_0=0.5,{\mu }_e=0.5,{\mu }_p=0.7,{\tilde{\nu }}_0=0.7,{\nu }_{-0}=0.3$, $\tau =1,q=1.0,$ and Q = 0.03.

Figure 5. Variation of ${\varphi }_1(\tau )$ with ${\nu }_{-0}$ for different ${\tilde{\nu }}_0$ when $L=0.86,V_0=0.5,\alpha =1.0,\sigma =1.1$, ${\mu }_e=0.5,{\mu }_p=0.7,{\nu }_{+0}=0.3,q=1.0$, and $\tau =1$ with (a) Q = 0.03; (b) Q = 2.1.

Figure 6. Variation of $W(\tau )$ with ${\nu }_{-0}$for different ${\tilde{\nu }}_0$ when $\alpha =1.0,L=0.86,\sigma =1.1,V_0=0.5,{\mu }_e=0.5,{\mu }_p=0.7,{\nu }_{+0}=0.3,q=1.0$, $\tau =1$, and Q = 0.03.

5. Conclusions

Nonextensive positron plasma mode has been investigated by the damped nonlinear DKP equation. Both damped compressive and rarefactive solitons are obtained. It was reported that the properties of existing solitons are damping or growing with time in the ionosphere plasma model and affecting by the parameter of nonextensivity and each positive and negative ion masses.

Acknowledgment

This project was supported financially by the Academy of Scientific Research and Technology (ASRT), Egypt [grant number 6493] under the project Science Up. (ASRT) is the 2nd affiliation of this research.

Disclosure statement

No potential conflict of interest was reported by the authors.