On the multiplicative Legendre equation

Abstract

When exponentials are employed to model procedures and efficacies appearing in real life, an additive derivative of this type of function does not exist. From this perspective, we define the Legendre equation in multiplicative analysis by several algebraic structures. Multiplicative Legendre polynomials of constituted problem are obtained by the power series solution method. Moreover, for the multiplicative Legendre equation, the generating function is obtained, and an integral presentation is constructed. Eventually, some fundamental spectral features of the multiplicative Legendre problem are analysed.

Keywords:

• Legendre equation
• multiplicative calculus
• multiplicative Sturm-Liouville equation
• non-Newtonian calculus

Mathematics Subject Classification (2020):

• 44A15
• 11N05

1. Introduction

In 1960s, multiplicative analysis was firstly presented as an alternative to usual analysis [1, 2]. At the same time, this analysis is entitled Geometric analysis, which is one of the sub-branches of Non-Newtonian analysis. Multiplicative analysis is a useful complement to usual analysis for problems consisting $\exp$-functions. This analysis changes the roles of known operations such as multiplication instead of addition and division instead of subtraction due to the properties of the logarithm. There are lots of causes to handle multiplicative analysis. It develops additive calculations circuitously. Some difficult problems in the usual analysis may be arranged incredibly easily here. In the usual analysis, each feature may be redefined in the multiplicative analysis by specific rules.

Many phenomena in real life change exponentially. For instance: populations of countries, the intensity of the earthquake [3] are affairs that behave this way. Therefore, considering multiplicative analysis in place of usual analysis lets better physical appraisal of these events. This analysis also yields better outcomes than the usual case in numerous fields such as finance, biology and demography. Limited edition of studies have been conducted on this analysis until the turn of millennium. Lately, numerous studies have been carried out on it and high-quality and efficacious outcomes have been acquired [4–13].

Legendre's equation is an equation that arises when solving Laplace and Helmotz equations in spherical coordinates and has important applications in physics and different technical fields [14]. Legendre equation is frequently encountered in classical and quantum mechanics, electromagnetic theory together with spherical coordinates. Solution functions of this equation are called Legendre polynomials. Legendre polynomials were first described by Legendre in 1785. Legendre polynomials also have an important place in the family of orthogonal polynomials. In classical case, this equation and the solution polynomials have been discussed in many studies (see Refs. [15–33]). Legendre equation, which has a very important place in a classical sense, and its solutions will be dealt with in a multiplicative sense and will be examined in detail.

In this study, out of the usual analysis, the Legendre equation and its features reconstruct in a multiplicative analysis with similar techniques analogous to the usual analysis. This equation will be called the multiplicative Legendre Equation (${}^{\ast }$Legendre Eq.). This equation is essentially a more complicated equation in the classical case. Firstly, we recall some notions and significant theorems of the multiplicative analysis from Ref. [4].

Definition 1.1

[4]

Let $\phi :E\subset \mathbb{R}\to {\mathbb{R}}^{+}$ be usual differentiable for all t. Provided that the following limit exists and positive ${\phi }^{\ast }\left(t\right)=\underset{ϵ\to 0}{lim}{\left[\frac{\phi (t+ϵ)}{\phi \left(t\right)}\right]}^{\frac{1}{ϵ}},$${\phi }^{\ast }\left(t\right)$ is entitled ${}^{\ast }$derivative (or multiplicative derivative) of φ at t. Futhermore, φ be usual differentiable at t, then ${\phi }^{\ast \left(n\right)}\left(t\right)=\exp \left\{{(\ln \circ \phi )}^{\left(n\right)}\left(t\right)\right\}.$

Theorem 1.1

[4]

Let $\phi ,\psi$ be ${}^{\ast }$differentiable and ϕ be usual differentiable at t. Below relations hold for ${}^{\ast }$derivative.

1. $\left(\alpha \phi {)}^{\ast }\right(t)={\phi }^{\ast }(t),\alpha \in {\mathbb{R}}^{+},$

2. $\left(\phi \psi {)}^{\ast }\right(t)={\phi }^{\ast }(t\left){\psi }^{\ast }\right(t),$

3. $\left(\phi /\psi {)}^{\ast }\right(t)={\phi }^{\ast }(t\left)/{\psi }^{\ast }\right(t),$

4. $\left({\phi }^{\varphi }{)}^{\ast }\right(t)={\phi }^{\ast }(t{)}^{\varphi \left(t\right)}\phi (t{)}^{{\varphi }^{\mathrm{\prime }}\left(t\right)},$

5. $(\phi \circ \varphi {)}^{\ast }(t)=({\phi }^{\ast }\circ \varphi \left)\right(t{)}^{{\varphi }^{\mathrm{\prime }}\left(t\right)},$

6. $(\phi +\psi {)}^{\ast }(t)={\phi }^{\ast }(t{)}^{\frac{\phi \left(t\right)}{\phi \left(t\right)+\psi \left(t\right)}}{\psi }^{\ast }(t{)}^{\frac{\psi \left(t\right)}{\phi \left(t\right)+\psi \left(t\right)}}.$

Since integration in multiplicative sense will occur while obtaining Legendre polynomials for ${}^{\ast }$Legendre Eq., let us express fundamental properties of multiplicative integration.

Definition 1.2

[4]

Let $\phi \in {\mathbb{R}}^{\mathbb{+}}$ is integrable on $[a,b]$, then ${\int }_a^b\phi (t{)}^{\mathrm{d}t}=\exp \left\{{\int }_a^b(\ln \circ \phi )\left(t\right)\mathrm{d}t\right\},$where ${\int }_a^b\phi (t{)}^{\mathrm{d}t}$ denotes the ${}^{\ast }$integral (or multiplicative integral) of φ on $[a,b]$.

Conversely, if ${}^{\ast }$integrability of φ on $[a,b]$ implies ${\int }_a^b\phi \left(t\right)\mathrm{d}t=\ln {\int }_a^b{\left({\mathrm{e}}^{\phi \left(t\right)}\right)}^{\mathrm{d}t}.$

Theorem 1.2

[4]

Let $\phi ,\psi >0$ be bounded, ${}^{\ast }$integrable and $\varphi >0$ be usual differentiable on $[a,b]$. Below relations hold for ${}^{\ast }$integral.

1. ${\int }_a^b\left[\phi \right(t{)}^{\alpha }{]}^{\mathrm{d}t}=\left[{\int }_a^b\phi \right(t{)}^{\mathrm{d}t}{]}^{\alpha },$ $\alpha \in \mathbb{R}$,

2. ${\int }_a^b\left[\phi \right(t\left)\psi \right(t){]}^{\mathrm{d}t}={\int }_a^b\phi (t{)}^{\mathrm{d}t}{\int }_a^b\psi (t{)}^{\mathrm{d}t},$

3. ${\int }_a^b[\frac{\phi \left(t\right)}{\psi \left(t\right)}{]}^{\mathrm{d}t}=\frac{{\int }_a^b\phi (t{)}^{\mathrm{d}t}}{{\int }_a^b\psi (t{)}^{\mathrm{d}t}},$

4. ${\int }_a^b\phi (t{)}^{\mathrm{d}t}={\int }_a^c\phi (t{)}^{\mathrm{d}t}{\int }_c^b\phi (t{)}^{\mathrm{d}t}$, $c\in [a,b]$,

5. ${}^{\ast }$integration by parts formula: $\begin{array}{rl}& {\int }_a^b{\left[{\phi }^{\ast }\right(t{)}^{\psi \left(t\right)}]}^{\mathrm{d}t}\\ & =\frac{\phi (b{)}^{\psi \left(b\right)}}{\phi (a{)}^{\psi \left(a\right)}}{\left\{{\int }_a^b{\left[\phi \right(t{)}^{{\psi }^{\mathrm{\prime }}\left(t\right)}]}^{\mathrm{d}t}\right\}}^{-1}.\end{array}$

Definition 1.3

[34]

Assume that $\mathrm{\Omega }\ne \mathrm{\varnothing }$ and $〈,{〉}_{\ast }:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{R}}^{+}$ is a function where below axioms hold for $\mathrm{\forall }\phi ,\psi ,\varphi \in \mathrm{\Omega }$

1. $〈\phi ,\phi {〉}_{\ast }\ge 1,$

2. $〈\phi ,\phi {〉}_{\ast }=1$ iff $\phi =1,$

3. $〈\phi \oplus \psi ,\varphi {〉}_{\ast }=〈\phi ,\varphi {〉}_{\ast }\oplus 〈\psi ,\varphi {〉}_{\ast },$

4. $〈{\mathrm{e}}^{\alpha }\odot \phi ,\psi {〉}_{\ast }={\mathrm{e}}^{\alpha }\odot 〈\phi ,\psi {〉}_{\ast },\alpha \in \mathbb{R}$

5. $〈\phi ,\psi {〉}_{\ast }=〈\psi ,\phi {〉}_{\ast }.$

Then, $(\mathrm{\Omega },〈,{〉}_{\ast })$ is ${}^{\ast }$inner product space where $〈,{〉}_{\ast }$ is ${}^{\ast }$inner product on Ω.

Lemma 1.1

[34]

${}^{\ast }{L}_2[a,b]=\{\phi \in {\mathbb{R}}^{+}:{\int }_a^b[\phi \left(t\right)\odot \phi \left(t\right){]}^{\mathrm{d}t}<\mathrm{\infty }\}$ is an ${}^{\ast }$inner product space with $\begin{array}{rl}& 〈,{〉}_{\ast }:{}^{\ast }{L}_2[a,b]\times {}^{\ast }{L}_2[a,b]\to {\mathbb{R}}^{+},\\ & 〈\phi ,\psi {〉}_{\ast }={\int }_a^b{\left[\phi \right(t)\odot \psi (t\left)\right]}^{\mathrm{d}t},\end{array}$where $\phi ,\psi \in {}^{\ast }{L}_2[a,b]$.

Proof.

It can be proved using features of ${}^{\ast }$inner product with ease.

The remainder of the study is edited as follows: next section, we construct ${}^{\ast }$Legendre Eq. by arithmetic operations. The expansions for ${}^{\ast }$eigenfunction of ${}^{\ast }$Legendre Eq. are constructed by series technique. Moreover, for ${}^{\ast }$Legendre Eq., the generating function is obtained and an integral presentations is constructed. Eventually, several spectral features of ${}^{\ast }$Legendre Eq. are investigated in the last section.

2. The Legendre equation on the multiplicative analysis

We give Legendre equation in the multiplicative analysis by several algebraic structures and Legendre polynomials of the obtained problem acquire. For this purpose, let us initially state algebraic structures that we will encounter while constructing and solving ${}^{\ast }$Legendre Eq. The arithmetic operations occurred by exp-functions are known as multiplicative algebraic operations. Let's denote some features of these operations with below arithmetic table for $\phi ,\psi \in {\mathbb{R}}^{+}.$ $p\ominus r=\frac{p}{r},p\oplus r=pr,p\odot r=p^{\ln r}=r^{\ln p}.$Above operations construct several algebraic structures. If $\oplus :E\times E\to E$ is an operation for $E\ne \mathrm{\varnothing }$ and $E\subset {\mathbb{R}}^{+},$ $(E,\oplus )$ is a ${}^{\ast }$group. Analogously, $(E,\oplus ,\odot )$ defines a ring in multiplicative sense [35].

nth order linear-homogeneous ${}^{\ast }$differential equation is indicated by $\begin{array}{rl}& {\left(y^{\ast \left(n\right)}\right)}^{a_n\left(t\right)}{\left(y^{\ast (n-1)}\right)}^{a_{n-1}\left(t\right)}\cdots \\ & {\left(y^{\ast \ast }\right)}^{a_2\left(t\right)}{\left(y^{\ast }\right)}^{a_1\left(t\right)}{y}^{a_0\left(t\right)}=1,\end{array}$where $a_n\left(t\right),\dots ,a_2\left(t\right),a_1\left(t\right),a_0\left(t\right)$ depend on t [13].

Consider the multiplicative Sturm-Liouville equation (1) $\begin{array}{rl}& \mathcal{L}\left[y\right]:=\left\{\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}({\mathrm{e}}^{p\left(t\right)}\odot \frac{{\mathrm{d}}^{\ast }y}{\mathrm{d}t})\right\}\oplus ({\mathrm{e}}^{q\left(t\right)}\odot y)\oplus \\ & ({\mathrm{e}}^{\lambda w\left(t\right)}\odot y)=1,\end{array}$(1) where λ is spectral parameter; $p\left(t\right)$, $q\left(t\right)$ and $w\left(t\right)$ are real-valued continuous functions [34]. If $p\left(t\right)=1-t^2,$ $q\left(t\right)=0,$ $w\left(t\right)=1$, Equation (1(1) $\begin{array}{rl}& \mathcal{L}\left[y\right]:=\left\{\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}({\mathrm{e}}^{p\left(t\right)}\odot \frac{{\mathrm{d}}^{\ast }y}{\mathrm{d}t})\right\}\oplus ({\mathrm{e}}^{q\left(t\right)}\odot y)\oplus \\ & ({\mathrm{e}}^{\lambda w\left(t\right)}\odot y)=1,\end{array}$(1) ) is converted to $\mathcal{L}\left[y\right]:={\left[{\left(y^{\ast }\right(t\left)\right)}^{(1-t^2)}\right]}^{\ast }{y}^{\lambda }=1,t\in [a,b]$or (2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) where $a,b\in \mathbb{R}$ and, λ is a spectral parameter. If we set $\lambda =n(n+1),$ Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) is called n-th order multiplicative Legendre equation (${}^{\ast }$Legendre Eq.). Here, $y(t,\lambda )>0$ is solution of above equation which is called multiplicative Legendre polynomial. The points $t=\pm 1$ and t = 0 are multiplicative singular points and a multiplicative ordinary point of Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ), respectively.

Let us examine solutions on the neighbourhood of this point.

Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) will be considered together with the below condition. (3) $\underset{t\to \pm 1}{lim}\left|y(t,\lambda )\right|<\mathrm{\infty }.$(3) Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) corresponds to the following nonlinear differential equation in a classical case. The spectral properties of ${}^{\ast }$Legendre Eq. coincide with the properties of this nonlinear equation on a classical sense $\begin{array}{rl}& [(1-t^2)y^{\mathrm{\prime }\mathrm{\prime }}-2t{y}^{\mathrm{\prime }}+\lambda y]y\\ & -[(1-t^2){\left(y^{\mathrm{\prime }}\right)}^2+\lambda y^2(1-\ln y)]=0.\end{array}$Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) has a series solution in the below form: (4) $y\left(t\right)=\prod _{k=0}^{\mathrm{\infty }}{c}_k^{t^k},$(4) where $c_k$ are real positive constants from [13, Theorem 3.1]. Taking 1st and 2nd ${}^{\ast }$derivatives of (4(4) $y\left(t\right)=\prod _{k=0}^{\mathrm{\infty }}{c}_k^{t^k},$(4) ), we acquire (5) $y^{\ast }\left(t\right)=\prod _{k=1}^{\mathrm{\infty }}{c}_k^{k{t}^{k-1}},y^{\ast \ast }\left(t\right)=\prod _{k=2}^{\mathrm{\infty }}{c}_k^{(k-1)k{t}^{k-2}}.$(5) By considering (4(4) $y\left(t\right)=\prod _{k=0}^{\mathrm{\infty }}{c}_k^{t^k},$(4) ) and (5(5) $y^{\ast }\left(t\right)=\prod _{k=1}^{\mathrm{\infty }}{c}_k^{k{t}^{k-1}},y^{\ast \ast }\left(t\right)=\prod _{k=2}^{\mathrm{\infty }}{c}_k^{(k-1)k{t}^{k-2}}.$(5) ) in Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ), it gives $\prod _{k=0}^{\mathrm{\infty }}{\left[c_{k+2}^{(k+1)(k+2)}{c}_k^{-k(k+1)+\lambda }\right]}^{t^k}=1.$If regulation is made according to coefficients, the below system is obtained: (6) $\begin{array}{rl}{c}_2^2{c}_0^{\lambda }& =1,\\ c_3^{2.3}{c}_1^{\lambda -2}& =1,\\ & ⋮\\ c_{k+2}^{(k+1)(k+2)}{c}_k^{-k(k+1)+\lambda }& =1.\end{array}$(6) That is, (7) $c_{k+2}=c_k^{-\frac{k(k+1)-\lambda }{(k+1)(k+2)}},k=2,3,4,\dots$(7) or $\begin{array}{rl}{c}_{2k}& =c_0^{(-1{)}^k\frac{\lambda (\lambda -2.3)(\lambda -4.5)\cdots (\lambda -(2k-2)(2k-1))}{\left(2k\right)!}},\\ c_{2k+1}& =c_1^{(-1{)}^k\frac{(\lambda -2)(\lambda -3.4)(\lambda -5.6)\cdots (\lambda -(2k-1)2k)}{(2k+1)!}},\\ & k=1,2,3,\dots .\end{array}$Thus, the general solution of ${}^{\ast }$Legendre Eq. (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) follows as $y(t,\lambda )=\prod _{k=0}^{\mathrm{\infty }}{c}_k^{t^k}=\prod _{k=0}^{\mathrm{\infty }}{c}_{2k}^{t^{2k}}\prod _{k=0}^{\mathrm{\infty }}{c}_{2k+1}^{t^{2k+1}},$or $\begin{array}{rl}y(x,\lambda )& =c_0^{1+\sum _{k=1}^{\mathrm{\infty }}(-1{)}^k\frac{\lambda (\lambda -2.3)(\lambda -4.5)\cdots (\lambda -(2k-2)(2k-1))}{\left(2k\right)!}{t}^{2k}}\\ & \times c_1^{x+\sum _{k=1}^{\mathrm{\infty }}(-1{)}^k\frac{(\lambda -2)(\lambda -3.4)(\lambda -5.6)\cdots (\lambda -(2k-1)2k)}{(2k+1)!}{t}^{2k+1}},\end{array}$where $c_0$ and $c_1$ are arbitrary constants. Both two series involved in the power of the solution are convergent for $\left|x\right|<1.$

Let ${\lambda }_n=n(n+1).$ Here, if n is even and odd, the functions $y_1\left(t\right)$ (the power of the $c_0$ term) and $y_2\left(t\right)$ (the power of the $c_1$ term) will be nth-degree polynomials, respectively. Furthermore, the ${}^{\ast }$eigenvalues of Legendre Prob. (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) )–(3(3) $\underset{t\to \pm 1}{lim}\left|y(t,\lambda )\right|<\mathrm{\infty }.$(3) ) are as follows: (8) ${\lambda }_n=n(n+1).$(8) ${}^{\ast }$Eigenfunctions ${\mathcal{P}}_n\left(t\right)$ are nth-degree multiplicative Legendre polynomials. Now let us compute these polynomials with two different methods.

Method 2.1

Suppose that $c_n$ is the basement of the highest power of t in the nth-degree polynomial. From recurrence formula (7(7) $c_{k+2}=c_k^{-\frac{k(k+1)-\lambda }{(k+1)(k+2)}},k=2,3,4,\dots$(7) ) and ${}^{\ast }$eigenvalues (8(8) ${\lambda }_n=n(n+1).$(8) ), we get $c_k=c_{k+2}^{-\frac{(k+1)(k+2)}{(n-k)(n+k+1)}}.$

Then, it can be written as (9) $c_{n-2m}=c_n^{(-1{)}^m\frac{n(n-1)(n-2)\cdots (n-2m+1)}{\mathrm{2.4.}\left(2m\right)(2n-1)(2n-3)\cdots (2n-2m+1)}},$(9) for $m=0,1,2,\dots .$ By considering below relations $\begin{array}{rl}& n(n-1)(n-2)\cdots (n-2m+1)=\frac{n!}{(n-2m)!},\\ & \left(2\right)\left(4\right)\cdots \left(2m\right)(2n-1)(2n-3)\cdots (2n-2m+1)\\ & =\frac{\left(2n\right)!(n-m)!m!}{(2n-2m)!n!},\end{array}$it yields $c_{n-2m}=c_n^{(-1{)}^m\frac{{(n!)}^2(2n-2m)!}{m!\left(2n\right)!(n-m)!(n-2m)!}}.$Therefore, (10) $y(t,\lambda )=\prod _{m=0}^{\left[\frac{n}{2}\right]}{c}_n^{(-1{)}^m\frac{{(n!)}^2(2n-2m)!}{m!\left(2n\right)!(n-m)!(n-2m)!}{t}^{n-2m}},$(10) where (11) $\left[\frac{n}{2}\right]=\{\begin{array}{ll}{\displaystyle \frac{n}{2}},& \mathrm{i}\mathrm{f}n\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\\ {\displaystyle \frac{n-1}{2}},& \mathrm{i}\mathrm{f}n\mathrm{o}\mathrm{d}\mathrm{d}\end{array}.$(11) Equation (10(10) $y(t,\lambda )=\prod _{m=0}^{\left[\frac{n}{2}\right]}{c}_n^{(-1{)}^m\frac{{(n!)}^2(2n-2m)!}{m!\left(2n\right)!(n-m)!(n-2m)!}{t}^{n-2m}},$(10) ) is general solution of Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) for all $c_n\in {\mathbb{R}}^{+}.$ By setting $c_n={\mathrm{e}}^{\frac{\left(2n\right)!}{2^n(n!{)}^2}}$, nth degree ${}^{\ast }$Legendre polynomial is acquired as follows, (12) ${\mathcal{P}}_n\left(t\right)=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{(-1{)}^m\frac{(2n-2m)!}{2^{n}m!(n-m)!(n-2m)!}{t}^{n-2m}}.$(12) Additionally, by taking the multiplicative derivative of the expansion $(t^2-1{)}^n=\sum _{m=0}^n{(-1)}^m\frac{n!}{m!(n-m)!}{t}^{2n-2m},$n-times, we get (13) ${\mathcal{P}}_n\left(t\right)={\left[\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{x}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right]}^{\frac{1}{2^{n}n!}},n=0,1,2,\dots .$(13) Here, the formula in (13(13) ${\mathcal{P}}_n\left(t\right)={\left[\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{x}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right]}^{\frac{1}{2^{n}n!}},n=0,1,2,\dots .$(13) ) is defined multiplicative Rodrigues formula.

Method 2.2

Let us consider the exponential functions $z={\mathrm{e}}^{(t^2-1{)}^n}.$ By taking n-times multiplicative derivative of this exponential functions, we get below multiplicative differential equation, ${\left(z^{\ast }\right)}^{t^2-1}{z}^{-2nt}=1.$

If we take the multiplicative derivative of the last equation, (14) ${\left[{\left(z^{\ast \left(n\right)}\right)}^{t^2-1}\right]}^{\ast }.{\left[z^{\ast \left(n\right)}\right]}^{-n(n+1)}=1,$(14) is obtained. Since Equations (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) and (14(14) ${\left[{\left(z^{\ast \left(n\right)}\right)}^{t^2-1}\right]}^{\ast }.{\left[z^{\ast \left(n\right)}\right]}^{-n(n+1)}=1,$(14) ) are identical, we get $y\left(t\right)={\left(z^{\ast \left(n\right)}\right)}^c,$where c is an arbitrary power. For $c=\frac{1}{2^{n}n!}$, the equality (13(13) ${\mathcal{P}}_n\left(t\right)={\left[\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{x}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right]}^{\frac{1}{2^{n}n!}},n=0,1,2,\dots .$(13) ) arises. This formula can also be expressed as follows, ${\mathcal{P}}_n\left(t\right)=={\mathrm{e}}^{\frac{1}{2^{n}n!}\frac{{\mathrm{d}}^n}{\mathrm{d}{x}^n}{(t^2-1)}^n}={\mathrm{e}}^{P_n\left(t\right)},n=0,1,2,\dots ,$where $P_n\left(t\right)$ is the usual Legendre polynomial.

Now, let us state some occasions of ${}^{\ast }$Legendre polynomials, which have an important place in applications.

Remark 2.1

By (13(13) ${\mathcal{P}}_n\left(t\right)={\left[\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{x}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right]}^{\frac{1}{2^{n}n!}},n=0,1,2,\dots .$(13) ), some ${}^{\ast }$Legendre polynomials are as follows. $\begin{array}{rl}{\mathcal{P}}_0\left(t\right)& =e,\\ {\mathcal{P}}_1\left(t\right)& ={\mathrm{e}}^t,\\ {\mathcal{P}}_2\left(t\right)& ={\mathrm{e}}^{\frac{1}{2}(3t^2-1)},\\ {\mathcal{P}}_3\left(t\right)& ={\mathrm{e}}^{\frac{1}{2}(5t^3-t)},\\ {\mathcal{P}}_4\left(t\right)& ={\mathrm{e}}^{\frac{1}{8}(35t^4-30t^2+3)}\\ & ⋮\end{array}$

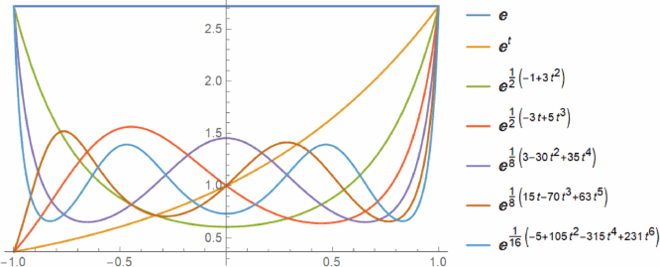
Features of usual Legendre polynomials [14] can be generalized to ${}^{\ast }$Legendre polynomials as follows:

Lemma 2.1

${}^{\ast }$Legendre polynomials provide the following properties:

1. ${\mathcal{P}}_n(-t)=\left[{\mathcal{P}}_n\right(t){]}^{(-1{)}^n},{\mathcal{P}}_n^{\ast }(-t)=[{\mathcal{P}}_n^{\ast }\left(t\right){]}^{(-1{)}^{n+1}},$

2. ${\mathcal{P}}_n^{\ast }\left(1\right)={\mathrm{e}}^{\frac{n(n+1)}{2}},{\mathcal{P}}_n^{\ast }(-1)={\mathrm{e}}^{(-1{)}^{n-1}\frac{n(n+1)}{2}},$

3. $\left[{\mathcal{P}}_{n+1}\right(t){]}^{n+1}=\frac{\left[{\mathcal{P}}_n\right(t){]}^{(2n+1)t}}{\left[{\mathcal{P}}_{n-1}\right(t){]}^n},$

4. ${\mathcal{P}}_n^{\ast }\left(t\right)=\left[{\mathcal{P}}_{n-1}^{\ast }\right(t\left){]}^t\right[{\mathcal{P}}_{n-1}^{\ast }\left(t\right){]}^n,$

5. ${\mathcal{P}}_n\left(t\right)=\left[{\mathcal{P}}_{n-1}\right(t\left){]}^t\right[{\mathcal{P}}_{n-1}^{\ast }\left(t\right){]}^{\frac{t^2-1}{n}},$

6. $\frac{{\mathcal{P}}_{n+1}^{\ast }\left(t\right)}{{\mathcal{P}}_{n-1}^{\ast }\left(t\right)}=\left[{\mathcal{P}}_n\right(t){]}^{2n+1},$

Proof.

From the multiplicative Rodrigues formula, the proofs of these features can be easily made similar to the classical situation.

Now, let us get generating function for ${}^{\ast }$Legendre Eq. and integral representations of ${}^{\ast }$Legendre polynomial:

Lemma 2.2

The generating function of ${}^{\ast }$Legendre polynomials has the following representation: (15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15)

Proof.

Consider the following function (16) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n\end{array}\right)x^n{(2t-x)}^n},$(16) where the binomial coefficients are in the form of $\left(\begin{array}{c}-\frac{1}{2}\\ n\end{array}\right)=\frac{{(-1)}^n\left(2n\right)!}{2^{2n}{(n!)}^2}.$Additionally, in (16(16) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n\end{array}\right)x^n{(2t-x)}^n},$(16) ), by considering the binomial expansion of the term ${\mathrm{e}}^{{(2t-x)}^n}$, we have $L(t,x)=\prod _{n=0}^{\mathrm{\infty }}\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n-m\end{array}\right)\left(\begin{array}{c}n-m\\ m\end{array}\right){\left(2x\right)}^{n-2m}{t}^n}.$In last equality, let us denote in the form below: (17) ${\mathcal{P}}_n\left(t\right)=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n-m\end{array}\right)\left(\begin{array}{c}n-m\\ m\end{array}\right){\left(2t\right)}^{n-2m}}.$(17) In (17(17) ${\mathcal{P}}_n\left(t\right)=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n-m\end{array}\right)\left(\begin{array}{c}n-m\\ m\end{array}\right){\left(2t\right)}^{n-2m}}.$(17) ), considering the following relation $\begin{array}{rl}& \left(\begin{array}{c}-\frac{1}{2}\\ n-m\end{array}\right)\left(\begin{array}{c}n-m\\ m\end{array}\right)\\ & =\frac{{(-1)}^{n-m}(2n-2m)!}{2^{2n-2m}(n-m)!m!(n-2m)!},\end{array}$we show that these polynomials are nth degree ${}^{\ast }$Legendre polynomials (12(12) ${\mathcal{P}}_n\left(t\right)=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{(-1{)}^m\frac{(2n-2m)!}{2^{n}m!(n-m)!(n-2m)!}{t}^{n-2m}}.$(12) ). It completes the proof.

Corollary 2.1

The Lemma 2.1 can also be proved by taking the necessary multiplicative derivatives of both sides of the equality (15(15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15) ).

Lemma 2.3

The integral representation of ${}^{\ast }$Legendre polynomials is as follows: (18) ${\mathcal{P}}_n\left(t\right)={\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}$(18)

Proof.

From the binomial expansion at the power of the exponential function in the integration on the right side of (18(18) ${\mathcal{P}}_n\left(t\right)={\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}$(18) ), we get (19) $\begin{array}{rl}& {\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}\\ & ={\int }_0^{\pi }{\left\{\prod _{m=0}^n{\mathrm{e}}^{\frac{1}{\pi }\left(\begin{array}{c}n\\ m\end{array}\right)t^{n-m}{(t^2-1)}^{\frac{m}{2}}{\cos }^{m}z}\right\}}^{\mathrm{d}z}\\ & ={\left\{\prod _{m=0}^n{\mathrm{e}}^{\left(\begin{array}{c}n\\ m\end{array}\right)t^{n-m}{(t^2-1)}^{\frac{m}{2}}}\right\}}^{\frac{1}{\pi }{\int }_0^{\pi }{\cos }^{m}z\mathrm{d}z}.\end{array}$(19) Using the calculation $\frac{1}{\pi }{\int }_0^{\pi }{\cos }^{m}z\mathrm{d}z=\{\begin{array}{ll}{\displaystyle \frac{\left(2k\right)!}{2^{2k}{(k!)}^2}},& m=2k\\ 0,& m=2k+1\end{array}$yields (20) $\begin{array}{rl}& {\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}\\ & =\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{\frac{n!}{2^{2m}(n-2m)!{(m!)}^2}{t}^{n-2m}{(t^2-1)}^m},\end{array}$(20) where $\left[\frac{n}{2}\right]$ is defined with (11(11) $\left[\frac{n}{2}\right]=\{\begin{array}{ll}{\displaystyle \frac{n}{2}},& \mathrm{i}\mathrm{f}n\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\\ {\displaystyle \frac{n-1}{2}},& \mathrm{i}\mathrm{f}n\mathrm{o}\mathrm{d}\mathrm{d}\end{array}.$(11) ).

Now, Let us show that the series on the right of equality (20(20) $\begin{array}{rl}& {\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}\\ & =\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{\frac{n!}{2^{2m}(n-2m)!{(m!)}^2}{t}^{n-2m}{(t^2-1)}^m},\end{array}$(20) ) is the ${}^{\ast }$Legendre polynomials:

Let the exponential function on the left side of equality (16(16) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\mathrm{e}}^{{(-1)}^n\left(\begin{array}{c}-\frac{1}{2}\\ n\end{array}\right)x^n{(2t-x)}^n},$(16) ) be differently represented by (21) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}={\mathrm{e}}^{\left(\frac{1}{1-tx}\right){(1-\frac{x^2(t^2-1)}{(1-tx{)}^2})}^{-\frac{1}{2}}}.$(21) By considering below relations $\begin{array}{rl}{\mathrm{e}}^{{\left(\frac{1}{1-tx}\right)}^{-\frac{1}{2}}}& =\prod _{s=0}^{\mathrm{\infty }}{\left(tx\right)}^s,\\ {(1-\frac{x^2(t^2-1)}{(1-tx{)}^2})}^{-\frac{1}{2}}& =\sum _{n=0}^{\mathrm{\infty }}{Q}_n^{x^n},\end{array}$the equality (21(21) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}={\mathrm{e}}^{\left(\frac{1}{1-tx}\right){(1-\frac{x^2(t^2-1)}{(1-tx{)}^2})}^{-\frac{1}{2}}}.$(21) ) is rearranged as $L(t,x)=\prod _{s=0}^{\mathrm{\infty }}{\left({\mathcal{P}}_n\right(t\left)\right)}^{x^n},$where (22) $Q_n=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{(-1{)}^{n-m}\left(\begin{array}{c}-\frac{1}{2}\\ m\end{array}\right)\left(\begin{array}{c}-2m\\ n-2m\end{array}\right)t^{n-2m}{(t^2-1)}^m},$(22) and (23) ${\mathcal{P}}_n\left(t\right)=\prod _{s=0}^{n-s}{\left(Q_{n-s}\right)}^{t^s}.$(23) By taking Equation (22(22) $Q_n=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{(-1{)}^{n-m}\left(\begin{array}{c}-\frac{1}{2}\\ m\end{array}\right)\left(\begin{array}{c}-2m\\ n-2m\end{array}\right)t^{n-2m}{(t^2-1)}^m},$(22) ) in (23(23) ${\mathcal{P}}_n\left(t\right)=\prod _{s=0}^{n-s}{\left(Q_{n-s}\right)}^{t^s}.$(23) ), we obtain $\begin{array}{rl}& {\mathcal{P}}_n\left(t\right)\\ & =\prod _{m=0}^{\left[\frac{n}{2}\right]}{\left(\prod _{s=0}^{n-2m}{\mathrm{e}}^{{(-1)}^{n-s}\left(\begin{array}{c}-2m\\ n-s-2m\end{array}\right)t^{n-2m}{(t^2-1)}^m}\right)}^{{(-1)}^{-m}\left(\begin{array}{c}-\frac{1}{2}\\ m\end{array}\right)}.\end{array}$Additionally, from the relation $\prod _{s=0}^{n-2m}{\mathrm{e}}^{{(-1)}^{n-s}\left(\begin{array}{c}-2m\\ n-s-2m\end{array}\right)}={\mathrm{e}}^{\frac{n!}{\left(2m\right)!(n-2m)!}},$we get ${\mathcal{P}}_n\left(t\right)=\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{{(-1)}^{-m}\left(\begin{array}{c}-\frac{1}{2}\\ m\end{array}\right)\frac{n!}{\left(2m\right)!(n-2m)!}{t}^{n-2m}{(t^2-1)}^m}.$If it is taken into account with (20(20) $\begin{array}{rl}& {\int }_0^{\pi }{\left\{{\mathrm{e}}^{\frac{1}{\pi }{(t+\sqrt{t^2-1}\cos z)}^n}\right\}}^{\mathrm{d}z}\\ & =\prod _{m=0}^{\left[\frac{n}{2}\right]}{\mathrm{e}}^{\frac{n!}{2^{2m}(n-2m)!{(m!)}^2}{t}^{n-2m}{(t^2-1)}^m},\end{array}$(20) ), the proof is completed.

3. Some spectral properties of multiplicative Legendre problem

We begin this section by reminding you of the general solution $y(t,\lambda )=\prod _{m=0}^{\left[\frac{n}{2}\right]}{c}_n^{(-1{)}^m\frac{{(n!)}^2(2n-2m)!}{m!\left(2n\right)!(n-m)!(n-2m)!}{t}^{n-2m}}$of ${}^{\ast }$Legendre Eq. (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) from Section 2.

Now let us state several spectral properties of ${}^{\ast }$Legendre polynomial.

Lemma 3.1

The ${}^{\ast }$Legendre polynomials ${\mathcal{P}}_n\left(t\right)$ and ${\mathcal{P}}_m\left(t\right)$ are orthogonal for $m\ne n.$ Furthermore, ${\int }_{-1}^1{\left[{\mathcal{P}}_n\right(t)\odot {\mathcal{P}}_m(t\left)\right]}^{\mathrm{d}x}=\{\begin{array}{ll}1,& \mathrm{i}\mathrm{f}m\ne n\\ {\mathrm{e}}^{\frac{2}{2n+1}},& \mathrm{i}\mathrm{f}m=n\end{array}.$

Proof.

Let's do the proof separately for two cases.

(i) Let $m\ne n$. Since ${}^{\ast }$Legendre polynomials ${\mathcal{P}}_n\left(t\right)$ and ${\mathcal{P}}_m\left(t\right)$ are solutions of Equation (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ), it yields (24) $\begin{array}{rl}& {\left[{\left({\mathcal{P}}_n^{\ast }\right(t\left)\right)}^{(1-t^2)}\right]}^{\ast }{\mathcal{P}}_n^{{\lambda }_n}=1,\end{array}$(24) (25) $\begin{array}{rl}& {\left[{\left({\mathcal{P}}_m^{\ast }\right(t\left)\right)}^{(1-t^2)}\right]}^{\ast }{\mathcal{P}}_m^{{\lambda }_m}=1.\end{array}$(25) Let us take $\ln {\mathcal{P}}_m$ and $\ln {\mathcal{P}}_n$th powers of (24(24) $\begin{array}{rl}& {\left[{\left({\mathcal{P}}_n^{\ast }\right(t\left)\right)}^{(1-t^2)}\right]}^{\ast }{\mathcal{P}}_n^{{\lambda }_n}=1,\end{array}$(24) ) and (25(25) $\begin{array}{rl}& {\left[{\left({\mathcal{P}}_m^{\ast }\right(t\left)\right)}^{(1-t^2)}\right]}^{\ast }{\mathcal{P}}_m^{{\lambda }_m}=1.\end{array}$(25) ), respectively. Then, if we use multiplicative integration to both sides on $[-1,1]$ after the obtained relations are divided by side, we get (26) $\begin{array}{rl}& {\left[{\int }_{-1}^1{\left({\mathcal{P}}_n^{\ln {\mathcal{P}}_m}\right)}^{\mathrm{d}t}\right]}^{{\lambda }_m-{\lambda }_n}\\ & ={\int }_{-1}^1{\left[\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}{\left(W({\mathcal{P}}_m,{\mathcal{P}}_n)\right)}^{(1-t^2)}\right]}^{\mathrm{d}t}=1,\end{array}$(26) where $W({\mathcal{P}}_m,{\mathcal{P}}_n)=({\mathcal{P}}_m\odot {\mathcal{P}}_n^{\ast })\ominus ({\mathcal{P}}_m^{\ast }\odot {\mathcal{P}}_n).$ Since ${\lambda }_m\ne {\lambda }_n,$ it gives ${\int }_{-1}^1{\left({\mathcal{P}}_n^{\ln {\mathcal{P}}_m}\right)}^{\mathrm{d}t}=1.$So, the proof is completed.

(ii) Let $m=n.$ By (13(13) ${\mathcal{P}}_n\left(t\right)={\left[\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{x}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right]}^{\frac{1}{2^{n}n!}},n=0,1,2,\dots .$(13) ), $\begin{array}{rl}& {\int }_{-1}^1{({\mathcal{P}}_n\odot {\mathcal{P}}_n)}^{\mathrm{d}t}\\ & ={\left\{{\int }_{-1}^1{\left[{\left(\frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{t}^n}{\mathrm{e}}^{{(t^2-1)}^n}\right)}^{\ln \frac{{\mathrm{d}}^{\ast \left(n\right)}}{\mathrm{d}{t}^n}{\mathrm{e}}^{{(t^2-1)}^n}}\right]}^{\mathrm{d}t}\right\}}^{\frac{1}{2^{2n}{(n!)}^2}},\end{array}$If multiplicative partial integration formula is applied to the right side of this equation n-times, (27) $\begin{array}{rl}& {\int }_{-1}^1{({\mathcal{P}}_n\odot {\mathcal{P}}_n)}^{\mathrm{d}t}\\ & ={\left\{{\int }_{-1}^1{\left[{\left({\mathrm{e}}^{{(t^2-1)}^n}\right)}^{\ln \frac{{\mathrm{d}}^{\ast \left(2n\right)}}{\mathrm{d}{t}^n}{\mathrm{e}}^{{(t^2-1)}^n}}\right]}^{\mathrm{d}t}\right\}}^{\frac{(-1{)}^n}{2^{2n}{(n!)}^2}}.\end{array}$(27) Here, considering the following relations, $\ln \frac{{\mathrm{d}}^{\ast \left(2n\right)}}{\mathrm{d}{t}^n}{\mathrm{e}}^{{(t^2-1)}^n}=\left(2n\right)!,$and ${\int }_{-1}^1{\left({\mathrm{e}}^{{(t^2-1)}^n}\right)}^{\mathrm{d}t}={\mathrm{e}}^{(-1{)}^{n}2\frac{\mathrm{2.4.}\cdots \left(2n\right)}{3.5\cdots (2n+1)}},$The equailty (27) turns into the equality ${\int }_{-1}^1{({\mathcal{P}}_n\odot {\mathcal{P}}_n)}^{\mathrm{d}t}={\mathrm{e}}^{\frac{2}{2n+1}}.$It completes the proof.

Lemma 3.2

Prob. (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) )–(3(3) $\underset{t\to \pm 1}{lim}\left|y(t,\lambda )\right|<\mathrm{\infty }.$(3) ) has only real ${}^{\ast }$eigenvalues.

Proof.

Suppose that λ and $\overline{\lambda }$ are ${}^{\ast }$eigenvalues corresponding to $y(t,\lambda ).$ and $\overline{y(t,\lambda )}$, respectively. From (26(26) $\begin{array}{rl}& {\left[{\int }_{-1}^1{\left({\mathcal{P}}_n^{\ln {\mathcal{P}}_m}\right)}^{\mathrm{d}t}\right]}^{{\lambda }_m-{\lambda }_n}\\ & ={\int }_{-1}^1{\left[\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}{\left(W({\mathcal{P}}_m,{\mathcal{P}}_n)\right)}^{(1-t^2)}\right]}^{\mathrm{d}t}=1,\end{array}$(26) ), ${\left\{{\int }_{-1}^1{\left[y^{\ln \overline{y}}\right]}^{\mathrm{d}t}\right\}}^{\lambda -\overline{\lambda }}=1.$By the notion of multiplicative integration, ${\left\{{\int }_{-1}^1{|\ln y|}^2\mathrm{d}t\right\}}^{\lambda -\overline{\lambda }}=0.$Since y must be a non-trivial solution, i.e. $y\ne 1,$ and ${\int }_{-1}^1|\ln y{|}^2\mathrm{d}t>0,$ we get $\lambda =\overline{\lambda }.$ This is the proof.

Lemma 3.3

${}^{\ast }$Legendre operator $\mathcal{L}$ (2(2) $\mathcal{L}\left[y\right]:={\left(y^{\ast \ast }\right)}^{1-t^2}{\left(y^{\ast }\right)}^{-2t}{y}^{\lambda }=1,t\in [a,b],$(2) ) is self-adjoint in ${}^{\ast }{L}_2[-1,1],$ formally.

Proof.

Assume that $\phi ,\psi \in C^{\ast \left(2\right)}$ are positive ${}^{\ast }$Legendre polynomials on $[-1,1]$. By the definition of ${}^{\ast }$Legendre operator and ${}^{\ast }$derivative, it is obtained that (28) $\frac{{\left(\mathcal{L}\psi \right)}^{\ln \phi }}{{\left(\mathcal{L}\phi \right)}^{\ln \psi }}=\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}\left[\right(W(\phi ,\psi ){)}^{1-t^2}].$(28) By multiplicative integrating both sides of (28(28) $\frac{{\left(\mathcal{L}\psi \right)}^{\ln \phi }}{{\left(\mathcal{L}\phi \right)}^{\ln \psi }}=\frac{{\mathrm{d}}^{\ast }}{\mathrm{d}t}\left[\right(W(\phi ,\psi ){)}^{1-t^2}].$(28) ) on $[-1,1],$ ${\int }_{-1}^1{\left[\frac{{\left(\mathcal{L}\psi \right)}^{\ln \phi }}{{\left(\mathcal{L}\phi \right)}^{\ln \psi }}\right]}^{\mathrm{d}t}=\frac{\underset{t\to 1^{-}}{lim}\left(W\right(\phi ,\psi ){)}^{1-t^2}}{\underset{t\to 1^{+}}{lim}\left(W\right(\phi ,\psi ){)}^{1-t^2}}$and using the properties of limit, we acquire $〈\mathcal{L}\phi ,\psi {〉}_{\ast }=〈\phi ,\mathcal{L}\psi {〉}_{\ast }$This indicates that the given ${}^{\ast }$Legendre operator is self-adjoint in ${}^{\ast }{L}_2[-1,1]$.

Self-adjointness is used in quantum mechanics. Accordingly, if the operator is self-adjoint, the evolution of the waves in time can be predicted, since the expansion of the operator is determined as a single type. Thus, the laws of physics do not lose their validity. However, the evolution of waves in time is unpredictable if the operator is not self-adjoint. The most important reason for this is that there can be no uniform expansion of the operator. In such a case, the space–time in question becomes quantum-mechanistically singular as well.

4. Some examples

In this section, some examples will be given to understand the study.

Example 4.1

Expand positive function $f\left(t\right)={\mathrm{e}}^{t(t-1)(t+1)}$ on $[-1,1]$.

It can be easily proved by a similar method in Ref. [36] that the positive and continuous function $f\left(t\right)$ in $[-1,1]$ has the following expansion in a series of ${}^{\ast }$Legendre polynomials: (29) $f\left(t\right)=\prod _{n=0}^{\mathrm{\infty }}{c}_n\odot {\mathcal{P}}_n\left(t\right),$(29) where $\begin{array}{rl}{c}_n& ={\left({\int }_{-1}^1{\left[f\right(t)\odot {\mathcal{P}}_n(t\left)\right]}^{\mathrm{d}t}\right)}^{\frac{2n+1}{2}}\\ & ={\mathrm{e}}^{\frac{2n+1}{2}{\int }_{-1}^1\ln f\left(t\right)\ln {\mathcal{P}}_n\left(t\right)\mathrm{d}t}.\end{array}$Because the exponent of $f\left(t\right)$ is a third-order polynomial, we calculate only for n = 0, 1, 2, 3, i.e. $c_0=1,c_1={\mathrm{e}}^{-\frac{2}{5}},c_2=1,c_3={\mathrm{e}}^{\frac{2}{5}}.$Consequently, from (29(29) $f\left(t\right)=\prod _{n=0}^{\mathrm{\infty }}{c}_n\odot {\mathcal{P}}_n\left(t\right),$(29) ), we verify that ${\mathrm{e}}^{t(t-1)(t+1)}={\left\{{\mathcal{P}}_1\right(t\left)\right\}}^{-\frac{2}{5}}{\left\{{\mathcal{P}}_3\right(t\left)\right\}}^{\frac{2}{5}}={\mathrm{e}}^{-\frac{2}{5}t+\frac{1}{5}(5t^3-3t)}.$

Example 4.2

We shall give some special values using the generating function (15(15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15) ).

Since the generating function (15(15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15) ) when t = 1, we arrive at ${\mathrm{e}}^{{(1-2t+t^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(1\right)\right\}}^{t^n}.$If left-hand side of last equality has a series representation as $\prod _{n=0}^{\mathrm{\infty }}{\mathrm{e}}^{t^n}$, then we get $\prod _{n=0}^{\mathrm{\infty }}{\mathrm{e}}^{t^n}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(1\right)\right\}}^{t^n}.$By comparing the exponents, the property ${\mathcal{P}}_n\left(1\right)=1$ is obtained.

Similarly, if we replace x by $-x$ and t by $-t$, then we get $\begin{array}{rl}{\mathrm{e}}^{{(1-2(-t\left)\right(-x)+{(-x)}^2)}^{-\frac{1}{2}}}& =\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n(-t)\right\}}^{{(-x)}^n}\\ \prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{{\left(x\right)}^n}& =\prod _{n=0}^{\mathrm{\infty }}{\left\{\mathcal{P}(-t)\right\}}^{{(-x)}^n}\end{array}$or ${\mathcal{P}}_n(-t)=\left[{\mathcal{P}}_n\right(x){]}^{(-1{)}^n}$. Consequently, the expression of the generating function (15(15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15) ) true.

Example 4.3

${}^{\ast }$Legendre polynomials appear in an expansion of the electrostatic potential in inverse radial powers [36]. The generating function (15(15) $L(t,x)={\mathrm{e}}^{{(1-2tx+x^2)}^{-\frac{1}{2}}}=\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n\left(t\right)\right\}}^{x^n}.$(15) ) is useful in solving this type of physical problems.

We want to state electrostatic potential in terms of a geometric coordinate system. We use two mutually orthogonal geometric real number lines [7]. Let an electric charge q be placed on the z-axis at $z={\mathrm{e}}^a$.

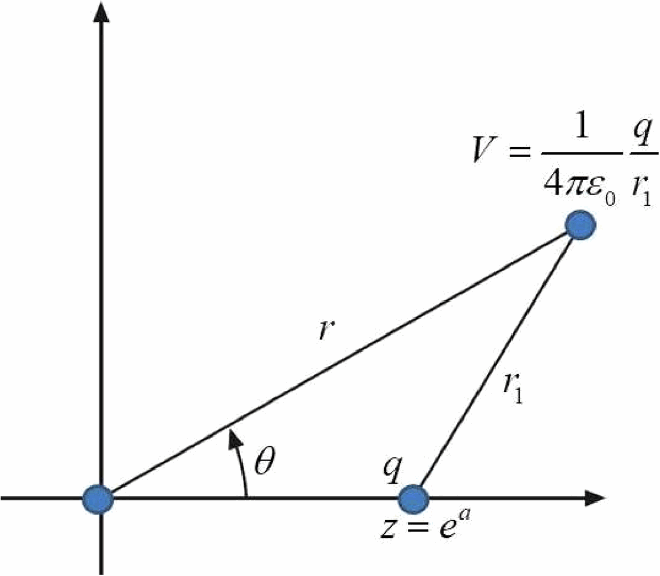
Since $x^{2_G}=x\odot x=x^{\ln x}$, $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{g}\theta ={\mathrm{e}}^{\cos \theta }$ and ${\left\{{\mathrm{e}}^{r_1}\right\}}^{2_G}\oplus ({\mathrm{e}}^{2ar}\odot \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{g}\theta )={\left\{{\mathrm{e}}^r\right\}}^{2_G}\oplus {\left\{{\mathrm{e}}^a\right\}}^{2_G}$or $1={\mathrm{e}}^{r^2+a^2-r_1^2-2ar\cos \theta },$the electrostatic potential at a non-axial point is given $\begin{array}{rl}V& =\frac{1}{4\pi {ϵ}_0}\frac{q}{r_1}\\ & =\frac{q}{4\pi {ϵ}_0}\frac{1}{\sqrt{1+{\left(\frac{a}{r}\right)}^2-2\left(\frac{a}{r}\right)\cos \theta }}\end{array}$Consider the case of $r>a$. The expression under the radical sign may be written as $(1-2tx+x^2{)}^{-\frac{1}{2}}$ where $t=\cos \theta$ and $x=\frac{a}{r}$. The Legendre polynomial ${\mathcal{P}}_n(\cos \theta )$ is defined as the coefficient of $(\frac{a}{r}{)}^n$ so that $V=\frac{q}{4\pi {ϵ}_{0}r}\ln \left\{\prod _{n=0}^{\mathrm{\infty }}{\left\{{\mathcal{P}}_n(\cos \theta )\right\}}^{{\left(\frac{a}{r}\right)}^n}\right\}.$

5. Conclusion

Legendre's differential equation is frequently encountered in physics and engineering. It arises in numerous problems, particularly in boundary value problems for spheres. Because Legendre polynomials with these equations and their solutions have such an important place, we carried these concepts to multiplicative analysis. First, we set up the Legendre equation in multiplicative analysis. Then, we obtained multiplicative Legendre polynomials for different situations using multiplicative series methods. Finally, we examined some spectral properties of these multiplicative polynomials. In fact, these investigations coincide with spectral properties of a much more complex nonlinear equation in the classical case.

Disclosure statement

No potential conflict of interest was reported by the author.