Effect of Mth coherent state on the interaction between two two-level atoms and two-mode quantized field

Abstract

The objective of this work is to measure the influence of the Mth coherent state on the optics model of two atoms interacting with two-mode quantized field. Also, two atoms interacting together is included in this optics model. The time-dependent wave function is computed analytically. The two-mode quantized field is in the Mth coherent state while the two atoms have two levels. The influence of the Mth coherent state on the quantum model is measured via studying the atomic inversion, von Neumann entropy, variance squeezing, correlation function and Husimi function. The influence of each mode of the quantized field separately and both modes together are discussed. The statistical measures indicate that the nonclassical quantized features increase in the presence of the Mth coherent state, and it features a controlling mechanism. This study opens up a wide range of a large number of serious applications for the quantum optics models.

Keywords:

• Atomic inversion
• von Neumann entropy
• variance squeezing
• correlation function
• Husimi function
• Mth coherent state

1. Introduction

The powerful additions in the quantum optics model are Jaynes–Cummings model [1] and Tavis–Cummings model [2]. They are widely used models and have many modern quantum applications as cryptography [3], teleportation [4,5] and quantum computing [6]. In addition, they are able to create some noteworthy nonclassical phenomena that verified empirically as the entangled states of two-trapped atom [7,8] and cavity QED [9]. Rempe et al [10] empirically evidenced the revival and collapse phenomena portended by the Jaynes–Cummings model. The quantum entanglement between the system components is the primary feature of modern quantum optics that is absent in classical mechanics. Entanglement is an essential feature due to its major role in processing devices for quantum information [11]. As a result, scientists have been interested in studying the nonclassical features of the interaction of the atom–field and the atom–atom [12] such as the collapse and revival [13,14], entanglement between system components [15,16] and field squeezing [17]. It should be noted that the rotating wave approximation (RWA) and Heisenberg equation of motion simplify the Hamiltonian operator so that it can be solved analytically. Recently, the effect of the atom–atom interaction on the quantum models related to the two atoms interacting with different types of the quantized field was discussed in [18–21]. In continuation of our previous works, we seek to complete the study of the nonclassical properties resulting from the quantum systems that have different initial states.

In most quantum optics models, the operating quantum electromagnetic field is the coherent state (CS), which verifies the minimum uncertainty relation [22,23]. The coherent state is also described as the maximum type of coherence and the eigenvector of the displacement operator. In this work, we wish to obtain a controlling mechanism for different physical dynamics by employing some quantum field state. The requested state has to be able to significantly modify the patterns of light–atom interaction but somehow preserve the major features of the coherent state interaction that is applied in most models. We hope that because we wish to maintain the advantages of utilizing the CS as discussed in many references such as [24–26].

Recently, a new kind of coherent states called the Mth coherent state (Mth CS) has been defined [27,28]. The Mth CS has appeared to have remarkable nonclassical effects while semi-preserving the statistical properties of the coherent state. Namely, the state has considerable sub-Poissonian statistics and significant squeezing as presented in [28]. Many similar quantum states have been represented and utilized in different applications. Examples of these are the entangled derivative of coherent state employed in a teleportation scheme [29], the two-mode ‘near’ coherent state used in entanglement [30]. In addition to this, the employment of near superposition in even and odd cat states [31], and the application of adding or depleting a photon from the near coherent state [32]. The analysis of these states and others reveals that the closest state to CS among them is the Mth CS [28].

The Mth CS has been operated for a single-level atom interacting with a single radiation field [33]. The results of the study displayed remarkable phenomena. One of these is the ability of the Mth CS to modulate the features of the physical dynamics while fairly sustaining the main aspects of applying the coherent state. Another emergent behaviour is the resolution phenomenon which provides a semi-periodic pattern in a certain period. Therefore, in this work, we aim to study the nonclassical effect of the Mth coherent state on the interaction between the asymmetric two two-level atoms and two-mode quantized field to investigate how these controlling effects emerge in our system.

The Hamiltonian operator of the proposed optics model using the RWA and including the two atoms interacting together can be formulated as follows($\hslash =1$): (1) $\begin{array}{rl}\hat{H}& ={\omega }_a\hat{n}+{\omega }_b\hat{m}\\ & +\sum _{j=1}^2[{\omega }_j{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}).\end{array}$(1) The first and second terms represent the first and second modes of quantized fields respectively, where ${\omega }_a$ and ${\omega }_b$ are the two-mode quantized field frequencies, $\hat{n}={\hat{a}}^{†}\hat{a}$ and $\hat{m}={\hat{b}}^{†}\hat{b}$ are the photon number operators, ${\hat{a}}^{†}$ ($\hat{a}$) and ${\hat{b}}^{†}$ ($\hat{b}$) are the creation (annihilation) operators that satisfy the relations $[\hat{a},{\hat{a}}^{†}]=1$, $[\hat{b},{\hat{b}}^{†}]=1$ and $[\hat{a},{\hat{b}}^{†}]=0$. The third term represents the sum of the asymmetric two atoms where ${\omega }_j,j=1,2$, is the j-atomic transition frequency. While other terms represent the interactions of atom–field and atom–atom where $g_j,j=1,2$, is the coupling constant of j-atom–field and λ is the coupling constant of atom–atom. The operators ${\hat{\sigma }}_{-}^{(j)}$, ${\hat{\sigma }}_{+}^{(j)}$ and ${\hat{\sigma }}_z^{(j)},j=1,2$, are spin atomic operators, which obey $[{\hat{\sigma }}_z^{(j)},{\hat{\sigma }}_{\pm }^{(j)}]=\pm 2{\hat{\sigma }}_{\pm }^{(j)},[{\hat{\sigma }}_{+}^{(i)},{\hat{\sigma }}_{-}^{(j)}]={\hat{\sigma }}_z^{(j)}{\delta }_{ij}$.

Let's point out that the suggested quantum system for symmetric two two-level atoms and one-mode radiation field was presented in [34] without atom–atom interaction. While, interacting asymmetric two two-level atoms and one-mode radiation field was presented in [18]. Finally, interacting asymmetric two two-level atoms and two-mode radiation field was presented in [21]. In these references, the initial quantized field is in the coherent state. While in this work, the two-mode quantized fields are initially in the Mth coherent states to study its nonclassical effects on the suggested quantum model. Notice that the last term in Hamiltonian operator (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a\hat{n}+{\omega }_b\hat{m}\\ & +\sum _{j=1}^2[{\omega }_j{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}).\end{array}$(1) ) was presented in the imaginary unit, so that Hamiltonian operator $\hat{H}$ is hermitian. And then we can find an analytical solution of this quantum model. Moreover, there is not any effect of the imaginary unit on the quantum properties.

Our aim in this work focus on the effect of the Mth coherent state on the components of the quantum system using some important indicators such as the atomic inversion, the von Neumann entropy, the variance squeezing, correlation function and the Husimi function. While the entanglement between two atoms had been studied in the previous work [21].

In this work, the wave function of the optics model is presented using Heisenberg equation of motion and the Mth coherent state in Section 2. The nonclassical features of the quantized system are discussed via the atomic inversion, the von Neumann entropy, the variance squeezing, correlation function and the Husimi function in Sections 3–7, respectively. Finally, the important conclusion points are recapped in Section 8.

2. Quantum model

Let us use the Heisenberg picture of motions, $i\frac{\mathrm{d}\hat{O}}{\mathrm{d}t}=[\hat{O},\hat{H}]$, to simplify the Hamiltonian operator (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a\hat{n}+{\omega }_b\hat{m}\\ & +\sum _{j=1}^2[{\omega }_j{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}).\end{array}$(1) ) as follows: (2) $\begin{array}{rl}i\frac{\mathrm{d}\hat{n}}{\mathrm{d}t}& =[\hat{n},\hat{H}]=\sum _{j=1}^2{g}_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}-\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)}),\\ i\frac{\mathrm{d}\hat{m}}{\mathrm{d}t}& =[\hat{m},\hat{H}]=-\sum _{j=1}^2{g}_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}-\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)}),\\ i\frac{\mathrm{d}{\hat{\sigma }}_z^{(1)}}{\mathrm{d}t}& =[{\hat{\sigma }}_z^{(1)},\hat{H}]=2g_1({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(1)}-\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(1)})\\ & +2i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}+{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}),\\ i\frac{\mathrm{d}{\hat{\sigma }}_z^{(2)}}{\mathrm{d}t}& =[{\hat{\sigma }}_z^{(2)},\hat{H}]=2g_2({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(2)}-\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(2)})\\ & -2i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}+{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}),\end{array}$(2) It is clear that (3) $\begin{array}{rl}i\frac{\mathrm{d}}{\mathrm{d}t}(\hat{n}-\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{(j)})& =0,\\ i\frac{\mathrm{d}}{\mathrm{d}t}(\hat{m}+\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{(j)})& =0.\end{array}$(3) Then, the operators $(\hat{n}-\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{(j)})$ and $(\hat{m}+\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{(j)})$ are constant operators. As a result, the Hamiltonian operator (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a\hat{n}+{\omega }_b\hat{m}\\ & +\sum _{j=1}^2[{\omega }_j{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}).\end{array}$(1) ) can be reduced to the effective Hamiltonian operator as (4) $\begin{array}{rl}{\hat{H}}_I& =\sum _{j=1}^2[\frac{{\mathrm{\Delta }}_j}{2}{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}),\end{array}$(4) where ${\mathrm{\Delta }}_j=2{\omega }_j-{\omega }_b+{\omega }_a,j=1,2$, called the detuning parameters.

The initial quantum state can be supposed as (5) $\begin{array}{rl}|\psi (0)⟩& =\{c_1|+,+⟩+c_2|+,-⟩+c_3|-,+⟩+c_4|-,-⟩\}\\ & \otimes |M_1(\alpha ),M_2(\beta )⟩\end{array}$(5) where $c_i,i=1,\dots ,4$, are the complex arbitrary constants which obey the normalization condition$\sum _{i=1}^4|c_i{|}^2=1$. Whilst $|M_1(\alpha ),M_2(\beta )⟩$ is the two-mode initial quantized field which are in the Mth coherent state as [28,33] (6) $\begin{array}{rl}|M_1(\alpha ),M_2(\beta )⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}Q(n,m)|n,m⟩,\\ Q(n,m)& =\frac{{\alpha }^n{\beta }^m}{\sqrt{n!m!}}\exp (-\frac{|\alpha {|}^2+|\beta {|}^2}{2})\\ & \times \frac{n^{M_1}{m}^{M_2}}{\sqrt{B_{2M_1}(|\alpha {|}^2)B_{2M_2}(|\beta {|}^2)}},\end{array}$(6) where $B_{2M_1}(|\alpha {|}^2)$ and $B_{2M_2}(|\beta {|}^2)$ represent the Bell polynomial which are defined as (7) $\begin{array}{rl}{B}_{2M_1}(|\alpha {|}^2)& ={\mathrm{e}}^{-|\alpha {|}^2}\sum _{k=0}^{\mathrm{\infty }}\frac{|\alpha {|}^{2k}{k}^{2M_1}}{k!},\\ B_{2M_2}(|\beta {|}^2)& ={\mathrm{e}}^{-|\beta {|}^2}\sum _{k=0}^{\mathrm{\infty }}\frac{|\beta {|}^{2k}{k}^{2M_2}}{k!}.\end{array}$(7) The employed values of $|\alpha |$ and $|\beta |$ are described in the peak representation [28,33]. That is the exact values of $|\alpha |$ and $|\beta |$ depend on the selected values of $M_1$ and $M_2$. The peak representation allows all Mth states of different M values to share the same peak in the photonic distribution, thus becoming comparable with the coherent state. They can be expressed as (8) $\begin{array}{rl}|\alpha |& =\exp [\frac{1}{2}\psi (|{\alpha }_0{|}^2+1)-\frac{M_1}{|{\alpha }_0{|}^2}],\\ |\beta |& =\exp [\frac{1}{2}\psi (|{\beta }_0{|}^2+1)-\frac{M_2}{|{\beta }_0{|}^2}],\end{array}$(8) where $\psi (x)$ is the digamma function, while $|{\alpha }_0|$ and $|{\beta }_0|$ are constants, their values are independent of $M_1$ and $M_2$. In our article, we assume $|{\alpha }_0|=|{\beta }_0|$. Applying this expression leads to approximately a steady average number of photons for any selected value of M.

To clearly study non-classical properties, the system should be in an exact resonance case. So, we proposed that the components of the proposed optics model are in exact resonance type, i.e. ${\omega }_1+{\omega }_2={\omega }_b-{\omega }_a$ or ${\mathrm{\Delta }}_1=-{\mathrm{\Delta }}_2=\mathrm{\Delta }$. Then, we can write the wave function of the optics model (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a\hat{n}+{\omega }_b\hat{m}\\ & +\sum _{j=1}^2[{\omega }_j{\hat{\sigma }}_z^{(j)}+g_j({\hat{a}}^{†}\hat{b}{\hat{\sigma }}_{+}^{(j)}+\hat{a}{\hat{b}}^{†}{\hat{\sigma }}_{-}^{(j)})]\\ & +i\lambda ({\hat{\sigma }}_{+}^{(1)}{\hat{\sigma }}_{-}^{(2)}-{\hat{\sigma }}_{-}^{(1)}{\hat{\sigma }}_{+}^{(2)}).\end{array}$(1) ) as (9) $\begin{array}{rl}|\psi (t)⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[A(n,m,t)|+,+;n,m⟩\\ & +B(n,m,t)|+,-;n-1,m+1⟩\\ & +C(n,m,t)|-,+;n-1,m+1⟩\\ & +D(n,m,t)|-,-;n-2,m+2⟩],\end{array}$(9) where $A(n,m,t),B(n,m,t),C(n,m,t)$ and $D(n,m,t)$ are arbitrary coefficients. We can compute them by the Schrödinger equation with the effective Hamiltonian operator as in  [21]. We select the value $|{\alpha }_0|=|{\beta }_0|$ to be 5 throughout the whole article.

In next sections, we intend to study the nonclassical effects of the Mth coherent state on the derived quantum model by discussing the temporal behaviour of some nonclassicality indicators such as the atomic inversion, the von Neumann entropy, the variance squeezing, the correlation function and the Husimi function. To determine these indicators, the density matrix of one atom takes the following formula: (10) $\begin{array}{rl}{\hat{\rho }}^{(j)}(t)& ={\rho }_{11}^{(j)}(t)|+{⟩}_{jj}⟨+|+{\rho }_{12}^{(j)}(t)|+{⟩}_{jj}⟨-|+{\rho }_{21}^{(j)}(t)|-{⟩}_{jj}\\ & \times ⟨+|+{\rho }_{22}^{(j)}(t)|-{⟩}_{jj}⟨-|\end{array}$(10) where (11) $\begin{array}{rl}{\rho }_{11}^{(1)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[|A(n,m,t){|}^2+|B(n,m,t){|}^2],\end{array}$(11) (12) $\begin{array}{rl}{\rho }_{22}^{(1)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[|C(n,m,t){|}^2+|D(n,m,t){|}^2],\end{array}$(12) (13) $\begin{array}{rl}{\rho }_{12}^{(1)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[A(n-1,m+1,t)C^{\ast }(n,t)\\ & +B(n-1,m+1,t)D^{\ast }(n,t)]={\rho }_{21}^{\ast (1)}(t),\end{array}$(13) (14) $\begin{array}{rl}{\rho }_{11}^{(2)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[|A(n,m,t){|}^2+|C(n,m,t){|}^2],\end{array}$(14) (15) $\begin{array}{rl}{\rho }_{22}^{(2)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[|B(n,m,t){|}^2+|D(n,m,t){|}^2],\end{array}$(15) (16) $\begin{array}{rl}{\rho }_{12}^{(2)}(t)& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[A(n-1,m+1,t)B^{\ast }(n,m,t)\\ & +C(n-1,m+1,t)D^{\ast }(n,m,t)]={\rho }_{21}^{\ast (2)}(t).\end{array}$(16)

3. Atomic inversion

The population inversion of the atom plays an effective role in determining the behaviour of the atom in the quantized field by the nonclassical phenomena called collapse and revival, which forms discrete packets in the evolution of the atomic inversion. The atomic population inversion is the difference between the probability that the atom is in the excited state and the probability that the atom is in the ground state as follows: (17) $W^{(j)}(t)={\rho }_{11}^{(j)}(t)-{\rho }_{22}^{(j)}(t),j=1,2.$(17) To study the effects of the Mth coherent state on the atomic inversion, let us plot the time-dependent atomic inversion for the asymmetric case at some values of the Mth coherent parameters $M_1$ and $M_2$ as shown in Figure 1. While the atomic inversion for the symmetric case is shown in Figure 2. In both cases, $W^{(j)}(t)$ represents the atomic inversion at the beginning of the interaction and in the resolution time, which is the period that produces a semi-periodic pattern when the atom interacts with the Mth CS. We model this period by applying the summation of five frequencies found in the elements of the population inversion [21]. In general, it is expected that the resolution phenomena for this model occur at (18) ${\tau }_{RS}=\frac{\frac{13\pi }{2}}{\begin{array}{c}4\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2)-[\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2+1)\\ +\eta (|{\alpha }_0{|}^2+1,|{\alpha }_0{|}^2)+\eta (|{\alpha }_0{|}^2-1,|{\alpha }_0{|}^2)\\ +\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2-1)]\end{array}},$(18) in which (19) $\eta (n,m)=\sqrt{(g_1^2+g_2^2)(2mn+3n-m-2)}.$(19) In our selected values, this resolution occurs around T = 327.

Figure 1. The atomic inversion for asymmetric two atoms ($g=g_1/g_2=0.5$) at $\delta =0$, $\lambda =1$; cases (A–D) black for $M_1=M_2=0$, blue for $M_1=M_2=20$, red for $M_1=M_2=40$, and green for $M_1=M_2=60$; while cases (E–H) black for $M_1=60$ and $M_2=0$, blue for $M_1=0$ and $M_2=60$, red for $M_1=40$ and $M_2=20$ and green for $M_1=20$ and $M_2=40$. (A) First Atom; (B) First Atom; (C) Second Atom; (D) Second Atom; (E) First Atom; (F) First Atom; (G) Second Atom; (H) Second Atom.

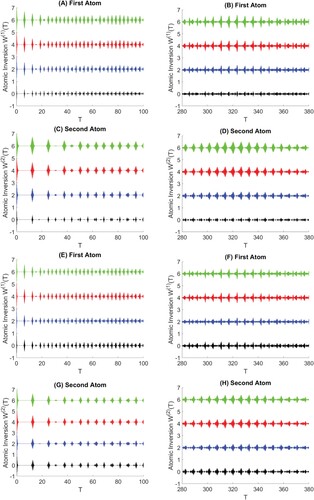
Figure 2. The atomic inversion for symmetric two atoms ($g=g_1/g_2=1$) at $\delta =0$, $\lambda =1$; cases (A–B) black for $M_1=M_2=0$, blue for $M_1=M_2=20$, red for $M_1=M_2=40$ and green for $M_1=M_2=60$, while cases (C–D) black for $M_1=60$ and $M_2=0$, blue for $M_1=0$ and $M_2=60$, red for $M_1=40$ and $M_2=20$ and green for $M_1=20$ and $M_2=40$.

For the asymmetric case, it is clear that the number of the first atom revivals is twice the number of the second atom revivals which means that the interactions of the first atom and field are twice the interactions of the second atom. This is a result of g = 0.5, the energy exchange rate during the first atom reaction with the field is twice as fast as the energy exchange rate through the second atom reaction with the field. In addition, the collapse regions shrink over time until they are absent as shown in Figure 1(E–H). While the values of the parameters $M_1$ and $M_2$ increase, we notice that the interval length of the revival regions increases. Sometimes, the nearest two revivals are merging to be one revival when the values of the parameters $M_1$ and $M_2$ increase as in Figure 1(A–D).

Notice that the sum of the values of the parameters $M_1$ and $M_2$ equals 60 in all curves of Figure 1(E–H). One can see that the effect of the two parameters together is greater than the effect of one of them only although its sum is equal.

We also note that the resolution phenomenon is present during the resolution period as shown in the left figures of Figure 1. And it is clearly present when either $M_1$ or $M_2$ are large, e.g. $=60$. While we observe that such a phenomenon is absent for the coherent state as visible in Figure 1(B,D). The semi-periodic pattern differs depending on the value of M and other parameters.

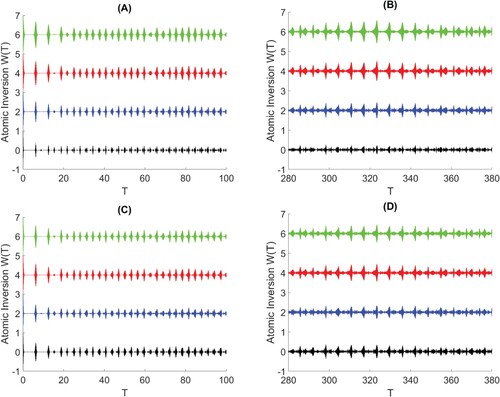
For the symmetric case, the same attitudes in the asymmetric case are appeared in Figure 2.

4. von Neumann entropy

The von Neumann entropy represents a measure of the atom-field entanglement and considers an extension of classical Gibbs entropy which can be evaluated as (20) $\begin{array}{r}{N}^{(j)}(t)=-{\mu }_{-}^{(j)}(t)\ln {\mu }_{-}^{(j)}(t)-{\mu }_{+}^{(j)}(t)\ln {\mu }_{+}^{(j)}(t),j=1,2\end{array}$(20) Here ${\mu }_{\pm }^{(j)}$ represent the eigenvalues of the atomic density matrix ${\hat{\rho }}^{(j)}(T)$. These eigenvalues defined as (21) $\begin{array}{rl}{\mu }_{\pm }^{(j)}(t)& =\frac{1}{2}\pm \frac{1}{2}\sqrt{{({\hat{\rho }}_x^{(j)}(t))}^2+{({\hat{\rho }}_y^{(j)}(t))}^2+{({\hat{\rho }}_z^{(j)}(t))}^2},\\ j& =1,2,\end{array}$(21) where (22) $\begin{array}{rl}{\hat{\rho }}_x^{(j)}(t)& =2\mathtt{\text{Re}}[{\hat{\rho }}_{12}^{(j)}(t)],{\hat{\rho }}_y^{(j)}(t)=2\mathtt{\text{Im}}[{\hat{\rho }}_{12}^{(j)}(t)],\\ {\hat{\rho }}_z^{(j)}(t)& ={\hat{\rho }}_{11}^{(j)}(t)-{\hat{\rho }}_{22}^{(j)}(t).\end{array}$(22) To study the effect of the Mth coherent state on the entanglement between one of the atoms and quantized field for asymmetric case, let us plot the first atom von Neumann entropy $N^{(1)}(t)$ and the second atom $N^{(2)}(t)$ at some values of the parameters $M_1$ and $M_2$. As known, the von Neumann entropy values are greater than 0 and less than 0.7 as seen in Figure 3. Also, it is a periodic function with a period that reduces over time. The period of the second atom is twice the period of the first atom. Moreover, the minimum values of von Neumann entropy decrease through increasing the $M_1$ and $M_2$ values. In Figure 3(E–H), although the total of the two parameters is equal ($M_1+M_2=60$), we notice that the effect of the two parameters together is bigger than the effect of one of them only. We also remark that the fluctuations for both atoms are larger at the resolution period for the Mth coherent state; however, these fluctuations are significantly lower for the coherent state.

Figure 3. The von Neumann entropy for asymmetric two atoms (g = 0.5) at $\delta =0$, $\lambda =1$; cases (A–D) black for $M_1=M_2=0$, blue for $M_1=M_2=20$, red for $M_1=M_2=40$, and green for $M_1=M_2=60$; while cases (E–H) black for $M_1=60$ and $M_2=0$, blue for $M_1=0$ and $M_2=60$, red for $M_1=40$ and $M_2=20$ and green for $M_1=20$ and $M_2=40$. (A) First Atom; (B) First Atom; (C) Second Atom; (D) Second Atom; (E) First Atom; (F) First Atom; (G) Second Atom; (H) Second Atom.

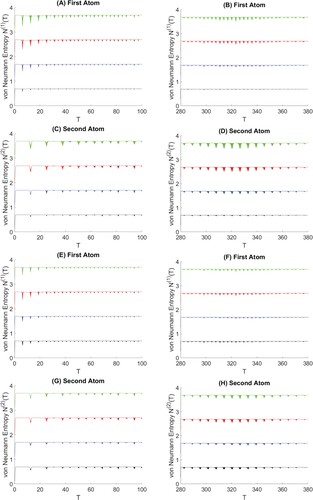
5. Variance squeezing

In the past three decades, squeezing has received great attention where considers an important phenomenon in quantum optics. The variance squeezing has two components $V_x^{(j)}(t)$ and $V_y^{(j)}(t)$ which can be defined as (23) $\begin{array}{rl}{V}_x^{(j)}(t)& =\sqrt{1-{[{\hat{\rho }}_x^{(j)}(t)]}^2}-\sqrt{|{\hat{\rho }}_z^{(j)}(t)|},\\ V_y^{(j)}(t)& =\sqrt{1-{[{\hat{\rho }}_y^{(j)}(t)]}^2}-\sqrt{|{\hat{\rho }}_z^{(j)}(t)|},\end{array}$(23) where ${\hat{\rho }}_x^{(j)}(t),{\hat{\rho }}_y^{(j)}(t)$ and ${\hat{\rho }}_z^{(j)}(t)$ defined in Equation (22(22) $\begin{array}{rl}{\hat{\rho }}_x^{(j)}(t)& =2\mathtt{\text{Re}}[{\hat{\rho }}_{12}^{(j)}(t)],{\hat{\rho }}_y^{(j)}(t)=2\mathtt{\text{Im}}[{\hat{\rho }}_{12}^{(j)}(t)],\\ {\hat{\rho }}_z^{(j)}(t)& ={\hat{\rho }}_{11}^{(j)}(t)-{\hat{\rho }}_{22}^{(j)}(t).\end{array}$(22) ).

Our aim is to study the effect of the parameters of Mth coherent state on one of the two components of the variance squeezing. The y-variance squeezing $V_y^{(j)}(t)$ is drawn in Figure 4 where j = 1 represents the first atom and j = 2 represents the second atom.

Figure 4. The y-component of the variance squeezing for asymmetric two atoms (g = 0.5) at $\delta =0$, $\lambda =1$; cases in the second column are the same cases in first column with different time. (A) First Atom; (B) First Atom; (C) Second Atom; (D) Second Atom; (E) First Atom; (F) First Atom; (G) Second Atom; (H) Second Atom.

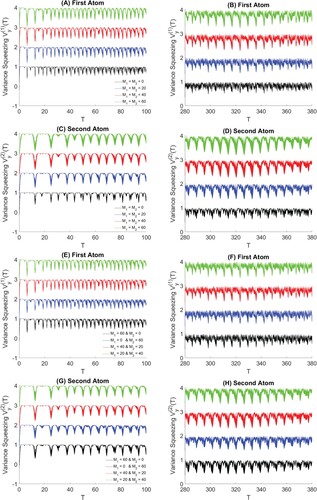
As shown in Figure 4, the y-component of the variance squeezing is less than zero at the initial time as shown in Figure 4. The variance squeezing components are periodic functions with a period reduces over time. The period of the variance squeezing for the second atom is twice the period of the first atom. The minimum values of the variance squeezing decrease until tend to zero in the presence of large values of parameters $M_1$ and $M_2$. When $M_1+M_2=60$, the effect of the two parameters together is greater than the effect of one of them ($M_1=60$ or $M_2=60$) as seen in Figures 4(E–H). Here also the resolution phenomenon is attending for the Mth CS and is missing with the coherent state $M_1=M_2=0$.

6. Correlation function

The Glauber correlation function is useful to determine the classical and nonclassical behaviours by the sub- and super-Poissonian features of the photons distribution where the classical aspect represents super-Poissonian distribution $G^{(j)}(t)>1$ and the nonclassical features represent the sub-Poissonian distribution $G^{(j)}(t)<1$, while $G^{(j)}(t)=1$ represents the coherent state. The second-order correlation functions for two-mode quantized field can be defined as (24) $G^{(1)}(t)=\frac{⟨{\hat{a}}^{†2}{\hat{a}}^2⟩}{⟨{\hat{a}}^{†}\hat{a}{⟩}^2},G^{(2)}(t)=\frac{⟨{\hat{b}}^{†2}{\hat{b}}^2⟩}{⟨{\hat{b}}^{†}\hat{b}{⟩}^2},$(24) where (25) $\begin{array}{rl}⟨{\hat{a}}^{†2}{\hat{a}}^2⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[n(n-1)|A(n,m,t){|}^2\\ & +(n-1)(n-2)(|B(n,m,t){|}^2+|C(n,m,t){|}^2)\\ & +(n-2)(n-3)|D(n,m,t){|}^2],\end{array}$(25) (26) $\begin{array}{rl}⟨{\hat{a}}^{†}\hat{a}⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[n|A(n,m,t){|}^2+(n-1)(|B(n,m,t){|}^2\\ & +|C(n,m,t){|}^2)+(n-2)|D(n,m,t){|}^2],\end{array}$(26) (27) $\begin{array}{rl}⟨{\hat{b}}^{†2}{\hat{b}}^2⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[m(m-1)|A(n,m,t){|}^2\\ & +m(m+1)(|B(n,m,t){|}^2+|C(n,m,t){|}^2)\\ & +(m+1)(m+2)|D(n,m,t){|}^2],\end{array}$(27) and (28) $\begin{array}{rl}⟨{\hat{b}}^{†}\hat{b}⟩& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}[m|A(n,m,t){|}^2+(m+1)(|B(n,m,t){|}^2\\ & +|C(n,m,t){|}^2)+(m+2)|D(n,m,t){|}^2].\end{array}$(28) Let us study the effect of the Mth coherent state on the correlation function by plotting the second-order correlation functions, $G^{(1)}(t)$ for first mode quantized field and $G^{(2)}(t)$ for second mode quantized field, at some values of the parameters $M_1$ and $M_2$ as seen in Figure 5 for asymmetric case.

Figure 5. The correlation function for asymmetric two atoms (g = 0.5) at $\delta =0$, $\lambda =1$; cases in the second column are the same cases in first column with different time. (A) First mode quantized field; (B) First mode quantized field; (C) Second mode quantized field; (D) Second mode quantized field; (E) First mode quantized field; (F) First mode quantized field; (G) Second mode quantized field; (H) Second mode quantized field.

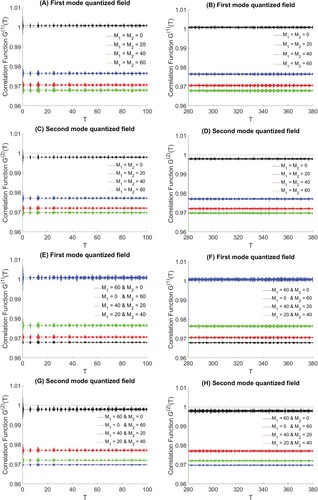
In the absence the parameters $M_1$ and $M_2$ (black curves in Figure 5(A–D)), notice that the correlation function for the first mode quantized field is upper than one while the correlation function for the second mode quantized field is lower than one. In other words, the first mode photon distribution is of the supper-Poissonian distribution while the second mode photon distribution is the sub-Poissonian distribution. That means there are nonclassical aspects of the second mode quantized field. In the presence the parameters $M_1$ and $M_2$, the correlation functions $G^{(1)}(t)$ and $G^{(2)}(t)$ shift down of one to become the sub-Poissonian distribution. This confirms that the Mth coherent state increases the nonclassical aspects. Moreover, we note that with a significant increase in values of parameters $M_1$ and $M_2$, the correlation functions $G^{(1)}(t)$ and $G^{(2)}(t)$ increase slowly.

In addition, although $M_1+M_2=60$, the effect of $M_1$ on the correlation function for first mode quantized field $G^{(1)}(t)$ increases with increasing the values of parameter $M_1$ and without any effect of the parameter $M_2$ as shown in Figure 5(E,F). While the effect of the parameter $M_2$ on the correlation function for second mode $G^{(2)}(t)$ increases with increasing the values of parameter $M_2$ and without any effect of the parameter $M_1$ as shown in Figure 5(G,H). This confirms that the parameter $M_1$ is not effect on the correlation function for second mode field and the parameter $M_2$ is not effect on the correlation function for first mode field.

Note that the correlation function is the clearest quantum indicators presented in this work to show the effect of the Mth coherent state on non-classical properties.

7. Husimi function

The Husimi function $\mathcal{Q}$ provides much information about the probability distribution of the state in the phase space. It measures the projection of the coherent state with the state of interest. For our problem with two modes, it can be defined as $M_1=M_2=0$. [35] (29) $\mathcal{Q}=\frac{⟨\gamma ,\eta |\hat{\rho }|\gamma ,\eta ⟩}{{\pi }^2},$(29) where $\gamma =x+iy$ and $\eta =X+iY$ are the variables of the coherent state. For our state it becomes (30) $\mathcal{Q}=\frac{|\mathcal{A}{|}^2+|\mathcal{B}{|}^2+|\mathcal{C}{|}^2+|\mathcal{D}{|}^2}{{\pi }^2}{\mathrm{e}}^{-(|\gamma {|}^2+|\eta {|}^2)},$(30) with (31) $\begin{array}{rl}\mathcal{A}& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}A(n,m,t)\frac{{\gamma }^{\ast n}{\eta }^{\ast m}}{\sqrt{n!m!}},\end{array}$(31) (32) $\begin{array}{rl}\mathcal{B}& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}B(n,m,t)\frac{{\gamma }^{\ast (n-1)}{\eta }^{\ast (m+1)}}{\sqrt{(n-1)!(m+1)!}},\end{array}$(32) (33) $\begin{array}{rl}\mathcal{C}& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}C(n,m,t)\frac{{\gamma }^{\ast (n-1)}{\eta }^{\ast (m+1)}}{\sqrt{(n-1)!(m+1)!}},\end{array}$(33) (34) $\begin{array}{rl}\mathcal{D}& =\sum _{n=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}D(n,m,t)\frac{{\gamma }^{\ast (n-2)}{\eta }^{\ast (m+2)}}{\sqrt{(n-2)!(m+2)!}}.\end{array}$(34) The Husimi function $\mathcal{Q}$ is plotted in Figure 6 for the asymmetric case for some selected moments. We here only consider the cases of M = 60 and M = 0 because they express the most pronounced features (larger revivals) among the others. When T = 0; as shown in the first column in the figure, we observe the initial distribution of the states before the interaction is started. At the moment T = 12.5, which is a moment of a revival for the first and second atoms as indicated in Figure 1, we see that the most localized distribution among them is for $M_1=M_2=60$ and this behaviour also appears in the moment T = 324. We also observe similarities between the case of the coherent states of $M_1=M_2=0$ and the case $M_1=60,M_2=0$ of the third column, where they both develop a similar pattern to a ring. However, the last case of $M_1=0,M_2=60$ of the last column has the most diverge behaviour.

Figure 6. The Husimi function $\mathcal{Q}$ for the asymmetric two atoms (g = 0.5) at $\delta =0$, $\lambda =1$ with $\gamma =x+iy=5$ and $\eta =X+iY$; first row represents $M_1=M_2=0$, second row for $M_1=M_2=60$, third row for $M_1=60$ and $M_2=0$, and the fourth row for $M_1=0$ and $M_2=60$; while the columns represent given moments. The first column for T = 0, second column for T = 12.5, third column for T = 20 and the fourth column T = 324.

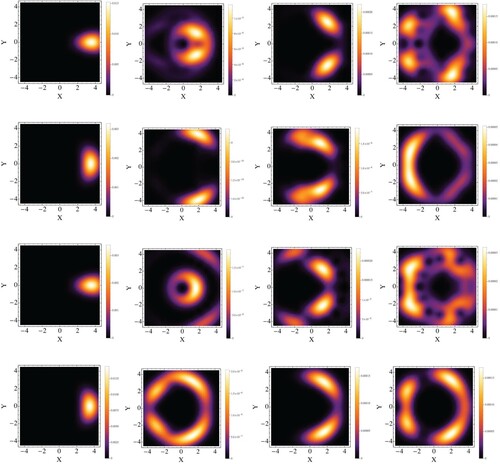
The next moment is T = 20, which is a moment of collapse for almost all states. They all roughly develop two regions with different distributions. The most localized one of them is for the coherent state of ($M_1=M_2=0$), while we notice that the case ($M_1=M_2=60$) constructs a long tail in both regions. The final studied time is T = 324, which is a moment in the resolution period. We detect that the most contained pattern is with $M_1=M_2=60$ and $M_1=0,M_2=60$, where they both yield peaks around a semi-circumference of circle centred at $(X,Y)=(0,0)$, while we see that the pattern of the cases $M_1=M_2=0$ and $M_1=60,M_2=0$ are similar and shattered in many regions. In general, the pattern produced by $\mathcal{Q}$ for the cases $M_1=M_2=0$ and $M_1=60,M_2=0$ are alike, and the other two cases are also similar. Furthermore, during the resolution period, we see that a smoother pattern occurs for the cases which have the most apparent resolution phenomenon.

8. Conclusion

The nonclassical quantum effect of the Mth coherent state on the quantum model for the two atoms with two levels and two-mode quantized field was studied. The two atoms interacting together is included in the quantum model. The initial states of two atoms are the excited states while the two-mode field is in the Mth coherent state. The rotating wave approximation and Heisenberg equation of motion were applied to simplify the Hamiltonian operator. The wave function was evaluated analytically. The results of the statistical measures such as the atomic inversion, the von Neumann entropy, the variance squeezing, the correlation function and the Husimi function were discussed. We note that for the asymmetric case, the rate of energy exchange between the first atom and the field is twice that between the second atom and the field.

The Mth coherent state delivers us to our aim stated in the introduction that we wish to control the evolution of different physical measurements while semi-maintaining the patterns that emerged from employing the coherent state. We can illustrate this by remarking the following points:

1. Applying the Mth state supplies a clear controlling mechanism to the characteristics of the collapse and revival patterns in all studied measurements for both atoms while preserving the behaviour of the CS. This apparently can be seen in figures such as Figure 1(A and C) or of Figure 3(A and C), where we notice that the size, width and height of the packets/peaks are modulated by altering $M_1$ and $M_2$.

2. The resolution period of Equation (18(18) ${\tau }_{RS}=\frac{\frac{13\pi }{2}}{\begin{array}{c}4\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2)-[\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2+1)\\ +\eta (|{\alpha }_0{|}^2+1,|{\alpha }_0{|}^2)+\eta (|{\alpha }_0{|}^2-1,|{\alpha }_0{|}^2)\\ +\eta (|{\alpha }_0{|}^2,|{\alpha }_0{|}^2-1)]\end{array}},$(18) ) yields a semi-periodic pattern that is pronounced and organized when applying significant values of $M_1$ and $M_2$. Moreover, we mostly witness that the repeated shape is not the same for all values of $M_1$ and $M_2$. An evident example of that is in Figure 1(B and D), where we observe that the semi-periodic shape is different from a circumstance to another. On the same time, we see that the case of the coherent state $M_1=M_2=0$, the behaviour tends to be more random than periodic.

3. Measuring the von Neumann entropy $N^{(1)}(T)$ with the Mth CS magnifies the results of the regular CS. We apparently detect this in Figure 3 of (A–D), in which we observe that the steady value of all of them is nearly the same, and the fluctuations have the same positions. However, these fluctuations have much more pronounced drops when applying the Mth fields with $M_1=M_2$ than the cases of regular CS.

4. The correlation function $G^{(i)}(T)$ indicates that the model with the Mth CS is always sub-Poissonian when $M_1=M_2$. In addition, it has more significant nonclassical values than the case of pure coherent states as can be seen in Figure 6 of (A–D).

5. The Husimi function $\mathcal{Q}$ with the Mth CS produces many phase distributions for a given moment, thus suggesting a method to control the phase properties of the scheme by modulating both $M_1$ and $M_2$.

As for the effect of first and second coherent parameters ($M_1,M_2$) together, we note that:

1. The first coherent parameter is not effect on the second mode quantized field and the second coherent parameter is not effect on the first mode quantized field.

2. The effect of the two parameters together is greater than one of them although the sum of all cases is equal.

3. The nonclassical quantized features increase slowly with a significant increase of the parameters.

In addition, the resolution phenomenon is present, and it has a well-pronounced growth with the Mth coherent state, and it is absent with the coherent state. Therefore, these results may open up a wide range of large number of the serious applications for the optics models in the presence the Mth coherent state.

Acknowledgments

Taibah University is strongly acknowledged for financially supporting this work.

Disclosure statement

No potential conflict of interest was reported by the author(s).