On the random search for a randomly moving particle

ABSTRACT

This paper discusses some methods based on the random search problem over the bound domain. The particle moves randomly with a bounded two-dimensional stochastic process in a bounded area. The physical phenomenon determines the boundaries of this area. We have a smart nanosensor tracks randomly for this particle. The necessary condition that maximizes the probability of the first meeting time between the nanosensor and the particle is derived.

KEYWORDS:

• Statistical physics
• bounded stochastic process
• random tracking method
• meeting probability
• wiener process

1. Introduction

In physics, the random search method is an important methodology to determine the meeting probability and the first hitting time between two randomly moving particles in the interactive medium. Also, this method concerns with multidiscipline range of real life applications, which include animal foraging search [1–3], high-capacity databases search [4], oil recovery from mature reservoirs [5,6] and facilitated target location in biological systems [7] (e.g. enhanced diffusion of regulatory proteins while “searching” for specific DNA target sites). In an earlier works, this method has also found interesting connections with human motion and related topics [8–10]. Concepts such as search strategy and efficiency make the approach to the problem naturally fit with the concepts and methods of statistical physics. Indeed, the input of concepts such as random walks, fractal geometry, scaling ideas, correlation functions, first-passage time processes and super diffusive dynamics has rendered great progress to this field. Actually, Levy flights and walks [1–8, 14], intermittent walks [11–13] and correlated random walks (CRW) [15] are among the most studied random walk models proposed as the best strategy in the random search problem.

Some recent works [18–27] have discussed the search problem when the target moves with a known stochastic process. These works presented extensive studies to present the existence of the optimal search strategy, which show the finiteness of the first meeting between the target and the searcher or sensor. Now, the question that arises here is, What happens when the searcher does not have a clear strategy? For example, if a smart sensor (like a nanosensor) is used to detect a specific virus within the bloodstream [29], then this problem will appear and we need to answer this question. The tremendous development in the field of Artificial Intelligence (AI) has helped open the door to technology for the work of high-precision exploration and sensor devices that move according to specific algorithms within the search area to find the target with minimum cost and maximum probability. Regarding this matter, Latif and Bozkurt [16] have created a mobile web of smart sensors that uses cockroaches to collect and transmit information, such as finding survivors in a building that’s been destroyed by an earthquake. The new technique developed by Latif’s team works by embedding a low-cost, light-weight, commercially available chip with a wireless receiver and transmitter onto each roach (they used Madagascar hissing cockroaches). They were able to use the microcontroller to precisely steer the roaches along a line that curves in different directions.

The problem of random search is evident when it comes to tracking a particular particle within the interactive medium to study its behaviour. It is concerned with known the first hitting time between this particle and the sensor that used to track it. Therefore, nanosensor that can perform the tracking process for this particle at an ultra-accurate level is required, as they can improve themselves based on the information they gather. From this point of view, the study of this problem contributes to improving the characteristics of some chemical compounds to raise the efficiency of their use in industry by studying the behaviour of a specific type of particles within the reaction medium. For example, particles that cause the dye to become unstable on fabric in the textile industry. If nanosensors are used within the dye compound to look for other compounds that stop the dye from working on the fabric, this prevents dye defects that cause a loss to the factory.

The main objective of this paper is to obtain the optimal tracking plan for the particle, which moves with a bounded two-dimensional stochastic process in a bounded known area (BKA) inside the reactive medium. The nanosensor tracks the particle as in Figure 1. Furthermore, the particle’s motion is independent of the tracking process and is not specifically aimed at evasion (i.e. the particle does not evade the nanosensor). We aim to maximize the probability of a meeting between the particle and the nanosensor. The nanosensors associated with AI systems can use their artificial cognitive ability to predict the particle’s position. The random movement of the particle has a direct impact on the random search path of the nanosensor. There are many studies to gain access to a high-resolution nanosensor with the ability to classify hyperspectral images [30]. As in [31], the spectroscopic imaging was improved by using the particle’s vibration amplitude to perform a continuous transformation of the wavelets produced by the interaction with the noise signal. This contributed to obtaining a high-resolution two-dimensional image. In [32–34], several algorithms have been improved to increase the efficiency of the work of the nanosensor to track the particle.

Figure 1. Random tracking path of the nanosensor in BKA.

This paper is organized as follows. Section 2 discusses the basic assumptions that describe our model. Section 3 gives the necessary condition that maximizes the meeting probability between the particle and the nanosensor. Finally, conclusions and ongoing research directions are highlighted.

2. Problem formulation

Our mathematical model, which is presented here, aims to find the meeting probability between the particle and the nanosensor. The particle moves on BKA inside the interactive medium with the following bounded random process [17], (1) $x(t)=\sum _{i=1}^2{A}_i\cos [{\omega }_{i}t+{\sigma }_i{B}_i(t)+{\theta }_i],$(1) where $A_i,i=1,2$ are the area boundaries (determined according to the physical phenomenon), ${\omega }_i{,}^{}{\sigma }_i$ are positive constants, $B_i(t)$ are unit wiener process and ${\theta }_i$ are uniformly distributed random variables on $[0,2\pi ]$. As in [17], the probability density function of the particle’s position can be calculated from: (2) $P_X(x)={\int }_D{P}_{Y_1}{(y_1)}^{}{P}_{Y_2}(x-y_1{)}^{}d{y_1}^{}d{y}_2,$(2) where, (3) $P_{Y_i}(y_i)=\frac{1}{\pi \sqrt{A_i^2-y_i^2}},i=1,2,$(3) and the integration domain $D$ is determined according to the particle’s position $x(t)$ and $A_i$.

Moreover, we assume that the nanosensor has a definite range law and moves randomly, as in Figure 1, and that there is no overlap in the nanosensor’s path. Also, let the following assumptions are true:

1. The path of the nanosensor is chosen at random but uniformly and independently of $A_i,i=1,2$;

2. No effort falls outside the tracking area.

It is hard to imagine a nanosensor’s path satisfying (a). However, an irregular nanosensor’s path that wanders throughout the BKA in such a way as to achieve a reasonably uniform path density over the BKA would approximately satisfy this assumption. Assumption (b) will be reasonably well satisfied when the maximum meeting range is much smaller than the dimensions of the tracking area and it is unlikely that the nanosensor’s path will wander outside the tracking area.

Consider that $g(h)$ be a conditional probability of meeting the particle along small increments $h$ of path length given failure to met the particle previously. By the uniformly assumption of (a), the particle’s distribution at time $t$ given failure to met the nanosensor is uniform over the BKA. Consequently, the probability of meeting the particle on this increment is $h/A_{}$ where $A=A_1{A}_2.$ Since the increment is placed independently of past path segments (assumption (a)), then the meeting probability on this increment of path is independent of the past meeting.

Define $b(z)$ to be a probability that the particle is met by the time which the nanosensor has travelled path length $z.$ Furthermore, we let the particle moves around its region (static equilibrium) with magnitude $x[h+\sin (h)]$. Then, $[1-b(z)]P_X(x[h+\sin (h)])$ is the probability of failing to met the particle by path length $z$ but succeeding in the next increment $h+\sin (h)$. Thus, $\begin{array}{rl}& b(z+h)=b(z)+[1-b(z)]P_X(x[h+\sin (h)]),\end{array}$ $\begin{array}{rl}& b(z+h)-b(z)=[1-b(z)]P_X(x[h+\sin (h)]),\end{array}$ then, $\underset{h\to 0}{lim}\frac{b(z+h)-b(z)}{h}=\underset{h\to 0}{{lim}^{}}[1-b(z)]\frac{P_X(x[h+\sin (h)])}{h}.$ Consequently, (4) $b^{\mathrm{\prime }}(z)=\underset{h\to 0}{{lim}^{}}[1-b(z)]\frac{P_X(x[h+\sin (h)])}{h}.$(4)

By using (2) we have, (5) $\begin{array}{rlr}& P_X(x[h+\sin (h)])& ={\int }_{D=2}{P_{Y_1}(y_1)}^{}{P}_{Y_2}(x[h+\sin (h)]-y_1)d{y_1}^{}d{y}_2.\end{array}$(5)

Without loss of generality, assume that $A_1\ge A_2,$ then (5) becomes, (6) $\begin{array}{rlr}& P_X(x[h+\sin (h)])& =\underset{a}{\overset{b}{\int }}\frac{dy}{{\pi }^2\sqrt{{(A_2^2-y^2)}^{}[A_1^2-{(x[h+\sin (h)]-y)}^2]}},\end{array}$(6) where the integration limits $a$ and $b$ are determined as follows:

1. $a=-A_2$, $b=x[h+\sin (h)]+A_1,$ for $-\frac{(A_1+A_2)}{h+\sin (h)}\le x\le -\frac{(A_1-A_2)}{h+\sin (h)},$

2. $a=-A_2$, $b=A_1,$ for $-\frac{(A_1-A_2)}{h+\sin (h)}<x<\frac{A_1-A_2}{h+\sin (h)}$ and

3. $a=x[h+\sin (h)]-A_1$, $b=A_2,$ for $\frac{A_1-A_2}{h+\sin (h)}\le x\le \frac{A_1+A_2}{h+\sin (h)}.$

Using Mathematica program the value of integration (6) is given by, (7) $\begin{array}{rlrlr}I& =\frac{1}{A_1{A}_2}\sum _{r=0}^{\mathrm{\infty }}\sum _{n=0}^r\sum _{k=0}^{2r-2n}{(-1)}^k\frac{{(x[h+\sin (h)])}^{2r-2n-k}}{A_1^{2r-2n}{A}_2^{2n}}& \times \left(\frac{2r!}{2^{r}r!}\right){\left(\frac{\left(\begin{array}{c}rn\end{array}\right)}{\left(\begin{array}{c}2r2n\end{array}\right)}\right)}^2& \times \left(\begin{array}{c}2r-2nk\end{array}\right)\left(\frac{b^{2n+k+1}-a^{2n+k+1}}{{}^{2n+k+1}}\right),& -1<\left|\frac{y}{A_2}\right|<1,-1<\left|\frac{y}{A_1}\right|<1.\end{array}$(7)

If we consider the limit integration (iii), then by substituting from (7) in (4) we obtain, (8) $b^{\mathrm{\prime }}(z)=[1-b(z)]\underset{h\to 0}{{lim}^{}}\frac{I}{h}.$(8)

Since $b(0)=0$, then for $z\ge 0$ (8) has a solution when $r=1+\alpha +\beta$, $k=1+2\alpha +2\gamma$, $n=\beta -\gamma$ where $\alpha ,\beta ,\gamma$ are random values determined by the reaction conditions and they are positive integers greater than or equal zero. Therefore, (8) has well known solution, $\begin{array}{rlrlr}I& =\underset{h\to 0}{{lim}^{}}[\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2}\frac{1}{A_1{A}_2}{(-1)}^{1+2\alpha +2\gamma }\frac{x[h+\sin (h)]}{h{A}_1^{2(1+\alpha -\gamma )}{A}_2^{2(\beta -\gamma )}}& \times \left(\frac{2(1+\alpha +\beta )!}{2^{1+\alpha +\beta }(1+\alpha +\beta )!}\right){\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2& \times \left(\begin{array}{l}2(1+\alpha -\gamma )1+2\alpha +2\gamma \end{array}\right)& \times \left(\frac{b^{2(1+\alpha -\beta )}-a^{2(1+\alpha -\beta )}}{{}^{2(1+\alpha -\beta )}}\right)\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2}]\end{array}$ $\begin{array}{rlrlr}& =[\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2}\frac{{(-1)}^{1+2\alpha +2\gamma }}{A_1^{2(\alpha -\gamma )+3}{A}_2^{2(\beta -\gamma )+1}}\left(\frac{2(1+\alpha +\beta )!}{2^{1+\alpha +\beta }(1+\alpha +\beta )!}\right)& \times {\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2\left(\begin{array}{l}2(1+\alpha -\gamma )1+2\alpha +2\gamma \end{array}\right)& \times \left(\frac{b^{2(1+\alpha -\beta )}-a^{2(1+\alpha -\beta )}}{{}^{2(1+\alpha -\beta )}}\right)\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2}]& \times \underset{h\to 0}{{lim}^{}}\frac{x[h+\sin (h)]}{h}\end{array}$ $\begin{array}{rlrlr}& =[\phantom{\times {\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2}\frac{2x^{}{(-1)}^{1+2\alpha +2\gamma }}{A_1^{2(\alpha -\gamma )+3}{A}_2^{2(\beta -\gamma )+1}}\left(\frac{2(1+\alpha +\beta )!}{2^{1+\alpha +\beta }(1+\alpha +\beta )!}\right)& \times {\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2& \times \left(\begin{array}{l}2(1+\alpha -\gamma )1+2\alpha +2\gamma \end{array}\right)\left(\frac{b^{2(1+\alpha -\beta )}-a^{2(1+\alpha -\beta )}}{{}^{2(1+\alpha -\beta )}}\right)\phantom{\times {\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta ){}_{}^{}2(\beta -\gamma )\end{array}\right)}\right)}^2}]& -1<\left|\frac{y}{A_2}\right|<1{,}^{}-1<\left|\frac{y}{A_1}\right|<1.\end{array}$

Consequently, $\begin{array}{rlrl}b(z)& =1-\exp (-z[\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2}\frac{2x^{}{(-1)}^{1+2\alpha +2\gamma }}{A_1^{2(\alpha -\gamma )+3}{A}_2^{2(\beta -\gamma )+1}}& \times \left(\frac{2(1+\alpha +\beta )!}{2^{1+\alpha +\beta }(1+\alpha +\beta )!}\right)& \times {\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2\end{array}$ (9) $\begin{array}{rlrl}& \times \left(\begin{array}{l}2(1+\alpha -\gamma )1+2\alpha +2\gamma \end{array}\right)& \times \left(\frac{b^{2(1+\alpha -\beta )}-a^{2(1+\alpha -\beta )}}{{}^{2(1+\alpha -\beta )}}\right)\phantom{{\left(\frac{\left(\begin{array}{l}1+\alpha +\beta \beta -\gamma \end{array}\right)}{\left(\begin{array}{l}2(1+\alpha +\beta )2(\beta -\gamma )\end{array}\right)}\right)}^2}]),& -1<\left|\frac{y}{A_2}\right|<1{,}^{}-1<\left|\frac{y}{A_1}\right|<1.\end{array}$(9)

This is similar to the random search formula of Koopman [28]. Since the tracking path was random, then this probability is usually lower than it would be if we had tracked systematically. Consequently, $b(z)$ is a lower bound for the actual meeting probability and is useful for approximation purposes. If we assume that a straight line path is necessary to track, then $b(z)$ becomes $\frac{z}{A_1{A}_2}.$ This estimation of $b(z)$ assumes ideal conditions and thus provides an upper bound for the probability.

3. Special case

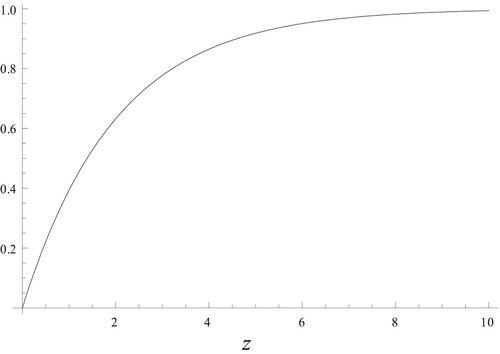
We are interested in studying a special case when the boundaries of BKA are fixed. (i.e. $\alpha =\beta =\gamma =0$). This means that the particle’s diffusion calms down inside the reaction medium. Consequently, the random tracking formula (9) will become, (10) $b(z)=1-\exp \left(\frac{-2xz(a^2-b^2)}{A_1^2{A}_2}\right),$(10) which is indicated in Figure 2.

Figure 2. The meeting probability of the random tracking path at $\alpha =\beta =\gamma =0.$

Let us examine an important property of the random tracking formula that is graphed in Figure 2. Initially, the slope of $b(z)$ equals $\frac{2x(a^2-b^2)}{A_1^2{A}_2}$, where at the beginning of the tracking process there is almost no chance of overlapping with the previous tracking process. However, as the tracking continues and the chance of overlap with previously tracked regions of the BKA increases, that slows the rate at which the probability of meeting increases. Thus, the random tracking formula shows a form of the law of diminishing returns. This is diminishing the return rate or decreasing the derivative of $b(z)$.

3.1. Necessary condition for optimal solution

Here we show how to implement the random tracking path of the nansensor used inside the BKA. The nansensor gives all points within the BKA the same priority and attention. The usefulness of the random tracking formula (9) appears in its properties. It has a high degree of mathematical simplicity and the ability to provide a lower bound on the effectiveness of a systematic tracking of the particle inside the BKA for most tracking situations. Thus, if we consider $\frac{A_1-A_2}{h+\sin (h)}\le x\le \frac{A_1+A_2}{h+\sin (h)}$, $A_1\ge A_2,$ and for the case $\alpha =\beta =\gamma =0$ (relative stability of the particle’s motion), then we can find the condition that maximizes the meeting probability of the particle after solving the following optimization problem: $\begin{array}{rl}& \text{Max}1-\exp \left(\frac{-2xz(a^2-b^2)}{A_1^2{A}_2}\right)\end{array}$ $\begin{array}{rl}& \text{Subject}\text{to}\frac{A_1-A_2}{h+\sin (h)}\le x\le \frac{A_1+A_2}{h+\sin (h)},A_1\ge A_2,\end{array}$ $\begin{array}{rl}& a=x[h+\sin (h)]-A_1,b=A_2,\end{array}$ $\begin{array}{rl}& A_1>0,A_2>0,h\ge 0,z\ge 0.\end{array}$

To maximize $b(z),$ it must be $a$ is greater than $b$ by a large magnitude i.e. $a-b>>0$, where $a$ and $b$are depend on $A_1$ and $A_2,$ see Figure 3.

Figure 3. The meeting probability of random tracking formula (9) for a system having $A_1=2$ and $A_2=4$. In the part (I) the values $(a,b)$ = (1.2,1) for $U$, $(a,b)$ = (2.2,1) for $S$ and $(a,b)$ =  (4.2,1) for $V$; in the part (II) the values $(a,b)$ = (1.4,1) for $U$, $(a,b)$ = (2.4,1) for $S$ and $(a,b)$ = (4.4,1) for $V$; in the part (III) the values $(a,b)$ = (2,1) for $U$, $(a,b)$ = (3,1) for $S$ and $(a,b)$ =  (5,1) for $V$ and in the part (IV) the values $(a,b)$ = (2.6,1) for $U$, $(a,b)$ = (3.6,1) for $S$ and $(a,b)$ = (5.6,1) for $V$.

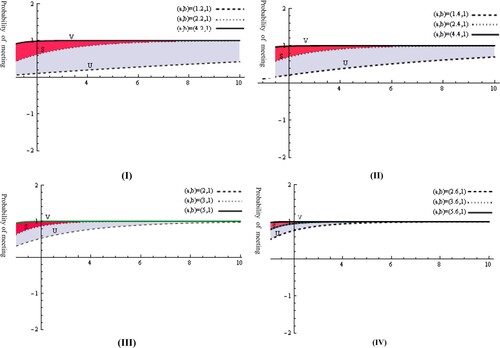
In the different parts of Figure 3, the meeting probability, the area between the curves $U$, $S$ and the area between the curves $S$, $V$ are decreasing as the values of $a$, $b$ grow. Due to the rapid movement of the particle in the interactive medium, the boundaries of the tracking area increase. This will reduce the meeting probability between the particle and the nanosensor. The nanosensor can modify its trajectory to predict the particle’s position based on the available information about the reaction, such as its speed. These results suggest that the meeting probability is increasing as the values of $a$ and $b$ grow where $a$ and $b$ depend on the boundaries $A_1$ and $A_2$. Furthermore, the maximization of meeting probability depends on the minimum values of $\alpha {,}^{}\beta$ and $\gamma$ where the values of $a$ and $b$ depend on them.

4. Conclusion and future work

A random tracking technique for a particle in BKA within an interactive medium has been proven. The particle moves with a bounded two-dimensional stochastic motion. The boundaries of the search area are determined by physical phenomena. The tracking process is done using a smart nanosensor, which moves randomly in BKA. The probability of meeting the particle has been found. A special case is discussed in detail when the interaction is stable. The necessary condition that maximizes the probability of the first meeting time between the nanosensor and the particle is derived.

In the future, the proposed model could be extended to consider a particle that moves with a bounded N-dimensional stochastic process.

Disclosure statement

No potential conflict of interest was reported by the author(s).