Controllability of damped dynamical systems modelled by Hilfer fractional derivatives

Abstract

In this article, we investigate the controllability of damped dynamical system modelled by Hilfer derivative of fractional order ${\tau }_1\in (1,2]$ and ${\tau }_2\in (0,1]$. The Mittag-Leffler matrix function of two parameters has been used to represent the solution of Hilfer fractional problem of damped dynamical system. With the use of the Schawder fixed point theorem and the contraction mapping theorem, the existence and uniqueness of the linear and non-linear system of Hilfer dynamical control system are determined. More specifically, fractional calculus are used to provide sufficient criteria for the controllability results. Finally, examples are given to show how the key results might be justified.

Keywords:

• Gramian matrix
• Laplace transform
• Mittag-Leffler function
• numerical technique
• successive approximation technique

1. Introduction

In recent decades, the theory of fractional calculus, which includes fractional differential equations, has made significant advances in science and development, primarily by providing sufficient results for models, particularly for real-world problems. Moreover, fractional differential equation is considered to be the generalised differential equations. It is possible to consider a field of mathematical physics which deals on integro-differential equations in which the integrals are of the convolution form and also have predominantly power law or logarithm type single kernels, the diff-integral being an operator that contains both integer-order integrals and integer-order derivatives as special cases is the motive why in present, fractional calculus becomes very popular and many application arise from the term diff-integral, we mean both the integral of arbitrary order and derivative of arbitrary order (see Refs. [1–3]). In this paper, we have considered diff-integrals of fractional order. Fluid flow, rheology, diffusive movement, power systems, probabilities, statistic, control theory of system dynamics, viscoelasticity, chemical quantum mechanics, optometry, data processing and several others are some of the fields where fractional calculus is used.

There are many definitions for fractional derivatives and fractional integrals in fractional calculus, but the Riemann-Liouville (R-L) and Caputo definitions are the most widely used (see, for instance, [4–8]). In recent years, a new term, the Hilfer fractional derivatives, has gained prominence among the definitions of other derivatives. Hilfer fractional derivative is an expanded form of Riemann-Liouville (R-L) and Caputo fractional derivatives proposed by Hilfer [9], which permits one to interpolate with another (for example, see Refs. [10–14]). The use of functions such as Mittag-Leffler (M-L), Wright type function turn out to play a fundamental yet powerful role in solving fractional differential equations.

Fractional-order differential equations have lately emerged as helpful tools for simulating the dynamics of processes in complicated media in a variety of applications. The literature reveals an increasing interest in fractional dynamical systems related concerns identified towards control theory. Concepts of observability, controllability and stability play a key role in the control system. Controllability is one of the most basic principles in mathematical control theory. It denotes that a dynamic system can be directed from any initial state to any final state by utilising a set of controls. In layman terms from the word controllability we mean, if one can control a system from one point to another point then that system possess a control, thus making the system controllable. The concept of controllability behaves as the most important path in both finite and infinite dimensional spaces of system which are used by both ordinary and partial differential equations. Controllability is considered as an important property of the control system as it defines the behaviour of that control system. The theory of controllability was proposed by R. Kalman in the year 1960 Kalman et al. [15]. Many authors have studied the linear and nonlinear functions of damped dynamical systems in recent years, and they have used the Gramian matrix and rank condition to predict controllability results in finite dimensional spaces, see Balachandran et al. [16], Balachandran and Park [17], Balachandran et al. [18], Boudjerida et al. [19]. Recent studies, Arthi et al. [20] established the controllability of fractional damped dynamical systems with distributed delays using Caputo derivatives for both linear and nonlinear cases. Authors Balachandran and Kokila [21] studied the controllability of linear and nonlinear fractional dynamical systems in finite dimensional spaces. Moreover stability, stabilizability of fractional-order stochastic system is also studied by various authors in Mchiri et al. [22], Zhu [23], Yang et al. [24] with delay which are few examples of the recent developments of fractional calculus. Many authors Kumar et al. [25], Darvishi et al. [26], Yaro et al. [27], Pratap et al. [28], Shah et al. [29] studied fractional wave equation, fractional-order neural networks with delay equation and much more which are a few applications of fractional differential equations.

In the literature, authors had investigated mechanical system $\begin{array}{rl}& m{D}^{2}h\left(t\right)+k_2{D}^{\text{β}}h\left(t\right)+k_{1}h\left(t\right)=f\left(t\right),\\ & t\ge 0,0<\text{β}<1,\end{array}$where $h\left(t\right)$ – a mass's position in relation to the other elements, f(t) – forcing function, $m,k_1,k_2$ - constants. This model is studied to analyse the dynamics of certain gases dissolved in a fluid and the dynamics of a sphere submerged in an incompressible viscous fluid for see Torvik and Bagley [30], Hartley and Lorenzo [31], Gorenflo et al. [32], Mainardi [33]. Control of the above system is very crucial which was studied by K. Balachandran et al. [34] by modifying certain terms and choosing apt constants $m,k_1,k_2,$ (1) $\{\begin{array}{ll}{}^{\mathcal{C}}{D}^{\tau }y\left(q\right)-\mathcal{P}& \begin{array}{l}{}^{\mathcal{C}}{D}^{\zeta }y\left(q\right)=h\left(q\right),\\ \zeta \in (0,1],\tau \in (1,2],\\ q\in [0,T]:=\mathbb{J},\end{array}\\ y\left(0\right)=y_0,& y^{\prime }\left(0\right)=y_0^{\prime },y\in \mathbb{R},\end{array}$(1) with ${\mathcal{P}}_{n\times n}$ is an matrix and $h:\mathbb{J}\to {\mathbb{R}}^n$ is a continuous function.

However, nowhere in the literature had the research on the controllability of a nonlinear Hilfer fractional dynamical system of order $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1$ has been examined. In order to fill this space, we use the Mittag-Leffler matrix function and the Gramian matrix, where the forcing function f is taken to be in terms of the control function u, to investigate the controllability of a nonlinear Hilfer fractional dynamical system of order $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1$ in a finite dimensional space.

Inspired by the previous works, controllability of Hilfer derivative of nonlinear fractional damped dynamical systems of the below form (2) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=h\left(q\right),& q\in [0,T]:=\mathbb{J},\\ I_t^{1-{\varphi }_1}y\left(0\right)=a,& I_t^{2-{\varphi }_1}y\left(0\right)=b,\\ I_t^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(2) where ${\varphi }_1={\tau }_1+2\zeta -{\tau }_1\zeta ,{\varphi }_2={\tau }_2+\zeta -{\tau }_2\zeta ,$ with $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1,y\in \mathbb{R},\mathcal{P}$ is an $n\times n$ matrix and $h:\mathbb{J}\to \mathbb{R}$ is continuous is determined. Here ${\tau }_1,{\tau }_2$ is the order of the fractional differential equation and ζ is the type-parameter which produces more types of stationary states and provide an extra degree of freedom on the initial condition. In the paper, Qiao et al. [35], bilinear method is used to solve the problem whereas we had analysed successive approximation method. In precise, Hilfer derivative helps in calculating the theoretical simulation of dielectric relaxation in glass-forming materials, rheological constitute modelling, polymer science, control theory, etc.

The following are the work's primary contribution:

• The Hilfer dynamical fractional problem $D^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=h\left(q\right)$ is solved based on Mittag-Leffler matrix function making use of Laplace convolution operator.

• Later, for the linear Hilfer dynamic control problem $D^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)q\in \mathbb{J}$, $I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,I_q^{1-{\varphi }_2}y\left(0\right)=c$ if the system is controllable or not is found out using the theorem involving controllability Grammian matrix.

• Then controllability of non-linear dynamical control problem $D^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)+h(q,y(q\left)\right),q\in \mathbb{J}$. $I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,I_q^{1-{\varphi }_2}y\left(0\right)=c$ is proved using Arzela – Ascoli theorem and Schawder fixed point theorem.

• Controllability of Hilfer Integro-differential systems $D^{{\nu }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\nu }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)+h(q,y(q),{\int }_0^{q}f(q,s,y\left(s\right)\left)\mathrm{d}s\right),q\in \mathbb{J}$ $I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,I_q^{1-{\omega }_2}y\left(0\right)=c$ is solved using contraction mapping theorem.

• At last, numerical result is obtained which validates our results.

The following is an overview of the paper's structure: Section 2 contains a list of preliminary concepts that are applicable to our results and will be helpful in the sections that follow. In Section 3, we studied the linear fractional dynamical system of Hilfer fractional derivative. Then we discuss the nonlinear dynamical system in Section 4. In Section 5, we study on integro-differential systems and then example is illustrated in Section 6.

2. Preliminaries

Definition 2.1

Hilfer [9]

The Hilfer differential equation of fractional order τ and parameter ζ of a function is described by the generalized R-L fractional derivative. It is known by ${}^H{D}^{\tau ,\zeta }h\left(q\right)=I^{\zeta (n-\tau )}{D}^n{I}^{(1-\zeta )(n-\tau )}h\left(q\right),$where $n-1<\tau <n,0\le \zeta \le 1,q>a,D=\frac{\mathrm{d}}{\mathrm{d}t}.$

Definition 2.2

Fahad et al. [36]

The Hilfer fractional derivative ${}_0{D}_t^{\tau ,\zeta }h\left(0\right)$ is taken as $D^{\tau ,\zeta }h\left(0\right)$. The Laplace transform of the Hilfer derivative is defined as $\begin{array}{rl}L\left\{{}_0{D}_t^{\tau ,\zeta }h\right(q\left)\right\}& =s^{\tau }L\left\{h\right(q\left)\right\}-\sum _{i=0}^{m-1}{s}^{n(1-\zeta )+\tau \zeta -i-1}\\ & \times \left({}_0{I}_t^{(1-\zeta )(n-\tau )-i}h\right)\left(0\right),\\ & n-1<\tau <n,0\le \zeta \le 1,\end{array}$exists for $s>\tau$.

Definition 2.3

Balachandran et al. [34]

General Mittag–Leffler function with two parameters has the form ${\mathbb{E}}_{\rho }{,}_{\mu }\left(\mathfrak{z}\right)=\sum _{k=0}^{\mathrm{\infty }}\frac{{\mathfrak{z}}^k}{\mathrm{\Gamma }(\rho k+\mu )},\rho ,\mu >0,$where $\mathfrak{z}\in \mathbb{C}.$

Definition 2.4

Balachandran et al. [34]

The Laplace transform of the Mittag–Leffler function in two parameters is $L\left\{q^{\mu -1}{\mathbb{E}}_{\rho ,\mu }\right(\lambda q^{\rho }\left)\right\}=\frac{s^{\rho -\mu }}{s^{\rho }+\lambda }.$

Solution Representations:

Consider the following Hilfer fractional problem (3) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=h\left(q\right),& q\in [0,T]:=\mathbb{J},\\ I_t^{1-{\varphi }_1}y\left(0\right)=a,I_t^{2-{\varphi }_1}y\left(0\right)=b,& I_t^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(3) where ${\varphi }_1={\tau }_1+2\zeta -{\tau }_1\zeta ,{\varphi }_2={\tau }_2+\zeta -{\tau }_2\zeta ,$ with $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1y\in \mathbb{R},\mathcal{P}\in {\mathbb{R}}^{n\times n}$ is a matrix, where h is a continuous function from $\mathbb{J}$ to $\mathbb{R}$. In order to identify the system's actual solution, we apply the Laplace transform to both sides of the above function, $\begin{array}{rl}& s^{{\tau }_1}Y\left(s\right)-s^{\zeta ({\tau }_1-2)+1}\left({}_0{I}_t^{(2-{\varphi }_1)}y\right)\left(0\right)\\ & -s^{\zeta ({\tau }_1-2)}\left({}_0{I}_t^{(1-{\varphi }_1)}y\right)\left(0\right)-\mathcal{P}{s}^{{\tau }_2}Y\left(s\right)\\ & +\mathcal{P}{s}^{\zeta ({\tau }_2-1)}\left({}_0{I}_t^{(1-{\varphi }_2)}y\right)\left(0\right)=H\left(s\right).\end{array}$Then $\begin{array}{rl}Y\left(s\right)& =\frac{s^{\zeta ({\tau }_1-2)+1}}{(s^{{\tau }_1}-\mathcal{P}{s}^{{\tau }_2})}b+\frac{s^{\zeta ({\tau }_1-2)}}{(s^{{\tau }_1}-\mathcal{P}{s}^{{\tau }_2})}a\\ & -\mathcal{P}\frac{s^{\zeta ({\tau }_2-1)}}{(s^{{\tau }_1}-\mathcal{P}{s}^{{\tau }_2})}c+\frac{H\left(s\right)}{(s^{{\tau }_1}-\mathcal{P}{s}^{{\tau }_2})}\\ & =\frac{s^{{\tau }_1-{\tau }_2+1-{\varphi }_1}}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}b+\frac{s^{{\tau }_1-{\tau }_2-{\varphi }_1}}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}a\\ & -\mathcal{P}\frac{s^{-{\varphi }_2}}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}c+H\left(s\right)\frac{s^{-{\tau }_2}}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}.\end{array}$Where I is the identity matrix, we will now take Laplace inverse transform for the above equation on both sides, $\begin{array}{rl}{L}^{-1}Y\left(s\right)& =L^{-1}\left\{s^{{\tau }_1-{\tau }_2+1-{\varphi }_1}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}^{-1}\right\}b\\ & +L^{-1}\left\{s^{{\tau }_1-{\tau }_2-{\varphi }_1}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}^{-1}\right\}a\\ & -\mathcal{P}{L}^{-1}\left\{s^{-{\varphi }_2}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}^{-1}\right\}c\\ & +L^{-1}\left\{H\right(s)\times s^{-{\tau }_2}{(s^{{\tau }_1-{\tau }_2}I-\mathcal{P})}^{-1}\}.\end{array}$If we replace the Laplace transform of the Mittag–Leffler function with the Laplace convolution operator in the above equation, we get the following result. (4) $\begin{array}{rl}y\left(q\right)& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +h\left(q\right)\ast q^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +{\int }_0^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})h\left(s\right)\mathrm{d}s.\end{array}$(4)

3. Linear system

Let us take the damped dynamical system of linear function in differential equation of fractional-order form which describes the hereditary and memory effects of complicated process. In this section, we will prove the controllability of system for fractional Hilfer derivative. (5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) with $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1y\in \mathbb{R},u\in L^2(\mathbb{J},{\mathbb{R}}^m),$ $\mathcal{P}\in {\mathbb{R}}^{n\times n}$ and $\mathcal{Q}\in {\mathbb{R}}^{n\times m}$ are matrices.

Definition 3.1

Balachandran et al. [34]

On $\mathbb{J}$, the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is considered to be controllable if, for each vector $a,b,c,x_1\in \mathbb{R}$ there exists a control $u\in L^2(\mathbb{J},{\mathbb{R}}^m)$ such that the corresponding solution of system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) with $y\left(0\right)=b,c$ satisfies $y\left(T\right)=x_1$.

We should notice that we are only interested with steering states in our controllability definition, not the velocity vector.

Theorem 3.1

The linear system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable on $\mathbb{J}$ iff the $n\times n$ Gramian matrix (6) $\begin{array}{rl}\mathbb{M}& ={\int }_0^T(T-s{)}^{2{\tau }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left({\mathcal{P}}^{\ast }\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathrm{d}s\end{array}$(6) is invertible.

Proof.

When $\mathbb{M}$ is invertible, the initial conditions a, b, c and $x_1$ are given. We have the option of selecting the input function $u\left(q\right)$ as $\begin{array}{rl}u\left(q\right)& =(T-q{)}^{{\tau }_1-1}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left({\mathcal{P}}^{\ast }\right(T-q{)}^{{\tau }_1-{\tau }_2}){\mathbb{M}}^{-1}{y}_1,q\in \mathbb{J},\end{array}$where, $\begin{array}{rl}{y}_1& =x_1-T^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)b\\ & -T^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)a\\ & +\mathcal{P}{T}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)c,\end{array}$and extend the control function which is continuous for all the values of q. let we take q = T, then y can be written as $\begin{array}{rl}y\left(T\right)& =b{T}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +a{T}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{T}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +{\int }_0^T(T-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u\left(s\right)\mathrm{d}s\\ & =b{T}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +a{T}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{T}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +{\int }_0^T(T-s{)}^{2{\tau }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left({\mathcal{P}}^{\ast }\right(T-q{)}^{{\tau }_1-{\tau }_2}){\mathbb{M}}^{-1}{y}_1\mathrm{d}s\\ & =b{T}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +a{T}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{T}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +\mathbb{M}{\mathbb{M}}^{-1}{y}_1\\ & =x_1.\end{array}$Therefore, the linear system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable on $\mathbb{J}$.

Assume that the state equation is controllable, but that the matrix $\mathbb{M}$ is not invertible for the purpose of a contradiction. If $\mathbb{M}$ cannot be inverted, therefore, the vector $\mathfrak{z}\ne 0$ exists. Such that $\begin{array}{rl}{\mathfrak{z}}^{\ast }\mathbb{M}\mathfrak{z}& =0={\int }_0^T{\mathfrak{z}}^{\ast }{(T-s)}^{2{\tau }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left({\mathcal{P}}^{\ast }\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathfrak{z}\mathrm{d}s,\end{array}$hence (7) ${\mathfrak{z}}^{\ast }{(T-s)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}=0,t\in \mathbb{J}.$(7) Let we take the initial and final condition, then if the system is controllable, there exists the control $u\left(q\right)$ on $\mathbb{J}$. It steers from 0 to $x_1=\mathfrak{z}$ at q = T. Then ${\int }_0^T{\mathfrak{z}}^{\ast }{(T-s)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u\left(s\right)\mathrm{d}s.$Using Equation (7(7) ${\mathfrak{z}}^{\ast }{(T-s)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}=0,t\in \mathbb{J}.$(7) ), ${\mathfrak{z}}^{\ast }$ is multiplied on both sides, yields $\mathfrak{z}{\mathfrak{z}}^{\ast }=0$, which is a contradiction. Therefore, the Gramian matrix is invertible, which proves the theorem.

Theorem 3.2

Linear damped dynamical system of differential equation of fractional-order system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable on $\mathbb{J}$ if and only if (8) $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}[\mathcal{Q},\mathcal{P}\mathcal{Q},{\mathcal{P}}^2\mathcal{Q},\cdots {\mathcal{P}}^{n-1}\mathcal{Q}]=n.$(8)

Proof.

To attempt, we show that the required condition has two cases.

Case 1:

Assume $T>\tau$, and our system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable for the values of a, b, c = 0 and initial control $\phi \left(0\right)$ for any $\mathfrak{y}\in {\mathbb{R}}^n$

Using the control system (3.1), there exists the control $u\left(s\right)$, such that (9) $\begin{array}{rl}\mathfrak{y}& ={\int }_0^{q+\tau }(q-s{)}^{\tau -1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}(\mathcal{P}(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u\left(s\right)\mathrm{d}s\\ & +{\int }_{q+\tau }^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2}\left)\mathcal{Q}u\right(s)\mathrm{d}s.\end{array}$(9) According to the Cayley Hamilton theorem, there are functions ${\gamma }_0\left(q\right),{\gamma }_1\left(q\right),{\gamma }_2\left(q\right),\dots {\gamma }_{n-1}\left(q\right)$ on the interval $[0,\mathrm{\infty })$. As a result (10) ${\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)=\sum _{i=0}^{n-1}{\gamma }_i\left(q\right){\mathcal{P}}^i.$(10) Let $〈\mathcal{P},\mathcal{Q}〉=\lambda +\mathcal{P}\lambda +{\mathcal{P}}^2\lambda +\cdots +{\mathcal{P}}^{n-1}\lambda$, where n is order of $\mathcal{P}$, λ is image $\mathcal{Q}$.

Now Equations (9(9) $\begin{array}{rl}\mathfrak{y}& ={\int }_0^{q+\tau }(q-s{)}^{\tau -1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}(\mathcal{P}(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u\left(s\right)\mathrm{d}s\\ & +{\int }_{q+\tau }^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2}\left)\mathcal{Q}u\right(s)\mathrm{d}s.\end{array}$(9) ), (10(10) ${\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)=\sum _{i=0}^{n-1}{\gamma }_i\left(q\right){\mathcal{P}}^i.$(10) ) imply $\mathfrak{y}\in 〈\mathcal{P},\mathcal{Q}〉$. Hence ${\mathbb{R}}^n=〈\mathcal{P},\mathcal{Q}〉$ thus holding Equation (8(8) $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}[\mathcal{Q},\mathcal{P}\mathcal{Q},{\mathcal{P}}^2\mathcal{Q},\cdots {\mathcal{P}}^{n-1}\mathcal{Q}]=n.$(8) ).

Case 2:

If $T\in [0,\tau )$, it is similar to case 1, so proof is ignored.

Next, the sufficient part is demonstrated in both cases.

Case 1:

For time $T>{\tau }_1$, we consider that the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) holds. Then for ${\mathbb{R}}^n=〈\mathcal{P},\mathcal{Q}〉$, $\overline{\mathfrak{y}}\in {\mathbb{R}}^n$, initial states a, b, c and control φ. Assume $\begin{array}{rl}\kappa & =\overline{\mathfrak{y}}-b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -{\int }_0^{q+\tau }(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}\phi \left(0\right)\mathrm{d}s\\ & -{\int }_{q+\tau }^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}\phi \left(0\right)\mathrm{d}s.\end{array}$For $\kappa \in {\mathbb{R}}^n=〈\mathcal{P},\mathcal{Q}〉$, we know that, the set $R(0,0)$ is equal to $〈\mathcal{P},\mathcal{Q}〉$.

Hence there exists the control $\vartheta \left(s\right)\in L^1(0,T)$, therefore, (11) $\begin{array}{rl}\mathfrak{y}& ={\int }_0^{q+\tau }(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2}\left)\mathcal{Q}{\vartheta }^{\ast }\right(s)\mathrm{d}s\\ & +{\int }_{q+\tau }^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2}\left)\mathcal{Q}{\vartheta }^{\ast }\right(s)\mathrm{d}s.\end{array}$(11) Letting $u\left(s\right)={\vartheta }^{\ast }\left(s\right)+\phi \left(0\right)$ we have $\begin{array}{rl}\overline{\mathfrak{y}}=& b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ +& {\int }_0^{q+\tau }(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u(s)\mathrm{d}s\\ & +{\int }_{q+\tau }^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}u\left(s\right)\mathrm{d}s.\end{array}$Which implies that the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable for $T>\tau$.

Case 2:

If $T\in (0,\tau )$, assume Equation (8(8) $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}[\mathcal{Q},\mathcal{P}\mathcal{Q},{\mathcal{P}}^2\mathcal{Q},\cdots {\mathcal{P}}^{n-1}\mathcal{Q}]=n.$(8) ) holds, then ${\mathbb{R}}^n=〈\mathcal{P},\mathcal{Q}〉$ for $\mathfrak{y}\in {\mathbb{R}}^n$ initial states $a,b,c.$ Let, $\begin{array}{rl}\kappa & =\overline{\mathfrak{y}}-b{T}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & -a{T}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)\\ & +\mathcal{P}c{T}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right).\end{array}$For $\kappa \in {\mathbb{R}}^n=〈\mathcal{P},\mathcal{Q}〉$, we get $\kappa \in R(0,0)$. Hence ${\vartheta }^{\ast }\left(s\right)\in L^1(0,T)$ exist and initial control ${\phi }^{\ast }\in L^1({\tau }_1,0)$ such that, $\kappa ={\int }_0^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}(\mathcal{P}(q-s{)}^{{\tau }_1{\tau }_2})\mathcal{Q}{\vartheta }^{\ast }\left(s\right)\mathrm{d}s,$thus we have, $\begin{array}{rl}\overline{\mathfrak{y}}& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +{\int }_0^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\mathcal{Q}{\vartheta }^{\ast }\left(s\right)\mathrm{d}s.\end{array}$Therefore, our linear damped dynamical system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable for $T\in (0,\tau ]$.

4. Nonlinear system

With having the results derived in the previous section, we shall now take the differential equation of fractional order nonlinear system of the form,

Case 1: Nonlinear function without control (12) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(12) where $0<{\tau }_2\le 1<{\tau }_1\le 2,0\le \zeta \le 1y\in \mathbb{R},u\in L^2(\mathbb{J},{\mathbb{R}}^m)$.

Consider the space $Y=\left\{y\right(q)\in C(\mathbb{J}:{\mathbb{R}}^n\left)\right\}$ and $D^{\tau ,\zeta }y\left(q\right)\in C(\mathbb{J}:{\mathbb{R}}^n)$ be a Banach space that possesses $\Vert y{\Vert }_Y=\underset{q\in \mathbb{J}}{max}|y\left(q\right)|+\underset{q\in \mathbb{J}}{max}|D^{{\tau }_2,\zeta }y\left(q\right)|$, where $0<{\tau }_2<1$. We shall define the following positive constants $b_1$ and $b_2$ such that $\begin{array}{rl}& \left(\mathbb{H}1\right)\Vert h(q,y(q\left)\right)\Vert \le b_1,q\in \mathbb{J},y\in {\mathbb{R}}^n.\\ & \left(\mathbb{H}2\right)\Vert h(q,x)-h(q,y)\Vert \le b_2\Vert x-y\Vert ,x,y\in {\mathbb{R}}^n.\end{array}$Let us describe, ${\eta }_1\left(q\right)=q^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\mathcal{P}{q}^{{\tau }_1-{\tau }_2},$  ${\eta }_2\left(q\right)=q^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\mathcal{P}{q}^{{\tau }_1-{\tau }_2},$  ${\eta }_3\left(q\right)=q^{{\tau }_1-{\tau }_2+{\varphi }_2-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2{,}_{{\tau }_1-{\tau }_2+{\varphi }_2}}\mathcal{P}{q}^{{\tau }_1-{\tau }_2},$  $a_1=\underset{q\in \mathbb{J}}{sup}\Vert {\eta }_1\left(q\right)\Vert ,a_2=\underset{q\in \mathbb{J}}{sup}\Vert {\eta }_2\left(q\right)\Vert ,a_3=\underset{q\in \mathbb{J}}{sup}\Vert {\eta }_3\left(q\right)\Vert ,\mathfrak{L}=\Vert b\Vert a_1+\Vert a\Vert a_2+\Vert c\Vert a_3,\mathfrak{M}=\Vert \eta \left(q\right)\Vert ,\mathfrak{N}=\Vert \mathcal{Q}\Vert$, $\mathfrak{K}=(T-q{)}^{{\tau }_1-1}\Vert {\mathcal{Q}}^{\ast }\eta (T-q){\mathbb{M}}^{-1}\Vert$.

Choose r>0, such that $\mathfrak{K}[\Vert y\Vert +\mathfrak{L}+\mathfrak{M}T{b}_1]=r$, $\begin{array}{rl}{\xi }_1& =\Vert {\mathbb{E}}_{{\tau }_1-{\tau }_2,1}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)b-\mathcal{P}{T}^{{\tau }_1-{\tau }_2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+1}\\ & \times \left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)a+T{\mathbb{E}}_{{\tau }_1-{\tau }_2,2}\left(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}\right)c\Vert ,\\ {\xi }_2& =\underset{s\in \mathbb{J}}{sup}\Vert {\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\Vert ,\\ {\xi }_3& =\underset{q\in \mathbb{J}}{sup}\Vert {\mathcal{Q}}^T\left[\right(T-q{)}^{{\tau }_1-1}\left]{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\right(\mathcal{P}{T}^{{\tau }_1-{\tau }_2}{)}^T\Vert ,\\ {\xi }_4& =T^{{\tau }_1}({\tau }_1{)}^{-1}.{\xi }_2||\mathcal{Q}||,\\ {ϵ}_1& =4{\xi }_3||{\mathbb{M}}^{-1}||(|x_1|+{\xi }_1),{ϵ}_2=4{\xi }_1,\\ ϵ& =max\{{ϵ}_1,{ϵ}_2\},\\ {\chi }_1& =4{\xi }_3||{\mathbb{M}}^{-1}||{\xi }_2{T}^{{\tau }_1}{\tau }_1^{-1},{\chi }_2=4{\xi }_2{T}^{{\tau }_1}{\tau }_1^{-1},\\ \chi & =max\{{\chi }_1,{\chi }_2\},\\ \xi & =max\{T{\xi }_4,1\},sup|h|=\left\{|h\right(s,z\left(s\right),v\left(s\right))|:s\in \mathbb{J}\}.\end{array}$

Theorem 4.1

If the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable then the system (12(12) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(12) ) is also controllable on $\mathbb{J}$, if there exists the function h which satisfies the condition $\left(\mathbb{H}1\right)-\left(\mathbb{H}2\right)$.

Proof.

We use the successive approximation technique to prove the results, hence we define (13) $\begin{array}{rl}{y}_0\left(q\right)& =y_0\\ y_{n+1}\left(q\right)& =b{a}_1+a{a}_2-c{a}_3+{\int }_0^q\eta (q-s)\mathcal{Q}{u}_n\left(s\right)\mathrm{d}s\\ & +{\int }_0^q\eta (q-s)h(s,x_n(s\left)\right)\mathrm{d}s,\end{array}$(13) where, (14) $\begin{array}{rl}{u}_n\left(q\right)& =(T-q{)}^{{\tau }_1-1}{\mathcal{Q}}^{\ast }{\eta }^{\ast }(T-q){\mathbb{M}}^{-1}\\ & \times \{\phantom{{\int }_0^T}{x}_1-{\eta }_1(q)b-{\eta }_2(q)a+{\eta }_3(q)c\\ & -{\int }_0^T\eta (T-s)h(s,y_n(s\left)\right)\mathrm{d}s\},\end{array}$(14) where $\mathrm{n}=0,1,2,\dots$ Since $y_0$ is a given vector, the sequence of the functions $\left\{y_n\right(q\left)\right\}$ is established. Now we must demonstrate that $\left\{y_n\right(q\left)\right\}$ in Y is a Cauchy sequence.

It is clear that, $\begin{array}{rl}\Vert u_n\left(q\right)\Vert & \le (T-q{)}^{{\tau }_1-1}\Vert {\mathcal{Q}}^{\ast }{\mathbb{M}}^{-1}\Vert \\ & \times [\phantom{{\int }_0^T}\Vert x_1\Vert +\Vert b\Vert \Vert {\eta }_1\left(q\right)\Vert +\Vert a\Vert \Vert {\eta }_2\left(q\right)\Vert \\ & +\Vert c\Vert \Vert {\eta }_3\left(q\right)\Vert \\ & +{\int }_0^T\Vert \eta (T-s)\Vert \Vert h(s,y_n(s\left)\right)\Vert \mathrm{d}s]\\ & \le \mathfrak{K}[\Vert x_1\Vert +\mathfrak{L}+\mathfrak{M}T{b}_1]=r\end{array}$and $\begin{array}{rl}\Vert u_n\left(q\right)-u_{n-1}\left(q\right)\Vert & \le (T-q{)}^{{\tau }_1-1}\Vert {\mathcal{Q}}^{\ast }{\eta }^{\ast }(T-q){\mathbb{M}}^{-1}\Vert \\ & \times {\int }_0^T\Vert \eta (T-s)\Vert \Vert h(s,y_{n-1}(s\left)\right)\\ & -h(s,y_n(s\left)\right)\Vert \mathrm{d}s\\ & \le \mathfrak{K}\mathfrak{M}T{b}_2\Vert y_{n-1}\left(q\right)-y_n\left(q\right)\Vert .\end{array}$Then $\begin{array}{rl}\Vert y_{n+1}\left(q\right)-y_n\left(q\right)\Vert & \le {\int }_0^q\Vert (T-q{)}^{{\tau }_1-1}\eta (q-s)\Vert \Vert \mathcal{Q}\Vert \\ & \times \Vert u_n\left(s\right)-u_{n-1}\left(s\right)\Vert \mathrm{d}s\\ & +{\int }_0^q\Vert (T-q{)}^{{\tau }_1-1}\eta (q-s)\Vert \\ & \times \Vert h(s,y_n(s\left)\right)-h(s,y_{n-1}(s\left)\right)\Vert \mathrm{d}s\\ & \le \mathfrak{N}\mathfrak{M}\left(\mathfrak{K}\mathfrak{M}T{b}_2\right)\\ & \times {\int }_0^q\Vert y_{n-1}\left(s\right)-y_n\left(s\right)\Vert \\ & +{\int }_0^q\mathfrak{M}{b}_2\Vert y_n\left(s\right)-y_{n-1}\left(s\right)\Vert \mathrm{d}s\\ & \le ({\mathfrak{M}}^2\mathfrak{N}\mathfrak{K}T{b}_2+\mathfrak{M}{b}_2)\\ & \times {\int }_0^q\Vert y_n\left(s\right)-y_{n-1}\left(s\right)\Vert \mathrm{d}s.\end{array}$Further, $\begin{array}{rl}\Vert y_1\left(q\right)-y_0\left(q\right)\Vert & \le \Vert b\Vert \Vert {\eta }_1\left(q\right)\Vert +\Vert a\Vert \Vert {\eta }_2\left(q\right)\Vert \\ & +\Vert c\Vert \Vert {\eta }_3\left(q\right)\Vert +\Vert y_0\Vert \\ & +{\int }_0^q\Vert \eta (q-s)\Vert \Vert \mathcal{Q}\Vert \Vert u_0\left(s\right)\Vert \\ & +{\int }_0^q\Vert \eta (q-s)\Vert \Vert h(s,y_0(s\left)\right)\Vert \mathrm{d}s\\ & \le \mathfrak{L}+\Vert y_0\Vert +(\mathfrak{M}\mathfrak{N}r+\mathfrak{M}{b}_1)T\\ & <\mathcal{P}T,\mathcal{P}<0.\end{array}$It is simple to obtain the estimation using this inequality and the induction method. $\Vert y_{n+1}\left(q\right)-y_n\left(q\right)\Vert \le \mathcal{P}({\mathfrak{M}}^2\mathfrak{N}\mathfrak{K}T{b}_2+\mathfrak{M}{b}_2)\frac{T^{n+1}}{(n+1)!}.$Because the right-hand side of the above estimation can be made arbitrarily small by choosing a large enough value for n, This means that in Y, $\left\{y_n\right(q\left)\right\}$ is a Cauchy sequence. The sequence $\left\{y_n\right(q\left)\right\}$ converges uniformly to a continuous function $y\left(q\right)$ on $\mathbb{J}$ since Y is complete. Thus we have $\begin{array}{rl}y\left(q\right)& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1-1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & -\mathcal{P}c{q}^{{\tau }_1-{\tau }_2+{\varphi }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+{\varphi }_1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)\\ & +{\int }_0^q(q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(q-s{)}^{{\tau }_1-{\tau }_2})\\ & \times \left(Bu\right(s)+f(s,y\left(s\right)\left)\right)\mathrm{d}s,\end{array}$where, $\begin{array}{rl}u\left(q\right)& =(T-s{)}^{2{\tau }_1-1}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left({\mathcal{P}}^{\ast }\right(T-q{)}^{{\tau }_1-{\tau }_2}){\mathbb{M}}^{-1}\\ & \times [y_1-{\int }_0^q(T-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left({\mathcal{P}}^{\ast }\right(T-q{)}^{{\tau }_1-{\tau }_2})f(s,y(s\left)\right)],t\in \mathbb{J}.\end{array}$Which is followed by defining the limit as $n\to \mathrm{\infty }$ on both sides of Equations (13(13) $\begin{array}{rl}{y}_0\left(q\right)& =y_0\\ y_{n+1}\left(q\right)& =b{a}_1+a{a}_2-c{a}_3+{\int }_0^q\eta (q-s)\mathcal{Q}{u}_n\left(s\right)\mathrm{d}s\\ & +{\int }_0^q\eta (q-s)h(s,x_n(s\left)\right)\mathrm{d}s,\end{array}$(13) ) and (14(14) $\begin{array}{rl}{u}_n\left(q\right)& =(T-q{)}^{{\tau }_1-1}{\mathcal{Q}}^{\ast }{\eta }^{\ast }(T-q){\mathbb{M}}^{-1}\\ & \times \{\phantom{{\int }_0^T}{x}_1-{\eta }_1(q)b-{\eta }_2(q)a+{\eta }_3(q)c\\ & -{\int }_0^T\eta (T-s)h(s,y_n(s\left)\right)\mathrm{d}s\},\end{array}$(14) ). Clearly $y\left(T\right)=x_1$ This indicates that if the system is controllable on $\mathbb{J}$, the control $u\left(q\right)$ leads the system from the initial state $a,b,c\to x_1$ in time T.

Case 2: Nonlinear function with control (15) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q),u(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\gamma }_1}y\left(0\right)=a,I_q^{2-{\gamma }_1}y\left(0\right)=b,& I_q^{1-{\gamma }_2}y\left(0\right)=c.\end{array}$(15)

Theorem 4.2

Let the continuous function h satisfy the condition (16) $\underset{|(y,u)|\to \mathrm{\infty }}{lim}\frac{\left|h\right(q,y,u\left)\right|}{|y,u|}=0$(16) uniformly in $q\in \mathbb{J}$ and if the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable then the system (15(15) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q),u(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\gamma }_1}y\left(0\right)=a,I_q^{2-{\gamma }_1}y\left(0\right)=b,& I_q^{1-{\gamma }_2}y\left(0\right)=c.\end{array}$(15) ) is also controllable on $\mathbb{J}$.

Proof.

Define $\mathcal{M}:\mathcal{N}\to \mathcal{N}$ by $\mathcal{M}(z,v)=(y,u)$, Then $\begin{array}{rl}\left|u\right(q\left)\right|& \le {\xi }_3||{\mathbb{M}}^{-1}||([|x_1|+{\xi }_1]+{\xi }_2{T}^{{\tau }_1}{\tau }_1^{-1}sup|h|)\\ & \le \frac{{ϵ}_1}{4a}+\frac{{\chi }_1}{4a}sup|h|\\ & \le \frac{1}{4a}[ϵ+\chi sup|h|]\end{array}$and $\begin{array}{rl}\left|y\right(q\left)\right|& \le {\xi }_1{\int }_0^q{\xi }_4(\frac{{ϵ}_1}{4a}+\frac{{\chi }_1}{4a}sup|h|)\mathrm{d}s\\ & +{\xi }_2{T}^{{\tau }_1}{\tau }_1^{-1}sup|h|\\ & \le \frac{{ϵ}_2}{4}+a(\frac{{ϵ}_1}{4a}+\frac{{\chi }_1}{4a}sup|h|)+\frac{{\chi }_2}{4}sup|h|\\ & \le \frac{\mathrm{d}}{2}+\frac{\chi }{2}sup|h|.\end{array}$The function h satisfies the following conditions. For each pair of positive constants χ and d, the positive constant r exists such that, if $|\mathcal{M}|\le r_1$, then (17) $\begin{array}{rl}& \chi |h(q,p)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J},\\ & \chi |h(q,z,v)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J}.\end{array}$(17) Also for given χ and ε, the Equation (17(17) $\begin{array}{rl}& \chi |h(q,p)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J},\\ & \chi |h(q,z,v)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J}.\end{array}$(17) ) satisfies for r which is a constant. Then any $r_1$ such that $r<r_1$, will also satisfy the Equation (17(17) $\begin{array}{rl}& \chi |h(q,p)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J},\\ & \chi |h(q,z,v)|+ϵ\le r,\mathrm{\forall }q\in \mathbb{J}.\end{array}$(17) ). Now take χ and ε as given above and let r be taken so that the mentioned inequality is satisfied.

Therefore, if $||z||\le r/2$ and $||V||\le r/2$ then $|z\left(s\right)|+|v\left(s\right)|\le r\mathrm{\forall }s\in \mathbb{J}$. It follows that $ϵ+\chi sup|h|\le r$, therefore, $|u\left(s\right)|\le r/4a\mathrm{\forall }s\in \mathbb{J}$ and hence $||u||\le r/4a$ which gives $||y||\le r/2\mathrm{\forall }s\in \mathbb{J}.$

Thus we have prove that if

$\mathcal{N}\left(r\right)=\left\{\right(z,v)\in \mathcal{N}:||z||\le r/2$ and $||v||\le R/2\}$

Then $\mathcal{M}$ is a mapping form $\mathcal{N}\left(r\right)$ into $\mathcal{N}\left(r\right)$. Because h is continuous, the operator is also continuous, and so the system is completely continuous when the Arzela – Ascoli theorem is applied. Since $\mathcal{N}\left(r\right)$ is closed, bounded and convex, from the Schawder fixed point theorem we can conclude that $\mathcal{M}$ has a fixed point $(z,v)\in \mathcal{N}\left(r\right)$ such that $\mathcal{M}(z,v)=(z,v)=(y,u)$.

Hence we have, $\begin{array}{rl}y\left(q\right)& ={\mathbb{E}}_{{\tau }_1-{\tau }_2,1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)b\\ & -\mathcal{P}{q}^{{\tau }_1-{\tau }_2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1-{\tau }_2+1}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)a\\ & +T{\mathbb{E}}_{{\tau }_1-{\tau }_2,2}\left(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\right)c\\ & +\int (q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\left)\mathcal{Q}u\right(s)\mathrm{d}s\\ & +\int (q-s{)}^{{\tau }_1-1}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}(\mathcal{P}{q}^{{\tau }_1-{\tau }_2}\left)h\right(s,y,u)\mathrm{d}s.\end{array}$Thus $y\left(q\right)$ is the solution of the system (15(15) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q),u(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\gamma }_1}y\left(0\right)=a,I_q^{2-{\gamma }_1}y\left(0\right)=b,& I_q^{1-{\gamma }_2}y\left(0\right)=c.\end{array}$(15) ), it is easy to verify that the $y\left(T\right)=x_1$.

Hence the system (15(15) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q),u(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\gamma }_1}y\left(0\right)=a,I_q^{2-{\gamma }_1}y\left(0\right)=b,& I_q^{1-{\gamma }_2}y\left(0\right)=c.\end{array}$(15) ) is controllable of $\mathbb{J}$.

5. Integro-differential systems

Consider the fractional differential equations that represent the nonlinear integro fractional dynamical system (18) $\begin{array}{r}\{\begin{array}{ll}\begin{array}{l}{D}^{{\nu }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\nu }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)\\ +h(q,y(q),{\displaystyle {\int }_0^{q}f(q,s,y(s\left)\right)\mathrm{d}s),}\end{array}& q\in \mathbb{J}\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\omega }_2}y\left(0\right)=c,\end{array}\end{array}$(18) where  $h:\mathbb{J}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ and $f:\mathbb{J}\times \mathbb{J}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ are continuous functions and $0<{\nu }_2\le 1<{\nu }_1\le 2,0\le \zeta \le 1y\in \mathbb{R}$. Also $\mathcal{P}$, $\mathcal{Q}$ and $C(\mathbb{J},{\mathbb{R}}^n)$ are defined as earlier.

Let us take the Nonlinear integro damped dynamical system, (19) $\begin{array}{r}\{\begin{array}{ll}\begin{array}{l}{D}^{{\nu }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\nu }_2,\zeta }\\ y\left(q\right)=\mathcal{Q}u\left(q\right)+h(q,z(q),\\ {\displaystyle {\int }_0^{q}f(q,s,z(s\left)\right)\mathrm{d}s),}\end{array}& q\in \mathbb{J}\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\omega }_2}y\left(0\right)=c.\end{array}\end{array}$(19) Then the solution of above equation is (20) $\begin{array}{rl}y\left(q\right)& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\nu }_1-{\nu }_{2,{\varphi }_1-1}}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_{2,{\varphi }_1}}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & -c\mathcal{P}{q}^{{\nu }_1-{\nu }_2+{\omega }_2-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1-{\nu }_2+{\omega }_2}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(q-s{)}^{{\nu }_1-{\nu }_2}\mathcal{Q}u\left(s\right)\mathrm{d}s\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(q-s{)}^{{\nu }_1-{\nu }_2}h\\ & \times (s,z(s),{\int }_0^{q}f(s,q,z\left(q\right)\mathrm{d}q\left)\right)\mathrm{d}s.\end{array}$(20) Assume the following conditions,

$\left(\mathbb{H}3\right)$ Let $b_3$ be a positive constant, such that for all $z\in C_n\left(\mathbb{J}\right)$, $t,s\in \mathbb{J}$, and the functions h and f are continuous such that, $\left|h(q,z(q),{\int }_0^{q}f(q,s,z\left(s\right)\left)\right)\right|\le b_3.$$\left(\mathbb{H}4\right)$ Let the function h is continuous and the constant $b_4>0$ exist, such that $\begin{array}{rl}& \Vert h(q,x_1,y_1)-h(q,x_2,y_2)\Vert \\ & \le b_4[\Vert x_1-x_2\Vert +\Vert y_1-y_2\Vert ],\\ & \mathrm{\forall }{x}_1,x_2,y_1,y_2\in {\mathbb{R}}^n.\end{array}$$\left(\mathbb{H}5\right)f:\mathbb{J}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is continuous and there exist constants $b_5>0$ such that, $\Vert f(q,s,x_1)-f(q,s,x_2)\Vert \le b_5\Vert x_1-x_2\Vert .$$\left(\mathbb{H}6\right)$ Let $q=(b_4+b_5)[\mathfrak{M}T\mathfrak{N}\mathfrak{K}+\mathfrak{M}T]$ be such that $0\le q<1$.

In short, let us define the following as per our problem variables, $\begin{array}{rl}\mu & =sup\Vert {\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\mathcal{P}(T-s{)}^{\nu -\zeta }\Vert \\ \eta (q-s)& ={\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(q-s{)}^{{\nu }_1-{\nu }_2}.\end{array}$

Theorem 5.1

Assume that the function h satisfies the conditions $\left(\mathbb{H}3\right)--\left(\mathbb{H}6\right)$. If the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is controllable, then the system (18(18) $\begin{array}{r}\{\begin{array}{ll}\begin{array}{l}{D}^{{\nu }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\nu }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)\\ +h(q,y(q),{\displaystyle {\int }_0^{q}f(q,s,y(s\left)\right)\mathrm{d}s),}\end{array}& q\in \mathbb{J}\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\omega }_2}y\left(0\right)=c,\end{array}\end{array}$(18) ) is also controllable on $\mathbb{J}$.

Proof.

Let us Define the operator $\tilde{\iota }:C_n\left(\mathbb{J}\right)\to C_n\left(\mathbb{J}\right)$ by (21) $\begin{array}{rl}\tilde{\iota }\left(z\right)\left(q\right)& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\varphi }_1-1}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\varphi }_1}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & -c.\mathcal{P}{q}^{{\nu }_1-{\nu }_2+{\omega }_2-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1-{\nu }_2+{\omega }_2}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\\ & \times \mathcal{P}(q-s{)}^{\nu -\zeta }\mathcal{Q}u(s)\mathrm{d}s\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(q-s{)}^{\nu -\zeta }\\ & \times h(s,z(s),{\int }_0^{s}f(s,q,z\left(q\right)\left)\mathrm{d}q\right)\mathrm{d}s,\end{array}$(21) where (22) $\begin{array}{rl}u\left(q\right)& =(T-q{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}{\mathcal{P}}^{\ast }(T-q{)}^{{\nu }_1-{\nu }_2}{\mathcal{Q}}^{\ast }{\mathbb{M}}^{-1}\\ & \times (x_1-{\eta }_1(q)b-{\eta }_2(q)a+{\eta }_3(q\left)c\right)\\ & -{\int }_0^T(T-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(T-s{)}^{{\nu }_1-{\nu }_2}\\ & \times h(s,z(s),{\int }_0^{s}f(s,q,z\left(q\right)\left)\mathrm{d}q\right)\mathrm{d}s.\end{array}$(22) We shall now define $\text{∼}\text{β}\left(r\right)=z\in C_n\left(\mathbb{J}\right):\Vert z\Vert \le r$, where $\text{∼}\text{β}\left(r\right)$ is a closed convex subset with $r=\mathfrak{L}+\left(\mu T^{{\tau }_1}{\tau }_1^{-1}\mathfrak{N}v\right)+\left(\mu T^{{\tau }_1}{\tau }_1^{-1}{b}_3\right),$where, $v=\mathfrak{K}\Vert {\mathbb{M}}^{-1}\Vert \left|x_1\right|+\mathfrak{L}+\mu T^{{\tau }_1}{\tau }_1^{-1}{b}_1).$It is very obvious that the operator $\tilde{\iota }$ maps $\text{∼}\text{β}\left(r\right)$ to $\text{∼}\text{β}\left(r\right)$, thus we can say that $\tilde{\iota }$ is completely continuous.

We can say that the fixed point $z\in \text{∼}\text{β}\left(r\right)$ exists using the Schauder Fixed Point theorem, such that $\tilde{\iota }$(z)$=z=y$. And by Contraction mapping theorem, we say that there exists a unique fixed point $y\in z$ such that $\tilde{\iota }y\left(q\right)=y\left(q\right)$.

Let us substitute Equation (22(22) $\begin{array}{rl}u\left(q\right)& =(T-q{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}{\mathcal{P}}^{\ast }(T-q{)}^{{\nu }_1-{\nu }_2}{\mathcal{Q}}^{\ast }{\mathbb{M}}^{-1}\\ & \times (x_1-{\eta }_1(q)b-{\eta }_2(q)a+{\eta }_3(q\left)c\right)\\ & -{\int }_0^T(T-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(T-s{)}^{{\nu }_1-{\nu }_2}\\ & \times h(s,z(s),{\int }_0^{s}f(s,q,z\left(q\right)\left)\mathrm{d}q\right)\mathrm{d}s.\end{array}$(22) ) in Equation (21(21) $\begin{array}{rl}\tilde{\iota }\left(z\right)\left(q\right)& =b{q}^{{\varphi }_1-2}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\varphi }_1-1}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +a{q}^{{\varphi }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\varphi }_1}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & -c.\mathcal{P}{q}^{{\nu }_1-{\nu }_2+{\omega }_2-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1-{\nu }_2+{\omega }_2}\mathcal{P}{q}^{{\nu }_1-{\nu }_2}\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\\ & \times \mathcal{P}(q-s{)}^{\nu -\zeta }\mathcal{Q}u(s)\mathrm{d}s\\ & +{\int }_0^q(q-s{)}^{{\nu }_1-1}{\mathbb{E}}_{{\nu }_1-{\nu }_2,{\nu }_1}\mathcal{P}(q-s{)}^{\nu -\zeta }\\ & \times h(s,z(s),{\int }_0^{s}f(s,q,z\left(q\right)\left)\mathrm{d}q\right)\mathrm{d}s,\end{array}$(21) ) to obtain $x_1$, that implies $y\left(T\right)=x_1$.

Hence the Non Linear Integro system is controllable.

6. Example

Example 6.1

(23) $\begin{array}{r}\{\begin{array}{l}{D}^{5/4,1/2}{y}_1\left(q\right)-D^{3/4,1/2}{y}_2\left(q\right)=0,\\ D^{5/4,1/2}{y}_2\left(q\right)-D^{3/4,1/2}{y}_1\left(q\right)=u\left(q\right).\end{array}\end{array}$(23) Comparing with linear system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ), we have

$\mathcal{P}=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],\mathcal{Q}=\left[\begin{array}{c}0\\ 1\end{array}\right],{\tau }_1=5/4,{\tau }_2=3/4,\zeta =1/2$.

The Mittag–Leffler matrix function for the given matrix $\mathcal{P}$ is $q^{1/2}{\mathbb{E}}_{1/2,5/4}\left(\mathcal{P}q\right)=\left[\begin{array}{cc}{N}_1\left(q\right)& N_2\left(q\right)\\ N_2\left(q\right)& N_1\left(q\right)\end{array}\right],$where $N_1\left(q\right)=\frac{\sqrt{q}}{2}\left[{\mathbb{E}}_{1/2,5/4}\right(q)+{\mathbb{E}}_{1/2,5/4}(-q\left)\right]$ and $N_2\left(q\right)=\frac{\sqrt{q}}{2}\left[{\mathbb{E}}_{1/2,5/4}\right(q)-{\mathbb{E}}_{1/2,5/4}(-q\left)\right].$ The controllability Gramian matrix (24) $\begin{array}{rl}\mathbb{M}& ={\int }_0^2(2-s){\mathbb{E}}_{1/2,5/4}\left(\mathcal{P}\right(2-s\left)\right)\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{1/2,5/4}\left({\mathcal{P}}^{\ast }\right(2-s\left)\right)\mathrm{d}s\\ & ={\int }_0^2\left[\begin{array}{cc}{N}_2^2(2-s)& N_1(2-s)N_2(2-s)\\ N_1(2-s)N_2(2-s)& N_1^2(2-s)\end{array}\right]\mathrm{d}s\\ \mathbb{M}& =\left[\begin{array}{cc}19.0621& 21.5817\\ 21.5817& 24.6211\end{array}\right].\end{array}$(24) By the definition of invertible, The controllability Gramian matrix $\mathbb{M}$ is invertible.

Therefore, the theorem (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ) is satisfied.

Example 6.2

(25) $\begin{array}{r}\{\begin{array}{l}{D}^{3/2,1/2}{y}_1\left(q\right)-D^{1/2,1/2}{y}_2\left(q\right)=\sin y\left(q\right),\\ D^{3/2,1/2}{y}_2\left(q\right)+2D^{1/2,1/2}{y}_1\left(q\right)=\sin \left(q\right)u_1\left(q\right)\\ +\cos \left(q\right)u_2\left(q\right).\end{array}\end{array}$(25) Comparing with the nonlinear system (15(15) $\{\begin{array}{ll}\begin{array}{l}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)\\ =\mathcal{Q}u\left(q\right)+h(q,y(q),u(q\left)\right),\end{array}& q\in \mathbb{J},\\ I_q^{1-{\gamma }_1}y\left(0\right)=a,I_q^{2-{\gamma }_1}y\left(0\right)=b,& I_q^{1-{\gamma }_2}y\left(0\right)=c.\end{array}$(15) ), then we have the matrix form of the above system is $\begin{array}{rl}\left[\begin{array}{c}{y}_1\left(q\right)\\ y_2\left(q\right)\end{array}\right]& =\left[\begin{array}{cc}0& 1\\ 1& -2\end{array}\right]\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]+\left[\begin{array}{cc}0& 0\\ \sin \left(q\right)& \cos \left(q\right)\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]\\ & +\left[\begin{array}{c}\sin \left(q\right)\\ 0\end{array}\right]y\left(q\right).\end{array}$For this system, on further calculations, we get the equation of controllability Gramian matrix (24(24) $\begin{array}{rl}\mathbb{M}& ={\int }_0^2(2-s){\mathbb{E}}_{1/2,5/4}\left(\mathcal{P}\right(2-s\left)\right)\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{1/2,5/4}\left({\mathcal{P}}^{\ast }\right(2-s\left)\right)\mathrm{d}s\\ & ={\int }_0^2\left[\begin{array}{cc}{N}_2^2(2-s)& N_1(2-s)N_2(2-s)\\ N_1(2-s)N_2(2-s)& N_1^2(2-s)\end{array}\right]\mathrm{d}s\\ \mathbb{M}& =\left[\begin{array}{cc}19.0621& 21.5817\\ 21.5817& 24.6211\end{array}\right].\end{array}$(24) ) to be non singular, also the non linear function h satisfies the Lipschitz condition. Therefore, the function $h(q,y(q),u(q\left)\right)$ is continuous and bounded. We can say that by Theorem (4.2), our nonlinear system (25(25) $\begin{array}{r}\{\begin{array}{l}{D}^{3/2,1/2}{y}_1\left(q\right)-D^{1/2,1/2}{y}_2\left(q\right)=\sin y\left(q\right),\\ D^{3/2,1/2}{y}_2\left(q\right)+2D^{1/2,1/2}{y}_1\left(q\right)=\sin \left(q\right)u_1\left(q\right)\\ +\cos \left(q\right)u_2\left(q\right).\end{array}\end{array}$(25) ) is completely controllable on $[0,2]$.

Example 6.3

Let we take the linear function of differential equation of fractional-order system with control function of the form (26) $\begin{array}{r}\{\begin{array}{l}{D}^{3/2,1/2}{y}_1\left(q\right)-D^{1/2,1/2}{y}_2\left(q\right)=u\left(q\right)\\ D^{3/2,1/2}{y}_2\left(q\right)+2D^{1/2,1/2}{y}_1\left(q\right)=0,\end{array}\end{array}$(26)

with initial condition $\left[\begin{array}{c}{y}_1\left(0\right)\\ y_2\left(0\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]and\left[\begin{array}{c}{y}_1^{\mathrm{\prime }}\left(0\right)\\ y_2^{\mathrm{\prime }}\left(0\right)\end{array}\right]=\left[\begin{array}{c}2\\ 2\end{array}\right]$. For every $0\le q\le 2$. Comparing with the system (5(5) $\{\begin{array}{ll}{D}^{{\tau }_1,\zeta }y\left(q\right)-\mathcal{P}{D}^{{\tau }_2,\zeta }y\left(q\right)=\mathcal{Q}u\left(q\right)& q\in \mathbb{J},\\ I_q^{1-{\varphi }_1}y\left(0\right)=a,I_q^{2-{\varphi }_1}y\left(0\right)=b,& I_q^{1-{\varphi }_2}y\left(0\right)=c,\end{array}$(5) ), we have

$\mathcal{P}=\left[\begin{array}{cc}0& 1\\ 1& -2\end{array}\right],\mathcal{Q}=\left[\begin{array}{c}1\\ 0\end{array}\right]$ and $y\left(q\right)=\left[\begin{array}{c}{y}_1\left(q\right)\\ y_1\left(q\right)\end{array}\right]$ Let us take $y\left(2\right)=\left[\begin{array}{c}{y}_1\left(2\right)\\ y_1\left(2\right)\end{array}\right]$ = $\left[\begin{array}{c}1\\ 2\end{array}\right]$ ${\tau }_1=3/2,{\tau }_2=1/2,\zeta =1/2$.

Using Equation (6(6) $\begin{array}{rl}\mathbb{M}& ={\int }_0^T(T-s{)}^{2{\tau }_1-2}{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\left(\mathcal{P}\right(T-s{)}^{{\tau }_1-{\tau }_2})\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{{\tau }_1-{\tau }_2,{\tau }_1}\\ & \times \left({\mathcal{P}}^{\ast }\right(T-s{)}^{{\tau }_1-{\tau }_2})\mathrm{d}s\end{array}$(6) ) the controllability Grammian matrix $\begin{array}{rl}\mathbb{M}& ={\int }_0^2(2-s){\mathbb{E}}_{1,3/2}\left(\mathcal{P}\right(2-s\left)\right)\\ & \times \mathcal{Q}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{1,3/2}\left({\mathcal{P}}^{\ast }\right(2-s\left)\right)\mathrm{d}s\\ & ={\int }_0^2\left[\begin{array}{cc}{N}_2^2(2-s)& N_1(2-s)N_2(2-s)\\ N_1(2-s)N_2(2-s)& N_1^2(2-s)\end{array}\right]\mathrm{d}s\\ \mathbb{M}& =\left[\begin{array}{cc}0.5297& 0.4424\\ 0.4424& 0.454\end{array}\right].\end{array}$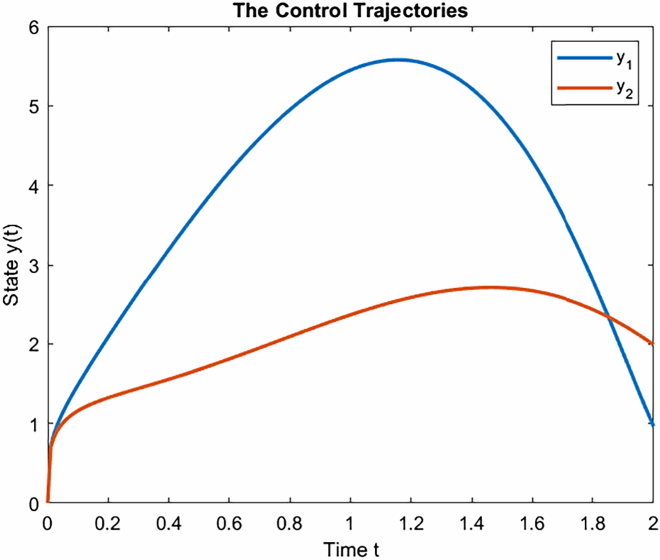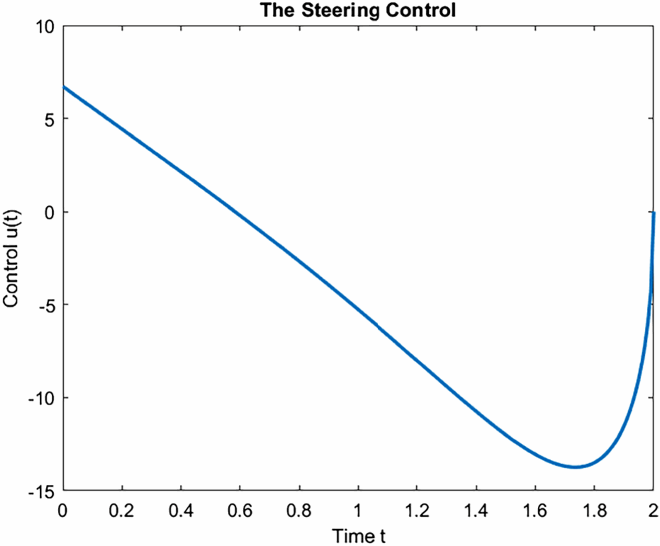Therefore, by the Theorem (3.1), the system is completely controllable. Using MATLAB, we complete the numerical solution $y\left(q\right)$ in (26(26) $\begin{array}{r}\{\begin{array}{l}{D}^{3/2,1/2}{y}_1\left(q\right)-D^{1/2,1/2}{y}_2\left(q\right)=u\left(q\right)\\ D^{3/2,1/2}{y}_2\left(q\right)+2D^{1/2,1/2}{y}_1\left(q\right)=0,\end{array}\end{array}$(26) ) in the interval [0,2]. The controlled trajectories of the system (26(26) $\begin{array}{r}\{\begin{array}{l}{D}^{3/2,1/2}{y}_1\left(q\right)-D^{1/2,1/2}{y}_2\left(q\right)=u\left(q\right)\\ D^{3/2,1/2}{y}_2\left(q\right)+2D^{1/2,1/2}{y}_1\left(q\right)=0,\end{array}\end{array}$(26) ) steering from the initial state y(0) = $\left[\begin{array}{c}0\\ 0\end{array}\right]$ to desired state y(2) = $\left[\begin{array}{c}1\\ 2\end{array}\right]$ during the interval [0,2], can be approximated from the following algorithm. $\begin{array}{rl}u\left(q\right)& =(2-q{)}^{3/2-1}{\mathcal{Q}}^{\ast }{\mathbb{E}}_{1,3/2}\left({\mathcal{P}}^{\ast }\right(2-q\left)\right){\mathbb{M}}^{-1}\\ & \times [y_1-{\int }_0^2(2-s{)}^{3/2-1}{\mathbb{E}}_{1,3/2}\\ & \times \left(\mathcal{P}\right(2-s\left)\right)f(s,x(s\left)\right)]\mathrm{d}s.\\ y\left(q\right)& ={\mathbb{E}}_{1,1}\left(\mathcal{P}q\right)b-q{\mathbb{E}}_{1,2}\left(\mathcal{P}q\right)a+\mathcal{P}{\mathbb{E}}_{1,2}\left(\mathcal{P}q\right)c\\ & +{\int }_0^2(q-s){\mathbb{E}}_{1,3/2}\mathcal{P}q\left[\mathcal{Q}u\right(s)+f(s,x\left(s\right)\left)\right]\mathrm{d}s.\end{array}$

Conclusion

The presented paper investigated the controllability criteria of fractional damped dynamical systems of Hilfer derivative of linear and non linear cases. Using some assumption of our controllability Gramian matrix and some fixed point theorem, the results are obtained for both linear and nonlinear systems. We also analysed the nonlinear integro-fractional dynamical system. We included numerical examples to justify our results. In the next work, we will analyse the stability of the Hilfer dynamical system and compare the results.

Disclosure statement

No potential conflict of interest was reported by the author(s).