Solving inverse heat conduction problem with discrete wavelet transform

Abstract

We consider as a test case the linear one-dimensional inverse heat conduction problem. Usual regularization methods are equivalent to filtering out high-frequency components, in a uniform way on the whole stretch of data. This sets a limit to the trade-off that can be obtained between good resolution and efficient noise reduction.

To overcome this limit, we propose the use of wavelet decomposition, which enables us to perform time–frequency analysis of the data content. A simple thresholding algorithm is used to eliminate noise components. The method is compared with the usual singular-value decomposition.

Preliminary results on simple test cases show that wavelet decomposition permits us to enhance the results of the inversion procedure, by giving smoother estimates of slow-varying parts of the solution while maintaining a sharp estimation of fast transients.

Keywords:

• Inverse heat conduction
• Regularization
• Wavelets
• Singular-value decomposition

1. Introduction

We consider the one-dimensional heat conduction problem in a slab of material: (---329--1) If T_m(t) is a measure of the temperature at x = 0.5, then finding T_s(t) such that T(x = 0.5,t) = T_m(t) is an inverse heat conduction problem (IHCP) [1,16,17]. This kind of problem has been extensively studied, and many inversion techniques have been tested on it [2–4,18,19].

In the frequency domain, the solution of the direct problem can be obtained from the Laplace transform: (---329--2) where p is the Laplace variable and (---329----1) and the solution of the inverse problem can be formally written as (---329--3)

The direct problem is stable, because G(p) is the transfer function of a low-pass filter: (---329---1) It ensues that G⁻¹(p) corresponds to a high-pass filter (---329---2) and the inverse problem is unstable, because a change of given amplitude in T_s can be obtained from a perturbation in T_m of arbitrarily small amplitude, by choosing the frequency of this perturbation high enough. Since noise (measurement noise or roundoff numerical noise) usually contains high-frequency components, this means that any attempt to solve the inverse problem will be totally submerged by amplified high-frequency noise, unless some degree of regularization is introduced.

All regularization methods introduce some kind of filtering of high-frequency components, eliminating noise that is responsible for the unstability but also high-frequency components of the desired solution. The higher the noise level, the lower the cutoff frequency of the filter. Regularization methods usually involve some design parameter, or regularization parameter, that enables us to adjust this cutoff frequency; all methods reach their optimal utilization when this adjustment is such that all frequencies at which the signal-to-noise ratio is small are eliminated. It has been remarked by several authors that the choice of one particular regularization method is not of prime importance, since all methods reach about the same results when correctly used [5].

This sets a bound to the efficiency of any method that can be analyzed (at least for linear problems) as filtering in the Fourier domain.

To overcome this limit, one has to recognize that the frequency content of the data varies with time: in our sample problem, the surface temperature may evolve slowly and then change suddenly under the application of a large heat flux. At one given frequency, the signal-to-noise ratio will be small at some times and large at other times. Some kind of time–frequency analysis should enable us to differentiate between these instants, and to adjust filtering accordingly, retaining higher frequencies when the signal contains rapid variations, and filtering more strongly when variations are slow.

Wavelets are a way to perform such an analysis, and in recent years much work has been devoted to develop an orthogonal basis of wavelets, both in the continuous and the discrete case [6]. Since engineering problems involve working with sampled data, we shall hereafter develop our analysis for the case of discrete systems only.

2. Solution of the time-sampled inverse problem by SVD

In applications, the measured temperature will not be known as a function but rather as a vector of values sampled at regular time intervals Δ t : (---329----2) , and we seek to reconstruct the surface temperature as a similar vector: T_s = (---329----3) .

Using T_s as data, the direct problem (1) is usually solved by some numerical scheme; in this study we chose a classic Crank–Nicholson scheme [7], with 200 nodes of space discretization and a time step equal to the sampling interval Δ t of 1s.

If θ is the temperature at the node x = 0.5, calculated by application of this scheme, and Θ the vector of sampled values of θ, then it can be shown that there exists a matrix A such that (---329--4)

Matrix A is easily determined by direct use of the numerical scheme with T_s, a unit-pulse vector (1, 0, 0, … 0).

Solving the inverse problem reduces to solving the linear system: (---329--5)

However, since this linear system is an approximation of the original unstable continuous problem, A will be badly conditioned; this means that the direct solution of this system will be of no interest, and sometimes even not computable. The preferred method to obtain an approximate but meaningful solution to (5)(---329--5) is the singular-value decomposition (SVD) [8], which is the exact counterpart for the discrete case of the Fourier decomposition outlined for the continuous case in the introduction.

The SVD of A is (---329--6) where Σ is a diagonal matrix with diagonal elements σ_i ordered by decreasing magnitude, U and V are orthogonal matrices, whose columns are vectors U_i and V_i.

The exact solution of (5)(---329--5) is given by (---329--7)

In this expression, the scalar products (---329----4) appear as the coefficients of the decomposition of T_m on the basis U_i); it has often been remarked, and it can be proved in some cases, that the vectors U_i are very close to sampled sines and cosines of frequencies increasing with index i. Coefficients σ_i appear as the values of the transfer function at these frequencies.

Solution (7)(---329--7) is unstable, because 1/σ_i will reach very large values while (---329----5) will be dominated by noise.

An approximate but stable solution will be given by the truncated SVD solution [9]: (---329--8)

The choice of the truncation index k is a major element for a good utilization of this regularization method, corresponding to the cutoff frequency in the continuous case. Several methods have been described to attempt an optimal choice of k [10]; however, direct inspection of the values (---329----6) and an educated guess at the noise level often provide a very good solution.

3. Solution of the inverse problem by DWT

3.1. Wavelet decomposition

The Fourier decomposition of a function corresponds to a projection of this function on a basis formed by sine and cosine functions of different frequencies. Since these functions are periodic, this decomposition does not allow to localize in time the presence of one frequency.

Wavelets [11] are analogous to sine functions in the sense that they are oscillatory functions with a given ‘frequency’, but they are localized in time: this means that an individual wavelet has a compact support, which is inversely proportional to its frequency. Wavelet transform thus enables a time–frequency analysis, similar to empirical methods like the so-called spectrogram; in fact wavelets were invented on an intuitive basis just to perform this kind of analysis.

Wavelet transforms have been proposed before to obtain regularized solutions to ill-posed problems originating from the heat diffusion equation. For the problem of reconstructing a surface flux from inner measurements in the case of a semi-infinite body, mathematical analysis [12,13] proved the convergence of regularization by projection onto a partial basis of wavelets. In the case of heat diffusion in an infinite medium, reconstruction of past history in the form of Dirac sources by use of Hermitian wavelets provides a family of stable solutions [14]. However, none of the above mathematical analyses were concerned about the possibility to improve the resolution for time-localized events, nor did they provide guidelines as to the application to engineering problems.

When working with discrete data, it is possible to define a discrete wavelet transform (DWT) analogous to the discrete Fourier transform. We chose to work with Daubechies wavelet of order 4 for simplicity. All details for implementation can be found in [15].

Figure 1 depicts two Daubechies wavelets, of different frequencies and located at different times. It can be seen how higher frequency wavelets have a narrower support, allowing a better time localization.

Figure 1. Two Daubechies wavelets, located at different times and with different frequencies.

The DWT of a vector is a vector of identical size, each component being the coefficient of the decomposition on the wavelet of corresponding index.

Since DWT is a linear operation, there exists a matrix W such that for some vector x (---329--9)

Note, however, that although this is a convenient notation for analysis, the DWT is not computed by this formula but rather by the recursive algorithm described in [15].

3.2. Thresholding procedure

Premultiplying (5)(---329--5) by W we obtain (---329--10)

(---329----7) represents the DWT of the data. Some components of this vector are dominated by noise, and we want to eliminate those. This can be performed by thresholding.

If we know that the noise level is at some value η, we set to 0 any components of (---329----8) that are smaller than η, thus defining a filtered data vector y*: (---329--11) Then the solution of the inverse problem is obtained by solving (---329--12)

Because some noise is still present in y*, it is necessary again to solve this equation by SVD, using the normal regularization procedure.

4. Application examples

4.1. Case 1

As a first example, to illustrate what can be expected from the method, we shall consider a not too realistic example.

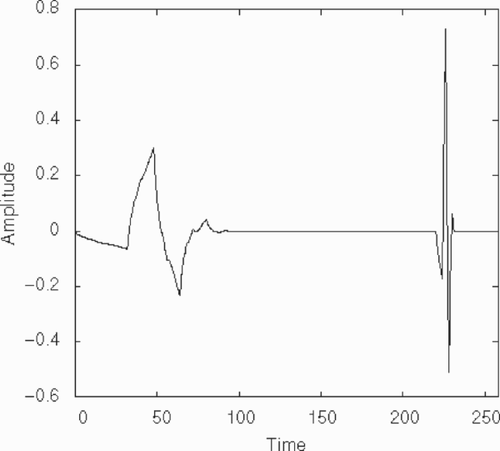
Surface temperature T_s is represented in figure 2(a) as a stretch of 256 data sampled at Δt = 0.05 s.

Figure 2. (a) Surface temperature T_s and (b) temperature measured (with noise) inside the slab T_m for case 1.

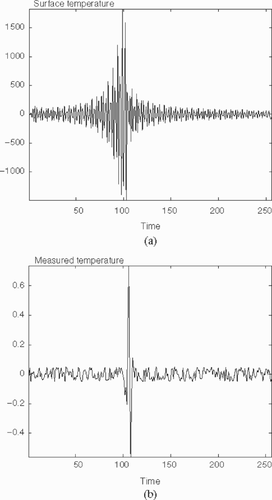
The measured temperature T_m was computed by the use of the numerical scheme, with diffusivity (---329----9) ; artificial noise was then introduced by adding to each component a random value equidistributed between −0.05 and 0.05. The result is plotted in figure 2(b); this is very nearly a single Daubechies wavelet. This is not an astonishing fact as the surface temperature was in fact specifically made up to reach this result.

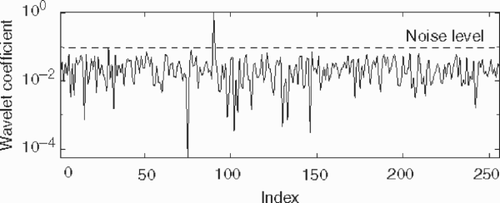
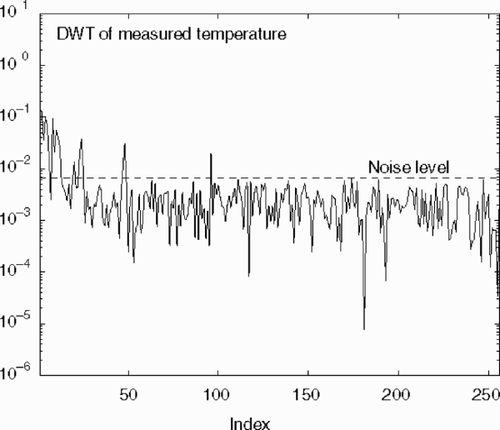
The DWT of T_m (figure 3) clearly shows this fact, and permits us to evaluate the noise level at around 1E − 1, which is in fact the true value.

Figure 3. Plot of components of the DWT of T_m.

Using this value as a threshold, the DWT of T_m is filtered to obtain y*. The inverse problem is then solved by SVD to eliminate numerical noise.

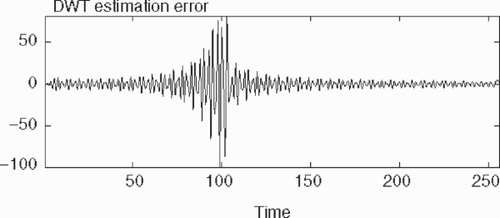
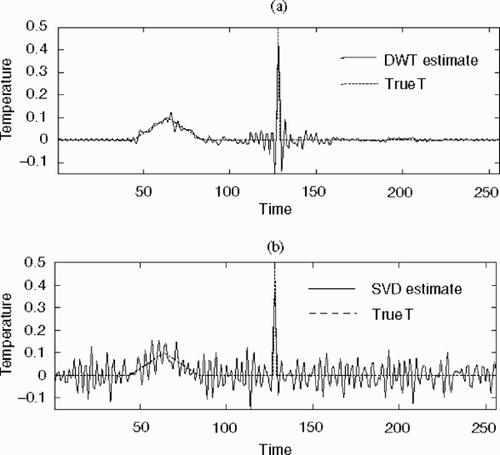
The results, as shown in figure 4, are quite good: it can be seen that the error on the reconstructed solution is around 5%. Notice that the estimation error is proportional to the original signal, because noise is still present on the single wavelet component.

Figure 4. Inversion by DWT, case 1.

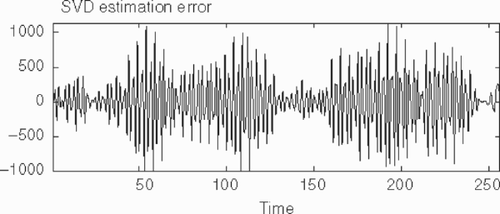
In opposition, the best result that could be obtained by direct truncated SVD is poor: the error is of the magnitude of the solution itself (figure 5). Noise here is spread out on the whole time stretch.

Figure 5. Inversion by SVD, case 1.

This example is a good illustration of the benefit that can be expected from DWT. Here, the signal is entirely concentrated on one component of the wavelet transform; all other components are noise. Thus by filtering in the wavelet domain, we keep all of the signal and eliminate a maximum of noise. By contrast, other decompositions, and the SVD decomposition itself, are distributed on a greater number of components; reduction of noise cannot be performed without eliminating some of the signals too.

4.2. Case 2

The previous case represents an ideal situation, and in fact was contrived to be so. We shall now present a more realistic situation.

This time the surface temperature consists of two parts: a rather slowly varying triangle, and a sudden spike (figure 6a). The difficulty in this example will be to obtain a good estimation of the spike amplitude, while preserving a smooth estimation of the triangle. The length of the data is again 256 samples at Δ t = 0.05 s, with diffusivity (---329----10) .

Figure 6. (a) Surface temperature T_s and (b) Temperature measured (with noise) inside the slab T_m for case 2.

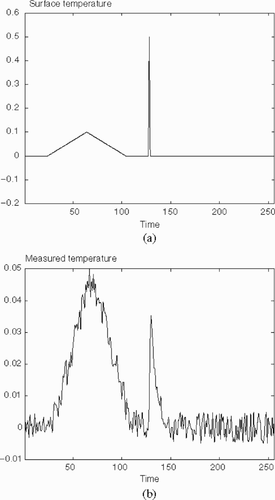
The inner temperature is again calculated, and artificial noise added, with amplitude 1E − 2 (figure 6b).

Again, the DWT transform (figure 7) clearly suggests the level of noise, and the threshold for filtering is chosen at η = 0.8E-2.

Figure 7. Plot of components of the DWT of T_m, case 2.

The results obtained by DWT and SVD are shown in figure 8. The truncation index was the same in both the cases (k = 170). Thus the height of the spike is estimated at very much the same value by both the procedures (0.4 and 0.36 for a theoretical value of 0.5); the level of noise during the spike period is also very similar. However, while DWT gives a smooth estimation outside of the spike, SVD has a high level of noise throughout the solution, blurring out almost completely the triangle shape. Lower noise could be obtained by diminishing the truncation parameter, but this would be at the expense of more bias on the estimated peak and some smoothing out of the triangle shape.

Figure 8. Results by DWT (a) and SVD (b), case 2.

5. Conclusion

We have shown that wavelet transform can help enhance the results of IHCPs; the main contribution is the ability to adjust the filtering strength to the frequency content of the data.

Although we presented illustrative results for the linear case only, the method can be used in conjunction with any inversion technique for non-linear problems.

However, the Daubechies wavelets we used in this study, though very simple, may not be ideally adapted to our purpose, since they are not continuous functions: this generates high-frequency components that still have to be eliminated in the inversion phase. Smoother classes of wavelets, although they no longer have a compact support, might be more interesting, since we expect the unnoised measurement signal to belong to a class of highly smooth functions.

A different approach to the same problem could be to use sequential inverse methods with adaptive strength of the filtering: this necessitates on-line estimation of the frequency content of the measurements. The results can be expected to be suboptimal by comparison to wavelet transform, but may be of more interest for engineering applications, and we intend to explore this possibility in the near future.