First- and second-order topological sensitivity analysis for inclusions

Abstract

The topological derivative provides the sensitivity of a given shape functional with respect to an infinitesimal domain perturbation. Classically, this derivative comes from the second term of the topological asymptotic expansion, dealing only with infinitesimal perturbations. Therefore, as a natural extension of this concept, we can consider higher-order terms in the expansion. In particular, the next one we recognize as the second-order topological derivative, which allows us to deal with perturbations of finite sizes. This term depends explicitly on higher-order gradients of the solution associated to the non-perturbed problem and also implicitly through the solution of an auxiliary variational problem. In this article, we calculate the explicit as well as implicit terms of the second-order topological asymptotic expansion for the total potential energy associated to the Laplace equation in the two-dimensional domain. The domain perturbation is done by the insertion of a small inclusion with a thermal conductivity coefficent value different from the bulk material. Finally, we present some numerical experiments showing the influence of the second-order term in the topological asymptotic expansion for several values of the thermal conductivity coefficent of the inclusion.

Keywords:

• first-order topological derivative
• second-order topological derivative
• finite domain peturbation
• asymptotic analysis
• complete second-order topological asymptotic expansion

1. Introduction

Topological sensitivity analysis gives the topological asymptotic expansion of a shape functional with respect to an infinitesimal domain perturbation, like the insertion of holes, inclusions or source term 1,2. The second term of this expansion provides the topological derivative, which has been applied in several problems, such as topology optimization, image processing and inverse problems 3–24. Such a technique has also been applied to non-invasive medical diagnosis and non-destructive evaluation of materials, for instance.

However, for practical applications, it is necessary to consider perturbations of finite size. In general, the first-order correction term only provides a good estimation for the shape functional for infinitesimal perturbations. In this case, we need to consider higher-order terms in the topological asymptotic expansion. The next one is recognized as the second-order topological derivative. These issues were addressed in our previous work 25, where we have shown that the second-order topological derivative provides a good estimation for the shape functional even for very large holes. Furthermore, we observe that in general the second-order topological derivative depends explicitly on higher-order gradients of the solution associated to the non-perturbed problem and also implicitly through the solution of an auxiliary variational problem. However, in 25 we have only calculated the explicit term of the second-order topological derivative. Therefore, as a natural extension of our work, in the present article we calculate the explicit as well as implicit terms of the second-order topological asymptotic expansion for the total potential energy associated to the Laplace equation in the two-dimensional domain. In addition, the domain perturbation is done by the insertion of a small inclusion, instead of a hole, with thermal conductivity coefficent value different from the bulk material. In summary, the main contribution of this article is the calculation of the complete second-order topological asymptotic expansion for inclusions, whose result is very useful for applications in the context of inverse problems, where we seek to identify a set of inclusions from boundary measurements (see, for instance 26,27).

In order to fix the basics ideas, let us consider an open bounded domain Ω ⊂ ℝ², with a smooth boundary ∂Ω. If the domain Ω is perturbed by introducing a small inclusion represented by ℐ_ϵ, which is a ball of radius ϵ centred at point , we have a perturbed domain Ω_ϵ = (Ω\ℋ_ϵ) ∪ ℐ_ϵ. From these elements, the topological asymptotic expansion of a given shape functional ψ, when exists, may be expressed as (1) where f₁(ϵ) and f₂(ϵ) are positive and smooth functions that decreases monotonically such that f₁(ϵ) → 0, f₂(ϵ) → 0 when ϵ → 0⁺ and (2) In addition, D_Tψ and are the first- and second-order topological derivatives of ψ, respectively. In fact, dividing Equation (1) by f₁(ϵ) and taking the limit ϵ → 0 we obtain (3) Moreover, dividing Equation (1) by f₂(ϵ) and taking the limit ϵ → 0 we have (4)

In this work, we apply the topological-shape sensitivity method developed in 28 to calculate D_Tψ and for the total potential energy associated to the Laplace equation in two-dimensional domain.

Finally, we present some numerical experiments showing the influence of the second-order term in the topological asymptotic expansion by taking different values for the parameter ϵ and several values of the thermal conductivity coefficent of the inclusion.

2. The topological-shape sensitivity method

The topological-shape sensitivity method 28 was proposed as an alternative procedure to calculate the topological derivative. A remarkable fact of this methodology is that it can be naturally extended to calculate higher-order topological derivatives. In particular, the following results holds:

THEOREM 1:

Let f₁(ϵ) be a function chosen in order to , then the (first-order) topological derivative given by Equation (3) can be written as (5)

THEOREM 2:

Let f₂(ϵ) be a function chosen in order to , then the second-order topological derivative is given by (6)

The derivative of the shape function with respect to the parameter ϵ that appears in Equations (5) and (6) may be seen as its classical shape sensitivity analysis 29. In particular, for inclusions given by a disk, the shape change velocity v is defined on the boundary ∂Ω_ϵ as (7) where n is the outward unit normal vector field. Then, the shape derivative of the shape functional results in an integral on the boundary ∂ℐ_ϵ, (8) where tensor Σ_ϵ can be interpreted as a generalization of the Eshelby energy–momentum tensor 30. As a consequence, this tensor plays a central role in the topological-shape sensitivity method and should be clearly identified according to the problem under consideration.

On the other hand, the topological asymptotic expansion may also be written as (9) which allows a straightforward identification of all terms in the above expansion.

Before applying the above methodology for a practical problem, let us present a simple one-dimensional diffusion–reaction example given by:

Example 3:

Let be a function u_ϵ ∈ 𝒰_ϵ satisfying (10) where 𝒰_ϵ = 𝒱_ϵ = {η ∈ H¹(Ω_ϵ) : η(0) = 0}, with . Then, let us consider a perturbation on the reaction coefficent c_ϵ(x) satisfying (11) Therefore, the above problem has exact solution, which is given by the following piecewise function

•	for (12)
•	for (13)
•	for (14)

In addition, let us consider a shape function associated to the solution u_ϵ evaluated at point x = 1, that is Finally, from these elements we may calculate the topological asymptotic expansion for this simple problem. In fact,

•	first-order topological derivative: applying Theorem 1, we have for f1(ϵ) = ϵ (15)
•	second-order topological derivative: applying Theorem 2, with f2(ϵ) = ϵ2, we obtain (16)

From the above results, we may build the following topological asymptotic expansion of the shape function (17) Let us fix the size of the inclusion, then we observe that the point which minimizes the shape function is given by for both approximations (18) (19) where function u is solution of Equation (10) for ϵ = 0. On the other hand, let us now fix . Then we take the size of the inclusion ϵ ∈ {0, 0.01, 0.02, …, 0.4}. Considering both approximations given by Equations (18) and (19), we can build the curves shown in Figure 1. From analysis of this graphic, we observe that the second-order topological derivative plays an important role in the estimation of the shape function, allowing a good approximation even for very large (finite) inclusions.

Figure 1. Estimation of u_ϵ(1) considering first- and second-order terms in the topological asymptotic expansion.

3. Topological derivative for the Laplace equation

As already mentioned, in this section we will calculate first- as well as second-order topological derivative for inclusions taking the total potential energy associated to the Laplace equation in two-dimensional domain as the shape functional.

The variational formulation for the Laplace equation associated to the perturbed domain Ω_ϵ can be stated as: find u_ϵ ∈ 𝒰_ϵ, such that (20) where the set 𝒰_ϵ is defined as and Γ_D and Γ_N are the Dirichlet and Neumann boundaries, such that , with Γ_D ∩ Γ_N = ∅. In addition, is the heat flux prescribed on Γ_N and the material property k_δ is defined, for δ ∈ ℝ⁺, as (21) The shape functional adopted will be the associated total potential energy, that is (22)

For this case, the Eshelby energy–momentum tensor is given by (23) Adopting an orthonormal coordinate system (t, n) on ∂ℐ_ϵ, the continuity condition of the solution u_ϵ on the boundary of the inclusion ∂ℐ_ϵ gives (24) where , and the jump condition associated to the normal derivative of u_ϵ comes from its respective variational formulation (Equation 20). Considering Equation (23) in Equation (8) and taking into account the above conditions, the shape derivative of the shape functional results (25)

Now, we need to know the behaviour of the solution u_ϵ in relation to ϵ, which, as a consequence of the methodology adopted, may be obtained from an asymptotic analysis of u_ϵ around the neighbourhood of the inclusion. In the present case, we have the following expansion for u_ϵ (Appendix) (26) where u is solution of (20) for ϵ = 0 (without inclusion), v_ϵ is such that |v_ϵ|_H¹(Ωϵ) ≤ Cϵ³, with C independent of ϵ, and function ũ is solution of the following variational problem: find ũ ∈ 𝒱, such that (27) where the admissible functions set 𝒱 and the admissible variations space 𝒲 are defined, respectively, as (28) and function g is given by (29)

Considering the expansion given by Equation (26) in Equation (25), we obtain (30) Finally, taking into account Equation (9), we get the following results for f₁(ϵ) = πϵ² and f₂(ϵ) = πϵ⁴ (31) (32)

Remark 4:

From Equation (32) we observe that the second-order topological derivative depends on higher-order gradients of the solution and also through the solution of an auxiliary variational problem (27).

Remark 5:

In the case of energy-based shape functional, we can obtain the topological asymptotic expansion for homogeneous Neumann boundary condition on the hole by simply taking the limit when the material property associated to the inclusion vanishes. Thus, after compute the limit δ → 0 in Equations (31) and (32), we have (33) (34)

4. Numerical experiments

Now, we shall study, through some examples, the influence of the second-order topological derivative in the topological asymptotic expansion. Therefore, we will compute the estimate for the shape functional taking into account only the first-order topological derivative (35) Then we will compare it with the estimate considering both first- and second-order topological derivatives, that is (36)

Remark 6:

Solution ũ(x) of the auxiliary problem (27) depends on the point where the inclusion is positioned. Thus, the incorporation of its contribution on the second-order topological derivative calculation is a quite cumbersome task and impracticable from the computational point of view. Therefore, the influence of function ũ(x) will be disregarded in the numerical experiments.

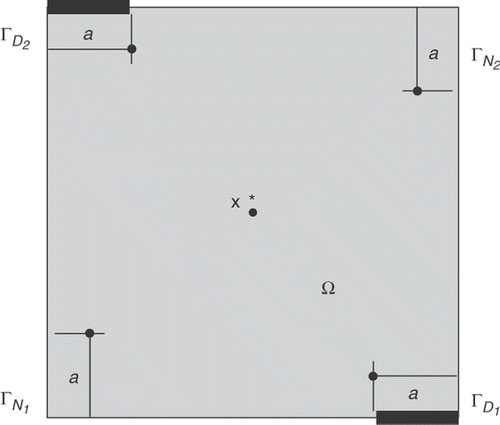
For that, let us consider a body represented by Ω = (0, 1) × (0, 1), submitted to a temperature = 0 on Γ_D1 and Γ_D2, and a heat flux on Γ_N1, on Γ_N2 and on , as shown in Figure 2, where a = 0.2. This body is perturbed by introducing inclusions with centre at x* = (0.5, 0.5), where δ ∈ {1/16, 1/8, 1/4, 1/2, 2, 4, 8, 16} and k = 1. Then, for each value of δ, we take ϵ ∈ {0.01, 0.02, 0.04, 0.08, 0.16}. Considering these values of ϵ and δ, we compute the topological asymptotic expansion associated to the domain Ω at x*. Then, in order to compute the shape functional values ψ(Ω_ϵ), we effectively insert the inclusions with centre at the fixed point x*. Finally, from these results, we can compare the accuracy obtained from both estimates given by Equations (35) and (36), taking into account the approximation in Remark 6.

Figure 2. Orginal domain Ω.

The solutions u and u_ϵ associated to the original Ω and perturbed Ω_ϵ domains, respectively, are approximated using the standard three node triangular finite element. In particular, the meshes were constructed maintaining the same number of elements ne = 120 along the boundary of the inclusion for whichever value of its radius ϵ. Since an automatic mesh generation was used, the following expected size h^e for the elements was adopted for all meshes (37)

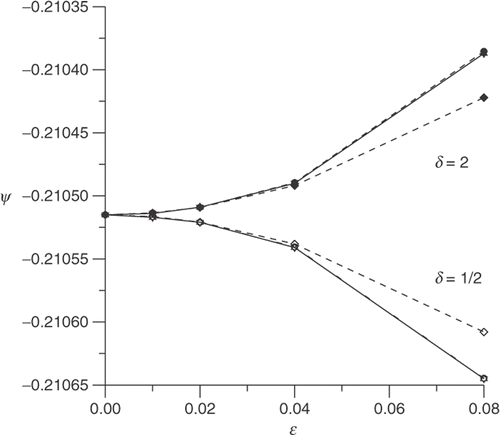
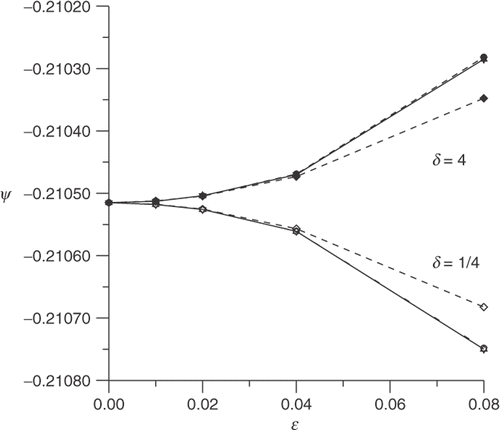
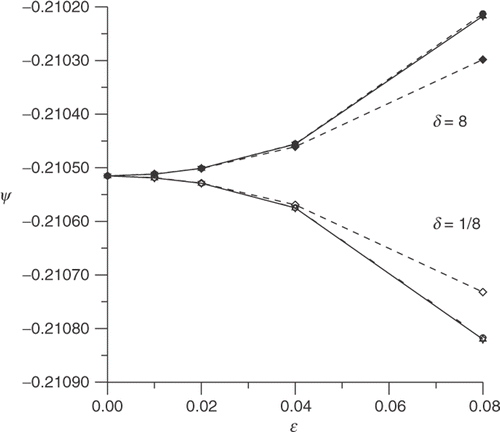
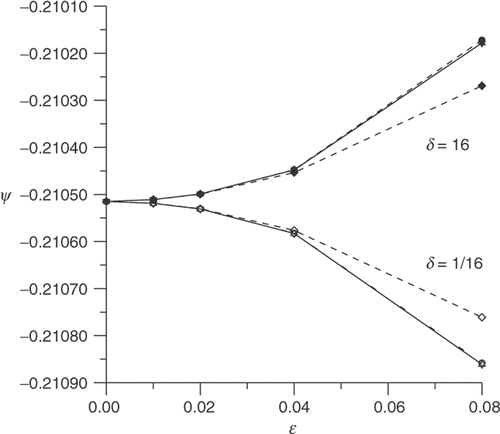
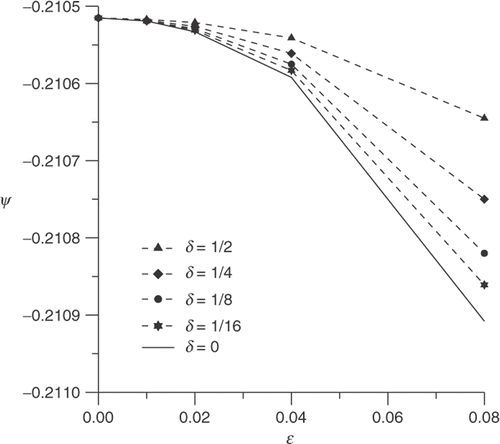
The behaviour of the topological asymptotic expansion as a function of ϵ, evaluated at x*, is shown in Figures 3–6 for different values of δ, where the label used to identify the curves is summarized in Table 1.

Figure 3. Estimate of ψ(Ω_ϵ) for δ = 1/2 and δ = 2.

Figure 4. Estimate of ψ(Ω_ϵ) for δ = 1/4 and δ = 4.

Figure 5. Estimate of ψ(Ω_ϵ) for δ = 1/8 and δ = 8.

Figure 6. Estimate of ψ(Ω_ϵ) for δ = 1/16 and δ = 16.

Table 1. Label of the graphics in Figures 3–6.

δ > 1	δ < 1

According to Remark 5, the limit case δ → 0 gives the topological asymptotic expansion for homogeneous Neumann boundary condition on the perturbation. Then, in Figure 7, we observe the behaviour of the topological asymptotic expansion when δ decreases to zero.

Figure 7. Behaviour of the topological asymptotic expansion when δ decreases to 0.

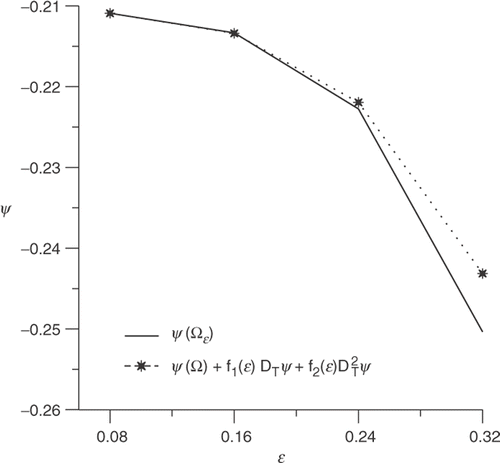
Finally, taking again δ = 0 and considering a larger variation of ϵ ∈ {0.08, 0.16, 0.24, 0.32}, we observe in Figure 8 that the discrepancy between the shape functional and its estimate considering first- and second-order topological derivatives (Equation 8) grows with ϵ. However, the estimation becomes bad only for very large holes (ϵ > 0.16).

Figure 8. Estimate of ψ(Ω_ϵ) considering the second-order term of the topological asymptotic expansion for ϵ ∈ {0.08, 0.16, 0.24, 0.32}.

5. Conclusions

In this work, we have obtained an explicit formula for the topological asymptotic expansion considering first- and second-order approximations. In particular, we have applied the topological-shape sensitivity method to calculate the first- and second-order topological derivatives for the total potential energy associated to the Laplace equation in two-dimensional domain, which was perturbed through the insertion of a small inclusion. Then, we have presented some numerical experiments showing the influence of the second-order approximation term in the topological asymptotic expansion. From these experiments, we have observed that the estimate considering only the explicit term of the second-order topological derivative remains precise even for very large inclusions or holes, allowing to deal with perturbations of finite size. This feature is very important in the development of topology optimization and reconstruction algorithms.

Acknowledgements

This research was partly supported by the Brazilian agencies CNPq, under grant 477212/2004-2, and CNPq/FAPERJ-PRONEX, under Grant E-26/171.99/2003. Jairo Rocha de Faria was partially supported by Brazilian government fellowship from CAPES. The support from these Institutions is greatly appreciated.

In this appendix, we present the derivation of the asymptotic formula given by Equation (26). Therefore, let us propose the following expansion (38) where u(x) is the solution of the problem stated in Equation (20) for δ = 1 (without perturbation) and w(x/ϵ) is the solution of the following exterior problem (39) whose explicit solution may be written as (40) (41) In addition, the remaining term of expansion (38) satisfies (42) where ξ is an intermediate point between x and .

In the same way, we assume that ũ_ϵ, solution of the boundary value problem (42), satisfies the expansion (43) where is the solution of the following exterior problem: find such that (44) which also has explicit solution, that is (45) Introducing the notation, (46) then (47) Thus, function ũ satisfies a boundary value problem stated as: find ũ such that (48) and the remaining term of expansion (43) solves: find v_ϵ such that (49) where ζ is an intermediate point between x and .

Finally, we have the following expansion for solution u_ϵ, (50) where v_ϵ satisfies the estimate below:

PROPOSITION 7:

Let v_ϵ satisfying the boundary value problem (49). Then, there exist a constant C, independent of ϵ, such that (51)

Proof

See 26,27,31▪

Remark 8:

The reader interested in asymptotic analysis for arbitrary-shaped inclusions may refer to 27, whose methodology may be extended to obtain higher-order expansions like the one given by (50).