An alternating boundary integral based method for a Cauchy problem for the Laplace equation in a quadrant

Abstract

We study the Cauchy problem for the Laplace equation in a quadrant (quarter-plane) containing a bounded inclusion. Given the values of the solution and its derivative on the edges of the quadrant the solution is reconstructed on the boundary of the inclusion. This is achieved using an alternating iterative method where at each iteration step mixed boundary value problems are being solved. A numerical method is also proposed and investigated for the direct mixed problems reducing these to integral equations over the inclusion. Numerical examples verify the efficiency of the proposed scheme.

Keywords:

• alternating method
• Cauchy problem
• Green's functions
• Laplace equation
• trigonometric- and sinc-quadrature rules
• unbounded domain
• quadrant

AMS Subject Classifications::

• Primary: 35R25
• Secondary: 35J05
• 65R20

1. Introduction

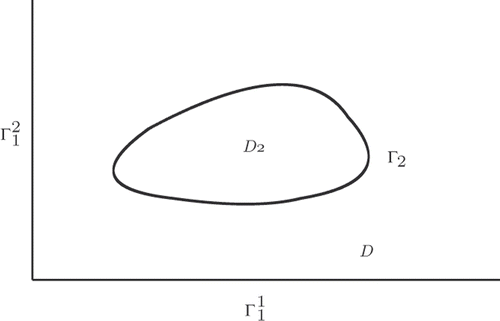
Let the region be the quadrant with (unbounded) boundary , where and . Moreover, let D₂ with be a bounded domain with boundary Γ₂. We put , and we assume that the boundary curve Γ₂ is given through a parametric representation (1) where is C² and -periodic with for all , see Figure 1 for an example of the configuration.

Figure 1. The quadrant with an inclusion D₂ and its boundaries.

We consider the Cauchy problem of finding a function satisfying the Laplace equation (2) and the boundary conditions (3) with u being uniformly bounded at infinity. In (1.3), ν denotes the outward unit normal to the boundary. Applications of this type of model occur, for example, in fluid mechanics with an inviscid and incompressible fluid flow.

For the uniqueness of a solution to the Cauchy problem (1.2–1.3) see, for example, 1,2. The solution does not, in general, depend continuously on the data, i.e. the problem is ill-posed in the sense of Hadamard, thus making classical methods inappropriate.

We shall employ the so-called alternating iterative method proposed in 3. This method was originally proposed for bounded domains and so we extend it to our unbounded setting. The situation of the Cauchy problem in a half-plane was recently considered in 4. The alternative method has successfully been applied in several engineering problems, see for example 5–10.

In each iteration, mixed direct problems are solved in the solution domain D. In most of the standard numerical methods for elliptic boundary value problems (the Finite Difference Method and the Finite Element Method) in unbounded domains an artificial boundary is introduced to reduce the problem to a finite domain, see, for example, 11. For the direct problems in this study, we propose and investigate a numerical boundary integral method which does not need any artificial boundary. Instead, the problems are each reduced to a boundary integral equation over Γ₂. This approach makes the implementation of the alternating method very efficient. Moreover, for the direct problems, there can be a singularity in the solution at the corner point (the origin) of the boundary Γ₁. However, since we reduce these problems to an integral equation over the boundary Γ₂ this singularity does not affect our numerical results.

For the contents of this article, in Section 2 the alternating method and the necessary direct problems are introduced. Also, convergence of the method is briefly discussed. In Section 3, the numerical method for the direct problems is introduced and analysis of the numerical approximation is undertaken. Finally, in Section 4 we present some numerical examples which show that the proposed method and approximations produce an accurate numerical solution to the Cauchy problem (1.2–1.3) in an efficient way.

2. An alternating method for the Cauchy problem (1.2)–(1.3

To formulate the alternating iterative procedure for solving (1.2–1.3), we introduce the following mixed boundary value problems: (4) (5) and (6) (7) By a solution to (2.1) and (2.2) or (2.3) and (2.4) we mean a classical solution which is uniformly bounded at infinity, i.e. (8) The alternating iterative procedure for constructing the solution to (1.2) and (1.3) runs as follows:

i.	The first approximation u0 to the solution u of (1.2)–(1.3) is constructed by solving problem (2.1)–(2.2) with , where h0 is an arbitrary initial guess.
ii.	Having constructed , we find by solving problems (2.3)–(2.4) with .
iii.	Then we find the element by solving problems (2.1)–(2.2) with .

2.1. Convergence and regularizing properties

Let U₀ be the solution to (2.1)–(2.2), with given (sufficiently smooth) function h and f₁ = 0. Further, let U₁ be the solution to (2.3) and (2.4) with f₂ = 0 and on Γ₂. The operator B is defined by (9) One can check that B is well defined, and, clearly, B is a linear operator. Similarly, let be the solution to (2.1)–(2.2) with h = 0, and let be the solution to (2.3)–(2.4) with on Γ₂. Denote (10) The Cauchy problem (1.1)–(1.2) is equivalent with the fixed point equation (11) Therefore, to investigate the convergence of the iterative alternating procedure it is enough to investigate the properties of the operator B. Following 3, it can be shown that B (using appropriate function spaces) is self-adjoint, non-negative, non-expansive and the number one is not an eigenvalue; thus convergence follows, see further 4.

For the case of noisy data and , where , and (12) due to the properties of B, the discrepancy principle can be employed as a stopping rule for fixed point iterations for equation (2.5), see 12, Chapt. 3, Section 3]. This implies in particular that if is the smallest integer with (13) for given , then converges to the exact solution of (2.5) when . Thus, the proposed alternating procedure is a regularizing method. In (2.5), for k ≥ 1 is obtained as described in (i)–(iii), where replaces the exact data (f₁, f₂) in (2.2) and (2.4).

3. Numerical approximation for the mixed problems

3.1. Dirichlet–Neumann mixed problem

We shall construct the solution of the mixed boundary value problem (2.3–2.5). For a quadrant the corresponding Green's function for the Neumann problem has the form with , , and . Note that for the planar case the above-introduced Green's function is unbounded at infinity. Using the single-layer potential approach with the Green's function N for the domain D₁, we can seek the solution of the mixed problem (2.3)–(2.4) in the form (14) with an unknown density ϕ on Γ₂ and a constant α. In order to satisfy the boundedness condition at infinity (2.5), the side condition is imposed 13. As it is evident from the approach (3.1), some additional conditions on the boundary function f₂ have to be imposed. First, for the existence of the integral the function f₂ is required to have an appropriate asymptotic behaviour on the real axis and second the integral of f₂ over the boundary Γ₁ has to vanish to satisfy the regularity condition at infinity. We summarize these properties as the following conditions: (15)

Using the continuity of the single-layer potentials and the properties of the Green's function, the problem (2.3–2.4) can be reduced to the pair of boundary integral equations (16) to be solved for the density ϕ and the constant α.

Using the parameterization (1.1) we can transform (3.3) into the parametric form (17) with the -periodic kernel the right-hand side (18) and the density . Here we used the notation , .

For the full discretization of the integral equation of the first kind (3.4), which has a logarithmic singularity, we apply a quadrature method together with the quadrature rule 14,15 based on trigonometric interpolation. For this purpose, we choose an equidistant mesh by setting (19) and use the quadrature rules (20) and (21) with weight functions These quadrature formulas are obtained by replacing a sufficiently smooth function with its trigonometric interpolation polynomial and then integrating exactly 15. We point out that in the case of a periodic and analytic function μ we obtain exponential convergence.

For the numerical calculation of the integral in (3.5) we apply the so-called sinc-quadrature rule (22) where . This quadrature formula is obtained by replacing f with a sinc approximation 16 and then integrating exactly. In the case of analytic functions f which satisfy for and some positive constant c, the quadrature (3.9) has exponential convergence. We note here, that for the change of the asymptotic of integrand in (3.9), if it is needed, some special transformations can be used 16.

Thus, after the application of the quadrature method to the integral Equations (3.3) and the quadrature rule (3.9) for the computation of the integral in the right-hand side of (3.5) we obtain the following system of linear equations (23) to be solved for for , and α, with a given right-hand side, A convergence and error analysis for this numerical scheme is described in 14 in a Hölder space setting and in 15 in a Sobolev space setting. This analysis exhibits the dependence of the convergence rate on the smoothness of the boundary curve Γ₂, i.e. the proposed method belongs to the class of algorithms without ‘saturation effect’.

In the alternating procedure, we have to obtain the normal derivative on the boundary part Γ₂. This derivative can be calculated from the above boundary integral formulation. Indeed, from the properties of the single-layer potentials, the normal derivative of the solution on Γ₂ can be calculated by the formula (24) for , where ν is the outward unit normal to Γ₂ and the kernels are given as and The approximation for (3.11) can be obtained by using the quadratures (3.7) and (3.9).

3.2. Neumann–Dirichlet mixed problem

We shall construct the solution of the mixed boundary value problem (2.1), (2.2) and (2.5).

For a quadrant, the corresponding Green function has the form where , , and . As one can check, this Green function is bounded at infinity. Thus, for the boundary value problems (2.1), (2.2) and (2.5) we again employ the single-layer potential approach (25) Then the problem given by the equations (2.1), (2.2) and (2.5) is reduced to the following integral equation of the second kind (26) We note here that in this mixed problem it is necessary to have the following asymptotic behaviour for the boundary function (27)

Taking into account (1.1) we can rewrite equation (3.13) in the parametric form (28) where , and and The numerical solution of the integral equation (3.15) is obtained by the Nyström method using the quadrature rules (3.7) and (3.9). The error and convergence analysis of this method can be found in 15.

From (3.12) we obtain the following parametric representation of the solution on Γ₂ for the mixed problem (2.1), (2.2) and (2.5) (29) where and the kernels have the form and for k = 1, 2, respectively. For the approximation of (3.16) the quadratures (3.8) and (3.9) are used.

4. Numerical examples

We shall present reconstructions for the Cauchy problem (1.1–1.2) for two different geometries and data. The Cauchy data on Γ₁ is constructed as follows: the mixed Dirichlet–Neumann problem (2.3–2.4) with boundary conditions u = g on Γ₂ and on Γ₁, is numerically solved by the boundary integral equation approach. Then, for the trace of the solution on Γ₁, the following representation holds (30) for and . For the numerical calculation of the first integral in this formula, we use the quadrature (3.7) and for the second integral we approximate the functions and on some interval via piecewise constant interpolation and then perform the exact integration. We shall also find the approximation of the boundary function on Γ₁ for noisy data.

To avoid an inverse crime we solve these integral equations on a finer mesh and choose the necessary values needed on a coarser mesh in the numerical examples below. Moreover, we also add random pointwise errors to the values of f₂ on Γ₁ with the percentage given in terms of the L²-norm.

Example 1

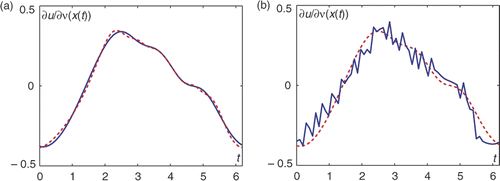
We investigate the case when the boundary curve Γ₂ is the unit circle with the distance d = 1.5 to the boundary Γ₁ Figure 2a.

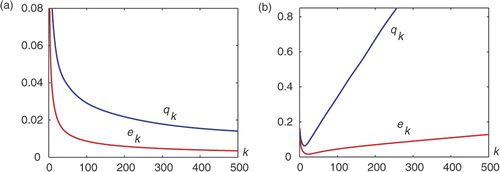
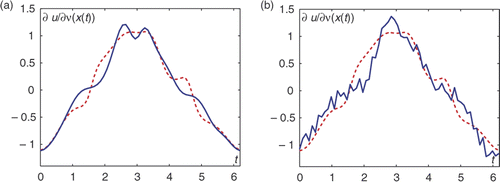
The data is found, as described in the beginning of this section, by solving the Dirichlet–Neumann mixed problem with on Γ₂ and on Γ₁, and by employing the approach (4.1). The results of the Cauchy data reconstructions (—) on Γ₂ in the case of exact and noisy data are presented in Figures 3 and 4, in comparison with the exact solutions (- - -), where k* is the number of iterations. The L²-errors and are shown in Figure 5. Here, we used the following discretization parameters: M = 32 and M₁ = 1000, and the initial guess was h₀ = 0 on Γ₂.

Figure 2. Geometry of the boundaries of the solution domains for the numerical examples; (a) Circle in a quadrant (b) Peanut in a quadrant.

Figure 3. Reconstruction of the boundary function on the circle in example 1, (a) Exact data, (b) 5% noise, .

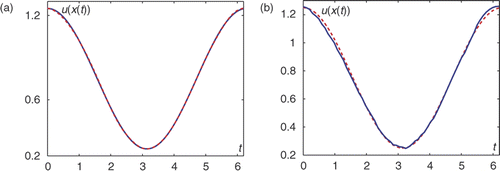
Figure 4. Reconstruction of the normal derivative on the circle in example 1, (a) Exact data, , (b) 5% noise, .

Figure 5. The L²-errors e_k and q_k on the circle in example 1, (a) Exact data, (b) 5% noise.

Example 2

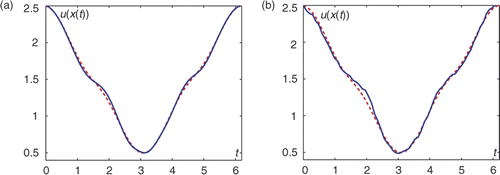
We now let Γ₂ have a more complicated geometry, and choose it as the peanut shaped curve (31) with the radial function and d = 1.5 (Figure 2b). Let and for , . The data is created as described in the beginning of this section.

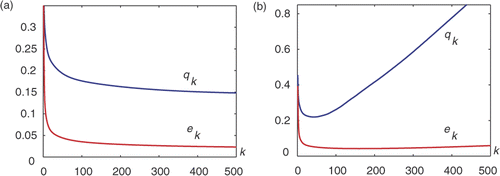
Figures 6 and 7 compare the exact solutions (dashed line) with the reconstructions (continuous line) on Γ₂ in the cases of exact data (f₁, f₂) and 5% data perturbation . The behaviours of the L²-errors e_k and q_k, introduced above, at every iteration step are presented in Figure 8. As in the previous example, we used the following discretization parameters: M = 32 and M₁ = 1000, and the initial guess was h₀ = 0 on Γ₂.

Figure 6. Reconstruction of the boundary function on the peanut in example 2, (a) Exact data, , (b) 5% noise, .

Figure 7. Reconstruction of the normal derivative on the peanut in example 2, (a) Exact data, , (b) 5% noise, .

Figure 8. The L²-errors e_k and q_k on the peanut in example 2, (a) Exact data, (b) 5% noise.

5 Conclusion

We have proposed and investigated an alternating iterative procedure for the reconstruction of a solution to the Laplace equation on the boundary Γ₂ of a bounded inclusion in an unbounded quadrant-type domain from given Cauchy data on the boundary of the quadrant. At each iteration step mixed boundary value problems need to be solved to update the function values on the boundary of the inclusion. Numerically these mixed problems are reduced to a system on the boundary part Γ₂. An advantage with this approach for the mixed problems compared with, for example, the Finite Element or Finite Difference Methods is that we only need to discretize the finite boundary Γ₂ and no artificial boundaries are needed to be introduced making the procedure more computationally efficient and reducing the dimension of the problem. A disadvantage is that an explicit expression for the fundamental solution is needed. The alternating procedure is a regularizing method and it preserves the original underlying physical model which is not the case with methods based on Tikhonov regularization such as the method of quasi-reversibility.

Future work includes extending this approach to unbounded three-dimensional solution domains. Also unsteady Cauchy problems in heat and fluid flow will be researched. Moreover, techniques to further increase the convergence rate will be investigated.