An iterative method for parameter identification and shape reconstruction

Abstract

An iterative strategy for the reconstruction of objects buried in a medium and the identification of their material parameters is analysed. The algorithm alternates guesses of the domains using topological derivatives with corrections of the parameters obtained by descent techniques. Numerical experiments in geometries with multiple scatterers show that our scheme predicts the number, location and shape of objects, together with their physical parameters, with reasonable accuracy in a few steps.

Keywords:

• topological derivative
• domain reconstruction
• parameter identification
• non-destructive testing
• scattering
• inverse transmission problems

1. Introduction

Numerical methods based on topological derivatives (TDs) are powerful tools for inverse scattering problems associated with shape reconstruction and non-destructive testing. Recent work on TDs focuses on problems where the nature of the scatterers is known 1–3. We address here the full problem, developing strategies to reconstruct objects buried in a medium or their physical properties 4,5. The medium and the objects are illuminated by an incident radiation (electromagnetic, thermal, and acoustic). The total field, composed of incident, scattered and transmitted waves, solves a transmission problem in the whole space. The inverse problem consists in reconstructing the objects and their material parameters from measurements of the total field at different locations. Adjoint state approaches based on FEM techniques are discussed in 1 or 6, where a boundary temperature is determined from interior temperature measurements. Other methods assume particular shape functions for the parameter distribution. FEM-based reconstructions of the stiffness parameters of scatterers based on this idea are studied in 7.

For numerical purposes, inverse scattering problems are often reformulated as constrained optimization problems. One seeks domains and parameters minimizing the difference between the data measured at the detector locations and the total field associated to a given set of scatterers. Our strategy consists in generating a sequence of approximations for the domains and their parameters along which the cost functional decreases. Guesses of the objects are updated by adding regions in which the TD of the cost functional is negative. This procedure provides good initial guesses of the scatterers without any a priori information about their shape or location. Each correction of the domains is followed by corrections of their parameters. Analytic expressions for such corrections are found by computing the variations of the cost functional along particular directions. Formulae for the required TDs and the parameter corrections were obtained in 4, where the idea is suggested and a simple test for piecewise constant parameters is shown. Here, we explore the performance of this iterative scheme in the general case in which the material properties of the objects and the background media are spatially dependent. Our implementation of the method is slightly different, in order to guarantee converging approximations. We introduce a systematic strategy to select the parameters controlling the algorithm, suppressing the need to visually check the values of the TDs around the obstacles each time the objects are updated. A few hints explaining why the scheme works are given. For other reconstruction strategies in homogenous media with heterogeneous inclusions or heterogenous media with homogeneous inclusions, see 5,8,9.

Reasonable reconstructions of the objects and their parameters are obtained in a few steps. Even if the predicted values of the parameters may deviate a bit from the exact ones due to noisy data, rough approximations are often useful to differentiate between different materials (in geophysics) or tissues (in biomedicine). Our techniques may be useful in digital image elasto-tomography for tumour detection 5,10, for instance: healthy tissue, benign tumours and malignant tumours are known to have different stiffness constants.

This article is organized as follows. Section 2 gives the constrained optimization reformulation of the inverse scattering problem. Section 3 details the reconstruction procedure and its properties. Numerical experiments are discussed in Section 4. Section 5 summarizes our conclusions.

2. Constrained optimization formulation of the inverse problem

Let us consider the medium ℝⁿ, n = 2 or 3, where a set of unknown objects are buried. This configuration is illuminated by an incident wave, which interacts with the medium and the obstacles. The total wave field (formed by incident U_inc, transmitted U_tr and scattered U_sc waves) solves the so-called forward problem, whose structure depends on the incident radiation (acoustic, electromagnetic, thermal, etc.).

To fix ideas, we consider the scalar acoustic problems for longitudinal or transversal waves in dimensionless form. Throughout this article, all the variables and parameters are assumed to be dimensionless. The total field U(x, t) is governed by a couple of wave equations with homogeneous transmission conditions at the interface Γ ≔ ∂Ω_i. Here Ω_i denotes the unknown objects and Ω_e the surrounding medium. The parameters ρ_e(x) and ρ_i(x) represent the densities of the medium and the inclusions, respectively. The parameters a_e(x) and a_i(x) are computed in terms of the elastic constants outside and inside the objects. The total field equals U_inc + U_sc outside the scatterers and U_tr inside. If the incident field is time harmonic, i.e. U_inc(x, t) = e^−ιωtu_inc(x) (ω > 0 is the frequency of the incident wave), the total field inherits that structure U(x, t) = e^−ιωtu(x). Then, its spatial amplitude solves the following transmission problem: (1) where and We assume that the real coefficients a_e, a_i, k_e, and k_i are bounded from below by positive constants and depend smoothly on x, becoming constant at infinity. We set The last condition in (1) is the Sommerfeld radiation condition, implying that only outgoing waves are allowed. The incident radiation is a plane wave u_inc(x) = e^ικ_ed·x with wave number κ_e.

The symbols ± denote traces and normal derivatives from each side of the boundary Γ. The normal vector points inside Ω_i. Transmission conditions are used when the obstacle is ‘penetrable’ by the radiation. Neumann (sound-hard obstacles) 2,4 or Dirichlet (sound-soft obstacles) conditions can be handled with similar techniques.

Analogous transmission problems are obtained for time harmonic radiations of a different nature. General acoustic waves are governed by Navier equations and we are left with vectorial transmission problems, more expensive to solve computationally. In electromagnetic scattering, time harmonic TM or TE waves lead also to (1), possibly with complex k_e and k_i due to attenuation in the media. For thermal waves, k_e and k_i are always complex. The techniques developed in this article apply in all these cases, with small modifications for complex k_e and k_i (see 11, which also explains how to handle non–time harmonic problems).

The total wave field is measured on Γ_meas for several incident waves (2) with incident directions d_m, m = 1, …, M. The inverse problem consists in finding the geometry and nature of the scatterers for which the solutions of the forward problems agree with the measured values on Γ_meas. This problem is ill–posed. For numerical purposes, it is convenient to reformulate it as an optimization problem: Find a domain Ω and functions a(x) and k(x) minimizing (3) when u_m solves (1) with Ω_i = Ω, a_i = a, k_i = k, and u_meas,m is the total field on Γ_meas when the incident wave is u_inc,m. If Γ_meas is just a set of point detectors, the integral over Γ_meas becomes the sum of the errors at each of them. For good guesses of the domains and the parameters, functional (3) should take small values.

3. Reconstruction scheme

The idea is to generate a sequence of approximate scatterers and parameters in such a way that the cost functional (3) decreases from one step to the next. To do so, we perform a double iteration. For a fixed value of the parameters, we improve our guesses of the obstacles computing the TD of the resulting functional and adding points at which the TD is negative. For a fixed approximation of the obstacles, we update our guesses of the parameters correcting them in a direction of descent. The algorithm stops either when the measure of the new regions added to the scatterers and the changes in the parameters are small enough or when a discrepancy principle is reached, i.e. when the difference between the measured data and the numerical solution for the reconstructed objects and parameters is approximately as large as the noise level in the measurements. Let us describe with more precision the different steps.

3.1. Initialization

To start the process we select constant first guesses for the inner parameters perturbing the background: a₀ = a_e(x₀) + α, k₀ = k_e(x₀) + κ, where x₀ may be any randomly chosen point. The resulting shape functional depends only on the domain Ω.

The TD of a shape functional J(ℛ) measures its sensitivity when infinitesimal balls are removed from the region ℛ at each point x 2: see Figure 1(a) for a graphical illustration of the geometry. Equivalently, For small scatterers B_ϵ(x) centred at a point x where D_T (x, ℛ) is negative, the functional J decreases, that is . When the TD at x is negative and large, one can expect that the functional still decreases by removing a large region about x, not just a small ball. TD methods exploit this idea and locate scatterers at the regions where the TD takes large negative values. For instance, Figure 2(a) represents the TD of the functional (3) for the obstacle configuration depicted in Figure 1(b) when ℛ = ℝ². Dark regions correspond to large negative values and light regions to the highest values. The contours of the objects are marked by white lines. Three dark regions are observed, which locate the three objects.

Figure 1. (a) Schematic geometry for computing TDs. (b, c) Geometry for the numerical examples with constant parameters.

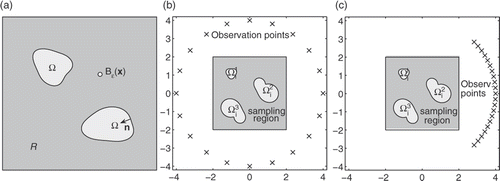
Figure 2. TD and first eight steps alternating several corrections of parameters with one correction of the domains.

Therefore, to construct a first guess for the geometry of a set of scatterers, we set ℛ = ℝⁿ, n = 2 or 3. An explicit expression for the TD of our particular type of functional in terms of forward and adjoint fields is given below. For any x ∈ ℝⁿ, the TD of the cost functional J(ℝⁿ; a₀, k₀) is (4) with a_i = a₀, k_i = k₀. The forward field u_m solves (1) with Ω_i = ∅ and u_inc = u_inc,m, i.e. (5) The adjoint field w_m solves (6) δ_Γmeas being the Dirac delta function on Γ_meas.

The proof can be found in 4. Notice that the true scatterers enter the TD through the presence of u_meas,m in the adjoint problems. When a_e and k_e are space dependent, the forward and adjoint fields have to be computed numerically. Otherwise, they have an explicit expression in terms of the incident wave or the fundamental solution of the differential operator. Similar adjoint and forward problems appear in other methods: adjoint methods 1, Green's function techniques 3, shape deformation or level sets 2.

For any fixed geometry, if the frequencies are low enough (ω small, and therefore small), the TD takes large negative values at solid regions located inside the scatterers. When the frequencies are high enough, the TD takes large negative values at annular regions marking the boundaries of the objects. In geometries with multiple obstacles, the reflections and interactions between different objects increase with the frequency, producing oscillations in the adjoint and forward fields. These oscillations persist in the TD, making it very difficult to distinguish between oscillations and contours at high frequencies. Therefore, we will implement our schemes for low frequencies. The interested reader can find a gallery of numerical examples comparing the behaviour of the TD at high and low frequencies in 4,13 for transmission problems in acoustics and in 11 for thermal waves.

By performing a test in a geometry with a known object, we find a threshold between ‘high’ and ‘low’ frequencies. In practice, the size and parameters of the objects are unknown, thus we calibrate a low frequency by checking that the TD is not oscillatory. Once a low frequency has been selected, our algorithm to generate an initial guess for the domains proceeds as follows. We evaluate (4) at a large grid of points and choose a first guess for the scatterer with the following structure: (7) Different procedures can be followed to define a smooth contour for Ω₁. We propose an approximation using trigonometric functions and adjust the coefficients by solving a least squares problem, see 4 for details.

The value −C₁ is computed as the largest negative value attained by the TD multiplied by a constant η₁. Initially, η₁ = 3/5. If , this value is accepted. Otherwise, we increase η₁ until the restriction is satisfied. Our initial choice of η₁ is usually sharp enough. The starting value η₁ = 3/5 was calibrated using (4) for a model problem with a single scatterer with known interior parameters. First, we selected a high frequency. Then, the TD located the boundary of the scatterer at an annular region. Next, we selected a low frequency. Then, η₁ was fitted in such a way that the boundary of Ω₁ agreed with the guess obtained using the high frequency. This yielded the value 3/5.

3.2. Correction of parameters

Once a guess Ω_j for the scatterers is available, we update our prediction of the parameters a_j−1 and k_j−1 inside it. To do so, we use a descent strategy. We fix the domain Ω_j and perturb the parameters following two fields φ and ψ, selected in such a way that the cost functional decreases. For any δ > 0, we set and seek δ, φ and ψ such that An explicit expression for this derivative provides analytical expressions for the corrections φ and ψ where u_m solves the forward problem (1) with u_inc = u_inc,m and Ω_i = Ω_j, a_i = a_j−1 and k_i = k_j−1. The adjoint fields w_m solve (8) with Ω_i = Ω_j, a_i = a_j−1 and k_i = k_j−1. The proof is given in 4. The forward and adjoint fields are computed numerically, either using a BEM in case of constant a_i and k_i, or combining BEM and FEM when these parameters are space dependent, as explained in 4,14, respectively. Setting (9) and (10) we guarantee for δ small. Typically, we set an initial guess for δ and check whether J decreases. If not, we divide δ by two until this restriction is fulfilled.

Notice that (9) makes sense everywhere. We may use it to define a_j and k_j everywhere or only inside Ω_j. Unlike 4, we have defined a_j and k_j by (9) inside the approximate scatterers and set a_j = a_j−1 and k_j = k_j−1 outside them. In this way, the parameters a_j and k_j are not continuous, showing a discontinuity at the boundary of the domains Ω_j.

If we are interested in locating homogeneous defects, that is, objects where the parameters a_i and k_i are constant, we can define the fields φ and ψ as follows: (11) If Ω_j is the union of a finite number of non-intersecting domains, , then the above definitions can trivially be adapted to define constant parameters inside each by replacing the integrals over Ω_j by integrals over . When we suspect that the sizes of the obstacles can be very different, we may divide each integral by the measure of in (11). In this case the interior parameters are only piecewise constant and we extend the definition to the exterior of the objects by simply setting a_j = a₀ and k_j = k₀.

3.3. Approximation of domains

Once we have updated the parameters a_j and k_j, we correct our guess of the scatterers. To do so, we consider the functional and compute its TD for It is given by formula (4) with a_i = a_j, k_i = k_j 4. The forward fields u_m and the adjoint fields w_m solve (1) and (8) with Ω_i = Ω_j, a_i = a_j, k_i = k_j and u_inc = u_inc,m, respectively. These fields must be computed numerically, for instance by BEM–FEM techniques. All these problems have the same structure and only differ in the right hand side. In practice, the numerical solutions are obtained by solving 2M systems of linear equations with the same matrix, but different right-hand sides. We refer to 14,15 for further details.

We construct a nested sequence of approximate obstacles Ω_j ⊂ Ω_j+1 as follows: Alternatively, we might update Ω_j in such a way that spurious points can be removed at any stage, as explained in 4. Such strategy is specially convenient if we want to detect objects with cavities (annular shapes, for instance) instead of solid objects.

The thresholds −C_j+1 are obtained multiplying the largest negative value attained by the TD by a factor η_j+1, 0 ≤ η_j+1 ≤ 1. In principle, we set η_j+1 = 9/10. In practice, it may happen that the new domain is too large, J increases and spurious points are added. Before accepting a threshold, we check that . If this is true, we accept the approximation Ω_j+1 and go ahead. If not, we increase η_j+1. To do so, we may use any function taking values in (0, 1) and tending to 1 as a parameter varies. For instance, we may set where μ ≥ 0, and increase μ until the restriction is fulfilled.

This strategy differs slightly from the one suggested in 4 in which the main goal was to ensure a large decrease in the magnitude of the TD. The TDs would vanish for the exact total field and the true scatterers and parameters, since the adjoint field would be zero. However, whether a reduction in the magnitude of the TD implies always a decrease in the value of the cost functional is unknown.

3.4. Convergence and stopping criteria

Following the procedure sketched above, the cost functional J decreases after each new choice of the parameters or the domains. We are generating a minimizing sequence that should converge to an optimal choice. Notice that the cost functional is positive but vanishes when u_m are the exact total fields corresponding to the true scatterers and parameters. The exact solution is therefore a global minimum. However, little is known about the properties of functional (3). In case additional local minima exist, the minimizing sequences we generate might converge to a spurious solution. This risk is reduced when the initial guess is sharp and increases when we use few incident waves, or when detectors are located in a narrow region.

Our reconstruction algorithm stops when the variation of the volume of the domains and the magnitude of the parameters is small enough (a Cauchy criterion). In the examples discussed in Section 4, the criterion is satisfied after a few iterations. Reasonable approximations of the scatterers and their properties are obtained, even for noisy data. The value of J at the last iteration is relatively small, which means we are approaching a solution. If we wish to improve the description of the shapes of the domains, we can further impose that the magnitude of the TD is small enough. An alternative stopping criteria would require the cost functional to become small enough. However, this might happen before both sequences stabilize to definite patterns and values, producing a poor approximation. It might also happen much later, resulting in a large number of iterations.

Our strategy to optimize the parameters could be combined with other descent methods to update the domains, such as shape optimization by deforming contours along vector fields or level-set-based techniques. However, none of them generates an initial guess for the obstacles. We should use TDs (Section 3.1) or other external approximation to start the iteration. Moreover, as discussed in 12, standard shape optimization methods can neither create missing objects nor destroy spurious ones. Unless the exact number of objects is known from the beginning, they will not converge. Instead, level-set methods 12,16 also allow for topological changes, the same as TD-based strategies. The computational cost for iteration in the three methods is roughly the same. The same adjoint and forward fields have to be computed. The main difference in the computational cost comes from the number of iterations. Most published papers on level-sets mention hundreds of iterations, see 17, or references in 16. We only need a few. The level-set method creates new approximations for the domains by solving Hamilton–Jacobi equations with a small time step. Unless an accelerating strategy is used, the variations from one step to the next with that method are small and the evolution of the sequence of domains is likely to be much slower than in our case.

4. Numerical experiments

In this section, we present numerical experiments illustrating the ability of our method to reconstruct the shape, size and location of buried objects, as well as their nature (described by the functions a_i and k_i) without any a priori information about them. In our simulations, the data vectors u_meas,m are given by = u(x_j) + ε_j, with x_j ∈ Γ_meas, where ε_j describe measurement errors. We generated the ‘exact’ data u(x_j) using a forward solver and added i.i.d. Gaussian random variables. For most tests, the relative error was 0.1% (numerical noise in our synthetic data due to discretization is less than 100 times smaller). We will see later that the TD is not overly sensitive to measurement errors and noisier data provide analogous results.

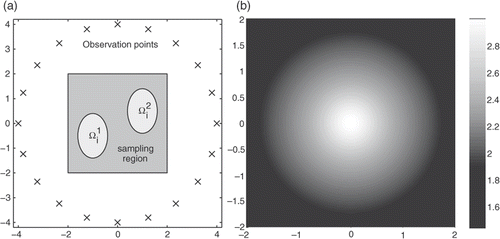
In all the tests that follow we made measurements at 20 observation points uniformly distributed on a circle of radius four centred at the origin (the points represented by crosses in Figure 1b). Data were generated for incident waves of the form (2) at 20 incident directions d_m = (cos θ_m, sin θ_m) for uniformly distributed angles θ_m in [0, 2π).

Let us start with a couple of tests with constant parameters to calibrate whether it is more convenient to alternate one correction of the domains and one correction of the parameters, or to carry out several iterations with respect to the parameters for each iteration with respect to the domain. We consider the configuration represented in Figure 1(b), consisting of three objects with different constant parameters. In the exterior medium, a_e = 1 and k_e = 2. The interior parameters inside the smaller object are and . The other two objects have exactly the same shape (up to a rotation), but different parameters. In the right-most object , and , whereas and in the object at the bottom. We take as initial guesses a₀ = 0.9 and k₀ = 1.8 which are a perturbation of the exterior parameters. Intuitively, we expect better reconstructions for large objects. We also expect better results when the gap between the interior and exterior parameters is large.

Figure 2(a) represents the values of the TD when Ω_i = ∅, a_i = a₀ and k_i = k₀, computed using formula (4) (with u_m and w_m solving (5) and (6), respectively) at a sampling grid defined in the square region represented in Figure 1(b). Dark colours indicate the regions where the TD takes large negative values, where objects should be located. The boundaries of the true defects are marked with white lines. Although we have two objects with exactly the same area, only the presence of , the right-most defect, is clearly distinguished. There is a bigger discrepancy between the interior and exterior parameters for than for The small object is also missed due to its size, although the parameters are quite different from the ones in the unbounded domain. Therefore, our first guess has only one component, which is the ball Ω₁ in Figure 2(b). We fix now Ω_i = Ω₁ and perform four iterations with respect to the parameters using formulae (10) and (11). The TD is recalculated for the parameters obtained in the fourth iteration with Ω_i = Ω₁, see Figure 2(b). Now the three objects are detected, although and seem to be much smaller than . This is the case for the true , but not for . The updated domains are represented in Figure 2(c). After four more iterations to improve the parameters, we recalculate the TD, as shown in Figure 2(c). The domains obtained by repeating this procedure are represented in Figure 2(d)–(i). A few iterations provide a reasonable reconstruction of and its parameters. Although we do not show the subsequent approximations, the reconstruction of was also quite satisfactory after two more steps, in spite of the small size of the object. As expected, the small gap between the true interior and exterior parameters for makes it difficult to get a good approximation for this object. The evolution of the interior parameters with the number of iterations is plotted in Figure 3(a) and (b). Notice that the different parameters are quite well identified. Two identical values of the parameters in the plot mark each iteration to improve the domains (the parameters are not updated).

Figure 3. (a, b) Evolution of the parameters a_i and k_i. The true values are , , and , , . (c) Values of the cost functional J at each iteration for the first and second examples.

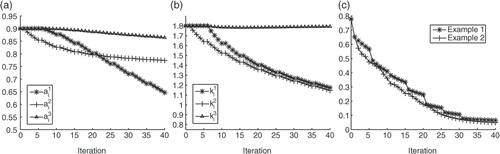
Let us repeat the test alternating one correction of the domains with one correction of the parameters. The initial guess for the domain is exactly the same as in the previous example (Figure 2b). Figure 4(a) shows the approximate scatterers at the 12th step. At this step, the area of the difference between the new and the old domains is negligible. The stopping criteria for the objects was therefore achieved and in the next iterations only the parameters are updated. The values of the parameters and , d = 1, 2, 3, at each iteration are shown in Figure 4(b) and (c), respectively. Comparing Figures 2(i) and 4(a), as well as Figures 3(a) and (b) and 4(b) and (c), we see that this method, which is more demanding in computer time, provides reconstructions of similar quality. The object looks better, but this is due to the fact that Figure 2 stops at the eighth step. In that case, the stopping criteria was satisfied after two more steps and the reconstruction of looked quite similar to the one in Figure 4(a).

Figure 4. (a) Approximate domain and TD at the 12th step alternating one correction of the domains and one correction of the parameters. (b) Values of the parameters , d = 1, 2, 3 versus the number of iterations. (c) Values of the parameters , d = 1, 2, 3 versus the number of iterations.

Figure 3(c) shows the reduction in the cost functional with both strategies. We observe that the cost functional decreases faster when updating domains than when updating parameters. However, its values at the last iteration are similar for both strategies. The first strategy is more efficient because it provides a similar quality of reconstruction at a lower cost. Each iteration with respect to the domain is more expensive than each iteration with respect to the parameters, due in part to the compared cost of computing forward and adjoint fields. For constant parameters, we solve adjoint and forward problems using the BEM with Brakhage–Werner potentials and trigonometric polynomials for the discretization. A detailed study of the method can be found in 18 (see also 4 for a brief description of the method in the exact setting we are using in this article). If we update the values of the parameters for a fixed domain, only the integral operators associated to the interior objects have to be recalculated. However, if we update the geometry of the objects without changing the values of the parameters, then all the integral operators are recalculated. Furthermore, each correction of the objects implies that we have to go through the list of the grid of sampling points to determine if each point belongs to the new object or not. Moreover, each time we update the obstacles we have to solve a least squares problem to determine the function that describes the parameterization of each obstacle.

We want to explore now the performance of our method for higher levels of noise. Figure 5(a) and (b) shows the final reconstructions for relative errors of orders 1% and 10%, respectively. Both have been obtained alternating one iteration for the domains with a few iterations for the parameters. The graphics illustrating the convergence of the parameters and , or of the cost functional J are analogous to the ones in Figure 3. A gallery of numerical tests exploring the sensitivity of the TD to noisy data for an exterior Neumann problem can be found in 2.

Figure 5. Final reconstruction of the objects with: (a) 1% noise and (b) 10% noise. (c) Seventh iteration of the method when receptors are located on a sector of the circle, see Figure 1(c).

Finally, we have also tested the method when measurements are collected on a non-circumscribing path with a 0.1% level of noise. Figure 5(c) shows the reconstructed objects at the seventh correction of the domains for the observation points represented by crosses in Figure 1(c). We show this intermediate reconstruction to empathize that, as expected, the closest object to the receptors is reconstructed faster and with more accuracy than the rest. Once this object is reasonably approximated, the remaining objects are also visible. This happened in our test at the fourth correction of the right-most object. Furthermore, the parts of the remaining objects that are close to the receptors are better reconstructed from the beginning (compare with Figure 2(h)). However, the final reconstruction was of the same quality as the ones in Figures 2(i) and 4(a). Reconstructions of shapes when detectors are located at the boundary of a half space and the material properties of the objects are known are discussed in 11 for time-dependent thermal waves. Some examples with detectors on a limited region of a circle (or sphere) for acoustic problems in two and three dimensions with constant and non-constant known parameters can be found in 4,13.

Let us discuss now the non-homogeneous case. At each step, the forward and adjoint fields are computed applying the mixed BEM–FEM scheme described in 14 (see also 15). Again, each iteration with respect to the domain is more expensive because we have to parameterize and mesh the new domains. Also, the matrices must be entirely recalculated. Therefore, we alternate one iteration for the domains with a few iterations for the parameters.

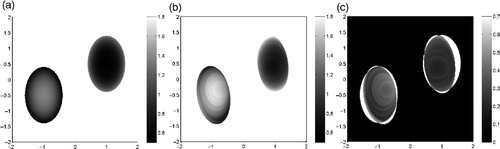
For the next test we have considered a simple geometry with two elliptical objects of the same size (Figure 6(a)). The interior parameters are in and in . The exterior parameter k_e is a radial function, (12) and a_e = 1. The function k_e is represented in Figure 6(b). The object on the left feels the strongest discrepancy between the exterior k_e and the interior k_i.

Figure 6. (a) Geometrical configuration and (b) function k_e for the examples with space-dependent parameters.

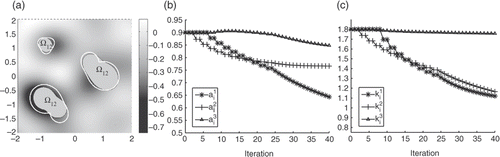
To initialize the iterative procedure we set a₀ = 0.9 and k₀ = 1.8, as in the previous example. Figure 7(a) depicts the TD when Ω_i = ∅. Our initial guess Ω₁ (shown in Figure 7(b)) consists of two circular objects approximately of the same size. We proceed now as in our first example, iterating four times to update the value of the parameters a_i and k_i. The TD after updating the parameters is plotted in Figure 7(b). The new domains are elliptical. After nine more steps of the combined method (one iteration for the objects and four for the parameters) our reconstruction is represented in Figure 7(c). The size of is underestimated, but the prediction of its location and shape is sharp. 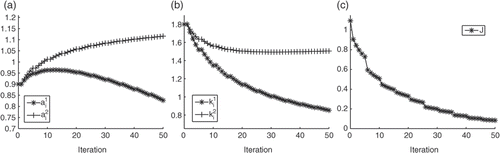The shape and size of are almost correct, but its location is slightly displaced to the left. Figure 8 plots the values of the parameters a_i and k_i and the cost functional J through the iterative procedure.

Figure 7. (a) TD with Ω_i = ∅, a_i = 0.9 and k_i = 1.8. (b) Initial guess Ω_i = Ω₁ and TD when Ω_i = Ω₁, and , d = 1, 2. (c) Final reconstruction at the 10th step.

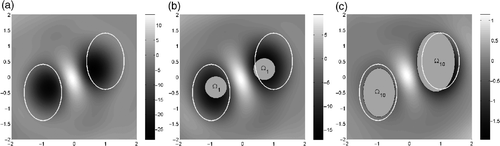
Figure 8. (a) Evolution of the parameters a_i. The true values are and . (b) Evolution of the parameters k_i. The true values are and . (c) Cost functional at each iteration.

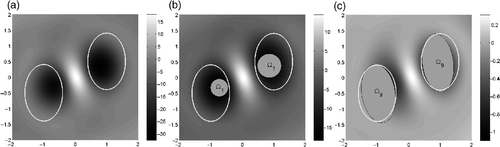
In our final example, we maintain the geometry described in Figure 6(a) and the function k_e defined in (12). The interior parameter k_i is given now by the space-dependent function (Figure 10(a))

To simplify the numerical procedure, we assume the interior parameters to be known. Our goal is to recover the objects and the function k_i. At each iteration, the approximate function k_i is defined by (9) and (10).

Figure 9(a) shows the TD when Ω_i = ∅, and our initial guess is represented in Figure 9(b). Our approximate objects at the final step of the iterative procedure are shown in Figure 9(c). The reconstruction of k_i at the last step is depicted in Figure 10(b), whereas the true k_i is represented in Figure 10(a). We concluded when the stopping criteria for the domains was attained. A few more iterations with respect to k_i would have improved the result. Discontinuities correspond to updates in the domains during the iterative procedure. As expected, the largest discrepancies between the exact and the approximate k_i are located in the regions added during the last step, since only four corrections of the parameters have been performed to improve the previous guess. This effect was not observed when recovering constant parameters since the integrals in (11) smooth out this contribution. The error in the approximation of k_i is plotted in Figure 10(c), where white regions also indicate the points that belong to the true objects, but not to the reconstructed ones, or vice versa. We do not find a sharp approximation of the function k_i, but we get reasonable information about its behaviour inside each object. We are able to recognize a radially increasing function inside and a radially decreasing function inside , with an average error about 0.3. In this case, the cost functional decreased from 1.26 to 0.17 in a similar way to Figures 3(c) and 8(c).

Figure 9. (a) TD with Ω_i = ∅. (b) Initial guess Ω_i = Ω₁ and TD when Ω_i = Ω₁. (c) Final reconstruction at the ninth step.

Figure 10. (a) Function k_i. (b) Reconstructed function k_i at the ninth step. (c) Error.

In comparison with the previous examples where the exterior parameters were constant, we notice that the fact that k_e is radial and reaches its maximum between both objects allows to get a very good approximation of parts of the boundaries placed far from Γ_meas where the interaction between objects is stronger.

5. Conclusions

We have discussed an iterative scheme to reconstruct objects buried in a medium and their material properties in a few steps. The idea is to generate a sequence of approximations for the objects and their parameters in such a way that the cost functional decreases. New objects are generated from previous ones by computing the TD of the functional and adding regions where it takes large negative values. Parameters are updated by adding corrections in a descent direction. The adjoint and forward fields needed to evaluate the TDs and the directions of descent are computed by hybrid BEM–FEMs. Our numerical experiments show that good reconstructions of the objects and their properties are obtained after a few steps even in the presence of noise and in heterogeneous media. When the material properties of the objects are space dependent, we are able to distinguish their spatial distribution. The quality of the predictions improves when objects are large and when the contrast between the interior and exterior parameters is high. The strategies we propose to update domains and parameters are independent. Our procedure to correct the parameters could be combined with different strategies to modify the domains ensuring a decrease in the magnitude of the functional, such as level-set-based methods 12,16.

Acknowledgements

The authors are partially supported by FIS2008-04921-C02-02, MEC–FEDER MTM2007-63204 and CM-910143 projects.