Estimation of target density functions in time-varying environments

Abstract

In this article, two different solutions are presented to the problem of estimation of time-varying range-angle in nonstationary environments. The first one utilizes a wideband signal with a certain bandlimitedness condition on the time variation of the target density function at each point in space. By choosing small successive processing time intervals, bandlimitedness of the time variation becomes much more realistic than assuming no time time variation or a specific time variation. The second one does not have this assumption and utilizes a narrowband signal with a continuous spectral content. Both provide a general methodology for imaging of nonstationary environments. In addition to nonstationarity, time-varying target density functions can also describe nonlinearity of a medium where each point distorts the transmitted wave by multiplying it with a time-varying function during reflection.

Keywords:

• range-direction target density functions
• nonstationary target environments
• time-varying target density functions
• joint range-angle beamforming
• radar imaging

1. Introduction

An essential goal of active sensors such as radar is to convey the reflectivity of each target at each point in space. This knowledge is reached via the bounced signal off the target and plays a primary role to obtain an image of the target area 1–11. The estimation of the target reflectivity at each point in a coordinate system simultaneously yields the target density function 2–6. The usual coordinate systems are range-angle or range-Doppler, only.

The target region in nonstationary environments cannot be assumed constant even during very small subintervals of time. This causes blurring of the target estimates, or scintillation. Nonstationarity of the target region is taken into consideration to some extent via Doppler 1–6. However, this is based on the constant radial velocity assumption during the processing subintervals.

In this work, the reflectivity point in a time-varying environment is considered as (t, R, D), where t is time, R is range and D is the direction cosines in three dimensional space as D = (β, γ, δ), where −1 ≤ β, γ, δ ≤ 1. The proposed techniques are studied in two sections, respectively. In Section 3, a joint range-direction approach is considered and the first technique is developed to jointly estimate the time-varying target density function h(t, R, D) for each time t, direction D and range R, using bandlimitedness assumption on the time variation. By applying this technique over small time intervals, the bandlimited time variation assumption on target density functions becomes much more realistic than assuming no time variation, or a specific type of time variation.

In Section 4, a narrowband approach is considered and an alternative technique is developed which does not have the bandlimitedness assumption on the time dependence of the target density function. This technique utilizes a narrowband signal with a continuous spectrum. Note that the nonlinearity of a medium where each point reflects the transmitted wave by distorting its shape by multiplying by a function of time can also be described by time-varying reflectivity.

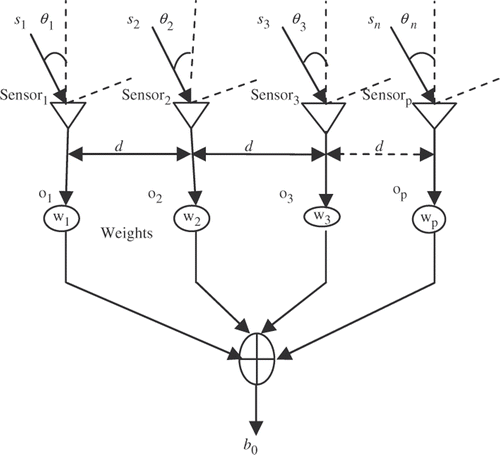
2. Preliminaries of array processing

A sensor array is a group of sensors located at spatially separated points. Sensor array processing focuses on data collected at the sensors to carry out a given estimation task. A schematic view of an array sensor system is shown in Figure 1. If p is the number of the elements in the array and the sensor elements are spaced arbitrarily with a distance in between d, using a set of weights and time delays to combine the signals from the sensors, the following well-known 12–15 structure is considered. Consider n signals from n targets with different angles θ_k (k = 1, 2, … , n), consisting of p sensor elements spaced with d distance. At a particular instant of time t, the total received signal at the i-th sensor is a combination of noise and n incoming signals: (1) where o_i(t) is the measure quantity at each of the sensors (i = 1, … , p) for a particular source at direction θ_k, s_k(t) is the incoming signal from the targets at direction θ_k, d is the element spacing and v is noise, ω = 2πf_c and λ = c/f_c, f_c is the carrier frequency, c is the speed of light, λ is the wavelength of the received signal and τ_k is the delay given by (2) From (1), the vector form of the received signal can be expressed as (3) where o(t) = [o₁(t), … , o_p(t)]^T, the steering matrix is A(θ) = [a(θ₁), … , a(θ_n)], the signal vector is s(t) = [s₁(t), … , s_n(t)]^T and the noise vector is v(t) = [v₁(t), … , v_p(t)]^T. The direction vector a(θ_k) is given by , where T is the transposition operator. The array output of the beamformer is (4) where denotes complex conjugate weight applied to o_i(t). Whereas the beamforming configurations are generally presented as in the scheme above, in this work, two different types of the beamformer are investigated in Section 3 and Section 4, respectively.

Figure 1. A general beamforming process.

3. Estimation of range-angle target density functions in nonstationary environments with bandlimited time variation

In this section, the range-angle target density function is estimated in a bandlimited time-varying environment. The proposed technique is studied to achieve focusing on the received signal with respect to both range and angle jointly via array processing. It exploits the capabilities of an array more fully, improving on the techniques which separate the processes of angular and range focusing on targets. The target space is upon a sphere with coordinates (R, D), where D is a multiple variable indicating the direction cosines in three-dimensional space as D = (β, γ, δ) where −1 ≤ β, γ, δ ≤ 1. R is denotes the range. Define R₁ to be an upper limit in the range from which there is backscattering, c is the speed of light. This configuration is important in terms of viewing a target globally, that is, in determining a complete picture of the target area. Define ω₀ as (5) where c is the speed of the waves. So that (6) Let (7) Let the transmitted wave-beam form be (8) This can be constructed using classical beamforming techniques for any finite integer M 16,17. In practice, W(D, t) can be modulated by multiplying by a high-frequency carrier , and M can be finite. However, for simplicity of notation we assume ω_c = 0. For the following analysis M can be finite or ∞. To include the carrier, simply replace kω₀ by ω_c + kω₀. In (9) q_k(D) can be arbitrary. The specific functions affect the beamforms that can be achieved. This is clarified in the following analysis.

For nonstationarity, each (R, D) reflectivity point is considered including t variable as (t, R, D). Thus, in a time-varying environment, each point (R, D) has a time-varying reflectivity, h(t, R, D) to an incoming wave, because the object at the point (R, D) can vary with time at least in orientation. Let H(ω, R, D) be defined as (9) H(ω, R, D) will be estimated. Define the variable X as

X = (x, y, z) = a point in the Cartesian coordinates.

The sensor at point X receives (10) where

XD = βx + γy + δz.

Equivalently, (11) Define (12) Let be expressed as a Fourier series for Rϵ[0, R₁] (13) where ϵ is a known normalizing constant, and (14) Thus (15) where (16) Assuming that h(t, R, D) is bandlimited to [ω₁, ω₂] with respect to t, and its bandwidth is less than for each k, demodulation via we can obtain over a finite time interval, at each point X. This uniquely determines L_k(t, X) for all t via extrapolation of a bandlimited function 16–19.

Hence, by extrapolation, we obtain from (16), (17) for ωϵ[ω₁, ω₂].

For each fixed ωϵ[ω₁, ω₂], is clearly a bandlimited function of each variable x, y, z of X, specified over a nonzero finite interval with respect to each variable, for fixed values of the other variables. Hence, from (17), via extrapolation (q_k(D)H_k(ω, D)) is uniquely determined, for each ωϵ[ω₁, ω₂]. From this H_k(ω, D) can be estimated over a certain directional region depending on q_k(D) (where q_k(D) ≠ 0). This is clearly the best which can be obtained for a given q_k(D). Then, from (12) and (13) H(ω, R, D) is obtained, as best as q_k(D)'s allow. For values of k and D for which q_k(D) = 0, the Fourier series terms of H(ω, R, D) will be missing, and we will obtain an orthogonal projection on for those k's where q_k(D) is not identically zero.

Remark 1 (Fixed range)

In first scenario, the range is taken as constant. If ranging is done by another means (such as pulsing), h(t, R, D) becomes h(t, D) and H(ω, R, D) becomes H(ω, D). Then H_k(ω, D) is the same (a constant multiple (ϵ)) of H(ω, D) for all k, and in fact, then L_k(t, X) become only one L(t, X) for each k, from which q_k(D)H_k(ω, D) for each k is estimated the same way, which yields an estimate of H(ω, D) for each ω. In this case, for each ω, one can also obtain the L₂-orthogonal projection of H(ω, D) on {q_k(D)}_k, by only considering the output of the sensor at the point X = 0 (i.e. using only one sensor), and a suitable W(t, D) such that {q_k(D)}_k forms a basis for L₂.

If over the directional region of interest at the fixed range, we can transmit a wave beam (18) (i.e. k = 1 = M = q_k(D)) then, using (17) and a finite nonzero aperture, we can uniquely determine W(t, D).

Remark 2 (Fixed direction)

In second scenario, the direction is taken as constant. Then H(ω, R, D) becomes H(ω, R). Then (12) becomes (19) and (13) and (14) become (20) (21) Hence, we can use only one sensor (X = 0), and (15) becomes (22) where now q_k is a known constant. By the same bandlimitedness assumption with respect to t, H_k(ω)q_k can be easily determined. If q_k ≠ 0 for all k, then H_k(ω) is uniquely determined. This yields H(ω, R) for all (ω, R). If some of the q_k's are zero, we obtain a Fourier series with those terms missing, which is an orthogonal projection.

Remark 3

Note that the function L_k(t, X) determined by demodulating the output of the sensor at point X via is a bandlimited function in each of its variables (t, β, γ, δ), specified on a nonzero region for each variable. Thus, it can be uniquely extrapolated with respect to all values of each variable for each known values of the other variables 16–19. Hence it can be uniquely extrapolated to all (t, β, γ, δ) and this can be done by successively extrapolating with respect to each variable one by one, to uniquely determine q_k(D)H_k(ω, D). In this case of point sensors this becomes a problem of extrapolation of a multivariable bandlimited function from its samples, which is a well-known problem with several proposed solution techniques 16–19.

Remark 4

Note that ω₀ is chosen according to an upper limit on the range of interest, (23) If R₁ can be made smaller, then ω₀ can be chosen larger. Then the allowed bandwidth of h(t, R, D) at each point (R, D) can be larger while demodulation via is still possible for each k. Note that for e.g., airborne or spaceborne radar platforms R₁ is already relatively small. For large values of R₁, the allowed bandwidth of the time variation is much larger than typical Doppler frequencies.

4. Estimation of range-angle target density functions in arbitrary time-varying environments

In the second method proposed in this article, an estimation technique without the bandlimitedness assumption on time dependence of the density functions is presented. This utilizes a narrowband signal with a continuous spectral content. Transmit a nonzero bandwidth signal with a continuous spectrum (24) i.e. H(ω) is such that there is at least one interval of nonzero length in [ω₁, ω₂] where H(ω) ≠ 0.

The signal returning from point (R, D) to the sensor at the point X is approximately (25) Over a time interval [0, T], express h(t, D, R) as (26) as a Fourier series. Hence, the total signal reaching point X from all the points (R, D) is (27) If F_k(u, v) is the multidimensional Fourier transform of f_k(D, R), then (28) By choice of W(t), the signal (29) is bandlimited to [ω₁, ω₂]. We choose T, ω₁, ω₂ such that ω₂ − ω₁ ≤ ω₀. Thus, then L_k(X, t) can be obtained from y(X, t) via demodulation. Since L_k(X, t) is bandlimited, its values for all t can be obtained from its values observed over any nonzero length interval 16–20. This yields (via extrapolation and Fourier transform) (30) for ωϵI, where I is a nonzero length subinterval of [ω₁, ω₂] (in fact, for all ω for which H(ω) ≠ 0). On the other hand, (31) Thus, for each ωϵI, F_k is a bandlimited function of X known over the finite aperture of the distributed sensor. Again, by 16–20, F_k can be extrapolated to all values of X.

Thus, for each ωϵI, and for each D from which there is a reflection, Q_k(D, ω) can be determined. But (32) Thus, for each D, Q_k(D, ω) is a bandlimited function in ω, known over the interval I. Then, for each D, Q_k(D, ω) can be uniquely extrapolated to all finite ω. This uniquely determines f_k(D, R) for each k. Thus, the density function h(t, D, R) is uniquely determined.

Remark 5

As in Section 3, specialization to cases of known fixed range or known fixed angle is obvious. Also, we assumed D to consist of three independent variables. It can consist of any number of variables (1, 2, …), and the techniques developed are equally valid. For two and three-dimensional spaces, for most applications it will consist of one or two independent variables, where these techniques apply as they are.

Remark 6

The situation with arrays of point sensors instead of continuously distributed sensors will lead to extrapolation problems from finite samples. These are well-studied problems 16–20.

5. Summary and conclusion

In this article, two solutions are proposed for estimation of time-varying target density functions in arbitrary nonstationary environments. Both provide a general methodology for imaging of nonstationary environments and are implementable using classical Fourier type techniques. Because the target density functions can be considered as the reflectivity of spatially continuously distributed targets, the developed target density functions are implementable for an active sensor imaging such as radar. Since an advantage of both techniques are the use of standard Fourier-based analysis, this makes it possible to use simple functions for global radar imaging in nonstationary environments.

The well-known works on target density functions are investigated in SAR/ISAR 7–11 and Fowle−Naparst works 2,3. Since both are developed in stationary environment, they differ from our work. Additionally, the Fowle−Naparst method is based on the complicated ambiguity functions rather than a standard Fourier theory used in our work. On the other hand, because our study is not based on the pointwise approach, it differs from the SAR/ ISAR method.