RTE-based bioluminescence tomography: A theoretical study

Abstract

Molecular imaging has become a rapidly developing area in biomedical imaging. Bioluminescence tomography (BLT) is an emerging and promising molecular imaging technology. Light propagation within biological media is accurately described by the radiative transfer equation (RTE). However, due to the difficulties in theoretical investigation and numerical simulations, so far, the study of BLT problems has been largely based on a diffusion approximation of the RTE. In this article, we provide a rigorous theoretical foundation for the study of the RTE-based BLT. After a discussion of the forward problem of the RTE and its numerical approximation, we establish a comprehensive mathematical framework for the RTE-based BLT problem through Tikhonov regularization. We show the solution existence, uniqueness and continuous dependence on the data for the regularized formulation. We then introduce stable numerical methods for the BLT reconstruction and show convergence of the numerical solutions. Finally, we present simulation results from a numerical example to demonstrate that reasonable numerical results can be expected from solving the RTE-based BLT problem via regularization.

Keywords:

• bioluminescence tomography
• radiative transfer equation
• inverse problem
• regularization
• numerical solution
• convergence

1. Introduction

Molecular imaging has become a rapidly developing area in biomedical imaging. According to 1, ‘molecular imaging techniques directly or indirectly monitor and record the spatiotemporal distribution of molecular or cellular processes for biochemical, biologic, diagnostic, or therapeutic applications’. Molecular imaging promises enabling platforms for in vivo studies of biological building blocks and pathways at cellular and sub-cellular levels. Imaging of molecular markers (e.g. gene expressions, proteins) and biological processes (e.g. interactions, pathway signalling) in unperturbed environments would provide unprecedented tools and rich information leading to earlier or predictive diagnosis, novel drug targets and design, and individualized yet adaptive therapies, which constitute the cornerstone of molecular medicine 1–3. Of particular interest is the optical molecular imaging for mouse studies, which has attracted great attention due to its superior performance, high versatility, ease-of-operation, and cost-effectiveness 4–7.

Among various optical molecular imaging techniques, bioluminescence imaging is of great importance due to its powerful probing and in vivo imaging capabilities, overcoming the sampling limitations of standard assay techniques. Despite genes being duplicated with cell division, the high sensitivity of bioluminescence imaging remains while with other techniques, such as magnetic resonance imaging (MRI), the probe signal decreases due to cell division. Without using excitation light, the background noise in bioluminescent imaging is rather low, yielding very favourable contrast-to-noise ratio. Bioluminescence tomography (BLT) is an emerging and promising molecular imaging technology that aims to reconstruct a 3D bioluminescent source distribution reflecting the concentration of bioluminescent cells in a living mouse from external views around the mouse. Similar to the development of X-ray computerized tomography (CT) after planar radiography, BLT allows a localized and quantitative analyses of bioluminescent source/probe distributions while existing planar bioluminescent imaging is primarily qualitative. BLT was first proposed in 2002 (8), and has been extensively studied since then.

Transmission of the bioluminescent photons through the biological tissue is subject to both scattering and absorption, and is accurately described by the radiative transfer equation (RTE). To describe the RTE, we first introduce some symbols. In this article, we study the BLT problem on spatial domains of dimension three. However, it is possible to develop our theory for any spatial dimension. Let X be a domain in ℝ³ with a Lipschitz boundary ∂X. The outward normal vector ν(x) exists almost everywhere (a.e.) on ∂X.

Denote by Ω the unit sphere in ℝ³. For each fixed direction ω ∈ Ω, we introduce a new Cartesian coordinate system (z₁, z₂, s) through the relation where z = z₁ω₁ + z₂ω₂ with (ω, ω₁, ω₂) forming an orthonormal basis of ℝ³, z₁, z₂, s ∈ ℝ. With respect to the new coordinate system, denote by X_ω the projection of X on the plane s = 0 in ℝ³, and by X_ω,z the intersection of the straight line {z + sω | s ∈ ℝ} with X. We assume the domain X is such that for any (ω, z) with z ∈ X_ω, X_ω,z is the union of a finite number of line segments: Here s_i,± = s_i,±(ω, z) depend on ω and z, and x_i,± ≡ z + s_i,±ω are the intersection points of the line {z + sω ∣ s ∈ ℝ} with ∂ X, and we assume sup_ω,z N(ω, z) < ∞. As an example, if X is a convex domain, then sup_ω,z N(ω, z) = 1. We then introduce the following subsets of ∂X: It can be shown that if ν(x_i,−) exists with x_i,− = z + s_i,−ω, then ν(x_i,−) · ω ≤ 0; if x ∈ ∂X and ν(x) · ω < 0, then x ∈ ∂X_ω,−. Similarly, if ν(x_i,+) exists with x_i,+ = z + s_i,+ω, then ν(x_i,+) · ω ≥ 0; if x ∈ ∂X and ν(x) · ω > 0, then x ∈ ∂X_ω,+. Now define the inflow boundary and the outgoing boundary These are subsets of Γ = ∂X × Ω.

Denote by dσ(ω) the infinitesimal area element on the unit sphere Ω. We will need the integral operator S defined by (1) with the phase function g normalized: In most applications, g is chosen to be independent of x. One well-known example is the Henyey–Greenstein phase function 9 (2) where the parameter η ∈ [−1, 1]. Throughout this article, the symbol ∇ denotes the gradient operator with respect to the x variable.

In RTE-based BLT, we determine a source function p such that the solution u of the boundary value problem (BVP) (3) (4) matches the boundary measurement u_m for the number of outgoing photons: (5) where, σ_t and σ_s are the total attenuation and scattering coefficients of the medium, X₀ is a Lipschitz subset of X, over which the light source function is to be determined and χ₀ is the characteristic function of X₀, i.e., its value is 1 in X₀, and is 0 in X\X₀. The set X₀ is called the permissible region.

As the RTE-based BLT is difficult to study theoretically and to solve numerically, so far, studies of BLT have been mainly limited to a case with a diffusion approximation of the RTE. The diffusion approximation is reasonable in the range of around 600 nm where photon scattering outperforms absorption in a mouse 10. Mathematical analysis and numerical approximations of the diffusion-based BLT problem can be found in numerous papers, for example in 11 a thorough theoretical investigation of the diffusion-based BLT in the form of a partially differential equation (PDE) constrained optimization problem with regularization, in 12 a study of a BLT approach that optimizes optical parameters when an underlying bioluminescent source distribution is reconstructed to match the measured data, in 13 a mathematical framework for multispectral BLT that allows simultaneous studies of multiple optical reporters, in 14 an expanded framework that allows a more accurate numerical solution of the BLT problem with a little additional computational cost, in 15 theoretical studies of a mathematical model for temperature-modulated BLT and in 16 a summarizing account.

However, as it is noted in 17, assumptions on which the diffusion approximation is based are not all satisfied by solutions of the RTE. This article intends to provide a rigorous theoretical foundation for a study of the RTE-based BLT problem. In Section 2, we study the forward problem of the RTE and its numerical approximation. In Section 3, we establish a comprehensive mathematical framework for the BLT problem through Tikhonov regularization; we demonstrate the solution existence, uniqueness and continuous dependence on the data. In Section 4, we introduce stable numerical methods for the BLT reconstruction and show convergence of the numerical solutions. In the final section, we present simulation results from a numerical example on the RTE-based BLT problem. Efficient numerical algorithms and their detailed error analysis for solving the RTE-based BLT problem are a topic for some forthcoming papers.

Inverse problems involving the RTE are a subject of current active research. For source inverse problems, similar to the one considered in this article, in 18, with a smallness assumption on the scattering, a uniqueness result is proved and a reconstruction algorithm is proposed based on a convergent Neumann series. In 19, some general uniqueness and stability results are established. We note that in these papers, data smoothness is assumed, for example σ_t is assumed to be in . In applications on optical tomography, however, σ_t is only piecewise smooth, and so the mathematical theories developed in those papers are not directly applicable to the BLT problem studied in this article; our smoothness assumption on σ_t is a realistic one: σ_t ∈ L^∞(X). Moreover, although the Neumann series is shown to be convergent in 18, the effectiveness and efficiency improvement of the related reconstruction algorithm for numerical simulations is a topic worth further exploration. A related coefficient inverse problem for the RTE has also been studied extensively, see e.g. 20 and the references therein. A general reference on inverse problems for PDEs is 21; in particular, Section 7.4 of the book presents some available results related to the RTE found in the literature, again under such smoothness assumptions as . The approach we adopt in this article for the reconstruction of the source function is through a least-squares approximation. A general reference on using the least-squares approach for identifying coefficients and/or source term is 22, where inverse problems are considered for elliptic and parabolic equations.

2. The forward problem and its numerical approximation

In this section, we consider the following forward problem (6) (7) where σ_t, σ_s and f are given functions, satisfying (8) and (9) The inner product in Q is

We need to introduce a function space V for the solution u of the BVP (2.1)–(2.2). Let and let be the subspace of functions with compact support in X for any ω ∈ Ω. For any u ∈ L¹(X × Ω), if there is a function w ∈ L¹(X × Ω) such that then we say w(x, ω) is the generalized derivative of u(x, ω) along the direction ω ∈ Ω, and write w(x, ω) = ω · ∇u(x, ω). We then introduce a space This is a Hilbert space with the inner product and the norm From 23, Lemma 2.1], we have the following density result.

Proposition 2.1

The space is dense in V.

We also need spaces over the boundary sets Γ₋, Γ₊, and Γ. For , we introduce the norm ‖v‖_QΓ− through the formula where dz = dz₁ dz₂. The space Q_Γ− is defined as the completion of the boundary values of functions with respect to the ‖ · ‖_QΓ− norm. Then Q_Γ− is a Hilbert space with the inner product (u, v)_QΓ− defined by We similarly define a Hilbert space Q_Γ+ over the set Γ₊. We further define a Hilbert space Q_Γ whose norm satisfies the relation

Definition 2.2

We call w ∈ Q_Γ+ the trace of a function v ∈ V on Γ₊ and write v|_Γ+ = w if for any sequence , Traces on Γ₋ and Γ are defined similarily for any function in V.

The following trace theorem holds (24).

Proposition 2.3

If v ∈ V, then it has a trace v|_Γ ∈ Q_Γ, and for some constant c depending only on X,

Corresponding to the RTE (2.1), we introduce a linear differential operator L by the formula Under the assumption (2.3), it can be shown that the following expression defines an equivalent norm over V (23): (10)

We introduce the following weak formulation for the BVP (2.1)–(2.2): (11) where (12) It is easy to see that if u is a smooth solution of the BVP (2.1)–(2.2), then it satisfies (2.6). Note that in the weak formulation (2.6), there is no requirement for the boundary condition (2.2). This property is important for a flexible FE discretization of the BVP.

Since (2.5) is an equivalent norm on V, we can show the boundedness and V-ellipticity of the bilinear form a(·, ·): (13) (14) Also recall the assumption (2.4). Applying the Lax–Milgram lemma 25, we conclude that the weak formulation (2.6) has a unique solution u ∈ V. Moreover, following 23, Theorem 3.2], for this u, (2.1) holds a.e. in X × Ω, and (2.2) holds a.e. on Γ₋, and there are two constants 0 < c₁ ≤ c₂ < ∞ such that

We now consider the numerical approximation of the forward problem (2.1)–(2.2) in an abstract form. Let V ^h be a finite-dimensional subspace of V, depending on a discretization parameter h. Then the discrete approximation of (2.6) is (15)

There are a variety of possible ways to construct the finite dimensional subspaces {V ^h}. Here, we describe one particular choice of V^h based on the finite element methods. For simplicity of presentation, assume the spatial domain X is a polyhedron. Let be a regular family of finite element partitions of into tetrahedrons 26,27. For the partition , write with each element X_i a tetrahedron. The meshsize of the partition is h_x = max_i diam(X_i). Then define a corresponding finite element space (16) where k ≥ 1 is an integer and P_k(X_i) is the space of the polynomials on X_i of total degrees less than or equal to k. Denote for the dimension of the space and let be the Lagrange basis functions of corresponding to a set of nodes . Then we also have Similarly, let be a family of partitions of the unit sphere Ω into regions with piecewise smooth boundaries. It is possible to create such partitions in several ways, for example 28. It is even possible to partition the unit sphere into regions of equal area and small diameter 29. For a partition : Ω = ∪ _jΩ_j, denote the meshsize h_ω = max_j diam(Ω_j), where the diameter diam(Ω_j) = sup{|ξ − η∣ ∣ ξ, η ∈ Ω_j}. We then define a finite element space (17) where l ≥ 0 is an integer and P_l(Ω_j) is a polynomial space of degrees less than or equal to l; P_l(Ω_j) could be the restriction of the polynomial space P_l(ℝ³) on Ω_j or the space of polynomials of degrees less than or equal to l in the two angular variables. Denote for the dimension of the space and let be the Lagrange basis functions of corresponding to a set of nodes . Then We now define an overall meshsize h = (h_x, h_ω); h → 0 means h_x → 0 and h_ω → 0. The overall finite element space is then the following: (18) i.e., any function v^h ∈ V^h can be written in the form From the construction, we know V^h is a subspace of V. Writing we can convert the finite element system (2.10) into a linear system for the coefficients {ξ_ij ∣ 1 ≤ i ≤ n_x, 1 ≤ j ≤ n_ω}: In practice, we can take k = 1 and l = 0, i.e., use finite element functions that are continuous and piecewise linear in x, and piecewise constant in ω. In this case, the finite element nodes for the space are the vertices of the tetrahedrons, and those for can be taken as the centroids of the regions .

Returning to the general framework, under the assumptions (2.3) and (2.4), we again apply the Lax–Milgram lemma to show that the discrete system (2.10) has a unique solution. Moreover, for the numerical solution error u − u^h, we have Ceá's inequality (19) From this, convergence of the discrete solution as h → 0 is a simple consequence of approximability of functions in V by finite element functions.

The Galerkin method (2.10) allows a straightforward a posteriori error estimate. Denote r^h = Lu^h − f for the residual. Then The a posteriori error bound can serve as a starting point for the development of an adaptive solution algorithm.

3. The BLT problem through regularization

We turn to a study of the RTE-based BLT problem (1.3)–(1.5). Throughout the article, we assume (2.3). The source function p will be sought in a closed convex subset Q_ad of the space Q₀ = L²(X₀). Usually it is taken to be the subset of the non-negatively valued functions in Q₀. As discussed in Section 2, for any p ∈ Q₀, the BVP (1.3)–(1.4) has a unique solution, and we denote the solution by u(p) = u(p; ·, ·). By definition, for q ∈ Q, (20) Following the idea of Tikhonov regularization (e.g. 30,31), we let (21) The regularization parameter ϵ is a small positive number.

We consider the following regularized RTE-based BLT problem.

Problem 3.1

Find p_ϵ ∈ Q_ad such that (22)

Obviously, the solution u(q) is linear in q. For p, q ∈ Q₀, we have the following formulae for the first and second derivatives of the functional J_ϵ: In particular, we observe that for ϵ > 0, J_ϵ is strictly convex on Q₀.

We now address the existence and uniqueness issue.

Theorem 3.2

For any ϵ > 0, Problem 3.1 has a unique solution p_ϵ ∈ Q_ad. Moreover, the solution p_ϵ ∈ Q_ad is characterized by a variational inequality (23) When Q_ad ⊂ Q₀ is a subspace, the inequality is reduced to a variational equation (24)

Proof

Note that Q₀ is a Hilbert space, Q_ad ⊂ Q₀ is convex and closed, J_ϵ : Q_ad → ℝ is strictly convex, continuous and coercive, i.e., J_ϵ(q) → ∞ as ‖q‖_Q0 → ∞. By a standard result on convex minimization (see e.g. 25, Theorem 3.3.12]), there is a unique solution p_ϵ ∈ Q_ad to Problem 3.1, and the solution is characterized by the relation (see 25, Theorem 5.3.19]) i.e., the relation (3.4).

Now assume Q_ad ⊂ Q₀ is a subspace. Take q = 0 and 2 p_ϵ, respectively, in (3.4) to conclude the equality (3.5).▪

We then consider the continuous dependence of the solution on the measurement data.

Theorem 3.3

The solution p_ϵ of Problem 3.1 depends continuously on the measurement u_m ∈ Q_Γ+. More precisely, there is a constant c > 0 such that for the solutions p_ϵ,1, p_ϵ,2 ∈ Q_ad of Problem 3.1 corresponding to two measurement data u_m,1, u_m,2 ∈ Q_Γ+, we have the bounds (25) (26) where u_ϵ,1 = u(p_ϵ,1) and u_ϵ,2 = u(p_ϵ,2).

Proof

In the inequality (3.4) for u_m = u_m,1 and p_ϵ = p_ϵ,1, we choose q = p_ϵ,2 to obtain Similarly, Add the preceding two inequalities, Then, (3.6) follows and we also have (27)

From (3.1), we have the equality Choose v = u_ϵ,1 − u_ϵ,2 in the above equality to obtain Combining this and (3.8), we deduce (3.7).▪

Actually, it can be shown that both p_ϵ and u(p_ϵ) also depend continuously on the other data of the problem.

Suppose only an approximate measurement data u_m,δ of (1.5) is known, (28) Denote by p_ϵ,δ ∈ Q_ad the solution of Problem 3.1 with u_m replaced by u_m,δ. Then the inequality (3.6) gives the error bound in the regularized source solution: (29) Therefore, assuming the data noise level δ is known, the regularization parameter ϵ = ϵ(δ) should be chosen such that Discussion of an optimal choice of the regularization parameter ϵ can be found in numerous references, e.g. 31, Section 3.2].

We now explore the solution behaviour when ϵ → 0+. Similar to the proof of (3.4), it can be shown that a solution p ∈ Q_ad of Problem 3.1 with ϵ = 0 is characterized by the inequality (30) Denote by S₀ ⊂ Q_ad the solution set of Problem 3.1. As in 11, the following result holds.

Proposition 3.4

Assume S₀ is non-empty. Then S₀ is closed and convex. Moreover, (31) where p₀ ∈ S₀ is the solution of Problem 3.1 for ϵ = 0 with minimal Q₀-norm: (32)

Proof

It is straightforward to show that S₀ is closed and convex, and so is weakly closed. Here we only prove (3.12). The element p₀ of (3.13) exists and is unique (e.g. 25). We take q = p₀ in (3.4), take q = p_ϵ in (3.11) for p = p₀, and add these two inequalities, Thus, (p_ϵ, p₀ − p_ϵ)_Q0 ≥ 0, ‖p_ϵ‖_Q0 ≤ ‖p₀‖_Q0 and so {p_ϵ} is bounded in the Hilbert space Q₀. Let {p_ϵ′} be a subsequence of {p_ϵ}, converging weakly to some element p ∈ Q₀. Since S₀ is weakly closed, p ∈ S₀. Moreover, Since p₀ is the unique element in S₀ with minimal Q₀-norm, p = p₀. Thus the limit p = p₀ does not depend on the subsequence selected; consequently, the entire family p_ϵ converges weakly to p₀ in Q₀ as ϵ → 0. To show strong convergence, we proceed as follows: Thus, ‖p_ϵ − p₀‖_Q0 → 0 as ϵ → 0.▪

Corollary 3.5

Suppose the solution set S₀ = {p} is a singleton. Then

Consider the situation where the level of the measurement data error is δ; see (3.9). Using (3.10), we have (33) We choose the regularization parameter ϵ = ϵ(δ) such that (34) Then from (3.14), we have the convergence

Note that p₀ ∈ S₀ is characterized as the unique solution of the variational inequality

We comment that if Q_ad is a bounded set, then S₀ is non-empty. This follows from applying a standard result on convex minimization, e.g. 25, Theorem 3.3.12]. Without further information on Q_ad though, we cannot ascertain uniqueness of a solution when ϵ = 0.

4. Numerical analysis of a Galerkin method for the BLT problem

We now turn to a discussion of numerical solutions of Problem 3.1 in an abstract frame. The admissible source function space Q_ad may or may not be discretized. In general, let be non-empty, closed and convex. In particular, without loss of generality, assume . As in Section 2, let V^h be a finite-dimensional subspace of V. In case is a discretized approximation of Q_ad with a discretization parameter , we will understand h as the collection of the discretization parameter h_V for the finite-dimensional subspace V^h_V (still denoted as V ^h for simplicity) and . Note that h → 0 means h_V → 0 and . For any q ∈ Q₀, let u^h = u^h(q) be the unique solution of the discrete problem We then introduce the following discretization of Problem 3.1.

Problem 4.1

Find such that (35) where (36)

A discrete analogue of Theorem 3.2 and Proposition 3.4 is the following result.

Proposition 4.2

For ϵ > 0, Problem 4.1 admits a unique solution which is characterized by the discrete variational inequality: (37) The solution depends continuously on the data. When is a subspace of Q₀, (4.3) reduces to a variational equation: (38)

Suppose Problem 4.1 for ϵ = 0 has a solution, and denote by the solution set. Then is closed and convex, and in Q₀ as ϵ → 0, where satisfies

Similar to Problem 3.1, we comment that if is a bounded set, then is non-empty. In concrete situations, it is possible to show the non-emptiness of the solution set directly.

The discrete analogue of (3.6) is Corresponding to (3.10), we then have

We now turn to a convergence analysis of the numerical solutions. For this purpose, we make the following assumptions.

ASSUMPTION 4.3

For any , there exists Π_V^hv ∈ V^h such that

ASSUMPTION 4.4

For any q ∈ Q_ad, there exists such that

We comment that both assumptions are naturally satisfied in practice. For instance, for the finite-dimensional subspace V^h constructed as in (2.13), Assumption 4.3 is valid following the standard finite element approximation theory 26,27; we may simply take Π_V^hv ∈ V^h to be the interpolant of v: Assumption 4.4 is valid if or if consists of piecewise constant functions on a finite element partition of ; in the latter case, we only need to take to be the piecewise constant projection of q with respect to the Q₀ inner product.

Theorem 4.5

Let ϵ > 0. Under Assumptions 4.3 and 4.4, we have the convergence (39)

Proof

The proof is divided into three steps.

	Step 1 Since is the solution of Problem 4.1, we deduce that the family is bounded. In (2.10) with , we take to obtain Applying the inequality (2.9), we obtain Thus, is also bounded. Therefore, there exist a sequence h′ → 0 and elements and u1 ∈ V such that as h′ → 0, (40) (41) We will show that p1 is the solution pϵ of Problem 3.1, and u1 = u(pϵ). Let v be a fixed yet arbitrary element in . In (2.10) with h = h′ and , we let vh′ = ΠVh′v from Assumption 4.3 to obtain (42) Write Then by taking the limit h′ → 0 in (4.8) and using (4.6)–(4.7), we obtain the relation (43) for any . By a density argument, (4.9) holds for any v ∈ V. Consequently, u1 = u(p1).
	Step 2 Since in Q0 and uh′ ⇀ u(p1) in V, we have (44)
	Step 3 Recall that pϵ denotes the solution of Problem 3.1. By Assumption 4.4, we have such that Consider the relations satisfied by uϵ = u(pϵ) and : Subtracting the two equalities with the same test function vh, we obtain Thus, using (2.9) and (2.8), we deduce the following inequality: (45) So by Assumptions 4.3 and 4.4, Thus, (46)

On the other hand, using (4.10) we have Together with (4.12), this implies By the uniqueness of a solution of Problem 3.1, p₁ = p_ϵ. Moreover, (47) Since the limit p_ϵ is unique, the entire family converges: (48) and (4.13) can be strengthened to (49)

To show the strong convergence (4.5), we note from (4.15) that This and the weak convergence (4.14) imply the strong convergence (4.5) 25, Exercise 2.7.3].▪

5. Numerical simulations

In this section, we report numerical results on a simple example. The purpose is to demonstrate that reasonable numerical results can be expected from solving the RTE-based BLT problem via regularization. For this purpose, we solve the BVP (1.3)–(1.4) on a reasonably fine (for our example below) spatial mesh with the S₄ formula for the numerical integration on the unit sphere, and observe the effects of the size and refinement degree of the permissible region on the accuracy of the reconstructed power and centre of the power, two important quantities from a BLT simulation. Discussion of efficient numerical methods and more sophisticated numerical simulations will appear in the sequel.

In the numerical experiments, we take X = (0, 1)² × (0, 0.01), σ_t = 1 and σ_s = 0.5. We use the Henyey–Greenstein phase function (1.2) with η = 0.5. The true source function is p(x) χ_Ω*(x) with p(x) = 100 and Ω_* a circular cylinder centreed at (x_c, y_c) = (0.6, 0.45) with radius 0.15 metre and height 0.01 metre. We use the numerical solution u_* computed with the upwind difference scheme over a uniform 1000 × 1000 × 5 mesh of the spatial region as the ‘true solution’ of the forward problem (1.3)–(1.4), and with the integral over the unit sphere being discretized with the S₄ formula 32. We then use u_* to define the measurement (1.5), and solve Problem 4.1 for a reconstruction of the source function. Here u^h is the upwind difference solution of the BVP (1.3)–(1.4) over a uniform 50 × 50 × 5 mesh of the spatial region and with the integral over the unit sphere again discretized with the S₄ formula. In the following, we report numerical simulation results corresponding to six choices of the permissible region for the source function reconstruction. Each permissible region is decomposed into certain number of pentahedral elements {T} with the thickness 0.01 metre in the z-direction, and the reconstructed light source function is assumed to be a constant on each element. Thus, for each admissible region and the associated decomposition into pentahedral elements, the discrete admissible set of Problem 4.1 consists of piecewise, non-negative constant functions. The problem (4.1) is reduced to a finite-dimensional optimization problem whose size equals the number of the pentahedral elements. The superscript h reminds us the use of the S₄ formula for integrals over the unit sphere, the spatial domain mesh used in solving the BVP (1.3)–(1.4), and the finite element partition of the admissible set. We pay particular attention to the reconstructed power and the reconstructed (horizontal cross-sectional) centre of the power where the summations are over all the elements T of the permissible region of p^h, and (x_T, y_T) are the (horizontal cross-sectional) coordinates of the geometric centre of the element T. Note that these quantities are meant to be approximate values of the exact power of the light source and (horizontal cross-sectional) centre of the power (x_c, y_c) = (0.6, 0.45).

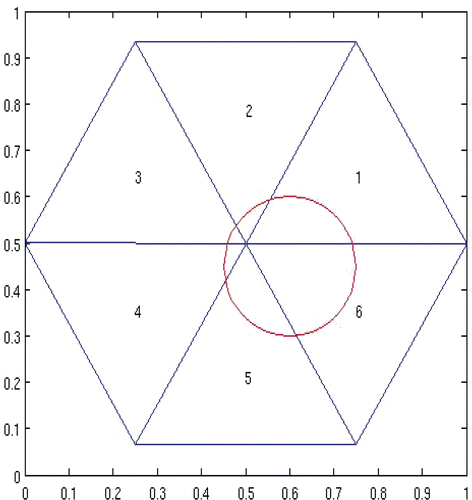
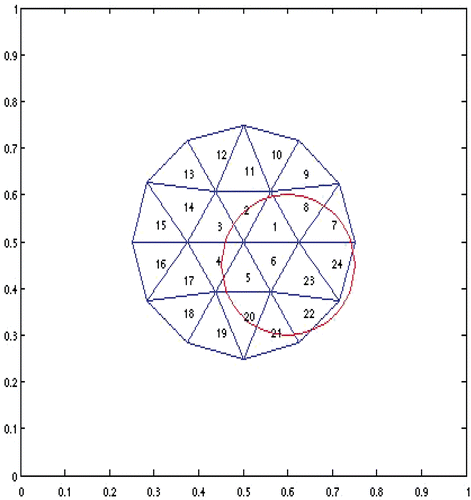
	Case 1 The horizontal cross-sectional view of the permissible region Ω1 and its partition are shown in Figure 1. Corresponding simulation results are given in Tables 1 and 2. Note that the permissible region Ω1 is much bigger than the true source region Ω*, and the partition of is rather coarse. Nevertheless, the reconstructed power is pretty accurate, whereas the reconstructed power centre is not close to the true one.
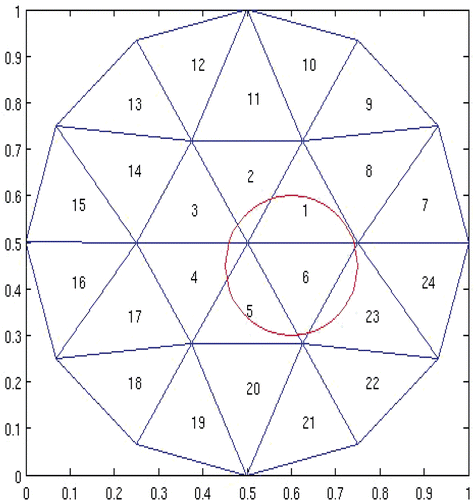
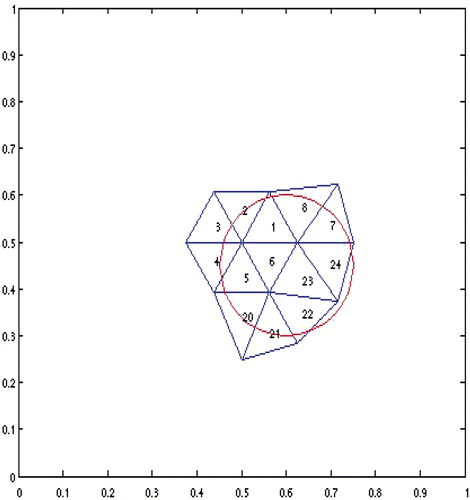
	Case 2 The horizontal cross-sectional view of the permissible region Ω2 and its partition are shown in Figure 2. Corresponding simulation results are given in Tables 3 and 4. In Table 3, results of the reconstructed source function are omitted for those elements if the values are between zero and 10−6. The permissible region Ω2 is about the same as Ω1; however, the partition of is finer. The reconstructed power is comparable to that from Case 1. There is a dramatic improvement in the accuracy of the reconstructed power centre.
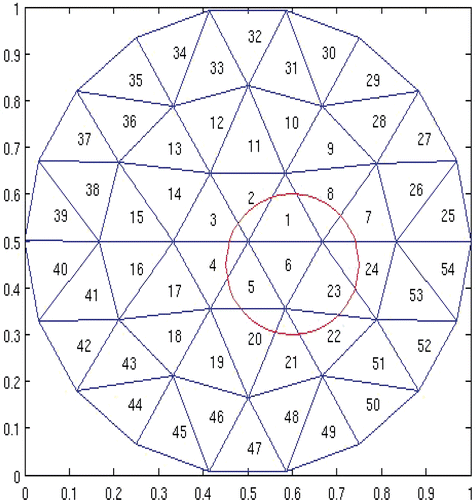
	Case 3 The horizontal cross-sectional view of the permissible region Ω3 and its partition are shown in Figure 3. Corresponding simulation results are given in Tables 5 and 6. In Table 5, results of the reconstructed source function are omitted for those elements if the values are between zero and 10−6. The permissible region Ω3 is nearly identical to Ω2, but a more refined partition is applied. Accuracy of the reconstructed power is somewhat increased, whereas the reconstructed power centre stays nearly the same as in Case 2.
	Case 4 The horizontal cross-sectional view of the permissible region Ω4 and its partition are shown in Figure 4. Corresponding simulation results are given in Tables 7 and 8. In Table 7, results of the reconstructed source function are omitted for those elements if the values are between zero and 2 × 10−3. Note that the partition of is even finer than that of . Compared to the results from Case 3, there is no further improvement in the reconstruction quality. Next, we shrink the permissible region to make it a better approximation of the true source region. Moreover, we allow a small portion of the true source region to lie outside the permissible region.
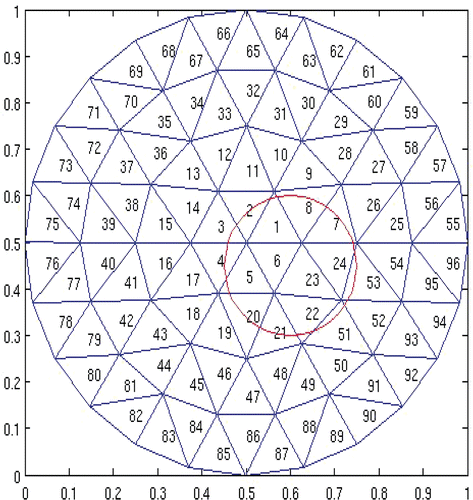
	Case 5 The horizontal cross-sectional view of the permissible region Ω5 and its partition are shown in Figure 5. Corresponding simulation results are given in Tables 9 and 10. In Table 9, results of the reconstructed source function are omitted for those elements if the values are between zero and 10−5. Compared with the results from Cases 1–4, we observe a substantial improvement in the quality of the reconstructed power and reconstructed power centre.
	Case 6 The horizontal cross-sectional view of the permissible region Ω6 and its partition are shown in Figure 6. Corresponding simulation results are given in Tables 11 and 12. The numerical results are comparable to that from Case 5.

Figure 1. Permissible region Ω₁ and the partition.

Figure 2. Permissible region Ω₂ and the partition.

Figure 3. Permissible region Ω₃ and the partition.

Figure 4. Permissible region Ω₄ and the partition.

Figure 5. Permissible region Ω₅ and the partition.

Figure 6. Permissible region Ω₆ and the partition.

Table 1. Reconstructed source function on each element, corresponding to Figure 1.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	12.715579	14.582576	14.604033	14.604248	14.604250
2	1.919267	2.139639	2.142075	2.142099	2.142100
3	0.392186	0.438764	0.439288	0.439293	0.439293
4	1.563244	1.721829	1.723552	1.723569	1.723569
5	12.464614	14.214264	14.234249	14.234449	14.234451
6	29.411168	33.525413	33.572371	33.572842	33.572846

Table 2. Reconstructed source power and center, corresponding to Figure 1.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06329	0.07212	0.07222	0.07222	0.07222
	0.8435	0.8448	0.8448	0.8448	0.8448
	0.3076	0.3077	0.3077	0.3077	0.3077

Table 3. Reconstructed source function on each element, corresponding to Figure 2.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	55.3263	64.7338	64.8465	64.8476	64.8476
2	6.6734	7.0689	7.0720	7.0720	7.0720
3	1.4302	1.6184	1.6219	1.6220	1.6220
4	4.8778	5.0045	5.0051	5.0051	5.0051
5	53.0525	61.2959	61.3921	61.3931	61.3931
6	95.8505	109.4079	109.5624	109.5639	109.5639
23	15.1867	16.8914	16.9102	16.9104	16.9104

Table 4. Reconstructed source power and center, corresponding to Figure 2.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06416	0.07340	0.07351	0.07351	0.07351
	0.6910	0.6916	0.6916	0.6916	0.6916
	0.3948	0.3953	0.3953	0.3953	0.3953

Table 5. Reconstructed source function on each element, corresponding to Figure 3.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	84.870568	101.694226	101.898442	101.900489	101.900509
2	14.213451	14.731308	14.733539	14.733561	14.733561
3	2.797054	3.141816	3.146271	3.146316	3.146317
4	11.309052	11.764974	11.768192	11.768224	11.768224
5	81.902810	93.851846	93.989819	93.991201	93.991215
6	93.424376	104.414441	104.535014	104.536220	104.536232
7	8.762242	9.897037	9.910247	9.910380	9.910381
8	22.941288	25.532779	25.560305	25.560581	25.560583
20	11.465727	12.566949	12.578447	12.578562	12.578563
21	9.716921	10.875681	10.888762	10.888893	10.888894
22	23.431565	26.232994	26.263572	26.263878	26.263881
23	80.848627	94.117825	94.273772	94.275334	94.275350
24	28.103102	30.898462	30.928100	30.928396	30.928399

Table 6. Reconstructed source power and center, corresponding to Figure 3.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06258	0.07129	0.07139	0.07139	0.07139
	0.6985	0.6992	0.6992	0.6992	0.6992
	0.3989	0.3997	0.3997	0.3997	0.3997

Table 7. Reconstructed source function on each element, corresponding to Figure 4.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	89.712931	109.276555	109.522163	109.524613	109.524638
2	32.197625	35.566044	35.599073	35.599408	35.599412
3	3.548439	3.286296	3.282148	3.282109	3.282109
4	22.811520	24.408401	24.422871	24.423020	24.423022
5	95.999311	111.685531	111.870345	111.872202	111.872220
6	91.837254	100.816507	100.908361	100.909287	100.909296
7	51.353625	59.988522	60.091196	60.092223	60.092233
8	59.827698	68.819725	68.920702	68.921717	68.921727
20	40.246607	46.036721	46.102573	46.103234	46.103241
21	48.737412	55.292398	55.366372	55.367114	55.367122
22	89.793535	103.531187	103.690184	103.691778	103.691794
23	87.427236	100.721543	100.876647	100.878202	100.878217
24	95.979403	108.687628	108.831452	108.832888	108.832902
51	3.238091	1.985510	1.967044	1.966858	1.966857
53	14.799574	15.764925	15.773740	15.773831	15.773832

Table 8. Reconstructed source power and center, corresponding to Figure 4.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06323	0.07225	0.07236	0.07236	0.07236
	0.6896	0.6895	0.6895	0.6895	0.6895
	0.4026	0.4039	0.4039	0.4039	0.4039

Table 9. Reconstructed source function on each element, corresponding to Figure 5.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	89.714319	109.279948	109.524345	109.526795	109.526820
2	32.197816	35.565782	35.599373	35.599709	35.599712
3	3.548404	3.286145	3.282252	3.282213	3.282213
4	22.811552	24.407758	24.422651	24.422800	24.422801
5	96.002998	111.691532	111.876862	111.878719	111.878737
6	91.798988	100.765690	100.858155	100.859079	100.859089
7	51.237846	59.798774	59.900201	59.901217	59.901228
8	59.825283	68.822368	68.923867	68.924884	68.924894
20	40.247400	46.038055	46.104075	46.104736	46.104743
21	48.711448	55.263504	55.337638	55.338381	55.338388
22	90.160964	103.836130	103.993890	103.995471	103.995486
23	87.468067	100.733561	100.888321	100.889871	100.889887
24	97.415525	110.473473	110.620942	110.622419	110.622433

Table 10. Reconstructed source power and center, corresponding to Figure 5.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06182	0.07088	0.07098	0.07098	0.07098
	0.5913	0.5917	0.5917	0.5917	0.5917
	0.4525	0.4528	0.4528	0.4528	0.4528

Table 11. Reconstructed source function on each element, corresponding to Figure 6.

Element	ϵ = 10^−1	ϵ = 10^−3	ϵ = 10^−5	ϵ = 10^−7	ϵ = 10^−9
1	89.714328	109.279932	109.524342	109.526792	109.526816
2	32.197845	35.565754	35.599345	35.599681	35.599685
3	3.548425	3.286113	3.282220	3.282181	3.282180
4	22.811563	24.407733	24.422626	24.422775	24.422776
5	96.002984	111.691524	111.876854	111.878710	111.878729
6	91.798970	100.765687	100.858152	100.859077	100.859086
7	51.237856	59.798776	59.900204	59.901220	59.901230
8	59.825289	68.822366	68.923865	68.924881	68.924891
20	40.247391	46.038060	46.104081	46.104742	46.104748
21	48.711433	55.263519	55.337654	55.338397	55.338404
22	90.160927	103.836143	103.993904	103.995484	103.995499
23	87.468071	100.733569	100.888329	100.889879	100.889895
24	97.415540	110.473476	110.620946	110.622422	110.622437

Table 12. Reconstructed source power and center, corresponding to Figure 6.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06182	0.07088	0.07098	0.07098	0.07098
	0.5913	0.5917	0.5917	0.5917	0.5917
	0.4525	0.4528	0.4528	0.4528	0.4528

From the above numerical results, we see that to have accurate reconstruction of the light source, it is crucial to have a permissible region not too much bigger than the true source region. Among such permissible regions, the reconstruction quality is rather stable with respect to the choice of the permissible region. In BLT practice, one may try to develop a hybrid physical, chemical and biological process that allows a somewhat acceptable prediction of the permissible region. Also, the idea of multi-spectral BLT 13 may be worth exploring in this regard. Note that when the partition of the permissible region is reasonably fine, further refinement does not help improving the reconstruction accuracy.

Next, consider the effect of noise in the measurement (1.5) on the reconstruction quality. The ‘true’ measurement data used above are multiplied by (1 + δr) for a uniformly distributed random variable r with values in [−1, 1]. We only report reconstructed source powers and centres corresponding to the permissible region Ω₅, in Tables 13–16. The results are similar to those of Table 10, with a higher level of noise leading to a bigger discrepancy in the numerical values. The reconstruction results appear quite stable with respect to the noise in the measurement data for this example. The reconstructed source function values on the elements are similar to those of Table 9, and are omitted.

Table 13. Results with permissible region Ω₅, noise level δ = 1%.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06182	0.07089	0.07099	0.07099	0.07099
	0.5913	0.5917	0.5917	0.5917	0.5917
	0.4525	0.4528	0.4528	0.4528	0.4528

Table 14. Results with permissible region Ω₅, noise level δ = 5%.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06183	0.07089	0.07100	0.07100	0.07100
	0.5913	0.5917	0.5917	0.5917	0.5917
	0.4524	0.4528	0.4528	0.4528	0.4528

Table 15. Results with permissible region Ω₅, noise level δ = 10%.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06183	0.07090	0.07100	0.07100	0.07100
	0.5912	0.5916	0.5916	0.5916	0.5916
	0.4525	0.4529	0.4529	0.4529	0.4529

Table 16. Results with permissible region Ω₅, noise level δ = 20%.

ϵ	10^−1	10^−3	10^−5	10^−7	10^−9
	0.06193	0.07101	0.07112	0.07112	0.07112
	0.5912	0.5916	0.5916	0.5916	0.5916
	0.4526	0.4526	0.4526	0.4526	0.4526

Acknowledgements

The first two authors were partially supported by the Mathematical and Physical Sciences Funding Program of the University of Iawa and NSF-DMS-0602242. The third author was partially supported by the NNSFC (10771138) and E-Institute of Shanghai Municipal Education Commission (N:E03004).